Introduction

Advances in nanotechnology and the development of nanorobots have led to a focus on manipulating nano-scale material1,2. Transporting nano-size particles and cargo for different purposes is one of the important applications in this field3,4. Therefore, investigating the movement of molecules or a cluster of atoms on a surface and trying to better control these particles by knowing the influencing variables in the system becomes important5,6,7,8. Natural nano-manipulators, such as motor proteins, transport cellular materials by converting chemical energy into motion, and DNA-based systems are used for building and manipulating molecules with high precision. These biological systems are incredibly efficient and versatile, inspiring researchers to develop artificial nanorobots9. Compared to natural nano-manipulators, the developed nanorobots have limitations such as several orders of magnitude larger than their payloads and the inability to operate on large numbers of diverse particles10,11. In this regard, the intend is to develop nanomanipulators with smaller sizes and higher complexity to perform precise tasks at the nanoscale10,12.

Molecular machines and Molecular motors have been developed to transport nano-scale materials known as nanocars and nanotrucks due to their car-like bodies and wheels10,11,13,14. Fullerenes are one of the most structures which, combined with chassis, make nanocars, nanotrucks, and other nanomanipulators14,15,16. Recently, the movement of fullerenes and nanocars on various gold, graphene, and silicon substrates has been analyzed14,15. The chemical stability and conductivity of the gold substrate are one of the significant advantages of fullerene, which has caused special attention for its use in nano trucks14,17,18,19. In addition to the type and size of the nanocar and molecular wheel, the shape of the substrate is also very effective in the movement of nanomanipulators. Flat, stepped, concave, cylindrical, and other types of surfaces have been investigated with respect to movement with fullerenes and other molecular wheels14,15,20,21,22,23.

Investigations with other types of wheels such as p-carbon and carbon nanotubes have also been conducted to investigate the effect of the chemical structure of the chassis and the crystal direction of the surface on the movement of nanocars24,25. The smallness of these nanocars provides the conditions for their use in large and diverse numbers, which increases the efficiency of cargo transportation7,20,25. Synthetic molecular machines have also been used to transport macroscopic cargoes and make connections between nanoscale and much larger dimensions26.

The motion class of nanocars is determined using computational or experimental methods. An experimental method is to use a scanning tunneling microscope (STM) to investigate the movement, which is suitable for analyzing a wide range of nanomachines27,28. Recent studies investigated the movement of nanomachines with C60 fullerene on a gold substrate under the influence of temperature gradient and even electric field29. However, STM outputs a limited number of low-detail images in a relatively long time and is also expensive to image27. Therefore, the use of computational molecular dynamics simulations to investigate the movement of nanocars is advantageous due to faster results they provide with an acceptable accuracy15,20.

Nemati et al. performed computational simulations to investigate the effect of temperature gradients on the movement of fullerene C60, nanocars, and nanotrucks with C60 acting as their wheels on a smooth gold surface in different conditions20,21. The results showed that high temperatures cause strong vibrations and frequent impacts of gold atoms, which increases the average distance of C60 from the substrate and reduces its binding energy. The temperature field caused C60 to move along with the temperature variation, while its diffusive motion remained unchanged perpendicular to the gradient. Increasing the temperature led to faster movement parallel to the gradient, and increasing the average bed temperature increased the diffusion coefficient in all directions. Like the C60, the temperature field affected the movement of the nanocars, but it had a more limited range due to the relatively larger, heavier, and more flexible chassis compared to the nanotruck. Large and heavy rolling molecules were less affected by the temperature field than small and light molecules20,21.

Kianzadeh et al. simulated the movement of C60 and nanocar with the C60 wheel on a hexagonal boron nitride and graphene hybrid substrate5,14. They found that the C60 molecules are more stable when they are located on the boron-nitride impurity regions of the substrate5,7. The motion of the molecules is limited by an energy barrier that only allows them to move in the boron-nitride region. To limit the surface movement of these molecules and nanocars at a temperature of 300 K, a nano-path made of boron nitride with graphene on its side was created so that all surface molecules remain in the boron-nitride nano-paths. A temperature gradient was applied to achieve unidirectional motion for C60 and nanocars on the surface. Due to the lower energy of the molecules in the colder parts, the molecules moved towards those regions of the nano-road5,14. This research provides us with a better understanding of the high controllability and maneuverability of fullerene-based thermal nanomachines. Moreover, gold nanotubes have emerged as a potential contender across various disciplines owing to their distinctive characteristics such as extensive surface area, exceptional adhesion properties, and immunity to corrosion. Recent research has demonstrated their efficacy in diverse areas including pharmaceuticals, biosensors, and electronic structure applications30,31,32. Gold nanotubes are regarded as exceptional nanomaterials due to their remarkable ability to bear heavy loads, while also being adaptable to various shapes and sizes30,33.

This study is one of the initial inquiries to investigate the effect of both temperature changes and a curved gold substrate on nanomachine migration. The choice of optimal cylindrical and concave substrates was based on previous studies for surface optimization and their similarity in contacting surfaces with the nanomachine wheels12,33. The main goal is to research and compare the characteristics and behavior of fullerene-based nanocars due to the change of different fullerene wheels. It has also been tried to identify the optimal fullerene wheel nanomachine for different applications with the desired target characteristics.

Methods

Analysis of the potential energy function

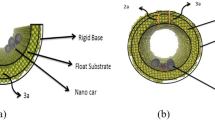
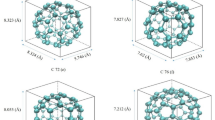
The motion of nanocars with different types of fullerene wheels on gold cylindrical and concave substrates is analyzed in this section using computational simulations that focus on the potential energy function. In this method, we aim to minimize the potential energy, as lower potential energy values correspond to more stable configurations and smoother movement of the nanocars along the substrates. For better control of the movement of the nanocarriers, cylindrical and concave surfaces were used22. The gold substrate was chosen to investigate the movement because fullerenes as molecular wheels have shown good performance on this substrate due to the high conductivity and excellent chemical stability of gold in recent research17,18,19,20,22,23. An inner layer (floating bed) and an outer layer (rigid bed) make up the surface of the gold bed for analysis (Fig. 1A). Six nanocars with different wheels are selected to investigate the effect of the fullerenes’ radii on their motion, their schematics are shown in Fig. 1B and C10. According to a report by Pishkenari et al., the potential energy of nanocar on a gold substrate was strongly influenced by their orientation. The study compared four different orientations of C60, considering both translational and rotational motion, and found that the Hexa-down orientation exhibited the most stable direction16.

Fig. 1
figure 1

(A) Substrates schematics. Cylinder (left) and concave (right) substrate. The substrates had the radii of 20 Å and 17.5 Å for nanocar and nanotruck, respectively, with the length of 27a. Green balls show gold substrates. (B) The initial composition of nanovehicles on the substrate form top (left) and front (right) view. (C) Different nanotrucks made of the selected fullerenes (i) A nanotruck made of C36 as the wheel. (ii) A nanotruck made of C50 as the wheel. (iii) A nanotruck made of C60 as the wheel. (iv) A nanotruck made of C76 as the wheel. (v) A nanotruck made of C80 as the wheel. (vi) A nanotruck made of C90 as the wheel. The figures were generated based on simulations coded in Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [available at https://www.lammps.org/] and visualized using the Visual Molecular Dynamics (VMD) package [version 1.9.4, available at http://www.ks.uiuc.edu/Research/vmd/].

Full size image

Simulation setup

Using atomistic dynamics, the present research examined the movement of nanocars with different sizes of wheels (Fig. 1C) on curved gold surfaces. Simulations were conducted at a variety of temperatures ranging from 75 K to 600 K, with various radii considered for the nanotruck (17.5 Å to 30 Å) and the nanocar (20 Å to 30 Å) on the curved surfaces. The minimum radius chosen was based on the size of the C60, nanocar, and nanotruck. Consequently, the substrates with radii of 20 Å and 17.5 Å were chosen for nanocar and nanotruck, respectively. Furthermore, previous studies have shown that the gold nanotube remains stable at high temperatures; although diffusion becomes intrusive at 900 K, atoms adhere to the walls and do not move until 1200 K34,35,36.

To assess how temperature and radii impact the mobility of C60, the length of the substrates was set to 27a, where a represents the gold lattice constant and was determined to be 4.078 Å37. Also, it is worth mentioning that atoms in the longitudinal direction are repeated periodically, and in other directions are fixed. The nanocar was positioned on the inner layer of the gold substrates, while the outer layer was deemed rigid. The Embedded Atom Method (EAM) is a widely used potential model in atomistic simulations for metals, where the total energy of an atom is determined by both the interactions between pairs of atoms and the embedding energy that depends on the local electron density around each atom. In this study, the EAM potential is employed to model the interactions among gold atoms on the substrate38. This method allows for accurate predictions of atomic behaviors, such as dislocations, and is particularly effective for simulating systems with complex interatomic interactions, such as those involving gold’s face-centered cubic (FCC) structure. By using EAM, we can capture the detailed atomic-scale interactions that influence the motion of the C60, nanocar, and nanotruck on the gold substrates, providing a more realistic simulation of their behavior under varying conditions39,40. The bonds and angles were formulated according to the harmonic style as follows in Eqs. (1) and (2):

$$\:{E}_{bond}={{K}_{b}\left(r-{r}_{0}\right)}^{2}$$
(1)
$$\:{E}_{angle}=\:{{K}_{a}\left(\theta\:-{\theta\:}_{0}\right)}^{2}$$
(2)

Kb denotes the stiffness of the bond, while r and r0 signify the bond distance and its equilibrium bond distance, respectively. Similarly, Ka represents the angle stiffness, where θ and θ0 stand for the angle and equilibrium angle correspondingly41. The dihedral term style is given by Eq. (3) subsequently:

$$\:{E}_{dihedral}=\:\frac{1}{2}{K}_{d1}\left(1+cos\varphi\:\right)+\frac{1}{2}{K}_{d2}\left(1-cos2\varphi\:\right)+\frac{1}{2}{K}_{d3}\left(1+cos3\varphi\:\right)+\frac{1}{2}{K}_{d4}\left(1-cos4\varphi\:\right)$$
(3)

The torsion stiffness parameters, Kd1 to Kd4, and dihedral angle \(\:\varphi\:\) were calculated using the MM3 force field. Table 1 provides the potential for these values assuming that the improper terms can be ignored during the simulations42,43,44, more information on atom types and other details are provided in31. The simulation was conducted with a large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) solver45 and the results were visualized using Visual Molecular Dynamics (VMD) software46.

Table 1 Parameters used in the simulation of the Nanocar and nanotruck.
Full size table

The Lennard-Jones 6–12 potential (Eq. (4)) was used to simulate the Van der Waals interactions between gold and carbon, hydrogen, as well as nitrogen atoms (C-Au, H-Au, and N-Au).

$$\:{E}_{Lj}=4\varepsilon\:\left[{\left(\frac{\sigma\:}{r}\right)}^{12}-{\left(\frac{\sigma\:}{r}\right)}^{6}\right]$$
(4)

The potential parameters, σ, ε, and r, are used to represent the well depth of the potential, the equilibrium distance, and the distance between carbon and gold atoms at equilibrium, respectively. To determine the values for the σ and ε parameters, Table 2 was utilized, assuming identical interaction parameters between both types of carbon atoms and gold. Furthermore, the gold substrate’s horizontal and thickness dimensions were considered large enough (three times the lattice constant), and a cut-off radius of rcut−off = 13 Å (where rcut−off > 4σ) was selected for accuracy47.

Table 2 Parameters of the Lj potential.
Full size table

To regulate the temperature of the substrate, nanocar, and nanotruck, two Nose-Hoover thermostats were implemented (Fig.S2 demonstrated the temperature of C76 based nanomachine and the substrate also provided the total energy of nanomachine and substrate). The calculation of charge distribution in the nanocar and nanotruck molecules was conducted through the use of the first principal theorem, or Restricted Hartree-Fock (RHF). This was done by making use of the NWChem 6.5 package and the 6-31G** (d, p) basis set48. Despite minimal charge distribution in the nanocar and nanotruck, it was deemed unnecessary to consider charge transfer between the nanomachines and the electrically neutral gold substrate. As such, the motion of the nanomachines on the gold substrate is not influenced by the electric field49. Also, worth mentioning that, the simulations were performed for \(\:8\:ns\) with the \(\:1\:fs\) time step .

Results and discussion

In this study, we aim to investigate the optimization of fullerene-based nanocarriers using the geometries proposed in previous studies. Two geometries, concave and cylindrical surfaces, are considered, and a radius of 25 Å is reported as the optimal radius for these surfaces. The primary parameter under investigation in this research is the distance traveled by each nanocarrier, as depicted in Fig. 2. The analysis reveals that the distance traveled by nanocarriers is nearly identical on both surfaces. However, upon comparing nanocarriers with varying wheel sizes, it becomes evident that as the wheel size of nanocarriers increases, resulting in a higher total mass of the nanomachine, the distance traveled by the nanocarrier decreases. A more detailed examination indicates that mass plays a crucial role in this effect. As the mass increases, it becomes the dominant factor in the interaction between the wheel and the gold surface. The trajectory plots and a supplementary video illustrating the motion of nanotrucks are provided in the Supporting Information.

Fig. 2
figure 2

Distance traveled of nanotrucks’ motion on different substrates. (A) Cylinder and (B) Concave.

Full size image

Considering that the primary application of these nanocarriers is the manipulation and carrying of materials at the nanoscale, the displacement of nanocarriers over the simulation time becomes one of the most significant criteria for comparing the nanomachines’ performance. Figure 3 illustrates the displacement of different nanocarriers under various conditions. It is evident from the results that the average displacement of nanocarriers on the cylindrical surface is higher than that of the concave surface. This difference can be attributed to the absence of high-energy points or points with a high surface-to-volume ratio in cylindrical geometry. These high-energy points in the concave geometry attract and restrict the long-range movement of nanomachines. This phenomenon is further intensified with an increase in temperature, as shown in Fig. 3.

Fig. 3
figure 3

Displacement of nanotrucks’ motion on different substrates. (A) Cylinder and (B) Concave.

Full size image

In the cylindrical substrate, when comparing nanocarriers with different wheel sizes, it becomes evident that nanomachines with larger wheels, such as C80 and C90, demonstrate higher displacements at low temperatures, specifically at 75 and 150 K. Nevertheless, as the temperature gradually increases, nanomachines with smaller wheels display improved performance, and they exhibit better results (the straight line movement) on the cylindrical surface at temperatures of 300 and above 400 K, on the cylindrical surface (Fig.S1 illustrates the trajectories of the nanomachines on cylindrical and concave substrates).

With further temperature increases, nanomachines with smaller wheels outperform those with larger wheels in terms of average displacement. At 500 K on the cylindrical surface, nanomachines with C80 wheels, and at 600 K on the same surface, nanomachines with C50 wheels show the highest displacements.

Additionally, on the concave surface, like cylindrical geometry, nanocarriers with larger wheels demonstrate greater displacement at lower temperatures. However, as the temperature rises to 300 and 400 K, nanocarriers with smaller wheels exhibit better performance. This phenomenon is attributed to their attraction towards high-energy points or surfaces, leading to reduced motion range. With further temperature increases to 500 and 600 K, nanomachines with smaller wheels surpass nanomachines with larger wheels due to increased energy surface, resulting in longer-range movement. Overall, Fig. 3 illustrates that nanomachines with C80 and C36 wheels on the cylindrical surface, and nanomachines with C80 and C50 wheels on the concave surface, show the highest displacements in terms of their average values for displacement.

For a more thorough analysis of these results, the diffusion coefficient of each nanomachine under different conditions is presented in Fig. 4. Considering the diffusive nature of nanocarriers’ movement, this coefficient serves as a critical parameter in determining the behavioral characteristics of nanocarriers. Based on Fig. 4, it is evident that on the concave surface, nanomachines exhibit a higher average diffusion coefficient compared to the cylindrical surface. This phenomenon is attributed to the presence of high-energy points or the higher surface-to-volume ratio on the concave substrate which leads to increased absorption and stronger interaction with the nanocarriers’ wheels.

On concave and cylindrical surfaces, nanomachines with larger wheels have a higher diffusion coefficient, because these nanomachines have larger wheels and thus have more interaction with the gold surface, resulting in a higher diffusion coefficient. With increasing the substrates’ temperatures, the diffusion coefficient of heavier nanomachines remains higher than that of the lighter ones. However, these results are contradictory to Fig. 3 where lighter nanomachines had much larger displacements at higher temperatures. However, by looking at this graph, they have a lower diffusion coefficient. To understand the reason behind this movement it is better to check the parameters related to the deviation.

By re-concerning Fig. 4, in almost all conditions, the coefficient of diffusion is higher than \(\:0.01\), which according to previous studies is the minimum coefficient of diffusion for nanomachines to have long-range movement. Nanocarriers have reached this minimum in these two substrates investigated in this research. As stated, in all cases, the coefficient of diffusion of nanomachines has reached this minimum, and this is proof of the validity of previous studies, which reported these geometries as optimal geometries22.

Fig. 4
figure 4

Diffusion coefficient (DC) of nanotrucks’ motion on different substrates. (A) Cylinder and (B) Concave.

Full size image

To investigate the effect of the considered geometries and the comparison of nanomachines, we will examine the characteristics that determine the amount of deviation of nanomachines, for this purpose, we will examine the recorded results of two parameters, the effective velocity, and the angular velocity. The effective speed of a nanomachine is defined as dividing the speed of the nanomachine in the desired direction, which in this study along the longitudinal axis of the cylinder and concave surfaces, by the total speed of a nanomachine, the results of which are shown in Fig. 5. Another parameter investigated is the angular velocity of a nanomachine in the direction perpendicular to the plane of movement, which is a suitable measure to detect the deviations of the nanomachines’ movement from the expected path. The results of this variable are also reported in Fig. 6.

According to the results presented in Fig. 5, in all cases, lighter nanocars with smaller wheels have a higher effective speed, which can be seen as the result of more dominance of the nanocar chassis on the nanocar when the wheels are smaller. By observing Fig. 5, the effective speed of nanocars has led to a slight decrease due to the increase in temperature. This has been an expected phenomenon because with the increase in temperature and kinetic energy of nanomachines, the desire to deviate from the main path also increases, but in this research it is clear that these two considered surfaces have been able to control the nanocars well even at high temperatures, because due to the increase in temperature, the effective speed of these nanomachines has seen less than 10% change, and this means that the movement path of the nanomachines is optimally limited from the sides and the nanomachines move the main part of their movement in the direction we expect.

Fig. 5
figure 5

Effective velocity of nanotrucks’ motion on different substrates. (A) Cylinder and (B) Concave.

Full size image

According to the results of Fig. 5 (A) and (B), the effective speed on the cylindrical surface in different situations is generally better than the concave surface, because the cylindrical surface, unlike the concave surface, does not have high-energy points on the edges, and this allows more movement and maneuvering of the nanocarriers and prevents them from being attracted to specific points.

By examining the results of the angular velocity of each nanomachine shown in Fig. 6, a better comparison and interpretation can be made regarding the deviation in the movement of the nanomachines. Based on the results presented in Fig. 6 (A) and (B), it can be emphasized why conducting this research was an important matter, as it is clear from the results of angular velocity, that the nanomachine that experiences the greatest deviation in the direction of movement (which pursues the highest angular velocity in the direction perpendicular to the movement) is a C60-based nanocar that has been studied in previous studies.

Fig. 6
figure 6

Angular velocity of nanotrucks’ motion on different substrates. (A) Cylinder and (B) Concave.

Full size image

As can be seen from the graph, in almost all situations, the C60-based nanomachine had the highest angular velocity or finally it had the same value as other nanomachines, and that is why we have to go to the synthesis of newer nanomachines to expand the applications of these nanocarriers or improve their performance. The functioning of these cases has been studied in this study.

According to the discussions in the previous sections and also the results of Fig. 6, the average angular speed of nanocars on a cylindrical surface is higher than on a concave surface, because the presence of surface effects on the concave surface and the attraction of nanocars to these points is a factor causing deviation, and as a result, the angular speed of nanocars increases.

In this research, our goal was to study the effect of changing the wheel of fullerene-based nanocars on the optimal substrates introduced in previous studies, that is, two concave and cylindrical surfaces. By examining the behavior of different nanomachines in the comparison of fullerene C60-based nanocar, the possibility of using other nanocars instead of this nanocar was investigated, and as the result, it was observed that other nanocars can show better performance than C60-based nanocar. Therefore, in Table 3, the optimal nanocars have been selected in each case. According to Table 3, the C60-based nanocar is not an optimal choice in any case, and other proposed nanocars have been able to show better performance, which is due to the unfavorable criteria related to checking the deviations of nanomachines, especially the amount of angular velocity of the C60-based nanocar.

Among other nanomachines, the performance of C80 and C36 as well as C50 is better than others and they have been able to occupy most of the optimal states. As expected, the obtained results, especially regarding the diffusion coefficient of C80-based nanomachines generally at low temperatures and lighter C36 and C50-based nanomachines have generally shown better performance at higher temperatures.

Table 3 Candidate fullerenes as the nanotrucks’ wheel at different conditions.
Full size table

Conclusion

With the progress of nanoscience, the fabrication of equipment and devices at the nanoscale has garnered more attention than ever before, leading to an increasing demand for nanocarriers and nanomanipulators. In recent years, research has focused on utilizing nanomachines and optimizing their performance to meet these emerging needs. The excessive costs associated with experimental studies have prompted researchers to explore the functionalities of these nanomachines through computer simulations and numerical investigations, which are considered precise and efficient methodologies.

In our previous studies, we explored different micro and nano-scale phenomena using numerical simulation50,51. This study introduces novel nanomachines based on spherical fullerene molecules as wheels, aiming to investigate the influence of wheel variations on nanomanipulators operating on two surfaces, namely concave and cylindrical. These surfaces have been previously identified as optimal platforms in earlier research. In addition to the well-known C60 fullerene, traditionally used as the wheel for nanomanipulators, new fullerene molecules, namely C36, C50, C76, C80, and C90, are proposed as alternative wheel options for nanomanipulators.

By utilizing cylindrical and concave substrates as curved surfaces, a significant improvement of approximately 50% in aligning nanocarriers with the desired direction was observed, a conclusion that was confirmed by analyzing the effective velocities and the angular velocity of the nanocarriers. Furthermore, a noteworthy finding in this research was the observation of the effect of mass and the interaction of the wheels with the gold surface. Nanomachines with larger wheels, despite having a higher number of carbon atoms in their structure and the expected improved motion, experienced limitations due to an increase in their overall mass, which restricted their movement. On the other hand, smaller nanomachines with fewer carbon atoms face challenges, particularly at low temperatures, especially when approaching the short-range diffusion limit. Nevertheless, as the temperature increased, these issues were resolved, and in more than 90% of the studied conditions, nanocarriers exhibited a higher diffusion coefficient, reaching close to 0.01, which grants them the ability for long-range motion. This observation is justified by the geometrical compatibility between the wheels and the gold surface, both of which exhibit curvature, facilitating more constructive interactions for the nanocarriers.

It was observed that nanocarriers with larger wheels had a higher incidence of interaction with the surface and exhibited higher diffusion coefficients, resulting in different expectations regarding their displacement. Specifically, at low temperatures, such as 75 and 150 K, these nanocarriers failed to demonstrate ideal performance. The obtained results for angular velocity, as a key characteristic to indicate the extent of nanocarrier deviations, revealed that larger nanomachines, due to their higher angular velocity, could not achieve desirable performance at low temperatures. Notably, among all the studied cases, the nanocarrier with the C60 fullerene wheel exhibited the highest deviation in its motion. Consequently, this highlights the need to replace this fullerene as a wheel and consider the use of newer nanocarriers.

Regarding the results obtained for various nanocarriers, it was evident that on the cylindrical surface, the deviation in nanocarriers’ motion was less pronounced. This was attributed to the absence of high-energy points, which are present on concave surfaces. In other words, the cylindrical surface, owing to this characteristic, could attract the nanocarriers towards itself and reduce the typical deviations in their motion.

Furthermore, through the examination of various characteristics of nanocarriers, we have not been able to demonstrate better performance than the typical nanocarrier with the C60 wheel in any of the cases. Additionally, among the other 5 nanocarriers studied, each one has been selected as the optimal nanocarrier for specific conditions at least once. Among these, nanocarriers with C80, C36, and C50 wheels have accounted for over 50% of the optimal cases and presented highly desirable performance.