Introduction

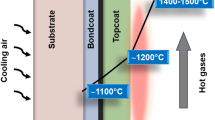
Environmental barrier coatings (EBCs) are used to protect SiC-based ceramic matrix composites (CMCs) from high-temperature corrosion in the hot-section of gas turbine engines1. Recently, rare-earth (RE) phosphates are found to have significant advantages over third-generation RE silicates for molten calcium-magnesium aluminosilicate (CMAS) corrosion resistance2,3,4,5. However, it is unclear if the advantages of corrosion resistance translate into improved fracture strength for RE phosphates compared to silicates. Improving fracture strength is crucial for EBCs to avoid microcracking, which is one of the primary reasons for spallation and eventual failure6,7,8. This work investigates the fracture behavior of RE phosphate (LuPO4) compared to RE silicate (Lu2SiO5) EBCs under CMAS corrosion using experiments and mesoscale simulations.

SiC-based CMCs have been proven to be a suitable replacement for Ni-based superalloys used in the hot section components of gas turbine engines due to their stable high-temperature performance1,9. However, when SiC-based CMCs are subject to high-temperature gas and debris at high speed within the gas turbines, they undergo different reactions and surface recession (corrosion)10. One of the leading causes of corrosion in CMCs is the reaction and penetration of molten CMAS formed from ingested debris, i.e., sand, dust or volcanic ash11. To protect CMCs from corrosion, environmental barrier coatings (EBCs) are used. EBCs are designed to be mechanically and chemically stable at high temperatures, providing a protective barrier between CMAS and CMCs12.

In the past several decades, numerous materials have been developed for EBC applications. These materials are broadly categorized into three generations based on their increasing high-temperature capability realized by introducing different high-temperature resistant compounds. The first generation EBCs contain mullite (Al2O3·SiO2), the second generation contain BSAS (BaO·SrO·Al2O3·SiO2) and the third generation contain rare-earth (RE) silicates (RE2Si2O7/RE2SiO5) in their composition13. Among these, the third-generation EBCs based on rare-earth disilicates are more durable and offer better protection against CMAS corrosion than earlier generations12. However, RE disilicates still corrode rapidly when exposed to molten CMAS at temperatures of 1300 °C and above, as the CMAS melt penetrates along the grain boundaries, forming large cracks and severe swelling14,15. Recently, this shortcoming has been addressed by replacing RE disilicates with RE phosphates, which form a continuous and dense reaction layer that halts CMAS penetration into the bulk pellet and limits corrosion4,5. With less CMAS corrosion, RE phosphates are considered a promising EBC material with durable high-temperature performance for hot sections of gas turbine engines.

This work investigates the effect of CMAS corrosion on the fracture characteristics of EBCs, which hasn’t been adequately studied. Most existing studies have focused on evaluating EBCs based on their thermomechanical and chemical compatibility with SiC CMCs4,5,16,17, while a few have specifically examined the fracture behavior8,14,18,19,20. However, most studies on the fracture behavior are qualitative and are limited in providing actionable insights to improve EBC performance. In this work, the effects of CMAS corrosion on the fracture behavior of RE-phosphate and -silicate EBCs are quantitatively studied to gain fundamental insights into the effects of different levels of CMAS penetration on EBC performance.

During CMAS corrosion, molten CMAS penetrates the EBC microstructure along the grain boundaries and causes structural changes5,14. The penetration into the microstructure is driven by total energy reduction through the formation of two CMAS-ceramic interfaces (low energy) replacing one ceramic-ceramic interface (high-energy grain boundary)21. The penetrated CMAS forms a brittle and glassy phase along ceramic grain boundaries that degrade the fracture strength of EBC12,14. Therefore, it is crucial to analyze and quantify the extent of degradation caused by penetrated CMAS, which might help understand the fracture performance of EBCs under CMAS corrosion. The structural degradation of EBC microstructures is analyzed by estimating fracture resistance for different CMAS penetration levels based on experimental observations.

However, an extensive experimental analysis may not be feasible for analyzing the fracture behavior of EBC materials with different levels of CMAS penetration. This would either require performing fracture tests on CMAS-exposed EBC coating samples (which are very thin) or creating multiple CMAS-EBC composite samples representing different levels of CMAS penetration. Both approaches may have several practical limitations in terms of feasibility, resources, and time. A computational fracture model offers a fast and economical alternative that can significantly reduce the number of experiments needed. Among the available computational fracture models for polycrystalline materials, phase field and cohesive zone-based models are the most frequently used22,23,24,25,26,27.

This work uses a mesoscale model based on the cohesive finite element method (CFEM) to analyze the fracture resistance of EBC microstructures28,29. The CFEM is chosen for its simplicity with fewer well-defined parameters and straightforward implementation for heterogeneous materials28,30,31. It can be easily implemented using cohesive finite elements available in many well-established commercial and open-source finite element software packages32. The cohesive zone model parameters are calibrated with the data obtained from experiments and literature31.

The CFEM is used to simulate fracture through EBC microstructures before and after CMAS penetration23. The microstructures used in the models consist of randomly oriented ceramic grains and their grain boundaries. The CMAS penetration is modeled by adding CMAS along the grain boundaries14. The fracture is tracked using cohesive elements inserted along all element edges throughout the model, as described in the “Materials and methods” section. The cohesive elements are assigned different traction–separation laws based on the material or interface they represent. Complex fracture patterns arising due to anisotropic ceramic grains, orientation-dependent grain boundaries, and the presence of CMAS are accounted using different material properties and traction separation laws. The fracture resistance of the EBC is estimated by computing J-integral33 and fracture toughness (KIc). The computed KIc is validated with the experimental KIc measured from indentation fracture tests on EBC samples before and after CMAS penetration. Additionally, statistical tests are performed to assess similarities or differences between the simulation results and experimental measurements.

Using experiments and fracture simulation, the present study aims to make the following contributions to the design and development of next-generation EBCs:

  1. 1.

    Provide a quantitative assessment of the fracture characteristics of RE phosphate and RE silicate EBC materials before and after CMAS penetration. This will help identify materials and microstructures that retain the fracture strength under CMAS corrosion.

  2. 2.

    Investigate and quantify the effect of CMAS reaction on the fracture characteristics of RE phosphate and RE silicate EBC materials. This will help identify materials that can retain fracture strength under different levels of CMAS corrosion.

  3. 3.

    Demonstrate the effectiveness of a combined methodology involving experiments and simulation to analyze EBC materials and emphasize its applicability for rapid assessment of potential EBC materials.

The remainder of the paper is organized as follows: The computational fracture model and experimental procedures for the microstructural characterization and measurement of fracture toughness of EBCs are described in “Materials and methods” section. The CFEM model validation and analysis of fracture characteristics of EBCs are provided in “Results” section. The fracture behavior of EBCs before and after CMAS penetration is discussed in relation to the experimental observations from CMAS corrosion tests in “Discussion” section, followed by conclusions in “Conclusion” section.

Materials and methods

This work uses a combination of experiments and computational modeling to get meaningful insights into the fracture behavior of the EBC materials under CMAS corrosion, as depicted in Fig. 1. The experimental procedures and computational methods used in this work are outlined in the following sections.

Fig. 1
figure 1

A schematic flow diagram showing the combined experiments and simulation approach adopted in this work. The cohesive finite element models (CFEM) are formulated using experimentally obtained electron backscattered diffraction (EBSD) micrographs of EBC samples. The CFEM is used for fracture simulations and fracture toughness (KIc) computation. The computed KIc is validated with the experimental KIc obtained using micro and nanoindentation tests34 performed on EBC samples before and after CMAS penetration. The validated model is then used to investigate the fracture characteristics of EBCs with CMAS penetration. The microstructural characterization of EBC samples is carried out using scanning electron microscopy (SEM) and energy-dispersive X-ray spectroscopy (EDS). The computed KIc values and microstructural characterization are used to compare the fracture resistance of rare-earth phosphate and silicate EBCs.

Full size image

Material preparation and CMAS reaction

Among the available rare-earth (RE) elements for EBC applications, lutetium (Lu) is chosen in this work to form lutetium phosphate (LuPO4) and lutetium silicate (Lu2SiO5). They exhibit better CMAS resistance and thermal expansion compatibility as EBC topcoats than other RE phosphates and silicates5,12,33. Unlike single-layered coating designs used in phosphate EBCs, multi-layered coating designs are generally adopted in silicate EBC applications4,12,35. The multi-layered design consists of Lu2SiO5 (monosilicate) topcoat and an interlayer of Lu2Si2O7 (disilicate) below the topcoat but above the bond coat. As a result, Lu2SiO5 (monosilicate), being the top coat, serves as the first line of defense against CMAS in a silicate EBC and is thus chosen for analysis in this work.

The LuPO4 and Lu2SiO5 EBC pellets were sintered using the spark plasma sintering (SPS) method. The LuPO4 powder used in the experiments was synthesized as reported by Bryce et al.35. Lu2SiO5 was synthesized via a solid-state reaction, where the appropriate ratios of Lu2O3 and SiO2 were milled together via high-energy ball milling (HEBM) at 500 rpm using ethanol as the mixing solvent and ZrO2 milling balls as the grinding material. The model CMAS (33CaO–9MgO–13AlO1.5–45SiO2) is prepared by mixing oxide powders CaO (99.99%, Sigma-Aldrich), MgO (99.99%, Sigma-Aldrich), Al2O3 (99.99%, Sigma-Aldrich), and SiO2 (99.9%, Alfa Aesar) according to the stoichiometric ratio. The mixture was then heated at a rate of 10 °C min−1 up to 1300 °C and held for 8 h and, finally, quenched in water to prepare the model CMAS. The LuPO4-CMAS and Lu2SiO5-CMAS composites (with 5 vol% and 8 vol% CMAS) were also synthesized via solid-state ball milling of LuPO4 and Lu2SiO5 powders with the model CMAS powder in their appropriate volume ratios. The milled powders were dried and then ground into fine powders, loaded into 10 mm diameter cylindrical graphite dies and sintered into dense pellets using SPS (Model 10-3 SPS system, Thermal Tech. LLC, Santa Rosa, CA). The samples were heated from room temperature to the sintering temperature of 1500 °C at a rate of 200 °C min−1, then held at 1500 °C and under a pressure of 50 MPa for 15 min. The sintered pellets were ground with SiC abrasive papers and then polished with colloidal silica suspension to achieve a mirror finish. The CMAS reactions on LuPO4 and Lu2SiO5 were performed in a box furnace with a heating rate of 10 °C min-1 to 1300 °C and held for 45 and 5 h, respectively. The reacted samples were cut in half, processed and polished for analysis.

Measurement of indentation fracture toughness

The fracture toughness of the EBC samples was estimated using micro and nanoindentation measurements. A micro-hardness tester (Leco M-400, LECO Corporation, USA) with Vickers indenter was used to create 10 indentations for each sample with a load of 1 kgf (~ 9.8 N), and each indentation lasted for 15 s. The indentation crack lengths were measured from the SEM image of each indentation linearly from the center of the indentation to the crack tip using ImageJ software (version 1.51, https://imagej.net/ij/docs/index.html)36 (see supplementary Figs. A.2 and A.3). Nanoindentation tests were also carried out for each sample with a load of 1000 μN to measure the hardness (H) and elastic modulus (E) of each sample. The fracture toughness (Kc) was evaluated using the half-penny cracks equation (Eq. (1)) given by Anstis et al.34,37,38,

$${K}_{c}=\delta {\left(\frac{E}{H}\right)}^{0.5} \frac{P}{{c}^{1.5}} ,$$
(1)

where P is the load for each micro indentation, c is the average value of all crack lengths from the micro indentation test and δ is the indenter geometry-related parameter.

The indentation fracture method used in this study is known to have significant uncertainty in the measurement of fracture toughness due to complex fracture mechanisms involved and material anisotropy at small scale39. For example, the effect of crystal anisotropy on fracture toughness of ZrB2 revealed that its indentation fracture toughness can vary with crystallographic orientation by more than 30%40. Measurements in piezoelectric materials showed significant variation while using indentation fracture toughness in the poled and unpoled directions41. A similar study on titanium nitride (TiN) ceramic demonstrated that intentionally designed grain boundaries can create “weak” and “tough” crack propagation directions indicating different fracture toughness in different directions42. These studies emphasize the role of microstructural features in influencing crack paths leading to anisotropic fracture toughness which might affect the accuracy of indentation fracture measurements43. However, in this work, the LuPO4 and Lu2SiO5 samples used for indentation-based mechanical property evaluations are considered homogenous and isotropic based on the following reasoning.

The LuPO4 and Lu2SiO5 samples were synthesized using chemical coprecipitation and solid-state reaction techniques, respectively, ensuring a uniform particle distribution and homogeneous composition. The synthesized powders were densified using spark plasma sintering (SPS), which facilitated high densification with minimal grain growth, resulting in fine-grained, highly dense ceramics with homogeneous microstructure44,45,46. The abovementioned processing approach yielded a relatively homogeneous bulk material. For measurements using micro indentation, a larger indentation area encompassing multiple grains was considered to effectively average out crystallographic anisotropy and non-homogenous composition, thus yielding isotropic and homogenous bulk property measurements47. In the case of nanoindentation, which probes localized regions, individual grains may exhibit anisotropic responses depending on their crystallographic orientation46. However, by performing multiple indentations across a larger area and averaging the results, the overall mechanical response can be reasonably approximated as isotropic at the macroscopic scale. Based on these considerations, SPS-sintered LuPO4 and Lu2SiO5 ceramics were assumed to exhibit isotropic and homogeneous behavior for indentation-based mechanical property evaluations. In the past, the fracture toughness of SPS-sintered rare earth phosphates was measured using similar techniques48. It is also noted that the indentation fracture method is well conceived for ceramics despite the uncertainties in the measurement49,50. In absence of adequate fracture toughness data for rare-earth ceramics in the literature, the measured indentation toughness values are assumed to describe fracture resistance of the materials51.

EBC microstructure models

This work uses the CFEM to simulate fracture through EBC microstructures before and after CMAS penetration28. The microstructures used in the models consist of randomly oriented ceramic grains and their grain boundaries. The microstructures are constructed from micrographs obtained using electron backscatter diffraction (EBSD). EBSD is a scanning electron microscope-based technique that scans the surface of a crystalline sample52. This work uses eight EBSD micrographs obtained by scanning different locations on the surface of a spark plasma sintered LuPO4 sample. The EBSD micrographs represent data as a 2D array of pixels representing multiple scanned points on the sample surface. The color of each pixel indicates a unique orientation, i.e., Euler angles: ϕ1, Φ, ϕ2, based on the crystal structure at a particular point on the sample surface. The scan size of each micrograph used is 40 × 40 μm2 with 133 × 133 pixels along the x and y directions (see Supplementary Fig. A.1).

The raw EBSD data (Fig. 2a) is processed through an open-source MATLAB toolbox MTEX (version 6.0, https://mtex-toolbox.github.io/)53. While processing, the microstructure is assumed to have no porosity, and missing data in the EBSD is filled using the nearest neighbor algorithm to get a microstructure with contiguous grains (Fig. 2b)52. After processing the EBSD data, a uniformly meshed grid of 2D plane strain quadrilateral finite elements is laid on the EBSD microstructure and sectioned according to different grains in the microstructure. Each section representing a different grain in the microstructure is assigned material properties based on their orientations. This creates the microstructure models before CMAS penetration (Fig. 2c). The microstructure models with CMAS penetration are generated by introducing CMAS along the grain boundaries. The grains are displaced to make space for CMAS by applying outward radial translation to their centroids with reference to the center of the entire microstructure. The outward radial translation is adjusted such that the overall empty spaces created along the grain boundaries reflect the desired level of CMAS penetration, i.e., 3%, 5%, 8%, 11% and 15% by volume, into the microstructure. Similar to the microstructure models without CMAS penetration, a uniform mesh of 2D plane strain quadrilateral finite elements is laid and sectioned based on different microstructure regions that include grains and CMAS along the grain boundaries (Fig. 2d–f).

Fig. 2
figure 2

Generation of Abaqus model from electron backscatter diffraction (EBSD) micrographs. Panel (a) shows the raw EBSD micrograph from experiments. Panel (b) shows the processed micrograph in which the non-indexed data is removed. Panel (c) shows the Abaqus model with different grains and grain boundaries. The panels in (d–f) show the microstructures with 3%, 8% and 15% CMAS penetration, respectively.

Full size image

Cohesive finite element model (CFEM)

A cohesive finite element model (CFEM) with zero-thickness cohesive elements embedded along the edges of all the 2D plane strain quadrilateral elements (Fig. 3a)28,29,30 is employed to investigate the fracture characteristics of EBCs. The CFEM model is implemented in Abaqus (version 2022, https://www.3ds.com/support/documentation/user-guides)32 and uses its standard bilinear traction separation law of the form,

$$\mathbf{t}=\left\{\begin{array}{c}{t}_{n}\\ {t}_{s}\end{array}\right\}=\left(1-D\right)\left[\begin{array}{cc}{K}_{nn}& 0\\ 0& {K}_{ss}\end{array}\right]\left\{\begin{array}{c}{\delta }_{n}\\ {\delta }_{s}\end{array}\right\},$$
(2)

where t is the traction vector on the cohesive element, D is scalar damage, K is the cohesive stiffness of the element, and δ is the separation between its faces. A linear scalar damage law is defined as,

$$D=\frac{{\delta }_{c}\left(\delta -{\delta }_{0}\right)}{\delta \left({\delta }_{c}-{\delta }_{0}\right)},$$
(3)

where δ is the current effective separation, i.e., \(\delta =\sqrt{{\delta }_{n}^{2}+{\delta }_{s}^{2}}\), δ0 is the initial separation for damage initiation, and δc is the critical separation at failure. The initial separation (δ0) is defined as the separation when the damage initiation criterion

$${\left\{{\left(\frac{{t}_{\text{n}}}{{T}_{\text{max}}}\right)}^{2}+{\left(\frac{{t}_{\text{s}}}{{T}_{\text{max}}}\right)}^{2}\right\}}^{0.5}=1,$$
(4)

based on quadratic traction is satisfied. The maximum traction Tmax is assumed to be the same for normal and shear directions28. The cohesive parameters used in this study are listed in Table 1.

Fig. 3
figure 3

Schematic representation of the (a) cohesive finite element discretization and (b) computational model for CFEM simulations subjected to surfing boundary condition.

Full size image
Table 1 Material properties and cohesive zone parameters.
Full size table

A schematic diagram of the computational model used in CFEM simulations is shown in Fig. 3b. A total of 32 CFEM simulations are performed by initiating crack along all four edges of each of the EBC microstructures obtained from eight EBSD images shown in the Supplementary Fig. A.1. The cohesive element size is taken as 0.3 μm to ensure convergence of fracture simulations for the given material properties and cohesive zone parameters28,31. Surfing boundary conditions are used to induce stable crack propagation through the microstructures as shown in Fig. 3b54. The J-integral is computed using a contour integral approach on a homogenous region surrounding the microstructures (Fig. 3b)54,55,56. All the materials in this work are considered brittle and their material properties are given in Table 1. The computed J-integral is used to estimate the fracture toughness using the relation, \({K}_{Ic}=\sqrt{\frac{J\overline{E} }{1-\overline{\nu }}}\), where J is the computed J-integral, \(\overline{E }\) is the effective Youngs modulus and \(\overline{\nu }\) is the effective Poisson’s ratio57. The homogeneous region surrounding the microstructure is assigned homogenized material properties of the microstructure it surrounds. The cohesive zone parameters based on bilinear traction separation laws are used for the cohesive elements inside the ceramic grains, i.e., LuPO4 and Lu2SiO5, and CMAS regions. For cohesive elements along the grain boundaries a sinusoidal fracture strength variation is assumed. It takes maximum and minimum value as 100% and 58% of the fracture strength of the grain, respectively28. The fracture strengths are assigned to the cohesive elements on grain boundaries based on misorientation between the adjacent grains30. The cohesive zone parameters are derived from the fracture toughness measured from indentation fracture experiments performed in this work. While the isotropic elastic properties are experimentally measured and the anisotropic elastic properties are taken from the literature2,58,59. The elastic properties of the homogenous regions surrounding CMAS-penetrated microstructures are computed using the rule of mixtures54.

Results

Validation of CFEM before CMAS penetration

The mesoscale simulations are carried out for LuPO4 and Lu2SiO5 using eight different microstructure (EBSD) images from fabricated EBC samples (see Supplementary Fig. A.1). A schematic representation of the CFEM model with boundary conditions is shown in Fig. 3b. A total of 32 simulations are carried out by initiating fracture on each of the four sides of the experimentally obtained microstructures. The simulation results for the LuPO4 and Lu2SiO5 without CMAS penetration are shown in Fig. 4. The pure EBCs exhibit a tortuous fracture propagation (Fig. 4a,b), which could be attributed to the material anisotropy and difference in the fracture strengths of grains and grain boundaries. The anisotropy and inhomogeneity in the microstructure cause the crack path to pass through grains (transgranular fracture) and along grain boundaries (intergranular fracture). The crack path is quantified using a crack path fraction parameter defined as fractions of crack path inside grains, i.e., \({H}_{\text{GR}}=\frac{{L}_{\text{GR}}}{{L}_{\text{GB}}+{L}_{\text{GR}}}\), and fraction of crack path along the grain boundaries, i.e., \({H}_{\text{GB}}=\frac{{L}_{\text{GB}}}{{L}_{\text{GR}}+{L}_{\text{GB}}}\), where LGB and LGR are crack lengths within grains and along grain boundaries, respectively28. The mean values of crack path fraction are found to be around 0.6 and 0.4 for the grains and grain boundaries, respectively, for both the LuPO4 and Lu2SiO5 EBCs (Fig. 4c). The similarity of the crack path fractions indicates the dominant effect of the microstructure on the fracture behaviour of EBCs, where the same set of microstructures are used for the fracture simulations of both EBCs.

Fig. 4
figure 4

Simulation results from cohesive finite element model (CFEM) for LuPO4 and Lu2SiO5 EBCs, and CMAS. Fracture patterns in the (a) LuPO4 and (b) Lu2SiO5 microstructures through grains and along grain boundaries (c) The box plots show crack path fractions for EBCs. The J-integral values for (d) LuPO4 and (e) Lu2SiO5 EBCs with evolving crack length. The variations in J-integral values for all the microstructures are shown as light-colored bands and their average is the dark-colored curve. Panel (f) compares fracture toughness (KIc) obtained from CFEM simulations with that of experimentally obtained values. The ‘*’ indicates similarity of the data from experiments and CFEM simulations based on two-sample t-test and Wilcoxon rank-sum test, see Supplementary Material for details.

Full size image

The model is validated by comparing fracture toughness KIc of the EBCs obtained from CFEM simulations to that of the experimentally measured values. The KIc is estimated from the J-integral values obtained from simulations using the relation outlined in “Cohesive finite element model (CFEM)” section. The J-integral values for LuPO4 and Lu2SiO5 EBCs with evolving crack length are shown in Fig. 4d,e, respectively. The noticeable variation in the J-integral values for different microstructures could be attributed to the tortuosity of the crack path (Fig. 4a,b)54. Hence, the mean J-integral values for the middle 50% of the sample length are used to estimate the KIc of the samples, mitigating the edge effects. The estimated KIc values for the LuPO4, Lu2SiO5, and CMAS samples are compared with that of the experimentally measured values in Fig. 4f30,55. Notice that the KIc for homogenous and isotropic CMAS is almost constant with zero variance (Fig. 4f).

For validation in Fig. 4f, 10, 11 and 15 experimental measurements of indentation fracture toughness (KIc) are used for LuPO4, Lu2SiO5 and CMAS respectively, with 32 values computed for each material from the simulations. The similarity between computed and experimentally measured KIc values is assessed using statistical tests based on a two-sample t-test and Wilcoxon rank-sum test with \(p<0.01\) (see Supplementary Table B.2). The tests show that the KIc values estimated from simulations are indeed statistically similar to that of experimentally measured values, thus validating simulation results for pure EBCs and CMAS. The observations demonstrate the ability of the CFEM to simulate fracture accurately in pure LuPO4, Lu2SiO5 and CMAS.

Validation of CFEM with CMAS penetration

The CFEM is further validated to describe the fracture behavior of CMAS-penetrated EBCs. Two levels of CMAS penetration, i.e., 5% and 8% by volume, are introduced along the grain boundaries within the microstructures obtained from the fabricated EBC samples. These two levels are chosen based on experimental observations in this work and the literature17 that indicate CMAS penetration along the grain boundaries within the 0 – 15% range by volume. The CFEM simulations use boundary conditions and material properties presented in “Cohesive finite element model (CFEM)” section. The KIc values estimated from the J-integral values are compared with the experimental KIc of LuPO4 and Lu2SiO5 with CMAS (5% and 8% by volume) measured from indentation fracture testing.

The simulation results for 5% and 8% CMAS-penetrated LuPO4 and Lu2SiO5 EBC samples are shown in Fig. 5. A total of 32 simulations are carried out for each of the EBCs with CMAS penetration by initiating fracture on each of the four sides of the microstructure obtained from eight EBSD images of EBCs. The tortuous fracture patterns observed in a LuPO4 microstructure at 5% and 8% CMAS penetration are shown in Fig. 5a–d. Fracture patterns show that the crack predominantly propagates through the penetrated CMAS regions. This behavior is expected as the fracture strength of CMAS and CMAS-grain interfaces are considered lower than the grains and grain boundaries (Table 1). The crack path fractions for the CMAS-penetrated microstructures are shown in Fig. 5e. The crack path fractions are defined as fractions of the crack path inside grains, i.e., \({H}_{\text{GR}}=\frac{{L}_{\text{GR}}}{{L}_{\text{GR}}+{L}_{\text{GB}}+{L}_{\text{CM}}+{L}_{\text{CI}}}\), along the grain boundaries, i.e., \({H}_{\text{GB}}=\frac{{L}_{\text{GB}}}{{L}_{\text{GR}}+{L}_{\text{GB}}+{L}_{\text{CM}}+{L}_{\text{CI}}}\), inside CMAS, i.e., \({H}_{\text{CM}}=\frac{{L}_{\text{CM}}}{{L}_{\text{GR}}+{L}_{\text{GB}}+{L}_{\text{CM}}+{L}_{\text{CI}}}\), and along grain-CMAS interface, i.e., \({H}_{\text{CI}}=\frac{{L}_{\text{CI}}}{{L}_{\text{GR}}+{L}_{\text{GB}}+{L}_{\text{CM}}+{L}_{\text{CI}}}\), where LGR, LGB, LCM and LCI are crack lengths within grains, along grain boundaries, within penetrated CMAS, and grain-CMAS interface, respectively. The crack path fractions indicate that increasing CMAS penetration from 5 to 8% causes increased crack propagation through CMAS-grain interfaces (CI) in both LuPO4 and Lu2SiO5 samples. Conversely, cracks passing through grains (GR) and grain boundaries (GB) decrease.

Fig. 5
figure 5

Simulation results from cohesive finite element model (CFEM) for 5% and 8% CMAS-penetrated LuPO4 and Lu2SiO5 EBCs. Panels (a–d) Show fracture patterns in the 5% and 8% CMAS-penetrated LuPO4 and Lu2SiO5 EBC microstructures respectively. The box plots in panel (e) shows crack path fractions for EBCs with CMAS penetration. The J-integral values for (f) LuPO4 and (g) Lu2SiO5 with and without CMAS penetration are compared with that of the pure CMAS with evolving crack length. The variations in J-integral values for all the microstructures are shown as light-colored bands and their average is presented with the dark-colored curve. Panel (h) compares fracture toughness (KIc) obtained from CFEM simulations with that of experimentally obtained values. The ‘*’ indicates similarity of the data from experiments and CFEM simulations based on two-sample t-test and Wilcoxon rank-sum test, see Supplementary Material for details.

Full size image

The J-integral values computed using CFEM simulations for CMAS-penetrated LuPO4 and Lu2SiO5 are shown in Fig. 5f,g as a function of evolving crack length. The mean value of J-integral for both 5% and 8% CMAS penetration lies below the J-integral value of pure LuPO4/Lu2SiO5, indicating degradation due to the presence of CMAS in the microstructure.

The model is validated by comparing fracture toughness KIc of CMAS-penetrated EBCs with that of the experimentally measured values. The J-integral from the middle 50% of the simulation length is used to estimate KIc to mitigate the edge effects. The distribution of KIc for EBCs with 5% and 8% CMAS penetration is presented using box plots in Fig. 5h. For validation in Fig. 5h, six and five values of experimentally measured indentation fracture toughness (KIc) are used for LuPO4 with 5% and 8% CMAS, respectively, with 32 values for each material from the simulations. While for Lu2SiO5, ten values of experimental KIc are used for both 5% and 8% CMAS penetrated microstructures. The KIc values obtained from simulations and experiments are compared and their similarity is assessed using statistical tests based on a two-sample t-test and Wilcoxon rank-sum test with \(p<0.01\).

The comparisons in Fig. 5h show that the estimated KIc is statistically similar to that of experimentally measured values for three out of four cases (see Supplementary Table B.3). The fracture toughness for LuPO4 with 8% CMAS penetration does not show statistical similarity with the experimental values (Fig. 5h). This could be due to insufficient experimental observations needed to test the statistical similarity between measured and computed KIc. Nonetheless, the comparison shows reasonable agreement for LuPO4 and Lu2SiO5 in most cases. In addition, it is seen that an increase in CMAS penetration from 5 to 8% led to a decrease in KIc, indicating higher degradation in fracture resistance with increasing CMAS penetration.

The statistical tests further reinforce the efficacy of CFEM in predicting the fracture behavior of CMAS-penetrated EBCs.

Fracture resistance of LuPO4 and Lu2SiO5 with CMAS penetration

The validated CFEM is employed to investigate the fracture behavior of LuPO4 and Lu2SiO5 EBCs with increasing CMAS penetration. Based on observations from CMAS reaction tests on EBC samples and literature17, five levels of CMAS penetration are considered for fracture simulations: 3%, 5%, 8%, 11% and 15% by volume. Similar to the validation studies, a total of 32 simulations are carried out for each penetration level, and their results are shown in Fig. 6.

Fig. 6
figure 6

Simulation results obtained using cohesive finite element model (CFEM) for LuPO4 and Lu2SiO5 microstructures at different levels of CMAS penetration. The fracture patterns in (a) LuPO4 and (b) Lu2SiO5 EBC microstructures are shown with 0% CMAS (pure), 3% CMAS, 8% CMAS and 15% CMAS penetration. Panels (c,d) show average crack path fractions before and after CMAS penetration in LuPO4 and Lu2SiO5, respectively. The J-integral values for (e) LuPO4 and (f) Lu2SiO5 before and after CMAS penetration are compared with that of the pure CMAS with evolving crack length. Panels (g,h) compare fracture toughness (KIc) and residual strength before and after CMAS penetration in LuPO4 and Lu2SiO5, respectively.

Full size image

The tortuous fracture patterns obtained using CFEM before and after CMAS penetration for both LuPO4 and Lu2SiO5 EBC microstructures are shown in Fig. 6a,b, respectively. The tortuosity of fracture in EBCs without CMAS penetration (pure EBC) is due to the anisotropy of grains. On the other hand, crack path tortuosity after CMAS penetration can be attributed to the presence of CMAS along the grain boundaries and its lower fracture strength than grains and grain boundaries. The lower fracture strength of CMAS and its interfaces causes the fracture to pass through CMAS regions in the CMAS-penetrated microstructures (Fig. 6a,b). It is observed that the fraction of total crack length passing through grains and grain boundaries decreases with increasing CMAS penetration, while the fraction of crack length passing through CMAS and CMAS-grain interface increases at the same time (Fig. 6c,d). Moreover, a steep decrease in the fraction of crack path passing through grains and grain boundaries at 3% CMAS penetration compared to pure LuPO4 and Lu2SiO5 indicates a significant change in fracture behavior caused by CMAS.

The average J-integral curves obtained from simulation for LuPO4 and Lu2SiO5 with different CMAS penetration levels are shown in Fig. 6e,f. For reference, the average J-integral curves of pure LuPO4, Lu2SiO5, and CMAS are shown as dashed curves at the top and bottom of the plots. It is observed that the average J-integral curves of CMAS-penetrated LuPO4 and Lu2SiO5 microstructures progressively degrade with increasing CMAS penetration levels and approach the average J-integral curve of CMAS. The J-integral values in the middle 50% sample lengths are used to estimate KIc. The distribution of KIc values estimated from all 32 simulations performed on eight experimentally obtained microstructures are plotted as box plots for CMAS-penetrated LuPO4 and Lu2SiO5 in Fig. 6g,h, respectively. The degradation due to CMAS penetration can be seen more clearly in the box plots. The KIc degradation at different levels of CMAS penetration is indicated as residual strength percentages by assuming the fracture strength of pure LuPO4 and Lu2SiO5 as 100% and that of the CMAS as 0%. The degradation of KIc in LuPO4 is observed to be higher than in Lu2SiO5. With a further increase in CMAS penetration, the KIc values degrade further and approach CMAS values. A steep drop in KIc caused by low levels of CMAS penetration in LuPO4 emphasizes the need for mechanisms that can limit CMAS penetration into the microstructures.

Discussion

The simulation results reveal that CMAS corrosion causes degradation of fracture resistance (KIc) in both LuPO4 and Lu2SiO5 EBCs, with more degradation observed in LuPO4 (Fig. 6g,h). It is seen that before CMAS penetration, the KIc of LuPO4 was slightly higher than that of Lu2SiO5. However, after CMAS penetration, the KIc values of LuPO4 are generally lower than Lu2SiO5. The lower values of KIc for LuPO4 are also observed experimentally in the indentation test results shown in Fig. 5h.

These observations indicate that the fracture resistance of CMAS-penetrated LuPO4 is lower than that of Lu2SiO5. Interestingly, it also emphasizes that a higher fracture resistance of LuPO4, in comparison with Lu2SiO5, could be achieved by eliminating or minimizing CMAS corrosion. To test this hypothesis, CMAS corrosion is experimentally studied in LuPO4 and Lu2SiO5 by exposing them to molten CMAS at 1300 °C for 45 and 5 h, respectively. Notice that the LuPO4 sample was subjected to a longer duration of reaction to observe its CMAS corrosion resistance.

The backscattered scanning electron microscopy (SEM) and energy dispersive X-ray spectroscopy (EDS) images of LuPO4 and Lu2SiO5 after the CMAS reaction are shown in Figs. 7 and 8, respectively. Figures 7a and 8a show the epoxy, CMAS, and bulk EBC pellet after CMAS reaction in LuPO4 and Lu2SiO5 samples. It is observed that Lu2SiO5 delaminates after the CMAS reaction of 5 h, whereas the LuPO4 remains intact even after 45 h. The delamination in Lu2SiO5 could be attributed to the mismatch in the coefficient of thermal expansion between Lu2SiO5 (~ 6.7 × 10–6 in the temperature range 200–1350 °C) and oxyapatite Ca2Lu8(SiO4)6O2 phase formed in the reaction layer58. Further investigation is needed to achieve a mechanistic understanding of the stress distribution and delamination in the Lu2SiO5.

Fig. 7
figure 7

SEM backscattered electron images of LuPO4 after interaction with molten CMAS at 1300 °C for 45 h. (a) Cross-section SEM image, (b) Higher resolution cross-section SEM image, (c) EDS elemental maps corresponding to the rectangular area in (b).

Full size image
Fig. 8
figure 8

SEM backscattered electron images of Lu2SiO5 after interaction with molten CMAS at 1300 °C for 5 h. (a) Cross-section SEM image, (b) Higher resolution cross-section SEM image, (c) EDS elemental maps corresponding to the rectangular area in (b).

Full size image

The high-resolution SEM images of the reaction zone in LuPO4 and Lu2SiO5 samples are shown in Figs. 7b and 8b, respectively. It is seen that a reaction layer is formed at the interface of CMAS and EBCs during the CMAS reaction. The average thicknesses of the reaction layer for LuPO4 and Lu2SiO5 are measured (at 20 locations on the SEM image) to be 32.8 ± 3.8 µm and 6.1 ± 1.4 μm, respectively. LuPO4 forms a continuous and thicker reaction layer than the Lu2SiO5. This aligns with the observations that RE silicates form porous and non-uniform reaction layers under CMAS corrosion16. At the same time, the RE phosphates have been observed to form continuous and denser reaction layers4.

The EDS maps of CMAS-LuPO4 and -Lu2SiO5 interfaces are shown in Figs. 7c and 8c, respectively. In LuPO4, calcium (Ca) did not penetrate the reaction layer. However, a noticeable penetration of Ca is seen in Lu2SiO5. The penetration of Ca in LuPO4 is restricted, possibly due to the formation of a continuous and dense reaction layer of Ca8MgLu(PO4)7 along the CMAS-LuPO4 interface. On the other hand, in Lu2SiO5, a porous and non-uniform reaction layer of oxyapatite Ca2Lu8(SiO4)6O2 may have allowed Ca to penetrate in bulk Lu2SiO5. Magnesium (Mg) and Aluminum (Al) penetration is observed to be similar in both LuPO4 and Lu2SiO5.

The color intensity of the EDS maps suggests that the amount of Lu present in the reaction layer is less in LuPO4 (Fig. 7c) than in Lu2SiO5 (Fig. 8c). This indicates that less LuPO4 is needed to form a dense reaction layer compared to Lu2SiO5. A lower stoichiometric ratio of Lu:Ca in Ca8MgLu(PO4)7 (at the CMAS-LuPO4 reaction layer) as compared to a higher Lu:Ca ratio in Ca2Lu8(SiO4)6O2 (at CMAS-Lu2SiO5 reaction layer) may have played a role in the amount of Lu in the reaction layer5. In contrast, a high concentration of Ca is required to form the Ca8MgLu(PO4)7 interfacial phase, limiting its penetration into the EBC matrix as compared with that of Lu2SiO5, and with the formation of the dense reaction layer at the interface, inhibiting the penetration of CMAS.

The abovementioned observations indicate that LuPO4 might perform better than Lu2SiO5 at restricting the amount of CMAS penetrating the bulk region by forming a dense and thicker reaction layer35 with higher contents of Ca and less Lu. As a result, LuPO4 might be able to avoid degradation of KIc from CMAS penetration and retain its fracture resistance for a longer duration of time with the formation of the dense interfacial layer. The dense reaction layer was also observed in the LuPO4 upon CMAS interaction at 5 h at 1300 °C with a thickness of 13.3 ± 1.9 μm60. The greater amount of CMAS penetration in the Lu2SiO5 may significantly alter the thermal expansion coefficient of the matrix as well, leading to the delamination of the bulk matrix underneath the reaction layer, in contrast to the well-maintained structural integrity of the LuPO4 matrix without cracking or delamination upon CMAS interaction at the same temperature even elongated duration. These experimental observations indicate that LuPO4 may be able to retain a higher fracture resistance (KIc) due to less CMAS penetration than Lu2SiO5 under similar CMAS corrosion conditions.

The experimental observations of the layered EBC structures show that, upon CMAS corrosion, EBCs macroscopically fail mainly by two mechanisms, i.e., penetration cracking and spallation18,20,61. In the penetration cracking, the crack initiates at the top layer and penetrates into the subsequent layers in the EBC perpendicular to the layer interfaces. On the other hand, spallation occurs when the interfaces between the layers is weaker than the adjacent layers. As a result, the crack propagates along the interfaces, eventually delaminating the layer above it and causing spallation20. Typically, penetration cracking occurs first and is caused by increased thermal residual stresses due to coefficient of thermal expansion mismatches of the EBC material and CMAS (and its reaction products)19. To this end, it is emphasized that the fracture in the EBCs is accelerated by CMAS corrosion due to its two-fold effect, that are, increase in the thermal residual stresses and degradation of fracture resistance. Therefore, it is crucial to limit the CMAS corrosion of the EBC top layer to avoid premature failure. The experimental observations and analyses from this work indicate that the LuPO4 might be better than the Lu2SiO5 at limiting the CMAS corrosion and avoiding EBC failures.

Conclusion

A combination of experiments and computational modeling is employed to investigate the effect of CMAS penetration on the fracture behavior of RE phosphate (LuPO4) and RE silicate (Lu2SiO5) EBCs. A computational framework based on cohesive finite element method (CFEM) is developed to quantify the fracture characteristics of EBCs. The CFEM model is developed using electron backscattered diffraction (EBSD) micrographs of EBCs. The model is validated with the experimentally measured fracture toughness and employed to investigate the fracture characteristics of LuPO4 and Lu2SiO5 with increasing CMAS penetration. Additionally, LuPO4 and Lu2SiO5 are subjected to experimental CMAS corrosion tests to evaluate their CMAS penetration resistance and the observations are correlated with the simulation predictions.

The major conclusions drawn from the experimental observations and computational fracture modeling for EBCs are as follows:

  1. 1.

    The LuPO4 EBC exhibits about 15% higher fracture resistance (KIc) than the Lu2SiO5 EBC before CMAS penetration. However, after CMAS penetration, Lu2SiO5 retains about 40–65% higher KIc than the LuPO4 across all levels of CMAS penetration.

  2. 2.

    The KIc of LuPO4 and Lu2SiO5 EBCs progressively degrade with increasing CMAS penetration to about 24% and 45%, respectively, of their original KIc after 15% CMAS penetration.

  3. 3.

    CMAS, a brittle and glassy phase with lower KIc than EBCs, causes significant degradation to the EBCs even at low penetration level. The LuPO4 and Lu2SiO5 degrade to about 57% and 91%, respectively, of their original KIc at 3% CMAS penetration.

  4. 4.

    Experimental CMAS corrosion tests show that LuPO4 EBC may perform better than Lu2SiO5 EBC despite lower residual KIc after CMAS penetration by forming a dense and thicker reaction layer (about 13.3 μm60 in contrast to 6.1 μm in Lu2SiO5) that can lower the amount of CMAS penetration.

The findings from this work indicate that EBC materials must be designed to resist the CMAS penetration for improved fracture resistance and avoid premature failure. The CMAS corrosion in EBCs is shown to substantially degrade their fracture resistance even at lower penetration levels, despite being thermomechanically compatible with SiC CMCs. Moreover, this work demonstrates the effectiveness of integrating computational modeling with experimental observations to rapidly evaluate material performance and, hence, accelerate their design and discovery.