Introduction

Zoonotic diseases, which are transmitted between animals and humans, present significant global health challenges. Human-non-human primate interactions, such as those involving baboons, pose complex epidemiological dynamics. Implementing preventive measures, such as improving sanitation and hygiene, is crucial for controlling zoonotic disease outbreaks. Regular monitoring and surveillance of wildlife and livestock can aid in the early detection of potential threats. Additionally, promoting education and awareness about the risks of zoonotic diseases can empower communities to adopt safer practices and reduce transmission.

Fractional calculus has gained significant attention for its applications in engineering1, physics2, plant epidemiology3, mathematical biology4, medicine5, as well as psychological and life sciences6. There are numerous interdisciplinary systems that can accurately be represented by fractional differential equations. These include viscoelasticity7, electromagnetic wave propagation8, quantum dynamics9, Lorenz systems10, Langevin systems11, and Liu systems12, Newton-Leipnik13,14,15, Diabetes16,17,18,19,20,21,22,23. In the field of fractional derivatives, one of the most highly regarded derivatives is the Atangana-Baleanu derivative, which has gained popularity due to its non-local and non-singular kernel, providing a more realistic representation of dynamic processes in biological systems. Several types of fractional derivatives are used in this field, including the Riemann-Liouville, Caputo, Caputo-Fabrizio, and AB operators. These have applications in engineering24, physics25,26,27, tobacco smoking models28, medicine29,30, influenza31, infectious diseases32, epidemics33, cancer34, coronavirus35, monkeypox36, zoonotic viral infections37, and alcohol-related models38. By bridging the gap between fractional modeling and zoonotic disease dynamics, this work advances the mathematical understanding of such diseases. It provides a foundation for future studies. The proposed model not only highlights the importance of integrating memory effects and spatial heterogeneity but also underscores the potential of fractal-fractional approaches to inform effective public health interventions in regions with significant human-wildlife interactions39,40,41. Despite the growing body of literature on fractional calculus in biological modeling, the integration of AB fractal-fractional derivatives in zoonotic disease transmission remains underexplored, particularly in the context of wildlife-human interactions. Existing studies have demonstrated the utility of fractional models for general epidemiological applications42. However, few have addressed the combined roles of fractal geometry and memory effects in zoonotic contexts. This gap is especially critical in regions like Al-Baha, where human-wildlife interactions create complex transmission dynamics. Fractional derivatives have found applications beyond epidemiology, particularly in dynamics and transport processes. Their ability to model memory effects and complex interactions makes them valuable in describing physical phenomena like fluid transport, diffusion processes, and biological signaling pathways. Incorporating these derivatives into zoonotic disease models offers both epidemiological accuracy and broad applicability to dynamic systems43,44,45,46,47.

Using fractional calculus and zoonotic modeling, this study advances our understanding of zoonotic disease dynamics in the Al-Baha region. Fractional Euler with Atangana-Baleanu scheme derivatives is demonstrated to incorporate memory effects and spatial heterogeneity, addressing critical gaps in existing models. This study uses Caputo derivatives to describe complex disease transmission dynamics using the fractional Euler method with the Atangana-Baleanu scheme. Informing public health strategies and enhancing epidemiological accuracy, it combines local and historical effects. Fixed-point theory establishes the existence and uniqueness of solutions, while stability analysis ensures model robustness. Numerical simulations demonstrate practical applications, such as limiting human-baboon interactions and managing food resources. Stability is evaluated with the Banach fixed-point theorem and Picard iterative method, while Lagrange polynomials represent state variables within the variable-order framework. By simulating system behavior and exploring control strategies-such as sterilization, food restriction, and reduced human interaction-the study offers a comprehensive framework for managing zoonotic disease risks. As a result, the fractional Euler method and Atangana-Baleanu scheme provide valuable insights for human-wildlife interactions in regions.

The manuscript is organized as follows: Section "Preliminary definitions": Preliminary definitions are discussed. Section "Model formulation" describes the dynamics of baboon and human populations in the context of zoonotic disease transmission. Section "Non-negativity, existence and uniqueness of solutions": Existence and uniqueness discusses the theoretical foundations for model validity. In Section "Hyers-Ulam stability", we introduce Hyers-Ulam stability. Section "Euler method involving Atangana-Baleanu operator" contains the Euler scheme involving the Atangana-Baleanu operator. Approximate Solutions presents numerical approximations for system components. In section "Numerical simulation", numerical simulations illustrate the system’s dynamic behavior under various scenarios. The Methodology Section are discussed in Section "Methodology section". Section "Discussion" and "Conclusion" contain the discussion and conclusion sections.

Preliminary definitions

Many new derivatives have been introduced to overcome this drawback, such as Caputo-Fabrizio (\(\texttt{CF}\))46 and Mittag-Leffler (\(\texttt{AB}\))47. In the \(\texttt{CF}\) derivative, the exponential function is used as the kernel, while in the \(\texttt{AB}\) derivative, the ML function is used. Here are the definitions of the AB Caputo operator.

Definition 1

(47) For \(\texttt{h} \in H^{1}(a, b)\) and \(0<\beta <1\), the \(\texttt{AB}\) derivative of order \(\beta\) is

$$\begin{aligned} _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta } \texttt{h}(t)=\frac{\texttt{B}(\beta )}{1-\beta } \int _{a}^{t} \frac{d \texttt{h}(\gamma )}{d \gamma } E_{\beta }\left[ -\beta (t-\gamma )^{\beta }\right] d \gamma , \end{aligned}$$

where \(\texttt{B}(\beta )\) with \(\texttt{B}(0)=\texttt{B}(1)=1\) denotes the normalization function, \(\beta =\frac{\beta }{1-\beta }\) and \(E_{\beta }\) is the ML function. Also, the corresponding \(\texttt {AB}\) fractional integral is

$$\begin{aligned} ^\texttt {AB} _{a} I_{t}^{\beta } \texttt {h}(t)=\frac{1-\beta }{\texttt {B}(\beta )} \texttt {h}(t)+\frac{\beta }{\texttt {B}(\beta ) \Gamma (\beta )} \int _{a}^{t} \texttt {h}(\gamma )(t-\gamma )^{\beta -1} d \gamma . \end{aligned}$$
(1)

Model formulation

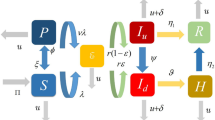
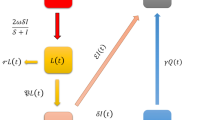
The following model aims to decribe the dynamics of baboon and human populations in the context of zoonotic disease transmission. The model incorporates control strategies such as sterilization, restricted food access, and reduced human-baboon interactions. The baboon population dynamics are modeled using the following equations, where we account for natural growth, disease transmission, and control actions. The combined system of equations modeling the dynamics of baboon and human populations with zoonotic disease transmission is:

$$\begin{aligned} \begin{aligned} \frac{d\texttt {S}_b}{dt}&= r \texttt {S}_b \Big ( 1 - \frac{\texttt {S}_b + \texttt {I}_b + \texttt {R}_b}{K} \Big ) - \beta _b \texttt {S}_b \texttt {I}_b - H_s(t) \texttt {S}_b - H_f(t) \texttt {S}_b, \\ \frac{d\texttt {I}_b}{dt}&= \beta _b \texttt {S}_b \texttt {I}_b - \texttt {S}_b \texttt {I}_b - H_s(t) \texttt {I}_b - H_f(t) \texttt {I}_b, \\ \frac{d\texttt {R}_b}{dt}&= \texttt {S}_b \texttt {I}_b - H_f(t) \texttt {R}_b, \\ \frac{d\texttt {S}_h}{dt}&= -\beta _h \texttt {S}_h \texttt {I}_b - H_i(t) \texttt {S}_h, \\ \frac{d\texttt {I}_h}{dt}&= \beta _h \texttt {S}_h \texttt {I}_b - \texttt {S}_h \texttt {I}_h - H_i(t) \texttt {I}_h, \\ \frac{d\texttt {R}_h}{dt}&= \texttt {S}_h \texttt {I}_h. \end{aligned} \end{aligned}$$
(2)

The components and parameters used in the baboon-human disease model are defined as follows: \(\texttt {S}_b\), \(\texttt {I}_b\), and \(\texttt {R}_b\) represent the susceptible, infected, and recovered populations of baboons, respectively, while \(\texttt{S}_h\), \(\texttt{I}_h\), and \(\texttt{R}_h\) denote the corresponding populations of humans. The model parameters include \(r\), the intrinsic growth rate of the baboon population; \(K\), the carrying capacity based on available food resources; \(\beta _b\), the transmission rate of disease among baboons; \(\beta _h\), the transmission rate of disease from baboons to humans; \(\texttt{S}_b\), the recovery rate of infected baboons; and \(\texttt{S}_h\), the recovery rate of infected humans. Additionally, \(H_s(t)\), \(H_f(t)\), and \(H_i(t)\) represent control measures affecting the baboon population, including sterilization control, food restriction, and human interaction reduction, respectively. These definitions provide a comprehensive framework for understanding the dynamics of disease transmission between baboons and humans within the model.

Model (2) can be written in sense of Atangana-Baleanu operator as:

$$\begin{aligned} \begin{aligned} _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{S}_b(\texttt{t})&= r \texttt{S}_b \Big ( 1 - \frac{\texttt{S}_b + \texttt{I}_b + \texttt{R}_b}{K} \Big ) - \beta _b \texttt{I}_b \texttt{I}_b - H_s(t) \texttt{S}_b - H_f(t) \texttt{S}_b, \\ _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{I}_b(\texttt{t})&= \beta _b \texttt{S}_b \texttt{I}_b - \texttt{S}_b \texttt{I}_b - H_s(t) \texttt{I}_b - H_f(t) \texttt{I}_b, \\ _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{R}_b(\texttt{t})&= \texttt{S}_b \texttt{I}_b - H_f(t) \texttt{R}_b, \\ _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{S}_h(\texttt{t})&= -\beta _h \texttt{S}_h \texttt{I}_b - H_i(t) \texttt{S}_h, \\ _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{I}_h(\texttt{t})&= \beta _h \texttt{S}_h \texttt{I}_b - \texttt{S}_h \texttt{I}_h - H_i(t) \texttt{I}_h, \\ _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{R}_h(\texttt{t})&= \texttt{S}_h \texttt{I}_h. \end{aligned} \end{aligned}$$
(3)

The AB fractional derivative provides a more flexible and generalized framework for fractional calculus, but it can be computationally demanding and complex to implement.

Non-negativity, existence and uniqueness of solutions

Theorem 1

The solutions to the system (3), which start at \({{\mathbb R}}^6_+\), are non-negative.

Proof

Negative values are not considered to be physically meaningful, so they are not considered when attempting to solve problems in biology. Positive bounded solutions are the most realistic and biologically relevant solutions, so they are often sought out when trying to solve biological problems. As a result, one has to

$$\begin{aligned} \begin{aligned} _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{S}_b(\texttt{t})|_{\texttt{S}_b=0} = r S_b> 0, _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{I}_b(\texttt{t})|_{\texttt{I}_b=0} = \beta _b S_b> 0, _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{R}_b(\texttt{t})|_{\texttt{R}_b=0} = \texttt{S}_b I_b> 0,\\ _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{S}_h(\texttt{t})|_{\texttt{S}_h=0} = 0, _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{I}_h(\texttt{t})|_{\texttt{I}_h=0} = \beta _h S_h I_b> 0, _{a}^\texttt{AB} \mathscr {D}_{t}^{\beta }\texttt{R}_h(\texttt{t})|_{\texttt{R}_h=0} = \texttt{S}_h I_h > 0. \end{aligned} \end{aligned}$$

It is concluded from48,49, the solution of model (3) semi-positive. \(\square \)

In Eq. (3), we use the fractional integral operator of Atangana-Baleanu:

$$\begin{aligned} \begin{aligned}&\texttt{S}_b(t) - \texttt{S}_b(0) = ^{\mathtt {\mathcal{A}\mathcal{B}}}I_{t}^{\beta } \left[ \mathscr {F}_1(t, \texttt{S}_b) \right] , \\&\texttt{I}_b(t) - \texttt{I}_b(0) = ^{\mathtt {\mathcal{A}\mathcal{B}}}I_{t}^{\beta } \left[ \mathscr {F}_2(t, \texttt{I}_b) \right] , \\&\texttt{R}_b(t) - \texttt{R}_b(0) = ^{\mathtt {\mathcal{A}\mathcal{B}}}I_{t}^{\beta } \left[ \mathscr {F}_3(t, \texttt{R}_b) \right] ,\\&\texttt{S}_h(t) - \texttt{S}_h(0) = ^{\mathtt {\mathcal{A}\mathcal{B}}}I_{t}^{\beta } \left[ \mathscr {F}_4(t, \texttt{S}_h) \right] , \\&\texttt{I}_h(t) - \texttt{I}_h(0) = ^{\mathtt {\mathcal{A}\mathcal{B}}}I_{t}^{\beta } \left[ \mathscr {F}_5(t, \texttt{I}_h) \right] , \\&\texttt{R}_h(t) - \texttt{R}_h(0) = ^{\mathtt {\mathcal{A}\mathcal{B}}}I_{t}^{\beta } \left[ \mathscr {F}_6(t, \texttt{R}_h) \right] , \end{aligned} \end{aligned}$$
(4)

with the initial conditions: \(\texttt{S}_b(0) = \texttt{S}_{b0}, \texttt{I}_b(0) = \texttt{I}_{b0}, \texttt{R}_b(0) = \texttt{R}_{b0},\) \(\texttt{S}_h(0) = \texttt{S}_{h0}, \texttt{I}_h(0) = \texttt{I}_{h0}, \texttt{R}_h(0) = \texttt{R}_{h0}\). Here, the kernels is given by:

$$\begin{aligned} \begin{aligned} \mathscr {F}_1(t, \texttt{S}_b)&= r \texttt{S}_b \Big ( 1 - \frac{\texttt{S}_b + \texttt{I}_b + \texttt{R}_b}{K} \Big ) - \beta _b \texttt{I}_b \texttt{I}_b - H_s(t) \texttt{S}_b - H_f(t) \texttt{S}_b, \\ \mathscr {F}_2(t, \texttt{I}_b)&= \beta _b \texttt{S}_b \texttt{I}_b - \texttt{S}_b \texttt{I}_b - H_s(t) \texttt{I}_b - H_f(t) \texttt{I}_b, \\ \mathscr {F}_3(t, \texttt{R}_b)&= \texttt{S}_b \texttt{I}_b - H_f(t) \texttt{R}_b, \\ \mathscr {F}_4(t, \texttt{S}_h)&= -\beta _h \texttt{S}_h \texttt{I}_b - H_i(t) \texttt{S}_h, \\ \mathscr {F}_5(t, \texttt{I}_h)&= \beta _h \texttt{S}_h \texttt{I}_b - \texttt{S}_h \texttt{I}_h - H_i(t) \texttt{I}_h, \\ \mathscr {F}_6(t, \texttt{R}_h)&= \texttt{S}_h \texttt{I}_h. \end{aligned} \end{aligned}$$
(5)

Using Eqs. (4) and (5), we get the Atangana-Baleanu fractional integral:

$$\begin{aligned} \begin{aligned}&\texttt{S}_b(t) - \texttt{S}_b(0) = \frac{1 - \beta }{\texttt{B}(\beta )} \mathscr {F}_1(t, \texttt{S}_b) + \frac{\beta }{\texttt{B}(\beta ) \Gamma (\beta )} \int _0^t \mathscr {F}_1(\upsilon , \texttt{S}_b)(t-\upsilon )^{\beta -1} \, d\upsilon , \\&\texttt{I}_b(t) - \texttt{I}_b(0) = \frac{1 - \beta }{\texttt{B}(\beta )} \mathscr {F}_2(t, \texttt{I}_b) + \frac{\beta }{\texttt{B}(\beta ) \Gamma (\beta )} \int _0^t \mathscr {F}_2(\upsilon , \texttt{I}_b)(t-\upsilon )^{\beta -1} \, d\upsilon , \\&\texttt{R}_b(t) - \texttt{R}_b(0) = \frac{1 - \beta }{\texttt{B}(\beta )} \mathscr {F}_3(t, \texttt{R}_b) + \frac{\beta }{\texttt{B}(\beta ) \Gamma (\beta )} \int _0^t \mathscr {F}_3(\upsilon , \texttt{R}_b)(t-\upsilon )^{\beta -1} \, d\upsilon ,\\&\texttt{S}_h(t) - \texttt{S}_h(0) = \frac{1 - \beta }{\texttt{B}(\beta )} \mathscr {F}_4(t, \texttt{S}_b) + \frac{\beta }{\texttt{B}(\beta ) \Gamma (\beta )} \int _0^t \mathscr {F}_4(\upsilon , \texttt{S}_b)(t-\upsilon )^{\beta -1} \, d\upsilon , \\&\texttt{I}_h(t) - \texttt{I}_h(0) = \frac{1 - \beta }{\texttt{B}(\beta )} \mathscr {F}_5(t, \texttt{I}_b) + \frac{\beta }{\texttt{B}(\beta ) \Gamma (\beta )} \int _0^t \mathscr {F}_5(\upsilon , \texttt{I}_b)(t-\upsilon )^{\beta -1} \, d\upsilon , \\&\texttt{R}_h(t) - \texttt{R}_h(0) = \frac{1 - \beta }{\texttt{B}(\beta )} \mathscr {F}_6(t, \texttt{R}_b) + \frac{\beta }{\texttt{B}(\beta ) \Gamma (\beta )} \int _0^t \mathscr {F}_6(\upsilon , \texttt{R}_b)(t-\upsilon )^{\beta -1} \, d\upsilon . \end{aligned} \end{aligned}$$

Let \((G^{*})\) denote the following assumptions: For all \(\iota \in [0, T]\), the functions \(S_b(\iota )\), \(I_b(\iota )\), \(R_b(\iota )\), \(S_h(\iota )\), \(I_h(\iota )\), and \(R_h(\iota )\) are nonnegative bounded functions, so that

$$\begin{aligned} \Vert S_b\Vert _{\infty } \le \texttt{K}_{S_b}, \Vert I_b\Vert _{\infty } \le \texttt{K}_{I_b}, \Vert R_b\Vert _{\infty } \le \texttt{K}_{R_b}, \Vert S_h\Vert _{\infty } \le \texttt{K}_{S_h}, \Vert I_h\Vert _{\infty } \le \texttt{K}_{I_h}, \Vert R_h\Vert _{\infty } \le \texttt{K}_{R_h}, \end{aligned}$$

where \(\texttt{K}_{S_b}\), \(\texttt{K}_{I_b}\), \(\texttt{K}_{R_b}\), \(\texttt{K}_{S_h}\), \(\texttt{K}_{I_h}\), \(\texttt{K}_{R_h}\) are some positive constants. Denote

$$\begin{aligned} \begin{aligned}&\gamma _{1} = r + \varsigma _b + H_s(t) + H_f(t), \\&\gamma _{2} = \varsigma _b + \texttt{S}_b + H_s(t) + H_f(t), \\&\gamma _{3} = \texttt{S}_b + H_f(t), \\&\gamma _{4} = \varsigma _h + H_i(t), \\&\gamma _{5} = \varsigma _h + \texttt{S}_h + H_i(t), \\&\gamma _{6} = \texttt{S}_h. \end{aligned} \end{aligned}$$

Theorem 2

(50) Suppose that \(G^{*}\) is satisfied, and assume the following inequality:

$$\begin{aligned} 0 \le M = \max \{\gamma _{1}, \gamma _{2}, \gamma _{3}, \gamma _{4}, \gamma _{5}, \gamma _{6}\} < 1, \end{aligned}$$

The kernels \(\mathscr {F}_1\), \(\mathscr {F}_2\), \(\mathscr {F}_3\), \(\mathscr {F}_4\), \(\mathscr {F}_5\), and \(\mathscr {F}_6\) satisfy the Lipschitz condition.

Proof

The kernel \(\mathscr {F}_1\) is considered. If we take \(\texttt{S}_b\) and \(\texttt{S}_{b1}\) as two functions, we get:

$$\begin{aligned} \begin{aligned} \Vert \mathscr {F}_1(t, \texttt{S}_b) - \mathscr {F}_1(t, \texttt{S}_{b1})\Vert&= \Vert (r + \varsigma _b + H_s(t) + H_f(t)) (\texttt{S}_b(t) - \texttt{S}_{b1}(t))\Vert \\&\le (r + \varsigma _b + H_s(t) + H_f(t)) \Vert \texttt{S}_b(t) - \texttt{S}_{b1}(t)\Vert \\&= \gamma _{1} \Vert \texttt{S}_b(t) - \texttt{S}_{b1}(t)\Vert . \end{aligned} \end{aligned}$$
(6)

Similar results hold for the kernels \(\mathscr {F}_2\), \(\mathscr {F}_3\), \(\mathscr {F}_4\), \(\mathscr {F}_5\), and \(\mathscr {F}_6\) using \(\{\texttt{I}_b, \texttt{I}_{b1}\}\) and \(\{\texttt{R}_b, \texttt{R}_{b1}\}\), \(\{\texttt{S}_h, \texttt{S}_{h1}\}\), \(\{\texttt{I}_h, \texttt{I}_{h1}\}\), \(\{\texttt{R}_h, \texttt{R}_{h1}\}\) respectively:

$$\begin{aligned} \begin{aligned}&\Vert \mathscr {F}_2(t, \texttt{I}_b) - \mathscr {F}_2(t, \texttt{I}_{b1})\Vert \le \gamma _{2} \Vert \texttt{I}_b(t) - \texttt{I}_{b1}(t)\Vert , \\&\Vert \mathscr {F}_3(t, \texttt{R}_b) - \mathscr {F}_3(t, \texttt{R}_{b1})\Vert \le \gamma _{3} \Vert \texttt{R}_b(t) - \texttt{R}_{b1}(t)\Vert ,\\&\Vert \mathscr {F}_4(t, \texttt{S}_h) - \mathscr {F}_4(t, \texttt{S}_{h1})\Vert \le \gamma _{4} \Vert \texttt{S}_h(t) - \texttt{S}_{h1}(t)\Vert ,\\&\Vert \mathscr {F}_5(t, \texttt{I}_h) - \mathscr {F}_5(t, \texttt{I}_{h1})\Vert \le \gamma _{5} \Vert \texttt{I}_h(t) - \texttt{I}_{h1}(t)\Vert , \\&\Vert \mathscr {F}_6(t, \texttt{R}_h) - \mathscr {F}_6(t, \texttt{R}_{h1})\Vert \le \gamma _{6} \Vert \texttt{R}_h(t) - \texttt{R}_{h1}(t)\Vert , \end{aligned} \end{aligned}$$

Thus, the Lipschitz conditions are satisfied for \(\mathscr {F}_1\), \(\mathscr {F}_2\), \(\mathscr {F}_3\), \(\mathscr {F}_4\), \(\mathscr {F}_5\), and \(\mathscr {F}_3\). Since \(0 \le M = \max \{\gamma _{1}, \gamma _{2}, \gamma _{3}, \gamma _{4}, \gamma _{5}, \gamma _{6}\} < 1\), the kernels are contractions. Due to the Banach fixed-point theorem, the solution of system (3) is unique. \(\square \)

Hyers-Ulam stability

This section aims to establish some results regarding Hyers-Ulam type stability.

Definition 2

(51,52) Model (3) is Hyers-Ulam stable if there exists a constant \(C_{\mathscr {G}} > 0\) with the following property: for each \(\varepsilon > 0\) and every solution \(U^{*} \in W\) satisfying the inequality

$$\begin{aligned} \left\| _{a}^{\mathcal{A}\mathcal{B}} \mathscr {D}_{0,t}^{\beta } U^{*}(t) - \mathscr {G}\left( t, U^{*}(t)\right) \right\| \le \varepsilon , t \in J, \end{aligned}$$

there exists a unique solution \(U \in W\) of Hyers-Ulam with initial condition \(U(0) = U^{*}(0)\) such that

$$\begin{aligned} \left\| U^{*}(t) - U(t)\right\| \le C_{\mathscr {G}} \varepsilon , \text {for all } t \in J, \end{aligned}$$

where

$$\begin{aligned} U^{*}(t) := \begin{pmatrix} \texttt{S}_b(t) \\ \texttt{I}_b(t) \\ \texttt{R}_b(t)\\ \texttt{S}_h(t) \\ \texttt{I}_h(t) \\ \texttt{R}_h(t) \end{pmatrix}, U^{*}(0) := \begin{pmatrix} \texttt{S}_b(0) \\ \texttt{I}_b(0) \\ \texttt{R}_b(0)\\ \texttt{S}_h(0) \\ \texttt{I}_h(0) \\ \texttt{R}_h(0) \end{pmatrix}, \text { and } \mathscr {G}\left( t, U^{*}(t)\right) := \begin{pmatrix} \mathscr {F}_1(t, \texttt{S}_b) \\ \mathscr {F}_2(t, \texttt{I}_b) \\ \mathscr {F}_3(t, \texttt{R}_b)\\ \mathscr {F}_4(t, \texttt{S}_h) \\ \mathscr {F}_5(t, \texttt{I}_h) \\ \mathscr {F}_6(t, \texttt{R}_h) \end{pmatrix}. \end{aligned}$$

Furthermore,

$$\begin{aligned} \varepsilon = \max \begin{pmatrix} \varepsilon _{1} \\ \varepsilon _{2} \\ \varepsilon _{3}\\ \varepsilon _{4} \\ \varepsilon _{5} \\ \varepsilon _{6} \end{pmatrix}, C_{\mathscr {G}} := \max \begin{pmatrix} C_{\mathscr {G}_{1}} \\ C_{\mathscr {G}_{2}} \\ C_{\mathscr {G}_{3}}\\ C_{\mathscr {G}_{4}} \\ C_{\mathscr {G}_{5}} \\ C_{\mathscr {G}_{6}} \end{pmatrix}. \end{aligned}$$

This \(C_{\mathscr {G}}\) is referred to as a Hyers-Ulam stability constant.

Definition 3

Whenever there is a continuous function \(\Pi _{\mathscr {G}}: J \rightarrow \mathbb {R}_{+}\) that solves the fractional problem Hyers-Ulam, it is said to be Hyers-Ulam stable. There exists a unique solution \(U^{*} \in W\) of Hyers-Ulam, satisfying

$$\begin{aligned} \left\| U^{*}(t) - U(t)\right\| \le \Pi _{\mathscr {G}}(\varepsilon ), \text {for all } t \in J. \end{aligned}$$

Remark 1

Considering the stability of the model, we take into account a small perturbation \(\Phi (t) \in C(J)\) such that \(\Phi (0) = 0\) and the following properties are satisfied:

  1. (i)

    \(|\Phi (t)| \le \varepsilon\) for \(t \in J\) and \(\varepsilon > 0\);

  2. (ii)

    \(_{0}^{\mathcal{A}\mathcal{B}} \mathscr {D}_{0,t}^{\beta } U^{*}(t) = \mathscr {G}\left( t, U^{*}(t)\right) + \Phi (t)\), for all \(t \in J\), where \(\Phi (t) = \begin{pmatrix} \Phi _{1}(t) \\ \Phi _{2}(t) \\ \Phi _{3}(t)\\ \Phi _{4}(t) \\ \Phi _{5}(t) \\ \Phi _{6}(t) \end{pmatrix}\).

Lemma 1

The solution \(U_{\Phi }^{*}(t)\) of the perturbed problem

$$\begin{aligned} \left\{ \begin{array}{l} _{a}^{\mathcal{A}\mathcal{B}} \mathscr {D}_{0,t}^{\beta } U^{*}(t) = \mathscr {G}\left( t, U^{*}(t)\right) + \Phi (t), t \in J, \\ U^{*}(0) = U_{0}^{*}, \end{array} \right. \end{aligned}$$

satisfies the inequality

$$\begin{aligned} \left| U_{\Phi }^{*}(t) - U^{*}(t)\right| \le \beta \varepsilon , \end{aligned}$$
(7)

where \(\beta := \left[ \frac{1-\beta }{\texttt{B}(\beta )} + \frac{T^{\beta }}{\texttt{B}(\beta ) \Gamma (\beta )}\right]\).

Proof

We have

$$\begin{aligned} U^{*}(t) = U_{0}^{*} + \frac{1-\beta }{\texttt{B}(\beta )} \mathscr {G}\left( t, U^{*}(t)\right) + \frac{\beta }{\texttt{B}(\beta ) \Gamma (\beta )} \int _{0}^{t}(t-s)^{\beta -1} \mathscr {G}\left( s, U^{*}(s)\right) ds. \end{aligned}$$

It follows from Remark 1 that

$$\begin{aligned} \left| U_{\Phi }^{*}(t) - U^{*}(t)\right|&\le \frac{1-\beta }{\texttt{B}(\beta )}|\Phi (t)| + \frac{\beta }{\texttt{B}(\beta ) \Gamma (\beta )} \int _{0}^{t}(t-s)^{\beta -1}|\Phi (s)| ds \\&\le \left[ \frac{1-\beta }{\texttt{B}(\beta )} + \frac{T^{\beta }}{\texttt{B}(\beta ) \Gamma (\beta )}\right] \varepsilon . \end{aligned}$$

Thus,

$$\begin{aligned} \left| U_{\Phi }^{*}(t) - U^{*}(t)\right| \le \beta \varepsilon . \end{aligned}$$

\(\square \)

Theorem 3

The AB fractional model Hyers-Ulam is Hyers-Ulam stable in W under Lemma 1if

$$\begin{aligned} 1 - \beta L_{\mathscr {G}} > 0. \end{aligned}$$

Consequently, the AB fractional model Hyers-Ulam is both Hyers-Ulam and generalized Hyers-Ulam stable in W.

Proof

Suppose \(U^{*} \in W\) satisfies the inequality (7), and \(U^{*}\) is the unique solution of problem Hyers-Ulam with the initial condition \(U(0) = U^{*}(0) \Longleftrightarrow U_{0} = U_{0}^{*}\). Then, by Lemma 1, we have

$$\begin{aligned} U(t) = U_{0}^{*} + \frac{1-\beta }{\texttt{B}(\beta )} \mathscr {G}(t, U(t)) + \frac{\beta }{\texttt{B}(\beta ) \Gamma (\beta )} \int _{0}^{t}(t-s)^{\beta -1} \mathscr {G}(s, U(s)) ds. \end{aligned}$$

Thus,

$$\begin{aligned} \left| U_{\Phi }^{*}(t) - U^{*}(t)\right| \le \beta \varepsilon . \end{aligned}$$

\(\square \)

Euler method involving Atangana-Baleanu operator

Using the fractional Euler method with the Atangana-Baleanu operator, we solve the model (3). By applying the fractional integral operator (3) to Eq. (3), we obtain:

$$\begin{aligned} \begin{aligned} \texttt{z}(t)=\texttt{z}_{0}+ _{0} I_{t}^{\rho _{1}} g(\texttt{z}(t)), \quad 0<t<b<\infty , \end{aligned} \end{aligned}$$
(8)

\(_{0} I_{t}^{\rho _{1}}\) indicates the integral operator corresponding to the fractional derivatives of \(\texttt{AB}\). The numerical scheme is designed based on a uniform grid on [0, b] with time steps of \(h=\frac{b-0}{N}\). We will use \(\texttt{z}_{k}\) to approximate \(\texttt{z}(t)\) at \(t=t_{k}\), where \(t_{k}=0+kh\) and \(k=0,1 \ldots , N\). By discretizing Eq. (8) using the Euler method53, we determine the following formulas for \(\texttt{AB}\).

$$\begin{aligned} \psi _{k+1}&=\psi _{0}+\frac{1-\beta }{\texttt{B}(\beta )} g\left( \psi _{k+1}\right) +\frac{h^{\beta }}{\texttt{B}(\beta ) \Gamma (\beta )} \sum _{i=0}^{k} \ell _{k+1, i} g\left( \psi _{i}\right) , k=0, \ldots , N-1, \end{aligned}$$
(9)

where \(\ell _{k+1, j}=(k+1-i)^{\beta }-(k-j)^{\beta }, j=0, \ldots , k\). According to Eq. (9), the discrete form of Eq. (3) is

$$\begin{aligned} \begin{aligned} \texttt{S}_{b, n+1}&=\texttt{S}_{b0}+\frac{1-\beta }{\texttt{B}(\beta )} [r \texttt{S}_{b, k+1} \Big ( 1 - \frac{\texttt{S}_{b, k+1} + \texttt{I}_{b, k+1} + \texttt{R}_{b, k+1}}{K} \Big ) - \beta _b \texttt{I}_{b, k+1} \texttt{I}_{b, k+1} - H_s(t) \texttt{S}_{b, k+1} - H_f(t) \texttt{S}_{b, k+1}]\\ &+\frac{h^{\beta }}{\texttt{B}(\beta ) \Gamma (\beta )}\sum _{j=0}^n\, \ell _{k+1, j}[r \texttt{S}_{b, j} \Big ( 1 - \frac{\texttt{S}_{b, j} + \texttt{I}_{b, j} + \texttt{R}_{b, j}}{K} \Big ) - \beta _b \texttt{I}_{b, j} \texttt{I}_{b, j} - H_s(t) \texttt{S}_{b, j} - H_f(t) \texttt{S}_{b, j}],\\ \texttt{I}_{b, n+1}&=\texttt{I}_{b0}+\frac{1-\beta }{\texttt{B}(\beta )} \left[ \beta _b \texttt{S}_{b, k+1} \texttt{I}_{b, k+1} - \texttt{S}_b \texttt{I}_{b, k+1} - H_s(t) \texttt{I}_{b, k+1} - H_f(t) \texttt{I}_{b, k+1}\right] \\ &+\frac{h^{\beta }}{\texttt{B}(\beta ) \Gamma (\beta )}\sum _{j=0}^n\, \ell _{k+1, j}\left[ \beta _b \texttt{S}_{b, j} \texttt{I}_{b, j} - \texttt{S}_b \texttt{I}_{b, j} - H_s(t) \texttt{I}_{b, j} - H_f(t) \texttt{I}_{b, j}\right] ,\\ \texttt{R}_{b, n+1}&=\texttt{R}_{b0}+\frac{1-\beta }{\texttt{B}(\beta )} \left[ \texttt{S}_b \texttt{I}_{b, k+1} - H_f(t) \texttt{R}_{b,k+1}\right] +\frac{h^{\beta }}{\texttt{B}(\beta ) \Gamma (\beta )}\sum _{j=0}^n\, \ell _{k+1,j}\left[ \texttt{S}_b \texttt{I}_{b, j} - H_f(t) \texttt{R}_{b, j}\right] ,\\ \texttt{S}_{h, n+1}&=\texttt{S}_{h0}+\frac{1-\beta }{\texttt{B}(\beta )} [-\beta _h \texttt{S}_{h, k+1} \texttt{I}_{b, k+1} - H_i(t) \texttt{S}_{h, k+1}]+\frac{h^{\beta }}{\texttt{B}(\beta ) \Gamma (\beta )}\sum _{j=0}^n\, \ell _{k+1, j}[-\beta _h \texttt{S}_{h, j} \texttt{I}_{b, j} - H_i(t) \texttt{S}_{h, j}],\\ \texttt{I}_{h, n+1}&=\texttt{I}_{h0}+\frac{1-\beta }{\texttt{B}(\beta )} \left[ \beta _h \texttt{S}_{h, k+1} \texttt{I}_{b, k+1} - \texttt{S}_h \texttt{I}_{h, k+1} - H_i(t) \texttt{I}_{h, k+1}\right] \\ &+\frac{h^{\beta }}{\texttt{B}(\beta ) \Gamma (\beta )}\sum _{j=0}^n\, \ell _{k+1, j}\left[ \beta _h \texttt{S}_{h, j} \texttt{I}_{b, j} - \texttt{S}_h \texttt{I}_{h, j} - H_i(t) \texttt{I}_{h, j}\right] ,\\ \texttt{R}_{h, n+1}&=\texttt{R}_{h0}+\frac{1-\beta }{\texttt{B}(\beta )} \left[ \texttt{S}_h \texttt{I}_{h, k+1}\right] +\frac{h^{\beta }}{\texttt{B}(\beta ) \Gamma (\beta )}\sum _{j=0}^n\, \ell _{k+1,j}\left[ \texttt{S}_h \texttt{I}_{h, j}\right] . \end{aligned} \end{aligned}$$

Numerical simulation

In order to support analytical results and evaluate the effectiveness of the control strategy, a numerical model (3) is proposed for different orders using the fractional Euler method with the Atangana-Baleanu scheme. Using Matlab, we constructed an algorithm to simulate the results. The numerical results have been presented for the initial 10 months \(\approx 300\) days. Data from the Ministry of Environment, Agriculture, and Water in Al-Baha have been incorporated into the analysis of Zoonotic Disease Transmission Between Baboons and Humans. The following table provides a summary of the parameter values and their respective sources with initial values \(\texttt{S}_{b}(0)= 5000\), \(\texttt{I}_{b}(0)\) = 150, \(\texttt{R}_{b}(0)\)=50, \(\texttt{S}_{h}(0)\)=8000, \(\texttt{I}_{h}(0)\) = 100, \(\texttt{R}_{h}(0)\) = 100:

Table 1 The values of parameters and initial populations used in the baboon-human model54.
Full size table

Disease-Free Equilibrium: Characterized by the absence of infections (\(I_b = I_h = 0\)). Populations remain constant in the susceptible and recovered compartments without new infections. Endemic Equilibrium: Characterized by persistent infections (\(I_b > 0\) and/or \(I_h > 0\)), where the disease stabilizes at a non-zero level in the populations. The trends in Fig. 1 suggest a shift toward the Endemic Equilibrium as the fractional orders decrease. This behavior reflects the persistence of infections in both populations due to memory effects and delayed recovery dynamics introduced by the fractional-order model. Figure 1 illustrates the dynamics of zoonotic disease transmission between baboons and humans as modeled by the Caputo fractional system. Each subplot in Fig. 1 corresponds to a specific population compartment: (a) Susceptible baboon population (\(S_b\)) over time. (b) Infected baboon population (\(I_b\)) over time. (c) Recovered baboon population (\(R_b\)) over time. (d) Susceptible human population (\(S_h\)) over time. (e) Infected human population (\(I_h\)) over time. (f) Recovered human population (\(R_h\)) over time. The plots showcase how the population dynamics evolve under different fractional orders \(\alpha\): \(1.0\), \(0.98\), \(0.90\), \(0.85\), and \(0.80\). These fractional orders represent the system’s memory effects, where smaller values indicate greater influence of past states. Figure 2 illustrates the transmission dynamics of zoonotic diseases between baboons and humans as modeled by the Caputo fractal-fractional system. Each subplot shows the population dynamics for different compartments under varying fractional orders \(\alpha : 1.0, 0.95, 0.90\), and \(0.85\). The following population compartments are represented: Susceptible baboons (\(S_b\)), Infected baboons (\(I_b\)), Recovered baboons (\(R_b\)), Susceptible humans (\(S_h\)), Infected humans (\(I_h\)), Recovered humans (\(R_h\)). The dynamics in each subplot reveal the interactions between the different populations over time, as influenced by the fractional order of the model. As the fractional order decreases (from \(1.0\) to \(0.85\)), the system demonstrates prolonged memory effects, leading to slower decay of infections and increased persistence of the disease in both baboon and human populations. For higher fractional orders (\(\alpha \approx 1.0\)), the system approaches the Disease-Free Equilibrium, with infections eventually vanishing. For lower fractional orders (\(\alpha = \le 0.90\)), the system exhibits characteristics of the Endemic Equilibrium, where infections persist over time in both populations. The results suggest that fractional-order dynamics are critical in understanding how past interactions influence current disease trends, particularly in zoonotic contexts.

Fig. 1
figure 1

Transmission dynamics of zoonotic diseases between baboons and humans in the Al-Baha region of system (3) illustrated in (a)-(f) for (\(\alpha\)): \(1.0\), \(0.98\), \(0.90\), \(0.85\), and \(0.80\).

Full size image
Fig. 2
figure 2

Transmission dynamics of zoonotic diseases between baboons and humans in the Al-Baha region of system (3) illustrated in (a)-(f) for (\(\alpha\)): \(1.0\), \(0.98\), \(0.90\), \(0.85\).

Full size image

Methodology section

The fractional Euler method with the Atangana-Baleanu (AB) operator is particularly well-suited for this zoonotic disease model compared to the Caputo or Riemann-Liouville derivatives due to the following reasons: Nonlocal and Non-Singular Kernel: The AB derivative incorporates the Mittag-Leffler (ML) function as its kernel, unlike Caputo and Riemann-Liouville, which use power-law kernels. This provides a more realistic representation of biological memory effects, essential for modeling infectious disease dynamics. Memory Effects and Spatial Heterogeneity: The model involves interactions between baboons and humans, where past infection states significantly influence future disease progression. The AB derivative better captures these long-term dependencies compared to Caputo, which assumes a weaker memory effect, and Riemann-Liouville, which lacks an initial value problem formulation. Numerical Stability and Accuracy: The fractional Euler method combined with AB derivatives ensures numerical stability while efficiently approximating solutions. The model employs Hyers-Ulam stability and the Banach fixed-point theorem to guarantee well-posedness, which is more challenging with Caputo and Riemann-Liouville operators. Extended Infection Persistence: The simulations show that lower fractional orders \((\alpha <1)\) lead to prolonged infections due to stronger memory effects, aligning well with real-world zoonotic disease transmission. Caputo derivatives may underestimate these effects, while Riemann-Liouville derivatives often require additional constraints for epidemiological models. Better Representation of Control Strategies: The AB-based model incorporates control measures like sterilization, food restriction, and reduced human-baboon interaction. The non-singular AB kernel allows these interventions to have a more gradual and cumulative impact, unlike Caputo derivatives, which might introduce abrupt changes due to weaker memory effects. Thus, the Atangana-Baleanu derivative offers a more flexible and realistic approach for modeling zoonotic disease transmission, making it a superior choice for this study.

Computational efficiency of variable-Order dynamics and Euler method with Atangana-Baleanu operator

The combination of variable-order dynamics and the Euler method involving the Atangana-Baleanu (AB) operator offers significant computational advantages over traditional multi-step schemes like the Adams-Bashforth-Moulton (ABM) method, especially in solving fractional differential equations (FDEs) for epidemiological modeling. In fractional-order models, the order of differentiation (\(\alpha\)) represents the strength of memory effects. The use of variable-order derivatives allows \(\alpha\) to change dynamically over time or based on state variables, adapting to different phases of disease transmission. Disease spread is not uniform over time; early-stage infections may exhibit different dynamics compared to later stages. A variable-order AB operator allows dynamic memory adjustments, unlike fixed-order Caputo or ABM schemes. Traditional fixed-order schemes require fine discretization to capture variations, increasing computational cost. Variable-order models achieve comparable accuracy with fewer points by adjusting the fractional order dynamically. Memory effects (e.g., lingering infections, delayed immunity) vary over time. A variable-order fractional model better captures these variations compared to constant-order schemes. The Euler-AB method with variable-order dynamics allows: Efficient modeling of zoonotic disease transmission with adaptive memory effects. Reduced computational burden compared to ABM by avoiding multi-step corrections. Better stability for long-term simulations, essential for studying disease persistence.

Banach fixed-point theorem

The Banach fixed-point theorem guarantees the existence and uniqueness of solutions under the condition that the underlying function is a contraction mapping. However, in the context of zoonotic disease modeling, the theorem has the following limitations:

  • It assumes a complete metric space, which may not always be the case for biological systems with stochastic influences.

  • The contraction condition may not hold for highly nonlinear disease dynamics, particularly in models with variable transmission rates or spatial heterogeneity.

  • The theorem does not account for external perturbations such as environmental factors that could affect disease transmission.

Picard iterative method

The Picard iterative method provides an approach to approximate solutions by successive iterations. While useful in deterministic settings, its limitations in zoonotic disease modeling include:

  • It requires an initial guess that is sufficiently close to the true solution for convergence, which may not always be feasible in complex epidemiological models.

  • Convergence may be slow or fail for models with strong nonlinearities or delayed effects inherent in zoonotic transmission.

  • It does not inherently handle stochastic fluctuations, which are crucial in real-world disease spread scenarios.

Epidemiological implications

The integration of variable-order dynamics and the Euler method with the Atangana-Baleanu operator significantly enhances the epidemiological modeling of zoonotic diseases. The key implications include:

  • Better Predictive Accuracy: Incorporating memory effects via fractional derivatives improves the accuracy of disease spread predictions compared to classical integer-order models.

  • Improved Control Strategy Design: The fractional approach provides a more nuanced understanding of intervention impacts, allowing for the optimization of measures like vaccination, sterilization, and habitat management.

  • Understanding Long-Term Disease Persistence: The ability to model memory-dependent transmission and recovery rates helps in assessing the risk of long-term endemic states versus eventual disease eradication.

  • Adaptability to Real-World Scenarios: The variable-order framework accommodates environmental changes and varying population behaviors, making it suitable for dynamic epidemiological conditions.

Discussion

The mathematical modeling of zoonotic disease transmission using fractional calculus provides deeper insights into the impact of memory effects and control strategies on disease dynamics. Our study employs the Atangana-Baleanu fractional derivative, which introduces a nonlocal and non-singular kernel, allowing for a more accurate representation of the interactions between baboon and human populations. The use of the fractional Euler method enhances the computational efficiency of the model while capturing the long-term effects of past infections. The numerical simulations reveal that the fractional-order model significantly influences disease persistence. Lower fractional orders \((\alpha <1)\) lead to extended infection durations due to the memory effect, which accounts for previous disease states and transmission history. This is particularly evident in the infected compartments, where the rate of decline in infections is slower compared to the classical integer-order model. Such behavior aligns with real-world zoonotic outbreaks, where disease transmission and recovery are influenced by factors such as environmental persistence of pathogens and immune response variations. The stability analysis confirms that the system remains dynamically stable under the fractional-order framework, with solutions bounded and biologically meaningful. Hyers-Ulam stability ensures the robustness of the model against small perturbations, making it a reliable tool for epidemiological forecasting. Moreover, the Banach fixed-point theorem and Picard iterative method validate the existence and uniqueness of solutions, reinforcing the theoretical foundation of the proposed model. Incorporating control strategies such as sterilization, restricted food access, and reduced human-baboon interactions demonstrates their potential in mitigating zoonotic disease transmission. The simulations suggest that a combination of these interventions is more effective than implementing a single control measure. Notably, sterilization of baboons helps regulate population growth, reducing the susceptible pool, while food access restriction minimizes congregation, lowering contact rates and transmission probabilities. Reduced human interaction further limits cross-species disease spillover. From a public health perspective, our findings underscore the importance of integrating fractional-order epidemiological models into decision-making processes. Traditional integer-order models may underestimate the impact of past infections, leading to inaccurate predictions. The fractional approach provides a more comprehensive framework, accounting for delayed recovery dynamics and long-term transmission effects. Policymakers and wildlife management authorities in the Al-Baha region can utilize this model to design and implement more effective zoonotic disease control strategies. Future work should explore the incorporation of stochastic elements into the fractional framework to account for random fluctuations in disease transmission. Additionally, incorporating real-time data on baboon movement patterns and human interactions could enhance model accuracy and predictive capabilities.

Conclusion

This study presents a novel fractional-order mathematical model for understanding zoonotic disease transmission between baboons and humans, incorporating the Atangana-Baleanu fractional derivative to account for memory effects and spatial heterogeneity. The fractional Euler method is employed to numerically solve the system, providing an efficient and accurate approach for capturing the complex dynamics of zoonotic infections. The results demonstrate that fractional-order models offer a more realistic depiction of disease spread, as lower fractional orders \((\alpha <1)\) lead to prolonged infection persistence due to historical dependence. This highlights the importance of memory effects in zoonotic disease modeling, particularly in regions where human-wildlife interactions contribute to recurring outbreaks. The stability analysis, supported by the Banach fixed-point theorem and Hyers-Ulam stability, confirms the reliability of the model, ensuring well-posedness and robustness in epidemiological predictions. The integration of control strategies-such as sterilization, food access restriction, and reduced human interaction-reveals their effectiveness in mitigating disease transmission. Numerical simulations indicate that a combination of these interventions significantly reduces infection levels, emphasizing the need for a multi-faceted approach to zoonotic disease management. These findings provide valuable insights for public health policymakers and wildlife conservationists in designing data-driven strategies to minimize the risks of zoonotic spillovers. In future research, the model can be extended to incorporate stochastic effects to account for environmental variability and unpredictable changes in disease transmission dynamics. Additionally, integrating real-world data on baboon movement, climate variations, and human interactions can further enhance the model’s predictive accuracy. By bridging mathematical modeling with practical epidemiological applications, this study contributes to the growing body of research on fractional-order disease models and their role in advancing public health interventions.