Introduction

The swift progress of contemporary industry and scientific apparatus has greatly amplified the needs for high-precision positioning systems, with applications in semiconductor manufacturing1,2,3, micromachining4,5,6,7, scientific instruments8,9,10,11,12,13,14, and biomedical device production. These applications demand systems that can achieve nanometer-scale accuracy and repeatability with rapid response to dynamic environments. Although traditional XY drive mechanisms are still widely adopted, they are avoided in large travel ranges, high-speed scanning, or high acceleration scenarios15. In this context, magnetic levitation (maglev) technology has been developed as a transformative solution that uses non-contact electromagnetic actuation to eliminate mechanical friction and backlash. Facilitating this leap in technological enhancement is the maglev system, which finds application in target tracking systems9,12, semiconductor fabrication16,17,18,19, precision material processing20,21, and biomedical device production22, making it the backbone of industrial automation22,23,24.

With the accelerating demand for multi-axis motion control, maglev planar motors have emerged as a revolutionary paradigm, enabling theoretically six-degree-of-freedom (6-DOF) in-plane motion via electromagnetic coupling. However, their full potential is limited by nonlinear electromagnetic interaction and also coupled dynamics that are inherent to multi-DOF systems15. Though the absence of mechanical constraints enables motion with zero friction, it magnifies the challenges of control (e.g. cross-axis decoupling and dynamic stabilization) as these characteristics represent an iterative blockade requiring more complex control schemes in order to translate the cycle-advancing geometric principles to the precision advantages promised in future generations of high-precision manufacturing and science.

One of the essential conditions to achieve accurate maglev control is to have an accurate wrench model, which encapsulates the forces and torques applied on the mover in its workspace. Multiple modeling techniques have emerged, each one striking a different trade-off between fidelity and computational efficiency. FTS-based approaches including finite element analysis (FEA) and surface charge models can precisely account for magnetic flux distribution and the end effects resulting from finite-sized magnet arrays. For example, Jansen et al.25 used a charge approach to model the edge effects of a Halbach magnet array, predicting forces with high accuracy. However, this is computationally expensive for real-time control and thus impractical for fast multi-axis motions. Methods such as parallel computing and lookup tables have been proposed to enhance the speed of these high-fidelity models26,27, but due to complexity or memory trade-offs, these methods are still quite restricted and will struggle with updating forces at kHz-level control frequencies.

But, for common maglev planar motor constructions, the adopted wrench models fall on analytical or harmonic-based models according to the requirements of real-time control. These approximated, analytical models represent the magnetic field with Fourier series or equivalent current distributions resulting in closed-form expressions for force/torque that can be efficiently computed. A harmonic model for a herringbone coil array, for example, is shown to match FEA results closely while providing a marked decrease in computation time25. Existing analytical models have also been adapted for situations with restricted rotational motion of the mover. Liu et al. by exploiting the rotational symmetry of circular coils28, established a planar motor model that encompasses yaw (rotation about the vertical axis). Similarly, Xu et al.29 developed a wrench model for a maglev positioning stage with 4 linear actuators that considers yaw angle in the force and torque equation. The infusion of this extra DOF increased multi-axis decoupling and control performance in these models. Van Lierop et al. A 5-DOF harmonic model (three translations plus two tilts) was introduced for a planar actuator, capturing the effect of small tilting motions with first order field harmonics30.

Harmonic-based models with added rotations are computationally efficient and beneficial for control, but they are not general as they are based on simplifying assumptions that limit their accuracy. In particular, the use of a single magnetic field and neglecting the magnet array finite-size edge effects lead to modeling errors for complex coil geometries. For example, the models by Liu et al.28, and Xu et al.29 included yaw but were forced to use a simplified coil shape, and therefore had to neglect edge field end effects, which can reduce accuracy in predicting the force and lead to less efficient usage of current. In addition, these models covered only single rotational DOF (yaw) or kept all rotations small. This gap leaves us unable to fully describe the wrench applied at the system level by the mover in the case of more complex rotations or larger-angle changes of orientation.

To achieve better modeling accuracy without compromising real-time feasibility, unified wrench models (UWM) were proposed to avoid coil simplifications. Zhu et al.31 proposed the UWM approach that expresses the wrench as a product of a pre-computed coefficient matrix and position-dependent functions that can be evaluated analytically for arbitrary coil configurations in real time. This approach obtains the high-fidelity and computational efficient simulations by integrating detailed flux distributions (end effects included) with relatively little number crunching. Building on this, Yuan et al. A magnet edge effects included extended UWM (EUWM) was proposed by32, claiming more compact push force as the mover approaches the edge of array. The UWM/EUWM formulations yield a sufficiently faster and more accurate representation of planar motor systems. Nevertheless, one critical limitation persisted: the formulation only describes the mover’s translations (X–Y travel and Z levitation) and omits rotations. And, in a similar vein, a closed-form relationship between rotational displacements (roll, pitch, yaw) and the wrench was not represented, since a planar motor’s mover was assumed to ideally remain level. The primary reason for such rigid assumptions is that due to small angular-angles or vibrations during motion, rotational effects cannot be neglected, in practice, making their omission introduce modeling errors consequently degrades control behavior. Recognizing this, Hu et al.33 developed analytical formulations for the six-degree-of-freedom (6-DOF) motion coordinates with respect to the generated wrench (i.e., force/torque vectors in three-dimensional magnitude and directional domains) for EUWM. Their approach maintains the unified modeling domain structure and single end-effector accuracy while extending the equivalent UWM concept into full 6-DOF space. This will give us a significant step toward the realistically 6-DOF controllability of maglev planar motors.

Despite these advances, existing 6-DOF models mainly focus on small-angle rotations and do not adequately handle cases-induced from large rotational maneuvers. Some applications require that the mover undergo significant rotations (e.g., a large yaw rotation) as part of its function. Dealing with these large-angle rotations in the control algorithm creates new challenges for such a method: the nonlinearity of the system becomes more and more prominent, and any model that is linearized about zero rotation will diminish in efficacy with increasing angles. Therefore, a modeling approach is still needed that not only covers full 6-DOF motion, but also holds true and is time efficient with respect to situations where a mover experiences large-angle rotations about one or more axes.

This paper presents a novel dynamic modeling and control framework for maglev planar motors capable of full 6-DOF control with large-angle (in particular, yaw angle φ) rotation. The developed method integrates the computational efficiency of harmonic based analytical models with the high-fidelity extended 6-DOF wrench model to attain a real-time capable whilst also accurate representation of the motor’s dynamics. An important novelty in our approach is that we include large-angle rotation modeling in the wrench computation. This is done through a Taylor series expansion of the rotational magnetic flux about select operating points throughout the trajectory of the mover, generating a linearized representation of the magnetic flux that is valid for a large span of orientations. This extended flux model is converted to an analytic wrench expression via Lorentz’s law, yielding closed-form equations (after suitable coordinate transformations and decoupling) that couple the motor to its complete 6-DOF. Unlike prior models that deal with the infinitesimal angle assumption, our formulation is capable of incorporating substantial yaw rotations in the motion plan while maintaining high accuracy. This ensures that the controller encodes the desired large-angle rotation already from the beginning of planning, instead of allowing it to be treated as just a perturbation. After the model is fitted with the reference trajectory, the trajectory segment with a big rotation angle will be locally linearized to calculate the magnetic flux, which ensures that the model is accurate and the control is robust when the trajectory changes during the trajectory. The resulting framework incorporates a fuller planar motor model and control scheme, being able to reproduce all relevant DOFs (and their cross couplings) while remaining computationally light enough for real-time implementation.

The rest of the paper is organized as follows: The design and modeling of the moving-magnet planar actuator are discussed in Section "Design and modeling of the moving-magnet planar actuator", which covers the theoretical background and the derivation of the dynamic equations according to Lorentz’s law. The NMPC-based nonlinear model predictive control (NMPC) trajectory tracking control strategy is presented in Section "Numerical verification experiments", including discussion on the global optimality of 6-DOF motion. Section "Motion control experiments" presents the description of the motion control experiments, including the experimental setup, the validation of the theoretical model, and the system performance evaluation under some operating conditions. Finally, Section "Conclusion" concludes the paper and reviews possible future research directions.

Design and modeling of the moving-magnet planar actuator

The moving-magnet planar actuator is engineered with a permanent magnet array and a coreless coil framework. It features a cubic magnet and dual 1-D coil arrays. The magnet configuration employs a 2D Halbach array to enhance magnetic flux density near the coil. This architecture allows the actuator to convert x-directional coil activity into y-directional propulsion, which optimizes force generation along a specified trajectory.

The force of the translator is derived using the Lorentz force equation, which is made possible by the coreless coil design. Computing the torque of the translator requires an analysis of the force distribution within the coil. These forces are theoretically represented as acting on the coil itself. Consequently, a “force arm” is defined as the distance from the center of mass of the translator to the spatial extent of the coil. This parameter is crucial for the functional effectiveness of the actuator.

In contrast, the force arm in a moving-coil planar actuator is independent of the position of the translator, as the coils are located on the moving part of the actuator.

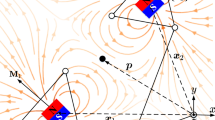
To assist in simulating actuator dynamics, a dual-reference frame approach is adopted, as shown in Fig. 1. A global coordinate system (GCS) is established at the center of the coil array of the stator, with the spatial orientation of the translator represented by the vector \({}^{c}\overrightarrow{d} = {[{}{}^{c}x {}{}^{c}y {}{}^{c}z]}^{T}\). Additionally, a local coordinate system (LCS) is established at the centroid of the translator, with the position of the magnet represented by the vector \({}^{m}\overrightarrow{d} = {[{}{}^{m}x {}{}^{m}y {}{}^{m}z]}^{T}\). The vector \({}^{c}\overrightarrow{p}={ [{}{}^{c}{p}_{x} {}{}^{c}{p}_{y} {}{}^{c}{p}_{z}]}^{T}\) describes the position of the local coordinate system relative to the global coordinate system, which includes the centroid of the translator. Transitioning coordinates between these systems requires an initial directional transformation followed by a translational adjustment, which enables accurate representation and manipulation of the spatial dynamics of the actuator.1

Fig. 1
figure 1

Schematics of the construction of the actuator for moving-magnet planar actuators with 2D Halbach permanent magnets: (a) side view, (b) top view, (c) side view, and (d) stator (coils).

Full size image
$${}^{m}\overrightarrow{d}={{}_{}^{\mathbf{m}}\mathbf{R}}_{\mathbf{c}}\left({}{}^{c}\overrightarrow{d}-{}{}^{c}\overrightarrow{p}\right)$$
(1)
$$\begin{aligned}{{}^{\mathbf{m}}\mathbf{R}}_{\mathbf{c}}&={{{}_{}^{\mathbf{c}}\mathbf{R}}_{\mathbf{m}}}^{{\varvec{T}}}={\left(\text{Rot}\left(\psi \right)\text{Rot}\left(\theta \right)\text{Rot}\left(\phi \right)\right)}^{T}\\ &={\text{Rot}\left(\phi \right)}^{T}{\text{Rot}\left(\theta \right)}^{T}{\text{Rot}\left(\psi \right)}^{T}\end{aligned}$$
(2)

where

$$Rot\left(\psi \right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& \text{cos}\left(\psi \right)& -\text{sin}\left(\psi \right)\\ 0& \text{sin}\left(\psi \right)& \text{cos}\left(\psi \right)\end{array}\right]$$
(3)
$$Rot\left(\theta \right)=\left[\begin{array}{ccc}\text{cos}\left(\theta \right)& 0& \text{sin}\left(\theta \right)\\ 0& 1& 0\\ -\text{sin}\left(\theta \right)& 0& \text{cos}\left(\theta \right)\end{array}\right]$$
(4)
$$Rot\left(\phi \right)=\left[\begin{array}{ccc}\text{cos}\left(\phi \right)& -\text{sin}\left(\phi \right)& 0\\ \text{sin}\left(\phi \right)& \text{cos}\left(\phi \right)& 0\\ 0& 0& 1\end{array}\right]$$
(5)

Within this framework, \(\psi ,\theta ,\text{ and }\phi\) represent the rotations about the \({}^{c}x- ,{}{}^{c}y -,\text{ and }{}{}^{c}z-\text{axes}\), respectively. All rotations are defined relative to the reference frame. Consequently, the position of the armature can be described using a 6-DOF model.

Magnetic field calculation model

In this section, we analyze the actuating forces produced by the magnet array in detail. We use a harmonic model to examine the distribution of the magnetic field from the magnets, as described by the equations below25. This method models the magnetic field in three dimensions using a double Fourier series and is particularly well-suited for predicting motor performance. The model accounts for the complex variations in the magnetic field owing to the geometry of the motor and the distribution of magnetic materials. The Fourier series approach provides an analytical solution that can be computed much more rapidly than numerical methods such as finite element analysis. The Fourier series approach is thus advantageous for the quick evaluation and optimization of motor designs.

$$\begin{aligned} ^{m} \vec{B}\left( {^{m} \vec{d}} \right) & = \sum\limits_{{k = 1}}^{\infty } {\mathop \sum \limits_{{l = 1}}^{\infty } } \\ & \quad- \mu _{0} Ke^{{\lambda ^{m} z}} \left[ {\begin{array}{*{20}c} {\omega _{k} cos(\omega _{k} ^{m} x)sin\left( {\omega _{l} ^{m} y} \right)} \\ {\omega _{l} sin(\omega _{k} ^{m} x)cos\left( {\omega _{l} ^{m} y} \right)} \\ {\lambda {\text{sin}}(\omega _{k} ^{m} x){\text{sin}}\left( {\omega _{l} ^{m} y} \right)} \\ \end{array} } \right] \\ \end{aligned}$$
(6)
$$\begin{aligned} K & = B_{r} \left( {e^{{ - m_{t} \lambda }} - e^{{ - m_{b} \lambda }} } \right) \\ & \quad\cdot \frac{{\left( {b_{k} b_{l} \pi \left( {k^{2} + l^{2} } \right) + a_{k} b_{l} k\lambda \left. {\tau + a_{l} b_{k} l\lambda \tau } \right)} \right.}}{{2\left( {k^{2} + l^{2} } \right)\pi \lambda \mu _{0} }} \\ \end{aligned}$$
(7)
$$a(k) = \frac{4}{{k\pi }}\cos \left( {\frac{{k\tau _{m} \pi }}{{2\tau }}} \right)\sin \left( {\frac{{k\pi }}{2}} \right)$$
(8)
$$b(k) = \frac{4}{{k\pi }}\sin \left( {\frac{{k\tau _{m} \pi }}{{2\tau }}} \right)\sin \left( {\frac{{k\pi }}{2}} \right)$$
(9)
$$\lambda = \sqrt {\omega _{k} ^{2} + \omega _{l} ^{2} }$$
(10)

Here, \({\omega }_{k}=\frac{k\pi }{\tau }\) and \({\omega }_{l}=\frac{l\pi }{\tau }\) are the spatial angular frequencies in the \({}^{m}x\) and \({}^{m}y\) directions, respectively. \(e\) is Euler number, \({\tau }_{m}\) is the size of the magnet magnetized in the \({}^{m}x-\) direction, and \({m}_{b}\) and \({m}_{t}\) are respectively the \({}^{m}z-\) of the bottom and top of the magnet array. \(\tau\) represents the size of the pole pitch. According to coordinate transformation, the magnetic flux at the point \({}^{c}\overrightarrow{d} = ({}{}^{c}x, {}{}^{c}y, {}{}^{c}z)\) can be expressed as

$$^{c} \vec{B}\left( {^{c} \vec{d},^{c} \vec{p},\psi ,\theta ,\phi } \right) = _{{}}^{{\mathbf{c}}} {\mathbf{R}}_{{\mathbf{m}}} ^{m} \vec{B}\left( {_{{}}^{{\mathbf{m}}} {\mathbf{R}}_{{\mathbf{c}}} \left( {^{c} \vec{d} - ^{c} \vec{p}} \right)} \right)$$
(11)

Electromagnetic force calculation model

In maglev planar motors, trajectory tracking control is crucial, especially owing to the lack of physical contact between the mover and the stator. The reference trajectory for the mover is defined as \(p(t)= {[{x}_{d}(t),{y}_{d}(t),{z}_{d}(t),{\psi }_{d}(t),{\theta }_{d}(t),{\phi }_{d}(t)]}^{T}\). The operational requirements for height stability and planar motion in maglev planar motors necessitate constraining rotational angles \(\psi\) and θ to small magnitudes. This assumption is grounded in three operational realities: vertical levitation control inherently suppresses out-of-plane tilting, mechanical designs physically restrict rotations, and planar positioning systems primarily require yaw adjustments (\(\phi\)) rather than significant pitch/roll motions. Consequently, the desired trajectory is adjusted to \({[{x}_{d}(t),{y}_{d}(t),{z}_{d},\text{0,0},{\phi }_{d}(t)]}^{T}\). Through the expansion of the Taylor series, the magnetic flux can be expressed as

$$\begin{aligned} ^{c} \vec{B} & \approx \left. {^{c} \vec{B}} \right|_{{\psi = 0,\theta = 0,\phi = \phi _{d} }} + \psi \cdot \frac{{\partial ^{c} \vec{B}}}{{\partial \psi }}\bigg|_{{\psi = 0,\theta = 0,\phi = \phi _{d} }} \\ & \quad+ \theta \cdot \frac{{\partial ^{c} \vec{B}}}{{\partial \theta }}\bigg|_{{\psi = 0,\theta = 0,\phi = \phi _{d} }} + \left( {\phi - \phi _{d} } \right) \\ & \quad\cdot \frac{{\partial ^{c} \vec{B}}}{{\partial \phi }}\bigg|_{{\psi = 0,\theta = 0,\phi = \phi _{d} }} \\ \end{aligned}$$
(12)

The FEM is impractical for predicting forces and torques in planar motors owing to the large volume involved in energy conversion, which requires a dense mesh for accurate simulation. Therefore, analytical techniques are employed for the analysis and design of these motors. Considering that the forces in coreless planar motors depend solely on the interactions between the permanent magnet array and the current-carrying coils, the forces and torques applied to the magnets are calculated using the Lorentz force law.

$$\begin{array}{c}\overrightarrow{{\varvec{F}}}=-{\iiint }_{{V}_{coil}} \overrightarrow{{\varvec{J}}}\times {}{}^{c}\overrightarrow{B}dV\#\left(13\right)\end{array}$$
(13)
$$\begin{array}{c}\overrightarrow{{\varvec{T}}}=-{\iiint }_{{V}_{coil}} {}{}^{c}\overrightarrow{d}\times \overrightarrow{{\varvec{J}}}\times {}{}^{c}\overrightarrow{B}dV\#\left(14\right)\end{array}$$
(14)

Considering that the current at the bottom flows only in the x- or y-direction, the current density becomes \(\overrightarrow{{\varvec{J}}}={[{J}_{x},\text{0,0}]}^{{\varvec{T}}}\). According to Eqs. (12) and (13), the force acting on the coil element can be determined as.

$$\begin{aligned}{{}^{c}{\varvec{F}}}^{\left(k,l\right)}dv&=\overrightarrow{{\varvec{J}}}\times \left({\left.{}{}^{c}\overrightarrow{B}\right|}_{\psi =0,\theta =0,\phi ={\phi }_{d}}+\psi \cdot \frac{\partial {}{}^{c}\overrightarrow{B}}{\partial \psi }\bigg|_{\psi =0,\theta =0,\phi ={\phi }_{d}}\right. \\ &\left.+\theta \cdot \frac{\partial {}{}^{c}\overrightarrow{B}}{\partial \theta }\bigg|_{\psi =0,\theta =0,\phi ={\phi }_{d}}+\left(\phi -{\phi }_{d}\right)\cdot \frac{\partial {}{}^{c}\overrightarrow{B}}{\partial \phi }\bigg|_{\psi =0,\theta =0,\phi ={\phi }_{d}}\right)dv\end{aligned}$$
(15)

Equation (15) is decomposed into four terms involving cross-products. The first term addresses a specific reference trajectory scenario, while the subsequent three terms examine the impact of rotation on force and torque, with particular emphasis on significant rotations around the \(\phi\) axis. We analyze the influence of the second term, angle \(\psi\), on the modeling of force and torque. By applying Eq. (11), the chain rule, and partial derivatives of the magnetic field intensity concerning angular variations, we obtain the following:

$$\frac{\partial {}{}^{c}\overrightarrow{B}}{\partial \psi }\bigg|_{\psi =0,\theta =0,\phi ={\phi }_{d}}=\frac{\partial {{}_{}^{\mathbf{c}}\mathbf{R}}_{\mathbf{m}}{}{}^{m}\overrightarrow{B}\left({{}_{}^{\mathbf{m}}\mathbf{R}}_{\mathbf{c}}\left({}{}^{c}\overrightarrow{d}-{}{}^{c}\overrightarrow{p}\right)\right)}{\partial \psi }\bigg|_{\psi =0,\theta =0,\phi ={\phi }_{d}}$$
$$\begin{aligned} \frac{{\partial ^{c} \vec{B}}}{{\partial \psi }}\bigg|_{{\psi = 0,\theta = 0,\phi = \phi _{d} }} & = \frac{{\partial _{{}}^{{\mathbf{c}}} {\mathbf{R}}_{{\mathbf{m}}} ^{m} \vec{B}\left( {_{{}}^{{\mathbf{m}}} {\mathbf{R}}_{{\mathbf{c}}} \left( {^{c} \vec{d} - ^{c} \vec{p}} \right)} \right)}}{{\partial \psi }}\bigg|_{{\psi = 0,\theta = 0,\phi = \phi _{d} }} \\ & = \frac{{\partial _{{}}^{{\mathbf{c}}} {\mathbf{R}}_{{\mathbf{m}}} }}{{\partial \psi }}\bigg|_{{\psi = 0,\theta = 0,\phi = \phi _{d} }} \cdot ^{m} \vec{B}\left( {_{{}}^{{\mathbf{m}}} {\mathbf{R}}_{{\mathbf{c}}} \left( {^{c} \vec{d} - ^{c} \vec{p}} \right)} \right)\bigg|_{{\psi = 0,\theta = 0,\phi = \phi _{d} }} \\ & \quad+ _{{}}^{{\mathbf{c}}} {\mathbf{R}}_{{\mathbf{m}}} |_{{\psi = 0,\theta = 0,\phi = \phi _{d} }} \bullet \frac{{\partial ^{m} \vec{B}\left( {_{{}}^{{\mathbf{m}}} {\mathbf{R}}_{{\mathbf{c}}} \left( {^{c} \vec{d} - ^{c} \vec{p}} \right)} \right)}}{{\partial \psi }}\bigg|_{{\psi = 0,\theta = 0,\phi = \phi _{d} }} \\ \end{aligned}$$
(16)

The full derivation of Eq. (16), including the explicit forms of rotation matrices, is detailed in Appendix A. The force induced by the angle \(\psi\) can be determined from the current density \(\overrightarrow{{\varvec{J}}}={[{J}_{x},\text{0,0}]}^{{\varvec{T}}}\) and the cross-product of the second term in Eq. (12). The cross-product of the current density \(\overrightarrow{{\varvec{J}}}\) with the first term in Eq. (16) yields

$$\begin{aligned}{{}^{c}{\varvec{F}}}^{\left(k,l\right)}dv&={\mu }_{0}K{e}^{\lambda {}{}^{m}z}\\ &\quad\times \left[\begin{array}{c}0\\ {J}_{x}{\omega }_{k}\text{sin}\left({\phi }_{d}\right)\text{cos}\left({\omega }_{k}\left[\text{cos}\left({\phi }_{d}\right)\left({}{}^{c}x-{}{}^{c}{p}_{x}\right)+\text{sin}\left({\phi }_{d}\right)\left({}{}^{c}y-{}{}^{c}{p}_{y}\right)\right]\right)\\ \text{sin}\left({\omega }_{l}\left[\text{cos}\left({\phi }_{d}\right)\left({}{}^{c}y-{}{}^{c}{p}_{y}\right)-\text{sin}\left({\phi }_{d}\right)\left({}{}^{c}x-{}{}^{c}{p}_{x}\right)\right]\right)\\ +{J}_{x}{\omega }_{l}\text{cos}\left({\phi }_{d}\right)\text{sin}\left({\omega }_{k}\left[\text{cos}\left({\phi }_{d}\right)\left({}{}^{c}x-{}{}^{c}{p}_{x}\right)+\text{sin}\left({\phi }_{d}\right)\left({}{}^{c}y-{}{}^{c}{p}_{y}\right)\right]\right)\\ \text{cos}\left({\omega }_{l}\left[\text{cos}\left({\phi }_{d}\right)\left({}{}^{c}y-{}{}^{c}{p}_{y}\right)-\text{sin}\left({\phi }_{d}\right)\left({}{}^{c}x-{}{}^{c}{p}_{x}\right)\right]\right)\\ {J}_{x}\lambda \text{sin}\left({\omega }_{k}\left[\text{cos}\left({\phi }_{d}\right)\left({}{}^{c}x-{}{}^{c}{p}_{x}\right)+\text{sin}\left({\phi }_{d}\right)\left({}{}^{c}y-{}{}^{c}{p}_{y}\right)\right]\right)\\ \text{sin}\left({\omega }_{l}\left[\text{cos}\left({\phi }_{d}\right)\left({}{}^{c}y-{}{}^{c}{p}_{y}\right)-\text{sin}\left({\phi }_{d}\right)\left({}{}^{c}x-{}{}^{c}{p}_{x}\right)\right]\right)\end{array}\right]dv\end{aligned}$$
(17)

We define the product of trigonometric functions as the canonical trigonometric product term (CTPT). In CTPTs, integral parameters (such as \({}^{c}x\) and \({}^{c}y\)) are closely related to positional parameters (such as \({}^{c}{p}_{x}\) and \({}^{c}{p}_{y}\)), which complicates accurate torque analysis. Additionally, incorporating trajectories further exacerbates these issues. To address these challenges, we use advanced trigonometric operations to effectively decouple positional parameters within CTPTs, which greatly enhances the accuracy and feasibility of torque analysis. The step-by-step derivation of this formulation, along with the expansion of CTPT expressions, is presented in Appendix A. Similarly, the cross-product of \(\overrightarrow{{\varvec{J}}}\) and the second term of (16) can be obtained as

$$\begin{aligned}&\overrightarrow{{\varvec{J}}}\times \left({{}_{}^{\mathbf{c}}\mathbf{R}}_{\mathbf{m}}{|}_{\psi =0,\theta =0,\phi ={\phi }_{d}}\cdot \frac{\partial {}{}^{m}\overrightarrow{B}\left({{}_{}^{\mathbf{m}}\mathbf{R}}_{\mathbf{c}}\left({}{}^{c}\overrightarrow{d}-{}{}^{c}\overrightarrow{p}\right)\right)}{\partial \psi }\bigg|_{\psi =0,\theta =0,\phi ={\phi }_{d}}\right)dv=-{\mu }_{0}K{e}^{\lambda \left({z}_{c}-{}{}^{c}{p}_{z}\right)}\\ &\quad\times \left.\left[\begin{array}{c}0\\ -{J}_{x}{B\psi }_{z}\\ {J}_{x}{B\psi }_{y}cos\left({\phi }_{d}\right)-{J}_{x}{B\psi }_{x}\text{sin}\left({\phi }_{d}\right)\end{array}\right.\right]dv\end{aligned}$$
(18)

Owing to space constraints, the specific expressions for \({B\psi }_{x}\), ​\({B\psi }_{y}\), and \({B\psi }_{z}\) are omitted in this paper. These expressions are computed using the chain rule for differentiation. As an example, we derive the computational result from the third-row element of Eq. (22). The detailed derivation process is provided in the appendix.

$$\begin{aligned}&{J}_{x}\text{cos}\left({\phi }_{d}\right){\left(\frac{\partial {}{}^{m}\overrightarrow{B}\left({{}_{}^{\mathbf{m}}\mathbf{R}}_{\mathbf{c}}\left({}{}^{c}\overrightarrow{d}-{}{}^{c}\overrightarrow{p}\right)\right)}{\partial \psi }\bigg|_{\psi =0,\theta =0,\phi ={\phi }_{d}}\right)}_{y}dv-{J}_{x}\text{sin}\left({\phi }_{d}\right){\left(\frac{\partial {}{}^{m}\overrightarrow{B}\left({{}_{}^{\mathbf{m}}\mathbf{R}}_{\mathbf{c}}\left({}{}^{c}\overrightarrow{d}-{}{}^{c}\overrightarrow{p}\right)\right)}{\partial \psi }\bigg|_{\psi =0,\theta =0,\phi ={\phi }_{d}}\right)}_{x}dv\\& \quad =-{J}_{x}\left({z}_{c}-{}{}^{c}{p}_{z}\right){{\omega }_{k}}^{2}\text{cos}\left(2{\phi }_{d}\right)\text{sin}\left({\omega }_{l}\left[\text{cos}\left({\phi }_{d}\right)\left({y}_{c}-{}{}^{c}{p}_{y}\right)-\text{sin}\left({\phi }_{d}\right)\left({x}_{c}-{}{}^{c}{p}_{x}\right)\right]\right)\\ & sin\left({\omega }_{k}\left[\text{cos}\left({\phi }_{d}\right)\left({x}_{c}-{}{}^{c}{p}_{x}\right)+\text{sin}\left({\phi }_{d}\right)\left({y}_{c}-{}{}^{c}{p}_{y}\right)\right]\right)dv\end{aligned}$$
(19)

The wrench on the coil in LCS can be obtained through the summation of all harmonics31:

$$\begin{array}{c}\left.\left[\begin{array}{c}{}^{c}{F}_{x}\\ {}_{\boldsymbol{ }}{}^{c}{F}_{y}\\ {}_{\boldsymbol{ }}{}^{c}{F}_{z}\\ {}_{\boldsymbol{ }}{}^{c}{T}_{x}\\ {}_{\boldsymbol{ }}{}^{c}{T}_{y}\\ {}_{\boldsymbol{ }}{}^{c}{T}_{z}\end{array}\right.\right]=\sum\limits_{k=1}^{\infty } \sum\limits_{l=1}^{\infty } \left.\left[\begin{array}{c}{}_{\boldsymbol{ }}{}^{c}{F}_{x}^{\left(k,l\right)}\\ {}_{\boldsymbol{ }}{}^{c}{F}_{y}^{\left(k,l\right)}\\ {}_{\boldsymbol{ }}{}^{c}{F}_{z}^{\left(k,l\right)}\\ {}_{\boldsymbol{ }}{}^{c}{T}_{x}^{\left(k,l\right)}\\ {}_{\boldsymbol{ }}{}^{c}{T}_{y}^{\left(k,l\right)}\\ {}_{\boldsymbol{ }}{}^{c}{T}_{z}^{\left(k,l\right)}\end{array}\right.\right]\end{array}$$
(20)

As detailed above, the moving-magnet planar actuator utilizes a 2D Halbach array to enhance magnetic flux density and optimize the conversion of x-directional coil activity into y-directional propulsion via Lorentz force equations. The modeling employs a dual-reference frame approach, accurately representing the 6-DOF of the translator in spatial dynamics. A harmonic model is employed for the rapid computation of the magnetic field distribution, with detailed equations that account for angular rotations. Analytical techniques are preferred over the FEM owing to the complex interactions within the system. A precise trajectory tracking control model is crucial for the performance of the actuator, especially under significant angular movements around the z-axis.

In summary, the proposed moving-magnet planar actuator model can accurately represent coils of arbitrary shapes without simplification, maintain low computational demands suitable for real-time control, and establish the relationship between the wrench and 6-DOF displacements in both central and edge regions. Therefore, the model introduced in this paper has substantial practical value and significant potential for application in advanced actuator systems.

Numerical verification experiments

To validate the accuracy of the proposed planar motor model, a series of comprehensive numerical simulation experiments were conducted to evaluate the performance of the model under various conditions and verify its reliability and precision compared with results from FEM software. By designing multiple experimental setups, we thoroughly analyzed the force and torque behaviors of the planar motor under different operating conditions and confirmed the applicability of the model. For comprehensive validation, we compared the results of our model with those obtained using FEM. During the experiments, we used FEM software to compare and validate the proposed model. The core of the experiments involved calculating the forces and torques of the planar motor under various conditions and comparing these results with theoretical values to verify the accuracy of the model. Preliminary experimental results indicated that the use of three harmonics met the accuracy requirements with a corresponding reduction in computation time. Consequently, we chose to use three harmonics for model simulation. We designed four sets of experiments, each with different angular settings and motion paths, to ensure the applicability of the model under various conditions.

The conductor–coil configuration used in the experiments is shown in Fig. 2; the configuration features coils of printed circuit board. Specific parameters are listed in Table 1. These setups allowed us to comprehensively analyze the planar performance of the motor in practical applications and verify the predictive capability of the model.

Fig. 2
figure 2

Magnet–coil configuration and verification setups: (a) bottom view; (b) cross-section view.

Full size image
Table 1 Physical parameters of the magnet–conductor configuration.
Full size table

Setup of simulations

To more effectively evaluate the applicability and accuracy of the model, we designed four distinct experimental trajectories, each with different angular settings and motion paths. The specific settings are as follows:

Set 1: For angles \(\psi\) of − 1.5°, 0°, and 1.5°, the origin of the coil moves linearly from (0, − 200, 0 mm) to (0, 200, 0 mm) in the global coordinate system (GCS). During this process, the position of the mover remains fixed at (40, 0, 5.5 mm), with a rotation angle \(\phi\) of − π/4. The purpose of this setup is to assess the accuracy of the force and torque modeling for the x-direction driving coil during linear motion.

Set 2: For angles \(\psi\) of − 1.5°, 0°, and 1.5°, the origin of the mover moves linearly from (− 200, 0, 0 mm) to (200, 0, 0 mm) in the GCS. During this process, the position of the coil remains fixed at (40, 0, 5.5 mm), with a rotation angle \(\phi\) of − π/4. This setup is similar to Set 1 but involves different movement directions. The purpose is to evaluate the accuracy of force and torque modeling for the y-direction driving coil during linear motion.

Set 3: For angles \(\psi\) of − 1.5°, 0°, and 1.5°, the origin of the mover is fixed at (40, − 25, 5.5 mm) in the GCS, with the rotation angle \(\phi\) varying from − π/4 to π/4. Throughout this process, the coil stays in the same spot at the GCS origin. This setup allows for the evaluation of the applicability of the model under changing angles by considering the rotational movement of the mover at a fixed position.

Set 4: For angles \(\psi\) of − 1.5°, 0°, and 1.5°, the origin of the coil moves linearly from (0, − 200, 0 mm) to (0, 200, 0 mm) in the GCS. During this process, the position of the mover remains fixed at (40, 0, 5.5 mm), with a rotation angle \(\phi\) of π/12. This setup allows for the evaluation of the accuracy of the force and torque modeling for the mover during linear motion at different \(\phi\) angles. This evaluation helps to further verify the model’s applicability. This assessment further confirms the model’s applicability.

Results and analysis

Experimental validation underlines the appropriate matching of the Large-Angle 6-DOF model to FEM benchmarks for various motion types. The model has the following configurations (Hardware: AMD Ryzen7 5700X, 32 GB RAM). The results of the four validation experiments are shown in Fig. 3. To avoid redundancy caused by overlapping curves, the following adjustments have been made: the \({F}_{y}\) curves for angles of − 1.5° and 1.5° are hidden in Fig. 3a,e; the \({F}_{x}\) curves for angles of − 1.5° and 1.5° are also hidden in Fig. 3a,e; the \({T}_{y}\) curves for angles of − 1.5° and 1.5° are hidden in Fig. 3b,h; and the \({T}_{z}\) curves for angles of − 1.5° and 1.5° are hidden in Fig. 3d,f.

Fig. 3
figure 3

Results of numerical verification experiments: (a) and (b) force and torque results for Set 1, (c) and (d) force and torque results of Set 2, (e) and (f) force and torque results of Set 3, and (g) and (h) force and torque results of Set 4.

Full size image

Numerical validation confirms that the proposed large-angle six-degree-of-freedom model satisfies high accuracy while maintaining a high computational efficiency as it closely follows the finite-element (FEM) results under small-angle deflection of a rigid body. As illustrated in Fig. 3 and tabulated in Table 2, in Test Sets 1 and 2, about 95% of the workspace has the prediction error below 1%, with only minor distortions close to the magnetic boundary, a consequence of end effects. Moreover, in contrast to traditional small-angle 6-DOF methods in Test Set 3, up to 5.3-times yaw angle torque prediction higher than conventional methods further demonstrates its incredible performance in high-angle testing. For example, in the case of Test Set4 which consists of 15° yaw during the compound translational motion, the multi-DOF coupling sacrifices a little overall accuracy, nevertheless, force/torque calculations stay within a feasible error rate. Moreover, the single-point computation for this model only costs approximately 3 ms (6800 times faster than FEM, 10 min per point), meeting the requirements of real time, high-frequency closed-loop control, which indicates broad prospects in engineering application such as precision manipulation, steady high-angle rotation, and long-travel motion.

Table 2 Performance comparison between the basic 6-DOF model and our large-angle 6-DOF model for set3.
Full size table

Trajectory tracking

This section describes the design and execution of two typical trajectory tracking experiments to validate the performance of the proposed control system under different path conditions. These experiments not only evaluate the system’s performance in the absence of noise but also investigate how the system’s stability and accuracy are affected by noise interference, which is common in practical operations.

Control system structure

The whole control system is made of four interconnected modules, as shown in Fig. 4, namely, the control strategy module, commutation module, maglev system module, and sensing system module. Central to the system is the control strategy module in which the controller computes the necessary force and torque components \(({F}_{x}, {F}_{y}, {F}_{z}, {T}_{x}, {T}_{y} {T}_{z})\) according to reference inputs and real-time sensory information. Moreover, a disturbance and state observer is included among the control system to estimate unmeasured states and external disturbances and adding robustness to the control system. These control outputs are fed into the commutation module where an inverse model uses them to produce the relevant coil current commands, which in turn are amplified and streamed into the coils array. Consequently, the magnetically levitated system module, comprising a coil array and a levitated translator, generates the requisite electromagnetic forces to control the translator’s motion with high accuracy and without the involvement of mechanical contact. The sensing system module, on the other hand, is responsible for real-time tracking of the position and orientation of the translator and providing this critical information to the control strategy module for effective closed-loop control. The close cooperation between these modules (illustrated in Fig. 4) enables the system to ensure precise trajectory tracking, disturbance resistance, and stable multi-degree-of-freedom movement, which is suitable for applications that demand high accuracy and dynamic control capabilities.

Fig.4
figure 4

Structure of the control system.

Full size image

Nonlinear model predictive control

To achieve high-precision trajectory tracking, the proposed control system employs Nonlinear Model Predictive Control (NMPC), which dynamically adjusts control inputs based on a predictive model to minimize deviations from the desired trajectory. Fundamentally, the desired spatial trajectory \(p(t)= {[{x}_{d}(t),{y}_{d}(t),{z}_{d}(t),{\psi }_{d}(t),{\theta }_{d}(t),{\phi }_{d}(t)]}^{\text{T}}\) may represent any temporally parameterized path. To align with the practical operating conditions of planar motors, which necessitate maintaining planarity and constant altitude in their operations, adjustments are made to conform to \({[{x}_{d}(t),{y}_{d}(t),{z}_{d},\text{0,0},{\phi }_{d}(t)]}^{\text{T}}\) in three-dimensional space, regardless of the desired temporal parameterization. Hence, the actual trajectory tracking challenge for planar motors is encapsulated by the pursuit of a trajectory within a plane at a specified height \({z}_{d}\), where \({z}_{d}\) is a constant, tracking a path on the \(x,y\) plane.

To achieve precise tracking of the desired trajectory, we define a cost function J, aimed at minimizing the trajectory tracking error and the energy expenditure of the control inputs. This function is instrumental in guiding the development of control strategies that are both efficient and effective, thereby facilitating the adherence to predetermined paths with minimal deviation and energy usage. This approach underscores the balance between precision in trajectory following and the pragmatic aspects of power consumption, presenting a methodologically sound basis for addressing the intricacies of planar motor motion control within the specified operational framework.

$$\begin{array}{*{20}l} {\mathop {{\text{min}}}\limits_{{\widehat{{\mathbf{u}}}(s,t_{0} )}} } \hfill & {J = \smallint _{0}^{T} \parallel \widehat{{\mathbf{x}}}(s,t_{0} ) - {\mathbf{x}}_{d} (t_{0} + s)\parallel _{Q}^{2} } \hfill \\ {} \hfill & { + \parallel \widehat{{\mathbf{u}}}\left( {s,t_{0} } \right)\parallel _{R}^{2} ds + \parallel \widehat{{\mathbf{x}}}\left( {T,t_{0} } \right) - {\mathbf{x}}_{d} \left( {t_{0} + T} \right)\parallel _{P}^{2} } \hfill \\ {{\text{s}}{\text{.t}}{\text{. }}} \hfill & {\mathop {\widehat{{\mathbf{x}}}}\limits^{.} (s,t_{0} ) = f(\widehat{{\mathbf{x}}}(s,t_{0} ),\widehat{{\mathbf{u}}}(s,t_{0} ))} \hfill \\ {} \hfill & {\widehat{{\mathbf{x}}}(0,t_{0} ) = x(t_{0} )} \hfill \\ {} \hfill & {{\mathbf{u}}_{{{\text{min}}}} \le \widehat{{\mathbf{u}}}(s,t_{0} ) \le {\mathbf{u}}_{{{\text{max}}}} } \hfill \\ \end{array}$$
(21)

Here, \({\mathbf{x}}_{d}(t)\) denotes the desired trajectory, while \(Q, R,\) and \(P\) represent weighting matrices that serve to equilibrate the significance of trajectory tracking error against the consumption of control energy. The control input \(\widehat{\mathbf{u}}(s,{t}_{0})\) must comply with the operational constraints of the planar motor, thereby ensuring that the implementation of control strategies adheres strictly to the physical and performance limitations inherent to the system.

$$\begin{aligned}& \begin{array}{*{20}l} {\mathop {{\text{min}}}\limits_{U} } \hfill & {J_{d} (U,x)} \hfill \\ {{\text{s}}{\text{.t}}{\text{.}}} \hfill & {{\mathbf{x}}_{{k + 1}} = f_{d} ({\mathbf{x}}_{k} ,{\mathbf{u}}_{k} )} \hfill \\ {} \hfill & {{\mathbf{x}}_{0} = x} \hfill \\ {} \hfill & {{\mathbf{u}}_{{min}} \le {\mathbf{u}}_{k} \le {\mathbf{u}}_{{max}} } \hfill \\ \end{array} \\ & \mathop {min}\limits_{{u\left( {s,t_{0} } \right)}} J\;{\text{subject to}}\;{\mkern 1mu} x\left( {s,t_{0} } \right) = f\left( {x\left( {s,t_{0} } \right),u\left( {s,t_{0} } \right)} \right), \\ & u_{{min}} \le u(s,t_{0} ) \le u_{{max}} \\ \end{aligned}$$
(22)

The controller uses NMPC to predict future states for a finite time horizon and optimally modify control inputs to minimize trajectory tracking errors. Other control methods like PID controllers or reinforcement, although advantageous in their specific applications, are not the focus of our research. In fact, this paper focuses on enhancing the accuracy of force and torque modeling of 6-DOF maglev planar motors, specifically in terms of large-angle z-axis rotations, against which conventional modeling frameworks do not sufficiently accommodate for cross-axis coupling effects and force alterations. Further, the use of NMPC-based control strategy that is integrated with this advanced modeling framework allows for fine-grained predictions of forces and torques in addition with dynamically optimized control inputs in real-time; This allows for better tracking precision, disturbance resilience, and enhanced system capability in high-fidelity scenarios. In the subsequent section, trajectory tracking experiments validate this approach.

Trajectory tracking simulation

In order to test the performance of the proposed control system, two trajectory tracking experiments were carried out with different paths. In particular, the first experiment consists of the tracking of a direct circular trajectory and the second of a more advanced eight-shaped trajectory. These experiments evaluate the performance of the system in terms of accurate tracking by rejecting disturbances and decoupling \(x-y\) reflections.

Case I—circular trajectory.

In the first experiment, the target trajectory was set as a circular path, defined as follows:

$$\mathbf{p}\left({\varvec{t}}\right)=\left\{\begin{array}{l}{x}_{d}=0.02\text{sin}\left(0.3t\right)\\ {y}_{d}=0.02\text{cos}\left(0.3t\right)\end{array}\right.\boldsymbol{ }\boldsymbol{ }$$
(23)

This trajectory was designed to test the system’s tracking performance during relatively simple periodic motion. Through this experiment, we evaluated the system’s response characteristics and control accuracy during continuous and smooth movements.

Figure 5 shows the trajectory tracking results under both noise-free and noisy conditions. The blue curve represents the system’s ability to accurately track the circular trajectory without noise, while the red curve shows that even with the addition of noise, the system maintains a high level of tracking accuracy. This demonstrates the robustness and adaptability of the proposed control method.

Fig. 5
figure 5

(a) 3D Trajectory tracking simulation of planar motor—case I; (b) trajectory in the xoy plane of planar motor—case I.

Full size image

Case II—eight-shaped trajectory.

In the second experiment, the target trajectory was set as an eight-shaped path, defined as follows:

$$\mathbf{p}({\varvec{t}})=\left\{\begin{array}{l}{x}_{d}=0.02sin(0.3t)\\ {y}_{d}=0.03cos(0.15t)\end{array}\right.$$
(24)

The eight-shaped trajectory is more challenging and was designed to evaluate the system’s control ability under complex path conditions. This experiment was used to observe the system’s performance during complex nonlinear motion, especially when the path includes sharp turns and continuous curves.

Figure 6 presents the trajectory tracking results for the eight-shaped path under both noise-free and noisy conditions. Despite the complexity of the path, the system effectively tracks the target trajectory. Although there is a slight decrease in tracking accuracy under noisy conditions, the system overall maintains stable control performance.

Fig. 6
figure 6

(a) 3D Trajectory tracking simulation of planar motor—case II; (b) trajectory in the xoy plane of planar motor—case II.

Full size image

Simulation results show that the proposed control system can achieve high-precision trajectory tracking for various paths. In both scenarios the tracking errors are minimized without compromising trajectory integrity by the NMPC-based controller. The system is very robust with respect to external disturbances, as the noise-induced deviation is only relatively small, which does not affect tracking accuracy more generally. The smoothness of these trajectories further verifies the validity of the controller as it dynamically adjusts control inputs while allowing the object to follow quickly changing motion states stably.

Thus the results suggest that proposed 6-DOF modeling and NMPC-based control framework works as per anticipation in dealing with trajectories of motion positively with vivid accuracy and stability. Further experimental validation via real-world motion control experiments is set out in the next section.

Motion control experiments

Experimental setup

To validate the planar motor control system’s performance, a motion control experiment was conducted using a high-precision planar motor system. The experimental configuration, depicted in Fig. 7a, comprises a mover, a sensor system, a driver, and a dSPACE controller. The mover incorporates a Halbach magnet array to enhance magnetic flux density.

Fig.7
figure 7

Experimental setup. (a) Schematic diagram of planar motor system. (b) Schematic diagram of planar motor measurements. (c) Overall layout of the maglev planar motor.

Full size image

The sensor system, depicted in Fig. 7b, includes three laser interferometers (Laser4, Laser5 and Laser6) for measuring the mover’s rotational motion (\(\psi ,\theta ,z\)), along with three laser interferometers (Laser1, Laser2 and Laser3) for measuring horizontal displacements (\(x,y\)) and rotational motion (\(\phi\)). The dSPACE controller processes the positioning and rotational data, generating control signals based on the motion control algorithm. These signals are converted into current by the driver module, which powers the planar motor coils to precisely control the mover’s motion. The experimental system is powered by a DC source, with real-time data monitoring and analysis facilitated through a connected computer interface. This setup allows for accurate testing and evaluation of the control algorithm and dynamic performance of the planar motor system across diverse operational scenarios. Additionally, Fig. 7c presents an overview of the planar motor system, showing the summary layout of stator—mover arrangement for the entire testing of the control algorithm and dynamic performance.

Experimental result

The performance of the developed planar motor control system was analyzed and evaluated based on experimental results as demonstrated in Fig. 8. Curve 1 shows that the actual motion trajectory of the x-axis is evidently consistent with the predefined reference trajectory and that tracking errors remain fluctuating in a small range (\(\pm 0.2\text{ mm}\)). This demonstrates that the control algorithm is very conducive to ensuring the accuracy of trajectory tracking.

Fig. 8
figure 8

Test of \({}^{c}x\)-axis motion and observed cross-axis positioning errors.

Full size image

The cross-axis coupling errors in the y and φ directions (as indicated by Curves 2 and 3 in the figure), respectively, oscillate around \(\pm 20\, \upmu \text{m}\) and \(\pm 0.5\text{ mrad}\), confirming the efficiency of the system’s decoupling mechanism. Yet, a closer inspection of the experimental data shows that even though the cross-axis errors are suppressed, there is still a finite amount of high-frequency noise. These outliers may be caused by noise in the sensor, outside environment (e.g. vibrations or temperature changes), or manufacturing imperfections in the platform.

The results show that the proposed method not only ensures the achievement of position and orientation targets like the method in the previous studies but also provides a good disturbance rejection and decoupling performance. Additional work on certain high-frequency incorrect predictions identified here might aid in tuning algorithms or including a disturbance observer to better handle the challenges when working at limiting accuracy levels, meant to improve robustness and practical usability.

Conclusion

This study introduces a 6-DOF dynamic modeling and control framework for magnetic levitation planar motors (MLPMs), specifically addressing large-angle yaw rotation challenges. By integrating harmonic-based analytical models with an extended 6-DOF wrench formulation, the method enables real-time dynamic representation with high fidelity. Taylor-series expansions of rotational magnetic flux and harmonic spectral analysis capture multi-DOF nonlinearities and coupling effects under large-angle conditions, achieving a 5.3-fold improvement in wrench prediction accuracy over conventional small-angle models. Numerical and experimental validations confirm the model’s computational efficiency and precision across operational regimes, including extreme yaw rotations, while maintaining real-time applicability. These advancements position the framework as a critical tool for high-precision industrial applications in semiconductor manufacturing, advanced robotics, and precision machining.

Potential extensions include adaptation to diverse coil configurations, integration with advanced trajectory-planning algorithms, and development of adaptive control strategies for enhanced disturbance rejection. Further exploration of higher-order magnetic flux dynamics could expand the framework’s applicability to extreme operational scenarios. This work bridges theoretical modeling and industrial implementation for maglev systems, offering a foundation for next-generation high-precision motion control technologies.