Hybrid-driven modeling using a BiLSTM–AdaBoost algorithm for diameter prediction in the constant diameter stage of Czochralski silicon single crystals

Abstract

During the preparation of electronic-grade silicon single crystals (SSC), accurately predicting the crystal diameter is crucial for obtaining high-quality crystals. In this paper, a hybrid-driven modeling method integrating Bidirectional Long Short-Term Memory network (BiLSTM) and Adaptive Boosting (AdaBoost) algorithm is proposed, aiming to improve the accuracy and stability of crystal diameter prediction in the medium diameter stage of the SSC growth by the Czochralski (CZ) method. First, the initial prediction of SSC diameter is performed using a mechanistic model and the prediction error is calculated; then, the time series data are processed using a BiLSTM network to generate the predicted values at each time point. Subsequently, the prediction results of the BiLSTM network are weighted and fused by the AdaBoost algorithm to obtain the final time series prediction output, and the prediction performance is further enhanced by iterative optimization. Compared with the traditional mechanistic model or a single data-driven model, this hybrid model retains the explanatory nature of the mechanistic model while also ensuring the accuracy of the data-driven model, which effectively overcomes the challenges posed by complex coupling and nonlinear problems.

Introduction

Electronic-grade silicon is an outstanding semiconductor material that allows efficient regulation of conductivity between conductors and insulators, and it is widely used in integrated circuits, automobiles, communications, and other fields. Electronic-grade SSC are commonly prepared in industrial production by the CZ method, which ensures uniform crystal growth by heating high-purity polysilicon to near 1400 °C, melting it into a liquid state, and then immersing SSC seed crystals into the molten silicon, pulling it upward slowly and rotating the seed crystals^1,2. During this process, the solution temperature and lifting speed are precisely controlled to make the silicon atoms orderly arranged according to a certain crystalline phase, forming a high-quality SSC structure.

In the semiconductor SSC growth process, the main factors influencing diameter variations include the heater power and the crystal lifting speed³. Notably, although adjusting the crystal pulling rate can quickly alter the crystal diameter, its adjustable range is relatively limited. Moreover, frequent pulling rate adjustments can cause large fluctuations at the growth interface, increasing the likelihood of crystal breakage and defects. In contrast, controlling the crystal diameter by adjusting the heater power is a slower process, but it has a wider adjustment range and is less likely to cause instability at the growth interface. Therefore, constructing a SSC growth model that accurately describes the relationship between heater power and crystal diameter, and designing an efficient diameter control system have become important issues in realizing high-quality SSC production.

One type of model commonly used in crystal diameter prediction is mechanistic modeling. Mechanistic modeling is an effective method to understand and analyze the dynamic properties of complex systems by quantitatively describing and predicting system behaviors and processes through scientific principles and physical laws. This modeling approach is widely used in the fields of physics, chemistry, biology, and engineering, which helps to deeply resolve the intrinsic mechanisms of a system.In their study, Winkler et al.^4,5 took the relationship between the variation in the crystal radius at the meniscus and the tilt angle of the crystal as a starting point to construct fluid-dynamic and geometric models for the CZ crystal growth process, thereby circumventing the complexity of thermodynamic modeling. Subsequently, Rahmanpour et al.^6,7 and Bukhari et al.⁸ thoroughly investigated and extended this work, and proposed a centralized parametric model (expressed in state-space form) incorporating the crystal growth kinetics and temperature kinetics, which further incorporated a simplified heat transfer model on the basis of the original hydrodynamic and geometrical model. In the context of the 300 mm CZ SSC growth process, Zheng et al.⁹ developed a centralized parameter model that integrates energy balance, mass balance, hydrodynamics, and geometric equations to enhance the understanding of CZ kinetics. This model was utilized for predicting the crystal radius and growth rate. For their investigation into the distribution parameter model concerning the CZ SSC growth process, Ng et al.^10,11,12 introduced a model that incorporates both the crystal radius and temperature variation, allowing for a more precise representation of system dynamics and temperature fluctuations within the crystal.In general, for lumped-parameter and distributed-parameter models to be applicable to real-world silicon single crystal growth control systems, strict assumptions regarding model accuracy must be satisfied. Moreover, in many of these mechanistic models of crystal growth, numerous parameters are either unknown or lack sufficient precision, and some practical parameter values may vary significantly across different operating conditions. For example, in the case of distributed-parameter models for the CZ crystal growth process, a primary challenge lies in the need to numerically solve complex partial differential equations. This requires powerful solvers and substantial computational resources, which are often impractical on the limited computing hardware available for process control in industrial environments. Additionally, information derived from numerical models (as well as the inverse solutions required for control purposes) may not be obtainable in real time. Furthermore, considerable effort is needed to adapt distributed-parameter models to actual crystal growth system designs and to determine the physical parameters and boundary conditions required by the solvers. In summary, mechanistic modeling approaches for CZ silicon single crystal growth inevitably face certain limitations, including high modeling costs, the need for extensive domain knowledge, the difficulty of obtaining key parameters online, and excessive model simplification that compromises accuracy in representing the system.

Another commonly adopted strategy is data-driven modeling. As computer hardware continues to advance, data analysis and machine learning approaches have increasingly become essential tools for investigating complex systems. Liang et al.^13,14 introduced a T-S fuzzy temperature identification algorithm aimed at modeling temperature changes during the growth of CZ SSC. Experimental results indicated that this fuzzy inference model achieves high accuracy in temperature prediction. Subsequently, Zhao et al.¹⁵ combined a T-S fuzzy model with an improved ant lion optimization (ALO) algorithm to establish a thermal model relating heating power to liquid surface temperature in the priming stage of CZ crystal growth. By applying the improved ALO algorithm to determine globally optimal parameters for the T-S fuzzy model, this method further enhanced the accuracy of predicting the liquid surface temperature.To expand deep learning applications in CZ SSC, Zhang et al.¹⁶ developed a data-driven model using a BP neural network to predict crystal diameter based on experimental data. Simulation outcomes showed not only high predictive accuracy but also strong stability, suggesting this approach can reliably guide crystal dimension control. Advancing these efforts, Zhang et al.¹⁷ introduced a deep learning model linking heater power to crystal diameter via an long short-term memory(LSTM) architecture, particularly effective for analyzing sequential data. Results from multiple simulations demonstrated that this LSTM-based model outperformed traditional techniques such as BP neural networks and support vector machines in predicting crystal diameter, indicating that LSTM integration can lead to more precise control of the crystal growth process.Although data-driven modeling offers advantages such as high prediction accuracy, ease of implementation, low cost, and no need to consider the inherent complexities of the crystal growth process, the resulting models are often black-box in nature, with limited interpretability and a lack of insight into the underlying dynamics of the CZ crystal growth process.

To harness the benefits of both mechanistic and data-driven models, we merge them in a way that the resultant model not only elucidates the fundamental physical processes but also maintains high predictive accuracy. Kato et al.¹⁸ developed a gray-box model aimed at forecasting the temperature gradient parameters of crystals at the solid–liquid interface, utilizing a mechanistic framework of the CZ SSC growth process, thereby establishing a groundwork for investigating the integration of data-driven approaches with mechanistic models in hybrid modeling techniques related to CZ SSC. Ren et al.¹⁹ introduced a Just-In-Time Learning–Stacked AutoEncoder–Extreme Learning Machine hybrid model, grounded in the concept of integrating data-driven and mechanistic elements, demonstrating its effectiveness in accurately predicting melt temperature and crystal growth rates. Wan et al.²⁰ proposed the mechanism- data-driven hybrid variable weighted stacked autoencoder random forest hybrid model, which was based on the mechanistic framework and industrial data, aimed at facilitating online monitoring of V/G. The distinctive feature of this hybrid-driven modeling strategy lies in its incorporation of the mechanistic model’s explanatory capabilities alongside the generalization strengths of data-driven models, enhancing the model’s robustness and adaptability, thus ensuring it better mirrors actual operational conditions. Although previous studies have explored data-driven approaches to predict crystal diameter using operational data, these efforts have primarily focused on establishing a direct mapping between process parameters (e.g., heater power) and crystal diameter, without considering the physical constraints provided by mechanistic models. The key distinction of this study lies in the seamless integration of mechanistic models—derived from energy balance, fluid dynamics, and geometric equations—with real production data through the BiLSTM-AdaBoost framework. Unlike purely data-driven methods, our hybrid model employs data-driven corrections to explicitly compensate for the residuals of the mechanistic model, thereby achieving both physical consistency and adaptability to process variations. This approach bridges the gap between theoretical modeling and industrial applicability, which has not been systematically addressed in prior work.

The main contributions of this study are as follows:

• 1. Application of Hybrid Modeling in Crystal Growth Prediction:

To address challenges such as nonlinearity, time delay, and difficulty in direct measurement of crystal diameter during the growth of electronic-grade semiconductor SSCs, a hybrid modeling approach combining mechanistic and data-driven models is proposed. The mechanistic model captures the dynamic behavior of crystal growth, while the data-driven model provides dynamic compensation for prediction results. This approach enhances prediction accuracy while maintaining model interpretability, offering theoretical support for quality control in SSC growth.

• 2. BiLSTM-AdaBoost-Based Prediction Algorithm:

To overcome the limitations of traditional single-model approaches, an ensemble learning framework combining Bidirectional Long Short-Term Memory (BiLSTM) networks and Adaptive Boosting (AdaBoost) is designed. Multiple comparative experiments (see Chapter 3) demonstrate that this algorithm significantly improves prediction accuracy and robustness compared to conventional methods, providing a new solution for parameter prediction in complex industrial processes.

• 3. Interdisciplinary Methodological Advancement in Semiconductor Crystal Growth:

By integrating control theory and machine learning, the proposed hybrid modeling framework offers a new perspective for research on semiconductor SSC growth. The method can be extended to related applications such as crystal defect detection and growth rate optimization, serving as a valuable reference for promoting intelligent development in semiconductor material manufacturing.

The structural content of this paper is organized as follows: Section "Proposed approach": A brief description of the mechanistic modeling of the SSC growth process and an in-depth introduction to the implementation details of the BiLSTM and Adaboost. Section "Heater to Crucible Thermal Radiation Transfer Rate for:": Through simulation experiments, the effectiveness and superiority of crystal diameter prediction based on BiLSTM and Adaboost algorithm are fully demonstrated, and the model performance is comprehensively discussed and analyzed. Concluding part: to summarize and conclude the work done in this paper, emphasizing the importance and practical application value of the research.

Proposed approach

Figure 1 illustrates the proposed hybrid-driven modeling method for diameter prediction in the constant diameter stage of CZ SSC using BiLSTM and the AdaBoost algorithm. The method comprises two modules: The first module is about the mechanistic modeling of the SSC growth process. Based on the mechanistic model established by the hydrodynamic model, energy balance model and geometric model of the CZ SSC growth process, the historical data of the actual SSC growth process is inputted into the mechanistic model to obtain the preliminary diameter prediction data and the error data of the diameter.

Fig. 1

Overall scheme of hybrid modeling.

The second module takes the error data in Module 1 and the historical data from the actual SSC growth process as inputs, sets the data of the corresponding step as the training samples, and sets them in proportion to the corresponding training and testing sets. Then, the data are normalized and modeled using BiLSTM network as a weak regressor to store the prediction results of each time step and calculate the weights. Finally, the weights of all the weak regressors are weighted and combined, and the final diameter time series prediction results are obtained after inverse normalization.

Mechanistic modeling of SSC growth systems

Mechanistic modeling is a scientific and highly explanatory modeling method for scenarios with a good understanding of the internal laws of the system. For the large time lag and nonlinear process such as the modeling of the SSC preparation process of the direct drawing method, the mechanistic modeling is used with a good explanatory nature.

$T_{h}$ represents the heater temperature, which controls the distribution of the thermal field and influences the silicon melt temperature and its melting state.$T_{c}$ denotes the crucible temperature, which is crucial for ensuring the uniformity and stability of the melt.$T_{m}$ indicates the melt temperature, a critical thermal parameter that impacts the melting, solidification, and the presence of crystal defects in silicon.$H_{m}$ refers to the melt height, which plays a significant role in maintaining thermal balance and the stability of crystal diameter.$R_{i}$ signifies the crystal radius, determining the diameter of the crystal rod and serving as an important indicator of process stability.$\alpha_{c}$ represents the crystal tilt angle; excessive deviation in the crystal axis offset angle adversely affects crystal quality.$V_{g}$ denotes the crystal growth rate, which influences the rate of crystal formation; both excessively fast and slow growth can compromise quality and efficiency. indicates the crystal length, which reflects the stability of growth and production efficiency. $H_{men}$ represents the height of the meniscus, the height difference between the melt and the crystal, which affects both the growth shape and quality.$V_{p}$ signifies the crystal pulling rate, impacting the balance between crystal quality and growth rate.$P_{in}$ represents the heater power, which regulates temperature and the thermal field, thereby indirectly influencing melt conditions and crystal growth.

Thermal transfer model

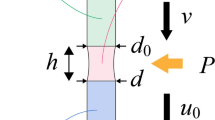
It is assumed that the heat released by the graphite heater is completely absorbed by the quartz crucible, with no energy loss. Utilizing the law of conservation of energy, we can develop a heat transfer model for the growth of silicon single crystals^7,21. Figure 2 shows the crystal growth model.

Fig. 2

Model of crystal growth set parameters.

• 1. Equation for heater temperature as a function of time $\dot{T}_{h}$ :

  $$\dot{T}_{h} = \frac{1}{{C_{h} }}\left( {P_{in} - q_{hc} } \right)$$

  (1)

  where the heater heat capacity $C_{h}$ is:

  $$C_{h} = S_{h} \times \rho_{h} \times V_{h}$$

  (2)

• 2. Heater volume $V_{h}$ is:

  $$V_{h} = \pi (R_{ho}^{2} - R_{hi}^{2} ) \times H_{h}$$

  (3)

• 3. Heater to Crucible Thermal Radiation Transfer Rate $q_{hc}$ for:

  $$q_{hc} = A_{c} \times \sigma \times \left( {T_{h}^{4} - T_{c}^{4} } \right)$$

  (4)

  The power of the heater is denoted as $P_{in}$, the specific heat capacity as $S_{h}$, the density as $\rho_{h}$, the outer diameter as $R_{ho}$, the inner diameter as $R_{hi}$, the height as $H_{h}$, the surface area of the crucible as $A_{c}$, the Stefan-Boltzmann constant as $\sigma$, the heater temperature as $T_{h}$, and the crucible temperature as $T_{c}$.

• 4. Equation for the variation of crucible temperature with time $\dot{T}_{c}$:

  $$\dot{T}_{c} = \frac{1}{{C_{c} }}\left( {q_{hc} - q_{co} - q_{cs} - q_{cm} } \right)$$

  (5)

  where the crucible heat capacity $C_{c}$ is calculated as:

  $$C_{c} = S_{c} \times \rho_{c} \times V_{c}$$

  (6)

• 5. Crucible volume $V_{c}$ is calculated as:

  $$V_{c} = \pi R_{c}^{2} \times H_{c}$$

  (7)

  where $q_{co}$ is the thermal radiation transfer rate from the crucible to the environment,$q_{cs}$ is the thermal radiation transfer rate from the crucible to the melt,$q_{cm}$ is the thermal conduction transfer rate from the crucible to the melt,$S_{c}$ is the specific heat capacity of the crucible,$\rho_{c}$ is the density of the crucible, and $H_{c}$ is the height of the crucible;

• 6. Based on the energy and mass conservation of the melt, the equation for the change in melt temperature over time as $\dot{T}_{m}$:

  $$\dot{T}_{m} = \frac{1}{{C_{m} }}\left( {q_{cm} + q_{cs} - q_{so} - q_{m} } \right) - \frac{{\dot{H}_{m} T_{m} }}{{H_{m} }}$$

  (8)

• 7. where the method for calculating the melt heat capacity as $C_{m}$:

  $$C_{m} = S_{m} \times \rho_{m} \times V_{m}$$

  (9)

• 8. The method for calculating the melt volume as $V_{m}$:

  $$V_{m} = \pi R_{c}^{2} \times H_{m}$$

  (10)

  where $q_{so}$ is the heat transfer rate from the melt to the surroundings, $q_{m}$ is the heat transfer rate from the melt to the curved surface, $\dot{H}_{m}$ is the rate of change of melt height, $T_{m}$ is the melt temperature, $H_{m}$ is the melt height, $S_{m}$ is the melt heat capacity, $\rho_{m}$ is the melt density, and $R_{c}$ is the crucible radius.

(4) At the solid–liquid interface of crystal growth, the growth rate of the crystal can be determined by calculating the difference between the heat flux from the melt to the growth interface ($Q_{mI}$) and the heat flux from the growth interface to the crystal ($Q_{Ii}$). This difference reflects the heat released by the crystal during the crystallization process .Therefore, based on the principle of energy conservation, we can derive the calculation formula for the crystal growth rate $V_{g}$⁷.

$$V_{g} = \frac{{Q_{Ii} - Q_{mI} }}{{H_{f} \rho_{s} }} = \frac{{q_{Ii} - q_{mI} }}{{H_{f} \rho_{s} \pi R_{i}^{2} }}$$

(11)

where $H_{f}$ is the latent heat of crystallization, $\rho_{s}$ is the crystal density, $q_{Ii}$ is the heat transfer rate from the solid–liquid interface to the crystal, $q_{mI}$ is the heat transfer rate from the melt to the solid–liquid interface, and $R_{i}$ is the crystal radius.

Geometric mode

• 1. Equation for the variation of melt height with time at the solid–liquid interface $\dot{H}_{m}$ ²²:

  $$\dot{H}_{m} = - \frac{{\rho_{s} R_{i}^{2} \left( {V_{p} - \dot{H}_{men} } \right)}}{{\rho_{m} R_{c}^{2} - \rho_{s} R_{i}^{2} }}$$

  (12)

  where $V_{p}$ represents the velocity at which the crystal rises,$\dot{H}_{men}$ indicates the rate at which the meniscus height changes,$\rho_{m}$ denotes the density of the melt, and $R_{c}$ refers to the radius of the crucible.

• 2. The equation for the height of the curved lunar surface is $H_{men}$ ²³:

  $$H_{men} = a\sqrt {\frac{{1 - \sin \left( {\alpha_{0} + \alpha_{c} } \right)}}{{1 + \frac{a}{{\left( {\sqrt 2 R_{i} } \right)}}}}}$$

  (13)

  From Eq. (13) it can be calculated that the

  $$\dot{H}_{men} = \frac{{\partial H_{men} }}{{\partial R_{i} }}\dot{R}_{i} + \frac{{\partial H_{men} }}{{\partial \alpha_{c} }}\dot{\alpha }_{c}$$

  (14)

  here $\dot{R}_{i}$ is the capillary length, also known as the Laplace constant, which is related to the surface tension $\dot{R}_{i}$ and melt density of the meniscus. The value of $\dot{R}_{i}$ is $\dot{R}_{i}$ ,$\dot{R}_{i}$ is the crystal growth angle, and $\dot{R}_{i}$ is the crystal tilt angle²⁴.

• 3. Relationship between the amount of change in crystal radius with time $\dot{R}_{i}$ and the growth rate $V_{g}$:

  $$\dot{R}_{i} = V_{g} \tan \alpha_{c}$$

  (15)

• 4. Change in angle of inclination over time $\dot{\alpha }_{c}$ ²⁵:

  $$\dot{\alpha }_{c} = \frac{{V_{p} - V_{cruc} - C_{\alpha z} V_{g} }}{{C_{\alpha n} }}$$

  (16)

  Among them

  $$C_{\alpha z} = 1 - \frac{{\rho_{s} R_{i}^{2} }}{{\rho_{m} R_{c}^{2} }} + \left[ {\left( {1 - \frac{{R_{i}^{2} }}{{R_{c}^{2} }}} \right)\frac{{\partial H_{men} }}{{\partial R_{i} }} - \frac{{2R_{i} H_{men} }}{{R_{c}^{2} }} - \frac{{a^{2} }}{{R_{c}^{2} }}cos\left( {\alpha_{0} + \alpha_{c} } \right)} \right]tan\alpha_{c}$$

  (17)
  $$C_{\alpha n} = \left( {1 - \frac{{R_{i}^{2} }}{{R_{c}^{2} }}} \right)\frac{{\partial H_{men} }}{{\partial \alpha_{c} }} + \frac{{a^{2} R_{i} }}{{R_{c}^{2} }}sin(\alpha_{0} + \alpha_{c} )$$

  (18)
  $$\frac{{\partial H_{men} }}{{\partial R_{i} }} = \frac{{a^{2} \left[ {1 - sin(\alpha_{0} + \alpha_{c} )} \right]}}{{2\sqrt 2 R_{i}^{2} \left( {1 + \frac{a}{{\sqrt 2 R_{i} }}} \right)S_{\alpha } }}$$

  (19)
  $$\frac{{\partial H_{men} }}{{\partial \alpha_{c} }} = - \frac{{acos\left( {\alpha_{0} + \alpha_{c} } \right)}}{{2S_{\alpha } }}$$

  (20)
  $$S_{\alpha } = \sqrt {\left[ {1 - \sin (\alpha_{0} + \alpha_{c} )} \right](1 + {a \mathord{\left/ {\vphantom {a {\sqrt 2 R_{i} }}} \right. \kern-0pt} {\sqrt 2 R_{i} }})}$$

  (21)

  where $V_{cruc}$ is the crucible rise rate.

• 5. The change in crystal length over time as $\dot{L}$:

  $$\dot{L} = V_{g}$$

  (22)

Long short-term memory (LSTM) network

In the diameter prediction in the constant diameter stage of direct-drawn SSC, the input data required for model construction comes from acquisition and simulation with significant time-series characteristics.The LSTM model, due to its efficient ability to capture the time dependence, is able to deeply mine the temporal correlations in the input data, while adapting to the complex relationships between different features in the multi-input task, and exhibits superior modeling results^21,26.

As explained in^22,27, the LSTM model is a widely recognized deep learning approach for handling sequential data. It includes three key components—the input gate, the forget gate, and the output gate—as well as a cell state. By discarding past information through the forget gate, integrating new information via the input gate, and determining the current hidden state through the output gate, the LSTM dynamically updates and transmits information within its cell state. Compared to conventional recurrent neural networks (RNN), LSTM more effectively capture long-term dependencies, thereby enhancing overall model performance.

RNN

A conventional RNN is a specific kind of neural network designed for handling sequential data. In contrast to feedforward neural networks, RNNs feature an internal recurrent structure that enables them to retain and leverage information from prior states while processing input sequences. This capability allows them to effectively capture temporal dependencies present in the data, as illustrated in Fig. 3.

Fig. 3

Schematic diagram of RNN.

The basic unit of RNN combines the current input with the hidden state of the previous moment through a circular connection to form a new hidden state. Its basic formula is as follows:

$$f_{t} = f(W_{h} \cdot h_{t - 1} + W_{x} \cdot x_{t} + b)$$

(23)

where $h_{t}$ is the hidden state at the current moment, $h_{t - 1}$ is the hidden state at the previous moment,${\text{x}}_{\text{t}}$ is the current input, $W_{h}$ and $W_{x}$ are the weight matrices, b is the bias, and f is usually a nonlinear activation function.

Gating mechanism

In order to improve the shortcomings of the traditional RNN, the LSTM introduces a gating mechanism that allows the network to dynamically select and manage the information at each time step by a combination of three gates to effectively capture long term dependencies, which control the flow of information by designing a series of “gates”. These gates serve to determine which information needs to be retained, updated, or exported, thus effectively managing the cell state and hidden state. This design makes LSTM more powerful and flexible when dealing with complex sequential data.

• 1. Amnesia Gate

The forgetting gate determines how much old information is discarded from the cellular state:

$$f_{t} = \sigma (W_{f} \cdot \left[ {h_{t - 1} ,x_{t} } \right] + b_{f} )$$

(24)

The output of the forgetting gate, denoted as $f_{t}$, varies between 0 and 1. The sigmod activation function, represented as $\sigma$, maps the input to a range of 0 to 1. Additionally,$W_{f}$ refers to the weight matrix,$h_{t - 1}$ indicates the hidden state from the previous time step,$x_{t}$ represents the current input, and $b_{f}$ is the bias term. Finally, the output $f_{t}$ governs the extent of information retained from the prior cell state,$C_{t - 1}$.

• 2. input gate

The input gate determines which new information will be added to the cell state:

$$i_{t} = \sigma (W_{i} \cdot \left[ {h_{t - 1} ,x_{t} } \right] + b_{i} )$$

(25)

where $i_{t}$ is the output of the input gate; $W_{i}$ is the weight matrix and $b_{i}$ is the bias term.

• 3. output gate

The output gate determines the hidden state of the next step :

$$o_{t} = \sigma (W_{o} \cdot \left[ {h_{t - 1} ,x_{t} } \right] + b_{o} )$$

(26)

$$h_{t} = o_{t} *\tanh (C_{t} )$$

(27)

where $o_{{\text{t}}}$ is the output of the output gate; $W_{O}$ is the weight matrix and $b_{O}$ is the bias term.

• 4. cell state

$$C_{t} = f_{t} *C_{t - 1} + i_{c} *\overline{{C_{t} }}$$

(28)

where $C_{t}$ is the weighted sum of the information retained by the previous cell state through the forget gate selection and the new information selected through the input gate.

At each time step, the LSTM’s forget gate decides how much of the previous information to discard, based on the current input. Simultaneously, the input gate selects which essential details to incorporate. Finally, the output gate determines which data from the cell state forms the hidden state, which then becomes the model’s output for the next layer. This synchronized process enables the LSTM to retain critical information over extended periods, effectively capturing long-term dependencies, as illustrated in Fig. 4.

Fig. 4

Schematic diagram of LSTM network.

BiLSTM

For diameter prediction in the constant diameter stage of CZ SSC, various types of data need to be linked to the past and future information related to the prediction point, and BiLSTM can better model complex feature interactions and dependencies for multiple input tasks such as simulated diameter, lifting speed, heater power, etc. in the training of the model^28,29.

The BiLSTM is an extended LSTM model that consists of two LSTM modules, one that reads from the forward to the time series (forward LSTM) and the other that reads from the backward to the time series (backward LSTM). This bi-directional structure enables the model to fully capture the contextual information and aims to improve the understanding of sequence data by considering both forward and backward information of the sequence.

The basic structure is a forward LSTM that needs to deal with the natural order of the sequence, from the first to the last time step $(x_{1} ,x_{2} ,...,x_{T} )$, and a backward LSTM that needs to deal with the reverse order input sequence, from the last time step to the first time step $(x_{T} ,x_{T - 1} ,...,x_{1} )$. In this model, the input signal passes through the forward LSTM layer output $\overrightarrow {{h_{t} }}$ and the backward LSTM layer output $\overleftarrow {{h_{t} }}$, which together determine the values passed into the hidden layer, to obtain the output of BiLSTM $y_{t}$, which is updated with the formula.

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{h_{t} }} = LSTM(x_{t} ,\mathop{h}\limits^{\rightharpoonup} _{t - 1} )$$

(29)

$$\overleftarrow {h}_{t} = LSTM(x_{t} ,\overleftarrow {h}_{t - 1} )$$

(30)

$$y_{t} = \overrightarrow {W} \overrightarrow {{h_{t} }} + \overleftarrow {W} \overleftarrow {{h_{t} }} + b$$

(31)

The hidden states of the forward and backward LSTM are spliced and the output is obtained:

$$h_{t}^{BILSTM} = [h_{t}^{forword} ,h_{t}^{backward} ]$$

(32)

The output of BILSTM is used as input for subsequent tasks. Further processing can be performed using a fully connected layer, as shown in Fig. 5.

Fig. 5

Schematic diagram of BILSTM network.

AdaBoost based prediction models

The growth process of direct-drawn SSC is complex, characterized by large hysteresis and high nonlinearity. Since a single BiLSTM model does not predict well when dealing with the multiple-input single-output case, it is particularly important to improve the model’s ability to model complex multi-class data features in practical applications. Such improvement can help us to better predict the diameter of direct-drawn SSC, thus improving production efficiency and quality^25,26,30,31.

In the field of crystal diameter prediction, commonly used ensemble learning methods include Gradient Boosting, XGBoost, Random Forest, and AdaBoost. Based on the specific requirements of the Czochralski process for crystal diameter prediction, Table 1 summarizes and compares the advantages and disadvantages of these algorithms, providing a reference for selecting an appropriate model.

Table 1 Advantages and disadvantages of each algorithm.

AdaBoost is a method of ensemble learning aimed at improving classifier performance. It creates a robust classifier by merging several weak classifiers, training each new model specifically on the mistakes made by the previous one. Through the modification of sample weights, AdaBoost highlights the samples that were misclassified, which ultimately leads to enhanced accuracy in the classification system.Therefore, we opt to use AdaBoost. The process of modeling can be summarized as follows:

• 1. Weight distribution:

The algorithm, for a given training dataset $T = \left\{ {(x_{1} ,y_{1} ),(x_{2} ,y_{2} )...(x_{t} ,y_{t} )} \right\}$, initializes the weights of each sample by assigning the same weights: $w_{i} = 1/N$, such that the initial weight distribution of the training sample set $D_{1} (i)$:

$$D_{1} (i) = \left( {w_{1} ,w_{2} , \ldots w_{N} } \right) = \left( {\frac{1}{N}, \ldots ,\frac{1}{N}} \right)$$

(33)

where $D_{1} (i)$ is the weight of sample N in round t.

• 2. Training a weak classifier

After completing several iterations, a weak classifier, denoted as $H_{t}$, is trained at round t utilizing the existing sample weights $D_{1} (i)$. The weak classifier h, which exhibits the smallest error rate at this point, is chosen as the tth basic classifier $H_{t}$. Subsequently, the weak classifier $H_{t} :X \to \left\{ { - 1,1} \right\}$ is computed, which incurs an error on the distribution $D_{t}$.

$$e_{t} = P(H_{t} (x_{i} ) \ne y_{i} ) = \sum\limits_{i = 1}^{N} {w_{ti} I} (H_{t} (x_{i} ) \ne y_{i} )$$

(34)

where the error rate of $H_{t} (x)$ on the training set $e_{t}$ is the sum of the weights of the samples misclassified by $H_{t} (x)$.

• 3. Calculate the weights of weak classifiers

Calculate the weights of the classifier $H_{t}$ based on the current error rate of the weak classifier:

$$a_{t} = \frac{1}{2}\ln (\frac{{1 - e_{t} }}{{e_{t} }})$$

(35)

where $a_{t}$ denotes the degree of contribution of weak classifiers.

• 4. Update sample weights

Update the weight distribution of the training samples $D_{t + 1}$:

$$D_{t + 1} = \frac{{D_{t} (i)\exp ( - a_{t} y_{i} H_{t} (x_{i} ))}}{{Z_{t} }}$$

(36)

where $Z_{t}$ is a normalization constant $Z_{t} = \sqrt {e_{t} (1 - e_{t} )}$.

• 5. Combinatorial weak classifier

Combine each weak classifier by its weight $a_{t}$ with the following formula:

$${\text{f}}(x) = \sum\limits_{t = 1}^{T} {a_{t} H_{t} (x)}$$

(37)

$$H_{final} = sign(f(x)) = sign(\sum\limits_{t = 1}^{T} {a_{t} H_{t} (x)} )$$

(38)

where T is the total number of weak classifiers and the sign function is used to transform the output into a classification result.

AdaBoost is a powerful ensemble learning method that can effectively enhance model performance by combining multiple weak classifiers. Figure 6 illustrates the AdaBoost training process, which includes key steps such as initialization of sample weights, training and weighting of weak classifiers, and the integration of the final model. To evaluate the model’s effectiveness, the previously mentioned metrics provide comprehensive insights into various aspects of performance. By appropriately adjusting parameters and model design, AdaBoost can achieve excellent results in many practical applications.

Fig. 6

ADABOOST training flow.

The advantages of AdaBoost are particularly evident in this study. Its iterative reweighting mechanism prioritizes samples with higher prediction errors, which is crucial for addressing the highly nonlinear and lag-dominated dynamic characteristics of the CZ crystal growth process. Unlike Bagging-based methods (e.g., Random Forest), which treat all samples equally, AdaBoost explicitly focuses on the residual errors of preceding weak learners, enabling targeted compensation for systematic biases in the mechanistic model’s predictions. Additionally, compared to methods like Gradient Boosting or XGBoost, which rely on gradient descent to optimize complex loss functions, AdaBoost’s additive model structure is more suitable for real-time control in industrial crystal growth environments. Its simplicity allows for seamless and efficient integration with BiLSTM outputs without introducing excessive computational overhead. Given that the features generated by BiLSTM inherently possess temporal dependencies and noise, AdaBoost effectively combines diverse weak regressors—even those with moderate individual accuracy—into a robust ensemble model. This helps mitigate the risk of overfitting, particularly in scenarios with limited training data, which is a common constraint in industrial settings.

Hybrid driven modeling approach based on BiLSTM and Adaboost algorithm

The proposed hybrid modeling approach integrates the BiLSTM algorithm and the Adaboost algorithm, where the former bi-directionally processes the data related to the prediction of the input crystal diameter through two independent LSTM networks in both the forward and backward directions, thus capturing the information of the past and future directions in the input sequences; and the latter iteratively trains multiple weak classifiers based on the data generated by the BiLSTM algorithm and gradually optimizes the overall prediction performance by assigning different weights to the results of each classifier. The latter iteratively trains multiple weak classifiers based on the data generated by the BiLSTM algorithm, and assigns different weights to the results of each classifier to gradually optimize the overall prediction performance.

As shown in Fig. 7, the steps to realize the prediction of crystal diameter during SSC growth are as follows:

• 1. Data Acquisition:Collecting data from the actual SSC growth process as well as the crystal growth model constructed based on the first-principles model under different working conditions in multiple furnaces to enrich the sample data set of the experiment.

• 2. mechanistic model simulation: Through Simlink simulation, input the lifting speed and heater power under actual working conditions, and get the prediction data of the diameter of the mechanistic model with large error.The diameter predicted by the purely mechanistic model only reaches about 70% of the actual crystal diameter.

• 3. Data preprocessing: the data to be put into the model training, the missing values, outliers processing, and filter out the random noise in the data, normalize the data, divided into training set and test set.

• 4. Training the BiLSTM Model: A bidirectional BiLSTM network is established to create the BiLSTM model. This network encompasses the following layers: an input layer, a bi-directional LSTM layer, a flattening layer, a fully connected layer, a ReLU activation layer, and an output layer. The data gathered in the earlier steps, including variables such as lifting speed, heater power, the diameter actually measured, and the discrepancy between the simulated and real diameters, are fed into the model. Subsequently, hyperparameters—including the learning rate, the number of training epochs, and the gradient threshold—are fine-tuned to optimize model training. The predictive outputs for the input samples from the trained individual BiLSTM model serve as a weak learner for the subsequent stage of the AdaBoost algorithm.

• 5. Adaboost Integrated Learning: This approach develops multiple weak classifiers by utilizing features produced by BiLSTM as input. Initially, each sample is assigned equal weights. The features generated by BiLSTM are iteratively trained to build the weak classifiers; if a sample is correctly classified, its weight is decreased for the next training set, while incorrectly classified samples see their weights increased. The adjusted sample set is then employed to train the subsequent classifier. Ultimately, all weak classifiers’ outputs are amalgamated to create a robust classifier. After the completion of training for each weak classifier, the weights of those with lower classification error rates are elevated, while weights for classifiers with higher error rates are diminished. The final bias compensation is based on the difference between the predicted actual diameter and the diameter modeled mechanically.

• 6. The prediction of crystal diameter during SSC growth can be realized by inputting the measured data into the constructed module of hybrid modeling after summing up the difference with the difference prediction value.

Fig. 7

Hybrid modeling predictions based on BILSTM-ADABOOST.

The bidirectional structure of BiLSTM can capture both past and future information simultaneously (such as the lag effects of pulling speed and heating power), thereby enhancing the feature extraction capability for time series data. AdaBoost, through iterative weighting of weak learners (BiLSTM), reduces the influence of high-error samples, decreases overfitting, and improves robustness. The hybrid modeling approach combines a mechanistic model with a data-driven model—the former provides physical constraints, while the latter corrects residual errors—achieving a balanced trade-off between interpretability and accuracy.

BiLSTM-AdaBoost feature importance analysis

In the BiLSTM–AdaBoost hybrid-driven modeling proposed in this paper, the base learner is a deep network (BiLSTM) rather than a decision tree, so it cannot directly output “feature importance” metrics like tree-based models. Therefore, the Permutation Feature Importance method is used to compare feature importance. The specific steps are as follows:

First, the model’s prediction error (MSE) on the unperturbed data is calculated as the baseline performance. Then, the values of a single feature are randomly permuted (i.e., shuffled), disrupting the association between that feature and the target variable, while keeping all other features unchanged. The prediction error (MSE) of the model on the perturbed data is then computed and compared with the baseline error. If the error increases significantly after the perturbation, it indicates that the feature is important for the model’s prediction. Conversely, if there is little to no change, the feature is considered unimportant.

For the initial dataset $D$, the mean squared error (MSE) of model $f_{k}$ is:

$$MSE_{k}^{{}} = \frac{1}{M}\sum\limits_{i = 1}^{M} {\left( {f_{k} \left( {X_{i}^{{}} } \right) - y_{i} } \right)^{2} }$$

(39)

Feature $j$ is permuted to generate the perturbed dataset $D^{(j)}$, and the mean squared error (MSE) of model $f_{k}$ on $D^{(j)}$ is:

$$MSE_{k}^{(j)} = \frac{1}{M}\sum\limits_{i = 1}^{M} {\left( {f_{k} \left( {X_{i}^{(j)} } \right) - y_{i} } \right)^{2} }$$

(40)

The importance score of feature $j$ for model $f_{k}$ is:

$$\Delta MSE_{k}^{(j)} = \frac{1}{M}\left[ {MSE_{K} - MSE_{K}^{(j)} } \right]$$

(41)

where $X_{i}$ is the dataset input, $y_{i}$ is the dataset output, and $f_{k}$ is the network model used—in this paper, it refers to the $k$-th BiLSTM model.

After integrating k weak learners, the global importance of feature $j$ is:

$$P_{j} = \sum\limits_{k = 1}^{K} {\left[ {\left( {\frac{1}{2}\ln (\frac{{1 - \varepsilon_{k} }}{{\varepsilon_{k} }})} \right).\left( {\Delta MSE_{k}^{(j)} } \right)} \right]}$$

(42)

where $\varepsilon_{k}$ is the weighted classification error, which is normalized to obtain a percentage form.

As shown in Fig. 8,The global feature importance scores are 0.1714, 0.2312, 0.1389, 0.2415, and 0.2169, respectively, indicating that Table 2 (heating power of the heater), Feature 4 (the discrepancy between the actual crystal radius and that predicted by mechanical models), and Feature 5 (radius measurement value) play a more significant role in model training. This is consistent with the previously mentioned Pearson correlation analysis and also aligns with real-world conditions.

Fig. 8

Feature importance analysis.

Table 2 Analysis of parameters for different feature values.

Weight distribution:

Industrial experiment simulation

In the previous section, we developed a hybrid BILSTM-ADABOOST driven model designed to more accurately predict the diameter of crystals during the growth of CZ SSC. In this section, we compare the performance of this model with other data-driven modeling methods.

Indicators for evaluating the performance of each model

To enable a comprehensive comparison of model performance, this study employs five evaluation metrics, summarized in Table 3. MSE measures the average of squared differences between actual and predicted values, highlighting the accuracy of the predictions. RMSE further indicates the magnitude of these errors. MAE tracks average absolute differences between observed and predicted outcomes, reflecting the model’s reliability. MAPE captures forecasting accuracy as a percentage error. Lastly, R2 gauges the proportion of variance in the dependent variable explained by the independent variables, delivering a thorough assessment of the model’s explanatory power.

Table 3 Model performance evaluation indicators.

Forecast results and analysis

In this instance, the SSC diameter during the CZ SSC growth process is established as the target variable. Utilizing data on the growth of the 12 inch SSC collected from the TDR-180 single crystal furnace between October 13 and October 20, 2020, the predictive capability of the proposed model is assessed by continuously sampling data throughout the constant diameter growth phase of the crystals. Figure 9 Actual diameter measurements in the constant diameter stage of the crystal.

Fig. 9

Actual diameter measurements in the constant diameter stage of the crystal.

In the experimental processing section, the core method for selecting 2,000 samples from 6,000 original time-series data points is based on a sliding window extraction mechanism and a data timeliness filtering principle. Using the sliding window approach, the window moves with a step size of 2, meaning each adjacent sample is spaced by 2 time points, thereby avoiding excessive data overlap. After theoretically generating approximately 3,000 candidate samples, the most recent 2,000 windowed samples at the end of the time series are retained with priority. This aims to optimize computational efficiency (reducing memory usage by 33%), enhance learning of recent dynamic patterns, and avoid interference from outdated data.

The dataset is partitioned using a non-random chronological split strategy (the first 80% for training, the last 20% for testing), strictly preserving temporal causality to prevent future data leakage, ensuring that model evaluation aligns with the physical constraints of real-world forecasting scenarios. This strategy adheres to common standards in the time-series prediction field, balancing engineering feasibility with academic rigor.

Handling outliers

When analyzing experimental data, a small number of data points may significantly deviate from the expected data distribution. If these outliers are not identified and removed, they can adversely affect the accuracy of To properly handle outliers in the dataset, this study adopts the 3-sigma rule. Let the actual measured value be $x_{1} ,x_{2} , \cdots ,x_{n}$, the arithmetic mean be $\overline{x} = 1{/}n \cdot (\sum\nolimits_{i = 1}^{n} {x_{i} } )$, the absolute error be $\Delta x_{i} = x_{i} - \overline{x}$, and the standard error be $\hat{\sigma } = [\sum {{{\Delta x_{i}^{2} } \mathord{\left/ {\vphantom {{\Delta x_{i}^{2} } {(n - 1)}}} \right. \kern-0pt} {(n - 1)}}} ]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$. If the absolute error $x_{d}$ of the measured value $\Delta x_{i}$ satisfies condition $\left| {\Delta x_{i} } \right| > 3\hat{\sigma }$, then $x_{d}$ is identified as an outlier and should be eliminated.

Data normalization processing

In data-driven soft sensing modeling, the use of auxiliary variables is essential. Due to potential differences in the numerical scales of various auxiliary variables, directly using raw values for computation may prolong the network’s learning time. Therefore, it is particularly important to perform normalization on both input and output data. Specifically, the normalization is carried out using the formula shown in Eq. (39).

$$\hat{x}_{i} = \frac{{x_{i} - \overline{x}}}{{x_{\max } - x_{\min } }}$$

(39)

In the equation:$x_{i}$ and $\overline{x}$ represent the $i$-th variable of $x$ and its mean value, respectively; $x_{\max }$ and $x_{\min }$ represent the maximum and minimum values of $x$, respectively; $\hat{x}_{i}$ is the normalization result.

The growth environment and process of CZ SSC is notably intricate, marked by a multitude of interrelated factors that can influence outcomes. This paper focuses on examining specific variables that pertain to the crystal radius at the constant diameter stage of growth. In a real industrial setting, various variables exert significant influence over the crystal radius. These include, among others, the speed at which the crystal is lifted, the rotation speed of the crystal, the lifting speed of the crucible, the rotation speed of the crucible, as well as the turn speed of the crystal and the rise speed of the crucible. In addition to these mechanical parameters, thermal factors such as the temperature of the liquid surface and the temperature within the hot field further contribute to the overall growth dynamics.To refine the prediction accuracy for the crystal diameter, the paper employs data gathered from practical crystal pulling experiments alongside statistical analysis through Pearson’s correlation coefficient. This analysis identifies several key variables that play a crucial role in diameter prediction, namely the heating power of the heater,pulling rate, the discrepancy between the actual crystal radius and that predicted by mechanical models, as well as the measured radius itself. Subsequently, these primary influencing variables are utilized in further modeling activities aimed at improving the predictive capabilities regarding the crystal diameter, enhancing the efficiency and quality of the crystal growth process.

In this paper, hybrid modeling is used to complete the crystal radius prediction, firstly, we need to get the diameter prediction value of the mechanistic model in simulink simulation, as shown in Fig. 10, and then make difference with the actual measurement value to compensate for the error of the simple mechanistic modeling and improve the prediction accuracy, and then we will use the difference value and other variables as the inputs and outputs to train the data-driven BILSTM-ADABOOST model.

Fig. 10

Mechanistic model crystal diameter predictions.

To evaluate the metrics of the BILSTM-ADABOOST model, various models including CNN, LSTM, GRU, CNN-BILSTM, CNN-LSTM, and LSTM are employed alongside BILSTM and the BILSTM-ADABOOST for diameter prediction and comparative analysis. The prediction outcomes of the BILSTM-ADABOOST algorithm, including prediction errors, are illustrated in Fig. 11. Figure 12 presents a comparison of the prediction performance of the different modeling approaches, while Fig. 13 depicts the prediction error comparison among these methods (Table 4).

Fig. 11

Prediction results of BILSTM-ADABOOST algorithm and prediction errors.

Fig. 12

Comparison of the prediction effect of each modeling method.

Fig. 13

Comparison of prediction errors between modelling methods.

Table 4 Parameter configuration for each algorithm.

Based on the data in Table 5, the comparison algorithms are CNN, GRU, CNN-BILSTM, CNN-LSTM, LSTM, BILSTM, and BILSTM-ADABOOST.From the R2 perspective, the value increases from 56.434% (CNN) to 95.483% (BILSTM-ADABOOST). This indicates that the latter can capture data trends and features more thoroughly, achieving the highest prediction accuracy.

Table 5 Predictive performance metrics for each model.

Table 5 presents the training times for each model. As shown in the table, the standalone models have relatively short training times, generally within 10 s. Due to the increased complexity of the hybrid model, its training time is comparatively longer. However, considering the slow-changing nature of semiconductor silicon single crystal production, the training time of the BiLSTM-AdaBoost model remains within practical limits. Furthermore, the training time can be reduced through model structure optimization (e.g., limiting the number of weak learners and adjusting the number of LSTM layers) as well as the use of parallel computing.

From the MSE/RMSE perspective, the BILSTM-ADABOOST model has the lowest MSE of 5.038 × 10⁻⁹, with a corresponding RMSE of only 7.098 × 10⁻5. This shows that BILSTM-ADABOOST has a smaller overall error in terms of numerical scale.From the MAE perspective, the absolute error decreases from 2.501 × 10⁻4 (CNN) to 5.917 × 10⁻5 (BILSTM-ADABOOST). This demonstrates that deeper or integrated deep learning methods have an advantage in reducing absolute error.From the MAPE perspective, all models have relatively small values (0.031%–0.131%), showing good overall performance. However, BILSTM-ADABOOST has the lowest MAPE of 0.031%, indicating a very small percentage error compared to the true value. This reflects higher predictive accuracy and stability.

In summary, hybrid models tend to achieve better results than single models, especially BILSTM-ADABOOST outperforms other comparative models in all indicators, suggesting that: the combination of two-way LSTM’s ability to capture time-series features and AdaBoost algorithm’s idea of iterative weighting of the weak learners jointly improves the model-fitting ability, significantly reduces the error,and improves the recognition accuracy.

Conclusion

This study proposes a novel hybrid-driven modeling approach for predicting the crystal diameter during the isothermal stage of CZ SSC growth. The method integrates a mechanistic model with a data-driven framework that combines BiLSTM networks and the AdaBoost algorithm. Compared to traditional mechanistic models and standalone data-driven models, the proposed hybrid model significantly improves prediction accuracy. Experimental results demonstrate that the BiLSTM-AdaBoost model achieves an R2 of 95.483%, a mean absolute error (MAE) of 5.917 × 10⁻5, and a mean absolute percentage error (MAPE) of 0.031%, indicating its superior capability to capture the complex nonlinear dynamics of the CZ process. Moreover, by leveraging AdaBoost’s error-driven adaptability and BiLSTM’s temporal dependency modeling, the hybrid model exhibits strong robustness to noise and fluctuations in input data, making it particularly suitable for real-time industrial applications with variable data quality. The lightweight ensemble structure of AdaBoost and the parallel processing capability of BiLSTM also ensure computational efficiency, enabling real-time control of crystal diameter under high-temperature, multi-physics environments. Importantly, this hybrid approach maintains the physical interpretability of mechanistic models while incorporating the flexibility of data-driven methods, ensuring that predictions align with the underlying physical dynamics of crystal growth. Overall, the proposed method provides a robust framework for real-time diameter control in industrial SSC production, contributing to defect reduction, yield improvement, and the advancement of semiconductor manufacturing technology.