Introduction

To resolve this energy problem, extensive research has been directed towards the discovery and modeling of new materials. The remarkable efficiency of lead-based organic and inorganic perovskites in converting solar energy into electrical energy has garnered significant attention1,2,3,4,5,6,7,8. The high charge carrier mobility and the nature of direct bandgap semiconductors characterize these materials as having an optimal dielectric constant, excellent diffusion, and strong absorption properties. These characteristics have enabled solar cell efficiency to reach 25%8,9,10,11. The mechanical, thermal, and chemical properties are crucial for ensuring the durability of materials in practical applications. The thermal and chemical stability of these materials can be inferred from their negative enthalpy values. Beyond their intriguing academic interest, these materials have significant technological and industrial potential. Additionally, these materials are utilized in diverse technological applications, such as laser and photo detectors12,13,14,15,16,17,18 X-ray instruments, and LEDs19,20,21,22. However, their use in photovoltaic devices is constrained by the harmful properties of lead23,24,25,26,27.

Owing to the toxicity of lead, research has shifted towards developing lead-free alternatives. M. Ilyas has author studied the elastic, electronic, and optical characteristics of CsXCl3 (X = Pd, Cd)28,29. Their findings indicated that CsCdCl3 behaved as an indirect bandgap semiconductor. Elastic studies have shown that this compound is elastically stable and exhibits ductile characteristics30. Additionally, research has revealed that these materials have a broad absorption spectrum, making them suitable for optical applications31,32. Ayaz et al. analyzed the properties of CsXCl3, where X is Be or Rh. They found that both materials exhibit metallic behavior when exposed to ultraviolet light, making them suitable for use in photodetectors and UV light emitters32,33,34,35. Similarly, A.A Mubarak and A.A Musa36 examined the electronic and optical characteristics of Li-based perovskite BaXF3, where X is Li, Na, K, or Rb. Their research indicated that these materials are semiconductors with a direct bandgap, and they predicted that these compounds could behave as metals at high incident photon energies. Raza et al. conducted a study on cubic perovskite compounds, RbXF3, where X represents ¼Mn, V, Co, and Fe. Their research focused on exploring the properties and potential applications of specific perovskite materials. Using GGA + U approximation within the WIEN2k code37,38,39,40. They reported that these compounds exhibited half-metallic and ferromagnetic properties, suggesting their potential use in spintronic devices. Somia et al. found that AMoO3 (A = Ca, Sr, and Ba) compounds exhibit metallic and paramagnetic behavior and are elastically and thermodynamically stable41,42. In this study, we examined the structural, electronic, elastic, and optical properties of Mg-based perovskite MgXCl3 (X = Rb, Ca) using the full potential linearized augmented plane wave method implemented in the WIEN2k code43,44,45,46,47,48. To the best of our knowledge, this is the first comprehensive analysis of these materials, as no previous studies have addressed their structural, electronic, optical, or elastic characteristics.

Computational methodology

Numerous properties of Mg-based perovskites MgXCl3 (X = Rb, Ca) have been analyzed using the full-potential linearized augmented plane wave (FPLAPW) method within the WIEN2k framework49,50,51,52,53,54,55,56,57,58. The exchange–correlation potential was treated using the Generalized Gradient Approximation (GGA) combined with an additional Hubbard U correction with a U value of 0.43 to obtain accurate results. Structural parameters were analyzed using Murnaghan’s state equation by adjusting the energy relative to the volume. The IR-Elast package, integrated within the WIEN2k code, was used to compute the elastic constants from which various elastic parameters were derived. A cutoff energy of − 6.0 Ry was specified for both materials, with an RMT value of 4.0 and a k-point value of 2000. The Gmax value was set as 12. The electronic properties were determined using density functional theory (DFT) calculations, with the band structure and density of states (DOS) computed to analyze the electronic characteristics. The optical properties were examined using the complex dielectric function ε(ω) = ε1(ω) + iε2(ω), with optical spectra computed using the finite displacement method and analyzed through the Phonopy code in conjunction with VASP. The elastic properties, including bulk modulus, shear modulus, Young’s modulus, and Poisson’s ratio, were derived from the calculated elastic constants. The 3D elastic properties were computed using Python 3.11.2, employing stress–strain analysis to extract the elastic stiffness tensor (Cij). The calculated elastic constants were then used to evaluate mechanical stability and anisotropy. The phonon dispersion calculations were performed using the density functional perturbation theory (DFPT) approach, which provided insight into the dynamical stability of the materials. These comprehensive analyses contribute to understanding the structural, electronic, optical, and mechanical behavior of the studied compounds59,60,61,62,63.

Result and discussion

In this portion, we will provide a comprehensive overview of the structural, elastic, electronic, and optical properties of Mg-based perovskites, highlighting key findings and insights into their behavior and potential applications MgXCl3 (X = Rb, Ca).

Structural properties

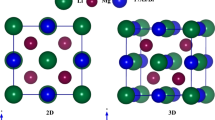
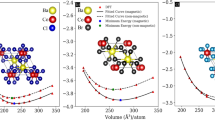
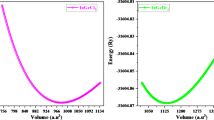
First, the fully optimized structures of the Mg-based perovskites MgXCl3 (X = Rb, Ca) were determined. Figure 1 shows the optimized and stable structures. Both structures are classified under the pm-3m (221) space group and display cubic symmetry. Wyckoff positions of the atoms are as follows: Mg at (0, 0, 0), Rb/Ca at (0.5, 0.5, 0.5), and Cl at (0, 0.5, 0.5). The structural parameters, including the lattice constant (a₀) and ground state energy (E₀), were obtained using the Birch-Murnaghan equation, which is a standard approach for analyzing the relationship between pressure and volume changes in materials. Furthermore, the bulk modulus (B₀), a measure of the material’s resistance to compression, and its derivative (B'), which describes how the bulk modulus changes with pressure, were also calculated to provide a comprehensive understanding of the material’s mechanical properties64,65. The bulk modulus of MgXCl3 (X = Rb, Ca) was found to be higher than that of MgXCl3 (X = Rb, Ca), which is attributed to the higher electronegativity of Ca (1.0 eV) compared to that of Rb (0.95 eV). All the calculated structural parameters are detailed in Table 1. To gain deeper insights into the structural stability of the studied compounds, energy versus volume curves were plotted and analyzed, as illustrated in Fig. 2. This analysis helps evaluate how the energy of the system changes with variations in volume, providing a measure of the stability of the compound. Additionally, to further assess the structural integrity of the perovskite compounds66, Goldschmidt’s tolerance factor (t)67 and octahedral factor (m) were applied. These factors were used to gauge the degree to which the compounds maintained their structural configuration. The formulas for determining the above factors are as follows:

Fig. 1
figure 1

Compute crystal structure of cubic perovskite of MgXCl3 (X = Rb, Ca).

Full size image
Table 1 The compute value of volume lattice constant and formation energy of cubic perovskite MgXCl3 where (X = Rb & Ca).
Full size table
Fig. 2
figure 2

Compute volume optimization of cubic perovskite of MgXCl3 (X = Rb, Ca).

Full size image
$$t=\frac{{r}_{j}+rL}{\sqrt{2}({r}_{k}+rL)}$$
(1)
$$u=\frac{{r}_{j}}{{r}_{k}}$$
(2)

In these equations, rJ and rK represent the radii of Mg and Cl/Rb, respectively, and rL denotes the radii of Cl. For a cubic perovskite structure, the Goldschmidt tolerance factor (t) should fall within the range of 0.7–1.0, and the octahedral factor (m) should be between 0.4 and 0.7. The calculated values for the structural parameters of these compounds are detailed in Table 1, and they fall within the specified ranges, confirming that both compositions exhibit a stable crystal structure characterized by cubic symmetry. This stability is crucial for practical applications of these materials.

The formation energy, which reflects the energy change associated with the formation of compounds from their constituent elements, is a key factor for evaluating their thermodynamic stability. A lower formation energy typically indicates greater stability and a more favorable formation process. To determine the formation energy of these compounds, the following equation is used

$$\Delta {H}_{f}={E}_{tot}-\mu A-\mu B-3\mu X$$
(3)

In Eq. (3), ΔHf represents the formation energy, which quantifies the energy change when the compound is formed from its constituent elements. The term Etot denotes the total energy of the compound under consideration, while μA, μB and μX are the chemical potentials of the elements Mg, X, and Cl66,67. These chemical potentials reflect the energy associated with the presence of each element in the reference state. The calculated formation energies ΔHf for the compounds are detailed in Table 1. A negative value for ΔHf signifies that the compound is energetically favorable to form, meaning that the formation of the compound releases energy and thus is thermodynamically stable. This implies that the compounds are not only stable but also likely to be synthetically feasible and maintain their structural integrity under typical laboratory.

Electronic response

To analyse the electronic structure of Mg-based perovskites MgXCl3 (where X = Rb, Ca), we conducted a detailed examination of both the energy bandgap and DOS. The results of this analysis are shown in Figs. 3 and 4, respectively. In these graphical representations, the zero- energy level is used as a reference point to delineate the energy band gap, which is characterized by the boundary between the conduction and valence bands. This approach provides insight into the fundamental electronic properties of perovskites, highlighting the energy ranges in which electron transitions occur. Figure 3 shows that both compounds behave as semiconductors. In these materials, the lowest energy level of the valence band is observed at the R-point, whereas the highest energy level of the conduction band is located at the G-point. This configuration resulted in an indirect bandgap (R–G) for both compounds. Specifically, the band gap energy is calculated to be 1.16 eV for MgRbCl3 and 0.853 eV for MgCaCl3. This indirect band gap implies that the transition of electrons between the valence and conduction bands involves a change in momentum, reflecting the semiconducting behavior of the compounds and influencing their electronic and optical properties.

Fig. 3
figure 3

Compute electronic band structure of cubic perovskite of MgXCl3 (X = Rb, Ca).

Full size image
Fig. 4
figure 4

Compute electronic partially density of state of cubic perovskite of MgXCl3 (X = Rb, Ca).

Full size image

The density of states (DOS) offers detailed insights into how different energy levels are distributed within the band structure of a material. Figure 4 illustrates the projected density of states (PDOS) of the studied perovskite compounds. This figure helps us to understand the contribution of specific atomic orbitals to the overall electronic structure of the compounds. The total density of states demonstrates that both MgRbCl3 and MgCaCl3 are wide-bandgap semiconductors, suggesting that they have significant energy separations between the valence and conduction bands. This separation is a key characteristic of semiconductors with large band gaps. In MgRbCl3, the PDOS shows that the Ag-d orbitals play a crucial role in the valence band, particularly within the energy interval of  − 1.8 eV to − 2.2 eV. This implies that these orbitals are significantl y involved in defining the electronic properties of the valence band within this energy range. In contrast, for MgCaCl3, the contribution of Ag-d orbitals is most significant in a slightly different energy range, from − 2.2 to − 2.6 eV, indicating their involvement in the valence band within this specific range. Chlorine (Cl-p) orbitals were also significant contributors to the valence band in both compounds. Their influence is prominent in the energy range 0 to − 2 eV, highlighting their role in shaping the valence band structure. For calcium (Ca) and strontium (Sr), their contributions extend across both the valence and conduction bands. Specifically, Ca-d orbitals play a role in the valence band in the energy interval between − 1 and − 2 eV. eV and extends into the conduction band at energies above 5.9 eV. This suggests that Ca-d orbitals have a dual role, affecting both the lower- and higher-energy regions. Similarly, Sr-d orbitals are involved in the valence band within the range of − 0.5 to − 2 eV, and their impact extends into the conduction band at energies greater than 6 eV. This dual contribution indicates the significant role of the Sr d orbitals in both the lower and upper parts of the band structure.

Elastic properties

The elastic properties of the cubic crystal structures are governed by three fundamental elastic constants: C11, C12, and C44. These constants describe how a material deforms under various types of stresses. In this investigation, the elastic constants for the Mg-based perovskites MgXCl3 (X = Rb, Ca) were determined using IR-Elast software, which is part of the WIEN2k computational package. The results, detailed in Table 2, show the calculated values of these elastic constants. The positive values obtained for C11, C12, and C44 adhere to the born stability criteria, which are necessary to ensure the mechanical stability. This indicates that both MgRbCl3 and MgCaCl3 possess structural resilience and are likely to remain stable under mechanical stress, confirming their mechanical robustness. Adherence to these criteria further supports the reliability of these materials in practical applications, where mechanical stability is crucial67. Furthermore, the value of C11 exceeded those of both C12 and C44, suggesting that the analyzed compounds exhibited greater resistance to compression along the x-axis. The bulk modulus (B) measures the solidity of a material; a higher B value indicates greater resistance to deformation under compression. The calculated bulk modulus of MgCaCl3 was higher than that of MgRbCl3, indicating that MgCaCl3 was harder. Consequently, MgCaCl3 experiences a smaller change in volume when subjected to uniform compression in all directions than MgRbCl3. This implies that MgCaCl3 exhibited superior hardness and structural stability under compressive forces. The shear modulus (G) of MgRbCl3 was higher than that of MgCaCl3, suggesting that MgRbCl3 can endure greater transverse deformation. The ductility or brittleness of a material is often evaluated using the Pugh’s ratio, which is defined as the ratio of the bulk modulus (B) to the shear modulus (G). According to Pugh’s criteria, if the B/G ratio exceeds 1.75, the material is considered to be ductile. If it is below this limit, then the material is considered brittle63. The computed Pugh ratio values for the perovskites under investigation are listed in Table 2. These values indicate that both MgRbCl3 and MgCaCl3 exhibit ductility and that they are capable of undergoing significant deformation before fracturing. The anisotropy factor (A) quantifies how a material’s properties differ with the direction, thereby characterizing its anisotropic nature. For the perovskite compound MgXCl3 (where X = Rb, Ca), the calculated anisotropy factors show deviations from the value of 1, which signifies that these materials exhibit anisotropic properties, meaning that their mechanical or physical characteristics vary with direction. The Cauchy pressure parameter, calculated as (C12–C44), provides insight into the type of bonding present within the material. Positive Cauchy pressure values suggest that the material exhibits predominantly ionic bonding, whereas negative values would indicate the presence of directional bonding. The observed positive values of the Cauchy pressure parameter in these compounds confirm that their bonding nature is primarily ionic.

Table 2 The computed elastic moduli, the young’s modulus E, bulk modulus B, Shear Modulus G, Poisson’s ratio (v), Pugh’s index ratio B/G, anisotropy factor A, and lattice constants Cij [GPa] at equilibrium volume.
Full size table

The Kleinman parameter (z) assesses internal strain and indicates the preferred mode of atomic bond deformation. This parameter helps to understand whether bond stretching or bending is favored within the material62. When the Kleinman parameter is close to unity, it suggests that bond stretching is more favorable, whereas a value approaching zero implies a preference for bond bending. For MgRbCl3 and MgCaCl3, the Kleinman parameter values were near zero, indicating that bond bending was the predominant deformation mode in these materials. This implies that the compounds are more likely to undergo bending of the atomic bonds rather than stretching under stress. Figure 5 show the 3D visualization of Young’s modulus for MgRbCl₃ and MgCaCl₃, illustrating their elastic anisotropy. In Fig. 5a, the Young’s modulus of MgRbCl₃ exhibits an irregular shape, indicating significant directional dependence of its stiffness. The deviation from a perfect sphere suggests variations in the material’s resistance to deformation across different crystallographic orientations, highlighting pronounced elastic anisotropy. In contrast, Fig. 5b illustrates the Young’s modulus of MgCaCl₃, which appears nearly spherical. This uniform shape implies minimal directional dependence, indicating an almost isotropic mechanical response. The comparison between these two compounds reveals that MgRbCl₃ exhibits stronger elastic anisotropy, while MgCaCl₃ demonstrates more uniform mechanical stability. These insights are crucial for potential applications, where isotropic materials ensure consistent mechanical performance, whereas anisotropic materials may offer direction-dependent advantages (Figs. 6, 7).

Fig. 5
figure 5

(a) 3D visualization of MgRbCl3 Young’s modulus & (b) 3D visualization of MgCaCl3 Young’s modulus.

Full size image
Fig. 6
figure 6

(a) 3D visualization of MgRbCl3 Poisson’s ratio & (b) 3D visualization of MgCaCl3 Poisson’s ratio.

Full size image
Fig. 7
figure 7

(a) 3D visualization of MgRbCl3 shear modulus & (b) 3D visualization of MgCaCl3 shear modulus.

Full size image

Optical response

Dielectric function

The dielectric function of a material characterizes its interaction with electromagnetic radiation, which quantifies its response to an electric field. This function provides insights into how the material polarizes in response to an applied electromagnetic field, influencing the propagation and absorption of electromagnetic waves through the material, and its formula is

$$\varepsilon \left(\omega \right)={\varepsilon }_{1}\left(\omega \right)+i{\varepsilon }_{2}\left(\omega \right)$$
(4)

It shows that it comprises the real component, ε1(ω) and an imaginary part, iε2(ω). Figure 8 displays the real component, ε1(ω) which reflects the material’s ability to store electrical energy and is directly related to its polarization characteristics67.

Fig. 8
figure 8

Compute optical dielectric function of cubic perovskite of MgXCl3 (X = Rb, Ca).

Full size image

An important parameter in this context is the static dielectric constant ε1(ω). This value represents the dielectric constant of the material at zero frequency and provides insight into the behavior of the material in the absence of an alternating electric field. The predicted values of ε1(ω) for the perovskite compounds MgXCl3 (X = Rb, Ca) are shown in the figure, highlighting their static dielectric properties. This information is crucial for understanding the performance of materials in applications involving constant or slowly varying electric fields. For the studied compounds, ε1(ω) (0) started at a maximum value from the zero-frequency limit, then decreased, and eventually dropped below zero within a certain energy range. The negative ε1 (0) value for MgRbCl3 at 15 eV confirms semiconductor behavior. The peak value was ε1(ω) max, which was found to be 49 at 0 eV for MgCaCl3 and 22 at 0 eV for MgRbCl3. The imaginary part of the dielectric function iε2(ω) plays a vital role in understanding how a material absorbs optical radiation and is directly linked to its electronic band structure65. This component of the dielectric function captures the extent to which the photons are absorbed as they interact with the crystal. Figure 8 displays the iε2(ω) spectra of MgCaCl3 and MgRbCl3, highlighting their optical absorption properties. For MgCaCl3, the absorption spectrum reaches a peak value of 18 at an energy of 1 eV, while MgRbCl3 shows a maximum absorption of 9.3 at the same energy. These results indicate that both compounds exhibit significant optical absorption at 1 eV, which is a critical factor for various optical applications.

The broad range of absorption spectra for both MgCaCl3 and MgRbCl3 suggests that they are capable of absorbing light over a wide range of photon energies. This broad absorption spectrum is advantageous for applications, such as photodetectors, light-emitting devices, and other optical technologies, where effective light absorption across different wavelengths is required. The ability of these materials to absorb a wide spectrum of light enhances their potential applications in advanced optical and electronic devices.

Refractive index n (ω)

The refractive index n (ω) is a key optical property that reveals how light slows down and bends when it travels through a material compared to its speed in a vacuum. This property is crucial for designing optical and photonic devices because it affects the propagation and interaction of light with the material. The refractive index is derived from the dielectric function of the material, which includes both real and imaginary components. The real part describes how the material stores electrical energy and its effect on light bending, whereas the imaginary part relates to light absorption. Together, these aspects provide a complete picture of the optical behavior of the material, which is essential for applications such as lenses and sensors. The formula to calculating the refractive index as:

$$n\left(\upomega \right)=\frac{1}{\sqrt{2}}([{{\upvarepsilon }_{1}}^{2}\left(\upomega \right)+{{\upvarepsilon }_{2}}^{2}\left(\upomega \right){]}^\frac{1}{2}+{\upvarepsilon }_{1}\left(\upomega \right){)}^\frac{1}{2}$$
(5)

This expression helps determine how a material interacts with electromagnetic waves, influencing its performance in various optical and photonic applications56.

Figure 9 illustrates the spectrum of the refractive index n (ω) for MgRbCl3 and MgCaCl3, revealing distinct patterns that are closely aligned with the behavior observed in the real part of the dielectric function. At zero frequency, the refractive indices n (0) for the two perovskites were 7 for MgCaCl3 and 4.89 MgRbCl3. These initial values indicate the baseline optical densities of the materials in the absence of photon energy. As the frequency increased, the refractive indices of both materials displayed pronounced peaks. For MgCaCl3, the refractive index reaches its maximum value of 2.3 at 3.6 eV, while MgRbCl3 achieves a peak value of 2.5 at a slightly lower energy of 3.3 eV. These peak values suggest that the materials exhibit enhanced optical properties at these specific energies, where they interact more strongly with the incoming photons. When the refractive index exceeds unity, it signifies that photons are effectively slowed as they traverse the material. This effect occurs because of the interaction between the photons and electrons within the perovskites, which influences the propagation of light through the materials. The observed peaks in the refractive index indicate specific energy levels where the interaction is most pronounced, potentially leading to enhanced optical effects, such as dispersion or refraction. These characteristics of the refractive index are crucial for applications involving light manipulation, such as optical coatings, lenses, and other photonic devices, where precise control over light propagation is required. The data from Fig. 6 highlight the potential of these materials for applications that leverage their unique refractive properties at different photon energies.

Fig. 9
figure 9

Compute optical refractive index of cubic perovskite of MgXCl3 (X = Rb, Ca).

Full size image

Absorption coefficient

The amount of light energy absorbed per unit length within a material is indicated by its absorption coefficient. The influences on this parameter include the molecular structure and band gap of the material. Absorption occurs when the frequency of an incoming photon aligns with the energy required to excite electrons from the valence band to the conduction band. Variations in the absorption coefficient with the photon frequency enable selective light absorption at specific wavelengths. For optical device design, understanding this property is essential for determining the light absorption efficiency of the material. The absorption coefficient can be determined using the following relationship:

$$\alpha \left(\omega \right)=\frac{2{\omega }_{44}k\left(\omega \right)}{4\pi }$$
(6)

Figure 10 presents a graph of the absorption coefficient, which provides an insight into the interaction of the material with incoming photons. This graph mirrors the behavior observed in the imaginary part of the optical conductivity, indicating a consistent pattern of the optical responses of the materials. The absorption of photons begins at different energy thresholds for the two perovskites; MgCaCl3 starts absorbing at approximately 1.3 eV, while MgRbCl3 begins at a higher energy of 1.8 eV. This difference in the onset energies reflects the variations in the electronic structures and bandgaps of the two materials. Further analysis of Fig. 7 reveals that both perovskites exhibit peak absorption coefficients at specific energy levels. For MgRbCl3, the peak absorption coefficient is 4.6 × 105 at 6 eV, whereas MgCaCl3 achieves its peak absorption coefficient of 3.7 × 1–5 at 7.3 eV. These peak values indicate the energy at which each material is most effective for absorbing photons. The higher peak absorption coefficient for MgRbCl3 at 6 eV suggests that it has a stronger capacity to absorb light at this energy level than MgCaCl3. Conversely, MgCaCl3 shows maximum absorption at a slightly higher energy, 7.3 eV, which implies a different energy profile for optimal photon absorption. This detailed absorption behavior can provide valuable information for designing applications where selective photon absorption is crucial, such as optical filters or sensors. The distinct absorption onset and peak values suggest that these materials can be tailored for specific optical applications based on their photon-absorption characteristics.

Fig. 10
figure 10

Compute optical absorption of cubic perovskite of MgXCl3 (X = Rb, Ca).

Full size image

Optical conductivity

The optical conductivity is denoted by σ(ω) and measured in units of (Ω. m)−1 It describes how well a material conducts electric current in response to an oscillating electric field and is calculated using the following mathematical expression65:

$$\sigma \left(\upomega \right)=\frac{\left(\upomega \right)}{4\pi \pi }{\upvarepsilon }_{2}\left(\upomega \right)$$
(7)

The relationship between the optical conductivity and the absorption spectrum is highlighted by the equation, illustrating that changes in one directly affect the other. Figure 11 shows the optical conductivity curves for the silver-based perovskites MgCaCl3 and MgRbCl3. These curves reveal that both materials possess a significant range of optical conductivity, ranging from 0 to 10 eV, indicating their potential for diverse optical applications. In the case of MgRbCl3, the optical conductivity reached its maximum value of 8 (Ω·m)⁻1 at an energy level of 9.1 eV. This peak suggests a strong response to electromagnetic radiation at this energy, making MgRbCl3 particularly noteworthy for applications that require high optical conductivity. Similarly, MgCaCl3 exhibits a peak optical conductivity of 5.9 (Ω·m)⁻1 at 8.7 eV. Although it is slightly lower than that of MgRbCl3, this peak still represents a significant level of optical activity. The broad range of optical conductivities observed in both materials, from the low energy levels to the higher end of the spectrum, underscores their versatility. This characteristic is essential for the development of optical devices that operate across various energy levels, making MgCaCl3 and MgRbCl3 promising candidates for future research and technological applications in fields such as photovoltaics, optoelectronics, and others where efficient light absorption and conductivity are crucial.

Fig. 11
figure 11

Compute optical conductivity of cubic perovskite of MgXCl3 (X = Rb, Ca).

Full size image

Reflectivity

The reflectivity of a compound can be determined by using formula:67

$$R\left(\upomega \right)=\frac{[n(\left(\upomega \right)-1{]}^{2}+{k}^{2}\left(\upomega \right)}{[n(\left(\upomega \right)+1{]}^{2}+{k}^{2}\left(\upomega \right)}$$
(8)

n represent is the real part and k represent is the imaginary part. Figure 12 provides a comprehensive view of the optical conductivity of MgCaCl3 and MgRbCl3. At zero energy, the optical conductivity values were notably high for both materials, with MgCaCl3 showing a value of 1.167 and MgRbCl3 at 0.36. This initial measurement indicated a strong response to electromagnetic radiation at very low energy levels. As the energy increases, the optical conductivity of both compounds increases, reflecting an enhancement in their ability to conduct optical signals. MgCaCl3 reaches its maximum optical conductivity of 0.37 at 1.2 eV, while MgRbCl3 achieves its peak conductivity of 0.48 at a higher energy of 6.9 eV. These optimal values signify the energy levels at which these materials are most efficient in conducting optical signals. Beyond these peak values, the conductivity began to fluctuate, which can be attributed to the complex interactions between the incident light and the electronic structure of the material. This fluctuation suggests that, while the materials are highly conductive at certain energies, their performance becomes less stable at higher energy levels. The decrease in the conductivity after reaching these peaks indicates that the materials may have limited effectiveness in a broad range of optical applications. However, the low reflectivity values of both MgCaCl3 and MgRbCl3 were noteworthy. Low reflectivity implies that these perovskites do not reflect much incident light, which is advantageous for lens-making applications, where minimizing reflection is crucial for improving light transmission and image clarity. The combination of their optical conductivity profile and low reflectivity suggests that MgCaCl3 and MgRbCl3 are promising candidates for use in advanced optical devices, such as high- performance lens.

Fig. 12
figure 12

Compute optical reflectivity of cubic perovskite (X = Rb, Ca).

Full size image

Phonopy dispersion

To assess the stability of Cubic Pervoskite of MgXCl3 (X = Rb, Ca) structures, we performed phonon dispersion calculations. The resulting phonon band spectrum along the high symmetry directions (G–X–M–W–Z) of the Brillouin zone shows no imaginary frequencies at the m-point, as illustrated in Fig. 13. This indicates the dynamical stability of these compounds, consistent with findings for AgXCl3 (X = Ca, Sr)67.

Fig. 13
figure 13

The compute phonon dispersion of cubic perovskite of MgXCl3 (X = Rb, Ca).

Full size image

Conclusion

Density Functional Theory has been extensively utilized to investigate the structural, elastic, electronic, and optical properties of Mg-based perovskites MgXCl3 (where X = Rb, Ca). Structural analysis confirmed that both MgRbCl3 and MgCaCl3 adopt a stable cubic configuration. This stability was substantiated by examining the tolerance factors, octahedral factors, and optimization curves, which collectively validated the robustness of the cubic structure. Electronic property studies reveal that both compounds exhibit indirect band gaps, with MgRbCl3 showing a band gap of 1.44 eV and MgCaCl3 having a slightly lower band gap of 0.853 eV. These bandgaps are crucial for understanding the electronic behavior and potential semiconductor applications of these materials. Investigations of the mechanical properties indicated that bond bending is the dominant bonding type within these perovskites. However, there is also evidence that directional bonding contributes to the mechanical characteristics of materials. Among the two, MgRbCl3 was found to be harder than MgCaCl3, suggesting higher resistance to deformation. Despite this difference in hardness, both compounds exhibited ductile behavior, which implies that they can sustain significant deformation before fracture. The optical properties demonstrate that these materials can absorb significant amounts of optical energy and serve as good optical conductors. The reflectivity of both compounds was relatively low up to the bandgap energy range, indicating transparency in this region. The phonon spectra confirmed the dynamic stability of the materials. Thermal studies suggest that both compounds exhibit favorable thermoelectric responses, making them promising alternatives for green-energy applications in thermoelectric devices. Furthermore, their optical properties indicate their potential applications in lens-making and other optoelectronic devices.