Optimizing resource allocation for IoT applications in the edge cloud continuum using hybrid metaheuristic algorithms

Abstract

The rise of Internet of Things (IoT) applications has heightened the need for efficient resource allocation across the edge-cloud continuum, combining low-latency edge nodes with high powered cloud servers. Optimizing this resource allocation is challenging, especially when balancing cost and task completion time (makespan). Traditional algorithms often fall short in these dynamic environments, leading to suboptimal solutions. This paper introduces a hybrid Flower Pollination Algorithm and Tabu Search (FPA–TS) algorithm to address IoT-specific requirements for multi objective optimization. The enhanced FPA incorporates adaptive probability based on solution diversity and dynamic levy flight control for effective global search, while Tabu Search contributes memory guided local refinement to further minimize makespan and costs. Extensive simulations with IoT scenarios show that the hybrid FPA–TS outperforms existing algorithms, offering a robust approach to optimizing resource allocation for IoT-driven applications in the edge-cloud continuum.

Introduction

The rapid adoption of the Internet of Things (IoT) has transformed various sectors, including healthcare, industrial automation, smart cities, and home automation¹. IoT enables the connection and real-time monitoring of billions of devices, generating unprecedented data volumes and continuous data streams². This explosion of data has driven the development of advanced architectures to address IoT’s unique requirements. One such architecture is the edge-cloud continuum³, which integrates the proximity and low-latency benefits of edge nodes with the robust computational power of cloud servers, providing a flexible environment to handle diverse IoT applications². Edge nodes process time-sensitive tasks close to the data source, while cloud servers manage computationally intensive tasks requiring significant processing and storage resources. Striking a balance between these tasks is critical to maintaining the responsiveness and efficiency that IoT applications demand³.

Resource allocation in IoT-driven edge-cloud environments presents a multifaceted challenge, as it involves optimizing conflicting objectives⁴. Two primary goals are minimizing computation costs and reducing makespan, the time needed to complete all tasks. This challenge is compounded by the heterogeneity of IoT devices and fluctuating network conditions⁵. For instance, smart city applications rely on real-time sensor data to make time-sensitive decisions, while delays in industrial IoT (IIoT) settings can disrupt productivity and compromise safety⁶. Consequently, resource allocation strategies must be adaptable, scalable, efficient, and capable of accommodating IoT’s diverse and dynamic requirements^7,8. Traditional optimization algorithms often fail to meet these demands⁹. Algorithms such as Genetic Algorithms (GA)¹⁰ and Particle Swarm Optimization (PSO)¹¹, initially designed for centralized cloud environments, focus on optimizing costs or computational efficiency. However, they lack the flexibility needed for distributed IoT environments, where dynamic workloads, resource heterogeneity, and stringent latency requirements must be addressed. IoT environments require dynamic task distribution across edge and cloud resources, accounting for both computational demands and latency constraints¹². This need for adaptable, real-time optimization often overwhelms conventional algorithms, which tend to converge prematurely on suboptimal solutions or struggle to respond to rapidly changing conditions.

To overcome these limitations; this paper introduces a hybrid metaheuristic optimization algorithm that integrates an enhanced Flower Pollination Algorithm (FPA) with Tabu Search (TS) for multi-objective optimization in IoT-specific edge-cloud environments. The hybridization of FPA and TS was specifically chosen to address the unique challenges of edge-cloud systems, including dynamic workloads, resource heterogeneity, and conflicting objectives. The global exploration ability of FPA enables the algorithm to adapt to rapidly changing workloads, while TS’s memory-based local refinement mechanism ensures efficient handling of heterogeneous resources and escaping local optima. These features make FPA–TS particularly suited for optimizing resource allocation in IoT environments where both cost and makespan must be minimized.

The enhanced FPA incorporates two key innovations: an adaptive probability function based on solution diversity and dynamic levy flight control. These improvements enhance global search capabilities, enabling the algorithm to thoroughly explore the solution space and avoid premature convergence. The Tabu Search component complements this by leveraging a memory-based local refinement mechanism, allowing the algorithm to escape local optima and improve resource allocation in promising regions of the solution space. The contribution of this paper includes the following:

• i. Develops a hybrid optimization algorithm by combining an enhanced Flower Pollination Algorithm (FPA) with Tabu Search (TS) to achieve multi-objective optimization in IoT edge-cloud environments.

• ii. It introduces adaptive probability and levy flight control in FPA to improve global search capabilities and prevent premature convergence.

• iii. Leverages the exploration strength of FPA and the local refinement capabilities of TS to achieve efficient resource allocation by balancing cost and makespan in dynamic IoT contexts.

• iv. Comprehensive evaluation of the proposed hybrid algorithm across different evaluation metrics.

The remainder of this paper is structured as follows: Section “Review of related work” reviews related work on resource allocation optimization in IoT-based edge-cloud environments. Section “Problem formulation” formulates the problem. Section “Proposed hybrid FPA–TS algorithm” describes the proposed hybrid algorithm in detail. Section “Experiment and result analysis” presents the results and discussion. Finally, Section “Conclusion” summarizes the study’s key findings and explores potential directions for future research in IoT-driven resource allocation.

Review of related work

Resource allocation in the IoT-driven edge-cloud continuum has become a critical research area, driven by the need for distributed computing solutions across diverse and heterogeneous environments¹³. The increasing complexity of IoT applications has highlighted the importance of optimizing multiple conflicting objectives, such as cost, makespan, energy consumption, latency, and reliability^3,4,14,15,16. Among these, balancing cost and makespan has emerged as a key challenge, particularly as modern applications demand economic efficiency alongside timely task completion. Early resource allocation strategies primarily targeted cloud-only environments, focusing on cost minimization through dynamic provisioning and pricing models for virtual machines (VMs), storage, and bandwidth¹⁷. These approaches achieved significant cost reductions by efficiently managing resources in centralized settings. However, they ignored the latency-sensitive, scalable and reliability-critical nature of many IoT applications, especially as edge computing gained prominence. The inclusion of an edge layer introduces unique challenges, such as real-time processing, energy consumption, and operational costs², which traditional strategies fail to address effectively. As a result, these methods often fall short in hybrid edge-cloud systems, where tasks must be distributed dynamically across geographically distributed resources to achieve both performance and reliability. Unreliable resource allocation algorithms pose significant challenges in edge-cloud systems. Failures due to resource unavailability, hardware malfunctions, or network disruptions can severely impact mission-critical applications^14,15,16.

Metaheuristic algorithms have emerged as powerful tools for addressing the complex resource allocation challenges within the edge-cloud continuum. These algorithms are well-suited for solving NP-hard problems, leveraging stochastic processes to explore and exploit the solution space effectively. Dynamic hybrid multi-objective metaheuristic algorithms, in particular, have gained significant attention due to their ability to optimize multiple conflicting objectives, such as makespan, cost, and energy efficiency. By integrating multiple heuristic approaches, these hybrid algorithms enhance solution diversity and convergence rates, addressing the limitations of single-method approaches. Recent studies highlight the use of adaptive mechanisms, such as reinforcement learning, chaotic maps, and fuzzy logic, within hybrid metaheuristics to dynamically adjust parameters and improve performance in real-time scenarios¹⁸. These advancements have laid the foundation for innovative resource scheduling and allocation frameworks, where the focus is on balancing exploration and exploitation to achieve superior performance in highly dynamic edge-cloud environments.

Recent advancements in task scheduling for cloud and edge-cloud systems have leveraged metaheuristic and hybrid approaches to address the inherent NP-hard complexities of these environments. Gabi et al. (2022) proposed a Fruit Fly-Based Simulated Annealing Optimization Scheme (FSAOS)³, which incorporates simulated annealing to enhance the balance between local and global search capabilities. While this method demonstrated significant reductions in makespan and execution costs, its scalability to dynamic and heterogeneous task workloads remains a limitation. Abdullahi et al. (2023) introduced an Adaptive Benefit Factor Symbiotic Organisms Search (ABFSOS) algorithm¹⁸, which dynamically adjusts control parameters to improve solution diversity and hypervolume, addressing Quality of Service (QoS) constraints effectively. Despite these improvements, ABFSOS suffers from computational overhead, especially when applied to larger-scale datasets. Dankolo et al. (2024) advanced scheduling in edge-cloud continuums with a Modified Flower Pollination Algorithm (FPA) that integrates chaotic maps and dynamic switches for better exploration and exploitation². However, while effective in reducing task delays and enhancing resource utilization, the algorithm struggles with scalability in highly heterogeneous environments. A comparison among these approaches reveals a shared focus on balancing exploration and exploitation through adaptive methods, but challenges such as computational cost and scalability persist, especially in scenarios involving dynamic workloads or heterogeneous infrastructures.

Furthermore, Malti et al.¹⁹ combined the Flower Pollination Algorithm with the Grey Wolf Optimizer (FPA–GWO), achieving improved makespan and resource utilization while mitigating the risk of local optima. However, the method does not adequately address task dependencies, limiting its effectiveness in more complex scheduling scenarios. Bansal et al.²⁰ proposed a Hybrid Particle Swarm Optimization–Whale Optimization Algorithm (PSO–WOA) for workflow scheduling in cloud-fog environments. This approach achieved notable reductions in execution cost and time while ensuring efficient resource utilization. However, it also introduced high computational demands, requiring extensive parameter tuning for optimal performance. Shukla and Pandey²¹ tackled the challenge of scheduling in fog-cloud systems with the MOTORS algorithm, integrating fuzzy clustering and hybrid heuristics to enhance task offloading and scheduling efficiency. While the method produced superior makespan-cost tradeoffs and minimized energy consumption, it faced challenges with scalability and relied heavily on fine-tuning parameters. Comparing these works reveals that while hybridization improves solution diversity and convergence rates, reliance on complex configurations and parameter dependencies remains a significant drawback, requiring further investigation to enhance automation and reduce computational demands.

Moreover, Robles-Enciso and Skarmeta²² proposed a custom Kubernetes scheduler for pod-node allocation, focusing on reducing latency and ensuring efficient resource utilization. However, its batch allocation approach struggles with real-time dynamic resource constraints. Fu et al.²³ introduced the Nautilus framework, which integrates reinforcement learning (RL) for microservice management, minimizing computational resource usage while maintaining QoS. Despite its efficiency, the RL-based approach introduces significant computational overhead. Cohen et al. (2023) tackled the challenges of service function chain deployment in hierarchical edge-cloud systems by using a bounded resource augmentation method to minimize latency, migration, and bandwidth costs²⁴. While the approach is innovative, scalability remains a limitation for larger deployments. Deng et al.²⁵ leveraged Spider Monkey Optimization to improve load balancing in cloud systems, achieving enhanced resource utilization and response times. However, the method is less adaptable to real-time workload fluctuations. Lingayya et al.²⁶ proposed a hybrid Stackelberg-Auction framework integrating dynamic task offloading and privacy preservation mechanisms for KubeEdge systems, which optimizes resource allocation and security but relies heavily on accurate task profiling for optimal results.

Guo et al.²⁷ tackled multi-resource allocation in cloud-edge systems using the Maximin Share Fairness mechanism with Bandwidth Compression (MMS-BC). This approach maximized resource utilization while ensuring fairness among users but faced complexity issues when user tasks varied significantly. Hao et al.²⁸ addressed delays in augmented reality (AR) applications through a delay prediction model, EPBN, and meta-heuristic optimization using PSO. While effective in reducing execution latency, it struggled with high dependencies among subtasks. Rajasekar and Santhiya²⁹ introduced a budget-based scheduling algorithm (BPS) for scientific workflows, achieving cost-efficiency and reduced makespan, though it was less adaptable to large-scale heterogeneous workflows. Salotagi and Mallapur³⁰ proposed Modified Emperor Penguin Optimization (MEPO) for IoT agriculture resource allocation, focusing on energy efficiency and QoS but encountered scalability limitations in dynamic environments. Afzali et al.³¹ applied Improved Binary PSO (IBPSO) for resource allocation in hybrid fog-cloud environments, excelling in latency reduction and load balancing but facing challenges in resource contention under high demand.

Liakath et al.³² introduced a Genetic Water Evaporation Optimization (GWEO) algorithm for efficient task scheduling in heterogeneous clouds. The approach minimized execution time and improved resource utilization but encountered high computational complexity for large-scale tasks. Mageswari et al.³³ tackled communication cost in IoT systems using the Elephant Herding Optimization (EHO) algorithm. While successful in reducing costs, its exploration capabilities were limited in diverse IoT environments. Mishra and Gupta³⁴ proposed the Dynamic Artificial Bee Colony (DRABC-LB) for cloud load balancing, achieving enhanced throughput and resource utilization. However, its sensitivity to workload variations remained a challenge. Kousar and Krishnan³⁵ developed the User Priority Resource Allocation (UPRA-MCTSS-LB) model for improving load balancing and resource utilization. Despite its benefits, the model lacked adaptability to real-time workload dynamics. Wang et al.³⁶ presented a Multi-Tier Computing Offloading Framework for next-generation wireless networks, optimizing task offloading and reducing latency. Nonetheless, scalability issues persisted in edge-heavy environments. The Table 2 below summarises the findings and the limitations of the current literature in resource allocation for IoT enabled edge-cloud continuum computing environment. The summary of the recent literature on resource allocation in the edge-cloud continuum is presented in Table 1.

Table 1 Literature review summary table.

The review of existing literature highlights significant advancements in resource allocation and task scheduling within cloud and edge-cloud continuum systems. However, persistent challenges remain, including scalability issues in handling dynamic and heterogeneous workloads, computational overhead from hybrid and reinforcement learning-based algorithms, and limited adaptability to real-time environments. Many of the reviewed approaches, while innovative, struggle with balancing exploration and exploitation in highly dynamic scenarios, particularly when optimizing multiple conflicting objectives such as cost, makespan, and energy efficiency. Additionally, the reliance on extensive parameter tuning and the inability to address task dependencies or resource contention further limit their applicability in complex edge-cloud systems. These gaps underscore the need for a robust, adaptive, and dynamic multi-objective hybrid metaheuristic algorithm capable of addressing these limitations. The proposed algorithm aims to provide scalable and efficient solutions by integrating advanced techniques for enhanced exploration, exploitation, and convergence in dynamic edge-cloud environments.

Flower pollination algorithm (FPA)

The Flower Pollination Algorithm (FPA) is a relatively recent addition to the family of nature-inspired optimization algorithms. Proposed by Yang³⁸, FPA is inspired by the pollination process of flowering plants, where pollinators such as insects and birds carry pollen from one flower to another, facilitating reproduction. FPA leverages this biological process by incorporating global and local search mechanisms, modelled as long-distance pollination (global search via levy flights) and local pollination (neighborhood search). FPA has demonstrated its effectiveness in various optimization problems due to its simplicity and the balance it strikes between exploration and exploitation^39,40,41,42. Its use of levy flights allows for wide exploration of the search space, enabling it to escape local optima and discover better global solutions. However, FPA has limitations when applied to complex, dynamic environments like the edge-cloud continuum. In such environments, FPA’s fixed parameters can hinder its performance, leading to premature convergence and suboptimal resource allocation.

Several researchers have attempted to enhance FPA to address these issues^43,44,45. Modifications such as adaptive control of the probability parameter and hybridization with other algorithms have shown promise in improving FPA’s performance. For example, studies have integrated FPA with Genetic Algorithms (GA) to improve solution diversity or with PSO to enhance convergence speed. Despite these improvements, FPA’s limitations in complex, multi-objective environments remain a challenge, motivating further research into hybrid approaches.

Tabu search (TS)

Tabu Search (TS) is a well-established metaheuristic algorithm used for solving combinatorial optimization problems developed by Glover in 1986, TS is characterized by its use of a memory structure (the tabu list) to guide the search process. The tabu list records recently visited solutions or attributes of solutions, preventing the algorithm from cycling back to these solutions and helping it escape local optima. TS is particularly effective in environments where local search can easily get trapped in suboptimal regions of the search space⁴⁶. By employing a memory-based approach, TS ensures that the search progresses toward better solutions, even when traditional local search methods fail. TS has been widely used in scheduling, network design, and load balancing problems, where its ability to exploit neighbourhood structures makes it well-suited for fine-tuning solutions after initial exploration by a global search algorithm⁴⁶.

One of the main strengths of TS is its flexibility; it can be easily adapted to a wide range of optimization problems and combined with other metaheuristics to form hybrid algorithms⁴⁷. In hybrid models, TS often serves as the local search component, refining solutions identified by a global search algorithm. This combination of global and local search has proven effective in complex multi-objective optimization problems, making TS an attractive candidate for hybridization with algorithms like FPA.

Problem formulation

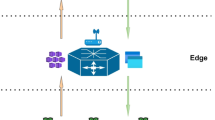
In the edge-cloud continuum, IoT resource allocation must balance conflicting objectives, such as minimizing the cost of computation and reducing the makespan. These objectives are critical for efficiently managing distributed computing resources across edge nodes and cloud servers. This research adopts a theoretical framework incorporating a distributed cloud resource provider (CRP) responsible for managing resources in the centralised remote cloud environment. The edge resource provider (ERP), which operates alongside the CRP to allocate resources to the pool of resource users (RUs) at the edge. The system framework is depicted in Fig. 1.

Fig. 1

Edge-cloud continuum computing model.

The resource scheduling algorithm is situated at the edge orchestrator, where tasks uploaded by IoT devices are received and evaluated based on QoS requirements and imposed constraints. The task schedule will then allocate either edge resources, cloud resources or both to the task based on optimal execution time and cost. The task execution cost is the cost of using resource provider’s resources (virtual machine) at a given period. The mode of cost charge of using a virtual machine ${v}_{j}$ depends on the resource provider. For example, Amazon ${EC}_{2}$ charges on hourly while Microsoft Azure charges per minute. In this research, cost charge on hourly basis is adopted. Hence the execution time of using a virtual machine will be converted to hours and the cost is calculated. It’s also assumed that the cost of using resources along the continuum to be one US dollar per hour $(\$1 /hour)$, and the cloud resources and edge resources belong to the same provider. Furthermore, to make ease the problem understanding, we present the list of notations in Table 2.

Table 2 Lista of notations.

Efficient resource allocation in the edge-cloud continuum involves assigning tasks ${T}_{i}$ to either edge or cloud resources while balancing two conflicting objectives: minimizing the makespan $\left({F}_{1}\right)$ and the total cost $({F}_{2}).$ The proposed hybrid optimization approach addresses these challenges through the following mathematical formulation:

Firstly, there are three (3) decision variables in the system as follows.

• i. ${x}_{i}\in \left\{\text{0,1}\right\}$: is a binary decision variable indicating the allocation of task ${T}_{i}$

  Where ${x}_{i}=1$ indicates task ${T}_{i}$ is executed on edge resources and ${x}_{i}=0$ indicates task ${T}_{i}$ is executed on cloud resources.

• ii. ${y}_{ij}\in \left\{\text{0,1}\right\}$: is a binary decision variable representing the assignment of task ${T}_{i}$ to resource $j$ (edge or cloud).

• iii ${z}_{ij}\ge 0$. : is a continuous decision variable representing the computational resources allocated to task ${T}_{i}$ on resource $j$.

To formulate the multi-objective optimization problem mathematically, Let ${T}_{comp}^{edge}(i)$ be the computation time on edge server, ${T}_{comp}^{cloud}(i)$ be the computation time on cloud server, ${T}_{comm}^{edge}(i)$ be the communication time from the IoT device to the edge server and ${T}_{comp}^{cloud}(i)$ be the communication time from the IoT device to the cloud server, then the computation time of task ${T}_{i}$ is determined by the processing speed ${R}_{edge}$ or ${R}_{cloud}$ of the edge-cloud continuum resources and the computational load ${L}_{i}$ of the task. Hence, the edge and cloud computational times are given by Eqs. (1) and (2) respectively.

$${T}_{comp}^{edge}\left(i\right)=\frac{{L}_{i}}{{R}_{edge}}$$

(1)

$${T}_{comp}^{cloud}\left(i\right)=\frac{{L}_{i}}{{R}_{cloud}}$$

(2)

The communication time, however, is determined by the size of the Tasks ${T}_{s}$ and the available network bandwidth on edge (${B}_{edge}$) or on cloud (${B}_{cloud}$). Hence, the commutation time is computed using Eqs. (3) and (4) for edge and cloud respectively.

$${T}_{comm}^{edge}\left(i\right)=\frac{{T}_{s}}{{B}_{edge}}$$

(3)

$${T}_{comm}^{cloud}\left(i\right)=\frac{{T}_{s}}{{B}_{cloud}}$$

(4)

However, the cost ${C(T}_{i})$ of executing task ${T}_{i}$ in an edge-cloud environment includes the computation cost and the communication cost on both edge and cloud environments. Fror task ${T}_{i}$, let ${C}_{comp}^{edge}\left(i\right)$ be the computation cost on the edge server, ${C}_{comp}^{cloud}\left(i\right)$ be the computation cost on the cloud server, ${C}_{comm}^{edge}\left(i\right)$ be the communication cost to the edge server, and ${C}_{comm}^{cloud}\left(i\right)$ be the communication cost to the cloud server. The computation cost is determined by the resource cost rate per unit time on edge server $({P}_{comp, edge})$ or cloud server $({P}_{comp, cloud})$ or both and the computation time required for the task. Hence, the computation cost of task ${T}_{i}$ on edge and on cloud servers is given by Eqs. (5) and (6) respectively.

$${C}_{comp}^{edge}\left(i\right)= {P}_{comp, edge}\times {T}_{comp}^{edge}(\text{i})$$

(5)

$${C}_{comp}^{cloud}\left(i\right)= {P}_{comp, cloud}\times {T}_{comp}^{cloud}(\text{i})$$

(6)

The communication cost on the other hand, is determined by data transfer cost rate ${P}_{comm, edge}$ to the edge server or ${P}_{comm, cloud}$ to the cloud server and the size of the task (${T}_{s})$. The communication cost to the edge and cloud servers is given by Eqs. (7) and (8) respectively.

$${C}_{comm}^{edge}\left(i\right)= {P}_{comm, edge}\times {T}_{s}$$

(7)

$${C}_{comm}^{cloud}\left(i\right)= {P}_{comm, cloud}\times {T}_{s}$$

(8)

Therefore, the total execution cost of task ${T}_{i}$ is given by Eq. (9).

$$C\left({T}_{i}\right)=\text{min}\left({C}_{comp}^{edge}\left(i\right)+{C}_{comm}^{edge}\left(i\right), {C}_{comp}^{cloud}\left(i\right)+{C}_{comm}^{cloud}\left(i\right)\right)$$

(9)

Let the objective function for makespan be ${F}_{1}$ and let the objective function for total execution cost be ${F}_{2}$ across all tasks. Then, the objective function for makespan and cost are computed using Eqs. (10) and (11) respectively.

$${F}_{1}=\underset{i\in \{\text{1,2},\dots ,N\}}{\text{max}}M({T}_{i})$$

(10)

$${F}_{2}=\sum_{i=1}^{N}C({T}_{i})$$

(11)

The multi-objective optimization problem aims to find a set of Pareto-optimal solutions that minimize both makespan and cost as follows:

$$\text{F}\left(\text{x}\right)=\text{min}\left({F}_{1}, {F}_{2}\right)$$

(12)

To ensure feasible and optimal task allocation, the following constraints are applied:

• i. Resource Allocation Constraint: Each task is assigned to exactly one resource:

  $$\sum_{j=1}^{M}{y}_{ij=1, \forall i \in \{\text{1,2},\dots ,N\}}$$

• ii. Resource Capacity Constraint: The total resources allocated to tasks on each resource must not exceed its capacity:

  $$\sum_{i=1}^{N}{z}_{ij\le {C}_{j} \forall i \in \{\text{1,2},\dots ,N\}}$$

• iii. Latency Constraint: The total execution time of each task must not exceed its deadline:

  $$M\left({T}_{i}\right)\le {D}_{i}, \forall i \in \{\text{1,2},\dots ,N\}$$

Proposed hybrid FPA–TS algorithm

This section provides a detailed explanation of the proposed hybrid algorithm, including the enhancements made to FPA, the integration of Tabu Search, and the mechanisms employed to achieve effective global exploration and local exploitation.

Enhanced flower pollination algorithm (EFPA)

The Flower Pollination Algorithm (FPA) is inspired by the natural process of pollination, where pollinators carry pollen between flowers to facilitate reproduction. FPA models this biological process through two phases: global pollination (long-distance pollination via levy flights) and local pollination (neighbourhood search). In optimization problem, FPA alternates between these two phases to explore and exploit the search space. However, despite its efficiency in global search, the basic FPA has limitations when applied to dynamic environments like the edge-cloud continuum. Specifically, its static parameters often lead to premature convergence and an inability to adapt effectively to changing conditions. To overcome these limitations, this paper proposes two key enhancements to the basic FPA.

Adaptive probability function based on solution diversity

In the standard FPA, a fixed probability, p, controls the switch between global pollination (exploration) and local pollination (exploitation). Typically, the value of p is set to a constant, mostly, 0.8, and is defined as follows:

$$x_{i}^{t + 1} = \left\{ {\begin{array}{*{20}c} {x_{i}^{t} + L\left( {x_{i}^{t} - g^{*} } \right),} & {with p \left( {global } \right)} \\ {x_{i}^{t} + \in \left( {x_{j}^{t} - x_{k}^{t} } \right),} & {with 1 - p \left( {local } \right)} \\ \end{array} } \right.$$

(13)

where ${x}_{i}^{t+1}$ is the position of the ${i}^{th}$ flower at time step t + 1, L is the levy flight step, ${g}^{*}$ is the best solution found so far, ϵ is a random number from a uniform distribution, ${x}_{j}^{t} and {x}_{k}^{t}$ are two random solutions.

In dynamic environments like the edge-cloud continuum, a static probability value limits the algorithm’s adaptability. The enhancement introduces an adaptive probability function based on solution diversity. Solution diversity D is measured as the average pairwise distance between solutions in the population. If diversity is high, local search is emphasized to exploit good regions; if the diversity is low, global search is favoured to explore new areas. The enhanced adaptive probability function is defined in Eq. (14).

$$p\left(t\right)=\frac{1}{1+{e}^{-k(D\left(t\right)-{D}_{avg}}}$$

(14)

where p(t) is the adaptive probability at time step t, D(t) is the diversity of the population at time step t, ${D}_{avg}$​ is the average diversity over all previous iterations, k is a constant controlling the steepness of the sigmoid function.

The solution diversity $D\left(t\right)$ is a measure used to quantify the variety or spread of solutions at a given iteration t in an optimization process. It helps in assessing whether the solutions are concentrated around a specific region of the search space or are widely dispersed. Mathematically, solution diversity $D\left(t\right)$ can be computed based on the distances between the solutions in the population. In this research, we compute the solution diversity by using the average Euclidean distance between each pair of solutions. Let $S\left(t\right)=\{{x}_{1}\left(t\right), {x}_{2}\left(t\right),\dots , {x}_{n}\left(t\right)\}$ represents the set of solutions at iteration $t$ where $N$ is the total number of solutions (or population). Let ${x}_{i}\left(t\right)$ represent the ${i}^{th}$ solution in the population at iteration. And let ${d(x}_{i}\left(t\right), {x}_{j}\left(t\right))$ be the Euclidean distance between solution ${x}_{i}\left(t\right)$ and ${x}_{j}\left(t\right)$. The Euclidian distance is computed as follows:

$${d(x}_{i}\left(t\right), {x}_{j}\left(t\right))=\sqrt{\sum_{k=1}^{n}{(x}_{i,k}\left(t\right)-{x}_{j,k}{(t))}^{2}}$$

(15)

Hence, the solution diversity is given by the following equation:

$$D\left(t\right)=\frac{2}{N(N-1)}{\sum }_{i=1}^{N-1}\sum_{j=i+1}^{N}{d(x}_{i}\left(t\right), {x}_{j}\left(t\right))$$

(16)

The formula for $D\left(t\right)$ calculates the average distance between all pairs of solutions in the population, giving an indication of how diverse the population is. If the solutions are widely spread, the diversity $D\left(t\right)$ will be large, indicating high exploration. If the solutions are concentrated around a single region of the search space, the diversity will be small, indicating that the algorithm might be converging or stuck in a local optimum. The adaptive probability p(t) then determines whether global pollination based on FPA or local pollination based on TA occurs as presented in algorithm 1.

Algorithm 1

Adaptive probability function.

Global pollination

The original FPA global pollination is performed using Levy flights, which model long-distance pollination. The movement equation for global pollination is given by Eq. (9)

$${x}_{i}^{t+1}={x}_{i}^{t}+L\left({x}_{i}^{t}-{g}^{*}\right)$$

(17)

where L is the levy distance drown from the levy distribution and is given by Eq. (18)

$$L = \frac{{\lambda \left( {1 + \lambda } \right)\sin \left( {\pi \lambda /2} \right)}}{{\pi \left( {1/s^{1} + \lambda } \right)}}$$

(18)

where $s$ is the step size, $\lambda$ is a constant.

In the original FPA, the step size of Levy flights is static, which can result in excessive exploration or premature convergence. The enhancement introduces a velocity clamping mechanism that dynamically adjusts the Levy step size based on the distance to the global best solution, preventing overly large or small steps. Velocity clamping is a technique used in optimization algorithms, particularly in Particle Swarm Optimization (PSO), to prevent the velocities of particles from becoming too large. By setting a maximum velocity, or clamp, it ensures that particles do not move too fast across the search space, which could cause them to miss optimal solutions. This helps balance exploration and exploitation within the search process, controlling how far particles move in each iteration while maintaining a steady convergence toward optimal solutions. The enhanced Levy flight step size L is adjusted by a velocity clamping factor ${v}_{clamp}$ given by Eq. (19)

$${L}_{clamp}=min({L}_{max},\mathit{max}\left({L}_{min}, {v}_{clamp})\right)$$

(19)

where ${L}_{max}$ and ${L}_{min}$ are predefined bounds for the levy step size, ${v}_{clamp}$ is a factor controlling the step size, calculated based on the distance from the current solution to the global best. Hence, the modified global pollination step is given by Eq. (20).

$${x}_{i}^{t+1}={x}_{i}^{t}+{L}_{clamp}\left({x}_{i}^{t}-{g}^{*}\right)$$

(20)

Therefore, the global pollination algorithm is presented in algorithm 2.

Algorithm 2

Global pollination.

Mathematical model of Tabu search for local refinement

In Tabu Search, neighbourhood solutions are generated by making slight modifications to the current solution. Let the current solution at iteration $t$ be represented as ${x}_{t}$, which consists of a vector of decision variables $[{x}_{t1}, {x}_{t2}, \dots , {x}_{tn}]$. To generate neighborhood solutions, each variable ${x}_{ti}$ is modified by applying a small perturbation, typically by adding or subtracting a value ${\Delta x}_{ti}$. This transformation creates new candidate solutions. Mathematically, the modified variable is expressed as:

$${x}_{t+1,i}={x}_{ti}+\Delta {x}_{i}$$

(21)

where $\Delta {x}_{i}$ s a small adjustment value. The objective is to explore different configurations of the solution by modifying one or more of the variables.

The neighbourhood ${N(x}_{t})$ is defined as the set of all possible solutions that can be generated by applying these small modifications to the current solution. This can be mathematically expressed as:

$$N(x_{t} ) = \left\{ {x^{\prime } |x_{i}^{\prime } = x_{ti} + \Delta x_{i} or x_{i}^{\prime } = x_{ti} - \Delta x_{i} } \right\}$$

(22)

This equation indicates that for each variable ${x}_{ti}$, new solutions are generated by either increasing or decreasing its value. If ${x}_{t}$ contains $n$ decision variables and each can be perturbed in two ways (increased or decreased), the total number of possible neighborhood solutions would be ${2}^{n}$. However, in practice, a subset of neighbors is typically chosen to control the computational complexity. When generating neighborhood solutions, it is important to ensure that the new solutions respect the problem constraints. For example, if each variable ${x}_{i}$ has a defined range $[a,b]$, then the modified values ${x}{\prime}$ must also fall within this range, ensuring:

$$a \le x_{i}^{\prime } \le b$$

(23)

If a perturbation causes the variable to exceed these bounds, adjustments are made to keep ${x}_{i}^{\prime}$ within the allowable limits. This step ensures that the neighborhood solutions remain feasible and adhere to all problem constraints. The equation for the adjustment is given as follows:

$$x_{i}^{\prime } = \left\{ {\begin{array}{*{20}l} {a\; if\; x_{i}^{\prime } < a } \\ {b \;if\; x_{i}^{\prime } > b } \\ { x_{i}^{\prime } \; if\; a \le x_{i}^{\prime } \le b} \\ \end{array} } \right.$$

(24)

Thus, when a perturbation causes ${x}_{i}^{\prime}$ to exceed its allowed bounds, it is reset to the nearest boundary, either $a$ or $b$, depending on whether it exceeds the upper or lower limit.

Once the neighbourhood has been generated, each candidate solution ${x}_{i}^{\prime}$ is evaluated based on the objective function $f(x)$, and the best neighbor is selected. Mathematically, the best neighbor is determined as follows:

$$x^{\prime } = \arg \mathop {\min }\limits_{{x^{\prime \prime } \in N\left( {x_{t} } \right)}} f\left( {x^{\prime \prime } } \right){ }$$

(25)

where the objective is to minimize the value of $f({x}^{{\prime}{\prime}})$. The selected solution must also not be part of the tabu list, which tracks previously visited solutions to avoid cycling. In cases where no non-tabu solution is found, or if the current neighbourhood does not lead to an improvement, an aspiration criterion is applied. The aspiration criterion allows the algorithm to override the tabu restriction if the new solution offers a significant improvement over the best-known solution so far. This is presented mathematically as follows:

$$x^{\prime } = \left\{ {\begin{array}{*{20}l} {x^{\prime } \; if \,x^{\prime } \notin T \left( {non - tabu\, solution} \right) } \\ {x^{\prime } \; if \,x^{\prime }\, \in T \,and\, f\left( {x^{\prime } } \right) < f_{best} } \\ {reject\, x^{\prime }\, if \,x^{\prime } \in T \,and\, f\left( {x^{\prime } } \right) \ge f_{best} } \\ \end{array} } \right.$$

(26)

Thus, if the solution ${x}^{\prime}$ is tabu (i.e., ${x}^{\prime}\in T$), but its objective value is better than the current best-known solution, it is accepted, even though it would normally be prohibited by the tabu list. Otherwise, the algorithm follows the standard tabu restriction and does not consider that solution. The process of generating neighborhood solutions and selecting the best candidate continues iteratively, allowing Tabu Search to explore the solution space effectively while avoiding local optima. By carefully generating and evaluating neighborhoods, the algorithm ensures progressive improvement of solution quality while adhering to problem constraints. This tabu search local refinement is summarized in algorithm 3.

Algorithm 3

Pseudocode of the tabu search stage.

Implementation of the Hybrid FPA–TS algorithm

To effectively address the multi-objective optimization problem of minimizing cost and makespan of executing IoT applications in the edge-cloud continuum, this study employs a Pareto-based optimization approach using the Flower Pollination Algorithm integrated with Tabu Search (FPA–TS). The aim is to explore a diverse set of solutions that form a Pareto front, representing the optimal trade-offs between the conflicting objectives of cost and makespan without explicitly combining them into a single objective function. The FPA–TS algorithm evaluates each solution based on both objectives independently during the optimization process. The algorithm seeks to maintain a set of solutions where no objective can be improved without worsening the other, thus forming a Pareto front. This approach ensures that the solutions reflect a wide range of trade-offs, giving the algorithm flexibility in choosing a solution that aligns with specific performance requirements. Let ${f}_{1}(x)$ represent the objective function for cost and ${f}_{2}(x)$ represent the objective function for makespan, with $x\in X$ denoting a solution from a feasible solution set $X$. A solution ${x}^{*}\in X$ is said to be Pareto optimal if there is no other solution $C$ such that:

$${f}_{1}\left(x\right)\le {f}_{1}\left({x}^{*}\right) \,and\, {f}_{2}\left(x\right)\le {f}_{2}\left({x}^{*}\right)$$

(27)

With at least one strict inequality:

$${f}_{1}\left(x\right)<{f}_{1}\left({x}^{*}\right) or {f}_{2}\left(x\right)<{f}_{2}\left({x}^{*}\right)$$

(28)

The Pareto front, denoted by F, is the set of all Pareto optimal solutions. Mathematically, the Pareto front is defined as:

$${F=\left\{x\in X \right|\nexists x\in X : f}_{1}\left(x\right)\le {f}_{1}\left({x}^{*}\right) and {f}_{2}\left(x\right)\le {f}_{2}\left({x}^{*}\right)\}$$

(29)

This set contains all non-dominated solutions, which represent the optimal trade-offs between cost and makespan. The multi-objective optimization problem is expressed as:

$${min\{f}_{1}\left(x\right), {f}_{2}\left(x\right), x\in X\}$$

(30)

subject to the constraints:${L}_{i}\le {L}_{treshold}$

where ${L}_{treshold}$ is the maximum allowable latency for a task executed on the edge, and ${L}_{i}$ is the expected latency for task ${T}_{i}$.

To achieve a balance between makespan (${f}_{1}\left(x\right))$ and execution cost (${f}_{2}\left(x\right)$), a trade-off factor β is introduced. The factor β enables adjustable weighting, where a higher β prioritizes minimizing makespan, while a lower β emphasizes reducing execution cost. Thus, the optimisation function can be presented as follows:

$${F\left(x\right)=\upbeta .f}_{1}\left(x\right)+\left(1-\upbeta \right).{f}_{2}\left(x\right)$$

(31)

where $\upbeta$ is the trade-off factor given by $0\le\upbeta \le 1$, $\upbeta =0$ indicates equal importance between makespan and cost, $\upbeta >0$ indicates higher wights for makespan (${f}_{1}\left(x\right))$ and $\upbeta <0$ indicates higher wights for cost (${f}_{2}\left(x\right)$). At the end of the optimization process, the Pareto front is a set $F$ given aas:

$$F={x}_{1}^{*}, {x}_{2}^{*},\dots , {x}_{n}^{*}$$

(32)

where each solution ${x}_{i}^{*}$ is a Pareto optimal solution in the objective space.

The algorithm begins with the standard FPA to explore the solution space broadly, using its global search mechanism based on levy flights. As the algorithm identifies promising regions, Tabu Search is incorporated to refine these solutions locally, enhancing the precision and quality of the solutions. Throughout this process, the solutions are evaluated based on their Pareto dominance solutions that dominate others (i.e., are better in at least one objective without being worse in the other) are retained as part of the Pareto front. At each iteration, the algorithm updates the Pareto front by comparing newly discovered solutions with existing ones. Only non-dominated solutions are added to the Pareto set, ensuring that the algorithm continuously converges toward a diverse and optimal set of trade-offs. By using this Pareto-based approach, the FPA–TS algorithm effectively captures the multi-objective nature of the problem, providing a set of Pareto-optimal solutions that can be analyzed to select the most suitable option based on the specific requirements and constraints of the edge-cloud environment. The hybrid FPA–TS algorithm is presented in algorithm 4.

Algorithm 4

Hybrid FPA-TS algorithm.

The success of the hybrid FPA–TS algorithm depends on the effective transition between the global exploration phase and the local refinement phase. The switching mechanism between these phases is critical to maintaining the balance between exploration and exploitation. The switch from global exploration to local refinement occurs when the enhanced FPA identifies a solution or set of solutions that demonstrate high potential for further optimization. This determination is made based on the objective function values and the diversity of the population. If the diversity is low and solutions appear to be converging toward local optima, the algorithm triggers the local refinement phase using TS. Once TS has refined the solutions and completed its local search, the algorithm returns to the global exploration phase to continue exploring the search space. This cyclical process ensures that the algorithm does not get stuck in a specific region and continues to search for globally optimal solutions.

Experiment and result analysis

This section presents the experimental setup used to evaluate the performance of the proposed hybrid Flower Pollination Algorithm (FPA) with Tabu Search (TS) and provides an in-depth analysis of the results. The experiments focus on assessing the algorithm’s ability to optimize cost and makespan in the edge-cloud continuum compared to existing benchmark algorithms.

Experimental setup

The experiments were conducted using edge-cloudsim simulator that simulate edge-cloud environments that mimic real-world task generation, resource availability, and network conditions. The environment settings of the edge-cloudsim are presented in the Table 3.

Table 3 Edge-cloudsim environment settings.

The simulated environment comprised multiple edge nodes and cloud servers, each with distinct resource capacities and associated costs. Edge nodes were configured to handle latency-sensitive tasks with limited resources, while cloud servers offered higher computational power but incurred higher costs. The experiments utilized two diverse datasets, NASA and HPC2N, to simulate real-world IoT workloads in the edge-cloud continuum. The NASA dataset represents high-performance computing workloads, including computationally intensive tasks with varying resource demands, such as AI inference and scientific simulations. These tasks reflect scenarios requiring a balance between computational efficiency and timely execution in dynamic IoT applications. On the other hand, the HPC2N dataset comprises heterogeneous task workloads often encountered in smart city and industrial IoT environments, characterized by diverse computational loads and strict deadlines. These datasets were chosen for their ability to emulate real-world IoT scenarios, capturing the heterogeneity, resource demands, and deadline constraints common in edge-cloud environments. The metrics used in evaluating the performance of the proposed algorithm include Makespan, Execution Cost, Resource Utilization, Percentage Improvement, Scalability and t-statistics assess the statistical significance of performance differences between algorithms as presented in Table 4. Hypervolume measures the quality of Pareto front solutions in the objective space, reflecting the diversity and optimality of solutions. These metrics collectively provide a comprehensive model for evaluating the proposed algorithm performance across various dimensions.

Table 4 Evaluation metrics.

Furthermore, in the experiment, Modified Emperor Penguin Optimization (MEPO) which is a hybrid of Emperor Penguin algorithm and Lionized golden eagle algorithm (Salotagi and Mallapur, 2024), Improved Binary PSO (IBPSO) (Afzali et al., 2023), and Fruit Fly-based Simulated Annealing Optimization Scheme (FSAOS) which is a hybrid or Fruit Fly algorithm and Simulated Annealing algorithm (Gabi et al., 2022) were selected as benchmark algorithms to compare with the proposed FPA–TS algorithm due to their diverse optimization mechanisms and relevance to multi-objective scheduling problems. All these algorithms are hybrid metaheuristics specifically implemented in the edge-cloud continuum, making them highly suitable for evaluating the performance of the proposed algorithm. IBPSO is known for its precision in exploring and exploiting solution spaces, making it effective for resource allocation challenges. MEPO balances solution diversity and convergence, demonstrating adaptability in dynamic environments. FSAOS, a hybrid algorithm combining fruit fly optimization and simulated annealing, excels in constrained optimization problems by enhancing local search capabilities. The parameter setting of the proposed hybrid FPA–TS algorithms is presented in Table 5.

Table 5 Algorithm parameter setting.

Results analysis

The results analysis and discussion focus on evaluating the performance of the proposed FPA–TS algorithm compared to three benchmark hybrid metaheuristics which are IBPSO, MEPO, and FSAOS across various performance metrics, including makespan, execution cost, resource utilization, scalability, and hypervolume. The analysis spans both edge and cloud environments using two datasets, HPC2N and NASA, to ensure comprehensive evaluation and robustness of the algorithms under diverse task sizes and configurations. Statistical significance tests are employed to validate the observed performance improvements, while key insights are derived from comparative evaluations across metrics. This section provides an in-depth analysis of the results, supported by tables, figures, and statistical findings, to highlight the strengths and limitations of the proposed algorithm relative to the benchmarks.

Makspan analysis

The makespan results across the datasets for both edge and cloud servers using the HPC2N and NASA datasets highlight the relative performance of the algorithms in processing tasks efficiently. In the HPC2N dataset on Edge (Fig. 2a), the proposed FPA–TS algorithm demonstrates the best performance with consistently lower makespan values across all task sizes. For instance, at a task size of 1000, FPA–TS achieves a makespan of 191.53 ms, which is 11.7% lower than the second-best algorithm, IBPSO (206.86 ms). As task size increases to 5000, FPA–TS maintains its superiority with a makespan of 869.64 ms, compared to IBPSO’s 998.63 ms, representing an improvement of approximately 12.9%. This highlights the robustness of FPA–TS in handling increasing workloads while maintaining efficiency.

Fig. 2

(a) Makespan on edge using HPC2N data. (b) Makespan on cloud using HPC2N data.

For the HPC2N dataset on Cloud (Fig. 2b), a similar trend is observed, where FPA–TS outperforms its competitors. At a task size of 1000, FPA–TS achieves a makespan of 961.05 ms, which is 16% lower than MEPO (1106.49 ms) and 18% lower than FSAOS (1144.64 ms). As the task size increases to 5000, FPA–TS maintains its edge with a makespan of 1860.30 ms, showcasing its scalability and effectiveness in cloud environments compared to IBPSO (1925.78 ms) and FSAOS (2075.22 ms).

On the other hand, the NASA dataset on Edge servers (Fig. 3a), FPA–TS also achieves the lowest makespan values, demonstrating its adaptability in a different workload setting. At a task size of 1000, FPA–TS records a makespan of 6372.32 ms, significantly outperforming MEPO (7132.31 ms) and FSAOS (7298.28 ms). The improvement becomes even more pronounced at higher task sizes, where FPA–TS achieves a makespan of 9085.92 ms at 5000 tasks, outperforming IBPSO (9613.33 ms) by 5.5% and FSAOS (9941.45 ms) by over 8.6%.

Fig. 3

(a) Makespan on edge using NASA data. (b) Makespan on cloud using NASA data.

Similarly, in the NASA Cloud dataset (Fig. 3b), FPA–TS remains the top performer with the lowest makespan across all task sizes. At 1000 tasks, FPA–TS achieves a makespan of 6393.15 ms, significantly outperforming FSAOS (7124.59 ms) and IBPSO (7237.99 ms). At the highest task size of 5000, FPA–TS records a makespan of 9380.30 ms, which is 3.3% lower than IBPSO (9698.11 ms) and a notable 11.9% lower than FSAOS (9663.95 ms). The comparative performance improvement of the proposed FPA–TS against the benchmark algorithms is presented in Table 6.

Table 6 Makespan performance percentage improvement.

The results across all datasets highlight FPA–TS’s consistency, scalability, and ability to outperform other algorithms in both edge and cloud environments. The algorithm demonstrates superior performance in reducing execution times, particularly in handling increasing workloads. While algorithms like IBPSO and MEPO perform well in smaller workloads, their performance deteriorates at larger task sizes, indicating potential limitations in task allocation and resource management strategies.

Cost analysis

The execution cost results across the datasets for both edge and cloud servers using the HPC2N and NASA datasets demonstrate the relative efficiency of the proposed FPA–TS algorithm in minimizing computational expenses during task execution. The task execution cost on Edge servers using HPC2N dataset (Fig. 4a), the proposed FPA–TS algorithm consistently achieves the lowest execution cost values across all task sizes. At a task size of 1000, FPA–TS records an execution cost of 41.76, outperforming the closest competitor, MEPO (49.83), by 16.2%. As the task size increases to 5000, FPA–TS maintains its superiority with a cost of 195.97, which is 10.7% lower than MEPO (224.23) and 13.5% lower than IBPSO (228.65). These results highlight FPA–TS’s ability to allocate resources efficiently, minimizing computational overhead. On the HPC2N Cloud dataset (Fig. 4b), a similar trend emerges, with FPA–TS outperforming its competitors at all task sizes. For example, at a task size of 1000, FPA–TS records a cost of 229.94, which is 20.7% lower than IBPSO (319.32) and 26.3% lower than FSAOS (290.29). As the task size scales to 5000, FPA–TS achieves a cost of 460.81, which is still lower than FSAOS (527.23) and MEPO (478.31). These findings indicate the robustness of FPA–TS in managing cloud-based workloads cost-effectively.

Fig. 4

(a) Execution cost on edge using HPC2N data. (b) Execution cost on cloud using HPC2N data.

In the NASA dataset at the Edge server (Fig. 5a), FPA–TS continues to outperform its competitors. At a task size of 1000, FPA–TS records an execution cost of 669.95, which is 24.1% lower than IBPSO (907.84) and 23.5% lower than MEPO (876.03). Even at higher task sizes, such as 5000, FPA–TS remains competitive with a cost of 1160.53, closely matching IBPSO but still outperforming MEPO (1089.26) and FSAOS (1105.05).

Fig. 5

(a) Execution cost on edge using NASA data. (b) Execution cost on cloud using NASA data.

On the Cloud servers (Fig. 5b), FPA–TS demonstrates its efficiency by recording the lowest execution costs at all task sizes. At 1000 tasks, FPA–TS achieves a cost of 203.94, which is significantly lower than MEPO (240.53) and IBPSO (234.57). At the largest task size of 5000, FPA–TS records a cost of 790.24, outperforming all other algorithms. The relative improvement over FSAOS (803.75) and IBPSO (832.05) emphasizes FPA–TS’s scalability and cost-effectiveness. The comparative performance improvements in task execution cost of the proposed FPA–TS against the benchmark algorithms is presented in Table 7.

Table 7 Execution cost performance percentage improvement.

Across all datasets, the results illustrate that the proposed FPA–TS algorithm is consistently more efficient in reducing execution costs compared to its competitors. The ability of FPA–TS to maintain low costs at varying task sizes and across different environments highlights its adaptability and robustness in resource optimization.

Resource utilization analysis

The resource utilization results across both edge and cloud servers using the HPC2N and NASA datasets highlight the performance of FPA–TS algorithms in efficiently leveraging available computational resources. Higher utilization reflects better use of the system’s capabilities, an essential metric for optimizing resource allocation strategies. On the edge servers using the HPC2N dataset (Fig. 6a), the proposed FPA–TS algorithm consistently achieves the highest resource utilization across all task sizes. At a task size of 1000, FPA–TS records a utilization of 5.86, surpassing IBPSO (5.00) by 17.2% and FSAOS (4.81) by 21.2%. At the largest task size of 5000, FPA–TS maintains its superiority with a utilization of 6.72, outperforming IBPSO (5.57) and FSAOS (5.76). This demonstrates FPA–TS’s ability to maximize resource efficiency, particularly as workloads increase.

Fig. 6

(a) Resource utilization on edge using HPC2N data. (b) Resource Utilization on cloud using HPC2N data.

On the Cloud servers using HPC2N dataset (Fig. 6b), FPA–TS continues to lead in resource utilization. At a task size of 1000, FPA–TS records a utilization of 5.96, outperforming MEPO (5.04) by 18.3% and FSAOS (5.64) by 5.8%. As the task size increases to 5000, FPA–TS achieves the highest utilization of 6.75, significantly higher than MEPO (5.90) and IBPSO (5.56). These results highlight FPA–TS’s ability to sustain high utilization across varying cloud workloads.

Furthermore, using NASA dataset, on the Edge servers (Fig. 7a), FPA–TS again outperforms its competitors, showcasing its adaptability to different workload patterns. At a task size of 1000, FPA–TS achieves a utilization of 0.29, which is more than double that of IBPSO (0.13) and FSAOS (0.13). At a task size of 5000, FPA–TS achieves a utilization of 0.64, outperforming MEPO (0.56) by 14.3% and IBPSO (0.55) by 15.9%. This indicates the algorithm’s ability to efficiently use resources even in scenarios with constrained computational capacity. However, on the cloud servers (Fig. 7b), FPA–TS demonstrates exceptional performance. At a task size of 1000, FPA–TS achieves a utilization of 0.93, which is 37.9% higher than IBPSO (0.67) and 33.1% higher than FSAOS (0.69). At the largest task size of 5000, FPA–TS achieves a utilization of 1.67, significantly outperforming IBPSO (1.29) and MEPO (1.33). This result underscores FPA–TS’s capacity to fully leverage resources even under high-demand conditions. The percentage performance improvement of the resource utilization is summarised in Table 8.

Fig. 7

(a) Resource utilization on edge using NASA data. (b) Resource utilization on cloud using NASA data.

Table 8 Resource utilization performance percentage improvement.

The resource utilization results across all datasets illustrate that the proposed FPA–TS algorithm is consistently more effective in utilizing resources compared to its competitors across edge and cloud computing environments.

Hypervolume analysis

The hypervolume metric serves as a key indicator for evaluating the quality of Pareto fronts in multi-objective optimization, particularly in balancing makespan and cost in resource allocation problems. It calculates the volume in objective space dominated by a set of non-dominated solutions and bounded by a defined reference point. For each algorithm (FPA–TS, MEPO, IBPSO, and FSAOS), Pareto fronts are generated from experimental results across varying task sizes for the HPC2N and NASA datasets as presented in Table 9. These objectives are normalized to ensure comparability, and a reference point is chosen just beyond the worst-case performance in both objectives. In dynamic edge-cloud environments where workloads are diverse, real-time, and often unpredictable, the hypervolume becomes essential. It captures not only how close solutions are to the optimal front but also how well they are spread across the trade-off space, thus indicating both convergence and diversity. A higher hypervolume reflects an algorithm’s robustness and adaptability in providing flexible trade-offs, which is crucial for managing time-sensitive or cost-sensitive tasks.

Table 9 Hypervolume improvement across task sizes.

In the HPC2N dataset (Fig. 8a), the proposed FPA–TS algorithm consistently outperformed the benchmark algorithms (MEPO, IBPSO, and FSAOS) across all task sizes. For instance, at a task size of 1000, FPA–TS achieved a hypervolume of 11.95, significantly higher than MEPO’s 9.64, IBPSO’s 8.27, and FSAOS’s 8.52. This trend persisted across task sizes, with FPA–TS maintaining its superiority. At the largest task size of 5000, FPA–TS recorded a hypervolume of 12.94, while MEPO, IBPSO, and FSAOS reached 9.67, 8.28, and 8.71, respectively. The results demonstrate the effectiveness of FPA–TS in optimizing multiple objectives and achieving superior Pareto fronts in the HPC2N dataset.

Fig. 8

(a) Hypervolume using HPC2N data. (b) Hypervolume using NASA data.

Similarly, the hypervolume analysis for the NASA dataset (Fig. 8b) showed FPA–TS as the best-performing algorithm across all task sizes. At a task size of 1000, FPA–TS achieved a hypervolume of 10.63, outperforming MEPO (8.58), IBPSO (7.36), and FSAOS (8.59). The advantage of FPA–TS became more evident at larger task sizes, where it consistently outperformed the benchmark algorithms. For instance, at a task size of 5000, FPA–TS recorded a hypervolume of 11.52, compared to MEPO (8.61), IBPSO (7.74), and FSAOS (10.12). This highlights the robustness of FPA–TS in handling diverse and large-scale tasks in the NASA dataset. Hence, the consistent performance of FPA–TS across varying task sizes and datasets demonstrates its adaptability and efficiency in optimizing multi-objective problems, making it a suitable choice for complex scheduling scenarios in edge-cloud environments.

Scalability analysis

Scalability analysis assesses how effectively an algorithm adapts to increasing task loads or computational resources, which is crucial for edge-cloud environments characterized by dynamic and heterogeneous workloads. In this study, scalability is measured by the reduction in makespan or execution cost when the number of virtual machines (VMs) is increased across different configurations using both HPC2N and NASA datasets. This quantification reflects the algorithm’s ability to utilize additional resources efficiently under growing demand. In dynamic IoT contexts, where workloads fluctuate and quality of service requirements are strict, a scalable algorithm ensures consistent performance without degradation. The analysis focuses on configurations with varying Virtual Machines (VMs) and task sizes across two datasets, HPC2N and NASA as presented in Table 10.

Table 10 Algorithms’ scalability.

In the HPC2N dataset, FPA–TS demonstrates superior scalability compared to the benchmark algorithms across all VM configurations. For the (1,2) configuration, FPA–TS achieves a scalability value of 0.642, outperforming FSAOS (0.562), MEPO (0.584), and IBPSO (0.457). As the configurations scale up, FPA–TS continues to maintain higher scalability. For example, in the (3,4) VM configuration, FPA–TS records the highest scalability value of 0.875, surpassing MEPO (0.828), IBPSO (0.728), and FSAOS (0.814). Even in the (4,5) configuration, where scalability typically declines due to resource saturation, FPA–TS achieves 0.775, outperforming MEPO (0.626) and matching IBPSO’s strong value of 0.747. In the NASA dataset, FPA–TS shows a similar trend of superior scalability. For the (1,2) configuration, FPA–TS achieves an impressive scalability value of 0.850, significantly outperforming FSAOS (0.612), MEPO (0.711), and IBPSO (0.601). As configurations increase, FPA–TS maintains its leading position. For instance, in the (2,3) configuration, FPA–TS achieves a scalability value of 0.921, higher than FSAOS (0.768), MEPO (0.731), and IBPSO (0.694). Even in the (4,5) configuration, where the scalability of other algorithms declines (e.g., IBPSO at 0.565), FPA–TS remains robust with a value of 0.775, outperforming all benchmarks. This highlights the efficiency of FPA–TS in adapting to increased resource configurations. Its hybrid nature, combining the Flower Pollination Algorithm with Tabu Search, ensures efficient exploration and exploitation, enabling it to fully leverage additional resources. MEPO exhibits competitive performance in some configurations but lacks consistency, particularly in the NASA dataset. FSAOS and IBPSO, while performing well in certain scenarios, show limited scalability as configurations increase, particularly in larger configurations like (4,5).

Runtime analysis

The runtime analysis reveals significant performance differences among the proposed FPA–TS algorithm and the benchmark algorithms (MEPO, IBPSO, and FSAOS) across varying task sizes and datasets. The results highlight the computational efficiency of FPA–TS, particularly in handling larger workloads, compared to the benchmarks as presented in Table 11.

Table 11 Algorithms’ runtime.

In the HPC2N dataset, FPA–TS consistently achieves shorter runtimes than MEPO and IBPSO across all task sizes. For instance, at 1000 tasks, the runtime of FPA–TS is 8.84 s, compared to 13.29 s for MEPO and 16.66 s for IBPSO. As the task size increases to 5000, FPA–TS maintains its advantage, recording a runtime of 41.72 s, significantly lower than MEPO (77.97 s) and IBPSO (83.84 s). However, FSAOS shows competitive performance at smaller task sizes, such as 1000 tasks, with a runtime of 7.74 s. Despite this, FSAOS experiences a more substantial runtime increase at larger task sizes, reaching 61.26 s at 5000 tasks, which FPA–TS outperforms by approximately 31.8%. In the NASA dataset, a similar trend is observed. FPA–TS consistently outperforms MEPO and IBPSO, with runtimes that increase more gradually as task sizes grow. For example, at 1000 tasks, FPA–TS achieves a runtime of 11.08 s, compared to 13.03 s for MEPO and 21.57 s for IBPSO. At 5000 tasks, FPA–TS maintains its efficiency with a runtime of 50.36 s, while MEPO and IBPSO record 68.98 s and 83.26 s, respectively. FSAOS, which demonstrates competitive performance for smaller task sizes with a runtime of 9.69 s at 1000 tasks, falls behind at larger workloads, reaching 60.49 s at 5000 tasks, compared to FPA–TS’s 50.36 s.

The scalability of FPA–TS is evident in its controlled runtime increase compared to the benchmark algorithms. For example, in the HPC2N dataset, the runtime increase from 1000 to 5000 tasks for FPA–TS is 372%, while MEPO and IBPSO exhibit increases of 486% and 403%, respectively. This demonstrates the ability of FPA–TS to maintain computational efficiency under increasing workloads. A similar pattern is observed in the NASA dataset, where FPA–TS exhibits a more stable runtime growth compared to the benchmarks, further highlighting its scalability and robustness.The efficiency of FPA–TS can be attributed to its hybrid structure, which combines the Flower Pollination Algorithm (FPA) with Tabu Search, optimizing the balance between exploration and exploitation. This adaptive nature reduces computational overhead, particularly in larger and more dynamic workloads, where MEPO and IBPSO struggle with excessive exploration or parameter dependencies.

Statistical analysis

The statistical analysis results for the proposed FPA–TS algorithm’s performance improvement across makespan, execution cost, and resource utilization highlight significant advantages over the benchmark algorithms (FSAOS, MEPO, and IBPSO) in both edge and cloud environments. A paired t-test was conducted to assess the significance of the performance improvements, and the results confirm statistical significance across all metrics.

For makespan, the results in Table 12 demonstrate that the proposed FPA–TS algorithm achieves significant improvements over the benchmark algorithms in both edge and cloud environments. The t-statistics for FPA–TS against FSAOS, MEPO, and IBPSO range from 10.15 to 13.68, with corresponding p-values all below 0.05. These results confirm that FPA–TS consistently outperforms the benchmark algorithms in reducing makespan, thereby optimizing task completion time. The improvements are particularly notable in the edge environment, where the adaptive nature of FPA–TS allows it to handle dynamic task sizes effectively, reducing delays caused by inefficient scheduling.

Table 12 Pair-wise t-test on makespan improvement.

For execution cost, Table 13 reveals that the proposed FPA–TS algorithm achieves statistically significant cost reductions compared to FSAOS, MEPO, and IBPSO in both edge and cloud environments. The t-statistics for FPA–TS against the benchmarks range from 6.77 to 15.88, with all p-values below 0.05. This demonstrates the efficiency of FPA–TS in minimizing resource consumption costs while maintaining quality of service. In the cloud environment, FPA–TS leverages its hybrid approach to adaptively allocate resources, leading to noticeable cost savings even for larger task sizes. This highlights the algorithm’s ability to balance cost efficiency and performance in diverse deployment scenarios.

Table 13 Pair-wise t-test on execution cost improvement.

For resource utilization, the results in Table 14 further emphasize the superior performance of FPA–TS. The t-statistics for FPA–TS against FSAOS, MEPO, and IBPSO range from 7.91 to 12.89, with all p-values below 0.05. These results confirm that FPA–TS optimizes resource usage more effectively than the benchmark algorithms. The improvements are especially pronounced in the edge environment, where resource constraints necessitate efficient utilization.

Table 14 Pair-wise t-test on resource utilization improvement.

The ability of FPA–TS to dynamically balance resource allocation across heterogeneous infrastructures ensures higher utilization rates, enhancing system efficiency and reducing wastage.

Results discussion

The results obtained across all metrics makespan, execution cost, resource utilization, scalability, and hypervolume clearly demonstrate the superiority of the proposed FPA–TS algorithm over the benchmark algorithms (FSAOS, MEPO, and IBPSO). This improved performance is attributed to the enhancements integrated into the FPA–TS algorithm, including adaptive probability switching, hybridization with Tabu Search, and dynamic control mechanisms. These enhancements enable a more balanced exploration and exploitation of the solution space, ensuring that the algorithm avoids premature convergence while effectively navigating complex optimization problems. This is particularly evident in makespan results, where FPA–TS consistently achieved shorter completion times across both edge and cloud environments, validating its robustness in managing workload diversity. The execution cost results further highlight the algorithm’s efficiency. The hybridization with Tabu Search allows FPA–TS to refine solutions locally, minimizing unnecessary resource usage and thereby reducing costs. By dynamically adapting the probability of global and local searches, the algorithm is able to optimize resource allocation strategies effectively, which directly translates into cost savings. Across both datasets, the proposed algorithm achieved significant reductions in execution costs compared to the benchmarks, reflecting its ability to address the challenges of resource optimization in highly dynamic and heterogeneous environments.

Furthermore, the resource utilization analysis showcases the algorithm’s ability to make optimal use of available computational resources. The proposed FPA–TS consistently demonstrated higher utilization rates across varying task sizes, outperforming the benchmarks in both edge and cloud scenarios. This is a direct result of the algorithm’s adaptive search mechanisms, which ensure that computational resources are leveraged effectively even under heavy workloads. The improvements in resource utilization highlight the algorithm’s capability to maximize system efficiency while maintaining performance under diverse operational conditions. Scalability analysis reinforces the adaptability of the FPA–TS algorithm, particularly when handling increased workloads and resource configurations. The algorithm exhibited a consistently higher ability to maintain or improve performance as the number of tasks and resource capacities increased, outperforming the benchmarks across all scalability scenarios. This scalability is crucial in edge-cloud environments, where workloads and resource availability can fluctuate unpredictably. The dynamic control of levy flight parameters and the integration of Tabu Search have proven instrumental in achieving this scalability, enabling FPA–TS to adapt seamlessly to changing operational demands. Moreover, the hypervolume results underscore the effectiveness of the proposed algorithm in generating diverse and high-quality Pareto front solutions. The integration of adaptive mechanisms, trade-off factor and hybrid metaheuristics ensure that the algorithm not only converges faster but also maintains solution diversity, a key factor in multi-objective optimization. This is critical for balancing trade-offs between conflicting objectives, such as minimizing makespan and execution cost while maximizing resource utilization. These findings collectively demonstrate the robustness, efficiency, and adaptability of the proposed FPA–TS algorithm, making it a highly promising solution for resource allocation and optimization in edge-cloud environments.

The practical deployment of the proposed FPA–TS algorithm in real-world edge-cloud environments requires addressing challenges such as network variability, hardware failures, and resource heterogeneity. Dynamic, network-aware scheduling strategies can mitigate issues like bandwidth constraints and connectivity disruptions by adjusting task allocation in real-time. Fault tolerance mechanisms, including checkpointing and redundant task allocation, enhance reliability during failures. Furthermore, scalable architectures and machine learning-based resource profiling can adapt to workload fluctuations and anticipate potential issues, ensuring robustness. These strategies make the FPA–TS algorithm suitable for dynamic and complex IoT edge-cloud systems.

Conclusion

This study proposed and evaluated a hybrid Flower Pollination Algorithm with Tabu Search (FPA–TS) for efficient resource allocation in edge-cloud environments. The algorithm incorporates adaptive probability switching, dynamic levy flight control, and hybridization with Tabu Search to balance exploration and exploitation in solving multi-objective optimization problems. Comprehensive experiments using two datasets (HPC2N and NASA) demonstrated the superior performance of FPA–TS compared to benchmark algorithms (FSAOS, MEPO, and IBPSO) across key performance metrics, including makespan, execution cost, resource utilization, scalability, and hypervolume. The results highlighted that FPA–TS consistently achieved lower makespan and execution costs, indicating its ability to optimize task completion time and reduce resource consumption effectively. Additionally, the algorithm achieved higher resource utilization rates and scalability, showcasing its robustness and adaptability to dynamic workloads and resource configurations in edge-cloud environments. The hypervolume analysis further validated FPA–TS’s capability to produce diverse and high-quality solutions for multi-objective optimization problems. Statistical significance testing confirmed that the observed improvements in FPA–TS’s performance were not only consistent but also statistically significant across all evaluation metrics. These findings underscore the algorithm’s suitability for real-world applications, where efficiency, adaptability, and scalability are crucial for effective resource allocation in edge-cloud environments. Despite the improvements made by the proposed algorithm, energy efficiency on edge nodes was not explicitly optimized, suggesting a potential limitation of the proposed algorithm. Future work could extend this research by incorporating energy consumption and fault-tolerance considerations into the optimization framework.