The effect of axial geometrical variations on the steady state characteristics of oil lubricated journal bearings using titanium dioxide nanoparticles as lubricant additives

Abstract

The current work examines journal bearings with axial geometrical configurations that are lubricated with nanofluids. Because of recent advancements in numerically controlled machine tools, accurate machining of complex shapes is now a realistic operation. A theoretical prediction of bearing characteristics for different complicated geometries with varying bearing length to shaft diameter ratios at varying eccentricity ratios is required prior to any experimental effort. The Reynolds like equation that governs the pressure distribution inside the bearing is provided. Four various bearing geometries with conical (wedge), concave, convex, and wavy surfaces are chosen to investigate the bearing characteristics while taking into account the impact of increasing nanoparticle concentrations and aggregate particle sizes. The modified Krieger–Dougherty viscosity model was used to investigate the influence of TiO₂ nanoparticle lubricant additives on the performance of the chosen journal bearings. The results show that the chosen shapes improve the bearing’s performance over the plain cylindrical bearing. The concave design is also shown to be better than the others; however the findings show that an optimization method may be required to acquire the geometry that provides the optimum bearing characteristics.

Introduction

Hydrodynamic journal bearings are in high demand nowadays because of their excellent characteristics such as long-term performance, low friction, and nearly no wear. There are two types of research articles: numerical studies and experimental studies. Numerical investigations are further characterized as isothermal studies with cavitation, isothermal studies without cavitation, and investigations that include thermal effects. More than 75% of the study is done theoretically utilizing numerical/computational approaches, while approximately 23% of the experiments have been carried out. In the literature, attempts to study the effect of geometrical variations on the performance of journal bearings have been reported in different manners. Some studies looked at non-circular geometrical shapes of the bearing bush, such as elliptical and multiple lobes^{1,2,3,4,5,6,7,8}. Others investigated the influence of the unavoidable geometrical changes generated by either angular misalignment or journal deflection^{9,10,11,12,13}. Leung et al.¹⁴ investigated journal bearings using spherical bushes. They concluded that the spherical journal bearing behaves similarly to a comparable cylindrical bearing. El-Gamal¹⁵ on the other hand, published a study for a cylindrical wedge-shaped bearing. His findings revealed that the wedge bearing at small wedge angles, particularly the long one, is better than the plain cylindrical bearing with the same side length. Pang et al.¹⁶ used AG, a genetic algorithm, to optimize the shape of hydrodynamic journal bearings in circumferential and axial wavy configurations. The Fourier series coefficients and axial waviness serve as design parameters in both circumferential and axial directions. Their findings indicated that the load capacity may be increased by around 10%. Green tribology aims to reduce friction and wear. Surface texturing on mating parts can minimize friction while increasing load capacity. Surface textures with various microgeometries, including dimples, grooves, and pits, have been proven to increase bearing performance. Textured bearing surfaces minimize friction while increasing load capacity. Researchers^{17,18,19,20,21,22} evaluated the influence of textural parameters such as the shape, depth, and dimensions of microgeometries, as well as their positions and distribution on the bearing surface, on journal bearing performance. Research results indicated that roughness characteristics and operating circumstances significantly impact journal bearing performance^20,21,22. Currently, as computer technology advances, more researchers are attempting to use commercial computational fluid dynamics (CFD) applications in their researches. The CFD code differs from other comparable codes in that it uses all of the Navier–Stokes equations to solve complex flow problems, whereas finite difference systems depend on the Reynolds equation. Furthermore, the CFD packages are applicable in highly complicated geometries. Many authors employed various computer codes to examine the parametric influence of hydrodynamic journal bearing, and their results are listed in Table 1.

Table 1 Summary of articles employing commercial computer codes.

Furthermore, the viscosity of the lubricant used has a significant impact on the steady-state performance of hydrodynamic journal bearings. Nanofluids have higher viscosity than conventional fluids in the absence of nanoparticle additions. Nanofluids’ effective viscosity is determined by the concentration and size of nanoparticles. Many classical models of nanofluid viscosities have been constructed in Refs.^{39,40,41,42,43,44,45,46,47}. There is also a scarcity of published data on how nanoparticle lubricant additives affect the dynamic responsiveness and stability of hydrodynamic lubrication. Many researchers investigated the steady-state characteristics of various hydrodynamic journal bearings operating with different nanoparticles as lubricant additives^{48,49,50,51,52}. Several prior studies have investigated the characteristics of journal bearings lubricated by couple stress fluids^{53,54,55,56,57,58,59,60}. They determined that friction causes a slight rise in lubricant temperature. There has been no mention of using nanolubricants to investigate bearing performance in advanced shapes. The current technology allows for the precise machining of extremely complex shapes. The effects of TiO₂ nanoparticle volume fraction and nanoparticle aggregate sizes on the steady state characteristics and stability limitations of plain journal bearings were investigated by Awad et al.⁶¹.

The current work is a continuation of Awad et al.⁶¹’s analysis to investigate the combined effects of axial changes in bearing geometrical shape and the use of nanoparticle additives with aggregation properties on bearing performance while keeping the radial clearance constant.

Materials and methods

Formulation

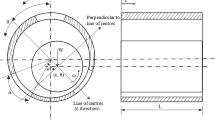
Figure 1 depicts the bearing arrangement and the suggested curvilinear coordinate system. When the Reynolds number is low, the fluid inertia forces may be ignored compared to the viscous forces, as is always the case with bearing problems. The research methodology used in the current study is depicted in Fig. 2, where a suggested work’s block diagram is presented in order to clarify and simplify the work description.

Fig. 1

Bearing geometry and curvilinear coordinate system.

Fig. 2

Steps of research methodology.

The equations governing the lubricant flow in the bearing, assuming that the flow is steady, laminar, and incompressible, are thus stated in Cartesian coordinates as,

$$\left. \begin{gathered} 0 = - \,\,\frac{1}{\rho }\,\frac{\partial \,p}{{\partial \,x}} + \nu \,\left( {\frac{{\partial^{2} \,u}}{{\partial \,x^{2} }} + \frac{{\partial^{2} \,u}}{{\partial \,y^{{\prime}{2}} }} + \frac{{\partial^{2} \,u}}{{\partial \,z^{{\prime}{2}} }}} \right)\, \hfill \\ 0 = \frac{\partial \,p}{{\partial \,y^{\prime}}} \hfill \\ 0 = - \,\,\frac{1}{\rho }\,\frac{\partial \,p}{{\partial \,z^{\prime}}} + \nu \,\left( {\frac{{\partial^{2} \,w^{\prime}}}{{\partial \,x^{2} }} + \frac{{\partial^{2} \,w^{\prime}}}{{\partial \,y^{{\prime}{2}} }} + \frac{{\partial^{2} \,w^{\prime}}}{{\partial \,z^{{\prime}{2}} }}} \right) \hfill \\ and \hfill \\ 0 = \,\frac{\partial \,u}{{\partial \,x}} + \frac{{\partial \,v^{\prime}}}{{\partial \,y^{\prime}}} + \frac{{\partial \,w^{\prime}}}{{\partial \,z^{\prime}}}\, \hfill \\ \end{gathered} \right\}$$

(1)

In terms of the curvilinear coordinates employed, we may write:

$$\left. \begin{gathered} \frac{\partial }{{\partial \,y^{\prime}}} = \frac{\partial }{\partial \,y}\,\,and\,\,\frac{{\partial^{2} }}{{\partial \,y^{{\prime}{2}} }} = \frac{{\partial^{2} }}{{\partial \,y^{2} }} \hfill \\ \frac{\partial }{{\partial \,z^{\prime}}} = \frac{1}{E}\left( {\frac{\partial }{\partial \,s} - \dot{H}\frac{\partial }{\partial \,y}} \right) \hfill \\ \frac{{\partial^{2} }}{{\partial \,z^{{\prime}{2}} }} = \frac{1}{{E^{2} }}\left[ {\left( {\dot{H}\frac{{\dot{E}}}{E} - \ddot{H}} \right)\frac{\partial }{\partial \,y}\, - \left( {\frac{{\dot{E}}}{E}} \right)\frac{\partial }{\partial \,s} + \frac{{\partial^{2} }}{{\partial \,s^{2} }} + \dot{H}^{2} \frac{{\partial^{2} }}{{\partial \,y^{2} }} - 2\,\dot{H}\frac{{\partial^{2} }}{\partial \,y\,\partial s}} \right] \hfill \\ \end{gathered} \right\}$$

(2)

With $y^{\prime} = y + H$, where $H = H(s)$ is a function that defines the geometrical configuration of the bearing (see Fig. 1) and must be supplied prior to any numerical computations. $E = E(s) = \sqrt {1 - \dot{H}^{2} }$, the dot denotes differentiation with respect to s. Referring to Fig. 1, we may also write, $w^{\prime} = E\,w\,\,and\,\,v^{\prime} = v + \dot{H}\,w$.

Using the relationships (2), Eqns. (1) can be expressed as follows:

$$\left. \begin{aligned} 0 = & - \frac{1}{\rho }\,\frac{\partial \,p}{{\partial \,x}} + \nu \,\left[ {\frac{{\partial^{2} \,u}}{{\partial \,x^{2} }} + \left( {1 + \frac{{\dot{H}^{2} }}{{E^{2} }}} \right)\,\frac{{\partial^{2} \,u}}{{\partial \,y^{2} }} + \frac{1}{{E^{2} }}\frac{{\partial^{2} \,u}}{{\partial \,s^{2} }} - \frac{{\dot{E}}}{{E^{3} }}\frac{\partial \,u}{{\partial \,s}}} \right. \\ & \left. { + \frac{1}{{E^{2} }}\left( {\dot{H}\frac{{\dot{E}}}{E} - \ddot{H}} \right)\frac{\partial \,u}{{\partial \,y}} - 2\frac{{\dot{H}}}{{E^{2} }}\frac{{\partial^{2} \,u}}{\partial y\,\partial s}} \right] & & & & & (a) \\ 0 = & \frac{\partial \,p}{{\partial \,y}} & & & & & \;\;\;\;\;\;\;\;(b) \\ 0 = & - \frac{1}{{\rho \,E^{2} }}\,\frac{\partial \,p}{{\partial \,s}} + \nu \,\left[ {\frac{{\partial^{2} \,w}}{{\partial \,x^{2} }} + \left( {1 + \frac{{\dot{H}^{2} }}{{E^{2} }}} \right)\,\frac{{\partial^{2} \,w}}{{\partial \,y^{2} }} + \frac{1}{{E^{2} }}\frac{{\partial^{2} \,w}}{{\partial \,s^{2} }} + \frac{{\dot{E}}}{E}\frac{\partial \,w}{{\partial \,s}}} \right. \\ & + \frac{1}{{E^{2} }}\frac{{\partial^{2} \,w}}{{\partial \,s^{2} }}\left. { - \frac{1}{{E^{2} }}\left( {\dot{H}\frac{{\dot{E}}}{E} + \ddot{H}} \right)\frac{\partial \,w}{{\partial \,y}} - 2\frac{{\dot{H}}}{{E^{2} }}\frac{{\partial^{2} \,w}}{\partial y\,\partial s} + \frac{1}{{E^{3} }}\left( {\ddot{E} - \frac{{\dot{E}^{2} }}{E}} \right)\,w} \right] & & & & & (c) \\ and \\ 0 = & \frac{\partial \,u}{{\partial \,x}} + \frac{\partial \,v}{{\partial \,y}} + \frac{\partial \,w}{{\partial \,s}} + \frac{{\dot{E}}}{E}\,w & & & & & (d) \\ \end{aligned} \right\}$$

(3)

Dimensionless quantities are introduced, such as:

$$\begin{gathered} \overline{y} = \frac{y}{c}\,\,,\,\,\theta = \frac{x}{R}\,\,,\,\,\overline{s} = \frac{s}{{S_{o} }}\,\,,\,\,\overline{H} = \frac{H}{{S_{o} }}\,\,,\,\,\overline{u} = \frac{u}{\omega \,R}\,\,,\,\,\overline{v} = \frac{v}{\omega \,R}\,\,,\,\,\overline{w} = \frac{w}{\omega \,R}\,\,,\,\,\Delta = \frac{\delta }{{S_{o} }}\,\, \hfill \\ \,and\,\,\overline{p} = \frac{{p\,\,c^{2} }}{{\mu_{bf} \,\omega \,R^{2} }} \hfill \\ \end{gathered}$$

(4)

Using the supplied dimensionless variables in (4) and assuming that ${c \mathord{\left/ {\vphantom {c {R < < 1}}} \right. \kern-0pt} {R < < 1}}\,\,and\,\,{c \mathord{\left/ {\vphantom {c {S_{o} < < 1}}} \right. \kern-0pt} {S_{o} < < 1}}$, Eq. (3) can be reduced to,

$$\left. \begin{aligned} 0 = & - \,\frac{{\partial \,\overline{p}}}{\partial \,\theta } + \frac{1}{{E^{2} }}\,\frac{{\partial^{2} \,\overline{u}}}{{\partial \,\overline{y}^{2} }} & & (a) \\ 0 = & \frac{{\partial \,\overline{p}}}{{\partial \,\overline{y}}} & & (b) \\ 0 = & - \left( {\frac{R}{{S_{o} }}} \right)\,\frac{{\partial \,\overline{p}}}{{\partial \,\overline{s}}} + \frac{{\partial^{2} \,\overline{w}}}{{\partial \,\overline{y}^{2} }} & & (c) \\ and \\ 0 = & \frac{{\partial \,\overline{u}}}{\partial \,\theta } + \left( \frac{R}{c} \right)\,\frac{{\partial \,\overline{v}}}{{\partial \,\overline{y}}} + \left( {\frac{R}{{S_{o} }}} \right)\,\left( {\frac{{\partial \,\overline{w}}}{{\partial \,\overline{s}}} + \frac{1}{E}\frac{d\,E}{{d\,\overline{s}}}\,\overline{w}} \right) & & (d) \\ \end{aligned} \right\}$$

(5)

The velocity components boundary conditions are as follows:

$$\left. \begin{aligned} At\,\,\overline{y} = 0: &\,\,\,\, \overline{u}\,\left( {\theta \,,\,\,\overline{s}\,,\,\,0} \right) = 0 \\ & \,\,\,\,\overline{w}\,\left( {\theta \,,\,\,\overline{s}\,,\,\,0} \right) = 0 \\ At\,\,\overline{y} = h^{*} : & \,\,\,\,\overline{u}\,\left( {\theta \,,\,\,\overline{s}\,,\,\,h^{*} } \right) = 1 + \frac{{S_{o} }}{R}\,\left( {\Delta - \overline{H}} \right) \\ & \,\,\,\,\overline{w}\,\left( {\theta \,,\,\,\overline{s}\,,\,\,h^{*} } \right) = 0 \\ \end{aligned} \right\}$$

(6)

where $h^{*}$ is the dimensionless film thickness, $h^{*} = {h \mathord{\left/ {\vphantom {h c}} \right. \kern-0pt} c} = 1 + \varepsilon \,\,\cos \,\,(\theta )$, and the dimensionless maximum variation of the geometry is defined as $\Delta = {\delta \mathord{\left/ {\vphantom {\delta {S_{o} }}} \right. \kern-0pt} {S_{o} }}$.

The velocity field can be obtained by integrating Eqs. (5a and c) twice with respect to $\overline{y}$ and applying the boundary conditions at $\overline{y} = 0\,\,and\,\,\overline{y} = h^{*}$. The velocity components and velocity gradients are,

$$\left. \begin{gathered} \overline{u} = \frac{{E^{2} }}{2}\left( {\overline{y}^{2} - \overline{y}\,h^{*} } \right)\,\frac{{\partial \,\overline{p}}}{\partial \,\theta } + \frac{{\overline{y}}}{{h^{*} }}\,\left[ {1 + \frac{{S_{o} }}{R}\,\left( {\Delta - \overline{H}} \right)} \right] \hfill \\ \overline{w} = \frac{1}{2}\left( {\frac{R}{{S_{o} }}} \right)\,\left( {\overline{y}^{2} - \overline{y}\,h^{*} } \right)\,\frac{{\partial \,\overline{p}}}{{\partial \,\overline{s}}} \hfill \\ \end{gathered} \right\}$$

(7a)

$$\left. \begin{gathered} \frac{{\partial \,\overline{u}}}{{\partial \,\overline{y}}} = \,E^{2} \left( {\overline{y} - \frac{{h^{*} }}{2}} \right)\,\frac{{\partial \,\overline{p}}}{\partial \,\theta } + \frac{1}{{h^{*} }}\,\left[ {1 + \frac{{S_{o} }}{R}\,\left( {\Delta - \overline{H}} \right)} \right] \hfill \\ \frac{{\partial \,\overline{w}}}{{\partial \,\overline{y}}} = \left( {\frac{R}{{S_{o} }}} \right)\,\left( {\overline{y} - \frac{{h^{*} }}{2}} \right)\,\frac{{\partial \,\overline{p}}}{{\partial \,\overline{s}}} \hfill \\ \end{gathered} \right\}$$

(7b)

Integrating Eq. (5d) with respect to $\overline{y}$ across the film yields,

$$\frac{\partial }{\partial \,\theta }\left( {E\,h^{{*^{3} }} \frac{{\partial \,\overline{p}}}{\partial \,\theta }} \right) + \left( {\frac{R}{{S_{o} \,E}}} \right)^{2} \,\frac{\partial }{{\partial \,\overline{s}}}\left( {E\,h^{{*^{3} }} \frac{{\partial \,\overline{p}}}{{\partial \,\overline{s}}}} \right) = \frac{6}{E}\,\left[ {1 + \frac{{S_{o} }}{R}\left( {\Delta - \overline{H}} \right)} \right]\,\frac{{\partial \,h^{*} }}{\partial \,\theta } + \frac{12}{E}\frac{{\partial \,h^{*} }}{{\partial \,\overline{t}}}$$

(8)

Equation (8) is a general form of Reynolds equation that governs the pressure inside a bearing with a variable axial shape. Axially, the radial clearance is always kept constant. Assuming steady state film operation, that is ${{\partial \,h^{*} } \mathord{\left/ {\vphantom {{\partial \,h^{*} } {\partial \,\mathop t\limits^{\_} = 0}}} \right. \kern-0pt} {\partial \,\mathop t\limits^{\_} = 0}}$,and substituting ${{\partial \,h^{*} } \mathord{\left/ {\vphantom {{\partial \,h^{*} } {\partial \,\theta = - \varepsilon \,\sin \,(\theta )}}} \right. \kern-0pt} {\partial \,\theta = - \varepsilon \,\sin \,(\theta )}}$ into Eq. (8) we have,

$$\frac{\partial }{\partial \,\theta }\left( {E\,h^{{*^{3} }} \frac{{\partial \,\overline{p}}}{\partial \,\theta }} \right) + \left( {\frac{R}{{S_{o} \,E}}} \right)^{2} \,\frac{\partial }{{\partial \,\overline{s}}}\left( {E\,h^{{*^{3} }} \frac{{\partial \,\overline{p}}}{{\partial \,\overline{s}}}} \right) = - \,\left( {\frac{6\,\varepsilon }{E}} \right)\,\left[ {1 + \frac{{S_{o} }}{R}\left( {\Delta - \overline{H}} \right)} \right]\,\,\sin \,(\theta )$$

(9)

The boundary conditions for the pressure variable $\overline{p}$ are,

$$\left. \begin{gathered} \overline{p}\,\left( {0\,,\,\,\overline{s}} \right) = 0\,\,,\,\,\,\,\overline{p}\,\left( {\theta_{eff} \,,\,\overline{s}} \right) = \left. {\frac{{\partial \,\overline{p}}}{\partial \,\theta }} \right|_{{\theta_{eff} }} = 0 \hfill \\ \frac{{\partial \,\overline{p}\,(\theta \,,\,\,0)}}{{\partial \,\overline{s}}} = 0\,,\,\,\overline{p}\,\left( {\theta \,,\,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \right) = 0 \hfill \\ \end{gathered} \right\}$$

(10)

In a dimensionless form, the radial and tangential load components can be represented as,

$$\left. \begin{gathered} \overline{W}_{r} = \frac{{W_{r} }}{{\left( {\frac{{\mu_{bf} \,\omega \,R^{3} S_{o} }}{{c^{2} }}} \right)}} = - \,2\,\,\int\limits_{0}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} {} \int\limits_{0}^{{\theta_{eff} }} {E\,\overline{p}} \left[ {1 + \left( {\frac{{S_{o} }}{R}} \right)\,\left( {\Delta - \overline{H}} \right)} \right]\,\,\cos \,(\theta )\,\,d\theta \,d\,\overline{s} \hfill \\ \overline{W}_{t} = \frac{{W_{t} }}{{\left( {\frac{{\mu_{bf} \,\omega \,R^{3} S_{o} }}{{c^{2} }}} \right)}} = \,\,\,2\,\,\int\limits_{0}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} {} \int\limits_{0}^{{\theta_{eff} }} {E\,\overline{p}} \left[ {1 + \left( {\frac{{S_{o} }}{R}} \right)\,\left( {\Delta - \overline{H}} \right)} \right]\,\,\,\sin \,(\theta )\,\,d\theta \,d\,\overline{s} \hfill \\ \end{gathered} \right\}$$

(11)

The dimensionless resultant load $\overline{W}$ and the attitude angle $\phi$ may be calculated from,

$$\overline{W} = \left( {\overline{W}_{r}^{2} + \overline{W}_{t}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \,\,,\,\,and\,\,\phi = \tan^{ - 1} \left( {\frac{{\overline{W}_{t} }}{{\overline{W}_{r} }}} \right)$$

Integrating the shear stress around the journal surface yields the friction force, which may be expressed in dimensionless form as,

$$\left. \begin{gathered} \overline{F}_{f} = \frac{{F_{f} }}{{\left( {\frac{{\mu_{bf} \,\omega \,R^{2} S_{o} }}{c}} \right)}} = \,2\,\,\int\limits_{0}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} {} \int\limits_{0}^{2\,\pi } {E\,\,\left. {\frac{{\partial \,\overline{u}}}{{\partial \,\overline{y}}}} \right|_{{\overline{y} = h^{*} }} \,} \left[ {1 + \left( {\frac{{S_{o} }}{R}} \right)\,\left( {\Delta - \overline{H}} \right)} \right]\,\,\,d\theta \,d\,\overline{s} \hfill \\ where\,\,\left. {\frac{{\partial \,\overline{u}}}{{\partial \,\overline{y}}}} \right|_{{\overline{y} = h^{*} }} = \frac{{E^{2} }}{2}\,h^{*} \frac{{\partial \,\overline{p}}}{\partial \,\theta } + \left( {\frac{1}{{h^{*} }}} \right)\,\left[ {1 + \left( {\frac{{S_{o} }}{R}} \right)\,\left( {\Delta - \overline{H}} \right)} \right] \hfill \\ \end{gathered} \right\}$$

(12)

In dimensionless form, the force acting normal to the journal surface is to be calculated from,

$$\overline{F}_{n} = \frac{{F_{n} }}{{\left( {\frac{{\mu_{bf} \,\omega \,R^{3} S_{o} }}{{c^{2} }}} \right)}} = \left( {\overline{F}_{{n_{r} }}^{2} + \overline{F}_{{n_{t} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$

(13)

where $\overline{F}_{{n_{r} }}^{{}} = \frac{{F_{{n_{r} }} }}{{\left( {\frac{{\mu_{bf} \,\omega \,R^{3} S_{o} }}{{c^{2} }}} \right)}} = - \,2\,\,\int\limits_{0}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} {} \int\limits_{0}^{{\theta_{eff} }} {\,\overline{p}} \,\cos \,(\theta )\,\left[ {1 + \left( {\frac{{S_{o} }}{R}} \right)\,\left( {\Delta - \overline{H}} \right)} \right]\,\,\,d\theta \,d\,\overline{s}$.

And $\overline{F}_{{n_{t} }} = \frac{{F_{{n_{t} }} }}{{\left( {\frac{{\mu_{bf} \,\omega \,R^{3} S_{o} }}{{c^{2} }}} \right)}} = \,\,\,2\,\,\int\limits_{0}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} {} \int\limits_{0}^{{\theta_{eff} }} {\,\overline{p}\,\sin \,(\theta )\,} \left[ {1 + \left( {\frac{{S_{o} }}{R}} \right)\,\left( {\Delta - \overline{H}} \right)} \right]\,\,\,d\theta \,d\,\overline{s}$.

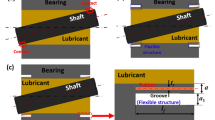
The friction parameter (variable) $C_{f} = f\,\left( {{R \mathord{\left/ {\vphantom {R c}} \right. \kern-0pt} c}} \right)$ may be calculated from $f\,\left( {{R \mathord{\left/ {\vphantom {R c}} \right. \kern-0pt} c}} \right) = {{\overline{F}_{f} } \mathord{\left/ {\vphantom {{\overline{F}_{f} } {\overline{F}_{n} }}} \right. \kern-0pt} {\overline{F}_{n} }}$, where $f\, = {{F_{f} } \mathord{\left/ {\vphantom {{F_{f} } {F_{n} }}} \right. \kern-0pt} {F_{n} }}$_. In Fig. 3, four geometrical bearing configurations are considered for comparison with the plain cylindrical bearing.

Fig. 3

Selected bearing geometrical configurations. (a) Wedge; (b) Concave; (c) Convex; (d) Wavy.

The axial surface profile of the journal is supposed to vary, and four types are considered:

$$\left. {\begin{array}{*{20}l} {Wedge\,\,bearing:} \hfill & {\overline{H} = 2 \Delta\,\,\overline{s}} \hfill \\ {Concave\,\,axially\,\,curved\,\,surfaces:} \hfill & {\overline{H} = 4{\mkern 1mu} \Delta {\mkern 1mu} {\mkern 1mu} \overline{s}^{2} } \hfill \\ {Convex\,\,axially\,\,curved\,\,surfaces:} \hfill & {\overline{H} = 4{\mkern 1mu} \Delta {\mkern 1mu} {\mkern 1mu} \left( {1 - \overline{s}} \right){\mkern 1mu} \overline{s}} \hfill \\ {Wavy\,\,surfaces:} \hfill & {\overline{H} = \frac{\Delta }{2}{\mkern 1mu} \left( {1 - \cos ({\mkern 1mu} 2{\mkern 1mu} \pi {\mkern 1mu} \overline{s}{\mkern 1mu} )} \right)} \hfill \\ \end{array} } \right\}$$

(14)

The coordinate $\overline{s}$ can be linked to the coordinate $\overline{z} = {{z^{\prime}} \mathord{\left/ {\vphantom {{z^{\prime}} {S_{o} }}} \right. \kern-0pt} {S_{o} }}$ by,

$\overline{z} = \int\limits_{0}^{{\overline{s}}} {\sqrt {1 - \left( {{{d\,\overline{H}} \mathord{\left/ {\vphantom {{d\,\overline{H}} {d\,\overline{s}}}} \right. \kern-0pt} {d\,\overline{s}}}} \right)^{2} } \,d\,\overline{s} = \int\limits_{0}^{{\overline{s}}} {E\,d\,\overline{s}} }$.

The common parameter for the geometries chosen is the greatest variation of the geometry $\overline{H}_{\max } = \Delta$, which should be practically <  < 1. In this paper, computations are conducted for $\Delta = 0.01\,,\,\,0.05\,,\,\,0.1\,,\,\,and\,\,0.15$.

Viscosity model $\left( {\overline{\mu }} \right)$

In the present study, the updated Krieger–Dougherty viscosity model may be used as¹⁹,

$$\overline{\mu } = \frac{{\mu_{nf} }}{{\mu_{bl} }} = \left( {1 - \frac{{\Phi_{a} }}{{\Phi_{m} }}} \right)^{{\, - 2.5\,\Phi_{m} }}$$

(15)

With $\Phi_{a} = \Phi \,\left( {\frac{{a_{a} }}{a}} \right)^{{3 - D^{*} }}$

Where,$a_{a} \,\,and\,\,a$, are the radii of aggregates and primary particles, D^* is the fractional index, which has a standard value of 1.8 for nanofluids⁴⁴. $\Phi_{m}$ is the maximum particle packing fraction, $\Phi_{m} = 0.605$ at high shear stress rates⁴⁴. Using the reported values of D^* and $\Phi_{m}$, the modified Kriegerr-Dougherty equation may be written as,

$$\overline{\mu } = \frac{{\mu_{nf} }}{{\mu_{bl} }} = \left( {1 - \frac{\Phi }{{\Phi_{m} }}\,\left( \beta \right)^{\,1.2} } \right)^{{\, - 2.5\,\Phi_{m} }}$$

(16)

where $\beta = \left( {{{a_{a} } \mathord{\left/ {\vphantom {{a_{a} } a}} \right. \kern-0pt} a}} \right)$ is the aggregate packing fraction, which depends on the type of the nanoparticles and their sizes. Binu et al.⁵⁰ carried out experimental measurements on TiO₂ nanoparticles of $a < 100\,{\text{nm}}$ and distributed in SAE30 engine oil at different volume fractions ranging from $\Phi = 0.0001\,\,to\,\,0.005$. They used the DLS analysis and found that the mean aggregate particle size $a_{a} = 777\,{\text{nm}}$ and the aggregate packing fraction was estimated to be $\beta = 7.77$. This means that the TiO₂ nanoparticle aggregates are roughly 7.77 times the primary particle size of 100 nm. They documented that Eq. (16) has a fairly good agreement with the measured viscosities for different values of volume fraction. In the present analysis, for comparison purpose, the study is carried out for volume fraction ranging from 0.001 to 0.01 with various values of aggregate particle packing fraction $\beta = 4\,,\,\,7.77\,\,and\,10$.

Solution methodology

The Reynolds-like Eq. (9) and boundary conditions (10) were numerically solved with the finite difference technique. To solve the sets of simultaneous equations, a FORTRAN-based computational algorithm⁶² is constructed in order to be used with the successive relaxation method. To consider a non-cavitating model, set all negative pressure variables to zero throughout the solution⁶¹. The iteration process continues until convergence with a relative tolerance of 0.01 is reached. The modified Krieger–Dougherty model (Eq. 16) is employed in the discretized Reynolds equations to calculate steady-state pressure distributions in the bearing lubricant film. The bearing properties of TiO₂ nanoparticle volume fractions are studied for different aggregate size values.

Results and discussions

The steady state journal bearing characteristics is affected significantly by using the journal bearing with an axial variation in geometrical shape as well as the use of nanoparticles as lubricant additives. Four different shapes for the bearing having wedge, concave, convex and wavy surfaces are made. Based on the experimental work of Binu et al.²⁶, the modified Krieger–Dougherty model, Eq. 16, is used to calculate the viscosity of the nanolubricant. In the formulation of nanolubricant, TiO₂ nanoparticles (scale 100 nm) and SAE30 engine oil are employed, with volume fractions ranging from 0.001 to 0.01 at various nanoparticle aggregate sizes. According to the authors’ knowledge, there are no published studies on how nanoparticle concentrations and aggregate particle sizes affect journal bearing performance using axial geometrical variations. In Refs^50,60, researchers examined the impact of titanium dioxide nanoparticles as lubricant additives on steady-state performance^50,60 and stability limitations⁶⁰. The current study found a high agreement between the model developed and data from the cited references for a cylindrical bearing operating under steady state conditions. El-Gamal¹⁵ provided an analysis of the steady state performance of a wedge-shaped hydrodynamic journal bearing, comparing the results of the dimensionless wedged-bearing load produced in the current work to the results obtained in¹⁵. A good qualitative agreement has been reached. The largest disparity in dimensionless load is 5.26% at eccentricity ratio 0.2, decreasing to 1.125% at eccentricity ratio 0.9.

Bearing characteristics for different geometries

The pressure distribution inside the bearing at the mid-plane is depicted in Figs. 4, 5 and 6.

Fig. 4

Effect of axial geometrical variations (bearing geometry) on pressure distribution along circumferential direction at bearing mid-plane at ${{\Phi = 0\,\,and\,\,S_{o} } \mathord{\left/ {\vphantom {{\Phi = 0\,\,and\,\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

Fig. 5

Effect of the maximum axial variation of the concave bearing geometry on pressure distribution along circumferential direction at bearing mid-plane with ${{\Phi = 0\,\,and\,\,S_{o} } \mathord{\left/ {\vphantom {{\Phi = 0\,\,and\,\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

Fig. 6

Effect of eccentricity ratio on pressure distribution along circumferential direction at bearing mid-plane for concave axial variation of the bearing geometry at ${{\Phi = 0\,\,and\,\,S_{o} } \mathord{\left/ {\vphantom {{\Phi = 0\,\,and\,\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

The findings reveal that a concave surface creates higher pressure levels inside the fluid film. The maximum geometric variation raises the pressure distribution values in the bearing oil film. Furthermore, the higher the eccentricity ratio, the higher the pressure values in the bearing fluid film. Figure 7 shows the results of the bearing characteristics $\overline{W}\,,\,\,\overline{F}_{f} \,,\,\,f\,({R \mathord{\left/ {\vphantom {R {c)}}} \right. \kern-0pt} {c)}}$ and $\phi$ obtained for the wedge, concave, convex and wavy shaped geometries selected. The results are presented for $\Delta = 0.1\,\,and\,\,{{S_{o} } \mathord{\left/ {\vphantom {{S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$ with $\Phi = 0$. The plain cylindrical bearing characteristics are also shown in the same Fig. 7a–d for comparison. It is remarkable that all geometries appear to have better load carrying capacity than a plain cylindrical bearing. This is the case at any eccentricity ratio. For all geometries, the load carrying capacity increases with the increase in eccentricity ratio. When the geometries are compared with each other, the concave geometry is found to give the largest load carrying capacity $\overline{W}$ at any eccentricity ratio $\varepsilon$. On the other hand, the convex shape is seen to give the smallest $\overline{W}$ at any $\varepsilon$. Figure 7c shows that the friction parameter $f(R/c)$ is seen to decrease for the geometries considered compared to the plain cylindrical journal bearing at any $\varepsilon$.The geometries considered show a negligible differences in attitude angle when compared to the plain cylindrical bearing at any $\varepsilon$, see Fig. 7d.

Fig. 7

Bearing characteristics (bearing load, friction force, friction parameter and attitude angle) for different geometries with ${{\Phi = 0\,\,and\,\,S_{o} } \mathord{\left/ {\vphantom {{\Phi = 0\,\,and\,\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

The superiority of concave geometry over other shapes can be seen. The results in Fig. 8a show that increasing the largest variation of the geometry $\Delta$ increases the bearing load capacity for concave axially curved surfaces. Furthermore, as shown in Fig. 8b, the largest change in the concave surface shape shows a significant reduction in the friction parameter at low eccentricity ratios.

Fig. 8

Effect of maximum axial variation on bearing characteristics (bearing load $\overline{W}$ and friction parameter $f\,(R/c)$) for concave bearing geometry at ${{\Phi = 0\,\,and\,\,S_{o} } \mathord{\left/ {\vphantom {{\Phi = 0\,\,and\,\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

Bearing characteristics using titanium dioxide nanoparticles as lubricant additive

The effect of TiO₂ nanoparticles with $\Phi = 0.005$ and aggregate packing fraction $\beta = 7.77$ on the pressure distribution in the oil film along the circumferential direction at the bearing mid-plane at $\varepsilon = 0.6$ is shown in Fig. 9. Figure 9 illustrates the pressure distribution along the circumferential direction at bearing mid-plane for all of the axial geometrical variations considered in the present investigation, namely wavy, concave, convex, and wavy. In comparison to the pressure distribution for plain bearings, the presence of any of the aforementioned axial variations causes an increase in the generated pressure inside the oil film. The findings reveal that the concave surface shape causes higher pressure distribution in the oil film than the other surface geometries.

Fig. 9

Effect of bearing geometry on pressure distribution along circumferential direction at bearing mid-plane at ${{\Phi = 0.005\,\,,\,\,\beta = 7.77\,\,and\,\,S_{o} } \mathord{\left/ {\vphantom {{\Phi = 0.005\,\,,\,\,\beta = 7.77\,\,and\,\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

Bearing characteristics (bearing load, friction force, friction parameter, and attitude angle) for various geometries using a TiO₂ lubricant additive with a volume fraction $\Phi = 0.005$ and aggregate packing fraction $\beta = 7.77$ are shown in Fig. 10. The bearing’s behavior is similar to that shown in Fig. 7, and the superiority of concave geometry over other shapes persists. For the concave surface geometry, the effect of TiO₂ volume fractions; ranging from 0 to 0.01; on the pressure distributions inside the bearing is explored in Fig. 11. It can be seen that as the volume fraction increases, the pressure inside the bearing increases. At higher volume fractions, the rise in pressure is found to be more pronounced. As shown in Fig. 12, the maximum value of the bearing oil film pressure distribution increases as the aggregate packing fraction value (described in viscosity model) increases. With increasing aggregate packing fractions, the pressure distribution becomes more pronounced.

Fig. 10

Bearing characteristics (bearing load $\overline{W}$, friction force $\overline{F}_{f}$, friction parameter $f\,(R/c)$ and attitude angle $\phi$) for different geometries with ${{\Phi = 0.005\,\,,\,\,\beta = 7.77\,\,\,and\,\,S_{o} } \mathord{\left/ {\vphantom {{\Phi = 0.005\,\,,\,\,\beta = 7.77\,\,\,and\,\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

Fig. 11

Effect of volume fraction $\Phi$ on pressure distribution along circumferential direction for concave bearing geometry at mid-plane with ${{\,S_{o} } \mathord{\left/ {\vphantom {{\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

Fig. 12

Effect of aggregate packing fraction $\beta$ on pressure distribution along circumferential direction for concave surface bearing geometry at mid-plane with ${{\Phi = 0.005\,\,and\,\,\,S_{o} } \mathord{\left/ {\vphantom {{\Phi = 0.005\,\,and\,\,\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

As demonstrated in Figure 13a, the effect of various TiO₂ volume fractions on bearing load capacity for concave surface bearing is analyzed and depicted. The findings show that the existence of TiO₂ nanoparticle lubricant additives increases the bearing load carrying ability. The increase in bearing load is found to be more pronounced at higher TiO₂ nanoparticle volume fraction values. According to Fig. 13b, increasing the volume fraction has no sensible effect on the bearing friction parameter.

Fig. 13

Effect of nanoparticle volume fraction on bearing characteristics (bearing load and friction parameter $f\,(R/c)$) for concave bearing geometry at ${{\Phi = 0.005\,\,,\,\,\beta = 7.77\,\,\,and\,\,S_{o} } \mathord{\left/ {\vphantom {{\Phi = 0.005\,\,,\,\,\beta = 7.77\,\,\,and\,\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

The results in Fig. 14a show that increasing the largest variation of the geometry $\Delta$ increases the bearing load capacity for concave axially curved surface. Furthermore, as shown in Fig. 14b, the largest change in the concave surface shape results in a significant reduction in the friction parameter. For a given volume fraction, the results show that increasing the aggregate packing fraction increases bearing load capacity (Fig. 15a) but has no sensible effect on friction parameter (Fig. 15b). Figure 16 shows the effect of bearing surface length to diameter ratio ${{(S_{o} } \mathord{\left/ {\vphantom {{(S_{o} } D}} \right. \kern-0pt} D})$ on bearing characteristics. The bearing load capacity increases as the length to diameter ratio increases, while the friction parameter decreases only slightly.

Fig. 14

Effect of maximum axial variation on bearing characteristics (bearing load $\overline{W}$ and friction parameter $f\,(R/c)$) for concave bearing geometry at ${{\Phi = 0.005\,\,,\,\,\beta = 7.77\,\,\,and\,\,S_{o} } \mathord{\left/ {\vphantom {{\Phi = 0.005\,\,,\,\,\beta = 7.77\,\,\,and\,\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

Fig. 15

Effect of packing volume fraction on bearing characteristics (bearing load $\overline{W}$ and friction parameter $f\,(R/c)$) for concave bearing geometry at ${{\Phi = 0.005\,\,\,and\,\,S_{o} } \mathord{\left/ {\vphantom {{\Phi = 0.005\,\,\,and\,\,S_{o} } {D = 1}}} \right. \kern-0pt} {D = 1}}$.

Fig. 16

Effect of $S_{o} /D$ on bearing characteristics (bearing load $\overline{W}$ and friction parameter $f\,(R/c)$) for different bearing geometries at $\Phi = 0.005\,\,and\,\,\beta = 7.77$.

The relative difference in bearing load carrying capacity as a result of surface geometry, nanofluid lubricant, and the combination of the two can be introduced as follows:

$$\begin{gathered} Surface\,\,geometry\,\,\,\,\,\,:\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\% \,W_{g} = \frac{{W_{g} - W_{\,cyl} }}{{W_{\,cyl} }}\, \times 100 \hfill \\ Nanofluid\,\,{\text{lub}} ricant:\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\% \,W_{\,n} = \frac{{W_{gn} - W_{g} }}{{W_{g} }}\, \times 100 \hfill \\ Combination\,\,of\,\,the\,\,two:\,\,\,\,\,\,\,\,\,\,\,\,\% \,W_{\,gn} = \frac{{W_{gn} - W_{\,cyl} }}{{W_{\,cyl} }}\, \times 100 \hfill \\ \end{gathered}$$

In the same manner, the relative difference in bearing friction parameter $\% \,C_{f}$ can be estimated. Table 2 shows the relative difference in bearing characteristics caused by using a concave bearing surface shape with a dimensionless maximum axial variation $\Delta = 0.1$ and a nanofluid lubricant with a volume fraction $\Phi = 0.005$ and an aggregate packing fraction $\beta = 7.77$.

Table 2 Bearing characteristics for concave bearing surface shape with and without lubricant additives.

In comparison to plain cylindrical bearing, the results for the bearing geometries under consideration demonstrate that the presence of variations in the axial shape of the bearing increases the load carrying capacity and decreases the friction parameter (variable). Concave geometry surpasses other shapes. Furthermore, using TiO₂ nanoparticles as a lubricant additive increases bearing load capacity while having no effect on friction parameters.

Conclusions

An axial geometrical configuration for hydrodynamic journal bearings lubricated with noanolubricant using titanium dioxide nanoparticles as lubricant additives is proposed here. The analysis assumed that the flow in the bearing was laminar incompressible and the lubricant was isoviscous. A curvilinear coordinate system is employed to develop the Reynolds-like equation that governs the pressure inside the bearing. A theoretical investigation of the effects of increasing nanofluid aggregate sizes and nanoparticle concentrations on the static performance of journal bearings has been presented. Several conclusions are drawn:

• Compared to a simple cylindrical bearing, variations in the bearing’s axial shape increase load carrying capacity while decreasing the friction parameter. This is especially apparent with reasonably long bearings.

• Concave geometry shows superiority over other forms.

• The effect of TiO₂ nanoparticle lubricant additives on the static characteristics of finite journal bearings is theoretically analyzed using the modified Krieger–Dougherty viscosity model. As the volume fraction and aggregate packing fraction increase, they cause a corresponding increase in the pressure distribution inside the bearing.

• The bearing load capacity increases significantly at higher values of the nanoparticle volume fraction while the friction parameter decreases. The bearing load capacity increases as the aggregate packing fraction increases with negligible effect on the friction parameter.

As a future work, it could be interesting to investigate the effect of axial geometrical variations on the stability limits of journal bearings lubricated by nanofluids.