Introduction

Compose of repeated ethylene oxide units, the synthetic polyethylene glycol (PEG) is known for its versatile properties and wide range of applications. It is produced through the polymerization of ethylene oxide, resulting in a linear, water-soluble polyether. One of the defining features of polyethylene glycol is its availability in a broad range of molar masses, typically ranging from as low as 200 g/mol to over 35,000 g/mol1,2,3,4. This diversity in molecular weight significantly influences its physical properties, such as viscosity, solubility, and melting point. PEGs with lower molar mass values are liquids or viscous fluids at room temperature, while higher-molecular-weight PEGs are solid and wax-like. PEG is non-toxic, biocompatible, and non-immunogenic, making it suitable for applications in pharmaceuticals, cosmetics, and food products5,6,7,8.

The diverse range of molar masses allows polyethylene glycol to serve various roles across industries. In the pharmaceutical sector, PEGs with lower molecular weights are often used as solvents, excipients, and laxatives, while higher-molecular-weight PEGs function as binders, drug carriers, or controlled-release agents9,10. In cosmetics, PEG acts as a moisturizer, emulsifier, and thickener due to its hydrophilic nature. Furthermore, PEG is employed in industrial processes as a lubricant, plasticizer, and anti-foaming agent. Its ability to conjugate with proteins and other molecules has also expanded its use in medical disciplines like tissue engineering and drug delivery systems11,12. This versatility, driven by the broad spectrum of molar masses, has solidified polyethylene glycol as a critical material in numerous scientific and commercial fields13.

Supercritical fluids like supercritical carbon dioxide (SC-CO2)14 have shown a great ability in various fields including extraction of essential oil15,16,17,18,19,20,21, seed oil22,23,24, solubility25,26,27, particle formation (RESS, RESSAS, US-RESS or US-RESoLVe,…)28,29,30,31,32,33,34,35,36, impregnation37,38, optimization and mathematical modeling20,39, polymer synthesis40, etc. The mixture of polyethylene glycol (PEG) and carbon dioxide (CO2) holds significant importance in various industrial and scientific applications due to their complementary properties41,42,43,44,45. PEG, with its hydrophilic and non-toxic nature, can act as a stabilizer, solvent, or carrier, while CO2, particularly in its supercritical state, serves as an environmentally friendly solvent and processing medium46,47,48,49. This combination is particularly valuable in green chemistry and sustainable processes, such as supercritical fluid extraction, polymer processing, and nanoparticle synthesis50,51. The PEG-CO2 mixture enables the creation of efficient, low-toxicity systems for drug delivery, where CO2 can act as a carrier to encapsulate or release active pharmaceutical ingredients stabilized by PEG. Additionally, in advanced material production, the mixture provides enhanced solubility, reduced viscosity, and tunable processing conditions, supporting the development of innovative and sustainable technologies. The solubility of CO2 in PEG is vital for gas separation and capture technologies, as PEG can absorb CO2 efficiently due to its strong affinity for the gas. This makes it valuable in carbon capture applications, helping to address environmental challenges like greenhouse gas emissions52,53. In pharmaceutical and biomedical applications, the solubility of CO2 in PEG facilitates the creation of drug delivery systems and foamed materials, where CO2 serves as a blowing or delivery agent while PEG stabilizes or encapsulates the target substances54,55,56. Thus, the high solubility of CO2 in PEG enables innovation in sustainable manufacturing, gas absorption processes, and advanced material design, enhancing their economic and environmental viability.

Accurate estimation of CO2 solubility in polyethylene glycol (PEG) is crucial for optimizing processes such as supercritical fluid extraction, carbon capture, and polymer modification, where CO2 acts as a solvent or carrier. Precise solubility data ensures efficient process design, enhances energy savings, and supports the development of sustainable, environmentally friendly technologies. It also enables better control over material properties in applications like drug delivery and advanced manufacturing. On the other hand, the experiential methods are costly, tedious and time-consuming. Given the laboratory data availability of carbon dioxide solubility in PEG polymer in the published literature, this study seeks to construct rigorous smart models based on several machine learning methods such as random forest (RF), decision tree (DT), adaptive boosting (AdaBoost), k-nearest neighbors (KNN), and ensemble learning (EL) to estimate CO2 solubility on PEG over a wide of range of values using data collected from previously published literature data. An outlier detection algorithm is applied to find the prospective suspected points prior to the model development and a sensitivity analysis is done to figure out the relevant impacts of each input parameter. The constructed model’s performance is highlighted through a number of evaluation metrics as well as plotting approaches.

Machine learning models

Decision tree

Decision tree (DT) is a widely used machine learning and statistical tool for dual tasks of regression and classification. The method originates from the concept of recursively partitioning data into subsets based on feature values to create a tree-like structure of decisions. At each internal node, a test is performed on a specific feature to determine the optimal split, directing the flow of data points to child nodes57. This procedure is continued until the pertinent data is sufficiently homogeneous or meets a stopping criterion, and the resulting leaf nodes represent the estimated outcomes or class labels. The simplicity of the decision tree model, along with its intuitive, hierarchical structure, makes it highly interpretable and suitable for various practical applications, including finance, healthcare, and engineering58,59,60.

Interpretability is known as one of the primary advantages of decision tree structures. Unlike more complex models like neural networks, decision trees visually represent the decision-making process, enabling users to understand how estimations are made. This makes decision trees particularly valuable in domains requiring transparency and accountability, such as medical diagnosis, where understanding the reasoning behind a classification is as important as the outcome itself. This combination of flexibility, interpretability, and efficiency makes decision trees a strong tool for solving an extensive range of classification and regression problems61.

Adaptive boosting

Adaptive Boosting (AdaBoost) is a powerful ensemble learning technique introduced by Yoav Freund and Robert Schapire, intended to enhance the performance of weak classifiers, this approach combines them to form a robust and more accurate classifier. AdaBoost works iteratively, where each subsequent weak learner (commonly decision stumps—simple decision trees with one split) focuses on the mistakes made by the previous learners. It assigns higher weights to misclassified data points, making them more influential in the next iteration. By adjusting the model’s focus to harder-to-predict samples, AdaBoost progressively reduces errors and enhances the accuracy of estimations. This iterative process keep going until a specified number of weak learners are trained or no further improvement can be achieved62.

One of the main advantages of AdaBoost is its capability in boosting the performance of weak learners while maintaining simplicity. Since it combines multiple weak classifiers rather than building a single complex model, AdaBoost avoids overfitting when appropriately tuned. Its capacity to adjust to the hardest-to-classify samples allows it to achieve high accuracy on both binary and multiclass classification tasks63,64,65.

K-nearest neighbors

The K-Nearest Neighbors (KNN) algorithm is an intuitive and effective non-parametric approach frequently applied to classification and regression problems. It operates on the principle that data points with similar features are usually located near each other within the feature space. To generate a estimation, the algorithm measures the distance between the query point and all other points in the dataset commonly using Euclidean distance and identifies the k closest neighbors. The outcome is then determined based on the values or labels of these nearest neighbors. In classification tasks, the output is determined by the most frequent class among the k nearest neighbors, whereas in regression, the estimation is calculated as the average value of these neighbors. Since KNN requires no prior model training and makes estimations directly from the data, it is referred to as a “lazy learning” algorithm66,67,68.

A key advantage of KNN lies in its simplicity and straightforward implementation. Unlike many other methods, it does not require any assumptions about the data distribution, which makes it highly flexible and well-suited for managing complex, non-linear patterns within the data. KNN can work effectively on both numerical and categorical datasets, and its performance improves with larger datasets and appropriately chosen k. Another key benefit is that KNN adapts well to multi-class classification problems without requiring extensive modifications. Its intuitive nature makes it widely used in real-world applications such as recommendation systems, anomaly detection, and pattern recognition tasks like image classification69,70.

Random forest

Random forest (RF) is a machine learning ensemble technique that improves estimation reliability and accuracy by aggregating the results of multiple decision trees. Developed by Leo Breiman, it works by constructing a “forest” of multiple decision trees, each trained on a random subset of the data using a technique called bagging (Bootstrap Aggregating). At each node where a split occurs in the tree, a randomly selected subset of features is evaluated, which introduces additional diversity among the trees. The final output is obtained by combining the estimations of all individual trees, using majority voting for classification tasks or averaging for regression. This ensemble strategy minimizes the likelihood of overfitting, a frequent problem with single decision trees, and improves the model’s ability to generalize to new, unseen data71,72,73.

One of the principal advantages of Random Forest is its capability to deliver high accuracy while maintaining robustness. By combining estimations from multiple trees, the model mitigates the impact of noisy data, outliers, or overfitting that could compromise the performance of a single tree. Additionally, Random Forest is highly versatile, capable of handling both classification and regression tasks, as well as mixed datasets with numerical and categorical features. Moreover, it exhibits excellent generalization capability, making it widely used in diverse fields such as finance (credit risk estimation), healthcare (disease diagnosis), and environmental sciences (climate modeling). By combining the interpretability of decision trees with ensemble learning techniques, Random Forest strikes an optimal balance between accuracy, robustness, and computational efficiency, making it a reliable tool for solving complicated real-world issues74,75.

Ensemble learning

Ensemble learning (EL) is a methodology in machine learning that integrates several individual models, often called “base learners” or “weak learners,” to produce a more accurate and reliable predictive model. The central idea is that while a single model may struggle with certain aspects of a dataset, combining the forecasts of numerous models can diminish errors and enhance generalization. Ensemble methods achieve this by leveraging the diversity among base models to minimize bias, variance, and noise. The primary techniques used in ensemble learning are boosting (like AdaBoost), bagging (such as Random Forest), and stacking, where multiple models contribute to the final estimation through averaging, majority voting, or a meta-model76,77.

One of the vital compensations of ensemble learning is its ability to significantly improve accuracy and robustness over single models. By combining outputs from multiple learners, ensemble techniques reduce the risk of overfitting, particularly on noisy or complex datasets. For example, bagging (Bootstrap Aggregating) trains models independently on randomly sampled subsets of the data, which reduces variance and enhances stability78,79.

Dada analysis and models’ evaluation metrics

To construct the smart models in this study, data were sourced from previously published research that experimentally measured CO2 solubility in different PEGs in terms of their molar masses, temperature and pressure80,81,82,83,84,85. The resulting dataset consists of 164 data points, for which statistical parameters such as the minimum, maximum, median, mode, kurtosis, standard deviation, skewness, and mean have been presented in Table 1.

Table 1 Statistical description with regard to input and output variables in this study.
Full size table

To assess how well each developed model performs in terms of estimation, various indices have been computed for comparison. These indices include mean square error (MSE), determination coefficient (R2), relative error percent (RE%), absolute relative error (ARE%) and average absolute relative error (AARE%) and the details are given in86,87,88.

For the development of predictive models, features contain PEG molecular weight, pressure and temperature, whereas CO2 solubility in PEG serves as the output variable. The dataset, consisting of 164 data points, is divided such that 90% is utilized for training and validation through the k-fold cross-validation approach with five folds, and the remaining 10% is reserved for evaluating the models’ performance. To minimize the effect of variability within the dataset, all input factors as well as the output variable are normalized beforehand according to the following simple equation89:

$$n_{norm} = \frac{{n - n_{\min } }}{{n_{\max } - n_{\min } }}$$
(1)

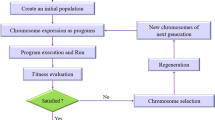
In this context, n refers to the actual data point, while nmin and nmax represent the minimum and maximum values in the dataset, respectively, and nnorm corresponds to the normalized data point. K-fold cross-validation is known as a methodology aimed at enhancing the accuracy of machine learning models by utilizing the entire dataset for repeated evaluations. The dataset is divided into K equal segments (folds), where each segment is used as a validation set once, while the remaining K − 1 segments are used for training. The outcomes from all K validation iterations are combined to produce a single performance estimate, reducing the bias associated with random data splitting. This approach also successfully decreases well-known overfitting phenomenon while training the data-driven models. A visual representation of the K-fold cross-validation algorithm is shown in Fig. 190,91. In this work, a five-fold cross-validation approach has been executed during the training phase for each machine learning model.

Fig. 1
figure 1

Schematic representation of k-fold cross-validation algorithm.

Full size image

Results and discussion

Outlier detection

The functionality and reliability of the developed models are significantly affected by the quality of the datasets used in their creation. To verify the trustworthiness of the data, the Leverage approach is utilized. In this method, the Hat matrix is expressed as92,93:

$$H = X\left( {X^{T} X} \right)^{ - 1} X^{T}$$
(2)

Herein, design matrix denoted by X can be defined with dimensions m × n, in which m indicates total count of datapoints, and n embodies count of input factors, which equals 3 in this study. The William’s plot provides a visual representation of the correlation amongst the normalized values and the Hat values, with the latter corresponding to the diagonal elements of the Hat matrix. This plot is particularly useful for identifying outliers, and the warning leverage is calculated using88,94:

$$H^{*} = 3\left( {n + 1} \right)/m$$
(3)

In this work, the warning leverage value has been calculated to be approximately 0.073. The standardized residuals are maintained within a range of − 3 to + 3. The William’s plot, shown in Fig. 2, visually highlights suspected and potential outlier data points. The vertical line indicates the warning leverage threshold, while the two horizontal lines define the standardized residual limits. Data points falling inside these boundaries are regarded as valid and trustworthy. As illustrated in Fig. 2, 12 data points are marked as suspected. However, to improve the generalizability of the developed models, all data points are incorporated into the algorithms.

Fig. 2
figure 2

Identification of outliers within the gathered experimental dataset.

Full size image

Sensitivity study

In this section, the goal is to analyze how each input parameter such as temperature, pressure, and PEG molecular weight affects the output variable, CO2 solubility in PEG. This is achieved through the application of sensitivity analysis to quantify the individual contributions and influence of these parameters88,95,96,97,98. This approach entails determining the relevancy index pertinent to every feature, which is computed using the following equation:

$$r_{j} = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {x_{j,i} - \overline{x}_{j} } \right)\left( {y_{i} - \overline{y}} \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {x_{j,i} - \overline{x}_{j} } \right)^{2} \sum\limits_{i = 1}^{n} {\left( {y_{i} - \overline{y}} \right)^{2} } } } }}\quad \left( {j = 1,2,3} \right)$$
(4)

The relevancy factor ranges from − 1 to 1, with two important points to note. Positive values signify a direct correlation with the output variable, whereas negative values represent an inverse relationship. Second, the greater the absolute value of the index, the stronger its impact on the output. Figure 3 presents the relevancy indices calculated for each input parameter. The results show that both pressure and PEG molecular weight have positive relevancy factors, suggesting a direct correlation with CO2 solubility in PEG polymer. On the other hand, temperature has a negative relevancy factor, indicating an inverse relationship with solubility. Among the parameters, pressure is observed to have the highest influence, whereas temperature is the least impactful on CO2 solubility in PEG.

Fig. 3
figure 3

Sensitivity study of temperature, pressure and PEG molar mass with respect to output parameter.

Full size image

Obtaining models’ hyperparameters

The training and validation subsets are used to identify the optimal parameters and hyperparameters for different algorithms. In the DT model, the max-depth hyperparameter is determined to be 6, as showed in Fig. 4. For the AdaBoost model, the optimal number of estimators is 12, as shown in Fig. 5. Similarly, Fig. 6 indicates that the number of estimators for the RF model is 11. For the KNN model, the value of K is determined to be 2, as illustrated in Fig. 7. It is notable that KNN, DT, RF, and AdaBoost models, with their respective optimized parameters, are considered components of the EL framework.

Fig. 4
figure 4

Coefficient of determination versus maximum depth for DT algorithm.

Full size image
Fig. 5
figure 5

R-squared in terms of number of estimators for AdaBoost algorithm.

Full size image
Fig. 6
figure 6

R-squared in terms of maximum depth hyperparameter for RF algorithm.

Full size image
Fig. 7
figure 7

R-squared in terms of number of neighbors hyperparameter in KNN algorithm.

Full size image

Performance of the developed models

Table 2 presents the evaluation metrics for training, test, and total datasets, showcasing the predictive performance of the data-driven models for CO2 solubility in PEG. To measure the effectiveness of the proposed soft computing techniques, three mathematical evaluation metrics are employed: R-squared, mean squared error (MSE), and the percent of average absolute relative errors. According to these metrics, the DT model demonstrates the highest accuracy in estimating solubility as it identified with lowest MSE, AARE% and highest R-squared for the unseen testing data. Note that AdaBoost and EL are detected with some degrees of overfitting due to considerable difference in MSE between train and test segments, even though they were empowered with k-fold cross validation during the training. Therefore, these two models are unreliable although their indicators for train and test are impressive.

Table 2 Assessment indices of the constructed smart models with regard to train, test and total datasets.
Full size table

This research employs two visualization methods, that is, crossplots and relative error plots to evaluate the accuracy of the machine learning algorithms. Figure 8 depict the comparison between actual and estimated solubility values for various models applied here. The DT predictive model demonstrates a close clustering of points near the bisector line, indicating a powerful correlation amongst the observed and estimated results. The resulted equations due to fitting lines to these datapoints are nearly identical to the y = x line, which confirms the model’ effectiveness in estimating solubility. Furthermore, scatter plots of relative errors in Fig. 9 reveal that the error values for the DT model are tightly concentrated around the x-axis, emphasizing its high accuracy. These visualization techniques provide strong evidence of the close match between the actual solubility values and the estimations generated by the DT model. Notice that the main limitation of the developed DT model is that they are eligible to applied only within the range of input parameters from which these models were developed.

Fig. 8
figure 8

Crossplots of the developed models, indicating modeled versus actual points based off of train and test portions.

Full size image
Fig. 9
figure 9

Crossplots of the developed models, indicating relative error percents versus actual points based off of train and test portions.

Full size image

Conclusions

This study aimed to develop advanced predictive models using numerous machine-learning techniques such as DT, RF, KNN, AdaBoost, and EL to estimate CO2 solubility in PEG under a variety of laboratory conditions. The data used to train and validate the models was collected from existing literature, and an outlier detection approach was applied beforehand to identify any irregular data points. Furthermore, sensitivity analysis was carried out to judge the relative contribution of each input parameter to the output variable. The findings demonstrated that DT model outperforms the other approaches, attaining highest R-squared (i.e., 0.801 and 0.991 for test and train, respectively) as well as smallest error metrics (MSE: 0.0009 and AARE%: 22.58 for test datapoints). The DT model is accurate, reliable, and user-friendly tool for estimating CO2 solubility in PEG, eliminating the need for experimental procedures, which are typically costly, labor-intensive, and time-consuming. Furthermore, it was observed that pressure and PEG molar mass have a direct impact on solubility, whereas temperature exhibits an inverse relationship with it.