Abstract
Knowledge graph embedding (KGE) is an effective method for link prediction in knowledge graphs, with numerous models demonstrating significant success. However, many existing KGE models struggle to effectively represent complex relationships and often face challenges related to a substantial number of missing triples. While enhancing KGE models through analogical reasoning offers a potential solution, current approaches typically depend on positive samples that are similar to the target for learning analogy embeddings. In real-world applications, data imbalance and incompleteness hinder the identification of sufficient positive examples, resulting in suboptimal performance in analogical inference. To this end, we propose a novel enhanced framework called Ne_AnKGE, which is based on negative analogical reasoning. First, Ne_AnKGE uses negative sample analogical reasoning to mitigate the scarcity of similar positive samples in analogical reasoning, while enhancing the link prediction ability of the basic model. Additionally, to enhance the model’s ability to represent complex relationships and overcome the limitations of relying on a single KGE model, the Ne_AnKGE framework integrates the outputs of TransE and RotatE, both of which have been enhanced through negative sample analogical reasoning. Extensive experiments on the FB15K-237 and WN18RR datasets demonstrate the competitive performance of Ne_AnKGE.
Similar content being viewed by others
A knowledge graph (KG) is a set of structured factual triples, structured as (head entity, relation, tail entity). Data from a knowledge graph can be depicted using a directed graph, where entities act as nodes, and the edges connecting these nodes indicate the relationships among the entities. In present, KGs have been extensively utilized across multiple domains, including medical diagnostic support, financial risk assessment, image and video processing, and social network analysis1. Freebase2, Yago3, WordNet4 and DBpedi5,etc., are some famous examples of knowledge graphs. However, most KGs are incomplete, making link prediction—a task focused on predicting missing links between entities—a prominent challenge within the knowledge graph domain. An effective strategy to address this challenge is knowledge graph embedding (KGE). The KGE models learn vector representations of entities and relations as inputs, then predict missing triples using predefined scoring functions6. Several KGE models, including TransE7, DistMult8, RotatE9, HAKE10, and TransRHS11 have achieved considerable success in KG link prediction.
The majority of existing KGE approaches fall into the category of inductive inference, in which a model learns embedding vectors based on existing factual triples, then calculates the triple scores using given scoring function, and ranks potential facts according to these scores12,13. However, large-scale KGs often contain a great many incomplete triples, so it is difficult to generalize from the memory-based inductive inference paradigm alone, which leads to the limitations of conventional KGE models. To mitigate these shortcomings, several models have integrated deep learning algorithms, including convolutional neural networks (CNNs), graph neural networks (GNNs), and attention mechanisms into KGE frameworks14. This integration facilitates richer representations of knowledge graph features, exemplified by models like ConvE15, RGCN16, and KBGAT17. Additionally, some models utilize innovation framework strategies to enhance the effectiveness of KGE approaches, including PUDA18 and REP19, etc.
A noteworthy model, AnKGE20, leverages analogical inference to extend the capabilities of KGE models. Analogical inference serves as a heuristic method for addressing novel problems by retrieving similar solutions. AnKGE learns analogical embeddings using positively analogous triples that are similar to the target triple as analogy objects, subsequently enhances the prediction performance of a given KGE model with the scores derived from these analogical embeddings. Nonetheless, practical datasets often encounter challenges related to data imbalance, where certain triples lack similar positive instances, thereby constraining the effectiveness of analogical inference. To alleviate this limitation, AnKGE employs adaptive weights that depend on the fraction of true positive triples among similar candidates. Despite this, when faced with data that lacks similar positive instances, AnKGE resorts to the original KGE model for predictions, which does not yield the expected improvements in performance.
Inspired by the AnKGE model, we also aim to utilize analogical inference to enhance the capabilities of base models. Unlike AnKGE, which sets the weight of analogical inference to zero when similar positive samples are absent, we introduce an innovative framework referred to as negative sample analogical inference enhanced KGE (Ne_AnKGE). The core idea of Ne_AnKGE is to utilize negative sample analogical inference to enhance the reasoning capabilities of the base KGE models, compensating for the scarcity of positive analogical instances. Firstly, the selected negative analogical objects are used as supervision signals to train the projection matrix, and the original entity embeddings are projected onto their corresponding analogical embeddings. The negative analogical inference score is computed by utilizing the analogical embeddings to improve the predictive capacity of the original KGE models. Subsequently, in order to alleviate the limitations of a single KGE model and better accommodate complex and imbalanced datasets, we incorporate negative analogy inference within a fusion framework that combines TransE and RotatE—two simple and easily explained KGE models—for the purpose of link prediction tasks. Theoretically, it is generally easier to construct an adequate amount of negative samples for a given triple than to find similar positive samples. This strategy addresses the limitation of the AnKGE model, allowing us to avoid the potential failure to produce the expected enhancement effect in such scenarios. Experimental findings on the FB15K-237 and WN18RR benchmark datasets confirm the superiority of Ne_AnKGE, demonstrating competitive performance across multiple evaluation metrics. This validation is supported by extensive link prediction experiments and ablation studies.
The key contributions of our research can be summarized as follows:
-
(1)
We propose a novel fusion framework, Ne_AnKGE. This framework integrates two KGE models are enhanced by negative sample analogy reasoning. Through flexible weight adjustment, Ne_AnKGE can better adapt to diverse knowledge graph datasets, enabling the model to be extensively applied in various scenarios.
-
(2)
We introduce a new negative entity analogy object retriever which has the capacity to extract high-quality negative entity analogy objects from randomly sampled negative entities. By this, it constructs more effective negative samples for the training process, thereby significantly enhancing the quality of training.
-
(3)
Our Ne_AnKGE model has been evaluated on two benchmark datasets, FB15K-237 and WN18RR, along with several baseline models and existing KGE models. The experimental results demonstrate that Ne_AnKGE outperforms them and achieves stable and superior performance, with outstanding compatibility and feasibility.
Related work
Knowledge graph embedding models
Conventional embedding models
Drawing upon the prior research conducted by Liang et al.21, KGE models can be categorized into translation models, tensor decompositional models and neural network models. The first two types of models are often considered conventional KGE models. Among them, TransE is a seminal translation model for knowledge graph embedding, specifically designed to tackle problems related to multi-relational data. Its fundamental concept involves mapping entities and relations into a vector space, where relationships between entities are represented through translational operations. The scoring function of the TransE model is based on the distance measurement using L1 or L2 norm. While effective, TransE struggles with certain complex relationship types, such as one-to-many, symmetric and transitive, and many-to-one relationships. Subsequently, several improved models derived from TransE have been introduced, including TransH22, TransR23, RotatE9, TransRHS11, HAKE10, PairRE24, and so on. For example, RotatE embeds entities as complex vectors with real and imaginary components, utilizing rotation operations on complex numbers to represent relations. Notably, RotatE adopts a self-adversarial negative sampling strategy to enhance model training and performance. Unlike traditional uniform negative sampling methods, this strategy generates negative samples by considering the specific context of each positive triple, thus allowing the model to learn relational patterns more accurately. HAKE focuses on improving the embedding quality and link prediction performance by capturing hierarchical information within the knowledge graphs. It utilizes a polar coordinate system to embed entities and relations, employing radial length and angle for representation, which has good scalability and flexibility. PairRE represents relations with paired vectors, enabling adaptive adjustments to model complex relationships effectively.
RESCAL25, the pioneering tensor decomposition model, utilizes tensor decomposition techniques to represent entities and relations. However, the model has high computational complexity and a substantial number of parameters that necessitate optimization. DistMult8 is another tensor decomposition model that embeds each relation as a diagonal matrix to decrease complexity, effectively halving the parameters compared to RESCAL, but it struggles to represent asymmetric relations adequately. The ComplEx model26, an extension of DistMult, is specifically designed to handle asymmetric relations through representing entities and relations in a complex vector space. DualE27 further projects embeddings into dual quaternion space to help the model deal with the diversity and complexity of knowledge graph data.
Neural network models
With advancements in artificial intelligence and deep neural networks, researchers begin to utilize the feature extraction capability of neural network algorithms to improve the representation ability of KGE models. SME28 is one of the earliest implementations of neural networks for KGE, aimed at capturing complex semantic information between entities and relations. To learn deeper features, recent literatures have proposed combining CNNs with KGE models. ConvE15 first proposes to use two-dimensional convolution to extract interaction features between these embedded vectors for knowledge graph inference, while ConvKB29 extends ConvE by removing reshaping operations to better capture global and transitional features within facts. ConEx30 enhances expressiveness by integrating affine transformations and Hermitian inner products on complex-valued embeddings with convolution operations.
Generally, KGE models employing CNNs tend to outperform traditional neural network models. However, complex information incorporated into the structures of knowledge graphs is difficult to learn well. Moreover, GNNs have been applied to KG reasoning tasks, exemplified by the RGCN model16, which enhances conventional graph convolutional network (GCN) by incorporating relation type embeddings and considering the influence of different relations separately. Despite this, RGCN may ignore entity differences, which can hinder the expression ability. To alleviate this situation, models like M-GNN31 and KBGAT17 integrate the attention mechanisms into their frameworks to improve the accuracy of knowledge graph information capture. CompGCN32 achieves accurate representation learning for multi-relational graphs through composite relation processing and efficient embedding techniques for nodes and relations. SE-GNN33 models three levels of semantic evidence as knowledge embeddings, facilitating a more comprehensive representation of knowledge.
Enhanced embedding models
Despite the great success have been made by the aforementioned models in relationship modeling, it is still a challenge to achieve comprehensive knowledge graph link prediction when relying solely on a single KGE model. Consequently, several frameworks and methodologies have been emerged to improve the effectiveness of KGE models, collectively known as enhanced KGE models. Notable examples include CAKE34, PUDA18 and REP19. CAKE is a knowledge graph enhanced model that significantly improves knowledge embedding performance by automatically extracting commonsense knowledge and generating commonsense enhancements. This process facilitates high-quality negative sampling, which is crucial for effective model training. Conversely, PUDA is a data augmentation strategy aimed at addressing issues related to false negatives and data sparsity. By expanding the training dataset, PUDA enhances the model’s generalization capabilities. REP, as a post-processing technique, focuses on better aligning pre-trained KGEs with graph contexts, thereby further refining the model’s overall performance.
Analogy-based embedding models
Analogical inference has also been instrumental in enhancing KGE models. ANALOGY35 is the first analogy-based KGE model that leverage robust analogy and flexible representation to address link prediction tasks. This model offers significant advantages in handling complex relationships, however, like other bilinear models, ANALOGY struggles to accurately capture the characteristics of asymmetric relations, leading to suboptimal performance. AnKGE also adopts analogical inference to enhance pre-train KGEs, exploring the knowledge graph link prediction task from a novel perspective. AnKGE20 proposes an effective retrieval method that encompasses three levels to identify suitable analogical objects. Specifically, AnKGE retrieves triples similar to the target triple and generates sets of similarity objects at the entity, relation, and triple levels, respectively. From these sets, the first n elements with the highest scores are selected, and their weighted summation are used as the supervisory signal for the analogical objects to guide the learning of the projection matrix. AnKGE then projects the original objects onto the appropriate analogical objects to derive analogical embeddings. Finally, it combines the original model’s score with the adaptively weighted analogical score to obtain the prediction. While AnKGE has achieved significant success in knowledge graph completion tasks, its effectiveness is influenced by the quality of the dataset, as it relies on similar positive samples. In contrast, our proposed Ne_AnKGE employs negative samples for analogical inference, theoretically, it is applicable to any knowledge graph datasets.
The proposed framework
Preliminaries on base models
In this paper, a KG is represented as \(\mathcal {G = (E, R, F)}\), where \(\mathcal {E}\) denotes the set of all entities, \(\mathcal {R}\) denotes the set of all relations, and \(\mathcal {F}\) is the collection of triples they form.
We employ TransE and RotatE as base models, both of which have good interpretability and relatively low computational complexity, and share some similarities in the design of the scoring function. The scoring functions for TransE and RotatE are given by Equations (1) and (2), respectively.
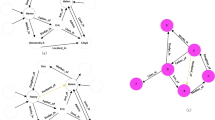
where, \(\circ\) denotes the vector rotation operation, and \(p=1\) or 2, indicating the use of L1 or L2 norm, respectively. Obviously, both models fundamentally rely on distance metrics to assess the quality of triples. The exploration of these two models reveals a significant difference between the positive and negative sample entities in KGE models. This distinction can be intuitively seen in Fig. 1. Specifically, for a query Q = (h, r, ?), both models aim to reduce the discrepancy between the head entity vector(represented as a black dot) after being transformed by the relationand the tail entity vector of the positive sample (denoted by red diamonds). Meanwhile, the models expect a significant difference between the head entity vector(black dot) after being transformed by the relation and the tail entity vectors of the negative samples (blue dots).
During the training process of the two base models, the widely adopted negative sampling loss function, as Eq. (3) introduced by RotatE9 is used:
In this equation, \(\gamma\) is a constant, \(\sigma\) is the sigmoid function, f(h, r, t) represents the score for the positive triple, \(f(h', r, t')\) represents the scores for the negative triples, and n denotes the number of negative triples during the training process. The self-adversarial weight \(p(h', r, t')\) for the negative triples is computed as:
Overall framework of Ne_AnKGE
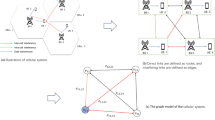
The overview of Ne_AnKGE is demonstrated as Fig. 2. Overall, Ne_AnKGE comprises three main modules: (1) A negative entity analogy object retriever responsible for generating negative entity analogy objects; (2) A negative sample analogy inference module responsible for enhancing the original KGE models; (3) A fusion module generating the final prediction.
Negative entity analogy object retriever
We generate a set of negative triples by replacing the head or tail entity in a given triple. For a triple (h, r, t), the corresponding set of negative sample triples can be represented as:
However, the number of negative instances corresponding to a specific triple can be substantial. Utilizing a vast number of negative samples to assist in predicting a triple is akin to using an exclusion method in an extensive dataset, which is impractical and ineffective. Therefore, it becomes crucial to determine how to select valid samples from the pool of negative samples.
For easily identifiable negative samples, the model has sufficient confidence to classify them as negative samples, rendering any enhancement of these samples subsequently insignificant. Therefore, we use the base model to score the constructed N negative samples and select the top n negative samples with the highest scores. For the negative samples that the model itself cannot differentiate well, we designate them as negative entity analogy objects. The objective is to improve the model’s ability to distinguish difficult-to-differentiate negative samples. Specifically, the sets of negative entity analogy objects are defined as:
where, \(E_{n}^{ert}\) represents negative samples from replacing a head entity, \(E_{n}^{hre}\) denotes negative samples from replacing a tail entity, and \(f(\, \, \ )\) is the scoring function of the original KGE model.
Negative sample analogy inference
For a missing triple (h, r, ?), the negative sample analogy inference does not directly predict the tail entity. Instead, it utilizes tail entities of known negative triples as negative entity analogy objects. The model assesses whether a candidate entity is negative based on the distance score between these negative entity analogy objects and the candidate entities. For example, given the triple (Jack, Biologicalfather, ?), we know that (Jack, Biologicalfather, Girl) is a negative triple. If the candidate tail entity is Lisa, and additional information indicates that Lisa is a girl, which means Lisa is sufficiently close to the negative sample, we can conclude that Lisa is also a negative entity sample.
Specifically, as shown in Fig. 3, we randomly select a batch of negative samples for each triple to simulate negative sample information available in real-world scenarios. We then use the negative entity analogy object retriever to filter out the required number of negative entity analogy objects from these samples. The vector representation of the candidate entity is mapped to its corresponding analogy vector using the projection matrix V. Next, we calculate the negative analogical inference score between this analogy embedding and the negative analogy objects to determine if the candidate entity is a negative sample. Finally, this negative analogical inference score is combined with the base model score as the final score of the triple.
Similar to AnKGE, we project the original embeddings through a projection matrix V to obtain the analogical embeddings, expressed as:
We use the vector representations of n negative samples as embeddings for negative entity analogy objects. The model computes distance scores between the candidate entity’s analogical embedding and these n embeddings, selecting the minimum score. Specifically, for each training triple (h, r, t), the model first constructs n negative entity analogy objects \(E_n=[e_{1}^{'}, e_{2}^{'}, \ldots , e_{n}^{'} ]\). It then calculates the L1 or L2 norm between the positive entity’s analogical embedding and all negative analogical entity embeddings to find the minimum value. Finally, the projection matrix V is trained using the loss function defined in Eq. (8).
where, \(e_i^a = V \times e_i\), and \(e_j^{-} = V \times e'_j\).
During the testing phase, we construct candidate triples through replacing the head and tail entities of each test triple with all possible entities, respectively. The candidate triples are evaluated using the base model’s score, augmented with a negative sample analogical score, to yield the final prediction. The ultimate scoring function is calculated as:
where f(h, r, t) represents the base model’s score, and \(Nar\_score\) denotes the negative analogical inference score. The \(Nar\_score\) is calculated as:
where MinMaxScaler is used to linearly transform the data to a range of \((-1, 1)\). The parameter p=1 or 2 indicates the use of L1 or L2 norm, respectively. \(h^a = V \times h\), and \(t^a = V \times t\).
Fusion module
The TransE model is well-suited for modeling simple one-to-one relationships, while the RotatE model excels in scenarios that require more complex relational modeling, especially in knowledge graph datasets involving symmetric or many-to-many relations. To better adapt to diverse datasets, we carry out extensive experiments that reveals the potential of integrating the outcomes of two models enhanced by negative sample analogical inference can improve the model’s performance. Specifically, for simpler datasets, the model relies on the results from the efficient and straightforward TransE model, whereas for more complex datasets, it more extensively utilize the results from the RotatE model. Therefore, during the testing phase, the following weighted score is employed to assess the quality of candidate triples:
where, S denotes the softmax function, \(\lambda\) is a weight hyperparameter, \(score_{TransE}\) and \(score_{RotatE}\) represent the scores calculated by Equation (9) based on the transE and rotatE models, respectively.
Experiments and analysis
Datasets
To verify the performance of our proposed Ne_AnKGE on link prediction, we conducted comprehensive experiments using two benchmark datasets: FB15K-237 and WN18RR, both of which are widely employed to assess various KG models. Each dateset is divided into training, validation and test sets. FB15K-237 is derived from FB15K, containing 14541 entities, 237 relations, and 310116 triples. The training, validation, and test sets contain 272115, 17535 and 20466 triples, respectively. Similarly, WN18RR is a subset of WN18, containing 40493 entities, 11 relations, and 93003 triples, with 86,835 in the training set, 3,034 in the validation set, and 3,134 in the test set. Their inherent diversity and challenges in terms of data scale, relation types, and entity categories enable a comprehensive assessment of the performance and robustness of knowledge graph models across different scenarios. The adoption of these two datasets ensures comparability and impartiality of the experimental results. A summary of the statistics for both datasets is presented in Table 1.
Evaluation metrics
We assess the Ne_AnKGE framework using four standard metrics: Mean Reciprocal Rank (MRR), which measures the inverse average rank of the correct entities within the entire entity set, and Hit@1, Hit@3, and Hit@10, which denote the percentage of correct entities ranked within the top 1, 3, and 10 positions among all candidates, respectively. When evaluating candidate triples, we adhere to a filtering protocol that removes any true triples found in the training, validation, and test datasets. The resulting filtered candidate triples are then ranked according to the scores of scoring function.
Implementation details
Our proposed Ne_AnKGE framework fuses two different KGE models: TransE and RotatE. First, we train the entity and relation vector representations for both TransE and RotatE on the selected datasets, with the training parameters detailed in Table 2. Subsequently, we train the projection matrix V for the two models on each dataset through the loss function given by Eq. (8).
A grid search is employed to select the hyperparameters. Specifically, we search for the following parameters: negative analogy inference weight: \(\beta \!\in \!\{1.0, 1.5, 2.0, 2.5\}\), weight assigned to the results of the TransE model \(\lambda \!\in \!\{0, 0.1, 0.2, \ldots , 0.9, 1.0\}\), learning rate \(r\in \{1e^{-3}, 5e^{-4}, 1e^{-4}, 5e^{-5}, 1e^{-5}\}\). For the constant \(\gamma\), we used the same setting as for RotatE (9), for the FB15K-237 dataset, we set the constant \(\gamma\) in the Eqs. (3) and (8) to 9.0, and for the WN18RR dataset, \(\gamma\) is set to 6.0. Additionally, for each triple, we randomly construct negative samples that account for a certain proportion of the overall number of entities. Let m represent the percentage of the extracted negative samples in the overall number of entities, that is, the quantity of negative samples N is determined by multiplying the number of entities in the dataset by m, with \(m\in \{30\%, 40\%, 50\%, 60\%\}\). A summary of the final experimental parameters can be found in Table 3.
Experimental results
Performance comparison
We evaluate the Ne_AnKGE framework’s performance against several widely used baseline models for link prediction. The baselines include: Conventional KGE models like TransE, ANALOGY, RotatE, HAKE, Rot-Pro36, PairRE, and DualE, as well as neural network-based models CompGCN and SE-GNN. We also include enhanced KGE frameworks PUDA and REP, along with the analogy-based enhanced KGE model AnKGE. The performance results for TransE and RotatE are obtained from models we trained, while results for the other models are sourced from their respective publications. Table 4 summarizes the experimental results for these baseline models alongside the Ne_AnKGE model on the FB15K-237 and WN18RR datasets, with the parameter \(m=60\%\).
The findings demonstrate that Ne_AnKGE surpasses all other approaches on the FB15K-237 dataset, achieving an MRR of 0.394. In comparison, the AnKGE method, which also employs analogical inference, shows the second-best performance with an MRR of 0.385. Although Ne_AnKGE scores 0.286 on Hit@1, slightly lower than AnKGE’s value of 0.288, the results of Ne_AnKGE remain competitive. Ne_AnKGE excels in other metrics, achieving Hit@3 and Hit@10 values of 0.433 and 0.606, respectively.
For the WN18RR dataset, Ne_AnKGE achieves an MRR of 0.505, further illustrating its superiority over other methods, including AnKGE, which has an MRR of 0.500. Although Ne_AnKGE achieves a Hit@1 value of 0.455, only slightly exceeding AnKGE’s score of 0.454, it demonstrates strong performance in other metrics, with Hit@3 and Hit@10 values of 0.526 and 0.603, respectively. These findings highlight the effectiveness of the proposed Ne_AnKGE framework in addressing link prediction tasks in knowledge graphs.
To further demonstrate the reliability of the above experimental results, we conduct a significance test in Table 4. Specifically, we implement 50 times independent experiments using Ne_AnKGE on the two datasets respectively. As shown in Fig. 4, the fluctuations in the four metric values across the 50 experiments for both datasets are negligible, with the standard deviations all below 0.002, indicating that the results of Ne_AnKGE are highly stable. Then, we take the 50 values for each of the four metrics as the observed values, and the corresponding values of the AnKGE model, which has the second-best performance, as the theoretical values, and perform a one-sample t-test. The result are shown in Table 5. The p-values of all metrics are less than the significance level of 0.05, indicate that Ne_AnKGE exhibits statistically significant differences from AnKGE. Ne_AnKGE significantly outperforms AnKGE on all metrics except for the Hit@1 metric on the FB15K-237 dataset. This indicates that the overall improvement of Ne_AnKGE is statistically signifcant compared with AnKGE.
Ablation study
To evaluate the effectiveness of Ne_AnKGE and to determine the impact of each module on the link prediction tasks, we conduct ablation experiments by removing different modules from the Ne_AnKGE framework on the FB15K-237 and WN18RR datasets. Six sub-models are included: (1) the complete Ne_AnKGE model, which incorporates the negative sample analogical reasoning module and the fusion module; (2) TransE+RotatE, which directly combines the original TransE and RotatE models (removing the negative sample analogical reasoning module); (3) Ne_AnKGE-TransE, which applies negative sample analogical reasoning enhancement only to TransE (enhancing a single model, removing the fusion module); (4) Ne_AnKGE-RotatE, which applies negative sample analogical reasoning enhancement only to RotatE (enhancing a single model, removing the fusion module); (5) TransE, the baseline model without any enhancement; (6) RotatE, the baseline model without any enhancement. The ablation experiment results are shown in Table 6.
From Table 6, we can conclude that:
-
(1)
Negative sample analogical reasoning module: Experimental results demonstrate that the fused TransE+RotatE model, after removing the negative sample analogical reasoning module, exhibits significant degradation across all four metrics compared to the complete Ne_AnKGE model. Specifically, on the FB15K-237 dataset, MRR decreased by 5.7%, Hit@1 decreased by 4.5%, Hit@3 decreased by 6.7%, and Hit@10 decreased by 7.1%. On the WN18RR dataset, more pronounced declines were observed: MRR decreased by 20.3%, Hit@1 decreased by 35.4%, Hit@3 decreased by 6.0%, and Hit@10 decreased by 3.5%. Additionally, the Ne_AnKGE-TransE model, which enhances TransE with negative sample analogical reasoning, outperformed the original TransE model on the FB15K-237 dataset by 5.7%, 4.8%, 6.8%, and 7.4% in the four metrics, respectively. On the WN18RR dataset, it achieved improvements of 1.7%, 0.6%, 2.8%, and 2.5%. Similarly, the Ne_AnKGE-RotatE model, which enhances RotatE with negative sample analogical reasoning, showed improvements of 5.2%, 4.3%, 6.1%, and 6.7% on the FB15K-237 dataset compared to the original RotatE model, and improvements of 2.8%, 2.7%, 2.7%, and 2.5% on the WN18RR dataset. These results demonstrate that the negative sample analogical reasoning module effectively enhances the model’s reasoning capability.
-
(2)
Fusion Module: Experimental results further demonstrate that removing the fusion module from the Ne_AnKGE framework-leaving only the individually enhanced KGE models (Ne_AnKGE-TransE and Ne_AnKGE-RotatE)-results in a consistent decline across all four metrics on the FB15K-237 dataset compared to the complete Ne_AnKGE model. This validates the necessity of integrating dual-model outputs via the fusion module, particularly for simple yet large-scale datasets. On the other hand, for more complex datasets, Ne_AnKGE can adapt to different datasets by flexibly adjusting the weights of each model, thus making the model more flexible.
The ablation study demonstrates that the negative sample analogical reasoning module substantially enhances core reasoning capabilities, while the fusion module ensures balanced performance across simple and complex data scenarios by dynamically integrating the complementary strengths of multiple models, thereby enhancing model adaptability.
Negative sample proportion discussion
The parameter m is the fraction of the extracted negative samples relative to the total number of entities. To validate the effectiveness of Ne_AnKGE and simulate various scenarios, we set m to 30%, 40%, 50%, 60%, reflecting the proportion of known negative samples. Figure 5 illustrates Ne_AnKGE’s performance across these varying m values. Notably, there is an observable improvement in the enhancement of base models through analogical inference with negative samples as m increases.
When m= 60%, Ne_AnKGE surpasses all baseline models in every metric except for Hit@1 on the FB15K-237 dataset, as shown in the previous Table 4. Specially, when m is set to 40% and Ne_AnKGE is applied to the two base models, significant improvements are observed across all metrics, as depicted in Table 7. The MRR values increase by approximately 3% for the FB15K-237 database, while the increases on WN18RR are 1.5% for TransE and 2.5% for RotatE. Additionally, the metrics of Hit@1, Hit@3 and Hit@10 show improvements ranging from 2.6% to 4.6% on FB15K-237, and about 2% on WN18RR. And when the base model is the same, compared to AnKGE, Ne_AnKGE demonstrates superior performance across all metrics, expect for Hit@1 value of Ne_AnKGE-TransE on WN18RR and the Hit@1 metric of Ne_AnKGE-RotatE on FB15K-237.
Unlike AnKGE, which generates candidate triples by substituting all entities and retrieves objects at three levels using a scoring function, Ne_AnKGE performs analogical inference by randomly sampling a certain number of negative samples. This approach better reflects real-world scenario where not all negative samples are available. The negative samples are ranked using scores generated by the base model, allowing for the screening of a small number of negative entity analogy objects. Specifically, we apply 128 and 384 negative entity analogy objects for each triple in the FB15K-237 and WN18RR datasets, respectively, accounting for less than 1% of the total entities in both datasets. Overall, Ne_AnKGE presents a more realistic framework by using a limited number of negative entity samples for each test triple. This methodology not only enhances the performance of KGE models but also improves implementation feasibility by significantly reducing computational complexity.
Model analysis
To further analyze the enhancement effect of the model, we compared the results of Ne_AnKGE with those of AnKGE. As illustrated in Table 7, the TransE model, upon augmentation with Ne_AnKGE, demonstrates a comparatively suboptimal outcome on the WN18RR dataset, particularly with regards to the Hit@1 metric. This can be attributed to TransE’s reliance on simple vector translations for learning. For complex relationships, such as symmetric relationships where both triples (A, B, C) and (C, B, A) exist, TransE tends to push the embedding of relation B towards zero while aligning A and C embeddings to be equal or similar. Consequently, in the presence of numerous symmetric relationships within the dataset, the embeddings of such relations tend to converge towards zero, impeding the model’s capability to effectively discern among these relation embeddings, as well as their corresponding head and tail entity embeddings.
However, Ne_AnKGE leverages the differences between positive and negative samples to enhance the model. This approach results in the observed suboptimal performance of the TransE model when enhanced by Ne_AnKGE on certain data. Moreover, compared to FB15K-237, the WN18RR dataset contains a greater number of entities and fewer relations, which leads to an increased number of entities connected by each relation. Accordingly, these relations require more complex representations that cannot be adequately captured by TransE’s vector translation mechanism. Therefore, for the WN18RR dataset, we solely rely on the results of the RotatE model for negative analogical inference, setting \(\lambda = 0\) in the Equation (8) for this dataset.
To effectively adapt to various datasets in real-world scenarios, we suggest an strategy: for datasets with complex relationships, we can reduce the weight of the TransE model and place greater reliance on the more sophisticated RotatE model for predictions. Conversely, when handling datasets characterized by an extensive array of relationships and triples but possessing relatively straightforward relational patterns, we can leverage the simplicity and efficiency of the TransE model more effectively. Thus, for the FB15K-237 dataset, we continue to utilize a combination of the two base models to generate the final predictions.
Time evaluation
The experiments in this study are divided into three parts: (1) embedding representations of the pre-trained base model; (2) training the analogy projection matrix; (3) model performance testing. To validate the feasibility of Ne_AnKGE, experiments were conducted on a machine with an Intel 12-core (16-thread) CPU, 16GB of RAM, and an NVIDIA GeForce RTX 4090 Laptop GPU (16GB VRAM), and the computation time for each stage was recorded. The experiments consisted of 100,000 training runs and 1 test. The detailed results are shown in Table 8. The results indicate that on the FB15K-237 dataset, the complete process takes approximately 36,682 seconds (about 10 hours), with the testing stage requiring only about 2,214 seconds (about 37 minutes); on the WN18RR dataset, the total time is approximately 46,891 seconds (about 13 hours), with the testing stage taking only 863 seconds (about 14 minutes). These results demonstrate that the Ne_AnKGE model can be efficiently deployed on standard hardware setups, with a low time cost during the testing phase, confirming its feasibility for practical applications.
Conclusion
In this paper, we introduce the Ne_AnKGE model, which utilizes negative sample analogical inference to enhance knowledge graph link prediction. This innovative approach enhances knowledge graph embedding by integrating a negative entity analogy object retriever specifically designed to identify negative analogy objects. The model learns a projection matrix using these negative analogy objects and projects the original entity embeddings onto a specific analogical embeddings to ensure that the analogical embeddings of positive entities are far away from those of negative analogy objects. Ultimately, we utilize negative analogy scores to guide and enhance the inference and prediction capabilities of the KGE models, and combine the results of the two enhanced KGE models as the final prediction of our model. Experimental results demonstrate that the Ne_AnKGE model is effective across a wide range of datasets and achieves promising results on the task of knowledge graph link prediction.
Despite the relatively strong performance of our model, there remains room for improvement in both the base model and its structure. In future work, we plan to develop a more generalizable framework capable of accommodating more complex models. We also expected to incorporate negative sample analogical inference into a broader array of KGE models, such as those based on multimodal KGs.
Data availability
Data or code used during the study are available from the corresponding author by request.
References
Han, Y. et al. A temporal knowledge graph embedding model based on variable translation. Tsinghua Sci. Technol. 29, 1554–1565. https://doi.org/10.26599/TST.2023.9010142 (2024).
Bollacker, K. D., Evans, C., Paritosh, P. K., Sturge, T. & Taylor, J. Freebase: a collaboratively created graph database for structuring human knowledge. In Proceedings of the SIGMOD Conference (2008).
Suchanek, F. M., Kasneci, G. & Weikum, G. Yago: A core of semantic knowledge. In Proceedings of the The Web Conference (2007).
Miller, G. A. Wordnet: A lexical database for english. Commun. ACM 38, 39–41 (1995).
Lehmann, J. et al. Dbpedia—a large-scale, multilingual knowledge base extracted from wikipedia. Semantic Web 6, 167–195 (2015).
Asmara, S. M., Sahabudin, N. A., Nadiah Ismail, N. S. & Ahmad Sabri, I. A. A review of knowledge graph embedding methods of transe, transh and transr for missing links. In 2023 IEEE 8th International Conference On Software Engineering and Computer Systems (ICSECS), 470–475, https://doi.org/10.1109/ICSECS58457.2023.10256354 (2023).
Bordes, A., Usunier, N., Garc-Duran, A., Weston, J. & Yakhnenko, O. Translating embeddings for modeling multi-relational data. In Proceedings of the Neural Information Processing Systems (2013).
Yang, B., Yih, W. T., He, X., Gao, J. & Deng, L. Embedding entities and relations for learning and inference in knowledge bases. In International Conference on Learning Representations (2014).
Sun, Z., Deng, Z., Nie, J. Y. & Tang, J. Rotate: Knowledge graph embedding by relational rotation in complex space. In 7th International Conference on Learning Representations, ICLR 2019 (2019).
Zhang, Z., Cai, J., Zhang, Y. & Wang, J. Learning hierarchy-aware knowledge graph embeddings for link prediction. In AAAI Conference on Artificial Intelligence (2019).
Zhang, F., Wang, X., Li, Z. & Li, J. Transrhs: A representation learning method for knowledge graphs with relation hierarchical structure. In International Joint Conference on Artificial Intelligence (2020).
Lu, Y., Yang, D., Wang, P., Rosso, P. & Cudre-Mauroux, P. Schema-aware hyper-relational knowledge graph embeddings for link prediction. IEEE Trans. Knowl. Data Eng. 36, 2614–2628. https://doi.org/10.1109/TKDE.2023.3323499 (2024).
Zhang, W., Du, T., Yang, C. & Li, X. A multimodal knowledge graph representation learning method based on hyperplane embedding. In Proceedings of the 2024 7th International Conference on Advanced Algorithms and Control Engineering (ICAACE), 434–437, https://doi.org/10.1109/ICAACE61206.2024.10549536 (2024).
Zhu, T., Tan, H., Chen, X. & Ren, Y. A transformer-based knowledge graph embedding model combining graph paths and local neighborhood. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), 1–9, https://doi.org/10.1109/IJCNN60899.2024.10650666 (2024).
Dettmers, T., Minervini, P., Stenetorp, P. & Riedel, S. Convolutional 2d knowledge graph embeddings. In AAAI Conference on Artificial Intelligence (2017).
Schlichtkrull, M. et al. Modeling relational data with graph convolutional networks. In Extended Semantic Web Conference (2017).
Nathani, D., Chauhan, J., Sharma, C. & Kaul, M. Learning attention-based embeddings for relation prediction in knowledge graphs. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 4710–4723, https://doi.org/10.18653/v1/P19-1466 (2019).
Tang, Z. et al. Positive-unlabeled learning with adversarial data augmentation for knowledge graph completion. In International Joint Conference on Artificial Intelligence (2022).
Wang, H. et al. Simple and effective relation-based embedding propagation for knowledge representation learning. In International Joint Conference on Artificial Intelligence (2022).
Yao, Z. et al. Analogical inference enhanced knowledge graph embedding. In AAAI Conference on Artificial Intelligence (2023).
Liang, K. Y. et al. A survey of knowledge graph inference on graph types: Static, dynamic, and multi-modal. IEEE Trans. Pattern Anal. Mach. Intell. 46, 9456–9478 (2022).
Wang, Z., Zhang, J., Feng, J. & Chen, Z. Knowledge graph embedding by translating on hyperplanes. In AAAI Conference on Artificial Intelligence (2014).
Lin, Y., Liu, Z., Sun, M., Liu, Y. & Zhu, X. Learning entity and relation embeddings for knowledge graph completion. In AAAI Conference on Artificial Intelligence (2015).
Chao, L., He, J., Wang, T. & Chu, W. Pairre: Knowledge graph embeddings via paired relation vectors. In Proceedings of the Annual Meeting of the Association for Computational Linguistics (Association for Computational Linguistics, 2020).
Nickel, M., Tresp, V. & Kriegel, H. P. A three-way model for collective learning on multi-relational data. In International Conference on Machine Learning (2011).
Trouillon, T., Welbl, J., Riedel, S., Gaussier, É. & Bouchard, G. Complex embeddings for simple link prediction. ArXiv abs/1606.06357 (2016).
Cao, Z., Xu, Q., Yang, Z., Cao, X. & Huang, Q. Dual quaternion knowledge graph embeddings. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI Press, 2021).
Glorot, X., Bordes, A., Weston, J. & Bengio, Y. A semantic matching energy function for learning with multi-relational data. Mach. Learn. 94, 233–259 (2013).
Nguyen, D. Q., Nguyen, T. D., Nguyen, D. Q. & Phung, D. Q. A novel embedding model for knowledge base completion based on convolutional neural network. In North American Chapter of the Association for Computational Linguistics (2017).
Demir, C. & Ngomo, A. C. Convolutional complex knowledge graph embeddings. In Extended Semantic Web Conference (2020).
Wang, Z., Ren, Z., He, C., Zhang, P. & Hu, Y. Robust embedding with multi-level structures for link prediction. In International Joint Conference on Artificial Intelligence (2019).
Vashishth, S., Sanyal, S., Nitin, V. & Talukdar, P. Composition-based multi-relational graph convolutional networks. arXiv preprint 1911.03082 (2020).
Li, R. et al. How does knowledge graph embedding extrapolate to unseen data: A semantic evidence view. arXiv preprint 2109.11800 (2022).
Niu, G., Li, B., Zhang, Y. & Pu, S. Cake: A scalable commonsense-aware framework for multi-view knowledge graph completion. In Annual Meeting of the Association for Computational Linguistics (2022).
Liu, H., Wu, Y. & Yang, Y. Analogical inference for multi-relational embeddings. ArXiv abs/1705.02426 (2017).
Song, T., Luo, J. & Huang, L. Rot-pro: Modeling transitivity by projection in knowledge graph embedding. In Advances in Neural Information Processing Systems, 24695–24706 (2021).
Funding
This research was funded by the National Natural Science Foundation of China (No. 62462069), Yunnan Province Graduate Quality Course Construction Project: Advanced mathematical statistics (Yun Degree [2022] No.8), the Research and Innovation Fund for Postgraduate Students of Yunnan Minzu University (No.2024SKY128) and the Open Research Fund of Yunnan Key Laboratory of Statistical Modeling and Data Analysis, Yunnan University (No.SMDAYB2023004).
Author information
Authors and Affiliations
Contributions
H.L. and Y.T. (Yuhu Tao) conceived the method and experiments, Y.T. (Yuhu Tao) and H.L. wrote the main manuscript text, D.C. and Y.T. (Yi Tang) analysed the results, J.W. and L.X. prepared figures. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Li, H., Tao, Y., Chen, D. et al. An enhanced framework for knowledge graph embedding based on negative sample analogical reasoning. Sci Rep 15, 14086 (2025). https://doi.org/10.1038/s41598-025-98550-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-98550-7