Exploration of the soliton solutions of the (n+1) dimensional generalized Kadomstev Petviashvili equation using an innovative approach

Abstract

In this paper, we deal with the (n+1)-dimensional generalized Kadomtsev-Petviashvili equation (dgKPE). This is an important model in nonlinear science, with applications in various fields. Its integrability and rich soliton dynamics continue to attract researchers interested in the field of nonlinear partial differential equations (NLPDEs). We are interested in the new auxiliary equation method (NAEM). We reduce the equation to an ordinary differential equation (ODE) with the help of an appropriate wave transformation and search for different types of soliton solutions. Additionally, we demonstrated the efficacy of the NAEM as a straightforward yet powerful mathematical instrument for handling challenging issues, highlighting its potential to resolve the challenging problems related to the study of nonlinear equations. This technique yields several types of solutions for (n+1)-dgKPE, including trigonometric, hyperbolic, shock wave, singular soliton, exponential, and rational functions. A range of graphs showcasing the results are reviewed, as well as the wave behavior for the solutions in different circumstances. The obtained data provide important information for studying hydrodynamic waves, plasma fluctuations, and optical solitons. They also aid in understanding the behavior of the KPE in different physical situations. We clarify in this article how the (n+1)-dgKPE, when combined with NAEM, can result in better data transmission rates, optimized optical systems, and the advancement of nonlinear optics toward more dependable and efficient communication technologies. The obtained information clarifies the equation and opens up new avenues for investigation. To our knowledge, for this equation, these methods of investigation have not been utilized before. The accuracy of each solution has been verified using the Maple software program.

Introduction

Nonlinear phenomena are useful in many fields, such as physics, mathematics, science, and engineering. One of the most important tasks in the study of nonlinear science is the explicit solution of NLPDEs. Many integral strategies are commonly used by researchers to find soliton solutions for these equations. Some of the primary techniques employed in this process are covered in this presentation. The unified method¹ , the Kudryashov method^2,3 , the new extended auxiliary equation method⁴ , the Khater II (Khat II) method⁵ , the Jacobi elliptic wave function method⁶ , the modified sub-equation method^7,8,9 , modifed exponential rational functional method¹⁰ , Lie symmetry analysis^11,12 , the extended sinh-Gordon equation expansion method¹³ , the exp-function method¹⁴ , modified extended auxiliary equation mapping method¹⁵ , the modified F-expansion method¹⁶ , the unified Riccati equation expansion method¹⁷ and much more.

Solitons are phenomena that arise in some solutions of evolution equations and reflect a careful balance between dispersion effects and nonlinear interactions. The literature discusses various varieties of solitons, such as lump, moving wave, single, and dark-bright solitons. A single-soliton solution, additionally known as a solitary wave, changes into one while maintaining its shape and speed throughout propagation when it is separated from other solitons¹⁸ .

This research indicates that numerous soliton-type wave solutions have been created for the (n+1)-dgKPE. Established thanks to Kadomtsev and Petviashvili¹⁹ , this equation was initially devised as a higher-dimensional expansion for the Korteweg-de Vries (KdV) equation to the examination of soliton solutions under modest transverse disturbances. Ever since it was introduced, the KPE has become the subject of numerous inquiries. By examining the integrability for the (n+1)-dgKPE, Xu and Wazwaz²⁰ intended to offer a more thorough foundation for the traditional KPE.

This study focuses to the (n+1)-dgKPE^20,21,22 :

$$\begin{aligned} {{\left( {{\Phi }_{t}}+{2{\theta }_{1}}\Phi {{\Phi }_{x_{1}}}+{{\theta }_{2}}{{\Phi }_{x_{1}x_{1}x_{1}}} \right) }_{x_{1}}}+{{\theta }_{3}}{{\Phi }_{x_{2}x_{2}}}+\sum \limits _{k=1}^{R}{{{\Theta }_{k}}{{\Phi }_{x_{1}x_{k}}}=0}. \end{aligned}$$

(1)

In the aforementioned equation, $\Phi$ denotes a differentiable function taking into account the temporal variable t and the spatial variables x. $R\ge 2$ is an integer. The subscripts in the formula indicate the partial derivatives of the functions. Xu and Wazwaz state that ${{\theta }_{1}}$, ${{\theta }_{2}}$, ${{\theta }_{3}}$, and ${{\Theta }_{k}}\left( k=1,2,3 \ldots R \right)$ are constant parameters²⁰ . Among other domains, dynamics of fluids, plasma physics, and non-linear optics all heavily rely on the (n+1)-dgKPE. Its exceptional adaptability for simulating multidimensional wave events substantially facilitates the study of a broad spectrum of physical systems. Because of its intricate mathematical structure and broad range of solutions, it is a crucial issue for researchers interested in mathematical science or nonlinear dynamics.

The KPE can be used to describe things like solitons, intricate wave interactions, and particles acting like particles. Its ability to depict and capture complex processes outside the scope of linear models is enhanced by its nonlinear characteristics. Therefore, the (n+1)-dgKPE is an especially powerful and insightful tool for examining complex behaviors in higher-dimensional scenarios.

The N-soliton solution and significant integrability features are shown by the (n+1)-dgKPE, as reported by Xu and Wazwaz’s study²⁰ . Using the dual Bell polynomial technique and the singularity manifold analysis, the equation’s complete integrability is shown by Bäcklund transformations, the Painlevé property, a Lax pair, and an infinite number of conservation laws. Raza et al.²¹ concentrated their investigation on getting Auto-Bäcklund transformations to the model via the extended homogeneous balance (HB) technique. They could also solve exponential functions by creating a bilinear Bäcklund transformation depending on the Hirota bilinear form. In addition, they looked at complexiton solutions for the KPE using the bilinear form and the extended transformed rational function approach.

This study emphasizes how new methods of problem-solving are required to identify the mathematical patterns that underlie actual physical systems. We offer an effective analytical method that generates novel and efficient wave solutions for the (n+1)-dgKPE via finite series expansion, demonstrating previously unreported outcomes. These techniques are useful resources for researchers working on complicated mathematical issues in various scientific domains. By offering efficient solutions, particularly for complex and high-dimensional systems, the proposed method addresses the constraints of the present approaches. In this sense, it provides useful and appropriate solutions to problems that are commonly found in the literature. Researchers can also create novel approaches and provide previous theories with more depth thanks to it.

This study is organized as follows: Sect. 2 gives a description of the NAEM. In Sect. 3, the offered method is applied to discover analytical solutions of the (n+1)-dgKPE. Comparisons are provided in Sect. 4. Numerical representations are given in Sect. 5 and Conclusions are presented in Sect. 6.

The NAEM

Consider the following NLPDE:

$$\begin{aligned} P(\Phi ,\Phi _{t},\Phi _{x_{1}},\Phi _{x_{2}},\dots ,\Phi _{R},\dots )=0, \end{aligned}$$

(2)

where an unknown function with its partial derivatives given $x_{1},x_{2},...,x_{R}$ and t is indicated by the expression $\Phi = \Phi (x_{1},x_{2},...,x_{R},t)$.

Thanks to the following wave transformation

$$\begin{aligned} \Phi (x_{1},x_{2},...,x_{R},t) = Q(\xi ), \quad \xi =\sum \limits _{k=1}^{R}{{{x }_{k}}-wt}, \end{aligned}$$

(3)

Eq. (2) is reduced to an ordinary differential equation (ODE) as follows:

$$\begin{aligned} D(Q,Q^{\prime },Q^{\prime \prime },Q^{\prime \prime \prime },\dots )=0. \end{aligned}$$

(4)

In Eq. (3), w is the wave speed.

The following will be the processes that are given for implementing the NAEM²³ :

Step 1. Eq. (4) has the following solution form:

$$\begin{aligned} Q(\xi ) = \sum \limits _{i=0}^{R} {{h}_{i}}{{L}^{g^i(\xi )}}, \end{aligned}$$

(5)

in which the real constants ${h}_{i}$ and the function $g(\xi )$ satisfy the first-order ODE given by:

$$\begin{aligned} \frac{\partial g(\xi )}{\partial \xi }=\frac{\left( \mu {{L}^{-g\left( \xi \right) }}+y+\lambda {{L}^{-g\left( \xi \right) }} \right) }{\ln \left( L \right) }, \quad L\ne 1, \quad L>0. \end{aligned}$$

(6)

Using $\lambda$, y, and $\mu$ are real constants, the application of Eq. (6) is described below:

Step 2. The principle of balance can be applied to Eq. (4) to determine the value of R.

Step 3. After Eq. (5) and its derivatives are inserted into Eq. (4) utilizing the wave transformation specified by Eq. (6), $L^{g(\xi )}$ becomes a polynomial. A system of equations is created by simplifying and setting as terms to zero. Computer algebra programs like Maple software can solve this system of equations effectively. The analytical solutions to Eq. (4) are obtained by solving this system.

Step 4. Finally, by using the transformation method from Eq. (3) and the solutions discovered from Eq. (4), we discover a range for analytical solutions to Eq. (2). Determine the solutions to Eq. (6) by employing a particular method.

Type 1. If $\lambda \ne 0$ and $4\lambda \mu -{{y}^{2}}<0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{y}{2\lambda }+\frac{\sqrt{4\lambda \mu -{{y}^{2}}}\tan \left( \frac{\sqrt{4\lambda \mu -{{y}^{2}}}\xi }{2} \right) }{2\lambda }, \end{aligned}$$

(7)

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{y}{2\lambda }-\frac{\sqrt{4\lambda \mu -{{y}^{2}}}\cot \left( \frac{\sqrt{4\lambda \mu -{{y}^{2}}}\xi }{2} \right) }{2\lambda }. \end{aligned}$$

(8)

Type 2. If $\lambda \ne 0$ and $4\lambda \mu -{{y}^{2}}>0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{y}{2\lambda }-\frac{\sqrt{-4\lambda \mu +{{y}^{2}}}\tanh \left( \frac{\sqrt{-4\lambda \mu +{{y}^{2}}}\xi }{2} \right) }{2\lambda }, \end{aligned}$$

(9)

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{y}{2\lambda }-\frac{\sqrt{-4\lambda \mu +{{y}^{2}}}\coth \left( \frac{\sqrt{-4\lambda \mu +{{y}^{2}}}\xi }{2} \right) }{2\lambda }. \end{aligned}$$

(10)

Type 3. If $-4{{\mu }^{2}}-{{y}^{2}}<0$, $\lambda =-\mu$ and $\lambda \ne 0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\frac{y}{2\mu }-\frac{\sqrt{-4{{\mu }^{2}}-{{y}^{2}}}\tan \left( \frac{\sqrt{-4{{\mu }^{2}}-{{y}^{2}}}\xi }{2} \right) }{2\mu }, \end{aligned}$$

(11)

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\frac{y}{2\mu }+\frac{\sqrt{-4{{\mu }^{2}}-{{y}^{2}}}\cot \left( \frac{\sqrt{-4{{\mu }^{2}}-{{y}^{2}}}\xi }{2} \right) }{2\mu }. \end{aligned}$$

(12)

Type 4. If $4{{\mu }^{2}}+{{y}^{2}}>0$ and $\lambda =-\mu$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\frac{y}{2\mu }+\frac{\sqrt{4{{\mu }^{2}}+{{y}^{2}}}\tanh \left( \frac{\sqrt{4{{\mu }^{2}}+{{y}^{2}}}\xi }{2} \right) }{2\mu }, \end{aligned}$$

(13)

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\frac{y}{2\mu }+\frac{\sqrt{4{{\mu }^{2}}+{{y}^{2}}}\coth \left( \frac{\sqrt{4{{\mu }^{2}}+{{y}^{2}}}\xi }{2} \right) }{2\mu }. \end{aligned}$$

(14)

Type 5. If $4{{\mu }^{2}}+{{y}^{2}}<0$ and $\lambda =\mu$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{y}{2\mu }+\frac{\sqrt{4{{\mu }^{2}}-{{y}^{2}}}\tan \left( \frac{\sqrt{4{{\mu }^{2}}-{{y}^{2}}}\xi }{2} \right) }{2\mu }, \end{aligned}$$

(15)

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{y}{2\mu }-\frac{\sqrt{4{{\mu }^{2}}-{{y}^{2}}}\cot \left( \frac{\sqrt{4{{\mu }^{2}}-{{y}^{2}}}\xi }{2} \right) }{2\mu }. \end{aligned}$$

(16)

Type 6. If $-4{{\mu }^{2}}+{{y}^{2}}>0$ and $\lambda =\mu$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{y}{2\mu }-\frac{\sqrt{-4{{\mu }^{2}}+{{y}^{2}}}\tanh \left( \frac{\sqrt{-4{{\mu }^{2}}+{{y}^{2}}}\xi }{2} \right) }{2\mu }, \end{aligned}$$

(17)

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{y}{2\mu }-\frac{\sqrt{-4{{\mu }^{2}}+{{y}^{2}}}\coth \left( \frac{\sqrt{-4{{\mu }^{2}}+{{y}^{2}}}\xi }{2} \right) }{2\mu }. \end{aligned}$$

(18)

Type 7. If ${{y}^{2}}=4{\mu }\lambda$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{y\xi +2}{2\lambda \xi }. \end{aligned}$$

(19)

Type 8. If ${\mu }\lambda <0$, $\lambda \ne 0$ and $y=0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\sqrt{-\frac{\mu }{\lambda }}\tanh \left( \sqrt{-\lambda \mu }\xi \right) , \end{aligned}$$

(20)

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\sqrt{-\frac{\mu }{\lambda }}\coth \left( \sqrt{-\lambda \mu }\xi \right) . \end{aligned}$$

(21)

Type 9. If ${\mu }=-\lambda$ and $y=0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{1+\exp \left( -2\lambda \xi \right) }{1-\exp \left( -2\lambda \xi \right) }. \end{aligned}$$

(22)

Type 10. If ${\mu }=\lambda =0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\sinh \left( y\xi \right) +\cosh \left( y\xi \right) . \end{aligned}$$

(23)

Type 11. If ${\mu }=K=y$ and $\lambda =0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\exp (K\xi )-1. \end{aligned}$$

(24)

Type 12. If ${\lambda }=K=y$ and $\mu =0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\frac{\exp (K\xi )}{1-\exp (K\xi )}. \end{aligned}$$

(25)

Type 13. If $y=\lambda +\mu$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{1-\mu \exp \left( \left( \mu -\lambda \right) \xi \right) }{1+\lambda \exp \left( \left( \mu -\lambda \right) \xi \right) }. \end{aligned}$$

(26)

Type 14. If $y=-\lambda -\mu$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\frac{\exp \left( \left( \mu -\lambda \right) \xi \right) -\mu }{\exp \left( \left( \mu -\lambda \right) \xi \right) -\lambda }. \end{aligned}$$

(27)

Type 15. If $\mu =0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\frac{y\exp \left( y\xi \right) }{1-\lambda \exp \left( y\xi \right) }. \end{aligned}$$

(28)

Type 16. If $\lambda =y=\mu \ne 0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\frac{\sqrt{3}\tan \left( \frac{\sqrt{3}\mu \xi }{2} \right) }{2}-\frac{1}{2}. \end{aligned}$$

(29)

Type 17. If $\lambda =y=0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\mu \xi . \end{aligned}$$

(30)

Type 18. If $\mu =y=0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=-\frac{1}{\lambda \xi }. \end{aligned}$$

(31)

Type 19. If $\mu =\lambda$ and $y=0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\tan \left( \mu \xi \right) . \end{aligned}$$

(32)

Type 20. If $\lambda =0$, then

$$\begin{aligned} {{L}^{g\left( \xi \right) }}=\exp \left( y\xi \right) -\frac{n}{l}. \end{aligned}$$

(33)

Here l and n are named deformation parameters and they are positive.

Extraction of soliton solutions

In this section, we develop the analytic solutions of the Eq. (1) using the NAEM.

Consider the following transformation:

$$\begin{aligned} \Phi (x_{1},x_{2},...,x_{R},t) = Q(\xi ), \quad \xi =\sum \limits _{k=1}^{R}{{x }_{k}} -wt. \end{aligned}$$

(34)

Substituting Eq. (34) into the Eq. (1), we get

$$\begin{aligned} {{\left( -w{Q}'+{{ 2{{\theta }_{1}}Q{Q}^{\prime }}}+{{\theta }_{2}}{Q}''' \right) }^{\prime }}+{{\theta }_{3}}{Q}''+\sum \limits _{k=1}^{R}{{{\Theta }_{k}}}{Q}''=0. \end{aligned}$$

(35)

Here, $\theta _{1}, \theta _{2}, \theta _{3}$ and ${\Theta }_{k}(k=1,2,3 \dots ,R)$ denote constant parameters. We integrate Eq. (35) twice concerning the variable $\xi$, assuming that the constants of integration are zero, to arrive at the following result:

$$\begin{aligned} \left( {{\theta }_{3}}-w+\sum \limits _{k=1}^{R}{{{\Theta }_{k}}} \right) Q+{{\theta }_{1}}{{Q}^{2}}+{{\theta }_{2}}{Q}''=0. \end{aligned}$$

(36)

Implementing the NAEM

In the event that $Q^2$ and $Q^{\prime \prime }$ are balanced, $R=2$ will be the outcome. Using Eq. (5), we obtain

$$\begin{aligned} Q(\xi )={{h}_{0}}+{{h}_{1}} {{L}^{g\left( \xi \right) }}+{{h}_{2}} \left( {{L}^{g\left( \xi \right) }}\right) ^2. \end{aligned}$$

(37)

Let $m=\sum \limits _{k=1}^{R}{{{\Theta }_{k}}}$ to simplify things. We derive the subsequent algebraic equations:

$$\begin{aligned} \left\{ \begin{aligned}&\left( {{L}^{g\left( \xi \right) }}\right) ^4: 6{{\lambda }^{2}}{{h}_{2}}{{\theta }_{2}}+h_{2}^{2}{{\theta }_{1}}=0, \\&\left( {{L}^{g\left( \xi \right) }}\right) ^3: 2{{\lambda }^{2}}{{h}_{1}}{{\theta }_{2}}+10\lambda y{{h}_{2}}{{\theta }_{2}}+2{{h}_{2}}{{\theta }_{1}}{{h}_{1}}=0, \\&\left( {{L}^{g\left( \xi \right) }}\right) ^2: 8{{h}_{2}}\lambda \mu {{\theta }_{2}}+3y\lambda {{h}_{1}}{{\theta }_{2}}+4{{h}_{2}}{{y}^{2}}{{\theta }_{2}}+2{{h}_{0}}{{h}_{2}}{{\theta }_{1}}+{{\theta }_{1}}h_{1}^{2}+m{{h}_{2}}-w{{h}_{2}}+{{h}_{2}}{{\theta }_{3}}=0, \\&\left( {{L}^{g\left( \xi \right) }}\right) ^1: 2\lambda \mu {{h}_{1}}{{\theta }_{2}}+6{{h}_{2}}y\mu {{\theta }_{2}}+{{y}^{2}}{{h}_{1}}{{\theta }_{2}}+2{{h}_{0}}{{h}_{1}}{{\theta }_{1}}+m{{h}_{1}}-w{{h}_{1}}+{{h}_{1}}{{\theta }_{3}}=0, \\&\left( {{L}^{g\left( \xi \right) }}\right) ^0: 2{{\theta }_{2}}{{h}_{2}}{{\mu }^{2}}+{{\theta }_{2}}{{h}_{1}}\mu y+{{\theta }_{1}}h_{0}^{2}+m{{h}_{0}}-w{{h}_{0}}+{{\theta }_{3}}{{h}_{0}}=0. \end{aligned} \right. \end{aligned}$$

(38)

We find two clusters of solutions by solving the Eq. (38):

Cluster 1.

$$\begin{aligned} \begin{aligned} \left\{ w=-4\lambda \mu {{\theta }_{2}}+{{y}^{2}}{{\theta }_{2}}+m+{{\theta }_{3}},\quad {{h}_{0}}=-\frac{6\lambda \mu {{\theta }_{2}}}{{{\theta }_{1}}},\quad {{h}_{1}}=-\frac{6\lambda y{{\theta }_{2}}}{{{\theta }_{1}}}, \quad {{h}_{2}}=-\frac{6{{\lambda }^{2}}{{\theta }_{2}}}{{{\theta }_{1}}}. \right\} \end{aligned} \end{aligned}$$

(39)

Eq. (1) is solved for the cases covered in the preceding section by using Eqs. (7)–(33) in conjunction with Eqs. (34) and (37). The following solutions occur in this situation:

Type 1. If $\lambda \ne 0$ and $4\lambda \mu -{{y}^{2}}<0$, then the next trigonometric solutions are obtained:

$$\begin{aligned}&{{\Phi }_{01}}\left( x_{1},x_{2},...,x_{R},t\right) = -\frac{3{{\theta }_{2}}\left( \tan {{\left( \frac{\sqrt{4\lambda \mu -{{y}^{2}}}\xi }{2} \right) }^{2}}+1 \right) \left( 4\lambda \mu -{{y}^{2}} \right) }{2{{\theta }_{1}}}, \end{aligned}$$

(40)

$$\begin{aligned}&{{\Phi }_{02}}\left( x_{1},x_{2},...,x_{R},t\right) =-\frac{3{{\theta }_{2}}\left( \cot {{\left( \frac{\sqrt{4\lambda \mu -{{y}^{2}}}\xi }{2} \right) }^{2}}+1 \right) \left( 4\lambda \mu -{{y}^{2}} \right) }{2{{\theta }_{1}}}. \end{aligned}$$

(41)

Type 2. If $\lambda \ne 0$ and $4\lambda \mu -{{y}^{2}}>0$, then the subsequent shock solution is expressed:

$$\begin{aligned} {{\Phi }_{03}}\left( x_{1},x_{2},...,x_{R},t \right) =\frac{3{{\theta }_{2}}\left( \tanh {{\left( \frac{\sqrt{-4\lambda \mu +{{y}^{2}}}\xi }{2} \right) }^{2}}-1 \right) \left( 4\lambda \mu -{{y}^{2}} \right) }{2{{\theta }_{1}}}. \end{aligned}$$

(42)

The singular solution is discovered as:

$$\begin{aligned} {{\Phi }_{04}}\left( x_{1},x_{2},...,x_{R},t\right) =\frac{3{{\theta }_{2}}\left( \coth {{\left( \frac{\sqrt{-4\lambda \mu +{{y}^{2}}}\xi }{2} \right) }^{2}}-1 \right) \left( 4\lambda \mu -{{y}^{2}} \right) }{2{{\theta }_{1}}}. \end{aligned}$$

(43)

Type 3. If $-4{{\mu }^{2}}-{{y}^{2}}<0$, $\lambda =-\mu$ and $\lambda \ne 0$, then the following trigonometric solutions are obtained:

$$\begin{aligned} {{\Phi }_{05}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{3 \theta _{2} \lambda }{\theta _{1} \mu ^2} \left( \begin{aligned}&-\frac{\lambda \left( 4 \mu ^2 + y^2 \right) \tan \left( \frac{\sqrt{-4 \mu ^2 - y^2} \xi }{2} \right) ^2}{2} \\&+ \mu y^2 + \frac{\lambda y^2}{2} + 2 \mu ^3 \\&- y \sqrt{-4 \mu ^2 - y^2} \left( \lambda + \mu \right) \tan \left( \frac{\sqrt{-4 \mu ^2 - y^2} \xi }{2} \right) \end{aligned} \right) , \end{aligned}$$

(44)

$$\begin{aligned} {{\Phi }_{06}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{3 \theta _{2} \lambda }{\theta _{1} \mu ^2} \left( \begin{aligned}&-\frac{\lambda \left( 4 \mu ^2 + y^2 \right) \cot \left( \frac{\sqrt{-4 \mu ^2 - y^2} \xi }{2} \right) ^2}{2} \\&+ \mu y^2 + \frac{\lambda y^2}{2} + 2 \mu ^3 \\&- y \sqrt{-4 \mu ^2 - y^2} \left( \lambda + \mu \right) \cot \left( \frac{\sqrt{-4 \mu ^2 - y^2} \xi }{2} \right) \end{aligned} \right) . \end{aligned}$$

(45)

Type 4. If $4{{\mu }^{2}}+{{y}^{2}}>0$ and $\lambda =-\mu$, then the next shock wave solution is found:

$$\begin{aligned} {{\Phi }_{07}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{3 \theta _{2} \lambda }{\theta _{1} \mu ^2} \left( \begin{aligned}&\frac{\lambda \left( 4 \mu ^2 + y^2 \right) \tanh \left( \frac{\sqrt{4 \mu ^2 + y^2} \xi }{2} \right) ^2}{2} \\&+ \mu y^2 + \frac{\lambda y^2}{2} + 2 \mu ^3 \\&+ y \sqrt{4 \mu ^2 + y^2} \left( \lambda + \mu \right) \tanh \left( \frac{\sqrt{4 \mu ^2 + y^2} \xi }{2} \right) \end{aligned} \right) . \end{aligned}$$

(46)

The singular solution is reached as:

$$\begin{aligned} {{\Phi }_{08}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{3 \theta _{2} \lambda }{\theta _{1} \mu ^2} \left( \begin{aligned}&\frac{\lambda \left( 4 \mu ^2 + y^2 \right) \coth \left( \frac{\sqrt{4 \mu ^2 + y^2} \xi }{2} \right) ^2}{2} \\&+ \mu y^2 + \frac{\lambda y^2}{2} + 2 \mu ^3 \\&+ y \sqrt{4 \mu ^2 + y^2} \left( \lambda + \mu \right) \coth \left( \frac{\sqrt{4 \mu ^2 + y^2} \xi }{2} \right) \end{aligned} \right) . \end{aligned}$$

(47)

Type 5. If $4{{\mu }^{2}}+{{y}^{2}}<0$ and $\lambda =\mu$, then the subsequent trigonometric solutions are obtained:

$$\begin{aligned}&{{\Phi }_{09}}\left( x_{1},x_{2},...,x_{R},t\right)&= \frac{3 \theta _{2} \lambda }{\theta _{1} \mu ^2} \left( \begin{aligned}&\lambda \left( \frac{y^2}{2} - 2 \mu ^2 \right) \tan \left( \frac{\sqrt{4 \mu ^2 - y^2} \xi }{2} \right) ^2 \\&+ \mu y^2 - \frac{\lambda y^2}{2} - 2 \mu ^3 \\&- y \sqrt{4 \mu ^2 - y^2} \left( -\lambda + \mu \right) \tan \left( \frac{\sqrt{4 \mu ^2 - y^2} \xi }{2} \right) \end{aligned} \right) , \end{aligned}$$

(48)

$$\begin{aligned}&{{\Phi }_{10}}\left( x_{1},x_{2},...,x_{R},t\right)&= \frac{3 \theta _{2} \lambda }{\theta _{1} \mu ^2} \left( \begin{aligned}&\lambda \left( \frac{y^2}{2} - 2 \mu ^2 \right) \cot \left( \frac{\sqrt{4 \mu ^2 - y^2} \xi }{2} \right) ^2\\&+ \mu y^2 - \frac{\lambda y^2}{2} - 2 \mu ^3 \\&- y \sqrt{4 \mu ^2 - y^2} \left( -\lambda + \mu \right) \cot \left( \frac{\sqrt{4 \mu ^2 - y^2} \xi }{2} \right) \end{aligned} \right) . \end{aligned}$$

(49)

Type 6. If $-4{{\mu }^{2}}+{{y}^{2}}>0$ and $\lambda =\mu$, then the following shock wave solution is attained:

$$\begin{aligned} {{\Phi }_{11}}\left( x_{1},x_{2},...,x_{R},t\right)&= \frac{3 \theta _{2} \lambda }{\theta _{1} \mu ^2} \left( \begin{aligned}&\lambda \left( -\frac{y^2}{2} + 2 \mu ^2 \right) \tanh \left( \frac{\sqrt{-4 \mu ^2 + y^2} \xi }{2} \right) ^2 \\&+ \mu y^2 - \frac{\lambda y^2}{2} - 2 \mu ^3 \\&+ y \sqrt{-4 \mu ^2 + y^2} \left( -\lambda + \mu \right) \tanh \left( \frac{\sqrt{-4 \mu ^2 + y^2} \xi }{2} \right) \end{aligned} \right) . \end{aligned}$$

(50)

The singular solution is discovered as:

$$\begin{aligned} {{\Phi }_{12}}\left( x_{1},x_{2},...,x_{R},t\right)&= \frac{3 \theta _{2} \lambda }{\theta _{1} \mu ^2} \left( \begin{aligned}&\lambda \left( -\frac{y^2}{2} + 2 \mu ^2 \right) \coth \left( \frac{\sqrt{-4 \mu ^2 + y^2} \xi }{2} \right) ^2 \\&+ \mu y^2 - \frac{\lambda y^2}{2} - 2 \mu ^3 \\&+ y \sqrt{-4 \mu ^2 + y^2} \left( -\lambda + \mu \right) \coth \left( \frac{\sqrt{-4 \mu ^2 + y^2} \xi }{2} \right) \end{aligned} \right) . \end{aligned}$$

(51)

Type 7. If ${{y}^{2}}=4{\mu }\lambda$, then the next only one solution is given:

$$\begin{aligned} {{\Phi }_{13}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{3{{\theta }_{2}}\left( 4\lambda \mu {{\xi }^{2}}-{{\xi }^{2}}{{y}^{2}}+4 \right) }{2{{\theta }_{1}}{{\xi }^{2}}}. \end{aligned}$$

(52)

Type 8. If ${\mu }\lambda <0$, $\lambda \ne 0$ and $y=0$, then the subsequent shock wave solution is reached:

$$\begin{aligned} {{\Phi }_{14}}\left( x_{1},x_{2},...,x_{R},t\right)&=\frac{6\lambda {{\theta }_{2}}\left( \sqrt{-\frac{\mu }{\lambda }}\tanh \left( \sqrt{-\lambda \mu }\xi \right) y+\tanh {{\left( \sqrt{-\lambda \mu }\xi \right) }^{2}}\mu -\mu \right) }{{{\theta }_{1}}}. \end{aligned}$$

(53)

The singular wave solution is attained as:

$$\begin{aligned} {{\Phi }_{15}}\left( x_{1},x_{2},...,x_{R},t\right)&=\frac{6\lambda {{\theta }_{2}}\left( \sqrt{-\frac{\mu }{\lambda }}\coth \left( \sqrt{-\lambda \mu }\xi \right) y+\coth {{\left( \sqrt{-\lambda \mu }\xi \right) }^{2}}\mu -\mu \right) }{{{\theta }_{1}}}. \end{aligned}$$

(54)

Type 9. If ${\mu }=-\lambda$ and $y=0$, then the next plane solution is obtained:

$$\begin{aligned} {{\Phi }_{16}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{6{{\theta }_{2}}\lambda \left( \left( \lambda +\mu +y \right) \exp \left( -4\lambda \xi \right) +\left( 2\lambda -2\mu \right) \exp \left( -2\lambda \xi \right) -y+\lambda +\mu \right) }{{{\theta }_{1}}{{\left( -1+\exp \left( -2\lambda \xi \right) \right) }^{2}}}. \end{aligned}$$

(55)

Type 10. If ${\mu }=\lambda =0$, then the subsequent mixed hyperbolic solutions are found:

$$\begin{aligned} {{\Phi }_{17}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{6\left( 2\cosh {{\left( y\xi \right) }^{2}}\lambda +\left( 2\lambda \sinh \left( y\xi \right) +y \right) \cosh \left( y\xi \right) +y\sinh \left( y\xi \right) +\mu -\lambda \right) {{\theta }_{2}}\lambda }{{{\theta }_{1}}}. \end{aligned}$$

(56)

Type 11. If ${\mu }=K=y$ and $\lambda =0$, then the following plane solution is obtained:

$$\begin{aligned} {{\Phi }_{18}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{6\left( \left( \lambda +\mu -y \right) \exp \left( 2K\xi \right) +\left( y-2\mu \right) \exp \left( K\xi \right) +\mu \right) {{\theta }_{2}}\lambda }{{{\theta }_{1}}{{\left( -1+\exp \left( K\xi \right) \right) }^{2}}}. \end{aligned}$$

(57)

Type 12. If ${\lambda }=K=y$ and $\mu =0$, then the next plane solution is found:

$$\begin{aligned} {{\Phi }_{19}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{\lambda ^2 \theta _{2}exp\left( K \xi \right) }{\theta _{1}\left( -1+exp(K \xi )\right) ^2}. \end{aligned}$$

(58)

Type 13. If $y=\lambda +\mu$, then the subsequent plane solution is reached:

$$\begin{aligned} {{\Phi }_{20}}\left( x_{1},x_{2},...,x_{R},t\right)&= \frac{6 \left( \begin{aligned}&\lambda \mu \left( y - \mu - \lambda \right) \exp \left( -2 \left( \lambda - \mu \right) \xi \right) \\&+ \left( \left( -y + 4 \mu \right) \lambda - y \mu \right) \exp \left( \left( -\lambda + \mu \right) \xi \right) \\&+ y - \mu - \lambda \end{aligned} \right) \theta _{2} \lambda }{{\theta _{1} \left( \exp \left( \left( -\lambda + \mu \right) \xi \right) \lambda - 1 \right) ^{2}}}. \end{aligned}$$

(59)

Type 14. If $y=-\lambda -\mu$, then the following plane solution is attained:

$$\begin{aligned} {{\Phi }_{21}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{6 \left( \begin{aligned}&\left( y + \mu + \lambda \right) \exp \left( -2 \left( \lambda - \mu \right) \xi \right) \\&+ \mu \lambda \left( y + \mu + \lambda \right) \\&+ \left( \left( -y - 4 \mu \right) \lambda - y \mu \right) \exp \left( \left( -\lambda + \mu \right) \xi \right) \end{aligned} \right) \theta _{2} \lambda }{{\theta _{1} \left( -\exp \left( \left( -\lambda + \mu \right) \xi \right) + \lambda \right) ^{2}}}. \end{aligned}$$

(60)

Type 15. If $\mu =0$, then the next plane solution is discovered:

$$\begin{aligned} {{\Phi }_{22}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{6\left( \exp \left( 2y\xi \right) {{\lambda }^{2}}\mu +\left( -2\lambda \mu +{{y}^{2}} \right) \exp \left( y\xi \right) +\mu \right) {{\theta }_{2}}\lambda }{{{\theta }_{1}}{{\left( \exp \left( y\xi \right) -1 \right) }^{2}}}. \end{aligned}$$

(61)

Type 16. If $\lambda =y=\mu \ne 0$, then the subsequent trigonometric solutions is given:

$$\begin{aligned} {{\Phi }_{23}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{3{{\theta }_{2}}\left( \frac{3\tan {{\left( \frac{\sqrt{3}\mu \xi }{2} \right) }^{2}}\lambda }{2}+\sqrt{3}\left( y-\lambda \right) \tan \left( \frac{\sqrt{3}\mu \xi }{2} \right) -y+2\mu +\frac{\lambda }{2} \right) \lambda }{{{\theta }_{1}}} . \end{aligned}$$

(62)

Type 17. If $\lambda =y=0$, then the following only one solution is yield:

$$\begin{aligned} {{\Phi }_{24}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{6\lambda \mu {{\theta }_{2}}\left( \lambda \mu {{\xi }^{2}}+y\xi +1 \right) }{{{\theta }_{1}}}. \end{aligned}$$

(63)

Type 18. If $\mu =y=0$, then the next only one solution is obtained:

$$\begin{aligned} {{\Phi }_{25}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{6{{\theta }_{2}}\left( \lambda \mu {{\xi }^{2}}-y\xi +1 \right) }{{{\theta }_{1}}{{\xi }^{2}}}. \end{aligned}$$

(64)

Type 19. If $\mu =\lambda$ and $y=0$, then the subsequent trigonometric solutions is discovered:

$$\begin{aligned} {{\Phi }_{26}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{6\lambda {{\theta }_{2}}\left( \tan {{\left( \mu \xi \right) }^{2}}\lambda +\tan \left( \mu \xi \right) y+\mu \right) }{{{\theta }_{1}}}. \end{aligned}$$

(65)

Type 20. If $\lambda =0$, then the following plane solution is reached:

$$\begin{aligned} {{\Phi }_{27}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{6\lambda {{\theta }_{2}}\left( \exp \left( 2y\xi \right) {{l}^{2}}\lambda +\exp \left( y\xi \right) {{l}^{2}}y-2\exp \left( y\xi \right) l\lambda n+\mu {{l}^{2}}-\ln y+\lambda {{n}^{2}} \right) }{{{\theta }_{1}}{{l}^{2}}}. \end{aligned}$$

(66)

Note: For solutions Eqs. (40)–(66), $\xi$ is given by $\xi =\sum \limits _{k=1}^{R}{{{x }_{k}}-\left( -4\lambda \mu {{\theta }_{2}}+{{y}^{2}}{{\theta }_{2}}+m+{{\theta }_{3}}\right) t}$.

Cluster 2.

$$\begin{aligned} \left\{ w=4\lambda \mu {{\theta }_{2}}-{{y}^{2}}{{\theta }_{2}}+m+{{\theta }_{3}},\quad {{h}_{0}}=-\frac{\left( 2\lambda \mu +{{y}^{2}} \right) {{\theta }_{2}}}{{{\theta }_{1}}},\quad {{h}_{1}}=-\frac{6\lambda y{{\theta }_{2}}}{{{\theta }_{1}}},\quad {{h}_{2}}=-\frac{6{{\lambda }^{2}}{{\theta }_{2}}}{{{\theta }_{1}}}.\right\} \end{aligned}$$

Utilizing the above parameters, we construct the following solutions:

Type 1. If $\lambda \ne 0$ and $4\lambda \mu -{{y}^{2}}<0$, then we get

$$\begin{aligned} {{\Phi }_{28}}\left( x_{1},x_{2},...,x_{R},t\right) = -\frac{{{\theta }_{2}}\left( 3\tan {{\left( \frac{\sqrt{4\lambda \mu -{{y}^{2}}}\xi }{2} \right) }^{2}}+1 \right) \left( 4\lambda \mu -{{y}^{2}} \right) }{2{{\theta }_{1}}}, \end{aligned}$$

(67)

$$\begin{aligned} {{\Phi }_{29}}\left( x_{1},x_{2},...,x_{R},t\right) =-\frac{{{\theta }_{2}}\left( \cot {{\left( \frac{\sqrt{4\lambda \mu -{{y}^{2}}}\xi }{2} \right) }^{2}}+1 \right) \left( 4\lambda \mu -{{y}^{2}} \right) }{2{{\theta }_{1}}}. \end{aligned}$$

(68)

Type 2. If $\lambda \ne 0$ and $4\lambda \mu -{{y}^{2}}>0$, then we obtain

$$\begin{aligned} {{\Phi }_{30}}\left( x_{1},x_{2},...,x_{R},t \right) = \frac{{{\theta }_{2}}\left( 3\tanh {{\left( \frac{\sqrt{-4\lambda \mu +{{y}^{2}}}\xi }{2} \right) }^{2}}-1 \right) \left( 4\lambda \mu -{{y}^{2}} \right) }{2{{\theta }_{1}}}, \end{aligned}$$

(69)

$$\begin{aligned} {{\Phi }_{31}}\left( x_{1},x_{2},...,x_{R},t\right) = \frac{{{\theta }_{2}}\left( 3\coth {{\left( \frac{\sqrt{-4\lambda \mu +{{y}^{2}}}\xi }{2} \right) }^{2}}-1 \right) \left( 4\lambda \mu -{{y}^{2}} \right) }{2{{\theta }_{1}}}. \end{aligned}$$

(70)

Type 3. If $-4{{\mu }^{2}}-{{y}^{2}}<0$, $\lambda =-\mu$ and $\lambda \ne 0$, then we reach

$$\begin{aligned} {{\Phi }_{32}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{{\theta _{2}} \left( \begin{aligned}&-\frac{3 \lambda \left( 4 \mu ^2 + y^2 \right) \tan \left( \frac{\sqrt{-4 \mu ^2 - y^2} \xi }{2} \right) ^2}{2} \\&+ \mu ^2 y^2 + \frac{3 \lambda ^2 y^2}{2} + \left( 2 \mu ^3 + 3 \mu y^2 \right) \lambda \\&+ 3 y \lambda \sqrt{-4 \mu ^2 - y^2} \left( \lambda + \mu \right) \tan \left( \frac{\sqrt{-4 \mu ^2 - y^2} \xi }{2} \right) \end{aligned} \right) }{{\theta _{1} \mu ^2}}, \end{aligned}$$

(71)

$$\begin{aligned} {{\Phi }_{33}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{{\theta _{2}} \left( \begin{aligned}&-\frac{3 \lambda \left( 4 \mu ^2 + y^2 \right) \cot \left( \frac{\sqrt{-4 \mu ^2 - y^2} \xi }{2} \right) ^2}{2} \\&+ \mu ^2 y^2 + \frac{3 \lambda ^2 y^2}{2} + \left( 2 \mu ^3 + 3 \mu y^2 \right) \lambda \\&- 3 y \lambda \sqrt{-4 \mu ^2 - y^2} \left( \lambda + \mu \right) \cot \left( \frac{\sqrt{-4 \mu ^2 - y^2} \xi }{2} \right) \end{aligned} \right) }{{\theta _{1} \mu ^2}}. \end{aligned}$$

(72)

Type 4. If $4{{\mu }^{2}}+{{y}^{2}}>0$ and $\lambda =-\mu$, then we discover

$$\begin{aligned}&{{\Phi }_{34}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{{\theta _{2}} \left( \begin{aligned}&\frac{3 \lambda ^2 \left( 4 \mu ^2 + y^2 \right) \tanh \left( \frac{\sqrt{4 \mu ^2 + y^2} \xi }{2} \right) ^2}{2} \\&+ \mu ^2 y^2 + \frac{3 \lambda ^2 y^2}{2} + \left( 2 \mu ^3 + 3 \mu y^2 \right) \lambda \\&+ 3 y \lambda \sqrt{4 \mu ^2 + y^2} \left( \lambda + \mu \right) \tanh \left( \frac{\sqrt{4 \mu ^2 + y^2} \xi }{2} \right) \end{aligned} \right) }{{\theta _{1} \mu ^2}}, \end{aligned}$$

(73)

$$\begin{aligned}&{{\Phi }_{35}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{{\theta _{2}} \left( \begin{aligned}&\frac{3 \lambda ^2 \left( 4 \mu ^2 + y^2 \right) \coth \left( \frac{\sqrt{4 \mu ^2 + y^2} \xi }{2} \right) ^2}{2} \\&+ \mu ^2 y^2 + \frac{3 \lambda ^2 y^2}{2} \\&+ \left( 2 \mu ^3 + 3 \mu y^2 \right) \lambda \\&+ 3 y \lambda \sqrt{4 \mu ^2 + y^2} \left( \lambda + \mu \right) \coth \left( \frac{\sqrt{4 \mu ^2 + y^2} \xi }{2} \right) \end{aligned} \right) }{{\theta _{1} \mu ^2}}. \end{aligned}$$

(74)

Type 5. If $4{{\mu }^{2}}+{{y}^{2}}<0$ and $\lambda =\mu$, then we find

$$\begin{aligned}&{{\Phi }_{36}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{{\theta _{2}} \left( \begin{aligned}&\lambda ^2 \left( -\frac{3 y^2}{2} + 6 \mu ^2 \right) \tan \left( \frac{\sqrt{4 \mu ^2 - y^2} \xi }{2} \right) ^2 \\&+ \mu ^2 y^2 + \frac{3 \lambda ^2 y^2}{2} + \left( 2 \mu ^3 - 3 \mu y^2 \right) \lambda \\&+ 3 \lambda y \sqrt{4 \mu ^2 - y^2} \left( -\lambda + \mu \right) \tan \left( \frac{\sqrt{4 \mu ^2 - y^2} \xi }{2} \right) \end{aligned} \right) }{{\theta _{1} \mu ^2}}, \end{aligned}$$

(75)

$$\begin{aligned}&{{\Phi }_{37}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{{\theta _{2}} \left( \begin{aligned}&\lambda ^2 \left( -\frac{3 y^2}{2} + 6 \mu ^2 \right) \cot \left( \frac{\sqrt{4 \mu ^2 - y^2} \xi }{2} \right) ^2 \\&+ \mu ^2 y^2 + \frac{3 \lambda ^2 y^2}{2} + \left( 2 \mu ^3 - 3 \mu y^2 \right) \lambda \\&- 3 \lambda y \sqrt{4 \mu ^2 - y^2} \left( -\lambda + \mu \right) \cot \left( \frac{\sqrt{4 \mu ^2 - y^2} \xi }{2} \right) \end{aligned} \right) }{{\theta _{1} \mu ^2}}. \end{aligned}$$

(76)

Type 6. If $-4{{\mu }^{2}}+{{y}^{2}}>0$ and $\lambda =\mu$, then we get

$$\begin{aligned}&{{\Phi }_{38}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{{\theta _{2}} \left( \begin{aligned}&\lambda ^2 \left( \frac{3 y^2}{2} - 6 \mu ^2 \right) \tanh \left( \frac{\sqrt{-4 \mu ^2 + y^2} \xi }{2} \right) ^2 \\&+ \mu ^2 y^2 + \frac{3 \lambda ^2 y^2}{2} + \left( 2 \mu ^3 - 3 \mu y^2 \right) \lambda \\&- 3 \lambda y \sqrt{-4 \mu ^2 + y^2} \left( -\lambda + \mu \right) \tanh \left( \frac{\sqrt{-4 \mu ^2 + y^2} \xi }{2} \right) \end{aligned} \right) }{{\theta _{1} \mu ^2}}, \end{aligned}$$

(77)

$$\begin{aligned}&{{\Phi }_{39}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{{\theta _{2}} \left( \begin{aligned}&\lambda ^2 \left( \frac{3 y^2}{2} - 6 \mu ^2 \right) \coth \left( \frac{\sqrt{-4 \mu ^2 + y^2} \xi }{2} \right) ^2 \\&+ \mu ^2 y^2 + \frac{3 \lambda ^2 y^2}{2} + \left( 2 \mu ^3 - 3 \mu y^2 \right) \lambda \\&- 3 \lambda y \sqrt{-4 \mu ^2 + y^2} \left( -\lambda + \mu \right) \coth \left( \frac{\sqrt{-4 \mu ^2 + y^2} \xi }{2} \right) \end{aligned} \right) }{{\theta _{1} \mu ^2}}. \end{aligned}$$

(78)

Type 7. If ${{y}^{2}}=4{\mu }\lambda$, then we attain

$$\begin{aligned} {{\Phi }_{40}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{{{\theta }_{2}}\left( 4\lambda \mu {{\xi }^{2}}-{{\xi }^{2}}{{y}^{2}}+12 \right) }{2{{\theta }_{1}}{{\xi }^{2}}}. \end{aligned}$$

(79)

Type 8. If ${\mu }\lambda <0$, $\lambda \ne 0$ and $y=0$, then we discover

$$\begin{aligned}&{{\Phi }_{41}}\left( x_{1},x_{2},...,x_{R},t\right)&=\frac{{{\theta }_{2}}\left( 6\lambda y\sqrt{-\frac{\mu }{\lambda }}\tanh \left( \sqrt{-\lambda \mu }\xi \right) +6\lambda \mu \tanh {{\left( \sqrt{-\lambda \mu }\xi \right) }^{2}}-2\lambda \mu -{{y}^{2}} \right) }{{{\theta }_{1}}}, \end{aligned}$$

(80)

$$\begin{aligned}&{{\Phi }_{42}}\left( x_{1},x_{2},...,x_{R},t\right)&=\frac{{{\theta }_{2}}\left( 6\lambda y\sqrt{-\frac{\mu }{\lambda }}\coth \left( \sqrt{-\lambda \mu }\xi \right) +6\lambda \mu \coth {{\left( \sqrt{-\lambda \mu }\xi \right) }^{2}}-2\lambda \mu -{{y}^{2}} \right) }{{{\theta }_{1}}}. \end{aligned}$$

(81)

Type 9. If ${\mu }=-\lambda$ and $y=0$, then we yield

$$\begin{aligned} {{\Phi }_{43}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{{\theta _{2}} \left( \begin{aligned}&\left( 6 \lambda ^2 + 2 \left( 3y + \mu \right) \lambda + y^2 \right) \exp \left( -4 \lambda \xi \right) \\&+ 2 \left( 6 \lambda ^2 - 2 \lambda \mu - y^2 \right) \exp \left( -2 \lambda \xi \right) \\&+ 6 \lambda ^2 + 2 \left( -3y + \mu \right) \lambda + y^2 \end{aligned} \right) }{{\theta _{1} \left( -1 + \exp \left( -2 \lambda \xi \right) \right) ^2}}. \end{aligned}$$

(82)

Type 10. If ${\mu }=\lambda =0$, then we have

$$\begin{aligned} {{\Phi }_{44}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{\left( \begin{aligned}&12 \cosh ^2 \left( y \xi \right) \lambda ^2 + 6 \lambda \left( 2 \lambda \sinh \left( y \xi \right) + y \right) \cosh \left( y \xi \right) \\&+ 6 \lambda y \sinh \left( y \xi \right) + y^2 + 2 \lambda \mu - 6 \lambda ^2 \end{aligned} \right) {\theta _{2}}}{{\theta _{1}}}. \end{aligned}$$

(83)

Type 11. If ${\mu }=K=y$ and $\lambda =0$, then we reach

$$\begin{aligned} {{\Phi }_{45}}\left( x_{1},x_{2},...,x_{R},t\right)&= \frac{2 \left( \begin{aligned}&\left( -3 \lambda ^2 + \left( 3y - \mu \right) \lambda - \frac{y^2}{2} \right) \exp \left( 2K\xi \right) \\&+ \left( \left( -3y + 2\mu \right) \lambda + y^2 \right) \exp \left( K\xi \right) \\&- \frac{y^2}{2} - \lambda \mu \end{aligned} \right) {\theta _{2}}}{{\theta _{1}} \left( -1 + \exp \left( K\xi \right) \right) ^2}. \end{aligned}$$

(84)

Type 12. If ${\lambda }=K=y$ and $\mu =0$, then we obtain

$$\begin{aligned} {{\Phi }_{46}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{\lambda ^2 \theta _{2}\left( exp(\lambda \xi )^2 +4exp(\lambda \xi ) +1\right) }{\theta _{1} \left( -1+exp(\lambda \xi ) \right) ^2}. \end{aligned}$$

(85)

Type 13. If $y=\lambda +\mu$, then we have

$$\begin{aligned} {{\Phi }_{47}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{ \left( \begin{aligned}&\lambda ^2 \left( 2\lambda \mu + 6\mu ^2 - 6y\mu + y^2 \right) \exp \left( -2 \left( \lambda - \mu \right) \xi \right) \\&- 2\lambda \left( \left( -3y + 8\mu \right) \lambda + y \left( y - 3\mu \right) \right) \exp \left( \left( -\lambda + \mu \right) \xi \right) \\&+ 6\lambda ^2 + \left( -6y + 2\mu \right) \lambda + y^2 \end{aligned} \right) {\theta _{2}}}{{\theta _{1}} \left( \lambda \exp \left( \left( -\lambda + \mu \right) \xi \right) - 1 \right) ^2}. \end{aligned}$$

(86)

Type 14. If $y=-\lambda -\mu$, then we obtain

$$\begin{aligned} {{\Phi }_{48}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{\left( \begin{aligned}&\lambda ^2 \left( 6\lambda ^2 + \left( 2\mu + 6y \right) \lambda + y^2 \right) \exp \left( -2 \left( \lambda - \mu \right) \xi \right) \\&+ \left( \left( -6y - 16\mu \right) \lambda - 2y \left( y + 3\mu \right) \right) \exp \left( \left( -\lambda + \mu \right) \xi \right) \\&+ \left( 6\mu ^2 + \left( 6y + 2\mu \right) \lambda + y^2 \right) \lambda \end{aligned} \right) \theta _{2}}{\theta _{1} \left( -\exp \left( \left( -\lambda + \mu \right) \xi \right) + \lambda \right) ^2}. \end{aligned}$$

(87)

Type 15. If $\mu =0$, then we get

$$\begin{aligned} {{\Phi }_{49}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{\left( \begin{aligned}&2 \lambda ^3 \mu \exp \left( 2 y \xi \right) + \lambda ^2 y^2 \exp \left( 2 y \xi \right) \\&- 4 \lambda ^2 \exp \left( y \xi \right) + 4 \lambda y^2 \exp \left( y \xi \right) \\&+ 2 \lambda \mu + y^2 \end{aligned} \right) \theta _{2}}{\theta _{1} \left( \lambda \exp \left( y \xi \right) - 1 \right) ^2}. \end{aligned}$$

(88)

Type 16. If $\lambda =y=\mu \ne 0$, then we reach

$$\begin{aligned} {{\Phi }_{50}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{\theta _{2} \left( \begin{aligned}&\frac{9 \tan ^2 \left( \frac{\sqrt{3} \mu \xi }{2} \right) \lambda ^2}{2} \\&+ 3 \lambda \sqrt{3} \left( y - \lambda \right) \tan \left( \frac{\sqrt{3} \mu \xi }{2} \right) \\&+ \left( -3 y + 2 \mu \right) \lambda + \frac{3 \lambda ^2}{2} + y^2 \end{aligned} \right) }{\theta _{1}}. \end{aligned}$$

(89)

Type 17. If $\lambda =y=0$, then we attain

$$\begin{aligned} {{\Phi }_{51}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{{{\theta }_{2}}\left( 6{{\lambda }^{2}}{{\mu }^{2}}{{\xi }^{2}}+6\lambda \mu \xi y+2\lambda \mu +{{y}^{2}} \right) }{{{\theta }_{1}}}. \end{aligned}$$

(90)

Type 18. If $\mu =y=0$, then we yield

$$\begin{aligned} {{\Phi }_{52}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{{{\theta }_{2}}\left( 2\lambda \mu {{\xi }^{2}}+{{\xi }^{2}}{{y}^{2}}-6y\xi +6 \right) }{{{\theta }_{1}}{{\xi }^{2}}}. \end{aligned}$$

(91)

Type 19. If $\mu =\lambda$ and $y=0$, then we have

$$\begin{aligned} {{\Phi }_{53}}\left( x_{1},x_{2},...,x_{R},t\right)&=-\frac{{{\theta }_{2}}\left( 6{{\lambda }^{2}}\tan {{\left( \lambda \mu \right) }^{2}}+6y\lambda \tan \left( \lambda \mu \right) +2\lambda \mu +{{y}^{2}} \right) }{{{\theta }_{1}}}. \end{aligned}$$

(92)

Type 20. If $\lambda =0$, then we obtain

$$\begin{aligned} {{\Phi }_{54}}\left( x_{1},x_{2},...,x_{R},t\right)&= -\frac{\theta _{2} \left( \begin{aligned}&6 \exp \left( 2y \xi \right) l^2 \lambda ^2 + 6 \exp \left( y \xi \right) l^2 \lambda y \\&- 12 \exp \left( y \xi \right) l \lambda ^2 n+ 2 \mu \lambda l^2 \\&+ l^2 y^2 - 6 l \lambda n y+ 6 \lambda ^2 n^2 \end{aligned} \right) }{\theta _{1} l^2}. \end{aligned}$$

(93)

For solutions Eqs. (67)–(93), $\xi$ is given by $\xi =\sum \limits _{k=1}^{R}{{{x }_{k}}-\left( 4\lambda \mu {{\theta }_{2}}-{{y}^{2}}{{\theta }_{2}}+m+{{\theta }_{3}}\right) t}$.

Comparisons

In this section, we will emphasize the importance of our proposed method. Xu and Wazwaz²⁰ examined the governing model and used the binary Bell polynomial method and singularity manifold analysis to find several analytical solutions. Even though they resulted in distinct wave models, our proposed method changes this approach to give a range of innovative soliton solutions, including plane, shock, singular, mixed trigonometric, and mixed hyperbolic types. We show the novelty and improvement of our results, which present novel solutions never published before, by comparing them with those of Xu and Wazwaz²⁰. These groundbreaking findings have important implications for the mathematics of physics and nonlinear optics as well as new directions to study higher-order PDEs. Our contributions provide a comprehensive and influential investigation of soliton solutions and their various wave phenomena.

Numerical representations

This part includes a detailed explanation of our findings using 3D and 2D figures, as well as a comprehensive analysis of density plots through parameter adjustments. The assumption used to generate graphs is that $x_{2},...,x_{M}=0$. In the past few years, a wide range of fields have shown a great deal of interest in the research of analytical solutions for NLPDEs and modeling of solitary wave phenomena, particularly optical science, plasma physics, and the biological sciences. We provide a study that looks at the physical characteristics of these solutions and considers their uses.

Fig. 1

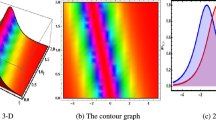
Visual interpretations of solution $\Phi _{01}(x_{1},t)$ for Eq. (40) is presented. (a) 3D plot, (b) 2D plot, and (c) density plot, where $\theta _{3}=3$, $\theta _{2}=2$, $\lambda =2$, $m=10$, $\theta _{1}=1$, $\mu =3$, $y=5$.

Fig. 2

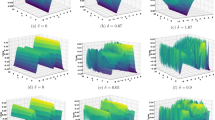
A graphical depiction of $\Phi _{11}(x_{1},t)$ for Eq. (50) is shown, (a) 3D plot, (b) 2D plot, and (c) density plot when $\theta _{3}=1.5$, $\theta _{2}=2$, $\lambda =2$, m=1, $\theta _{1}=1$, $\mu =2$, $y=5$.

Fig. 3

A graphical depiction of $\Phi _{15}(x_{1},t)$ for Eq. (54) is shown, (a) 3D plot, (b) 2D plot, and (c) density plot when $\lambda =1$, $\theta _{3}=1$, $\theta _{2}=1$, m=1, $\theta _{1}=1$, $\mu =1$, $y=1$.

Fig. 4

The graphical representation of $\Phi _{18}(x_{1},t)$ for Eq. (57) is presented. (a) 3D plot, (b) 2D plot, and (c) density plot, where $\theta _{3}=1$, $\theta _{2}=1$, $m=2$, $\theta _{1}=1$, $\mu =1$, $\lambda =1$, $y=1$.

Fig. 5

Graphical interpretations for solution $\Phi _{20}(x_{1},t)$ for Eq. (59) using $\theta _{3}=1$, $\theta _{2}=1$, $m=2$, $\theta _{1}=1$, $\mu =1.5$, $\lambda =-0.5$, $y=1$.

The research data highlight several noteworthy physical properties. The transformations selected for the variables and coefficients are essential to understanding the model’s analytical solutions as well as their practical applications. These results suggest that different types of solitary wave solutions are generated in optical fibers by maintaining the form and speed of the waves during propagation while balancing nonlinear interactions and dispersive effects. By carefully choosing the settings, these solitons can be handled effectively.

Conclusions

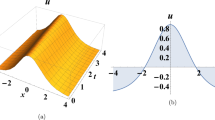
This work aims at the (n+1)-dgKPE, which describes a wide variety of applications in a variety of physical systems, including fluid physics, plasma physics, Bose-Einstein condensates, and optical fibers. In this study we used NAEM. Numerous soliton solutions, including singular periodic wave solutions, shock wave solutions, mixed trigonometric solutions, exponential function solutions, and hyperbolic solutions, were obtained as possible results of the NAEM. 3D, 2D, and density plots that enhance the visualization of the solution set under various parameter changes, Fig. 1, 2, 3, 4, and 5 supporting the main results of the study. Figure 1 shows that we achieve a bright soliton for the trigonometric function solution Eq. (40) for different parameter values, while Figure 2 shows that we find a kink soliton solution for the shock wave solution Eq. (50). Figure 3 shows that we attain a periodic soliton for the singular wave solution of Eq. (54). Figure 4 shows the existence of the dark soliton, which is observed as a plane solution in the solution of Eq. (57). Figure 5 shows that we attain a plane solution for the bright soliton solution of Eq. (59). A thorough overview of the solutions was given by these graphs. Appropriate parameter values are essential to avoiding infinities and achieving realistic findings, which are necessary for physically meaningful results. Furthermore included is a comparison of the outcomes. In addition to its many uses in simulating the propagation and interaction of soliton waves, (n+1)-dgKPE is essential for comprehending wave behavior in fluid dynamics, plasma physics, and optical fibers. The (n+1)-dgKPE solutions that are developed in this context serve as a crucial foundation for future study and applications in related domains and aid in our understanding and control of complicated dynamics in physical systems. Efficient approaches have been employed in several investigations to get analytic solutions, and the resulting outcomes have made significant contributions to both mathematics and physics. When the findings are displayed visually and are the subject of comparison analysis, these investigations are more thorough and accurate. Future studies could examine the various behaviors of these solutions and the effects of other parameters or approaches on the proposed model to discover novel phenomena.