Introduction

Tobacco is a significant cash crop in many countries, including China, India, Brazil, the United States, and Indonesia1,2,3. After removing moisture from the fresh tobacco leaves during the curing process, the leaves go through the threshing process, a key step in the post-harvest processing of tobacco, which involves separating the lamina from the stem of the tobacco leaf4,5. To obtain a qualified size of fragment of leaf lamina, and avoid the small or large ones, in recent years, substantial research and development efforts have been made to improve the technology of threshing. For instance, tobacco threshing parameters, such as temperature, feed flow, roll speed, were optimized by combining the Particle Swarm Optimization-Back Propagation (PSO-BP) neural network with the non-dominated sorting genetic algorithm-II (NSGA-II) algorithm6. This approach significantly improved the quality of post-threshing tobacco leaves, reducing the mean square error of the predictions and demonstrating the model’s accuracy. Those optimized threshing parameters can serve as a valuable reference for threshing process design. To address the challenging issue of a lower large slice rate compared to high and medium slice rates after tobacco leaf-threshing, the discrete element method has been utilized to configure different roller speeds for sharp diamond, hollow diamond, and diamond frame columns and to conduct numerical simulations on the cutting process7. The tobacco leaf model was established via the single distribution particle model and the leaf separation process was modelled via bonding contact model. Although the method demonstrates the potential to model the threshing process and the leaf was simplified as elastic material governed by Young’s modulus and Poisson’s ratio. However, the tobacco leaf was an anisotropic nonlinear material due to its complicated cellular microstructures and the properties of the phase constituents. Therefore, comprehending the mechanical behavior of the leaf tissue is essential for an effective design and optimization of the threshing technology.

Experimental studies have been conducted to characterize the mechanical properties of plant leaf or tissue and to investigate the factors that determine them. Henry et al.8 measured the stress-strain of 72 fire-cured tobacco leaves, including 3 parts of the leaves, 4 moisture contents, and 2 tensile loading rates. Wang et al.9 quantitated the ultimate strength of leaves and the hardness of leaf surface for seven spices via the universal testing machine and nanoidenter tester, respectively. Zhang et al.10 discovered that the effects of moisture content of leaf have a significant effect on the mechanical properties of tobacco leaves from Zimbabwe and four different regions in China. The moisture contents of leaves are prepared in a climate chamber. However, the experimental studies are usually time-consuming and cost-intensive and are highly sensitive to the availability of the seasonal plant, as well as the testing and storage environment, such as temperature and humidity. Meanwhile, the plant tissue, including the plant leaf, has a hierarchical cellular structure, which enables the distinct mechanical properties of plant tissue11,12,13,14. Therefore, it’s not possible to understand the underpinning mechanisms of deformation and failure of the plant tissue only through the experimental test at tissue scale.

To overcome the limitation of experimental test and better the understanding of mechanical behaviors of the plant tissue at different scales, Discrete Element Method (DEM) and Finite Element Method (FEM) have been utilized to simulate the mechanical behavior of plant tissue. DEM is a discontinuous-based numerical method proposed by Cundall and Strack15 for granular media. The method has been utilized to simulate the tensile behaviors of various heterogenous media, including plant fiber16, biological tissue17, fiber reinforced composites4,18. Recently, the method has been utilized to simulate the tensile test of tobacco leaf19. The method shows a good prediction on the tensile strength by choosing suitable parameters of the bonds. However, the method is not able to predict the nonlinear response of the plant tissue illustrated in the experimental test, due to the lack of consideration of the cellular hierarchical structures.

Micromechanics approaches play an important role in predicting the mechanical behaviors of biomaterials and bio-inspired materials through establishment of direct link between function and microstructure20,21,22. Specifically, they illuminate the importance of various deformation mechanisms contributing to the macroscopic response, thereby providing an economic and efficient virtual laboratory towards a better understanding of the biomaterials and a better support of material development23,24,25. Recently, finite element-based micromechanics has been adopted to simulate the macro response and local deformation of plant tissue by constructing a RVE model, which contains a representative multicellular material system. Faisal et al.11 constructed a Voronoi model based on 2-D Finite Edge Centroidal Voronoi tessellation algorithm and calculated the effective elastic properties of the cellular tissue. The Voronoi cell formulated with straight lines may be suitable to represent the cellular shape of petiole tissue, whose cellular shapes are relative regular with limited curvature. Pieczywek et al.12 developed a finite element model to simulate the nonlinear tensile test of onion tissue based on a real tissue geometry. However, in contrast with the leaf tissue, characterized by irregular wavy cell geometries forming jigsaw puzzle patterns14, the onion tissue cells are regular and arranged in a brick-mortar pattern. Similarly, Zamil et al.13 proposed a multiscale Finite Element Analysis (FEA) framework to study the tissue-scale mechanical properties of onion tissue. However, the RVE model was created based on an idealized tissue patch. The RVE model has only been utilized to study the effective mechanical properties of the onion tissue and the tissue nonlinear behavior and toughening mechanism have not been discussed in terms of the RVE model. To the best knowledge of the authors, there is no micromechanics model based on the real tissue geometries at cellular level, characterized by irregular wavy shapes, has been proposed for plant leaves and there is also a lack of quantitative prediction for the nonlinear behavior and understanding of the toughening mechanism.

Herein, for the first time, we developed a RVE model of the tobacco leaf based on the real cellular topology, characterized by distinct irregular wavy cells and a complicated mechanical wall network. Six tensile tests have been performed and the stress-strain response shows a distinct stiffening behavior. The proposed RVE model is able to produce a good agreement with the averaged tensile response under 25% strain loading. With the validated RVE model, the relation between tissue-level response and the cellular-level deformation has been examined and the corresponding toughening mechanism has been uncovered. Further, the RVE model has been applied to evaluate the effect of loading direction and investigate the underpinning deformation mechanism of the cellular network.

Material characterization

Mechanical characterization

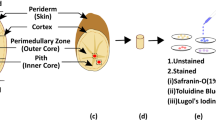
The tobacco leaves are grown in production area of Yuxi, Yunnan, China and provided by the by Zhejiang China Tobacco Company. During the pre-preparation stage in the factory, the tobacco leaves processing conditions are meticulously controlled to adhere to the standardized industrial production process. After the harvest of the tobacco leaves, the flesh tobacco leaves are flue-cured to create desired appearance and internal quality through imposition of appropriate temperature and humidity in the flue-curing barn26 and Fig. 1a is a typical flue-cured tobacco leaf with yellow color. As shown in Fig. 1a., the sampling position is located at quadrilateral area surrounded by the midrib and two parallel secondary veins in the middle position of the tobacco leaf, because this location has the largest area of leaf flesh that facilitates the leaf specimen cut. And the longer side of the sample edge is parallel with the secondary veins27. With respect to the quadrilateral area, the thickness of the leaf flesh is not uniform. The side close to the midrib is thicker than other areas and the side close to the leaf margin is thinner. Therefore, the cutting position is away from both midrib and leaf margin. During this study, six leaf specimen samples have been cut out with a rectangular cutter, as shown in Fig. 1b, from six pieces of leaves at the same location. When the cutting position closest to the midrib is 1.5 cm away and the size of regular cutter is 50 mm in length and 20 mm in width, the leaf sample can maintain a uniform thickness. Although the effects of vein distribution on leaf properties are beyond the scope of this paper, it’s worth to mention the major veins are much stiffer than the leaf flesh and impose a strong anisotropy towards the leaf tissue27.

The leaf samples were first dried and then were placed in temperature and humidity control chamber for 30 min. The final water content of the leaf specimen was 16%. The tensile testing was conducted via a Zwick/Roell Z020 universal material testing machine, as shown in Fig. 1c. During the test, the machine displays the force, displacement value, deformation value, loading speed, as well as testing curves in real time. Figure 2 illustrated the stress-strain responses of six tests, which are highly nonlinear and characterized by three distinctive phases. The loading was quasi-static with the speed of 5 mm/min. The first (A-B segment) and final phases (C-D segment) are characterized by linear responses, represented by initial Young’s modulus,\({E_1}\)and the secondary Young’s Modulus, \({E_2}\). The second phase between them is a transitional phase, which is characterized by a nonlinear hardening process (B-C segment). Meanwhile, the stress-strain test data possess a considerable variation due to the intrinsic variations of microstructures and material properties of cellular wall and protoplast12,14. Table 1 lists out the initial Young’s modulus and secondary Young’s modulus for the six tests. The initial Young’s modulus varies at the range of [1.29 2.21] MPa, its mean value is 1.66 MPa and its Standard Deviation (SD) is 0.296 MPa. The secondary Young’s modulus varies at the range of [2.85 5.39] MPa, its mean value is 3.88 MPa and its SD is 0.823 MPa. However, all six tests possess the same deformation trend, and the averaged stress-strain response was shown in Fig. 2.

Fig. 1
figure 1

Tensile test setup for tobacco leaf: (a) Digital photograph of the tobacco leaf; (b) Rectangular cutter; (c) Tensile test of tobacco leaf samples.

Full size image
Fig. 2
figure 2

Stress-strain responses of six tobacco leaf specimens.

Full size image
Table 1 Initial and secondary Young’s moduli of six leaf specimens.
Full size table

Microstructure characterization

To main intact cell structures of the biological specimens and avoid the usage of expensive and hazardous processing materials, a procedure proposed by Golinejad et al.28 to prepare plant cells for SEM analysis was adopted in this study. The water content of the flue-cured leaf samples was around 18%, obtained by measuring the weight difference before and after the drying process in a vacuum oven at 80 degrees for 12 h. The tobacco leaves were washed with dust free paper moistened with distilled water and then the sample was dehydrated through a series of ethanol (30%, 50%, 70%, 85%, 90% and 100%) for 15 min each step. The samples were then frozen at -80 °C and dried in a freeze-drying oven (SCIENTZ-12 N, Xinzhi Bio-Tech Co, Ningbo) for 12 h. The samples were adhered to the scanning electron microscope (SEM) sample columns with conductive adhesive, and the samples were sprayed with gold using a vacuum ion coater. Figure 3a and b shows the cellular structure of the plant leave and the enlarged image. Unlike the well-studied onion tissue with regular cellular shape, the epidermal tissues of tobacco leaves exhibit irregular, wavy cell shapes that create jigsaw puzzle-like patterns. The cross-sectional morphological characteristics of plant leaves were obtained using a scanning electron microscopy (SEM) (Phenom proX-SED, Phenom, Netherlands) operated at an acceleration voltage of 15 kV. The thickness of the leave is around 78\({\text{\varvec{\upmu}m}}\)and the total wall thickness of two bonded cells is around 2\({\text{\varvec{\upmu}m}}\), as shown in Fig. 3c and d, respectively.

Fig. 3
figure 3

Microstructure characterization of tobacco leaves: (a) SEM of epidermal tissues; (b) Cell shape with irregular and wavy pattern; (c) SEM of cross-section of the tobacco leave; (d) Enlargement of the SEM of cross-section of the tobacco leave.

Full size image

Cellular microstructures based RVE model of plant leaf

Finite element model of plant leaf with cellular microstructures

The RVE model includes the creation of the finite element model of the representative microstructure of tobacco leaves and the specification of periodic boundary conditions (PBC) and loadings. The finite element model was created based on the SEM image of tobacco leaves. The epidermal cells have an irregular and wavy cellular shape, and they are bonded together by middle lamella. Figure 4 shows the process to create the finite element of the microstructures of tobacco leave in Abaqus based on the SEM microstructure characterization images. As shown in Fig. 4b, the SEM image was utilized to generate cellular microstructure images of the tobacco leaf sample and the window size for the RVE model is \(167\upmu m \times 167\upmu m\) and it contains 16 plant cells. Drago and Pindera20 investigated the effects of inclusion number on homogenized properties and they showed that the maximal error of effective moduli is below 5% when the inclusion number is 16. In addition, the selected SEM image area for RVE model was equal to one-fourth of the entire SEM image. The SEM image for RVE has a good statistically representation towards the whole SEM image, since the difference between the averaged cell size in the RVE model and the averaged cell size of the whole SEM image is below 10%. Then, the SEM image was imported into SOLIDWORKS, and the corresponding cellular outline was carefully drawn out, as shown in Fig. 4c. However, the current CAD model does not qualify as a RVE because of the non-periodic positioning of cells next to the boundary29. The problem is overcome by slightly adjusting the cellular distributions around four boundary sides without altering its essential features. After adjustment, the cell walls along top and bottom sides connect and formulate intact cells. The similar treatment has been conducted for those cells at left and right sides of the RVE. The RVE with modified boundaries that satisfies the imposition of the periodic boundary conditions was shown in Fig. 4e, and was further discretized in HyperMesh via 2D triangular and quadrilateral element, as shown in Fig. 4f.

Fig. 4
figure 4

Process to generate finite element model of plant leaf microstructures based on SEM images: (a) tobacco leaf sample cutting; (b) SEM characterization of cellular microstructure and the selected area for RVE model; (c) The enlarged SEM image of RVE model (d) Cellular boundary identification in SOLIDWORKS; (e) CAD model of processed cellular structure; (f) Finite element model of tobacco leaf with detailed cellular structure.

Full size image

The discretization detail of a single cell and its cellular walls are carefully illustrated in Fig. 5. The red cell is connected to adjacent six cells, as shown in Fig. 5a and it possesses a highly irregular and wavy cellular walls, as shown in Fig. 5b. In general, the connection between cells could be divided into two types, as shown in Fig. 5c. Type I is the line connection that two cells are connected by a line formulated by two adjacent cell walls. Type II is the triangular connection, where multiple cells are bonded together.

Fig. 5
figure 5

Illustration of tobacco leaf RVE model: (a) Discretization detail of a single cell; (b) Triangular area of cell; (c) Connection types between cells.

Full size image

Imposition of PBC and macroscopic loading

Proper periodic boundary conditions must be applied to above RVE model to accurately capture the material’s response under different loading conditions. One direct method to impose periodic boundary conditions is using the “Constraint Equation” function in ABAQUS30,31, but this requires extensive manual work to create numerous constraint equations. Another more efficient way is to utilize an open-source ABAQUS CAE plug-in, EasyPBC32 or the Micromechanics Plugin for Abaqus/CAE developed by Dassault Systems33, which automates the imposition of six sets of periodic boundary conditions and the calculation of homogenized properties. Recently, those tools have been utilized to prepare RVE model for cellular materials with triply periodic conditions34,35. In addition, Tian and Qi36 proposed an algorithm to unified periodic boundary condition for homogenizing the thermo-mechanical properties of composites and this could benefit the development of future commercial finite element commercial software packages.

Figure 6 depicts the method of imposing boundary conditions in this paper. Equation (1) adopts the method of imposing periodic nodes in EasyPBC for 2D RVE models, which can be obtained directly by running the script. It consists of the following two sets of constraint Eq. 

$$\begin{gathered} {\text{ Equation 1:}}\left\{ \begin{gathered} U_{{Right}}^{1} - U_{{Left}}^{1}=U_{{RP4}}^{1}; \hfill \\ U_{{Right}}^{2} - U_{{Left}}^{2}=0; \hfill \\ \end{gathered} \right. \hfill \\ {\text{Equation 2: }}\left\{ \begin{gathered} U_{{Top}}^{1} - U_{{Bottom}}^{1}=0; \hfill \\ U_{{Top}}^{2} - U_{{Bottom}}^{2}=U_{{RP5}}^{2}; \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
(1)

Where Right-Left, and Top-Bottom correspond to the periodic nodes on the boundary of \(U_{{Right}}^{1}\) is the displacement of Right in the 1-direction. 1 and 2 represent the X-axis and Y-axis in the ABAQUS software, respectively.

In addition, in order to obtain the tensile stress-strain response of the RVE model corresponding to the experimental data, we adjusted the loading method of the above RVE model. For instance, with respects to unidirectional loading along X axis, displacement increment loading is applied in terms of RP4 (reference point) and the displacement associated with RP5 is set to zero. The similar setup is utilized for the unidirectional loading along Y axis. Finally, in the post-processing of the model, the resultant force can be extracted from the reference point and the stress-strain response can be obtained from Eq. (2).

$$\begin{gathered} \sigma {\text{=}}\frac{{{F^{\left( {{\text{RP}}} \right)}}}}{S}{\text{=}}\frac{{F_{{{\text{RT}}}}^{{\left( {{\text{RP}}} \right)}}}}{{W \times T}}; \hfill \\ \varepsilon {\text{=}}\frac{{{U^{RP}}}}{L} \hfill \\ \end{gathered}$$
(2)

where\(F_{{{\text{RT}}}}^{{\left( {{\text{RP}}} \right)}}\)is the resultant force and\({U^{RP}}\)is the applied displacement. W, L and T represent the width, length, and thickness of the RVE model. The default value of thickness is unit 1 for the 2D model.

Fig. 6
figure 6

PBC specification for unidirectional loading.

Full size image

Numerical results

Identification of cellular material properties

Besides the accurate characterization of the microstructures of tobacco leaf, the identification of mechanical properties of the cell wall and protoplast plays a critical role in determining the homogenized response of the RVE model, as well as the localized stress and strain response at cellular scale. Previous studies have demonstrated that the mechanical properties of different plant tissues vary. The elastic modulus of the cell wall varies between 75 and 150MPa37,38 and the turgor pressure, which determines the stiffness of protoplast varies between 0.1 and 0.4MPa38. In terms of nanoindentation tests and finite element simulation at cellular level, Forouzesh et al.38 proposed an indirect approach to decouple and measure cell wall properties and the turgor pressure effects. The poisson’s ratio of the cell wall and protoplast are 0.4913 and 0.3439, respectively. The stiff cell wall is modelled via isotropic elastic material model13. The elastic material properties range of cell wall are summarized in Table 2 and E and \(\nu\) represent the Young’s modulus and Poisson’s ration, respectively. The soft protoplast phase is modelled via a compressible neo-Hookean model, which was utilized to model a soft collagen bio-tissue undergoing unidirectional large deformation24. The knowledge of Young’s moduli range and Poisson’s ratio facilitate the calculation of the initial shear modulus range from the isotropic relationship \(\mu =E/2(1+\nu )\) and hence the bulk modulus range from \(\kappa =2\mu (1+\nu )/3(1 - 2\nu )\). \({c_1}\)and \({c_2}\) are the material parameters of generalized Mooney-Rivlin material with. By assuming \({c_2}=0\), the generalized Mooney-Rivlin material was reduced to a compressible neo-Hookean model.

Table 2 Material properties of cell wall and protoplast.
Full size table

Further, to determine the exact Young’s modulus of cell wall, \({E_{CW}}\) and protoplast, \({E_P}\), a parametric study has been conducted towards the cell wall and protoplast within the range of [75 150] MPa and [0.1 0.4] MPa, respectively. An error function, Eq. (3), has been utilized to evaluate the error between the homogenized response predicted by the RVE model and the experiment test24. To eliminate the test variation, the averaged test result is utilized, as shown in Fig. 3.

$$error({{\mathbf{x}}_i})=\frac{{\sum\limits_{{k=1}}^{N} {|{{\left( {{\sigma ^{RVE}}\left( {{{\mathbf{x}}_i}} \right)} \right)}_k} - {{\left( {\sigma _{{\exp }}^{{AVE}}} \right)}_k}|} }}{{\sum\limits_{{k=1}}^{N} {{{\left( {\sigma _{{\exp }}^{{AVE}}} \right)}_k}} }}$$
(3)

Where \({{\mathbf{x}}_i}\) contains variables of \({E_{CW}}\) and \({E_P}\), \({\sigma ^{RVE}}\) represents the homogenized stress along the unidirectional loading direction, \(\sigma _{{\exp }}^{{AVE}}\) represents the averaged stress of six experimental test, and k represents the number of data points along the stress-strain curve.

Figure 7a illustrates the error variation as a function of the cell wall’s modulus and protoplast’s modulus in terms of MATLAB40. The minimum error is 0.123, equivalent to 12.3%. The corresponding cell wall’s modulus and protoplast’s modulus are identified, and their value are 135 MPa and 0.1 MPa, respectively. Further, Fig. 7b shows the comparison of stress-strain response between the RVE’s prediction with above identified material properties and averaged experimental test. In general, the RVE’s prediction has a very good agreement with the testing data, particularly for the initial elastic stage, A-B segment and the nonlinear hardening stage, B-C segment. During the second elastic stage, the RVE’s prediction is slightly more compliant than the experimental test. In contrast, without identified material properties, the homogenized response could be much stiffer or more compliant than the experimental test data, as illustrated in Fig. 7b.

Fig. 7
figure 7

Parametric study of Young’s modulus of cell wall and protoplast on the homogenized responses of tobacco leaf: (a) The effect of Young’s modulus of cell wall and protoplast on the homogenized response error relative to the averaged experimental data; (b) Comparison of simulation and experimental averages.

Full size image

Microstructure deformation under monotonic loading

Figure 8 illustrates the von Mises stress evolution inside the cellular RVE at different strain level for the homogenized response based on the identified material properties at cellular level (Fig. 7b). As expected, the stress is mainly distributed along the network formulated by the connected cellular walls due to their high stiffness. During the initial elastic stage, A-B segment in Fig. 7b, most of the cells can extend equally and the stress is distributed relatively evenly along the cellular walls, except those triangular areas connecting different cells, as shown in Fig. 8a. As the increase of stretching, the major loading paths begin to formulate. As shown in Fig. 8, when the loading strain reaches 8% (Fig. 7b), two dominant loading paths, path 1 and 2, have been established. In contrast with loading path 1 and 2, other loading paths, such as loading path 3, are wavier and more prone to unfold. Further, comparing with loading path 1, loading path 2 formulates later because of its less severe waviness.

During the second stage, individual cells inside the RVE have the trend to extend along the loading direction and shrink along the transverse direction. However, their deformations are not uniform due to their shape irregularities. Therefore, the nonlinear response has been induced, as well as the wavy deformation of four RVE boundaries. When the loading strain reaches 18% (Fig. 7b), the homogenized response enters the third stage, and the response becomes linear again. The corresponding Young’s modulus, \({E_2}\), increases to 2.65 MPa from 1.67 MPa, that is the initial Young’s modulus, \({E_1}\). During the third stage, a new loading path, path 3, just below the loading path 1, appears and the stress along other cellular walls maintains without a significant increase.

Fig. 8
figure 8

Von Mises stress evolution of RVE under 25% along x directional tensile loading.

Full size image

Loading direction effects

Figure 9 shows the homogenized stress-strain responses of RVE under monotonic loading along x direction, parallel to the secondary veins and along y direction, perpendicular to the secondary veins, respectively. With respects to the magnitude of the homogenized stress-strain response, the homogenized response under unidirectional loading along y direction shows a significant difference with the response under the loading along x direction, as shown in Fig. 9a. However, when the tensile strain was increased to 40%, the deformation characteristics, shown in Fig. 9b are aligned with the response of the RVE under x directional tensile loading. During the small loading range between 2% and 10%, the stress-strain response is linear with Young’s modulus, \({E_1}\) of 0.33 MPa, followed by a nonlinear transitional stage between 10% and 35% loading strain. When the loading strain reaches 35%, the stress-stain response becomes linear again and possesses a stiffer response with Young’s modulus, \({E_2}\) of 0.52 MPa.

Fig. 9
figure 9

(a) Homogenized stress-strain response under 25% monotonic unidirectional loading under x and y direction, respectively; (b) Homogenized stress-strain response under 40% y directional tensile loading.

Full size image

The anisotropic behaviors of the leaf flesh originate from the cellular arrangement. Figure 10 illustrates the von Mises distributions under different loading levels. Similar with the stress distribution pattern, the stress is primary distributed along the cellular walls. However, the stress magnitude is significantly smaller than previous case under uniaxial tensile loading along x direction. Because the connected cellular walls are much wavier along y direction, and this offers a higher extensivity along y direction. When the loading level is small, that is below 4%, as shown in Fig. 10a, the stress distribution is relatively even, except for the triangular connecting area. As the applied strain increased to 8%, two major loading paths, path 1 and 2 appear, as shown in Fig. 10c. As shown in Fig. 10d-e, the loading path 1 and 2 not only straighten out, but also rotate along y direction. For instance, the inclined angle of the loading path 2 is 18 degree under applied strain of 10%. When the applied strain increases, the inclined angle also decrease. When the applied strain reaches 35%, the beginning of stiffening stage, the inclined angle reaches 10 degrees and maintains the inclined angle.

Fig. 10
figure 10

Von Mises stress evolution of RVE under 40% along y directional tensile loading.

Full size image

Conclusions

In this paper, the cellular microstructure of tobacco leaf has been characterized via SEM and the corresponding mechanical behaviors under uniaxial tensile loading parallel to the secondary vein have been calibrated. In terms of the SEM images of the cellular microstructures, a finite element based RVE model was created, consisting of the stiff phase, cellular walls and the soft phase, protoplast. The unknown Young’s modulus of cellular walls and protoplast were backed out by minimizing the difference between the averaged experimental tensile test response and the prediction via the RVE model.

Further, the relationship between the homogenized response and the microstructure deformation have been studied in detail for both the uniaxial tensile loading parallel to the secondary vein and perpendicular to the secondary vein, respectively. In general, the homogenized response can be divided into three stages: the initial linear response, followed by a nonlinear transitional phase, and then followed by a linear stiffening response. During the first stage of linear behavior, the von Mises stress distribution inside the cellular network is relatively even. At the second stage, as the increase of the applied strain, the cellular network was gradually straightened out and major loading paths formulated along the connected cellular walls with less wavy shape. At the third stage, the major loading paths were fully extended and RVE response become linear again, but with a stiffer response. In addition, the homogenized response of the RVE model has a strong directional effect, due to the significant variation of the waviness of the connected cellular walls at different directions, which directly impact the extensibility of the tobacco leaf. The unique biomaterial hardening mechanism has been closely related with the cellular level deformation. Those findings could offer insights to make high performance bio-inspired material through microstructure design.