Quaternion generative adversarial -driven Soc estimation using Tyrannosaurus optimizer for improving hybrid electric vehicles renewably powered energy management

Abstract

The change in transportation efficiency in the last several years has seen several new engine technologies like EVs and HEVs being more prevalent. Integration of RES wind energy technique, solar photovoltaics, and bio-energies becomes a requirement during the transition from conventional houses to smart houses and from conventional cars for energy efficient electric or hybrid vehicles. The battery of an HEV can only be charged to a certain level and similarly it should not be discharged beyond a certain limit, hence the battery state of charge (SOC) in HEVs has to be supervised by a smart battery management system (BMS). However, the current method requires improvement of the performance of SOC estimate on HEVs. Therefore, development of new SOC estimation method with DL for safe renewable energy management (REM) framework for Hybrid EV (Electric vehicles) is the prime focus of this paper is developed as DLSOC-REM. For more accurate SOC estimate, the proposed approach employs a Quaternion Generative Adversarial Network (QGAN) model. When hyper parameter tuning, the prototype is invigorated employing the Tyrannosaurus optimization algorithm (TOA) to fine-tune SOC estimate outcomes of the QGAN model. Using the QGAN model simplifies the modeling process and gives a correct representation of the battery model’s input–output relationship. The work’s originality is demonstrated by the design of the TOA-based QGAN model for SOC estimation. The suggested approach shows excellent accuracy with few errors for various drive cycles and temperatures: for US06, the RMSE stabilizes at about 0.05%, the MAE drops to 0.1%, and the MSE reaches 0.0025%.

Introduction

Ecological deterioration and energy scarcity have recently gained international attention, especially as vehicle engineering requirements have gotten more stringent¹. Few new energy cars, such as EVs and hybrid EVs (HEVs) have been proposed to take the role of conventional gasoline-powered automobiles in order to lower waste gas emissions and conserve energy when driving². Currently, the HEV has the advantages of more speed and high-distance travel over EVs, making it a highly viable alternative propulsion system³. HEVs’ efficient BMS plays a key role in increasing driving range, lowering costs, prolonging life of battery, and improving vehicle safety⁴. Numerous BMSs are installed for problem diagnostics, equalization management, etc.⁵. Finding the current, voltage, and temperature signals is one of the sampling circuit’s primary functions. The control circuit then uses the signals to estimate the batteries’ state of health (SOH), SOC, state of life (SOL), and state of power (SOP)⁶. In the meantime, the vehicle controller manages the circuits and ensures that the energy and power distribution of the car is managed⁷. A conventional fuel car’s fuel meter is analogous to the SOC of the batteries in a BMS. Connecting the driver to the battery’s natural state and avoiding problems like overcharging and over discharging are the main functions of the SOC⁸.

There are three primary methods for determining the SOC approximation of Li-ion batteries: traditional, model-based, and machine learning (ML). Although they are less complicated, the classical models are not appropriate for online use⁹. Additionally, the method-based techniques are quite effective at accurately simulating the properties of Li-ion batteries. They struggle, nonetheless, to create a useful model for estimating the SOC of Li-ion batteries¹⁰. As an alternative, ML-based SOC estimation method employ an abundance of data and powerful processors to estimate the SOC with little prior knowledge about the intriguing aspects of the battery and chemical reaction¹¹. However, both the volume and quality of the training data have a major impact on how effective ML models are. For efficient SOC estimate, on the other hand, recently created deep learning (DL) models can be applied¹². An LSTM model for SOC estimation, the observed voltage, current, and temperature are instantly sent to the derived network that learns the mapping between the input time series and the target SOC¹³. Similarly, the gated recurrent neural network and LSTM are used for SOC estimation. The LSTM’s prediction results are smoothed using an unscented Kalman filter (UKF). These studies have provided accurate SOC estimates for a range of dynamic profiles, like the Federal Urban Driving Schedule (FUDS), the US06 test, and the dynamic stress test (DST). However, because they vary by locale, driver, and duration, the batteries’ actual EV driving profile differs from the typical dynamic profile.

Previous research on energy management in hybrid electric vehicles (HEVs) that utilize renewable energy sources has made notable advancements, yet it has also encountered several challenges. One major issue is the failure to account for the variability and intermittency of renewable energy sources like solar and wind. Many studies operate under the assumption of ideal conditions, neglecting the real-world difficulties posed by fluctuating energy availability. Moreover, current energy management strategies often do not fully incorporate advanced optimization techniques, which can result in less effective performance when it comes to balancing power demands and energy storage. Another challenge is the insufficient integration of various energy storage systems, such as batteries and supercapacitors, which could improve system efficiency but are often not fully utilized. Additionally, many strategies focus on short-term benefits without considering the long-term sustainability of energy resources. The ability to scale these methods to fit different vehicle models and driving conditions also presents a challenge, which limits their practical use^14,15. The novelty and contributions of this work are given below,

• The proposed method is introduced to enhance the accuracy of SOC estimation in HEVs by integrating deep learning techniques with REM, addressing key challenges in energy storage and distribution.

• QGAN model leverages quaternion mathematics to increase the accuracy and robustness of renewable energy management systems, focusing on precise SOC estimation in HEVs by handling multidimensional data and complex interactions in energy systems.

• TOA fine-tunes the hyperparameters of the QGAN model, enhancing its predictive capabilities by ensuring optimal configuration, leading to better SOC estimation and overall system performance in managing renewable energy in HEVs.

• The proposed technique is tested across various driving cycles like BJDST, FUDS, US06 to assess its reliability and accuracy in real-world conditions, evaluating performance metrics like MSE, RMSE, MAE, and MAPE to ensure robust SOC estimation.

Some of the recent papers related to this work are described below,

In 2022, Maheshwari, A, and Nageswari, S¹⁶ proposed Sunflower Optimization technique (SFO) to find the best noise covariance matrices prior to SOC estimation where EKF is applied for online SOC estimation. As the iterative SFO is only run once, the AIC’s instantaneous response is not impacted by EKF. Compared with various versions of adaptive extended Kalman filters, genetic algorithms and trial–error techniques, the indexes of the algorithm are low. Regardless of the quality of the initial SOC it quickly corrects itself to the right value. Proof of concept and enhanced performance is established through SFO-EKF algorithm through qualitative and quantitative results on five challenging datasets which includes constant current discharge and high drive cycle situations in a pressure sensor. Simulation results also reveal that for both static and dynamic operating conditions, estimations of SOC could better approximate and produce a higher rate of convergence.

In 2023, Zafar, M.H. et al.¹⁷ designed a hybrid multi-layer deep neural network (HMDNN) approach for SoC approximation for electric cars (EVs). The technique utilizes the relationship between SoC and the voltage/current of the EV battery for training with the Mountain Gazelle Optimizer MGO algorithm. Samples of real data of EV charging are introduced to evaluate the methodology, and comparison to the standard methods is made. An analysis of the technique yields an average of 0.1% NMSE and 0.3% RMSE using a total of four Li-ion battery datasets. The results prove that the suggested method can quickly and almost without any error approach a more efficient course of operation as a means of increasing battery life.

In 2022, Vasanthkumar, P et al.¹⁸ proposed an advanced edition of the WFO for IoT-based HEVs through deep learning. The BMS presented here adopts the ABiGRU technique for SOC estimation in HEVs with high accuracy. IHymo algorithm is employed for optimizing hyperparameters so that ABiGRU technique’s SOC estimate performance will be enhanced. It has also been found that the input is better represented and simpler when the ABiGRU model is used. The author conducted a comprehensive simulation result and shown how the proposed IWHODL-BMS model was optimal to the other approaches on several aspects.

In 2024, Zafar, M.H, et al.¹⁹ presented a new architecture that improves state of charge (SoC) estimate performance: the new named Fusion-Fission Optimization (FuFi based) Convolutional Neural Network with Bi-Long Short Term Memory Network as FuFi-CNN-Bi-LSTM. FuFi optimization is applied to tune hyperparameters and CNN-Bi-LSTM is engulded in the model. The effectiveness and the shortcomings of several models described by the FuFi Algorithm is analyzed comparatively. The ability of the model to accurately predict SoC under different temperatures is established by subjecting the model to real operational settings as well as drive cycle tests.

In 2023, Varatharajalu, K, et al.²⁰ proposed hybrid War Strategy Optimization algorithm along with the WSO-HDLNN to find out the dynamic electrical characteristic of battery pressurized by physical force. To minimize battery voltage inaccuracy, the technology integrates the WSO-HDLNN technique. The technique determines the battery’s characteristics and forecasts how the battery will react to deformation using the WSO-HDLNN. By lowering estimated and measured voltage errors, the technique efficiently determines parameters. With a time of 0.7 s and reduced computing time and error than current approaches, the method works better than existing methods. The simulation results show the efficiency of the method.

In 2022, Cui, Z, et al.²¹ suggested a CNN-BWGRU network hybrid approach to maximize battery information influence. The technique learns feature parameters using a bidirectional network and a multi-moment input structure. While the BWGRU enhances fitting performance at low temperatures, the CNN gains knowledge from the input. The suggested network exhibits robustness, estimation accuracy, and good generalization capabilities. Compared to other networks, experimental results demonstrate greater accuracy and stability, as well as the capacity to overcome initial SOC effects. The CNN-BWGRU network gives recommendations for stable and safe battery operation in natural settings as well as a novel approach to battery SOC calculation.

In 2024, Hong, J, et al.²² used a hybrid LSTM and gate recurrent unit (LSTM-GRU) neural network to forecast real-world automotive battery systems. The study employs a similarity metric method to decrease parameter dimensionality and examines correlation analysis properties. Experimental and real-world vehicle data are used to compare the benefits of LSTM-GRU, LSTM, GRU, and LSTM-CNN. By including noise data in the input variables, the resilience of the method is confirmed, and its accuracy and efficacy are illustrated. The findings, which had a minimal MAPE and MAE of 1.03% and 0.73 for summer conditions and 0.06% for experimental settings, were confirmed using actual vehicle data collected in the spring, summer, fall, and winter.

In 2022, Hamida, M.A., et al.²³ presented the artificial hummingbird optimization technique (AHOT), which is intended to identify unknown parameters of Li-Ion batteries used in EV. The unique flying abilities and foraging techniques of hummingbirds in the wild are replicated by the AHOT, such as axial, diagonal, omnidirectional, directed, territorial, and migrant foraging methods. The standard deviation error and objective function on the dynamic Li-Ion battery model are used to validate the method. The results are compared also with other methods and experimental uses of the ARTEMIS driving cycle pattern and 40 Ah Kokam Li-Ion batteries. Nonetheless, the AHOT gets the lowest the worst-case objective basis of 0.004467 than other techniques for the ARTEMIS cycle.

Comparisons of different methods for SoC are listed in Table 1, where the merits and demerits of each of them are also indicated. It is actually seen that the SFO-EKF, HMDNN, FuFi-CNN-Bi-LSTM are accurate and efficient approaches but there are still some issues such as pre-estimations, data demands, or overlearning. AHOT and LSTM-GRU methods are demonstrated as good at adaptation but they may face certain difficulties if some conditions are met or tend to over fitting.

Table 1 Comparison of the existing approaches.

Approximating the SOC in HEV is a cumbersome and important operation for the efficient and immediate battery efficiency and life expectancy. For renewable energy power substation. Prior techniques like conventional regression techniques and basic artificial neural networks have their own drawbacks like high calculating burden, dependency upon huge set of data, and organizational sophistication not to mention the fact that they becoming obsolete in view of present day dynamic environment. These methods often do not incorporate change in different environmental conditions and hence they lead to wrong SoC estimation. Moreover, most methods do not allow online usage or are burdened with prescreening, thus having scalability issues in realistic situations.

This manuscript is organized as follows: The the suggested technique is described in Sect “Proposed estimation model”, the results and discussion are presented in Sect “Result and discussion”, and future work is concluded in Sect “Conclusion”.

Proposed estimation model

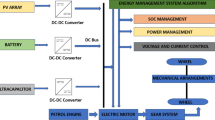
In present, there lies a need for accurate estimation of SOC primarily to enhance the energy management in HEVs. DL based a proposed SOC estimation model called as the Renewable energy management SOC estimation model based on a hybrid technique^26,27,28. Two major parts of the model include a QGAN for SOC prediction and TOA for hyperparameters tuning and improving prediction accuracy.

The Fig. 1 portrays, a QGAN for SOC estimation in HEV. It employs voltage data, current data and temperature data gathered from the vehicle. In this paper, the estimated SOC is obtained through the least-squares method for the difference between real and modeled voltage, and with the TOA for adjusting the parameters.

Fig. 1

(a) Overall structure of the proposed model (b) Schematic process.

Detailed dissection of the suggested model

This section discusses the creation of a new method for estimating state of charge (SOC) using deep learning (DL) within a safe Renewable Energy Management (REM) framework designed for Hybrid Electric Vehicles (HEVs), referred to as DLSOC-REM. To enhance the accuracy and reliability of SOC estimates, the framework utilizes a QGAN model. The QGAN effectively captures the complex relationships between inputs and outputs of the battery model, making the modeling process simpler and improving estimation accuracy. To further enhance the SOC estimation results, the model incorporates the TOA for hyperparameter tuning. TOA boosts the QGAN’s performance by optimizing its parameters, which in turn increases the robustness and precision of SOC predictions. This method ensures a well-adjusted model that can adapt to various battery types and operating conditions. The uniqueness of this work lies in the combined use of the QGAN model with TOA, offering an innovative solution for precise and efficient SOC estimation in renewable energy-driven HEVs.

Defining model inputs and outputs

Taking into account the requirements of the neural network, it can be noted that such inputs and outputs of the model are distinguished. The battery’s current condition is represented by the SOC measurement at a discrete time step $S$, which is an input to the model and is written as $SOC(s)$. SOC is affected by variables that have a non-linear relationship with SOC, like as the battery’s terminal voltage and current drawn^28,29.

Current and voltage as model variables

One of the key inputs is the current’s direct parameter $I(s)$. The model’s output is defined as the battery terminal voltage at step $S$,$V(s)$. The voltage at the previous time step $V(s - 1)$ is also given as an input to record the historical data. By taking into account former conditions, this prior voltage enhances the accuracy of the model by offering insight into the battery’s previous operational status.

Defining terminal voltage at current step $V(s)$

The following represents the terminal voltage $V(s)$ at time step $S$ is given in Eq. (1).

$$V(k) = OCV(SOC(s)) + R_{b} I(s) + U_{RC} (s)$$

(1)

where, $OCV(SOC(s))$ indicates the open-circuit voltage, a process of SOC, $R_{b}$ denotes the internal resistance of battery, and $U_{RC} (s)$ signifies the voltage associated with the RC circuit of the battery, which depends on $U_{RC} (s - 1)$.

Direct measurement of variables

The RC circuit voltage at the previous stage $U_{RC} (s - 1)$, is merged into $V(s - 1)$ in order to directly measure the model inputs. Because $V(s - 1)$ closely correlates with $V(s)$, the dependence structure is made simpler and the learning model is able to create a function that connects the input variables to the output voltage.

Synthesized function for terminal voltage

The function $f$, which connects the current inputs, is used to express the terminal voltage at time step $S$ is given in Eq. (2)^30,31.

$$V(s) = f(V(s - 1),I(s),SOC(s))$$

(2)

The QGAN learning model approximates this function $f$ and is subsequently trained to accurately predict $V(s)$.

Defining input and output vectors

The input and output vectors are defined in a systematic manner by the battery model. At time step $S$, the input vector is given in Eq. (3)³².

$$p(s) = [V(s - 1)I\,SOC(s)]^{T}$$

(3)

where the output at time $S$ is the terminal voltage $V(s)$, and $T$ denotes the transposition.

Formulating the functional mapping

The model’s functional mapping can then be shown as follows in Eq. (4).

$$F(p(s)) = V(s)$$

(4)

And the input vector $p(s)$ is mapped to the terminal voltage $V(s)$ by the function F.

Model training process

Prior to training, the input–output pairings $\{ p(s)\sim V(s)\}$ are generated and gathered. The training set can be defined as follows if denote each input $p(s)$ as $x_{j}$ and each output $V(s)$ as $t_{j}$ is given in Eq. (5).

$$\{ (x_{j} ,t_{j} )|x_{j} \in R^{n} ,t_{j} \in R^{m} ,j = 1,.....,N\}$$

(5)

where, there are $N$ total training examples, and $x_{j}$ is an n-dimensional input vector and $t_{j}$ is an m-dimensional output vector. In the REM-SOCQGAN model, where the QGAN predicts SOC and the TOA adjusts the model’s hyperparameters for maximum accuracy, this dataset structure is essential for efficient training and SOC prediction.

QGAN based estimation of SOC

The Quaternion Generative Adversarial Network (QGAN) and the Tyrannosaurus Optimization Algorithm (TOA) present notable benefits over traditional methods for predicting the State of Charge (SOC) in hybrid electric vehicles. QGAN is particularly effective at modeling the intricate, multidimensional relationships between input and output variables, thanks to its capability to process quaternion-valued data. This results in a more precise and thorough depiction of battery dynamics, simplifying the modeling process and improving the reliability of SOC predictions compared to standard neural networks. Meanwhile, TOA enhances performance by effectively fine-tuning the hyperparameters of QGAN, leading to optimized SOC estimation across different operating conditions. In contrast to typical optimization algorithms, TOA offers faster convergence, avoids getting stuck in local minima, and adapts well to high-dimensional, nonlinear optimization challenges, which are prevalent in energy management. The integration of QGAN and TOA boosts prediction accuracy, computational efficiency, and adaptability, positioning them as a state-of-the-art solution for SOC estimation in hybrid electric vehicles powered by renewable energy. In order to effectively manage renewable energy resources inside their EMS, HEVs must have their SOC estimated. Accurately forecasting the battery’s power availability under changing operating and load conditions is difficult. Figure 2 give the representation of a QGAN.

Fig. 2

Representation of a quaternion generative adversarial network.

Because of their limited adaptability to dynamic battery conditions, noise sensitivity, and simplified battery models, traditional SoC estimate techniques which rely on electrochemical data-driven approaches or simplified battery models frequently struggle with real-time accuracy. Use a Quaternion Generative Adversarial Network (QGAN), which optimizes the representation and processing of SoC-related data by fusing the power of quaternions with generative adversarial models, to overcome these constraints.

Quaternion deconvolution for SoC feature extraction

The Quaternion generative adversarial network (QGAN) is a sophisticated machine learning model that efficiently processes and models multidimensional data using quaternion algebra. Unlike traditional GANs that work with real numbers, QGANs utilize quaternions—hypercomplex numbers with four components—to more naturally handle multi-channel inputs, such as spatial–temporal data. This approach allows the model to capture intricate relationships between features while minimizing computational demands. In a QGAN, the generator creates data that mimics real samples, while the discriminator differentiates between real and synthetic data. The design of QGAN promotes quicker convergence, improved feature representation, and less parameterization, making it particularly suitable for applications like battery state of charge (SOC) estimation and signal processing. To train the QGAN-TOA model effectively, it is crucial to have a diverse dataset that encompasses various driving cycles, battery states, temperatures, and charging/discharging scenarios. Generally, tens of thousands of samples are necessary to achieve precise SOC estimation, with the exact data volume depending on the model’s complexity and the variability of driving conditions. Quaternion deconvolution is used in this QGAN model to extract multi-dimensional SoC features, which improves battery data representation and processing. Here, quaternion deconvolution is modified to handle data encoded in quaternion structures from several sensor sources, including temperature, voltage, and current. Assume that the quaternion vector output represented by $O \in Q^{m}$, is the SoC estimate. It is obtained from input data, $I \in Q^{n}$, and a sparse quaternion matrix $K \in Q^{m}$, which includes the kernel’s convolution components. One way to express the forward propagation of SoC estimate is as follows in Eq. (6).

$$O = \hat{R}\,I$$

(6)

If the backpropagation is applicable and $\hat{R}$ is a quaternion rotation matrix with scaled components is given in Eq. (7).

$$\frac{\partial loss}{{\partial I}} = \hat{R}^{T} \frac{\partial loss}{{\partial O}}$$

(7)

Given the extremely dynamic environment of the HEV, quaternion convolution is essential for capturing the spatial–temporal correlation in SoC data and minimizing potential model over fitting through implicit regularization.

Quaternion batch normalization (QBN) for stability

By standardizing quaternion data across all layers, quaternion batch normalization (QBN) minimizes the internal covariance shift (ICS) that might happen in quaternion space and stabilizes the SoC estimation procedure. QBN normalizes each quaternion input $I_{k}$ as follows in Eq. (8).

$$\hat{I}_{k} = \frac{{I_{k} - E[I_{k} ]}}{{\sqrt {Var[I_{k} ] + \in } }}$$

(8)

In which, $Var[I_{k} ]$ and $E[I_{k} ]$ denotes the variance and mean for each dimension. The expressive power is then preserved by a linear transformation in Eq. (9).

$$O_{k} = \lambda_{k} \hat{I}_{k} + \beta_{k}$$

(9)

where, $\beta_{k}$ is the quaternion bias and $\lambda_{k}$ is a real scaling factor. This allows for real-time data fluctuations, improving the accuracy of the SOC estimation.

QGAN for SoC prediction

A quaternion-based generator in the QGAN model creates realistic SoC estimates, and the discriminator helps to refine the generator’s output by separating real from synthetic SoC data. The loss function is minimized by the generator in Eq. (10).

$$_{\,\,G\,\,\,\,\,\,\,\,D}^{\min \,\,\,\max } \,V(G,D) = E_{{I\sim p_{data} }} [\log (D(I))] + E_{{z\sim p_{z} }} [\log (1 - D(G(z)))]$$

(10)

The QGAN generator uses quaternion convolution to maximize SoC prediction, and all of its elements have quaternion values. Because it preserves rotational invariance and takes into consideration the multidimensional nature of SoC-related data, this quaternion-based method is more reliable than scalar GANs.

Loss function for SoC optimization

By maintaining uncorrupted, crucial data regions, the QGAN uses a quaternion context loss $Loss_{c}$ to guarantee correct SoC estimations is given in Eq. (11).

$$Loss_{c} (z|O,M) = ||M.G(z) - M.O||_{1}$$

(11)

where, $M$ is a quaternion matrix mask that represents the availability of data. Sensitivity to crucial SoC data is increased by a weighted term $W$, which accounts for the significance of nearby data points is given in Eq. (12).

$$Loss_{c} (z) = ||W.(G(z) - O)||_{1}$$

(12)

Lastly, by striking a balance between precisely learnt data and the synthesized SoC output, a quaternion priori loss $Loss_{p} (z)$ aids the generator in producing realistic SoC estimates is given in Eq. (13).

$$Loss_{p} (z) = \gamma \log (1 - D(G(z)))$$

(13)

where,$\gamma$ optimizes SoC estimate by balancing the context and past losses.

Through these procedures, quaternion generative adversarial network (QGAN) gives a complex and precise SoC estimation method for HEV renewable energy controlling systems. Using quaternion deconvolution, batch normalization, and well-defined loss function, a high level of prediction accuracy with the improved robustness and adaptability to dynamic SoC estimation problem, QGAN presents itself as the potential solution to the traditional problems.

Parameters tuning using TOA

In order to introduce the TOA for improving the estimation of SOC in HEVs, envisage that the use of such behaviour of T-Rex to adjust weight, bias and loss function of a Quaternion Generative Adversarial Network (QGAN). Based on the simulation of the predator–prey relationship, the algorithm developed in this paper can be used to support enhancing the HEV systems such as the renewable energy management application, and the parameter tuning of complicated models like QGANs.

Inspiration for the TOA in SoC estimation

The strategy of optimization is borrowed from the fact of T-Rex’s role of both scavenger and the predator of top rank. The search and convergence mechanism of the algorithm is reflected by the T-Rex white pattern, which switches between charging and randomly wandering. Thanks to the population-oriented approach, TOA is able to predict person’s selection (exploitation) and search (exploration).

• Apex predator (exploitation): Similar to how TOA takes advantage of the best-performing solutions (weights and biases) during the optimization process, the T-Rex tracks and captures prey using its powerful hunting skills.

• Scavenger (exploration): When there is no prey, the T-Rex scavenges and searches new areas for potential prey. This feature is similar to TOA’s exploration phase, in which local minima are escaped by random searches.

Mathematical model of TOA

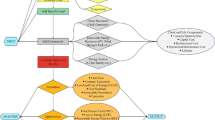
Step 1: initialization (Prey location/parameter initialization).

The prey’s starting locations are chosen at random from a predetermined search space. These “prey locations” in the context of QGAN are the model’s weights and biases, which are initialized at random within a higher and lower bound. For each prey (i.e., a possible solution in the search space), let $T_{i}$ represent the starting parameter set is given in Eq. (14).

$$T_{i} = rand(NP,\dim ) \times (Ub - Lb) + Lb$$

(14)

where, the prey’s position, or the weight/bias of the QGAN model at iteration $i$, is denoted by $T_{i}$, the number of populations, or individual solutions, is denoted by $NP$. The number of dimensions (for each weight and bias parameter) is denoted by $\dim$, and the lower and upper boundaries of the weight and bias values are denoted by $Lb$ and $Ub$.This initialization guarantees a broad search throughout the QGAN model’s parameter space in order to identify the best solutions for SoC estimation.

Step 2: Hunting and chasing (parameter update—exploitation phase).

The T-Rex uses a pursuit technique to find its prey (the ideal weight/bias) during the hunting phase. Similar to this, TOA updates the prey placements (weights and biases) by assessing the current solution’s fitness and shifting the positions in the direction of the most promising areas. If the T-Rex is successful in hunting the prey (i.e., the optimization is successful), let $T_{new}$ represent the revised location (new weights and biases) is given in Eq. (15).

$$T_{new} = \left\{ \begin{gathered} t_{new} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,rand() < E_{r} \hfill \\ Random\,\,\,\,\,\,\,otherwise \hfill \\ \end{gathered} \right.$$

(15)

where, the likelihood of successfully reaching the prey, denoted by $E_{r}$, is determined by the fitness function. The updated position, denoted by $t_{new}$, is determined by the hunting formula is given in Eq. (16).

$$t_{new} = t + rand() \times s_{r} \times (x_{pos} \times x_{r} - t\arg et \times p_{r} )$$

(16)

where, $t$ is the prey’s current location (weight/bias).The T-Rex is in position $x_{pos}$. The algorithm converges at a pace denoted by $x_{r}$, which represents the T-Rex’s running rate. The hunting success rate $s_{r}$, affects how much the position shifts. The prey’s running speed, represented by $p_{r}$ is a metaphor for the pace at which the weight or bias changes. In this stage, the algorithm adjusts the parameters in order to move them in the direction of a better solution based on the fitness value of the weights and biases.

Step 3: selection (exploitation phase—choosing the best weights and biases).

Following the hunting phase, the selection phase uses the fitness value to decide whether to accept or reject the new prey position. Let the fitness function (such as the loss function for the QGAN model be represented by $f(T)$. The following is the selection procedure is given in Eq. (17).

$$T_{k + 1} = \left\{ \begin{gathered} if\,f(T) < f(T_{ne} )\,\,\,\,\,\,\,update\,t\arg et\,position\, \hfill \\ Otherwise\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t\arg et\,is\,zero \hfill \\ \end{gathered} \right.$$

(17)

where, the fitness function assessed at the present position (current weights and biases) is denoted by $f(T)$.The fitness function assessed at the new position (with updated weights and biases) is denoted by $f(T_{new} )$.The prey (weights and biases) is updated if the new position provides a better solution (i.e., reduced loss); if not, the prey stays at the old location.

In this case, the loss function utilized in QGAN for SoC estimate is the fitness function $f(T)$. In order to get the estimated SoC of the HEV as near to the actual amount as possible, the QGAN model’s loss (or accuracy) must be minimized. The step by step procedure of TOA is given in Fig. 3.

Fig. 3

Step by step process of TOA.

By following these optimization procedures, TOA assists in optimizing the settings of the QGAN, guaranteeing precise SoC estimation for HEVs, which results in improved battery life and effective energy management. In the optimization process, the balance between exploration and exploitation is symbolized by the hunting and scavenging behavior of Tyrannosaurus Rex.

Result and discussion

The outputs and discussion of the introduced scheme is described in this section. To validate the effectiveness of the proposed QGAN-TOA based SoC estimation model, tests were conducted using standard drive cycles: Federal Urban Driving Schedule (FUDS), Beijing Dynamic Stress Test (BJDST) & US06. The four drive cycles give new information about the availability of the model under actual driving scenarios and the energy requirements on the battery system in HEVs.

• FUDS

Known also as Urban Dynamometer Driving Schedule (UDDS), the FUDS replicate stop-and-go traffic of cities. It depicts often acceleration, deceleration, and staking that are unique for the urban mobility. These conditions can lead to so called SO/C (State of Charge) change due to frequent changes in power request.

• BJDST

The Beijing Dynamic Stress Test (BJDST) is a work cycle designed for HEVs and reflects the traffic congestion characteristic of Beijing. It also must contain periods of high acceleration and high speed and high average power which makes it a virtuous stressor for SoC estimators.

• US06 drive cycle

That is why, the US06 drive cycle imitates both Franken- urban and high-speed freeway mobility with cruising and acceleration maneuvers. This cycle is much higher than FUDS and BJDST, which examines high speed behaviors and mixed driving profiles, including frequent acceleration, deceleration and steady state, additionally testing the model. By using these drive cycles, the QGAN-TOA based SoC estimation model undergoes a comprehensive evaluation across different driving scenarios, capturing both typical city driving (FUDS), high-stress urban conditions (BJDST), and aggressive, mixed driving (US06). The effectiveness of the QGAN-TOA model in these tests showcases its adaptability and robustness in accurately predicting SoC under varied driving patterns and battery demand conditions.

Performance metrics

The examination of the proposed algorithm based on the performance metrics which are RMSE, MSE, MAE, and MAPE are explored and as well use comparison of the proposed QGAN-TOA method with some existing method such as SFO-EKF¹⁶, HMDNN¹⁷, IWHODL-BMS¹⁸, WSO-HDLNN²⁰ and CNN-BWGRU²¹. The performance metrics’ equations are as follows:

RMSE

It is also common to use such measures as the Root mean square error (RMSE) that indicates the difference between expected and observed values. It indicates how far off a model’s predictions are. For the same reason, a lower value of RMSE is an indication that the model is providing a more accurate estimate since the difference between the true and predicted scores is relatively small. This can be expressed in Eq. (18).

$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {(y_{i} - \hat{y}_{i} )^{2} } }$$

(18)

where, $n$ denotes the count of observations, $y_{i}$ indicates the true value for the $i^{th}$ observation, $\hat{y}_{i}$ indicates the predicted score of the $i^{th}$ observation, and $(y_{i} - \hat{y}_{i} )^{2}$ indicates the squared variation between each observation’s actual and expected values.

MSE

The mean squared discrepancies between the actual values and the expected is a well-known measure of a model’s performance known as mean squared error, MSE. Thus, relating to the fact that MSE does not feature the square root as is seen in the RMSE, it squares the differences making great errors more prominent. It can be expressed in Eq. (19).

$$MSE = \frac{1}{n}\sum\limits_{i = 1}^{n} {(y_{i} - \hat{y}_{i} )^{2} }$$

(19)

MAPE

The size of errors obtained by comparing the means of the forecast and true values is expressed as the mean absolute percentage error (MAPE). Because it computes error in %, which is more comprehensible on any given scale, it is often used for its simplicity. The MAPE is formulated in Eq. (20).

$$MAPE = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {\frac{{y_{i} - \hat{y}_{i} }}{{y_{i} }}} \right|} \times 100$$

(20)

where, $\left| {\frac{{y_{i} - \hat{y}_{i} }}{{y_{i} }}} \right| \times 100$ denotes the absolute percentage error for each observation.

MAE

The generalization of the measure of the divergence between the anticipated and true values is based on the mean absolute error (MAE) measure. Another useful measure for intended accuracy as it calculates the average of errors to a series of predictions without recognizing the direction of the failure. This can be expressed in Eq. (21).

$$MAE = \frac{1}{n}\sum\limits_{i = 1}^{n} | y_{i} - \hat{y}_{i} |$$

(21)

where, $|y_{i} - \hat{y}_{i} |$ indicates the absolute error for each observation.

Performance evaluation

In this section, the effectiveness analysis of the developed method is related with existing methods.RMSE, MSE, MAE and MAPE, examinationproposed algorithm are investigated and to analyze the effectiveness of the developed QGAN-TOA method, it is related with the some existing methods such as SFO-EKF¹⁶, HMDNN¹⁷, IWHODL-BMS¹⁸, WSO-HDLNN²⁰, and CNN-BWGRU²¹.

Performance analysis of proposed method

The performance analysis of the proposed method is clarified in this section. The proposed technique effectively estimates SOC with the least RMSE, MAE, MSE, and MAPE values.

The Fig. 4 shows RMSE (%) across Epochs for Different drive cycles (US06, RUDRST, and FUDS) over 100 training epochs. For US06, RMSE decreases with more epochs, starting around 0.06% at epoch 10 and stabilizing around 0.05% by epoch 100. For RUDRST, RMSE remains close to 0.13%, with minor variations across epochs. In the FUDS drive cycle, RMSE values stay consistent near 0.1%. This pattern suggests that the model’s performance improves over epochs for US06, while it remains relatively stable for RUDRST and FUDS.

Fig. 4

Proposed method RMSE analysis with different drive cycles and epochs.

The Fig. 5 shows MAE percentages for the proposed method across three drive cycles (US06, BJDST, and FUDS) over 100 epochs. In the US06 cycle, MAE decreases from around 0.15% at epoch 10 to approximately 0.1% by epoch 100, indicating improved accuracy with more training. For BJDST, MAE remains steady at roughly 0.3% across all epochs, while in FUDS, MAE fluctuates slightly but stabilizes around 0.35%. The results suggest that the proposed method reduces MAE in US06 over time but has minimal impact on BJDST and FUDS across epochs.

Fig. 5

Proposed method MAE analysis with different drive cycles and epochs.

The Fig. 6 presents MAPE percentages for the proposed method across three drive cycles (US06, BJDST, and FUDS) over 100 epochs. In the US06 cycle, MAPE is minimal, starting below 0.5% and further decreasing to nearly zero by epoch 100, indicating high accuracy. For BJDST, MAPE stabilizes around 3% across all epochs, showing little variation with training. In the FUDS cycle, MAPE remains consistently around 4.5% across epochs, with minor fluctuations. These results suggest that proposed effectively reduces MAPE in the US06 cycle but shows limited improvement for BJDST and FUDS.

Fig. 6

Proposed method MAPE analysis with different drive cycles and epochs.

The Fig. 7 illustrates the MSE performance of the proposed method across different epochs (from 10 to 100) and drive cycles (US06, BJDST, and FUDS). For the US06 cycle, MSE reduces with increased epochs, starting at about 0.004% at epoch 10 and gradually declining to around 0.0025% by epoch 100. In the BJDST cycle, MSE stabilizes around 0.008% across epochs, showing minimal variation. For the FUDS cycle, MSE consistently remains close to 0.01%, indicating less impact of epoch changes on error reduction. The method achieves optimal performance in the US06 drive cycle with lower MSE values.

Fig. 7

Proposed method MSE analysis with different drive cycles and epochs.

The Fig. 8 displays the SOC estimation using the proposed method compared to the true SOC over time under the BJDST drive cycle at temperatures of 0 °C, 25 °C, and 45 °C. In all cases, the proposed method (red line) closely follows the true SOC (blue line), indicating high accuracy. At 0 °C, SOC decreases from 1 to around 0.25 over 10,000 s. At 25 °C, SOC drops similarly but slightly faster. At 45 °C, the SOC decreases more quickly, reaching around 0.15 at the same time. The method consistently tracks the true SOC trend across varying temperatures.

Fig. 8

Proposed method SOC analysis on BJDST.

The Fig. 9 presents SOC (State of Charge) estimations using the proposed method against the true SOC over time under the US06 driving cycle at temperatures of 0 °C, 25 °C, and 45 °C. At each temperature, the proposed method (red line) aligns closely with the true SOC (blue line), indicating effective accuracy. At 0 °C, the SOC decreases from 1 to about 0.15 over 10,000 s. At 25 °C, the SOC reduces similarly, with a slight decrease in alignment. At 45 °C, SOC also drops to approximately 0.15 within 10,000 s. The proposed method maintains a strong fit to the true SOC across temperatures.

Fig. 9

Proposed method SOC analysis on the US06.

The Fig. 10 displays the performance of the proposed method for estimating the SOC of a battery over time under different temperatures (0 °C, 25 °C, and 45 °C) using the FUDS drive cycle. The graphs compare the estimated SOC (red line) with the true SOC (blue line). At 0 °C, the estimated SOC closely matches the true SOC, although a slight deviation occurs as time progresses. At 25 °C, the estimation aligns almost perfectly with the true SOC throughout the cycle. At 45 °C, a similar accuracy is observed, demonstrating that the proposed method maintains reliable SOC estimation across different temperatures.

Fig. 10

Proposed method SOC analysis on FUDS.

The Fig. 11 presents the pairwise correlation analysis of variables (Current, Discharge (Disch), State of Charge (SoC), and Voltage) across three different drive cycles: BJDST, US06, and FUDS. Each subplot displays scatter plots with correlation coefficients, where colors highlight correlation intensity. Histograms along the diagonal illustrate the distribution of each variable. Negative correlations are more prominent in the BJDST cycle, shown by red-colored coefficients, particularly between Current and Voltage. The US06 cycle exhibits weaker correlations, while FUDS has a mixed pattern with moderate correlations between SoC and Discharge (Disch) variables. This analysis provides insight into how each variable interacts under different driving conditions, useful for battery management in electric vehicles.

Fig. 11

Pairwise correlation analysis of BJDST, US06, and FUDS drive cycles.

The Fig. 12 illustrates the behavior of voltage, temperature, and current SOC over time for a battery under the FUDS driving cycle at 0 °C. The Voltage (orange) remains stable with minor fluctuations, while the current exhibits periodic oscillations, indicating variable load demands in the cycle. The SoC line reduces slightly because of gradual discharge of battery, temperature remains almost near zero showing less heat produced. This data assists in understanding the performance of battery for low temperature dynamic drive cycle.

Fig. 12

Battery voltage, current, temperature, and SoC for FUDS Dataset at 0°.

The current, voltage, temperature, and the SOC figures are generated for a battery under BJDST driving cycle for a battery temperature of 0 °C as shown in the Fig. 13. It is drawn against the time steps in seconds in the x-axis and against parameter values in the y-axis. Voltage is maintain the constant level slightly varying while Current has a fluctuating type of graph implying dynamic load changes. The SoC decreases gradually over the protection cycle as it represents energy consumption in the cycle. The Temperature line is slightly oscillating, meaning that there is a very small thermal effect at this temperature. This analysis is effective for knowledge of battery characteristics and discharge performance in cold condition for BJDST cycle.

Fig. 13

Battery voltage, current, temperature, and SoC for the BJDST Dataset at 0°.

The Fig. 14 shows the different battery parameters for a US06 drive cycle dataset at 0 °C. The horizontal axis samples the time in seconds from 2000 to 8000 and the vertical axis shows values are in the range of − 2 to 5. The voltage as well maintains a small range difference of only 4 V, which signifies that this parameter does not vary much. The current changes within cycle and now it is about − 2 to 2A, which indicates current draws in the low range. They are always constant and present a flat line pattern to the rest of the temperature parameter. The SoC tracks how much of the battery capacity has been used and whether the discharge is gradual, as a graph demonstrates. By using this graph it is possible to evaluate battery stability and power consumption while using the US06 dataset at 0 °C.

Fig. 14

Battery voltage, current, temperature, and SoC for US06 Dataset at 0°.

Performance comparison between the suggested strategy and current techniques

In this section, the effectiveness analyses of developed method compared with the existing methods are analyzed for three drive cycles. It indicates that the effectiveness of the developed QGAN-TOA method, in some ways is relevant to some existing methods including SFO-EKF¹⁶, HMDNN¹⁷, IWHODL-BMS¹⁸, WSO-HDLNN²⁰, and CNN-BWGRU²¹.

The Table 2 compares various methods for SOC estimation across three drive cycles: B calibrations BJ DST, US06 and FUDS which have been tested using statistics such as RMSE, MSE, MAE and MAPE. Specifically, the proposed method provides the lowest error rate consistently against the metrics and drive cycles, which suggests better performance and accuracy relative to SFO-EKF, HMDNN, IWHODL-BMS, WSO-HDLNN, CNN-BWGRU.

Table 2 Performance comparison of SoC estimation methods across different drive cycles.

Gragner causality test

One of the methods of verifying if the past and present values of other variable time series data termed “cause” variables influences the future values of another set of variable time series data referred to as the “effect” variables is termed the Granger Causality Test (GCT). GCT aids in the analysis of time series patterns for State of Charge (SoC) prediction when modelling cyclic processes as a series of occurrences. Data should be preprocessed to eliminate unit roots and autocorrelation, which might skew test results, in order to get trustworthy results. The Granger causality method’s primary phases are described in Table 3, and the GCT findings are compiled in Table 4.

Table 3 Comparison of RE using the Granger causality test.

Table 4 The SOC estimator error’s statistical findings.

According to the hypothesis, each lag coefficient $\alpha_{j} = 0$ is examined using Eqs. (22), (23) for all lags $j$.

$$x(s) = \sum\limits_{i = 1}^{\infty } {\beta_{i} } x(s - i) + c_{1} + v_{1} (s)$$

(22)

$$x(s) = \sum\limits_{i = 1}^{\infty } {\beta_{i} } x(s - i) + \sum\limits_{j = 1}^{\infty } {\gamma_{j} } x(s - j) + c_{2} + v_{2} (s)$$

(23)

To determine, if $x(s)$ Granger-causes $y(s)$ Eqs. (24), (25) are applied.

$$x(s) = \sum\limits_{i = 1}^{\infty } {\beta_{i} } x(s - i) + c_{1} + u_{1} (s)$$

(24)

$$x(s) = \sum\limits_{i = 1}^{\infty } {\beta_{i} } x(s - i) + \sum\limits_{j = 1}^{\infty } {\gamma_{j} } x(s - j) + c_{2} + u_{2} (s)$$

(25)

To compute the F-statistic, use Eq. (22).

$$F = \frac{{(ESS_{R} - ESS_{UR} )/q}}{{ESS_{UR} /(n - k)}}$$

(26)

The outcomes are summarised in Table 3, which gives that the GCT analysis validates the significant correlation between the suggested QGAN-TOA approach and SoC estimation across different drive cycles.

The Table 3 compares relative error (RE) for different methods using the Granger causality test across three drive cycles (BJDST, US06, FUDS). The proposed method consistently achieves lower SE (standard error) and T statistic values, indicating higher accuracy and reliability, with F-value and P-value values close to or below competitive benchmarks, especially in the FUDS cycle.

The Table 4 presents statistical findings on the SOC estimator error. For voltage, the maximum error is 74.62 mV, with a standard deviation of 11.31 mV, a mean error of − 0.01 mV, and a duration of 47.584 s. For SOC, the maximum error is 0.03%, with a standard deviation of 0.01% and a mean error of − 14.29%.

Discussion

The proposed method combines Quaternion Generative Adversarial Networks (QGAN) for SOC prediction with the TOA for hyperparameter tuning, enhancing accuracy and adaptability in hybrid electric vehicles.

Advantages of the proposed estimation model

• Adaptive optimization: The Tyrannosaurus Optimization Algorithm (TOA) tunes hyperparameters dynamically, which helps enhance prediction performance and adaptability to varying conditions.

• Robust data handling: The model is also able to process multiple inputs in the inputs space (voltage, current and temperature) at the same time, ideal for HEVs.

Disadvantages of the proposed estimation model

• Complexity: The new combination of QGAN and TOA also increases computational complexity in terms of processing power and memory effect.

• Dependence on data quality: This approach relies on data input, and therefore, the quality of data used in the model affects the precise results that get when solving real-world.

• Training time: Generally, GAN-based models may take longer time in order to be trained, thus implying a relative reduction of the speed at which it is possible to deploy them.

The proposed model, which integrates QGAN and TOA, significantly outperforms traditional methods in state of charge (SOC) estimation. It achieves high accuracy and reliability across different driving cycles and temperature conditions. The model’s ability to handle noisy or incomplete data stems from its robust design, which accurately captures battery behavior. With a root mean square error (RMSE) close to 0.05%, a mean absolute error (MAE) of 0.1%, and a mean square error (MSE) around 0.0025%, the model shows stability even with data fluctuations. This capability ensures effective battery management, enhancing performance and longevity, and making it well-suited for real-world applications.

Conclusion

It is important and useful that the authors investigated and proposed a QGAN model and TOA, where SOC estimation in HEVs is optimised with higher accuracy and reliability than conventional methods. The model shows great efficiency near and far from the reference values with almost no mistakes during various drive cycles and temperatures. More specifically, to estimate the SOC of the battery for cycling of the US06 drive, it has been observed that RMSE becomes almost constant and fluctuates in the range of 0.05%, MAE reaches its minimum of 0.1% and MSE is approximately 0.0025% which shows that battery SOC is being predicted with high accuracy. This high accuracy ensures more efficient management of the battery, making the HEV perform better and last longer key factors for the broader adoption of HEVs and integration of renewable energy. The effectiveness of the method in particular depends on quality data and range of the data used in the training. Investigating how real driving conditions differ from test protocols or battery degradation is not well considered, and impacts the model’s applicability. In future, use more variety of data set, real-life driving data to incorporate a new model under different conditions, will provide a better handling model. Future research could investigate the integration of the proposed framework with real-time energy management systems tailored for various hybrid EV models. Improvements in QGAN architectures and the creation of hybrid optimization techniques may enhance the accuracy of SOC estimation. Furthermore, broadening the framework to include multiple renewable energy sources and grid connectivity presents significant opportunities. Upcoming studies will focus on how our approach can be incorporated into battery management systems (BMS) for hybrid electric vehicles (HEVs), including the necessary hardware infrastructure like sensors, computational units, and communication systems.