Posture configuration optimization method and system for folding booms of the pump truck under life extension control

Abstract

The service process of the pump truck typically requires subjective control of the folding boom to achieve the desired pouring position. However, such the posture of the boom controlled by the operator’s experience, can lead to additional fatigue damage, ultimately reducing the fatigue life of the boom structure. To address this issue, this paper proposes a posture configuration optimization method for folding booms of the pump truck under life extension control. A multifunctional integrated system platform has also been developed. First, the dataset of “behavioral-performance” characteristics for the folding booms of the pump truck is obtained using a synergistic method of “acquisition-simulation-correction”. After evaluating the fatigue life, the dataset is transformed into a fatigue life sample dataset. The Extra Trees model, enhanced by Bayesian Optimization, is then developed to realize rapid predictions of fatigue life for various boom postures. Second, the posture configuration optimization model for the boom is developed with two primary objectives: maximizing fatigue life and minimizing the distance between the end of the boom and the pouring point. Subsequently, the optimization model is solved using the improved Ant Colony Algorithm. This configuration optimization yields the optimal boom posture for a specific pouring point. Finally, the “posture configuration system for the folding booms of the pump truck under life extension control” is constructed through algorithm encapsulation and function integration. This system provides a visual and interactive intelligent computing platform for the aforementioned processes.

Introduction

With the acceleration of urbanization both domestically and internationally, concrete pump trucks play a crucial role in national infrastructure construction due to its high pouring efficiency and flexibility¹. The flourishing development of the construction industry has put forward higher requirements on the operational efficiency, precision and safety of concrete pump trucks. This trend promotes the development of concrete pump trucks towards multi-jointed booms, long distances, substantial capacity, and intelligent systems. It has also led to increased complexity in the posture configuration of folding booms². During pumping operations, the operator generally performs the following steps to configure the posture of the folding boom. First, the operator determines the exact position for pouring concrete through visual observation, defining the required conveying distance and height. Second, the operator manipulates the folding booms of the pump truck to execute various actions. These actions include rotating and pitching the main boom, telescoping and adjusting the angle of the remaining boom, and precisely positioning the end hose. In this process, they need to repeatedly perform small-amplitude boom spreading operation. Through visual confirmation, or communication and collaboration with the ground commanders, the position of the boom is continuously fine-tuned. This action continues until the end of the boom is aligned with the pouring point. The entire operation process requires the operator to possess extensive experience, strong spatial awareness, and precise operational skills³.

The folding boom is responsible for load carrying and transferring within the entire pumping machine. For a particular pouring position, the posture of the folding boom is not unique⁴. If the posture configuration of the folding boom is carried out purely by manual subjective experience, it can only barely meet the most basic pouring requirements. On the one hand, this process is very time-consuming. It requires operators to repeatedly observe and adjust several times with their eyes. This will seriously affect the construction progress. On the other hand, the continuously generated vibration response will accelerate the fatigue damage of the boom during the continuous adjustment process. Moreover, due to the lack of precise quantification of manual operation, it is difficult to accurately predict the stress impact of each action on the folding boom. This will lead to the fatigue damage of the boom being accidental and unknown⁵. Under long-term frequent operation, it greatly increases the risk of folding boom failure. According to incomplete statistics, in addition to the whole machine tipping over, more than 80% of pump truck accidents are related to structural fatigue failure⁶. For example, in June 2022, a site in Huai’an, the fatigue fracture of the pump truck boom caused injuries and fatalities to the workers during the construction process. In May 2021, at the construction site of a campus in Nanshan, the boom shook significantly and caused casualties when the driver operated the boom. From the point of view of force, the fatigue failure of pump truck folding boom is mainly attributed to factors such as tilt angles of booms, pressure of the cylinder, dynamic load effect of pumping. However, the above factors can be covered by the posture configuration of the boom.

In terms of fatigue damage to folding booms, the degree of fatigue damage in the folding boom is typically reflected by its remaining fatigue life. Commonly used methods for assessing the fatigue life of mechanical equipment include the nominal stress method⁷, hot spot stress method⁸, fracture mechanics method⁹, and structural stress method¹⁰. Compared with other methods, the fracture mechanics method is able to analyze the size and expansion rate of the crack. It can clearly grasp the fatigue crack expansion process of the folding boom^11,12,13,14. However, it needs to be based on a large amount of stress history data in practice. Traditional simulation and measurement methods often struggle to ensure the timeliness, sustainability, and accuracy of data acquisition^15,16. In recent years, data-driven methods based on machine learning have gradually emerged in the field of fatigue life prediction¹⁷. Notably, Shen et al.¹⁸ proposed a boom damage prediction framework to address the challenges of detecting damage in large boom structures. They selected key features using the Random Forest model and employed the Gaussian Process Regression algorithm for training and fitting the data. This resulted in accurate predictions of damage levels in the boom structures of wheeled cranes. Cao et al.¹⁹ highlighted the importance of time–frequency domain analysis for rotating machinery, building upon traditional deep learning models. They proposed a complex domain extension network that integrates multi-channel information fusion. This network was applied to predict the fatigue life of rotating machinery under various operating conditions. Jiao et al.²⁰ introduced a prediction model based on an optimized Long Short Term Memory network (LSTM). They employed the Adaptive Moment Estimation (AME) algorithm to offer independent adaptive learning rates for different grid parameters of LSTM. This significantly enhances the prediction accuracy of fatigue life for wind turbine blades. From the above study, a single prediction model may exhibit uncertainty in its fitting capability when handling diverse data. Therefore, it is essential to explore improvements in the model through model construction methods and hyperparameter optimization.

In terms of the posture configuration of folding booms, in order to quickly and accurately solve for the posture of the boom inversely based on the pouring position, the kinematics analysis of the folding boom must be conducted. This analysis aims to determine the correlation between the position of the end of the boom and the dimensional and operational parameters of each section. However, the folding boom is a typical multi-degree-of-freedom tandem system. Several challenges exist in the kinematic inverse solution of its positional state. Firstly, establishing kinematic equations is more complex²¹. The complexity of these equations increases with the number of links and joints in the system. Second, the kinematic equations at high degrees of freedom are highly nonlinear. It is computationally intensive and complex to solve²². Third, there are multiple sets of solutions in the system that can achieve the same pouring position²³. To address these issues, current research primarily employs geometric algebraic methods, numerical solution methods, and optimization algorithms. Among them, Chai et al.²⁴ proposed an inverse kinematics analysis method specifically for parallel robots. This method employs geometric algebra to integrate geometric representation with computation. Taking 3-degree-of-freedom and 6-degree-of-freedom parallel robots as examples, the feasibility of the proposed method was validated. The solution of forward–backward stochastic differential equations driven by G-Brownian motion (G-FBSDEs) is quite complex. To address this complexity, Hu et al.²⁵ proposed a numerical solution method that first approximates the G expectation and derives feasible motion distributions. Specific solution results are obtained through discrete schemes. The effectiveness of this method has been demonstrated through convergence analysis and numerical experiments. Wang et al.²⁶ proposed a 2-norm optimal solution extraction method to address the multiple inverse kinematics problem in mobile robots resulting from high redundancy. This method solves the kinematic equation using the 2-norm of the angle difference before and after rotation as the shortest stroke index. This approach shortens the motion path of robots and enhances its smoothness. The aforementioned methods illustrate that geometric algebraic methods transform complex kinematic problems into geometric or algebraic forms for resolution. While it simplifies the calculation process, it becomes challenging to implement for highly complex or nonlinear problems. Numerical solution methods employ numerical algorithms to solve equations of motion. They have a wide range of applications. However, they heavily rely on algorithm stability and typically require numerous iterative operations. The above two methods can yield multiple feasible solutions. To achieve a unique solution, necessary constraints must be imposed. Optimization algorithms can provide a unique and optimal solution based on defined objectives. They can effectively address complex nonlinear problems involving multiple objectives and constraints. Thus, to ensure that the kinematic inverse solution results are both unique and meet target requirements, optimization algorithms are more suitable.

Additionally, to address user needs, a “posture configuration system for the folding booms of the pump truck under life extension control” has been developed through functional integration. This system will significantly enhance computational efficiency. Several studies have explored the development of system platforms. Moi et al.²⁷ constructed a digital twin system for a small crane. This system not only facilitates status monitoring of the device but also implements real-time simulation within a nonlinear finite element program using the payload as input. He et al.²⁸ developed a mechanism-data fusion digital twin framework for a gantry crane. This achieves real-time mapping from physical space to virtual space during the operation of major mechanical equipment. It is evident that the existing technology is sufficient for real-time monitoring and performance evaluation of mechanical equipment. However, how to fully utilize monitoring data and evaluation results to optimize the operational status of mechanical equipment is still a problem. Systematic integration of various functions and optimization results into interactive interfaces requires further research.

Considering the above issues, this article proposes a posture configuration optimization method for folding booms of the pump truck under life extension control. Additionally, a corresponding multifunctional integrated system platform has been developed. The main contributions are as follows:

• 1. Taking behavioral characteristics (posture of the boom and pumping pressure) as inputs and performance characteristics (fatigue life of the boom) as outputs, the fatigue life prediction model (BO-ET) for the folding booms of the pump truck has been constructed. This model facilitates fast and accurate predictions for the fatigue life of folding booms.

• 2. Kinematic analysis of the boom system is conducted using the D-H coordinate system. The kinematic relationships, both positive and negative, between each parameter of the boom system and the end of the boom are derived. The included angle of the boom serves as the design variable, while the unfolding range of each boom under different postures acts as a constraint. The shortest Euclidean distance from the end of the boom to the pouring position and the longest fatigue life of the boom structure are defined as dual-objective functions, leading to the construction of the posture configuration optimization method for folding booms of the pump truck.

• 3. Through algorithm encapsulation and function integration, the “posture configuration system for the folding booms of the pump truck under life extension control” is constructed. The system integrates monitoring of equipment service information, fatigue life prediction, and posture configuration optimization. It provides visual real-time feedback on the service information of the equipment. Additionally, it visualizes the results of the posture configuration. The system provides convenience for practical application in engineering.

Pouring scene of pump trucks

Concrete pump trucks facilitate efficient and precise transportation of concrete. They are suitable for construction sites of various types and scales. The work cycle consists of three stages: ① Preparation stage. The operator determines the parking position of the pump truck based on specific requirements and the layout of the construction site. This ensures that the reachable area at the end of the boom covers the pouring range of construction. ② Pumping phase. The pump truck and concrete mixing plant are positioned in designated locations. The legs of the chassis are extended and secured on the ground. Each boom is unfolded to ensure that the end of the boom reaches the pouring point before pumping begins. ③ Reflux adjustment and pipeline cleaning. The reflux valve is opened after pumping is completed. The discharge of concrete from the pipeline is controlled. This prevents residual concrete in the pipeline from solidifying and causing blockages. Finally, the pipeline is washed with water, and the boom and legs are retracted after completion. The specific scenario is illustrated in Fig. 1.

Fig. 1

Pouring scene of concrete pump trucks. This figure was created by Unity 3D 2021.3.37 (https://unity.cn/releases#undefined).

This explanation uses a six-section folding boom concrete pump truck as an example. The initial position is defined as boom #1 horizontally, and the remaining booms are retracted. The connection between the root of each boom and the head of the preceding boom is the rotation center. When extending, boom #4 deploys in a clockwise direction outward. The remaining booms deploy in a counterclockwise direction. Each boom can extend to a maximum angle of φ_i (i = 1, 2, …, 6). The angle between the boom and the horizontal is referred to as the tilt angle of boom θ_i. Angles above the horizontal line are considered positive, while those below are negative. Both positive and negative angles must not exceed 180°. The angle at which each boom rotates relative to the previous boom is referred to as the included angle of boom A_i. Positive values are measured clockwise, while negative values are measured counterclockwise. As shown in Fig. 2a), a schematic diagram illustrates the tilt angle and included angle of the arch-shaped posture of the boom. During the working cycle of the concrete pump truck, the posture of the folding boom is controlled to achieve various working heights and amplitudes at the end of the boom. This enables the completion of pouring tasks in various scenarios. From this, it can be seen that commonly used postures, as illustrated in Fig. 2b), include upright, conventional arch, M-shaped, and quasi-horizontal postures. The upright posture is suitable for high-height, low-amplitude pouring scenarios. Conventional arches and M-shapes are suitable for medium-height, medium-amplitude pouring scenarios. Quasi-horizontal and deep arch postures are suitable for low-height, high-amplitude pouring scenarios. Under different postures, the tilt angle and included angle of the boom satisfy Eq. (1):

$$\left\{ \begin{aligned} & A_{1} = \theta _{1} \\ & A_{i} = 180^\circ {\text{ + }}\theta _{i} - \theta _{{i - 1}} ,\;i = 2 \sim 6i \in N^{ + } \\ \end{aligned} \right.$$

(1)

Fig. 2

Angle definition and typical postures of the boom.

Acquisition of service information for pump trucks

Regarding the acquisition of service information for concrete pump trucks, the direct acquisition method gathers objective data in real service scenarios. This method offers better data timeliness. However, this approach necessitates the purchase of suitable sensing equipment and a data acquisition system. Additionally, the use of sensors presents several challenges²⁹. First, sensors are fragile and require regular maintenance and replacement. Second, improper arrangement can affect measurement accuracy. Third, limited coverage makes comprehensive monitoring challenging. Fourth, the signal transmission process may encounter issues such as interference and signal loss. The finite element simulation method can comprehensively and safely assess the operational and safety performance characteristics of equipment in a virtual environment. This method can significantly reduce the costs and risks associated with real measurements. However, the reliability of the simulation results largely depends on the accuracy of various factors, including models, boundary conditions, and material parameters. Additionally, solving complex models may require substantial computational resources and time³⁰. Therefore, based on the above two methods, this article proposes a collaborative data acquisition method of “acquisition-simulation-correction”. This method is employed to obtain a dataset of the “behavioral-performance” characteristics of the folding booms of the pump truck. The specific scheme is illustrated in Fig. 3.

Fig. 3

Scheme of information acquisition for pump trucks. This figure was created by SolidWorks 2019 software (https://www.solidworks.com/zh-hans) and Ansys 2021 software (https://www.ansys.com/zh-cn).

In terms of data collection, the concrete pump truck information acquisition system is utilized to complete the collection of boom information data. It includes the following three parts: (1) the placement of detection points. Based on the structural and load characteristics of the folding booms of the pump truck, it is simplified as a cantilever beam in the rotational plane. It is also simplified as a simply supported beam in the amplitude plane. According to the analysis method of the structural influence line, the maximum bending moment and shear force occur near the root of each boom. A statistical analysis is conducted to investigate the actual damage locations of the boom structure. Considering the feasibility of the actual layout, the sections at the root of the first four booms are identified as dangerous sections (i.e., sections 1–1 to 4–4). The distance of each section from the boom root of each boom is 3045 mm, 3004 mm, 1200 mm and 900 mm respectively. The weld areas between the main web plate and the upper flange plate in each dangerous section are designated as stress detection points M1 ~ M4. Figure 4 shows the details. (2) Hardware Components. This system contains various types of sensors (such as CXL200 tilt angle sensors, P3MBP pressure sensors, K-RY61 strain gauges), HBM testing system, MIC-7500 Industrial Personal Computer (IPC) and Zoomlion Box. Among them, the tilt angle sensors are installed parallel to the surface of the boom. They are used to measure the angle between each boom and the horizontal line. The pressure sensors are installed inside the oil cylinder. They are used to measure the pressure when the hydraulic oil is delivered. The strain gauges are affixed to the detection points M1 ~ M4. The testing system and the industrial personal computer are responsible for data transmission and processing. (3) Implementation process. The pump truck is controlled to pump in different postures for a period of time. The sensors will collect the “behavioral-performance” characteristic data of the folding boom during the pumping process and transmit them to the HBM testing system. The data will be initially converted and processed by the industrial personal computer. The processed data will be stored to Zoomlion Cloud server through Zoomlion Box by Wifi transmission. Users can download and apply the data from the cloud server with terminal devices.

Fig. 4

Placement of detection points.

The finite element simulation should be based on the theory of limit state design. When analyzing the stress situation of the folding boom structure, the dynamic load effect must be considered, as per the industry standard QC/T 718-2013 “Concrete Pump Truck”³¹. This involves applying a static load, such as multiplying the self-weight load by a coefficient of 1.2 and the working load by a coefficient of 1.3. The mechanical model is illustrated in Fig. 5. A finite element simulation model of the pump truck is established using ANSYS software. Load steps are applied to analyze the stress history at each grid node of the boom structure.

Fig. 5

Mechanical model of folding booms.

In terms of data correction, data correction is to use the finite element simulation model to correct the pre-processed anomalous data again on the basis of information data pre-processing. It is of great significance in improving data quality, model prediction performance and computational efficiency. As far as information data preprocessing is concerned, different information categories are prone to inconsistent sampling frequencies. This can lead to a lack of correlation between heterogeneous data and cannot be used directly. In this case, the least squares method³² can be used for time alignment. Sensors can be damaged by environmental disturbances during use leading to signal loss, anomalies and other problems. Linear interpolation³³ can be used to fill in the missing parts. Meanwhile, the interquartile range (IQR)³⁴ of the box plot is utilized to monitor the outliers and remove them. In order to ensure the consistency between the measured data and the simulation data in the stress history dataset S, the measured strain data should be converted into stress data through Eq. (2). The specific data processing method for the collected information can be referred to Ref.³⁵. As far as anomaly data correction is concerned, it is centered around the detection points M1 to M4 on the dangerous section 1-1 to section 4-4. The pre-processed valid informatics data are utilized to correct the above finite element simulation model. The pre-processed anomaly data are validated and corrected using the corrected simulation model. Eventually, the stress history dataset S* for life calculation is formed.

$$\sigma = {{E\varepsilon } \mathord{\left/ {\vphantom {{E\varepsilon } {10^{6} }}} \right. \kern-0pt} {10^{6} }}$$

(2)

where, E is the elastic modulus of the material, E = 2.06 × 10⁵ MPa. $\varepsilon$ is the microstrain, measured in με. $\sigma$ is the stress value, measured in MPa.

Fatigue life prediction of the folding boom structure

Under the guidance of fracture mechanics theory, the Rain Flow Counting Method is employed to extract an eight-level dual-parameter spectrum of stress for each detection point at every posture of the boom from dataset S*. The influence of the stress ratio is mitigated using the Goodman curve. The Paris formula is employed to calculate the life of crack propagation at each detection point for each level of the stress spectrum. Subsequently, cumulative fatigue damage and remaining fatigue life for each detection point under the corresponding posture are calculated using Miner’s theory. A fatigue life sample dataset is created with the posture of the boom and pumping pressure as inputs, and residual fatigue life of detection points as outputs. Building on this, the Extra Trees model³⁷, enhanced by Bayesian Optimization³⁶ (BO-ET) is introduced to fit the mapping relationship between the posture of the boom, pumping pressure, and fatigue life. This allows for rapid fatigue life prediction of the folding boom structure across different postures.

Construction of fatigue life samples

The fatigue life sample data set Q = {$\theta_{i}$,$F_{p}$,$N_{sk}$} is constructed using postures of the boom $\theta_{i}$ and pumping pressure F_p as inputs, with the fatigue remaining life $N_{sk}$ of detection point k as the output. The boom structure is assembled by welding multiple steel plates or profiles. During welding and assembly, factors like uneven material properties, welding defects, and poor joint design will inevitably lead to initial cracks near the weld. Under complex alternating loads, the cracks will expand until failure occurs. It can be seen that the alternating stress from these loads is a direct cause of fatigue damage to the structure. It can be represented by the stress range. Therefore, based on the corrected stress history data set S*, the Rain Flow Counting Method⁸ is employed to extract an 8-level mean spectrum and amplitude spectrum of stress for detection point k in the same posture. The stress spectrum at each level is converted into a stress range using the Goodman curve:

$$\sigma_{vki} = 2{{(\sigma_{fki} + {{\sigma_{ - 1} \sigma_{jki} } \mathord{\left/ {\vphantom {{\sigma_{ - 1} \sigma_{jki} } {\sigma_{u} }}} \right. \kern-0pt} {\sigma_{u} }})} \mathord{\left/ {\vphantom {{(\sigma_{fki} + {{\sigma_{ - 1} \sigma_{jki} } \mathord{\left/ {\vphantom {{\sigma_{ - 1} \sigma_{jki} } {\sigma_{u} }}} \right. \kern-0pt} {\sigma_{u} }})} {(1 + {{\sigma_{ - 1} } \mathord{\left/ {\vphantom {{\sigma_{ - 1} } {\sigma_{u} }}} \right. \kern-0pt} {\sigma_{u} }})}}} \right. \kern-0pt} {(1 + {{\sigma_{ - 1} } \mathord{\left/ {\vphantom {{\sigma_{ - 1} } {\sigma_{u} }}} \right. \kern-0pt} {\sigma_{u} }})}}$$

(3)

where, $\sigma_{vki}$ is the stress range after eliminating the influence of the stress ratio, measured in MPa, $i = 1 \sim 8$ ($i \in N*$). $\sigma_{fki}$ is the amplitude value of stress. $\sigma_{jki}$ is the mean value of stress. $\sigma_{ - 1}$ is the fatigue strength of the material when the stress cycle characteristic R = -1. $\sigma_{u}$ is the ultimate strength of the material.

According to the Paris formula, under a single-stage stress range, the number of stress cycles N_i from the initial crack l₀ to the critical crack l_d is:

$$N_{i} = \int_{{l_{0} }}^{{l_{d} }} {C_{0}^{ - 1} \left( {\Psi \sigma_{vi} \sqrt {\pi l} } \right)}^{ - m} {\rm {d}}l$$

(4)

where, C₀ and m are material parameters. They can be obtained through fatigue fracture tests of standard parts. $\Psi$ is the geometric correction factor. According to “Handbook of stress intensity factors (Revised edition)”³⁸, combined with the characteristics of the boom structure, it can be calculated by Eq. (5):

$$\Psi = \left\{ \begin{aligned} & \Psi _{1} = \left[ {1 - 0.025\left( {l_{m} /d} \right)^{2} - 0.06\left( {l_{m} /d} \right)^{4} } \right]\sqrt {\sec \left( {\pi l_{m} /2d} \right)} \\ & \Psi _{2} = 1.12 - 0.231\left( {l_{n} /D} \right) + 10.55\left( {l_{n} /D} \right)^{2} - 21.72\left( {l_{n} /D} \right)^{3} + 30.39\left( {l_{n} /D} \right)^{4} \\ \end{aligned} \right.$$

(5)

where, $\Psi_{1}$ is the geometric correction factor applicable to the plate with the center crack. $\Psi_{2}$ is the geometric correction factor applicable to the plate with the edge crack. According to Ref.³⁹, when the crack size is much smaller than the plate thickness, $\Psi_{1} = 1$ and $\Psi_{2} = 1.12$ are usually taken. l_m is half of the length of the center crack. l_n is the length of the edge crack. Crack lengths can be measured by non-destructive testing. d is half of the width of the plate with the center crack. D is the width of the plate with the edge crack. Specific width of the board is subject to design parameters.

Assume that the number of times the stress spectrum of each level occurs is n_i. The number of stress cycles corresponding to the fatigue failure of the structure obtained by formula (4) is N_i. According to Miner’s theory, the value of fatigue cumulative damage M_k for detection point k on the boom structure is:

$$M_{k} = \sum\limits_{{i = 1}}^{8} {n_{{k_{i} }} /N_{{k_{i} }} }$$

(6)

0 ≤ M_k < 1 indicates that the boom structure has fatigue damage. M_k = 0 indicates that the boom structure has reached its critical life and needs to be stopped. M_k > 1 indicates that the boom structure may break at any time.

Assume that the boom of the pump truck maintains the same posture for multiple pumping within t hours. At this time, the value of fatigue cumulative damage for detection point k is M_k. Assume that the number of working days of the pump truck in a year is B. If the number of working hours per day is T, then the fatigue residual life of detection point k in a specific posture can be expressed as:

$$N_{sk} = t/\left( {M_{k} TB} \right)$$

(7)

where, $N_{sk}$ is the fatigue remaining life of detection point k in a certain posture, measured in year.

BO-ET model for fatigue life prediction

This chapter introduces the Extra Trees model (ET)³⁷ to train and test the fatigue life sample data set Q. During this process, the key hyperparameters of the ET model (i.e., max_depth and n_estimators) need to be determined. The Bayesian Optimization Algorithm³⁶ can be used to solve it. This enhances the learning and fitting capabilities of the BO-ET model while improving computational efficiency.

Extra trees (ET)

The fatigue life dataset Q have high feature dimensions and obvious nonlinear situations. The prediction task needs to balance the prediction accuracy and prediction efficiency. In terms of model selection, among many machine learning models, Extra Trees model (ET)³⁷ is characterized by strong robustness and fast training speed. It is suitable for high-dimensional nonlinear data. Therefore, the ET model is selected as the base model for the prediction task.

The ET model is an integrated learning algorithm based on decision trees and Bagging framework proposed by PierreGeurts et al. in 2006. The core idea is to use all training set data as root nodes. Randomly select feature subsets and thresholds (cut points) to bifurcate the root node recursively to form multiple decision trees. Ultimately, the average of the prediction results of all decision trees is used as the prediction result of the ET model. The specific construction process includes: 1) the fatigue life dataset Q is divided into training set Q-1 and test set Q-2 in a ratio of 8:2. All the data in the training set Q-1 are taken as the root nodes. The same number of root nodes are generated according to the maximum decision tree trees (n_estimators) set by the ET model. 2) The root nodes are split recursively using the binary tree construction method. The feature subsets and feature cut points are completely randomized during the splitting process. Until all the decision trees grow to the maximum depth (max_depth), the splitting is stopped, and the prediction results of each decision tree are outputted. 3) The average of the prediction results of all the decision trees is taken as the prediction result of the ET model. The test set Q-2 is used to obtain the model evaluation index.

Bayesian optimization algorithm (BO)

The performance, generalization ability, and computational efficiency of the machine learning model largely depend on the hyperparameter settings. Among the commonly used hyperparameter optimization methods, Bayesian optimization³⁶ has certain advantages: (1) adaptive search. An agent model of the parameter space is constructed during the search process. The evaluation results of previous searches are utilized to dynamically adjust the search direction and intelligently mine potential optimal solutions. (2) Wide range of application. Good optimization effect can be achieved for both high-dimensional/low-dimensional and continuous/intermittent parameter search space. (3) High computational efficiency. Due to the ability of adaptive search, Bayesian optimization can find the optimal solution with fewer iterations.

BO algorithm takes SMBO as the core framework. It mainly consists of two parts: the probabilistic agent model and the acquisition function. The former is used to construct the mapping relationship between the input parameters and the objective function. Then the prediction model of the objective function is formed. The overall core idea lies in transforming a priori information and historical data into a posteriori probability distribution through a probabilistic agent model. In turn, the next search direction is actively selected. A large number of iterative processes are reduced thus shortening the search time. In this paper, Gaussian regression process is chosen as the probabilistic agent model, and EI function is the collection function. The specific implementation process of the BO algorithm is as follows:

Assuming that the hyperparameters to be optimized are u = (u₁, u₂,…, u_i) and the objective function is g(u). The number of randomly generated sets of hyperparameters is w and the corresponding objective function is computed. This constitutes the prior sample data set D_1~w = {(u₁, g₁), (u₂, g₂), …, (u_w, g_w)} used to initialize the model. The Gaussian regression process is utilized to learn and fit this data set. The vector consisting of all objective functions follows a multivariate Gaussian distribution (prior probability distribution, denoted p(D_1~w)):

$$g_{1\sim w} \sim N\left( {\mu \left( {u_{1\sim w} } \right),\Sigma \left( {u_{1 - w} ,u^{\prime}_{1\sim w} } \right)} \right)$$

(8)

where, $\mu \left( {u_{1\sim w} } \right)$ is the mean function of the variable u. It is usually taken as 0 under Gaussian distribution.$\Sigma \left( {u_{1\sim w} ,u^{\prime}_{1\sim w} } \right)$ is the covariance matrix, also known as the kernel function K.

$$\Sigma \left( {u_{1\sim w} ,u^{\prime}_{1\sim w} } \right) = K_{1\sim w} = \left( {\begin{array}{*{20}c} {k\left( {u_{1} ,u^{\prime}_{1} } \right)} & \cdots & {k\left( {u_{1} ,u^{\prime}_{w} } \right)} \\ \vdots & {} & \vdots \\ {k\left( {u_{w} ,u^{\prime}_{1} } \right)} & \cdots & {k\left( {u_{w} ,u^{\prime}_{w} } \right)} \\ \end{array} } \right)$$

(9)

The fitted Gaussian regression process is used to calculate the function $g_{{{\text{w + }}1}}$ corresponding to the new sampling point $u_{w + 1}$. Under the assumption of Gaussian distribution, $g_{{1\sim {\text{w}} + 1}}$ should conform to the w + 1 dimensional Gaussian distribution (joint probability distribution, denoted as $p\left( {D_{1\sim w} \left| {g_{w + 1} } \right.} \right)$):

$$\left[ \begin{gathered} g_{1\sim w} \hfill \\ g_{w + 1} \hfill \\ \end{gathered} \right] \sim \left( {0,\left[ {\begin{array}{*{20}c} {K_{1\sim w} } & {k_{ * } } \\ {k_{ * }^{{\text{T}}} } & {k\left( {u_{w + 1} ,u^{\prime}_{w + 1} } \right)} \\ \end{array} } \right]} \right)$$

(10)

where, $k_{ * } = [k\left( {u_{w + 1} ,u_{1} } \right),k\left( {u_{w + 1} ,u_{2} } \right), \cdots ,k\left( {u_{w + 1} ,u_{w} } \right)]$.

The prior probability distribution of $g_{{{\text{w + }}1}}$ is denoted as $p\left( {g_{w + 1} } \right)$. According to Bayes’ theorem, the posterior probability distribution $p\left( {g_{w + 1} \left| {D_{1\sim w} } \right.} \right)$ of $g_{{{\text{w + }}1}}$ is:

$$p\left( {g_{w + 1} \left| {D_{1\sim w} } \right.} \right) = {{p\left( {D_{1\sim w} \left| {g_{w + 1} } \right.} \right)p\left( {g_{w + 1} } \right)} \mathord{\left/ {\vphantom {{p\left( {D_{1\sim w} \left| {g_{w + 1} } \right.} \right)p\left( {g_{w + 1} } \right)} {p\left( {D_{1\sim w} } \right)}}} \right. \kern-0pt} {p\left( {D_{1\sim w} } \right)}}$$

(11)

According to the posterior probability distribution of $g_{{{\text{w + }}1}}$, the search direction of $g_{{{\text{w + }}1}}$ is updated by minimizing the objective function value. In this way, the values of the optimal hyperparameters are determined. The process of hyperparameter optimization should consider the global nature and interpretability. In this section, the Expected Improvement (EI) function is chosen as the collection function. Based on the modeling results of Gaussian regression process, the balance between the current optimal point information and the unknown region is found. Thus, the global optimal solution in the search space is obtained.

The difference between the objective function value $g_{{{\text{w + }}1}}$ corresponding to the new sampling point and the optimal value $g_{best}$ in the current sample dataset D_1-w can be expressed as the degree of improvement $I\left( g \right)$.

$$I\left( g \right) = \max \left\{ {0,g_{w + 1} - g_{best} } \right\}$$

(12)

The expected value of $I\left( g \right)$ is calculated by using the EI function:

$$EI\left( {I\left( g \right)} \right) = \left\{ {\begin{array}{*{20}l} {\left( {\Psi \sigma \left( g \right)} \right)\Phi \left( \Psi \right) + \sigma \left( g \right)\phi \left( \Psi \right),} \hfill & {\sigma \left( g \right) > 0} \hfill \\ {0,} \hfill & {\sigma \left( g \right) = 0} \hfill \\ \end{array} } \right.$$

(13)

$$\Psi = {{\left( {\Omega \left( g \right) - g_{best} } \right)} \mathord{\left/ {\vphantom {{\left( {\Omega \left( g \right) - g_{best} } \right)} {\sigma \left( g \right)}}} \right. \kern-0pt} {\sigma \left( g \right)}}$$

(14)

where, $\Omega \left( g \right)$ and $\sigma \left( g \right)$ are the mean and standard deviation of the objective function for all sample points, respectively. $\Phi \left( x \right)$ and $\phi \left( x \right)$ are the distribution function and probability density function of the standard normal distribution, respectively:

$$\left\{ \begin{aligned} & \Phi \left( x \right) = \left( {2\pi } \right)^{{ - 1/2}} \int_{{ - \infty }}^{x} {e^{{ - t^{2} /2}} dt} \\ & \phi \left( x \right) = \left( {2\pi } \right)^{{ - 1/2}} e^{{ - t^{2} /2}} \\ \end{aligned} \right.$$

(15)

When the expected value of $I\left( g \right)$ takes the maximum value, the corresponding independent variable is the next sampling point. This is the optimal hyperparameter obtained from the optimization.

Construction process of the BO-ET model

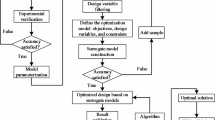
In order to facilitate the understanding and application, the specific construction process of the BO-ET model is given, as shown in Fig. 6. The detailed steps are as follows:

Fig. 6

Construction process of BO-ET model.

Step 1 Division of the dataset. The fatigue life dataset Q is divided into training set Q-1 and test set Q-2 in a ratio of 8:2.

Step 2 Obtaining of the mapping relationship between hyperparameters and loss function. First, the value ranges for the key hyperparameters are defined. Second, the ET model with various key hyperparameters is employed to learn and fit the training set Q-1. During the fitting process, the fivefold cross-validation method⁴⁰ is incorporated. It allows for a more stable and accurate estimation of the loss function g(u) for each set of hyperparameters u = (u₁, u₂, …, u_w). This forms a mapping relationship between hyperparameters and loss functions. Subsequently, this mapping will serve as the prior sample data D_1~w = {(u₁, g₁), (u₂, g₂), …, (u_w, g_w)} for the BO algorithm.

STEP 3 Obtaining of the posterior probability distribution of the loss function g_w+1 corresponding to the new sampling point u_w+1. Gaussian Process Regression is employed to learn and fit the prior sample data D_1~w. The prior probability distribution of the loss function g_w+1 corresponding to the new sampling point u_w+1 is updated. The posterior probability distribution of g_w+1 is calculated using Bayes’ theorem.

STEP 4 Determination of the value of the optimal hyperparameter u_w+1. The difference between g_w+1 and the optimal value g_best in the current sample data set D_1~w is expressed as the degree of improvement I(g). During this process, the expected value of I(g) is calculated by selecting the Expected Improvement (EI) function as the acquisition function. Based on the posterior probability distribution of g_w+1, the maximum expected value is used to continuously update the direction of search for the hyperparameters. This approach determines the global optimal solution u_w+1 in the search space.

STEP 5 Evaluation of the model. The BO-ET model with the optimal hyperparameter u_w+1 serves as the fatigue life prediction model. The model is tested using the test set Q-2. During this period, the coefficient of determination (R²) and the Mean Absolute Error (MAE) are chosen as model evaluation metrics⁴¹. The calculation formulas are presented in formula (16). Specifically, R² indicates the fit degree between predicted values and true values of the model, typically ranging from 0 to 1. The closer R² is to 1, the better the model fits the sample data. MAE measures the difference between predicted values and true values of the model. It represents the average of the absolute errors. The closer MAE is to 0, the higher the prediction accuracy of the model.

$$\left\{ \begin{aligned} & {\rm {MAE}} = n^{{ - 1}} \sum\limits_{{i = 1}}^{n} {|\hat{y}_{i} - y_{i} |} \\ & {\rm{R}}^{2} = 1 - {{\sum _{{i = 1}}^{n} (\hat{y}_{i} - y_{i} )^{2} } \mathord{\left/ {\vphantom {{\sum _{{i = 1}}^{n} (\hat{y}_{i} - y_{i} )^{2} } {\sum _{{i = 1}}^{n} (\bar{y}_{i} - y_{i} )^{2} }}} \right. \kern-\nulldelimiterspace} {\sum _{{i = 1}}^{n} (\bar{y}_{i} - y_{i} )^{2} }} \\ \end{aligned} \right.$$

(16)

where, $y_{i}$ is the true value of the sample data. $\hat{y}_{i}$ is the predicted value of the regression model. $\overline{y}_{i}$ is the average of the true values of the sample data. n is the number of samples.

Posture configuration optimization method for folding booms of the pump truck under life extension control

Kinematic analysis of the folding boom

The folding boom of the pump truck is analogous to a series of robots with six degrees of freedom in space. It can be simplified into a rigid structural system. The D-H coordinate system can be employed for the kinematic modeling and theoretical analysis of the folding boom. This system comprises four specific parameters: kinematic pairs (either rotation or translation) at each joint, the direction of the joint axis, the length of the joint, and the angle of the joint. In this coordinate system, the spatial position of the end of the boom can be expressed based on the motion parameters of each joint. Conversely, the motion parameters of each joint can be reversely solved according to the spatial position of the end of the boom. Consequently, the joint coordinate system for the structural system is established using the D-H coordinate system, as shown in Fig. 7. The relevant D-H parameters are listed in Table 1.

Fig. 7

The joint coordinate system for folding booms.

Table 1 D-H parameters of the folding boom system.

α_i and β_i are both vectors. Counterclockwise is positive and clockwise is negative. L_i and l_i are also vectors. α_i and A_i satisfy Eq. (17):

$$\left\{ \begin{aligned} & \alpha _{2} = A_{1} \\ & \alpha _{{i + 1}} = A_{i} - 180^\circ ,i = 2 \sim 6,i \in N^{ + } \\ \end{aligned} \right.$$

(17)

By utilizing the transformation matrix of homogeneous coordinates ${}_{i}^{i - 1} E\left( {\alpha_{i - 1} } \right)$ (see formula (18)), the coordinate system of the boom joint point i-1 is transformed into that of joint point i. Therefore, $[X_{0} ,Y_{0} ,Z_{0} ]$ is taken as the base coordinate system. The transformation matrix for the coordinate system $[X_{8} ,Y_{8} ,Z_{8} ]$ at the end of the boom, relative to the base coordinate system, is presented in formula (19):

$${}_{i}^{i - 1} E\left( {\alpha_{i - 1} } \right) = \left[ {\begin{array}{*{20}c} {\cos \alpha_{i} } & { - \sin \alpha_{i} \cos \beta_{i} } & {\sin \alpha_{i} \cos \beta_{i} } & {l_{i} \cos \alpha_{i} } \\ {\sin \alpha_{i} } & {\cos \alpha_{i} \cos \beta_{i} } & { - \sin \beta_{i} \cos \alpha_{i} } & {l_{i} \sin \alpha_{i} } \\ 0 & {\sin \beta_{i} } & {\cos \beta_{i} } & {L_{i} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$

(18)

$${}_{8}^{0} E\left( {\alpha_{i - 1} } \right) = {}_{1}^{0} E\left( {\alpha_{0} } \right){}_{2}^{1} E\left( {\alpha_{1} } \right){}_{3}^{2} E\left( {\alpha_{2} } \right){}_{4}^{3} E\left( {\alpha_{3} } \right){}_{5}^{4} E\left( {\alpha_{4} } \right){}_{6}^{5} E\left( {\alpha_{5} } \right){}_{7}^{6} E\left( {\alpha_{6} } \right){}_{8}^{7} E\left( {\alpha_{7} } \right)$$

(19)

By combining Eqs. (18) and (19), the various parameters of the boom are incorporated into the transformation matrix of the coordinate system. Consequently, the coordinate $(x,y,z)$ of the end of the boom in the base coordinate system is obtained as:

$$\left\{ \begin{aligned} & x = c_{1} (l_{2} c_{2} + l_{3} c_{{2 - 3}} + l_{4} c_{{2 - 4}} + l_{5} c_{{2 - 5}} + l_{6} c_{{2 - 6}} + l_{7} c_{{2 - 7}} ) + s_{1} \sum L_{i} \\ & y = s_{1} (l_{2} c_{2} + l_{3} c_{{2 - 3}} + l_{4} c_{{2 - 4}} + l_{5} c_{{2 - 5}} + l_{6} c_{{2 - 6}} + l_{7} c_{{2 - 7}} ) + c_{1} \sum L_{i} \\ & z = l_{2} s_{2} + l_{3} s_{{2 - 3}} + l_{4} s_{{2 - 4}} + l_{5} s_{{2 - 5}} + l_{6} s_{{2 - 6}} + l_{7} s_{{2 - 7}} + L_{{1 - 2}} \\ \end{aligned} \right.$$

(20)

where, $L_{1 - 2}$ represents the distance from Z₁ to Z₂ along Z₁. $c_{i} = \cos \alpha_{i}$. $c_{i - n} = \cos (\alpha_{i} + \alpha_{i + 1} + ... + \alpha_{n} )$. $s_{i} = \sin \alpha_{i}$. $s_{i - n} = \sin (\alpha_{i} + \alpha_{i + 1} + ... + \alpha_{n} )$.

Posture configuration optimization for folding booms of the pump truck

Construction of optimization model

Once the pouring point is determined, it is incorporated into the kinematic analysis from “Construction of fatigue life sample” section to solve for the posture inversely. Various postures of the boom can achieve the specified conveying distance and height. It is currently impossible to identify a single optimal posture for a specific conveying task. Therefore, a mathematical model for posture configuration optimization is developed to minimize damage and extend lifespan. The model considers the included angle A_i of the folding boom as a design variable. Simultaneously, the fatigue life of the boom structure is set as the first objective function. Additionally, to minimize the Euclidean distance e_j (j = 1,2,3,4) from the end of the boom (x_j, z_j) to the target pouring point (x^*, z^*), this distance must be minimized. Thus, the Euclidean distance e_j is designated as the secondary objective function. This optimization model aims to determine the optimal posture of the folding booms of the pump truck. The specific formulation of the objective function is presented in Eq. (21).

$$\left\{ \begin{gathered} \max N_{sk} = F(\theta_{i} ,F_{p} ) = F(f(A_{i} ),F_{p} ) \hfill \\ \min e_{j} = \sqrt {(z_{j} - z^{ * } )^{2} + (x_{j} - x^{ * } )^{2} } \hfill \\ \end{gathered} \right.$$

(21)

where, $N_{sk}$ is the fatigue remaining life of detection point k. $F(\theta_{i} ,F_{p} )$ is the fatigue life prediction model based on the BO-ET model (see 4.2), where, $\theta_{i} = f(A_{i} )$, it can be converted according to formula (1).

For constraints, the regional planning method is employed to divide the pouring area in conjunction with the typical posture of the folding boom. Corresponding constraints are established for the divided areas. The motion trajectory of folding booms of the pump truck shows that the reachable area at the end of the boom forms a spatial hemispherical shape. The turntable defines the overall orientation of the folding boom. Therefore, for any rotation angle α₁, the reachable area at the end of the boom forms a right-angle fan (see Fig. 8). This coordinate system is equivalent to the base coordinate system in the D-H coordinate system. The self-constraints of the boom can be established based on its overall morphological characteristics in the typical posture. The value range for the included angle A_i of the boom within the reachable area is specified in formula (22). Based on the pouring range achievable by the typical posture of the boom, the corresponding reachable areas R_j (j = 1,2,3,4) are defined. Specifically, the reachable area of the upright end of the boom P₁(x₁, z₁) is defined as 0 < x₁ ≤ x_s and z_m ≤ z₁ ≤ z_b. The reachable area of the quasi-horizontal end of the boom P₄(x₄, z₄) is defined as x_m ≤ x₄ ≤ x_b and 0 ≤ z₄ ≤ z_s. The remaining areas within the right-angle fan are designated as the reachable areas for the conventional arched end of the boom P₂(x₂, z₂) and the M-shaped end of the boom P₃(x₃, z₃).

$$\left\{ \begin{aligned} & A_{{j,i\min }} \le A_{i} \le A_{{j,i\max }} \\ & (x_{j} ,z_{j} ) \in R_{j} \\ \end{aligned} \right.$$

(22)

Fig. 8

Division of reachable areas of the end of the boom.

where, $A_{j,i\min }$ and $A_{j,i\max }$ are the minimum and maximum values of the included angles of each boom set in region R_j, respectively.

Solution of the optimization model

Ant Colony Optimization (ACO)⁴² is a heuristic algorithm introduced by Marco Dorigo in 1990. During foraging, ants release and detect pheromones, dynamically adjusting their search directions. ACO simulates this behavior to identify optimal solutions. It offers high adaptability, flexibility, and parallel processing capabilities. It is particularly effective in solving mathematical model for posture configuration optimization. Common methods for multi-objective optimization include the weighting method, ε-constraint method, Pareto ranking, and objective aggregation. Among these, the ε-constraint method⁴³ is highly flexible. It systematically explores the entire solution space, effectively reducing subjectivity in selecting objective function weights. Therefore, this article applies the ε-constraint method to convert the multi-objective optimization model into a single-objective one. This significantly simplifies the solution process and enhances computational efficiency.

Existing studies indicate that the quality of the initial solution of the ACO and the concentration of pheromones significantly influence both the solution process and outcomes⁴⁴. To address this, improvements are made to the search for the ACO’s initial solution and adjustment of pheromones. The constraints on the coordinates of the end of the boom in the optimization model are stringent. Finding a high-quality initial solution that meets these constraints is challenging. Consequently, a local search strategy based on neighborhood perturbation is applied. Each dimension of the current initial solution is slightly perturbed and evaluated to retain the superior solution. The locally optimal solution, discovered through iterations, serves as the initial solution for the ACO. To enhance the capability of global search and efficiency of convergence of the algorithm, the fixed pheromone is replaced with the adaptive pheromone. Pheromone levels of better solutions are increased while older pheromones decay over time. This guides the ant colony toward the correct direction of search. The implementation flow of the improved ACO is shown in Fig. 9. The detailed solution steps are as follows:

Fig. 9

Implementation flow of improved ACO.

Step 1 Conversion from multi-objective to single objective. Applying the ε-constraint method, the first objective function ($\max N_{sk}$) is treated as the primary objective. The second objective function ($\min e$) is converted into a constraint that meets Eq. (23). This method reduces the dual-objective optimization model to a single-objective model.

$$e_{j} \le \varepsilon$$

(23)

where, ε is the maximum distance from the end of the boom to the pouring point. It can be determined according to requirements of accuracy.

Step 2 Parameter initialization. Parameters of the algorithm are initialized in this process. They include the number of ants (num_ants), maximum iterations (num_iterations) S, pheromone importance factor (alpha), heuristic importance factor (beta), pheromone decay factor (decay), maximum heuristic searches (iterations) s, neighborhood perturbation range (Δt), maximum distance ε from the end of the boom to the pouring point, and the coordinates of the pouring point.

Step 3 Heuristic search for initial solution. Ants are dispatched to explore feasible paths, and a set of initial solutions h_o is randomly selected. Then small perturbations up to Δt are applied to each dimension of h_o. A new initial solution h_o-new will be generated. The better solution h_o-better is retained by evaluating and comparing h_o and h_o-new. This process of “perturbation— > h_o-new— > h_o-better” needs to be repeated until the number of iterations k reaches maximum heuristic searches s. The retained solution is output as the locally optimal initial solution h_o-best.

Step 4 Adaptive adjustment of pheromones. The concentration of pheromones on the searching path is updated according to h_o-best (see Eq. (24)). All the ants are deployed, and the colony is directed towards the path with a high concentration of pheromones. Thus, a new solution h_new is generated. h_new is evaluated and compared with the previous solution h_before. If h_new outperforms h_before, the concentration of pheromones on the new path is increased. If not, the original concentration of pheromones is retained. The process of “concentration of pheromones updating— > h_new” needs to be repeated until the number of iterations q reaches the maximum iterations S. The final path chosen by the colony (i.e., the global optimal solution h_all-best) is output.

$$\tau_{ij} (t + 1) = (t + 1)\tau_{ij} (t) + \vartriangle \tau_{ij}$$

(24)

where, $\rho$ is the volatilization factor of pheromones. It reflects the natural decay of pheromones over time. $\vartriangle \tau_{ij}$ is the increase in the concentration of pheromones.

Step 5 Output of solution results. The output result of STEP 3 h_all-best is required to be a set of included angles of the boom. It should be converted into a set of tilt angles of the boom. As a result of improved ACO for solving optimization models, the H_all-best is obtained. If the coordinates of the pouring point fall within regions R₂ and R₃, the optimal solutions obtained in each of the two postures need to be compared. The optimal solution is taken as the final output result.

Posture configuration system for folding booms of the pump truck

Based on the aforementioned theories and methods, the “Posture configuration system for folding booms of the pump truck under life extension control” has been developed through algorithm encapsulation and module integration. This system enables multifunctional control of a single platform. The operation process in actual engineering applications is also simplified. In addition, intuitive real-time feedback of equipment information and display of posture configuration results are provided through the visualization interface.

In terms of system functionality, four main functional modules are contained within the system. (1) Equipment information module. The equipment parameters of the concrete pump truck are displayed by this module, including type of equipment, size of whole machine, and size of structure. This facilitates a comprehensive understanding for the information of the machine. (2) Equipment monitoring and data visualization module. The service processes of both the physical machine and the virtual machine are demonstrated in real-time through virtual-real synchronization. The behavioral and performance characteristics of the data collected by sensors are displayed in real-time. (3) Fatigue life assessment and visualization module. Simulation data are integrated with the collected data. Fatigue life evaluation results for each set of behavioral characteristics are obtained and displayed according to the construction method of the fatigue life sample (see “Construction of fatigue life sample” section). (4) Posture configuration module for the boom. The constructed fatigue life prediction model BO-ET, combined with the posture configuration method (see “Posture configuration optimization for folding booms of the pump truck” section), is used to determine the optimal posture under any conveying distance and height. Once the conveying distance and height from the bottom of the turntable to the desired pouring point are input, the optimal posture is presented in the form of data and virtual machine images. At the same time, commands are pushed to the operator.

In terms of the process of system development, it involves the joint development of several software programs. Several elements, such as data acquisition and integrated processing, fatigue life evaluation, rapid fatigue life prediction, and posture configuration of the boom, are included. The process of specific development is illustrated in Fig. 10. The virtual machine is constructed through the combined use of “Solidworks modeling— > 3Ds Max rendering— > Unity 3D interactive environment”. The motion relationship of the virtual model is defined using C# scripts. Images of the real machine, captured by the industrial camera, are processed and rendered using OpenCV and OpenGL libraries. Then they are transferred to the front-end interface. Real-time monitoring of the real machine is achieved in this way. At the same time, the system interface transfers the acquired service information (see Chapter 3) from the local server to C# via Javascript. The linkage between the virtual machine and the real machine is achieved. The fatigue life evaluation algorithm, the fatigue life prediction model BO-ET, and the posture optimization algorithm of the boom are developed using Python. The fast solution of the optimal posture for a specific pouring task and the rapid fatigue life prediction are achieved. The results are transmitted to the display area of the posture configuration module via Javascript.

Fig. 10

The process of system development.

In terms of visualization presentation, an interactive interface for macro display and user operation is provided, as shown in Fig. 11. The method for fatigue life prediction and position configuration method for the boom guide the functions of the interface. The artistic design concepts of simplicity, balance, and hierarchy are incorporated into the interface.

Fig. 11

System visualization interface. This figure was created by Visual Studio Code 2019 version 1.41 software (https://code.visualstudio.com/updates/v1_41) and Unity 3D 2021.3.37 (https://unity.cn/releases#undefined).

As shown in Fig. 11, the main interface of the system is built using the Visual Studio Code editor, integrating four functional modules. Elements such as click buttons, hover buttons, input boxes, an image display box, and a data display box are included. The specific realization process is outlined as follows. (1) The structure and content of the web page are defined through HTML. CSS is used to enhance the appearance and layout of the web page and to control the style of each element. The interactive functions and dynamic behaviors of each element are implemented through JavaScript. Different realization elements are configured under each functional module. ①Three click buttons are configured under the equipment information module. When clicked, these buttons direct the interface to specific content. ②A square hover button, a round hover button, and a synchronized screen display are configured under the equipment monitoring and data visualization module. When the mouse hovers over these buttons, the data collected by the corresponding sensors is displayed in real-time as dynamic line graphs. ③A round hover button is also provided under the fatigue life assessment and visualization module. It is used to display the evaluation results for the fatigue life of booms in different postures in real-time. ④The posture configuration module for the boom is designed as the main interactive area. It contains user input boxes (for inputting conveying distance and height), click buttons (for running the calculation program when clicked), a data display box, and an image display box. (2) The operator can write the conveying distance and height of the determined pouring point into the corresponding input boxes. Clicking the “CALCULATE” button activates the fatigue life prediction and posture configuration optimization algorithm (written in Python). The results are presented as data and images in their respective display boxes. This allows the operator to precisely control the real machine based on the results.

Instance validation

Experiment validation

To validate the feasibility of the proposed method, A three-section boom small pump truck folding boom experimental bench has been constructed, as shown in Fig. 12. Based on the principle of easy to difficult, experimental and then practical application, the engineering problem of the posture optimization of the boom is reasonably simplified, specifically including the following four aspects.

• 1. Physical modeling. For a certain pouring position in the actual construction process, the pump truck boom can reach the pouring position at the end of the boom through a variety of different posture configurations. However, the experimental conditions have certain restrictions, the experimental space has limitations, and the experiment is difficult. Therefore, when conducting the relevant experiments, the number of the boom of the experimental pump truck was selected as three. Such a program, on the one hand, can ensure the existence of multiple sets of boom postures can meet the pouring requirements. On the other hand, it is also sufficient to effectively verify the proposed method. Starting from simulating the function of the real machine, the experimental bench should have the luffing mechanism and pumping system similar to the real machine. The real machine adopts hydraulic cylinders to control the luffing movement of the boom system. It also adopts high-pressure piston pumps and alloy steel pipes to pump the concrete. In order to realize the same operation action, the experimental bench is equipped with BST-YF-JF DC actuator motor. Its parameters include thrust force of 4000N, stroke of 150 mm, and voltage of 24V. Full coverage of the posture of the folding boom is realized by controlling the expansion and contraction of the actuator. At the same time, the sludge pump with power 400W and PVC pipe with inner diameter 20mm are used to realize the pumping of fluid. The purpose of the experiment is mainly to verify the feasibility of the posture optimization method. Therefore, in terms of structure and material selection, the material used for the experimental bench is Q235. The boom structure is a box-type welded structure with a plate thickness of 2 mm.

• 2. Validation indicators. The proposed method contains the indicators mainly include the tilt angle of the boom, pumping pressure and the stress history data of the dangerous points on the dangerous section. In the experiment, the dangerous points in the section at the boom root of the first two sections of the boom are also taken as the detection points. The tilt angle of the boom and the stress history data of the dangerous points are taken as indicators. The pumping system can be used in the way of variable pressure.

• 3. Experimental method. The YBM-78A tool-type surface strain gauges are installed at the boom roots (detection points MS1 and MS2) of the first and second boom using a full-bridge connection. Based on the acquisition scheme and analysis process of the real machine, the experimental bench is controlled to pump in different bit positions. The analog signals collected by the strain gages are converted to digital signals by the DH5902N (32CH) rugged data acquisition device. They are then stored in the ITA-3650 industrial computer for subsequent analysis and calculations.

• 4. Data analysis. Taking the posture configuration optimization method for the folding boom under life extension control proposed in this paper as the theoretical basis, the posture configuration optimization model for the experimental bench is constructed. Subsequently, the improved ant colony algorithm is used to solve it. The optimal posture of a specific pouring location is obtained. The specific analysis results are shown in “Fatigue life prediction” and Posture configuration optimization for folding booms of the pump truck” sections.

Fig. 12

The test bench for small folding booms of the pump truck.

Fatigue life prediction

Fatigue life dataset

To enhance the applicability of the experimental data, uniform sampling is applied across the rotation range of each boom. The sampling results are combined to generate multiple postures of the boom. The pumping system operates at rated power for the boom in different postures. Strain data from detection points MS1 and MS2 are collected during stable pumping conditions at an acquisition frequency of 10 Hz. Using the fatigue life calculation method (refer to “Construction of fatigue life sample” section), the strain data are converted into a fatigue life dataset. For material Q235, parameters C₀ = 2.61 × 10^–13 and m = 3.07 are used in the calculations. The initial crack length l₀ of each boom is measured via nondestructive flaw detection, with a tolerance of 0.5mm. The critical crack length l_d is determined by the plate thickness of each boom. The critical crack length of the first and second boom are taken as 2mm and 1mm in turn. It is assumed that the process of pumping at the same posture lasts 2 min, with an annual average of 300 experimental days and 10 h per day. The fatigue life dataset comprises a total of 68 data sets (see Fig. 13).

Fig. 13

Experimental dataset of fatigue life.

Fatigue life prediction results

The BO-ET model is utilized to train and tests the dataset. The hyperparameter search space for n_estimators and max_depth in Bayesian Optimization is set to [100, 800] and [5, 40], respectively, with integer-only values. The search process is conducted over 200 iterations. This study uses an Intel Core i7-8750H processor, an NVIDIA GTX1050Ti 4GB GDDR5 GPU, 8GB of RAM, and the Windows 10 operating system. All tests are performed on this hardware for consistency. Figure 14 presents the specific test results.

Fig. 14

Test results of BO-ET model.

As shown in Fig. 14, most coordinate points formed by the true and predicted values lie near the contour line. The linear regression line also closely aligns with the contour line. It indicates that the BO-ET model demonstrates a strong fitting ability. The fitting accuracies for stress detection points MS1 and MS2 both exceed 0.96. Regarding prediction error, the MAE value is positively correlated with the true value. Specifically, the MAE for MS1 is approximately 6.23% of its value, while the MAE for MS2 reaches 15.32% due to a few points with significant prediction deviations. These results demonstrate the high prediction accuracy of the BO-ET model. It enables fast fatigue life predictions for the folding boom. Regarding the learning time of the model, given the hyperparameter search space, number of iterations, and hardware setup, the BO-ET model completes training in 403s and 386s. Compared to traditional methods, this represents a significant improvement in the efficiency of fatigue life assessment.

Posture configuration optimization for folding booms of the pump truck

The kinematic positive solution analysis method described in “Kinematic analysis of the folding boom” section establishes the D-H coordinate system of the test bench for small folding booms of the pump truck. Taking the bottom center of the turntable as the origin and combined with Eq. (25), the coordinate equation of the end of the boom relative to the base coordinate system is obtained. The relevant D-H parameters are presented in Table 2.

Table 2 D-H parameters of the test bench for small folding booms of the pump truck.

The parameters in Table 2 indicate that the test bench can only achieve the conventional arch posture. The constraints for the area planning method (see “Posture configuration optimization for folding booms of the pump truck” section) are expressed as follows:

$$0^\circ \le A_{1} \le 90^\circ ,0^\circ \le A_{2} \le 70^\circ ,180^\circ \le A_{3} \le 230^\circ$$

(25)

Five pouring points (1.2, 0.4), (0.85, 0.22), (0.98, 0.17), (1.03, 0.1), and (0.91, 0.36) are randomly selected from the reachable area of the end of the boom. They are solved separately using the posture configuration optimization method from “Posture configuration optimization for folding booms of the pump truck” section. As shown in Fig. 12, the fatigue life at detection point MS2 is generally lower than that at MS1. Therefore, the fatigue life of MS2 is selected as the objective function. The maximum Euclidean distance from the end of the boom to the pouring point is set to ε = 0.7. The parameters settings for the improved ACO model include: num_ants = 100, num_iterations = 500, alpha = 1, beta = 1, decay = 0.95, iterations = 50, and Δt = 0.1. The specific results obtained using the proposed method are presented in Table 3.

Table 3 Solving results for improved ACO.

Coordinate of one of the pouring points is selected and input into the “posture configuration system for folding booms of the pump truck”. Using (0.98, 0.17) as an example, the solution result is systematically demonstrated in Fig. 15.

Fig. 15

Posture configuration result of the test bench for small folding booms of the pump truck. This figure was created by Visual Studio Code 2019 version 1.41 software (https://code.visualstudio.com/updates/v1_41) and Unity 3D 2021.3.37 (https://unity.cn/releases#undefined).

From the above analysis, it can be seen that the experimental bench validates the proposed posture configuration optimization method through functional equivalent design and reasonable simplification. In the functional equivalent design, the experimental bench simulates the motion control and stress detection of the folding boom. In terms of reasonable simplification, a 3-section boom structure is adopted and Q235 material is selected. At the same time, the experimental bench carries out validation work around the core indicators such as stress distribution and posture configuration. The results show that the experimental bench not only effectively validates the feasibility of the posture optimization method, but also highly correlates with the application of the real machine. The results of the experiment provide a solid theoretical basis for the posture configuration optimization of the folding boom in the actual project.

Engineering validation

The 56X-6RZ concrete pump truck from Zoomlion Heavy Industry Science and Technology Co., Ltd serves as the research object in this section. The proposed posture configuration optimization method for folding booms of the pump truck determines the optimal posture of the boom at a specific pouring point within the scenario. The results are presented using the self-developed system. For the concrete pump truck, the maximum theoretical conveying capacity stands at 180m³/h, and the rated working pressure is 42 MPa. The maximum concrete outlet pressure is recorded at 11.3 MPa. The pumping frequency is 0.4333 Hz. The diameter and stroke of the concrete cylinder are Φ260 mm and 2100 mm. The structural configuration of its boom is identified as 56X-6RZ. The maximum height × radius × depth of the boom is 56 × 51 × 40.2 mm. The corresponding minimum spread height of the boom is 15.8 m. The inner and outer diameters of conveying pipes are Φ123 × 133 mm.

Fatigue life prediction

Fatigue life dataset

The stress history dataset S* is constructed using the data acquisition method described in “Construction of fatigue life sample” section, which combines the “measurement + simulation” method. Among them, the measured data are provided by Zoomlion Heavy Industry Science and Technology Co., Ltd. They are collected in real-time through the self-constructed concrete pump truck information acquisition system. One operational cycle consists of seven working days, with 2.4 million data sets selected from the database, see Table 4. The simulation data, obtained using ANSYS software, are used to supplement the measured data.

Table 4 Statistical table of concrete pump truck information acquisition.

The stress history dataset S is then processed and condensed through data preprocessing (The exact process can be found in Ref.³⁴). Based on the fatigue life calculation method (see “Construction of fatigue life sample” section), the processed dataset S^* is transformed into engineering dataset Q of fatigue life (see Fig. 16), comprising 1137 datasets.

Fig. 16

Engineering dataset of fatigue life.

Fatigue life prediction results

The BO-ET model is also utilized to train and test the fatigue life dataset. In this case, the relevant parameter settings for the Bayesian optimization and the hardware configuration used to run the algorithm are identical to those in “Experiment validation” section. The detailed test results are presented in Fig. 17.

Fig. 17

Prediction results of BO-ET model.

As shown in Fig. 17, the BO-ET model exhibits a strong fitting capability in engineering validation. The fitting accuracies for the stress detection points M1 to M3 exceed 0.99, while the accuracy for M4 exceeds 0.96. In terms of prediction error, the MAE values for M1 to M3 range from 0.72% to 1.44% of their respective values. However, the MAE value of M4 is higher, at 13.13%, due to larger deviations at certain individual points. The learning time of the model ranges from 650 to 760s. In practical engineering applications, the efficiency of fatigue life assessment is significantly enhanced.

Posture configuration optimization for folding booms of the pump truck

The kinematic positive solution analysis method described in “Kinematic analysis of the folding boom” section establishes the D-H coordinate system of the 56X-6RZ concrete folding booms of the pump truck. Taking the bottom center of the turntable as the origin and combined with Eq. (26), the coordinate equation of the end of the boom relative to the base coordinate system is obtained. The relevant D-H parameters are presented in Table 5.

Table 5 D-H parameters of the 56X-6RZ concrete folding booms of the pump truck.

Based on the parameters in Table 5, the conveying distances and heights for each region in the regional planning method (see “Posture configuration optimization for folding booms of the pump truck” section) are determined to be: x_b = z_b = 52.96 m, z_m = x_m = 40 m, z_s = x_s = 20 m. The constraints for the regions R₁ ~ R₄ can be specifically expressed as follows:

$$\left\{ \begin{gathered} \left\{ \begin{aligned} & R_{1} :75^\circ \le A_{1} \le 90^\circ ,160^\circ \le A_{{2,3,5}} \le 180^\circ ,180^\circ \le A_{4} \le 220^\circ ,150^\circ \le A_{6} \le 180^\circ \\ & R_{2} :0 \le A_{1} \le 15^\circ ,160^\circ \le A_{{2,3,5}} \le 180^\circ ,165^\circ \le A_{4} \le 195^\circ ,120^\circ \le A_{6} \le 180^\circ \\ & R_{3} :\left\{ \begin{aligned} & 15^\circ < A_{1} < 90^\circ ,150^\circ < A_{2} < 180^\circ ,0 < A_{3} < 150^\circ ,195^\circ < A_{4} < 360^\circ ,45^\circ < A_{5} < 175^\circ ,0 < A_{6} < 175^\circ \\ & 15^\circ < A_{1} < 90^\circ ,150^\circ < A_{2} < 180^\circ ,0 < A_{3} < 150^\circ ,120^\circ < A_{4} < 165^\circ ,185^\circ < A_{5} < 195^\circ ,0 < A_{6} < 175^\circ \\ & 15^\circ < A_{1} < 90^\circ ,0 < A_{2} \le 150^\circ ,195^\circ \le A_{4} \le 360^\circ \\ \end{aligned} \right. \\ & R_{4} :15^\circ < A_{1} < 90^\circ ,\theta _{2} \ge 0^\circ ,45^\circ \le A_{3} \le 180^\circ ,120^\circ < A_{4} \le 180^\circ ,90^\circ \le A_{5} \le 180^\circ \\ \end{aligned} \right. \hfill \\ \left( {x_{j} ,z_{j} } \right) \in R_{j} \hfill \\ \end{gathered} \right.$$

(26)

One pouring point (15.2, 48.8) and (50.6, 8.1) is selected from region R₁ and R₄, respectively. Two pouring points (20.1, 31.6) and (39.2, 17.4) are selected from regions R₂ and R₃. The optimal postures of the boom for these points are determined using the posture configuration optimization method outlined in “Posture configuration optimization for folding booms of the pump truck” section. As discussed in “Fatigue life prediction” section, the fatigue life of detection points M1 ~ M4 follows the same pattern. The fatigue life of M3 is always to be the shortest. Therefore, the fatigue life of M3 is selected as the objective function. The maximum Euclidean distance from the end of the boom to the pouring point is set to ε = 0.15. The parameter settings for the improved ACO model are consistent with those in “Experiment validation” section Table 6 presents the specific solution results. Using (20.1, 31.6) as an example, the systematic presentation of the solution results is shown in Fig. 18.

Table 6 Solving results for improved ACO.

Fig. 18

Detailed explanation of the system interface for solving results. This figure was created by Visual Studio Code 2019 version 1.41 software (https://code.visualstudio.com/updates/v1_41) and Unity 3D 2021.3.37 (https://unity.cn/releases#undefined).

Method comparison and discussion

The uncertainty in the optimization model and solution process of the boom posture configuration mainly comes from the determination of the value of the first objective function (i.e., the fatigue life prediction result). Therefore, the accuracy of the fatigue life prediction model will directly affect the optimization result of the posture. In this section, the accuracy of the BO-ET model in fatigue life prediction is further discussed using engineering validation as an example. It is divided into two aspects: horizontal comparison and vertical comparison.

Horizontal comparison

The more commonly used Random Forest model (RF)⁴⁵, Adaptive Boosting model (Adaboost)⁴⁶, and Support Vector Machine model (SVM)⁴⁷ are selected from a wide range of machine learning models for comparison with ET model. The comparison process ensures that the dataset is divided consistently. Default parameters are used for each model. The test results of each model are shown in Fig. 19.

Fig. 19

Test results for each model under horizontal comparision.

As shown in Fig. 19, the ET model has the most outstanding prediction accuracy. The R² of ET model always occupy the highest position and MAE always the lowest. Compared with the ET model, the R² of the remaining models is lower by 0.68% to 12.09%. Meanwhile, the MAE is 27.9% to 577.42% higher. This can verify the validity and superiority of the ET model as a basic prediction model.

Vertical comparison

To verify the effectiveness of the BO algorithm for the optimization of the ET model, the BO-ET model is compared with the single ET model. The details can be seen in Table 7.

Table 7 Test results of each model under vertical comparison.

Table 7 clearly reflects the superiority of the BO-ET model. Compared with the ET model, the accuracy of the BO-ET model is improved by 0.96–4.07%. Meanwhile the error is reduced by 18.25–79.78%. From this, it can be judged that the BO algorithm has a positive optimization effect on the ET model.

Combining the above two comparisons and analyses, it can be seen that the BO-ET model performs best on the fatigue life prediction task. It is sufficient to provide accurate objective function prediction values for posture optimization of the boom.

Conclusion

This paper proposes a posture configuration optimization method for folding booms of the pump truck under life extension control. The optimal posture of the boom under the dual objectives is successfully realized. It reduces fatigue damage during operation and extends the fatigue life of the boom while ensuring pouring requirements are met. In addition, an independently developed system platform is provided. The main conclusions are as follows:

• 1. This article proposes a data-driven BO-ET model for rapid fatigue life prediction of folding booms of the pump trucks. In experimental validation, the fitting accuracy (R²) of the model ranges from 0.96 to 0.98. The MAE is between 6.23 and 15.32% of the true value. In engineering validation, the R² exceeds 0.96, reaching up to 0.99. While the MAE ranges from 0.72 to 13.13%. These results demonstrate the strong fitting capability and high accuracy of the model. It significantly improves the efficiency of fatigue life assessment.

• 2. A posture configuration optimization method for folding booms of the pump truck is developed based on the concept of life extension control. The solution process of the improved ACO algorithm is given. This method enables the intelligent configuration for the posture of the boom. It can effectively minimize fatigue damage caused by manual control. Experimental validation and engineering validation confirm the feasibility of the proposed method.

• 3. To meet market and user needs, this paper develops a “posture configuration system for folding booms of the pump truck”. The system offers real-time equipment monitoring and multifunctional control on a unified platform. It significantly simplifies the operation process for engineering applications.