Generalized fractional modeling and optimal control of respiratory syncytial virus infections in Florida

Abstract

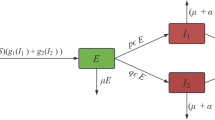
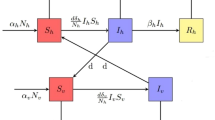
This study explores and investigates a human respiratory syncytial virus (RSV) infection using a generalized fractional-order susceptible-exposed-infected-recovered (SEIR) model. The model incorporates the recently introduced fractional derivative operator, the $\psi$-Caputo derivative, defined with respect to an auxiliary function, $\psi (t)$. The formulation allows flexible depiction of memory and genetic effects in disease dynamics, beyond integer-order models. A rigorous mathematical framework proves the existence and uniqueness of solutions to the $\psi$-Caputo fractional initial-value problem (IVP), proving the model’s theoretical well-posedness. We also offer an innovative and efficient numerical approach for solving the fractional model, with verified convergence and a valid error bound. Comprehensive simulations and analyses are conducted to the applicability of the model. In particular, the model represents diverse dynamic behaviors by varying the fractional order $\alpha$ within the range (0, 1]. These results indicate that the system’s reaction is sensitive to the fractional order $\alpha$, with classical integer-order dynamics regained when $\alpha \rightarrow 1$. Furthermore, the fractional SEIR model with an optimal control framework uses treatment as a control variable to evaluate intervention options. Simulation results indicate that the fractional $\psi$-Caputo model, with optimal control, better decreases infectious people than standard integer-order models. These findings demonstrate the modeling and control approach’s potential to analyze, predict, and mitigate RSV infections in real-world circumstances.