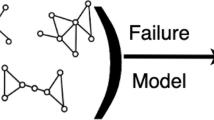
Abstract
According to control theory, a dynamical system is controllable if, with a suitable choice of inputs, it can be driven from any initial state to any desired final state within a finite time. Most dynamic characteristics of real networks are nonlinear, so achieving target control is more practical and necessary. The network’s control energy is also a problem that must be considered. Whether and how to control the complex system of the industrial chain has high theoretical and practical significance. In this study, we use the GARCH model, DCC model, and network structure control theory comprehensively to study the price fluctuation risk of the mining stock market from the perspective of the industry chain and network control dynamics and obtain interesting results. (1) Risk conduction among stocks has a prominent industry-driving effect, and the risk conduction ability of upper and middle stocks is stronger. (2) The risk regulation cost, time cost, and node number cost of the whole-industry chain are all higher than those of the two-tier chain, which indicates that the correlation complexity of the network has a positive relationship with risk control. (3) Key risk nodes play an essential role in risk control, so monitoring key stocks from the industrial chain perspective is necessary to control risks in time. This work can provide valuable suggestions for market regulators and policy-makers in terms of risk management and control.
Similar content being viewed by others
Introduction
With the rise and vigorous development of complex network research, structural controllability has attracted extensive attention and much research from relevant researchers in physics (Zhao et al., 2023), biology (Newby et al., 2022), and economics (Galbiati et al., 2013) because of its importance in systems engineering applications. In complex system research, we always hope that the state of each node in the system can change to the desired state, which is the problem of complex network system control (Liu et al., 2011). The financial market is a complex system, and research on its risk control is highly important. In recent years, China has put forward the goal of “carbon neutrality”, proposing to optimize the structural reform of the supply side of energy and resources and give play to the role of mining as a “booster” in carbon reduction. This will inevitably lead to uncertainty in China’s mining financial market and the risk of sharp fluctuations in stock prices. This will inevitably lead to uncertainty in China’s mining financial market and the risk of large stock price fluctuations, increasing the uncontrollability of the system and attracting greater attention from scholars and managers. Recently, there has been much research on price volatility transmission and risk conduction (Xie et al., 2021; Zhang et al., 2023). With the requirement of “focusing on improving the toughness and safety level of the industrial chain”, it is necessary to understand how the risk of stock price volatility in the mining industry chain is transmitted and how to control it. Solving this problem can provide suggestions for policy-makers and market regulators to monitor the mining stock market better and prevent risks in time.
At present, studies on price fluctuations focus mainly on time series analysis and use methods such as the Pearson correlation (Li et al., 2022; Yuan et al., 2020), Granger causality (Gao et al., 2018; Wang et al., 2020) and pattern causality (Sun et al., 2024) to define the correlation between stock prices. An increasing number of scholars are studying the spillover relationship of price volatility using the copula model (Dai et al., 2020; Wang et al., 2021b), the DCC model (Jiang et al., 2022; Kim et al., 2020) and the GARCH model (Chen et al., 2020). Some scholars have constructed the GARCH time-varying copula-CoVaR model to dynamically study the price spillover relationship (Xu et al., 2021), while others study the spillover relationship of stock prices based on the basis of the BEKK-GARCH model (Ahmed and Huo, 2021; Xie et al., 2021). At present, the econometric model is still the mainstream model of risk measurement. Many scholars have adopted Granger causality (Gao et al., 2018; Wang et al., 2021a), and the entropy model (Niu and Lu, 2021) to analyze the risk contagion. An increasing number of scholars have measured CoVaR and delta CoVaR, which are good measures of the systemic risk contribution, spillovers of financial individuals, and even tail risks. The DCC (Zhang et al., 2023) and GARCH models (Abuzayed et al., 2021) are the main methods used for measuring risk. Compared with quantile regression or the copula method, the GARCH model can better describe the nonlinear structure and dynamic characteristics of time series data, which is consistent with the research purpose of this paper. Therefore, we adopt BEKK-GARCH and DCC-GARCH to measure the spillover effect of stock price volatility and the risk spillover relationship.
In terms of risk control, previous scholars have focused on macroeconomic indicators (Christensen and Li, 2014; Kaminsky and Reinhart, 1999), corporate financial information (Shang et al., 2021), capital market information (Tan et al., 2023), etc., and built a risk indicator system and a risk early warning index system. At present, machine learning models such as quantile random forests, support vector machines, and deep neural networks, provide practical tools for effectively predicting financial risk (Aprillia et al., 2021; Huang et al., 2021; Ristolainen 2018). Some scholars carry out risk control according to monetary and fiscal policies, with monetary policy playing a more critical role (Fratzscher and Rieth, 2019). With the proposal of the new regulatory concept of “too connected to fail”, an increasing number of scholars have begun to conduct risk control from the network perspective. Some scholars have constructed a global economy risk network and proposed a control strategy (Brissette et al., 2021). Some scholars have used combinatorial optimization to control contagion regarding complete information in the interbank network (Fukker and Kok, 2024). Some have investigated how the two risk control strategies inhibit credit risk contagion among enterprises in the network (Qian et al., 2023). Current risk control is more inclined to control multiple complex relationships rather than superficial relationships.
Lombardi A first proposed the concept of network controllability (Lombardi and Hrnquist, 2007) and, for the first time, equated the state transition matrix of a linear system to the weighted adjacency matrix of a network system. In 2011, scholars combined traditional control theory with complex networks (Liu et al., 2011), and the problem of selecting control nodes in large-scale network systems was solved. Some scholars subsequently proposed the criterion and theory of accurate controllability (Yuan et al., 2013), further developing the controllability of complex networks. Many scholars have conducted relevant studies on network control, including optimal control of complex network ageing (Sun et al., 2020), structure control of complex networks on the basis of nonlinear dynamics (Zañudo et al., 2017), and network structure control and dynamic control (Gates and Rocha, 2016). Scholars have proposed dynamic control theories and methods for nodes or edges in networks (Gao et al., 2015; Lu et al., 2020). This method provides a new research idea and direction for risk control in the network. Introducing network structure control theory into the study of financial risk control is valuable.
Hence, we attempt to construct a research framework that combines econometrics, cascade conduction, and structural control theories to realize the risk control of price fluctuations in the industrial chain. First, on the basis of the BEKK-GARCH model and sliding window, we measure the volatility spillover effect of stocks under different windows. Second, on the basis of the DCC-GARCH model, the systematic spillover risk (Delta CoVaR) among stocks is calculated, and the risk cascade conduction network model based on CoVaR is then constructed. Third, we construct the risk control network model by combining the structural control and energy consumption minimization theories. Finally, combined with the industrial chain, we set up different cases of the industrial chain and analyzed the risk regulation signals and control strategies under different cases.
This paper makes two contributions. To our knowledge, this paper is the first to provide insights into the risk control of price fluctuations in mining stock, combining the network control dynamics model and industry chain theory. This study can provide market managers and policy-makers with a reference for risk control. Second, this study is the first to apply network structure control theory to risk control in the stock market and explore risk control signals and strategies in different situations, significantly expanding the methods and means of stock market risk control research.
Data and methods
Data description
The data are from the Choice database. Listed mining companies belong to the mining, smelting, and manufacturing industries under the China Securities Regulatory Commission (CSRC) industry classification. They are in the industrial chain’s upper, middle, and lower reaches. We went through a process that selected 83 companies; the detailed information can be found in Table S1 in the supplementary information. The closing prices of 83 listed mining companies are selected as the research data. The study period is from January 2, 2020, to December 31, 2021, for a total of 486 trading days. The closing price measures the volatility spillover effect and risk spillover value between stocks.
Methods
Volatility spillover effect based on BEKK-GARCH
The BEKK-GARCH model is used to calculate the spillover effect between stocks. We adopted a binary BEKK-GARCH model, which consists of two parts: the mean value equation and the variance equation, as shown in Formulas (1)–(3).
Mean equation:
Variance equation:
The spillover effect includes the shock and the volatility effects. The shock effect from stock 1 to stock 2 is represented by \({a}_{12}\); the volatility effect from stock 1 to stock 2 is represented by \({b}_{12}\). The total volatility spillover effect (SP) of stock 1 to stock 2 is shown in Formula (4):
Risk cascade conduction network model based on DCC-GARCH-CoVaR
The concept of conditional value at risk (CoVaR) can measure financial individuals’ degree of systemic risk contribution and risk spillover effect (Adrian and Brunnermeier, 2016). Moreover, delta CoVaR is good at capturing tail risk in extreme situations (Rodríguez-Moreno and Peña, 2013). The DCC-GARCH model is widely used to study the time-varying correlation between variables. We use it to fit the stock return, and the time-varying \(\Delta {{CoVaR}}_{q}^{{i|j}}\) is obtained (Engle, 2002). The dynamic correlation coefficient \({\rho }_{t}^{{ij}}\) is obtained, and the expressions of the VaR and CoVaR can be written as:
where \({\hat{\mu }}_{t}^{i}\) is the average value estimated by the GARCH model and Q(q) is the q quantile value of the distribution. The key to solving \({{VaR}}_{q,t}^{i}\) is to obtain the conditional standard deviation by fitting the univariate GARCH model, and the key to solving \(\triangle {{CoVaR}}_{q,t}^{\left.i\right|j}\) is to find the dynamic correlation coefficient \({\rho }_{t}^{{ij}}\) by using the DCC function.
Combined with the sliding window method, we construct a dynamic network with a window length of \(k\) and a sliding step length of \(s\). We set the sizes of k and s to 240 and 5, respectively, which is mainly considered from a realistic perspective and by the characteristics of stock price data. Stock price data are high-frequency time series data. The window length of 240 days is exactly one year, and the opening time of the stock price is 5 days a week. This setting can be analyzed not only from a long-term perspective but also in combination with short-term changes, which helps us gain a comprehensive understanding of stock price fluctuations.
Listed mining companies are located in different industrial chain positions, so the industrial driving coefficient is considered when setting the risk conduction rules. Combined with the input‒output table, we calculated the backwards correlation as the industry-driving effect size (risk amplification ability) among stocks. We determined the antirisk ability according to enterprise financial operations. The financial operation of an enterprise is reflected by the Z value index, which comprehensively considers factors such as the asset scale, liquidity, profitability, financial structure, and debt-paying ability and can reflect the ability of an enterprise to resist risk. When the Z value is greater than 2.675, the enterprise’s ability to resist risk is greater; in contrast, the ability of enterprises to resist risk is weak. The Z value of each company is very different, so the logarithm of the Z value is calculated with a base of 2.675 as the antirisk ability index. We build a risk conduction network model with stock as the node, the stock volatility spillover relationship as the edge, and the adjusted risk spillover value as the edge weight. The details are shown i Formula (9).
where \({{IPC}}_{i,j}={{x}_{{sz}}^{i}* b}_{i,j}\), \({x}_{{sz}}^{i}\) is the market value of \(i\), and \({b}_{i,j}\) is the industrial driving coefficient between stocks\(\,i\) and \(j\). \((1+{{IPC}}_{i,j}){\Delta {{CoVaR}}_{q}^{i,j}}^{[T_{1+s\left(w-1\right)},{T}_{k+s(w-1)}]}\) indicates the strength of risk conduction between stocks under a specific window.
Risk control network model based on network control dynamics
Network structure control and minimum energy consumption theory
According to control theory, a dynamic system is controllable if appropriate external inputs can move the system’s internal state from any initial state to any reachable final state in a finite time interval (Kalman, 1963). The same is true for the study of complex networks. The dynamic characteristics of real networks are mostly nonlinear, but they can be transformed into linear systems to be studied (Slotine, 2004). The dynamics formulas of linear time-invariant networks are shown as (10)–(12):
where \(x\left(t\right)\in {{\mathbb{R}}}^{n}\), \(u\left(t\right)\in {{\mathbb{R}}}^{m}\), and \(y\left(t\right)\in {{\mathbb{R}}}^{p}\) represent the network’s state, input, and output, respectively, at time \(t\). \(A\in {{\mathbb{R}}}^{{\rm{n}}\times {\rm{n}}}\) is an \(n\times n\) matrix, \(B\in {{\mathbb{R}}}^{n\times m}\) is an \(n\times m\) matrix, which is a node matrix controlled by an external input signal, and \(C\in {{\mathbb{R}}}^{p\times {n}}\) is a \(p\times n\) matrix of output nodes. The linear time-invariant network dynamics formula is converted to the network structure-directed graph formula:
where \({a}_{{ij}}\) represents the directed weighted adjacency matrix of the risk conduction network, \({b}_{{ij}}\) is the control node matrix, and \({u}_{j}\) is an external input signal. The controllability of the system is judged on the basis of the Kalman condition, and the system controllability must satisfy the controllability matrix C full rank:
The system (A, B, C) is said to be target controllable concerning a given target node set C if there exists a time-dependent input vector \(u\left(t\right)=({u}_{1}(t)\)…\({u}_{m}{(t))}^{T}\), that can drive the state \({x}_{0}\) of the target nodes to any desired final state \({x}_{f}\) in finite time. Each input of \(u\left(t\right)\) brings a node in the network closer from its initial state, \({x}_{0}\), to its final state, \({x}_{f}\). Finally, the network output \(y(t)\) is guided from the initial value \({y(0)=y}_{0}\) to the expected value \({y(0)=y}_{f}\) in a finite number of steps t, as shown in Fig. 1.
To quantify the state transition cost on the system, we can consider the control input \(u\left(t\right)\) that minimizes the energy input (Lindmark and Altafini, 2018). The function expression is shown in Formula (14), and the corresponding transition cost is shown in Formula (15).
where \({W}_{r}^{-1}({t}_{f})={\sum }_{0}^{t}{e}^{A\tau }B{B}^{T}{e}^{{A}^{T}\tau }d\tau\) is called the controllability Gramian matrix. The control of state transition achieved at minimum cost can be more precisely expressed as Formula (16), which is used as the node risk control cost:
Risk conduction control network model based on the VaR and CoVaR
We calculate the risk conduction matrix of stocks under 50 windows in 2020 and 2021 and construct the risk conduction control network model. The risk cascade conduction network evolution model is obtained, as shown in Formulas (17–20).
where there are \({n}_{1}\) nodes in the network when \({t}=0\). After the t unit time evolution of the network, some new nodes \(\triangle {n}_{t}\) will appear and some nodes \({V}_{t}^{m}\) will disappear due to the influence of interdependent behavior, collective behavior, etc. Then, the node set in the network at \(t\) is \({{\boldsymbol{V}}}_{t}\). \({e}_{{ij}}^{t}\) represents an edge in the network at time \(t\). If the absolute value of risk conduction between stock nodes \(i\) and \(j\) is greater than 0, there is a connected edge between them; otherwise, there is no connected edge.
According to the risk conduction network evolution model, some edges may occur only once, indicating that the probability of their occurrence is minuscule and has no significant impact on the overall risk conduction. Therefore, the edge of the network was screened, and the edges with a cumulative proportion of 80% were extracted. That is, the edge with a frequency greater than 10, and the risk conduction control network model is finally built:
where V represents the node set in the network, E represents a set of edges in a network, and \({P}_{i,j}\ge 10\) indicates that the number of risk conduction relationships between nodes is greater than or equal to 10; then, there is an edge between them; otherwise, there is no edge. W represents the edge weights between nodes, \({P}_{k}\) represents the frequency of the edge, and \(m\) represents the number of all edges with a frequency greater than 10.
Our ultimate goal is to control the network’s risk transmission to reduce the risk. Therefore, combined with the above calculation and the actual risk size (VaR fluctuates approximately 10%), the initial state VaR and the final state 0.9*VaR were set in this paper, and the risk conduction control formula was finally obtained as follows:
where A represents the adjacency matrix of risk conduction in different networks, B represents the driver node matrix, \({x}_{0}\) represents the initial state VaR, \({x}_{f}\) represents the final state, and U(t) represents the value of risk regulation. Its absolute value represents the cost of risk regulation, and T represents the control time.
Results
Identification of key risk conduction nodes
The listed mining companies are located in different positions in the industrial chain, and we believe that risk conduction between stocks is affected by industry drive. Different layers have different industrial driving effects. Therefore, to better reveal the risk transmission characteristics of stocks from the perspective of the industrial chain, we set different layers for analysis. We set up four cases, including the whole-industrial chain network (WICN), upper- and middle-layer network (UMN), upper- and lower-layer network (ULN), and middle- and lower-layer network (MLN). This not only provides certain risk point prevention and control suggestions for decision-makers and market managers from the perspective of the industrial chain but also provides a certain basis for subsequent risk control.
The characteristics of risk conduction are mainly considered in three main aspects: conduction range, conduction strength, and conduction number. In this paper, the conduction range refers to the length of the conduction time, which is the point in time when no new node can be conducted and how many time steps are counted. For example, we set the original time t = 0. When t = 1, risk conduction occurs in stock a, and when t = n, risk conduction stops. The conduction step is n; that is, the conduction range of node a is n. The conduction intensity represents the cumulative value of the risk conduction of the node. The conduction number indicates how often the whole network node is infected with risk.
We comprehensively considered the three indicators of conduction range, strength, and number and constructed three-dimensional graphs under different situations, as shown in Fig. 2. The conduction range, strength, and number exhibited positive distributions. This means that the other two are more considerable when one is more extensive. The probability that the number of nodes’ risk conduction is above 40 is less than 20%, which aligns with the “80/20 law”. This shows that only a few nodes in the mining finance network play a more critical role in risk conduction.
The frequency of the top ten stocks in each dimension is calculated according to the three dimensions, and the stock with the greatest frequency is extracted. If the frequency is the same, reference is made to its conduction strength. The final results are shown in Table 1.
In the WICN and UMN, the metal smelting industry in the middle reaches accounts for the most significant proportion and plays a more critical role in risk conduction. In the MLN, the metal smelting stocks, also in the middle layer, play a more critical role in risk conduction. In the ULN, the upstream mining industry is more critical in risk conduction. In the mining financial network, the nodes in the middle layer play the most vital role in the network to which they belong. They also connect to the industrial chain, indicating that the industrial drive affects risk conduction. Managers should focus effectively on and control the few stocks marked in the table to reduce large-scale risk transmission. For example, 600508.SH, 600307.SH, 600231.SH, 600971.SH and 600188.SH plays an important role in each case.
Dynamic simulation of risk control in a two-layer case based on key risk stocks
We construct a risk control network model and then divide the two-layer and three-layer network cases. The two- or three-layer network not only includes the relationships between the nodes of a single layer but also includes the relationships between the layers. Therefore, we did not analyze the single-layer situation but focused on analyzing the two-layer and the whole-industrial chain from the perspective of the industrial chain. The networks are the upper-middle layer network (UMN), upper-lower layer network (ULN), lower-middle layer network (MLN), and three-layer network (WICN). The control difficulty and control strategy in different situations are compared. The cost of risk control includes the cost of risk regulation, time, and the number of nodes. The higher the risk control cost, the more difficult it is to control. The risk regulation cost refers to the absolute sum of the control signal energy consumption within a particular control time, the time cost refers to the final control time, and the number of nodes cost refers to the minimum number of drive nodes under complete control.
First, the network in the two-layer case is analyzed, and the top ten key risk nodes are taken as the driver nodes individually. The ratio of driver nodes and control nodes of networks is shown in Fig. 3. Under the same drive node, the control ratio of the ULN is the highest, followed by those of the MLN and UMN. They need 5, 6, and 6 nodes to achieve global control. This high probability indicates that controlling the upper-lower layer is easier, whereas controlling the upper-middle layer is more complicated.
The changing trend of the control signal of the double-layer network under complete control is shown in Fig. 4, where the horizontal coordinate is time t, and the vertical coordinate is the control signal \({u}_{t}\) of the drive node. When t = 24, the network control effect is better in the two-layer case, and the control signal converges infinitely and is close to 0. When t = 1, the control signal is enormous, and the control signal gradually decreases with increasing time. The figure shows that if the overall risk value in the network is reduced by 10% within the time of t = 8, the control signal that must be input is enormous; that is, the risk regulation cost is high, and the unit is 10,000. Over time, the control signal clearly tends to decrease. When t = 16, the control signal decreases to hundreds of digits, and when t = 24, the control signal decreases to less than ten and approaches 0 indefinitely. This shows that with increasing time costs, the cost of its control signal continues to decrease. To obtain the shortest time and most effective control, it is necessary to input a considerable signal energy cost. Therefore, the arrival purpose of less energy consumption can choose t = 24 as an adequate control time. The control signal forms and specific control strategies of different stocks are now analyzed.
-
(1)
Control strategy for six key risk stocks in the UMN case
In Fig. 5, 600231.SH and 600307.SH are ferrous metal smelting and rolling industry stocks in the middle layer, while the remaining four are coal mining stocks in the upper layer. The stock nodes in the upper layer have an extensive industry-driving coefficient to the stock nodes in the middle layer, indicating that a decrease in the risk value of the upper layer nodes is more conducive to a decrease in the risk value of the middle layer nodes. Therefore, in this situation, more attention and control should be given to the coal mining and selection stocks in the upper layer. From the perspective of controlling signal energy consumption, the risk control cost of stocks is 600231.SH, 600188.SH and 600971.SH is larger, and midstream enterprises have a more significant industry-driving effect on their industries. They also play an essential role in reducing the risk value in their industries. The top nodes in the upper and middle layers have strong risk transmission ability and must strengthen prevention.
-
(2)
Control strategy for five key risk nodes in the ULN case
In Fig. 6, 600326.SH belongs to the lower layer, whereas the other four are mining and selection industries in the upper layer. This indicates that more attention should be given to the upstream nodes when controlling risks in the ULN case. From the perspective of industry driving, the upstream industry has a more significant industrial driving coefficient than the downstream industry, indicating that the risk control of upstream nodes is more conducive to overall risk reduction in the ULN case. Therefore, in this situation, more control should be carried out on the coal mining and selection industry in the upper layer. From the perspective of controlling signal energy consumption, 600028.SH and 600326.SH has a large signal input, while the risk control costs of the other three are lower.
-
(3)
Control strategy for six key risk nodes in the MLN case
Stocks 600425.SH and 600992.SH belongs to the mineral products industry in the lower layer, while the other four are the metal smelting and processing industry stocks in the middle layer. In terms of the industrial driving effect, metal smelting and processing in the middle layer has a significant driving effect on its industry, with considerable risk conduction strength and range. Therefore, we should strengthen the control of the midstream stock nodes. From the perspective of the control signal energy consumption, 600549.SH, 600992.SH and 600231.SH has enormous risk control costs, and it is still necessary to strengthen the control of midstream stock nodes to achieve a decrease in the overall risk value (Fig. 7).
Overall, risk control under the two-layer case is considered in three aspects. First, the upstream stocks have a large industrial driving coefficient, accounting for a relatively high proportion, especially for coal enterprises. Therefore, we should pay more attention to large coal enterprises upstream. Second, midstream stocks play the role of “connecting the preceding and the following” in the industrial chain and have large risk conduction intensity and scope. We should control risk for metal smelting enterprises. The third is to adopt incentive or tightening policy signals.
Dynamic simulation of risk control in a three-layer case based on key risk stocks
In Fig. 8, less than 15% of the driver nodes can control more than 90% of the network nodes; however, to achieve global control, the proportion of driver nodes must account for approximately 18%. Approximately 13% of the nodes can be globally controlled for a two-layer case. The larger the network scale, the denser the correlation relationship, and the more subsystems must be controlled; thus, its difficulty increases suddenly. This is consistent with the effective global control of the stock and futures markets in reality and with the findings of previous studies. The network size and density in the mining finance network are large, so more driving nodes are needed to achieve global control.
After calculation, global controllability can be achieved only when the number of drive nodes is 11. Finally, when t = 18, the control signal continues to approach 0, and when t = 20, the total energy consumption of the control signal increases, as shown in Fig. 9.
Therefore, t = 18 is set as the final control time, according to which, the corresponding control strategy is proposed. The figure shows that at time t = 6, if the overall risk value in the network is reduced by 10%, the magnitude of the input control signal is in the tens of thousands. At t = 12, it falls below 10. The energy consumption of the control signal decreases the fastest with time, and a small energy consumption can be achieved in the shortest time, indicating that the control efficiency is greater than that of the double layer. Through calculation, the cost of risk regulation in the three-layer case is more significant than that in the upper-lower and upper-middle layers, and the cost of the number of control nodes is higher than that in the two-layer case. However, the control time cost is reduced. This shows that controlling the risk in the three-layer case is more complicated.
Control strategy for eleven key risk nodes in the WICN case
When t = 18, the control signal trend of each stock node is shown in Fig. 10. Stocks 600508.SH, 600971.SH, 600188.SH and 600028.SH belongs to the mining and selection industry in the upper layer, 600307.SH and 600231.SH belongs to the middle layer of the ferrous metal smelting industry, 600326.SH is a nonmetallic mineral product, and the other four stocks are from the nonferrous metal smelting and processing industry. This indicates that more controls should be implemented in the metal smelting industry in the middle layer. Because they are in the middle layer of the industrial chain, they connect the upper and lower layers, which means they are more likely to transmit risk. Therefore, greater control over the middle layer nodes is more conducive to reducing global risk.
From the point of view of signal energy consumption, the risk control cost of stocks is 600508.SH, 600307.SH, 600961.SH, and 600971.SH is higher, indicating that more signal control should be applied to these stocks. The signal input of each stock is increasing, suggesting that active monetary policy measures can be taken to control the risk in the mining financial market. For example, market managers can inject more capital into stocks, increase their liquidity in the market, ensure the stability of the financial market, and then reduce the overall risk value. Among them, 600508.SH, 600971.SH, 600188.SH, 600307.SH, 600231.SH stocks appear the most frequently in different situations, most of which are stock nodes in the middle and upper layers. In the two-layer case, the upper-layer stock nodes are more critical to risk reduction, whereas the middle-layer nodes are more critical in the three-layer case. Therefore, these stocks should be given more attention and risk control according to different cases.
It is known from the above that the signal input of these stocks is increasing and approaching the signal trend of 0, which can be understood as loose monetary policy. The above research shows that stock price volatility has intensified in the past two years. In the postepidemic era, the risks in the mining financial market are relatively significant, which is most likely because the weakness of the macroeconomy has led to the limited development of the real economy of the mining industry. Financing difficulties in the mining financial market increase investor panic and lead to stock market volatility, resulting in a wide range of stock price fluctuations and triggering a wide range of risk conduction. When China suffered a stock market crash in 2015, the government adopted interest rate and reserve ratio cuts to promote capital injection and flow in the stock market. The national team took the initiative to increase capital investment, buy some essential stocks, and restore liquidity in the stock market. Therefore, risk control in the mining financial market in the postepidemic era can also adopt the same loose monetary means.
Discussion and conclusions
In this work, we conduct risk control in the mining stock of the industrial chain by synthetically adopting the GARCH, DCC, and complex network dynamics models. A risk conduction and control network is constructed, and several risk control strategies are proposed accordingly. The primary conclusions are as follows:
The conduction range, conduction strength, and conduction number of nodes show a positive trend. The number of stocks with high-risk conduction strength in the network is less than 20%, which aligns with the Pareto principle. The stock nodes in the upper and middle layers of the industrial chain have a higher probability of bringing risks to the overall situation; thus, more attention and management should be given to such nodes. For example, 600508.SH (Shanghai Datun Energy Resources Co., Ltd.), 600971.SH (Anhui Hengyuan Coal Industry and Electricity Power Co., Ltd.) and 600231.SH (Lingyuan Iron & Steel Co., Ltd.) are stocks of large mining enterprises in China that significantly impact the development of the entire mining industry. A large range of strong risk conductions will occur when they have a risk impact. Key risk points in the network can be controlled according to different situations. Risk prevention can move from the traditional “too big to fail” regulatory concept to the “too connected to fail” regulatory concept.
Approximately 13% of the nodes can achieve global control in the two-layer case, whereas approximately 18% is required in the three-layer case. In the two-layer case, the risk control time is t = 24, while in the three-layer case, it is t = 18. Considering the risk control cost, time cost, and node number cost comprehensively, the risk control difficulty and cost are the lowest in the upper–low layer case. In contrast, the risk control difficulty is more significant in the upper–mid and middle-low layer cases. The node cost in the three-layer case is approximately twice that in the two-layer case, and the regulation cost is also greater. Although the time cost has decreased, the overall control difficulty is greater than in the two-layer case. This shows that for a network with a higher average degree, the more complex the correlation, the more difficult it is to control. Under the final control strategy, the control signal tends to increase or decrease over time and approaches 0. Market managers should take incentives or tightening policy signals to reduce the transmission of risks. In the postepidemic era, the government should strengthen the control of key risk stocks, adopt relatively loose monetary policies, increase the injection of funds in the market, and stabilize the development of the stock market.
Key risk nodes such as 600508.SH (Shanghai Datun Energy Resources Co., Ltd.), 600971.SH (Anhui Hengyuan Coal Industry and Electricity Power Co., Ltd.), 600188.SH (Yankuang Energy Group Company Limited), 600307.SH (Gansu Jiu Steel Group Hongxing Iron and Steel Co., Ltd.) and 600231.SH (Lingyuan Iron & Steel Co., Ltd.) is the most common in different cases, indicating that these stocks play a more critical role in risk control and reduction. The coal mining industry is in the upper layer, while the metal smelting and processing industry is in the middle layer. They are large mining companies, most of which are located in the middle stream of the industrial chain and play a “connecting role”. It is necessary to pay more attention to the risk-conduction characteristics of these stocks to prevent risks and ensure timely control. The industry-driving effect plays a vital role in risk conduction, which is necessary for risk management from the perspective of the industrial chain.
In summary, this paper provides a clear framework for studying the risk control of Chinese mining stocks in the industrial chain. This provides market managers and policy-makers with a more comprehensive risk control scheme. At present, the risk control model is constructed on the basis of the principles of network dynamics and structural control theory without considering risk supervision concepts and policies in the actual mining financial market, which will be taken into consideration in the future.
Data availability
All data generated or analyzed during this study are included in this published article and its supplementary information and supplementary data files. The supplementary information is in Table S1. The supplementary data files include the raw data in excel called 50 window data, the files of the control data of the middle and lower layers, the upper and lower layers, the upper and middle layers, and the whole layer.
References
Abuzayed B, Bouri E, Al-Fayoumi N, Jalkh N (2021) Systemic risk spillover across global and country stock markets during the COVID-19 pandemic. Econ Anal Policy 71:180–197. https://doi.org/10.1016/j.eap.2021.04.010
Adrian T, Brunnermeier MK (2016) CoVaR. Am Econ Rev 106:1705–1741. https://doi.org/10.1257/aer.20120555
Ahmed AD, Huo R (2021) Volatility transmissions across international oil market, commodity futures and stock markets: empirical evidence from China. Energy Econ 93:104741. https://doi.org/10.1016/j.eneco.2020.104741
Aprillia H, Yang HT, Huang CM (2021) Statistical load forecasting using optimal quantile regression random forest and risk assessment index. IEEE Trans Smart Grid 12:1467–1480. https://doi.org/10.1109/tsg.2020.3034194
Brissette C, Niu X, Jiang CH, Gao JX, Korniss G, Szymanski BK (2021) Heuristic assessment of choices for risk network control. Sci Rep 11:7645. https://doi.org/10.1038/s41598-021-85432-x
Chen YF, Zheng B, Qu F (2020) Modeling the nexus of crude oil, new energy and rare earth in China: an asymmetric VAR-BEKK (DCC)-GARCH approach. Resour Policy 65:101545. https://doi.org/10.1016/j.resourpol.2019.101545
Christensen I, Li FC (2014) Predicting financial stress events: a signal extraction approach. J Financ Stab 14:54–65. https://doi.org/10.1016/j.jfs.2014.08.005
Dai X, Wang Q, Zha D, Zhou D (2020) Multi-scale dependence structure and risk contagion between oil, gold, and US exchange rate: a wavelet-based vine-copula approach. Energy Econ 88:104774
Engle R (2002) Dynamic conditional correlation. J Bus Econ Stat 20:339–350
Fratzscher M, Rieth M (2019) Monetary policy, bank bailouts and the sovereign-bank risk nexus in the Euro area. Rev Financ 23:745–775
Fukker G, Kok C (2024) On the optimal control of interbank contagion in the euro area banking system. J Financ Stab 71:101225. https://doi.org/10.1016/j.jfs.2024.101225
Galbiati M, Delpini D, Battiston S (2013) The power to control. Nat Phys 9:126–128. https://doi.org/10.1038/nphys2581
Gao J, Liu YY, D’Souza RM, Barabási A-L (2015) Target control of complex networks. Nat Commun 5:5415
Gao X, Huang S, Sun X, Hao X, An F (2018) Modelling cointegration and Granger causality network to detect long-term equilibrium and diffusion paths in the financial system. R Soc Open Sci 5:172092. https://doi.org/10.1098/rsos.172092
Gates AJ, Rocha LM (2016) Control of complex networks requires both structure and dynamics. Sci Rep 6:24456. https://doi.org/10.1038/srep24456
Huang BN, Wei JK, Tang YH, Liu C (2021) Enterprise risk assessment based on machine learning. Comput Intell Neurosci 2021:6049195. https://doi.org/10.1155/2021/6049195
Jiang S, Zhou J, Qiu S (2022) Is there any correlation between digital currency price fluctuation? Based on the DCC-GARCH and wavelet coherence analysis. Econ Res-Ekonomska Istrazivanja. https://doi.org/10.1080/1331677x.2022.2134901
Kalman RE (1963) Mathematical description of linear dynamical systems. J Soc Ind Appl Math Ser A Control 1:152–192
Kaminsky GL, Reinhart CM (1999) The twin crises: the causes of banking and balance-of-payments problems. Am Econ Rev 89:473–500. https://doi.org/10.1257/aer.89.3.473
Kim JM, Kim ST, Kim S (2020) On the relationship of cryptocurrency price with US stock and gold price using copula models. Mathematics 8:1859. https://doi.org/10.3390/math8111859
Li GZ, Zhang AN, Zhang QZ, Wu D, Zhan CJ (2022) Pearson correlation coefficient-based performance enhancement of broad learning system for stock price prediction. IEEE Trans Circuits Syst II-Express Briefs 69:2413–2417. https://doi.org/10.1109/tcsii.2022.3160266
Lindmark G, Altafini C (2018) Minimum energy control for complex networks. Sci Rep 8:3188. https://doi.org/10.1038/s41598-018-21398-7
Liu YY, Slotine JJ, Barabasi AL (2011) Controllability of complex networks. Nature 473:167–173. https://doi.org/10.1038/nature10011
Lombardi A, Hrnquist M (2007) Controllability analysis of networks. Phys rev e 75:056110
Lu F, Yang K, Qian Y (2020) Target control based on edge dynamics in complex networks. Sci Rep 10:9991. https://doi.org/10.1038/s41598-020-66524-6
Newby E, Zañudo JGT, Albert R (2022) Structure-based approach to identifying small sets of driver nodes in biological networks. Chaos 32:063102. https://doi.org/10.1063/5.0080843
Niu HL, Lu YF (2021) Multiscale entropy and asynchronies of percolation-based price model and Chinese stock market. Int J Mod Phys C 32:2150073. https://doi.org/10.1142/s012918312150073x
Qian Q, Chao XR, Feng HR (2023) Internal or external control? How to respond to credit risk contagion in complex enterprises network. Int Rev Financ Anal 87:102604. https://doi.org/10.1016/j.irfa.2023.102604
Ristolainen K (2018) Predicting banking crises with artificial neural networks: the role of nonlinearity and heterogeneity. Scand J Econ 120: 31–62
Rodríguez-Moreno M, Peña JI (2013) Systemic risk measures: the simpler the better? J Bank Financ 37:1817–1831. https://doi.org/10.1016/j.jbankfin.2012.07.010
Shang HY, Lu D, Zhou QY (2021) Early warning of enterprise finance risk of big data mining in internet of things based on fuzzy association rules. Neural Comput Appl 33:3901–3909. https://doi.org/10.1007/s00521-020-05510-5
Slotine JJE (2004) Applied nonlinear control. Prentice-Hall
Sun ED, Michaels TCT, Mahadevan L (2020) Optimal control of aging in complex networks. Proc Natl Acad Sci USA 117:20404–20410. https://doi.org/10.1073/pnas.2006375117
Sun QR, Zhao WQ, Bai ZS, Guo S, Liang JL, Xi ZL (2024) Multi-scale pattern causality of the price fluctuation in energy stock market. Nonlinear Dyn 112:7291–7307. https://doi.org/10.1007/s11071-024-09279-3
Tan BY, Gan ZQ, Wu Y (2023) The measurement and early warning of daily financial stability index based on XGBoost and SHAP: evidence from China. Expert Syst Appl 227:120375. https://doi.org/10.1016/j.eswa.2023.120375
Wang GJ, Yi SY, Xie C, Stanley HE (2020) Multilayer information spillover networks: measuring interconnectedness of financial institutions. Quant Financ 23. https://doi.org/10.1080/14697688.2020.1831047
Wang GJ, Yi SY, Xie C, Stanley HE (2021a) Multilayer information spillover networks: measuring interconnectedness of financial institutions. Quant Financ 21:1163–1185. https://doi.org/10.1080/14697688.2020.1831047
Wang H, Yuan Y, Li Y, Wang X (2021b) Financial contagion and contagion channels in the forex market: a new approach via the dynamic mixture copula-extreme value theory. Econ Model 94:401–414. https://doi.org/10.1016/j.econmod.2020.10.002
Xie QW, Liu RR, Qian T, Li JY (2021) Linkages between the international crude oil market and the Chinese stock market: a BEKK-GARCH-AFD approach. Energy Econ 102:105484. https://doi.org/10.1016/j.eneco.2021.105484
Xu J, Lian D, Yang D (2021) Risk spillover: a new perspective on the study of financing difficulties for SMEs—evidence from China. Discrete Dynamics in Nature and Society
Yuan JH, Li XY, Shi Y, Chan FTS, Ruan JH, Zhu YC (2020) Linkages between Chinese stock price index and exchange rates-an evidence from the belt and road initiative. IEEE Access 8:95403–95416. https://doi.org/10.1109/access.2020.2995941
Yuan ZZ, Zhao C, Di ZR, Wang WX, Lai YC (2013) Exact controllability of complex networks. Nat Commun 4:2447. https://doi.org/10.1038/ncomms3447
Zañudo JGT, Yang G, Albert R (2017) Structure-based control of complex networks with nonlinear dynamics. Proc Natl Acad Sci USA 114:7234–7239. https://doi.org/10.1073/pnas.1617387114
Zhang P, Lv ZX, Pei ZF, Zhao YH (2023) Systemic risk spillover of financial institutions in China: a copula-DCC-GARCH approach. J Eng Res 11:100078. https://doi.org/10.1016/j.jer.2023.100078
Zhao YN, Gu P, Zhu FL, Liu TY, Shen RJ (2023) Security control scheme for cyber-physical system with a complex network in physical layer against false data injection attacks. Appl Math Comput 447:127908. https://doi.org/10.1016/j.amc.2023.127908
Acknowledgements
This work was supported by the Basic Science Center Project of the National Natural Science Foundation of China [No. 72088101, the Theory and Application of Resource and Environment Management in the Digital Economy Era], the National Natural Science Foundation of China [Nos. 72371229, 71991485, 71991481, and 71991480], the Integrated Project of the Major Research Plan of the National Natural Science Foundation of China [No. 92162321], the Fundamental Research Funds for the Central Universities (3-7-8-2023-01), and the Geological Survey project of China Geological Survey (DD20243234). We appreciate the valuable comments and suggestions of Professor Anjian Wang and associate professor Weiqiong Zhong.
Author information
Authors and Affiliations
Contributions
XX wrote the main manuscript text, XG carried on the logical sorting and content discussion, XS and HZ gave methodological support, and CW conducted the review and content discussion of the article. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethical approval
Ethical approval is not applicable because this article does not contain any studies with human or animal subjects.
Informed consent
Informed consent is not applicable because this article does not contain any studies with human or animal subjects.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Xi, X., Gao, X., Sun, X. et al. Dynamic analysis and application of network structure control in risk conduction in the industrial chain. Humanit Soc Sci Commun 11, 1468 (2024). https://doi.org/10.1057/s41599-024-04001-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-024-04001-5