Introduction

The high quality and efficiency of prefabricated construction is predicated on the stability of the prefabricated construction supply chain (PCSC) and on the effective coordination of their interdependent entities: the prefabrication factories, transportation enterprises, and construction companies (Jaillon et al. 2009). The complexity of the prefabricated construction supply chain invokes numerous risks. However, traditional engineering project management practices overlook the interactions between stakeholders within the prefabricated construction supply chain. (Wang et al. 2023). The construction company acts as the general contractor of projects and undertakes on-site assembly. It subcontracts production and transportation services to prefabrication factories and transportation companies. The stable development of prefabricated construction is thus dependent on the seamless integration of all actors, and expectations of sufficient profit for all.

However, the potential instability in the PCSC threaten to undermine or even nullify the benefits of prefabricated building construction (Zhai et al. 2016). For instance, workers often spend considerable time at assembly sites awaiting the arrival of delayed prefabricated components. This in turn arises from the uncertainties faced by manufacturers during production processes in regards to material shortages, machine malfunctions, and extended preventive maintenance. (Koranda et al. 2012). Given that construction materials account for approximately 50% of the total budget of any project, the untimely delivery of these materials not only negatively impacts manufacturers but also disrupts assemblers and the entire supply chain. Therefore, ensuring punctual delivery of prefabricated components is crucial to maintaining stability in the PCSC. In most prior studies, assemblers have been regarded as leaders within the supply chain, and thus devised strategies to ensure on-time delivery by manufacturers while safeguarding their own interest. Key manufacturer focused strategies include incentivizing early delivery while penalizing delays (Wang and Gerchak, 2001), or providing false delivery dates to manufacturers before actual component delivery occurs (Zhai et al. 2016).

In fact, due to the short construction period and high efficiency of prefabricated buildings, target customers primarily consist of time-sensitive clients (Jiang et al. 2023). Consequently, the manufacturer’s profitability is closely tied to its production efficiency, with shorter delivery times for prefabricated components leading to increased consumer demand and ultimately higher profits. In other words, manufacturers actively adopt a crashing strategy in an effort to attract more consumers while enhancing their own profitability by reducing the delivery time of prefabricated components. At this point, the manufacturer must strike a balance between an increase in crashing costs and an increase in sales. For prefabricated building assemblers, reduced delivery times result in heightened consumer demand while simultaneously decreasing component inventory costs. To expedite the manufacturer’s production process, assemblers may offer to share a portion of the incurred crashing costs. Similar incentives have been implemented in practical scenarios with remarkable outcomes. For instance, the EPC contract of a prominent chemical company in the United States specified that the owner can share certain crashing costs with the contractor in order to minimize production time. In the case of the production of the 787 aircraft (Richard, 2024), Boeing collaborated with contractors to distribute the expenses incurred due to delivery delays, effectively alleviating scheduling pressures and in the process achieving a 30 percent crashing-cost reduction (Gaynor, 2015). Such precedents reveal the imperative to devise a rational incentive-based mechanism by which supply chain efficiency may be augmented.

In the existing literature, limited research has been conducted on power structures in the PCSC. In fact, where there are large companies in the supply chain, which is common in prefabricated construction, the power structure can easily shift. The presence of large assemblers in the construction sector, such as Country Garden, Vanke, and Gensler, for example, give them greater power in the supply chain. Similarly, where there are strong manufacturers in the prefabricated construction supply chain, such as Skanska in US, the Turner Corporation, and the China State Construction Corporation, these will dominate the supply chain. The party with greater power can take the lead in making decisions that while beneficial to themselves, may undermine the overall efficiency of the supply chain in total (Shi et al. 2018). In order to identify decision strategies that may improve the profitability of prefabrication enterprises operating under various environments, while at the same time strengthening the stability of the PCSC, this paper introduces the concept of power structure into the PCSC.

This paper investigates the decision optimization of PCSC under different power structures, by considering lead-time incentives. The research contributes to the existing studies in several ways. Firstly, we introduce an incentive mechanism in respect of lead-time into the prefabricated construction supply chain, with the aim of developing strategies that give supply chain members greater lead-time stability and profit. Secondly, we analyze the impact of the power structure on the decision of supply chain participants by establishing crashing models, given lead-time incentives. Finally, by comparing three scenarios, we introduce a dynamic wholesale price contract and a revenue-sharing and cost-sharing contract, able to coordinate the supply chain under different circumstances. This research attempts to address the following questions: (1) What are the optimal pricing, crashing and lead-time incentive decisions of both the assembler and manufacturer under different power structures? (2) When should assemblers adopt lead-time incentives? (3) What impact does the introduction of lead-time incentives have on optimal decisions and profits of the PCSC? (4) Can an optimal decision by the manufacturer and assembler maximize the profit of the supply chain under different power structures? (5) How should the optimal decision of supply chain participants acting under decentralized decision-making conditions be coordinated?

The remaining part of this paper is organized as follows. Section “Literature review” reviews relevant literature. Section “Problem and model description” describes the problem investigated along with assumptions, and notations. In section “Crshing models with lead-time incentive”, the crashing models are developed with lead-time incentives under three different power structures. In section “Coordinating model”, a dynamic wholesale price contract and a revenue-sharing and cost-sharing contract are illustrated. In section 6, numerical analysis is used to estimate the influence of different parameters and models on supply chain profits. Section 7 reiterates conclusions and considers future research directions.

Literature review

This study aims to extend the following two streams of literature: (1) Production strategies of prefabrication manufacturers (2) Supply chain management under conditions of varying power structures.

Production strategies of prefabrication manufacturers

Professor Koskela of Stanford University was the first to propose the idea of construction supply chain management (Koskela, 1992). Only in recent years has PCSC gained significant attention, beginning with Vrijhoef and Koskela (2000), who introduced supply chain management strategies into the PCSC in the effort to optimize it. The decision optimization of PCSC has emerged as a research priority in the industry (Rahman, 2013). Kim et al. (2016) established a time-driven cost model for the PCSC and applied it to a construction project. Yang et al. (2018) analyzed the characteristics of PCSC and provided prefabricated component order strategies for contractors. Wang et al. (2018) predicted the cost of prefabricated construction supply chains in the case of uncertain demand, and identified the key cost reduction nodes across the whole supply chain. Du et al. (2022) established a series of models to investigate contractors’ optimal rate of assembly under various government subsidies. Chen et al. (2023) considered an assembly supply chain model comprising two manufacturers and one assembler, in order to investigate pricing and carbon emission decisions. They found that the assembler will produce products with lower carbon emissions and expand market share where manufacturers enhance carbon emission reduction abilities. Jiang et al. (2024) investigated pricing and assembly rate strategies, as well as coordination mechanisms in a two-tier prefabricated construction supply chain consisting of a manufacturer and an assembler, under various subsidy schemes.

In addition to making decisions about production strategies, manufacturers are also faced with a variety of uncertainties that can lead to delays in the delivery of prefabricated components. Consequently, the incentive of lead-time was introduced to assure compliance with construction scheduling. The incentive mechanism can effectively facilitate collaboration among enterprises in the construction supply chain and enhance construction quality. Mol et al. (2004) first proposed that the success of construction projects was not only affected by factors such as effort level, core competence and payment cost of organization members, but also by interactive decisions such as reward and punishment mechanisms. Hosseinian and Carmichael (2013) then established an optimal incentive model for owners and contractors based on different risk preferences. They went further to extend this across a variety of incentive models (including duration, cost and safety) under conditions of non-cooperation. Jiang et al. (2010) optimized the decision of an expressway project by designing feasible incentive contracts, and further determined the reward and punishment reference points for the optimal construction period. Meng and Gallagher (2012) studied the influence of incentive contracts in construction projects and found that the combination of reward and punishment mechanisms could not only be used for cost goals, but also for performance goals. Lin and Zhang (2020) considered the incentive mechanism of construction supply chains including one contractor and multiple subcontractors, and establish a supply chain model in which the contractor is the leader and the subcontractor is the follower. Han et al. (2022) studied the influence of reputation incentives in large-scale projects and found that the contractor would be more inclined to make optimal efforts in large-scale projects once reputational effects are introduced. He (2023) constructed incentive models with and without user involvement, examined the impact of user involvement on the effort level of construction contractors and the performance of construction projects, and designed a refined incentive mechanism.

The above studies serve as a foundation and reference of departure for this study. However, the majority of existing literature focuses on examining the incentives of owners and governments towards construction enterprises, with limited research conducted on incentive mechanisms among construction enterprises themselves. Furthermore, most existing studies on the internal incentive mechanism within the construction supply chain primarily concentrate on optimizing construction duration and costs, neglecting considerations regarding incentives for manufacturers’ crashing strategies.

Supply chain management under conditions of varying power structures

Previous research has considered the influence of unequal power structures on supply chain decisions. Specifically, power is shown to disrupt optimal decisions and the subsequent profits of supply chain participants (Gaski and Nevin, 1985; Kolay and Shaffer, 2013). Choi (1991) studied the supply chain pricing decisions of two manufacturers and a common retailer based on linear and nonlinear demand across three kinds of non-cooperative games, and found that various cooperative modes had a divergent impact on supply chain decisions. Ertek and Griffin (2002) and Raju and Zhang (2005), confirmed that channel structure could be coordinated by volume discount contracts. Kim and Kwak (2007) established two models to describe the bargaining process between suppliers and buyers under long-term replenishment contracts. Zhang et al. (2012) used game theory to investigate the substitutability of products under different power structures. Shi et al. (2013) studied the influence of power structures and demand models on the performance of supply chain members, finding that the impact of power structures not only depends on the expected demand model, but also on demand shock. Li et al. (2021) considered a retailer-dominated Stackelberg game model in a decentralized two-level supply chain, and found that retailers, manufacturers, and consumers could all be better off under the retailer-sponsored gift card strategy. Li and Mizuno (2022) considered three possible power structures between manufacturer and retailer in the dual-channel supply chain, and found that optimal pricing and inventory decisions are affected by the power structure. Andriani and Tseng (2023) examined the pricing and joint investment decisions of a two-echelon supply chain with a manufacturer and a retailer by constructing centralized, manufacturer-led decentralized, and retailer-led decentralized models. They found that in decentralized models, the Stackelberg game determines the optimal price and investment decisions.

In addition to the common power structure with unequal powers, the research on supply chain structure based on the comparison of unequal powers and equal powers has become a topic of interest in related academic fields in recent years. Yang et al. (2005) analyzed a two-echelon supply chain composed of one manufacturer and two competitive retailers. The different competitive behaviors of two retailers are analyzed from the perspective of Stackelberg and vertical Nash games led by supplier and retailers respectively. Cai et al. (2009) analyzed the influence of price discount and price scheme on the competition of dual-channel supply chain under different power structures. They found that a vertical Nash game can make supply chain participants reach equilibrium, with a balanced power structure being most beneficial to the whole supply chain. Zheng et al. (2019) considered a closed-loop supply chain with unequal power, and studied the optimal decision and profit under five non-cooperative and cooperative Stackelberg game models. They proposed a variable weighted Shapley value to coordinate the closed-loop supply chain. Li et al. (2022) investigated the implication of fairness in conjunction with channel coordination and contracting mechanisms by developing a game-theoretic utility model where the Nash bargaining fairness reference is leveraged to capture the impact of fairness preferences on three widely used contracting mechanisms—wholesale price, buy-back, and revenue-sharing.

The aforementioned studies demonstrate that power structures vary widely in supply chains and exert significant influence on supply chain decisions and profits. However, the concept of power structures has been largely overlooked in PCSC. In fact, unequal powers are common in the prefabricated construction supply chain due to the existence of large companies. Moreover, the introduction of lead-time incentive further magnifies the influence of variable power structures on supply chain decisions.

The extant literature serves as the foundation for this research. This study incorporates manufacturer crashing strategies and delivery time incentives into a PCSC. By employing optimization theory, Nash Game theory, and Stackelberg game theory, we establish a profit optimization model for PCSC under three different power structures: the Nash game model and two Stackelberg models led by the assembler and the manufacturer. We then employ the derivation, reverse solution method, and MATLAB to solve these three models. Consequently, this study formulates pricing strategies for prefabricated construction enterprises and their supply chains under different power structures as well as manufacturers’ crashing strategies and assemblers’ crashing incentive strategies. Additionally, revenue-sharing contracts, cost-sharing contracts, and dynamic wholesale price contracts are designed for each power structure in order to achieve supply chain coordination. Finally, numerical analysis not only validates our conclusions but also provides further implications. This research is of great significance in promoting the development of prefabricated construction by offering optimal prices, delivery times, and crashing incentives for PC enterprises to achieve supply chain coordination under different power structures.

Problem and model description

Prefabrication component manufacturers’ high crashing costs are an important factor limiting their ability to attract clientele. While the supply chain is subject to a large number of exogenous variables, both manufacturers and assemblers have few alternative responses beyond price adjustment. A solution proposed here, therefore, is to introduce a lead-time incentive for assemblers in the PCSC, and for assemblers to share some of the crashing costs with manufacturers such that manufacturers are incentivized to accelerate prefabricated component production, when needed. Ideally, assemblers would choose to take on as little crashing cost as possible while manufacturers would choose to raise wholesale prices as much as demand will bear. Consequently, apportionment of crashing costs is dependent on the supply/demand market power of the supply chain. Thus, we introduce a dynamic wholesale price contract to coordinate the decentralized decision of PCSC under the assembler Stackelberg game model. It is calculated that the separate revenue sharing contact and cost-sharing contract is insufficient to coordinate the supply chain. Therefore, we design a revenue-sharing and cost-sharing contract to coordinate the supply chain. The notations of the parameters and variables in this paper are presented in Table 1.

Table 1 Notations of parameters and variables.
Full size table

We propose the following assumptions prior to calculation, and certain symbols are defined as follows:

(1) This paper investigates a two-echelon supply chain comprising an assembler and a manufacturer, with the exclusion of other stakeholders in the PCSC. It is assumed that both parties possess symmetrical information, while disregarding moral hazard within the construction supply chain. In a decentralized decision scenario, both sides act rationally to maximize their individual interests. Under centralized decisions, both parties pursue profit maximization for the entire supply chain.

(2) The prefabricated components of a prefabricated construction can be categorized into standard and nonstandard components. The assembler may proactively procure standard components in order to minimize construction time uncertainty. Therefore, this study assumes that the assembler possesses an inventory of standard components and procures non-standard components from the manufacturer upon receiving an order. During the waiting period for the arrival of non-standard components, the assembler shall bear the inventory cost of the standard components htD.

(3) This study assumes that the materials required for a prefabricated building consist of one standardized prefabricated component and one non-standardized prefabricated component. Therefore, consumer demand (D) can represent the quantity of either standardized or non-standardized prefabricated components required throughout the entire production cycle.

(4) The study only considers the production time of the manufacturer’s non-standard prefabricated components, disregarding the transportation and construction time of these components. Thus, the manufacturing duration for non-standard prefabricated components directly represents consumers’ waiting time for prefabricated buildings. Upon implementing a crashing strategy by manufacturers, consumers experience a waiting time denoted as t. The adoption of a crashing strategy results in saved time for manufacturers (i.e., reduced waiting time for consumers), represented as\(\,{t}_{1}-t\).

(5) The demand for prefabricated buildings by consumers is influenced by both the price (p) and delivery time (t). Previous research suggests that consumer demand follows a negative exponential growth pattern in response to changes in building price and delivery time, expressed as \(D\left(p,t\right)=a{p}^{-b}{t}^{-\lambda }\) (Doğan, 2015).

(6) The crashing cost of the manufacturer exhibits a positive correlation with both the time saved and the quantity of prefabricated components required for crashing, denoted as \(sD({t}_{1}-t)\).

Crashing models with lead-time incentive

This section considers the optimal decision, sensitivity analysis and impact analysis of the lead-time incentive of PCSC under variable power structures. The decision environment of supply chain members becomes more complicated with the introduction of the lead-time incentive. Three crashing models are constructed: (1) manufacturer Stackelberg game model, (2) Nash game model with equal power, and (3) assembler Stackelberg game model.

The manufacturer Stackelberg model

In this section, we consider the optimal decision of PCSC enterprises under a manufacturer Stackelberg model with lead-time incentives (MSL). Here, the power of the manufacturer is significantly higher than that of the assembler. The sequence of events is as follows: First, the manufacturer sets the production time of non-standard components and sets the wholesale price of prefabricated components. Then the assembler accepts the manufacturer's decisions passively, and on that basis sets the price for prefabricated constructions. The extent of crashing cost shared by the assembler is negotiated at the start of the sales period.

Modeling and optimal decisions

The decision problem faced by the manufacturer in the MSL model is as follows:

$${\pi }_{{\rm {M}}}^{{{\rm {MSL}}}}\left(t,\omega \right)=\left(\omega -c\right)a{p}^{-b}{t}^{-\lambda }-({s-\tau }_{0})({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }$$
(1)

The first item on the right of the equation is the manufacturer's profit from selling prefabricated components, and the second item is the crashing cost of producing non-standard components when shared with the assembler.

The decision problem faced by the assembler in the MSL model is as follows:

$${\pi }_{{\rm {A}}}^{{{\rm {MSL}}}}\left(p\right)=\left(p-\omega \right)a{p}^{-b}{t}^{-\lambda }-{hta}{p}^{-b}{t}^{-\lambda }-{\tau }_{0}({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }$$
(2)

The first item on the right of the equation is the profit from selling prefabricated constructions, the second is the cost of stocking standard components while waiting for the manufacturer to deliver non-standard components, and the third item is the crashing cost that the assembler has shared.

Proposition 1. Under the MSL model, the optimal production time of non-standard components is

$${t}^{{{\rm {MSL}}}}=\frac{\left(1-b\right)\left(h-{\tau }_{0}\right)-\lambda (s{t}_{1}+c)}{\lambda (h-s)}$$
(3)

The optimal wholesale price of the prefabricated component is

$${\omega }^{{{\rm {MSL}}}}=\frac{\lambda h\left(c+s{t}_{1}-{\tau }_{0}{t}_{1}\right)+\left(h-{\tau }_{0}\right)\left[{\tau }_{0}\left(1-b\right)+{bs}-h\right]-\lambda c{\tau }_{0}}{\lambda (h-s)}$$
(4)

And the optimal price of prefabricated construction is

$${p}^{{{\rm {MSL}}}}=\frac{{b}^{2}({\tau }_{0}-h)}{\lambda (b-1)}$$
(5)

The proof is in Appendix.

From Proposition 1, it can be seen that the delivery time of non-standard components, price of prefabricated constructions and the wholesale price of prefabricated components all decrease with an increase of consumers' time sensitivity \(\lambda\). This is explained by the fact that prefabricated construction companies have to cut their price or accelerate production as time sensitivity increases in order to attract customers. A lower construction price implies the assembler is impacted by time-sensitive consumers. Thus, to keep supply stable, the manufacturer needs to lower the wholesale price. As for the price sensitivity of consumers, it can be seen that with the increase of \(b\), the delivery time of the prefabricated construction is shortened and the price decreases. Similarly, where consumers’ price sensitivities are high, the supply chain members need to cut price and implement crashing.

Sensitivity analysis

In this section, we analyze the sensitivity of the assembler' and manufacturer' optimal decisions under the MSL model, and the influence of \(s\) and \({\tau }_{0}\) are analyzed.

Proposition 2.

(1) \(\frac{\partial {t}^{{{\rm {MSL}}}}}{\partial s} > 0\), \(\frac{\partial {\omega }^{{{\rm {MSL}}}}}{\partial s} > 0\);

(2) \(\frac{\partial {t}^{{{\rm {MSL}}}}}{\partial {\tau }_{0}} < 0\), \(\frac{\partial {\omega }^{{{\rm {MSL}}}}}{\partial {\tau }_{0}} < 0\), \(\frac{\partial {p}^{{{\rm {MSL}}}}}{\partial {\tau }_{0}} > 0\).

The proof is in the Appendix.

From Proposition 2, it can be seen that after introducing the lead-time incentive, with the increase of unit crashing cost, the manufacturer's cost increases, the delivery time of prefabricated components increases, and the wholesale price of prefabricated components increases. With the increase of crashing cost shared by the assembler, the cost of manufacturing is reduced indirectly, the delivery time of components being shortened. As the proportion of crashing cost sharing by the assembler increases, the manufacturer can discount the wholesale price, leading ultimately to increasing customer demand.

Impact analysis of Lead-time incentive

In this section, we compare the optimal delivery time and price of prefabricated constructions in the Lead-time incentive Stackelberg game model with that in the model without Lead-time incentive. Without Lead-time incentive (MS model), we have \({\tau }_{0}=0\). In this scenario, the manufacturer has more power than the assembler, which is sufficient to determine the crash time of nonstandard components. The wholesale price of prefabricated components is a fixed value,\(\,\omega ={\omega }_{0}\). From Eqs. (1) and (2) and proposition 1, we have \({t}^{{{\rm {MS}}}}=\frac{{\omega }_{0}+{bh}({\omega }_{0}-s{t}_{1})}{h(b-1)}\), \({p}^{{{\rm {MS}}}}=\frac{b}{b-1}\left({\omega }_{0}+h{t}^{{{\rm {MS}}}}\right)\). We summarize the significance and value of Lead-time incentive through comparative analysis.

Proposition 3. By comparing MSL model and MS model, we have the following conclusions:

When \(\frac{h(b-1)\left(\left(b-1\right)\left({\tau }_{0}-h\right)-\lambda \left(s{t}_{1}+c\right)\right)}{\lambda (h-s)({\omega }_{0}+{bh}({\omega }_{0}-s{t}_{1}))}\ge 1\), \({t}^{{{\rm {MSL}}}}\ge {t}^{{{\rm {MS}}}}\); when \(\frac{h(b-1)(\left(b-1\right)\left({\tau }_{0}-h\right)-\lambda \left(s{t}_{1}+c\right))}{\lambda (h-s)({\omega }_{0}+{bh}({\omega }_{0}-s{t}_{1}))} < 1\), \({t}^{{{\rm {MSL}}}} < {t}^{{{\rm {MS}}}}\).

When \({\omega }^{{\rm {{MSL}}}}-{\omega }_{0}+{\tau }_{0}({t}_{1}-{t}^{{\rm {{MSL}}}})\ge h({t}^{{{\rm {MS}}}}-{t}^{{{\rm {MSL}}}})\), \({p}^{{{\rm {MSL}}}}\ge {p}^{{{\rm {MS}}}}\); when \({\omega }^{{{\rm {MSL}}}}-{\omega }_{0}+{\tau }_{0}\left({t}_{1}-{t}^{{{\rm {MSL}}}}\right) < h({t}^{{{\rm {MS}}}}-{t}^{{{\rm {MSL}}}})\), \({p}^{{{\rm {MSL}}}} < {p}^{{{\rm {MS}}}}\).

The proof is in the Appendix.

From Proposition 3, after introducing the lead-time incentive into the PCSC, the construction price will depend on the impact of the lead-time incentive on the delivery time of the prefabricated construction. Where the construction delivery time remains stable, the construction price will increase. Thus, the introduction of the lead-time incentive fails to attract a large number of consumers, yet increases the construction price, and is therefore counterproductive. However, if the construction delivery time can be shortened by introducing the lead-time incentive, the construction price will be reduced.

The Nash game model

This section studies the optimal decision of prefabricated construction supply chain enterprises under the vertical Nash game model with the lead-time incentive (NGL). Under the NGL model, the manufacturer and the assembler are similar in bargaining power. Neither dominate the supply chain. Therefore, in the NGL model, the manufacturer cannot alone determine the wholesale price of prefabricated components, and the assembler cannot decide the amount of crashing cost that it shared. The sequence of events is as follows: the assembler and the manufacturer make decisions at the same time, both sides aim at maximizing their own profits and cannot make decisions based on the reactions of the other party.

Modeling and optimal decision

The decision problems faced by the manufacturer in NGL model are as follows:

$${\pi }_{\rm {{M}}}^{{{\rm {NGL}}}}\left(t\right)=\left({\omega }_{{\rm {l}}}-c\right)a{p}^{-b}{t}^{-\lambda }-({s-\tau }_{0})({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }$$
(6)

The decision problems faced by the assembler is

$${\pi }_{{\rm {A}}}^{{{\rm {NGL}}}}\left(p\right)=\left(p-{\omega }_{{\rm {l}}}\right)a{p}^{-b}{t}^{-\lambda }-{hta}{p}^{-b}{t}^{-\lambda }-{\tau }_{0}({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }$$
(7)

The meaning of function is consistent with that in MSL model and we do not repeat here.

Proposition 4. Under the NGL model, the optimal crash time of non-standard components for manufacturer is

$${t}^{{{\rm {NGL}}}}=\frac{\lambda ({\omega }_{l}-c-\left({s-\tau }_{0}\right){t}_{1})}{(1-\lambda )({s-\tau }_{0})}$$
(8)

The optimal price of prefabricated construction for assembler is

$${p}^{{{\rm {NGL}}}}=\frac{b}{b-1}({\omega }_{l}+{\tau }_{0}{t}_{1}+\frac{\lambda ({h-\tau }_{0})({\omega }_{l}-c-\left({s-\tau }_{0}\right){t}_{1})}{(1-\lambda )({s-\tau }_{0})})$$
(9)

The proof is in the Appendix.

From Proposition 4, we find that with the increase of consumer price sensitivity, the price of prefabricated constructions decreases. The assembler can only reduce prices in order to attract more consumers. However, as the wholesale price of prefabricated components increases, the assembler has to raise construction prices to maintain profit. For the manufacturer, the most important factors affecting the producing time of non-standard prefabricated components are the time sensitivity of consumers and their crashing cost.

Sensitivity analysis

This section conducts a sensitivity analysis on the optimal decisions of the assembler and manufacturer under the NGL model. We analyze the effects of the wholesale price of prefabricated components, unit crashing cost and the amount of crashing cost that the assembler shared.

Proposition 5.

(1) \(\frac{\partial {t}^{{{\rm {NGL}}}}}{\partial {\omega }_{{\rm {l}}}} < 0\), \(\frac{\partial {p}^{{{\rm {NGL}}}}}{\partial {\omega }_{{\rm {l}}}} > 0\);

(2) \(\frac{\partial {t}^{{{\rm {NGL}}}}}{\partial s} > 0\), \(\frac{\partial {p}^{{{\rm {NGL}}}}}{\partial s} < 0\);

(3) \(\frac{\partial {t}^{{{\rm {NGL}}}}}{\partial {\tau }_{0}} < 0\), \(\frac{\partial {p}^{{{\rm {NGL}}}}}{\partial {\tau }_{0}} > 0\).

The proof is in the Appendix.

Proposition 5 shows that with the Lead-time incentive, the delivery time of prefabricated components is negatively correlated with the wholesale price of prefabricated components. Prefabricated construction price is positively correlated with the wholesale price of prefabricated components. Component delivery time is positively correlated with unit crashing cost and negatively correlated with the amount of crashing cost shared by the assembler. Construction price is negatively correlated with unit crashing cost.

Impact analysis of Lead-time incentive

In this section, we compare the optimal delivery time and price of prefabricated constructions in the Lead-time incentive Nash game model with that in the model without Lead-time incentive. Without Lead-incentive (NG model), we have \({\tau }_{0}=0\). In this scenario, the assembler and manufacturer have equal power. The wholesale price of prefabricated components is a fixed value,\(\,\omega ={\omega }_{0}\). From Eqs. (6) and (7) and Proposition 4, we have \({t}^{{NG}}=\frac{\lambda ({\omega }_{0}-s{t}_{1})}{S(1-\lambda )}\), \({p}^{{MS}}=\frac{b}{b-1}\left({\omega }_{0}+h{t}^{{NG}}\right)\). We summarize the significance and value of the Lead-time incentive through comparative analysis.

Proposition 6. By comparing NGL model and NG model, we have the following conclusions:

When \(\frac{s[{\omega }_{{\rm {l}}}-c-\left({s-\tau }_{0}\right){t}_{1}]}{({s-\tau }_{0})({\omega }_{0}-s{t}_{1})}\ge 1\), \({t}^{{{\rm {NGL}}}}\ge {t}^{{{\rm {NG}}}}\); when \(\frac{s[{\omega }_{{\rm {l}}}-c-\left({s-\tau }_{0}\right){t}_{1}]}{({s-\tau }_{0})({\omega }_{0}-s{t}_{1})} < 1\), \({t}^{{{\rm {NGL}}}} < {t}^{{{\rm {NG}}}}\).

When \({\omega }_{{\rm {l}}}-{\omega }_{0}+{\tau }_{0}({t}_{1}-{t}^{{{\rm {NGL}}}})\ge h({t}^{{{\rm {NG}}}}-{t}^{{{\rm {NGL}}}})\), \({p}^{{{\rm {NGL}}}}\ge {p}^{{{\rm {NG}}}}\); when \({\omega }_{l}-{\omega }_{0}+{\tau }_{0}\left({t}_{1}-{t}^{{{\rm {NGL}}}}\right) < h({t}^{{{\rm {NG}}}}-{t}^{{{\rm {NGL}}}})\), \({p}^{{NGL}} < {p}^{{NG}}\).

The proof is in the Appendix.

Proposition 6 shows that in the vertical Nash game model with lead-time incentive, the manufacturer cannot determine the wholesale price of prefabricated components, but can set the crashing time, while the assembler cannot determine the crashing cost shared, but can set the price of construction. Therefore, in the NGL model, the decision variables are consistent with the vertical Nash game without the incentive mechanism. Therefore, the comparison of the optimal decision depends on the allocation of crashing cost shared by the assembler and the wholesale price of prefabricated components, discussed before the cycle starts.

The assembler Stackelberg model

This section considers the optimal decision of PCSC enterprises under assembler Stackelberg model with lead-time incentive (ASL). Here, the assembler has power in the supply chain, being able to decide the price of prefabricated constructions, as well as the extent of crashing costs to be shared with the manufacturer. The manufacturer, as follower, can only passively accept the decisions of the assembler and decide the production time of non-standard prefabricated components. The wholesale price of prefabricated components has been negotiated by both parties before the start of the sales period and is an exogenous variable. Therefore, the sequence of events in the supply chain is as follows: First, the assembler decides the price of the prefabricated construction and the amount of crashing cost shared to maximize profit. Then the manufacturer decides the production time of non-standard components based on the decision of the assembler to maximize profit.

Modeling and optimal decision

In the ASL model, the decision problem faced by the assembler is as follows:

$${\pi }_{{\rm {A}}}^{{{\rm {ASL}}}}\left(p,\tau \right)=\left(p-{\omega }_{l}\right)a{p}^{-b}{t}^{-\lambda }-{hta}{p}^{-b}{t}^{-\lambda }-\tau ({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }$$
(10)

The decision problem faced by the manufacturer is

$${\pi }_{{\rm {M}}}^{{{\rm {ASL}}}}\left(t\right)=\left({\omega }_{l}-c\right)a{p}^{-b}{t}^{-\lambda }-(s-\tau )({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }$$
(11)

The meaning of function is consistent with that in MSL model and we do not repeat here.

Proposition 7. Under the ASL model, the optimal crash time of non-standard components for manufacturer is

$${t}^{{{\rm {ASL}}}}=\frac{{\lambda }^{2}{t}_{1}}{1-\lambda }$$
(12)

The optimal price of prefabricated construction for assembler is

$${p}^{{{\rm {ASL}}}}=\frac{b}{b-1}({\omega }_{{\rm {l}}}+{\lambda }^{2}h{t}_{1}-s{t}_{1}+\frac{{\omega }_{{\rm {l}}}-c}{1-\lambda })$$
(13)

The amount of crashing cost that the assembler shared is

$${\tau }^{{{\rm {ASL}}}}=s-\frac{{\omega }_{{\rm {l}}}-c}{(1-\lambda ){t}_{1}}$$
(14)

The proof is in Appendix.

Proposition 7 shows that in the ASL model, as the time-sensitive of consumers increase, the manufacturer will no longer be willing to sacrifice their own costs to attract consumers. For the assembler, in order to maintain the stability of supply chain, he can only choose to share the crashing cost for the manufacturer to maintain his own profit. In this case, in order to maintain his own profit, assembler choose to increase construction price. As leader of supply chain, assembler is willing to lower price to attract more consumers when the price sensitivity of consumers increases. When the assembler leads the supply chain, the price of construction is a more controlled factor than the delivery time. Therefore, the target consumers of the assembler are mostly price sensitive and delivery time insensitive.

Sensitivity analysis

This section conducts sensitivity analysis on the optimal decisions of the assembler and manufacturer under the ASL model, respectively. We analyze the effects of the wholesale price of prefabricated components and unit crashing cost on related variables.

Proposition 8.

(1) \(\frac{\partial {p}^{{{\rm {ASL}}}}}{\partial {\omega }_{{\rm {l}}}} >\, 0\), \(\frac{\partial {\tau }^{{{\rm {ASL}}}}}{\partial {\omega }_{{\rm {l}}}} <\, 0\);

(2) \(\frac{\partial {p}^{{{\rm {ASL}}}}}{\partial s} <\, 0\), \(\frac{\partial {\tau }^{{{\rm {ASL}}}}}{\partial s} >\, 0\).

The proof is in Appendix.

Proposition 8 shows that after the introduction of the lead-time incentive. In the ASL model, the price of prefabricated constructions is proportional to the wholesale price of prefabricated components and inversely proportional to the unit crashing cost. The amount of crashing cost that the assembler shared is inversely proportional to the wholesale price of prefabricated components. When the wholesale price is high, the assembler will no longer share the crashing cost with the manufacturer. The amount of crashing cost that the assembler shared is proportional to the unit crashing cost. When the unit crashing cost is high, the assembler needs to absorb more crashing cost in order to keep the supply chain stable.

Impact analysis of Lead-time incentive

In this section, we compare the optimal delivery time and price of prefabricated constructions in the lead-time incentive Stackelberg game model with that in the model without Lead-time incentive. Without Lead-time incentive (AS model), we have \({\tau }_{0}=0\). In this scenario, the assembler has greater power than the manufacturer, being able to decide the price. The wholesale price of prefabricated components is a fixed value,\(\omega ={\omega }_{0}\). From Eqs. (10), (11) and Proposition 7, we have \({t}^{{{\rm {AS}}}}=\frac{\lambda (s{t}_{1}-{\omega }_{0})}{S(\lambda -1)}\), \({p}^{{{\rm {AS}}}}=\frac{b}{b-1}\left({\omega }_{0}+h{t}^{{{\rm {AS}}}}\right)\). We summarize the significance and value of the lead-time incentive through comparative analysis.

Proposition 9. By comparing ASL model and AS model, we have the following conclusions:

When \(\frac{\lambda s{t}_{1}}{{\omega }_{0}-s{t}_{1}}\ge 1\), \({t}^{{{\rm {ASL}}}}\ge {t}^{{{\rm {AS}}}}\); when \(\frac{\lambda s{t}_{1}}{{\omega }_{0}-s{t}_{1}} < 1\), \({t}^{{{\rm {ASL}}}} < {t}^{{{\rm {AS}}}}\).

When \({\omega }_{{\rm {l}}}-{\omega }_{0}+{\tau }^{{{\rm {ASL}}}}({t}_{1}-{t}^{{{\rm {ASL}}}})\ge h({t}^{{{\rm {AS}}}}-{t}^{{{\rm {ASL}}}})\), \({p}^{{{\rm {ASL}}}}\ge {p}^{{{\rm {AS}}}}\); when \({\omega }_{{\rm {l}}}-{\omega }_{0}+{\tau }^{{{\rm {ASL}}}}\left({t}_{1}-{t}^{{{\rm {ASL}}}}\right) < h({t}^{{{\rm {AS}}}}-{t}^{{{\rm {ASL}}}})\), \({p}^{{{\rm {ASL}}}} < {p}^{{{\rm {AS}}}}\).

The proof is in Appendix.

Proposition 9 shows that in the ASL model the assembler decides the crashing cost shared. The manufacturer cannot decide the wholesale price of prefabricated components, but can decide the delivery time of non-standard components. Therefore, when the assembler is more powerful, compared with the crashing model without lead-time incentive, the assembler can set reasonable crashing cost sharing to motivate the manufacturer to crash and ensure their own profits. As a result, the assembler is able to keep construction prices high while reducing the delivery time of non-stand components.

Influence analysis on different power structures

In this section, we compare the price of prefabricated construction (PC), the delivery time of non-standard components, the wholesale price of prefabricated components, the amount of crashing cost shared by the assembler, and the profits of both parties in the Nash game model and the two Stackelberg game models with the lead-time incentive. The features and performance of the three crash models are presented in Table 2.

Table 2 . Features and performance of three models.
Full size table

Proposition 10. By comparing NGL model, MSL model and ASL model, we have the following conclusions:

(1) When \(\frac{(1-\lambda )({s-\tau }_{0})(\left(b-1\right)\left({\tau }_{0}-h\right)-\lambda (s{t}_{1}+c))}{{\lambda }^{2}(h-s)({\omega }_{l}-c-\left({s-\tau }_{0}\right){t}_{1})}\ge 1\), \({t}^{{{\rm {MSL}}}}\ge {t}^{{{\rm {NGL}}}}\); when \(\frac{(1-\lambda )({s-\tau }_{0})(\left(b-1\right)\left({\tau }_{0}-h\right)-\lambda (s{t}_{1}+c))}{{\lambda }^{2}(h-s)({\omega }_{l}-c-\left({s-\tau }_{0}\right){t}_{1})} < 1\), \({t}^{{{\rm {MSL}}}} < {t}^{{{\rm {NGL}}}}\).

When \(\frac{(1-\lambda )(\left(b-1\right)\left({\tau }_{0}-h\right)-\lambda (s{t}_{1}+c))}{{\lambda }^{3}(h-s){t}_{1}}\ge 1\), \({t}^{{{\rm {MSL}}}}\ge {t}^{{{\rm {ASL}}}}\); when \(\frac{(1-\lambda )(\left(b-1\right)\left({\tau }_{0}-h\right)-\lambda (s{t}_{1}+c))}{{\lambda }^{3}(h-s){t}_{1}} < 1\), \({t}^{{{\rm {MSL}}}} < {t}^{{{\rm {ASL}}}}\).

When \(\frac{{\omega }_{l}-c-\left({s-\tau }_{0}\right){t}_{1}}{\lambda {t}_{1}({s-\tau }_{0})}\ge 1\), \({t}^{{{\rm {NGL}}}}\ge {t}^{{{\rm {ASL}}}}\); when \(\frac{{\omega }_{{\rm {l}}}-c-\left({s-\tau }_{0}\right){t}_{1}}{\lambda {t}_{1}({s-\tau }_{0})} < 1\), \({t}^{{{\rm {NGL}}}} < {t}^{{{\rm {ASL}}}}\).

(2) \({\omega }^{{{\rm {MSL}}}}\ge {\omega }_{{\rm {l}}}\) and \({\tau }^{{{\rm {ASL}}}}\le {\tau }_{0}\).

(3) When \({\omega }^{{{\rm {MSL}}}}-{\omega }_{{\rm {l}}}\ge \left({\tau }_{0}-h\right)\left({t}^{{{\rm {MSL}}}}-{t}^{{{\rm {NGL}}}}\right)\), \({p}^{{{\rm {MSL}}}}\ge {p}^{{{\rm {NGL}}}}\); when \({\omega }^{{{\rm {MSL}}}}-{\omega }_{{\rm {l}}} < \left({\tau }_{0}-h\right)\left({t}^{{{\rm {MSL}}}}-{t}^{{{\rm {NGL}}}}\right)\), \({p}^{{{\rm {MSL}}}} < {p}^{{{\rm {NGL}}}}\).

When \({\omega }^{{\rm {{MSL}}}}-{\omega }_{{\rm {l}}}\ge h\left({t}^{{{\rm {ASL}}}}-{t}^{{{\rm {MSL}}}}\right)+{\tau }_{0}\left({t}^{{{\rm {MSL}}}}-{t}_{1}\right)+\tau \left({t}_{1}-{t}^{{{\rm {ASL}}}}\right)\), \({p}^{{{\rm {MSL}}}}\ge {p}^{{{\rm {ASL}}}}\); when \({\omega }^{{{\rm {MSL}}}}-{\omega }_{{\rm {l}}} < h\left({t}^{{{\rm {ASL}}}}-{t}^{{{\rm {MSL}}}}\right)+{\tau }_{0}\left({t}^{{{\rm {MSL}}}}-{t}_{1}\right)+\tau \left({t}_{1}-{t}^{{{\rm {ASL}}}}\right)\), \({p}^{{{\rm {MSL}}}} < {p}^{{{\rm {ASL}}}}\).

When \(h\left({t}^{{{\rm {NGl}}}}-{t}^{{{\rm {ASL}}}}\right)\ge \left(\tau -{\tau }_{0}\right){t}_{1}+{\tau }_{0}{t}^{{{\rm {NGl}}}}-\tau {t}^{{{\rm {ASL}}}}\), \({p}^{{{\rm {NGL}}}}\ge {p}^{{{\rm {ASL}}}}\); when \(h\left({t}^{{{\rm {NGl}}}}-{t}^{{{\rm {ASL}}}}\right) < \left(\tau -{\tau }_{0}\right){t}_{1}+{\tau }_{0}{t}^{{{\rm {NGl}}}}-\tau {t}^{{{\rm {ASL}}}}\), \({p}^{{{\rm {NGL}}}} < {p}^{{{\rm {ASL}}}}\).

(4) For the manufacturer’s profit \({\pi }_{{\rm {M}}}^{{{\rm {MSL}}}}\ge {\pi }_{{\rm {M}}}^{{{\rm {NGL}}}}\) and \({\pi }_{{\rm {M}}}^{{{\rm {MSL}}}}\ge {\pi }_{{\rm {M}}}^{{{\rm {ASL}}}}\). When \(\frac{{\omega }_{{\rm {l}}}-c-\left({s-\tau }_{0}\right){t}_{1}}{\lambda {t}_{1}({s-\tau }_{0})}\ge 1\), \({\pi }_{{\rm {M}}}^{{{\rm {NGL}}}}\ge {\pi }_{{\rm {M}}}^{{{\rm {ASL}}}}\); when \(\frac{{\omega }_{{\rm {l}}}-c-\left({s-\tau }_{0}\right){t}_{1}}{\lambda {t}_{1}({s-\tau }_{0})} < 1\), \({\pi }_{{\rm {M}}}^{{{\rm {NGL}}}} < {\pi }_{{\rm {M}}}^{{{\rm {ASL}}}}\).

For the assembler’s profit \({\pi }_{{\rm {A}}}^{{{\rm {ASL}}}}\ge {\pi }_{{\rm {A}}}^{{{\rm {NGL}}}}\) and \({\pi }_{A}^{{{\rm {ASL}}}}\ge {\pi }_{{\rm {A}}}^{{{\rm {MSL}}}}\). When \({\omega }^{{{\rm {MSL}}}}-{\omega }_{{\rm {l}}}\le \left({\tau }_{0}-h\right)\left({t}^{{{\rm {MSL}}}}-{t}^{{{\rm {NGL}}}}\right)\), \({\pi }_{{\rm {A}}}^{{{\rm {MSL}}}}\ge {\pi }_{{\rm {A}}}^{{{\rm {NGL}}}}\); when \({\omega }^{{{\rm {MSL}}}}-{\omega }_{{\rm {l}}} > \left({\tau }_{0}-h\right)\left({t}^{{\rm {{MSL}}}}-{t}^{{{\rm {NGL}}}}\right)\), \({\pi }_{{\rm {A}}}^{{{\rm {MSL}}}} < {\pi }_{{\rm {A}}}^{{{\rm {NGL}}}}\).

The proof is in Appendix.

Proposition 10 shows that the delivery time for prefabricated constructions is critically important. It has a great impact on the subsequent construction price formulation and the optimal profit of supply chain members. Where the manufacturer leads the supply chain, the wholesale price must not be lower than the standard wholesale price under other power structures. Similarly, where the assembler leads the supply chain, the crashing cost shared must not be higher than that under other power structures. As for the price of prefabricated constructions, the delivery time, the wholesale price of prefabricated components, the amount of crashing cost shared by the assembler, and the inventory cost of prefabricated components should all be considered. Moreover, profits are maximized for whoever it is that leads the supply chain.

Coordinating model

In this section we consider PCSC coordination strategies with the lead-time incentive under different power structures. The purpose of coordination is to introduce corresponding contracts to make the total profit of the supply chain under decentralized decision match the profit under centralized decision, where none of the supply chain members are worse off. We introduce two revenue-sharing and cost-sharing contracts and a dynamic wholesale price contract to coordinate and optimize the PCSC under three different power structures respectively.

Influence analysis on different power structures

This part considers the global optimal model with lead-time incentive (GOL).

Modeling and optimal decision

According to the sum of Eqs. (1) and (2), (6) and (7), and (10) and (11), we have the decisions faced by both sides of the supply chain under the global optimal model with lead-time incentive, as follows:

$${\pi }^{{{\rm {GOL}}}}\left(p,t\right)=(p-c)a{p}^{-b}{t}^{-\lambda }-{hta}{p}^{-b}{t}^{-\lambda }-s({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }$$
(15)

The first item on the right of the equation is the profit from selling prefabricated constructions, the second is the cost of stocking standard components while waiting for the manufacturer to delivery non-standard components, and the third item is the crashing cost of producing non-standard components.

Proposition 11. Under the GOL model, the optimal crash time of non-standard components for manufacturer is

$${{t}}^{{\rm{GOL}}}=\frac{{\lambda }({c}+{s}{{t}}_{{1}})}{({b}+{\lambda }-{1})({s}-{h})}$$
(16)

The optimal price of prefabricated construction for assembler is

$${{\boldsymbol{p}}}^{{\boldsymbol{GOL}}}=\frac{{\boldsymbol{b}}({\boldsymbol{c}}+{\boldsymbol{s}}{{\boldsymbol{t}}}_{{\bf{1}}})}{{\boldsymbol{b}}+{\boldsymbol{\lambda }}-{\bf{1}}}$$
(17)

The optimal profit of supply chain is

$${{\pi }}^{{\rm {GOL}}}=\frac{{a}{({b}+{\lambda }-{1})}^{{b}+{\lambda }-{1}}{({s}-{h})}^{{\lambda }}}{{{b}}^{{b}}{{\lambda }}^{{\lambda }}{({{c}+{st}}_{{1}})}^{{b}+{\lambda }-{1}}}$$
(18)

The proof is in Appendix.

Proposition 11 shows that in the GOL model, under complete cooperation, the assembler and the manufacturer ignore their own profits when prioritizing whole of supply chain profit.

The comparison between decentralized and centralized decision

This section focuses on the comparison and analysis of the overall profit of the supply chain.

Proposition 12. The comparison of overall profit of the prefabricated construction supply chain under different competitive environment are as follows:

\({\pi }^{{{\rm {GOL}}}} > {\pi }^{{{\rm {NGL}}}},\,{\pi }^{{{\rm {GOL}}}} > {\pi }^{{{\rm {ASL}}}}\) and \({\pi }^{{{\rm {GOL}}}} > {\pi }^{{{\rm {MSL}}}}\)

The proof is in Appendix.

Proposition 12 shows that after introducing the lead-time incentive, supply chain profit under centralized decision is still higher than that under decentralized decision. This is because the supply chain members aim to maximize individual profits, and while the supply chain under centralized decision eliminates the double marginal effect in order to achieve maximum profit.

Manufacturer Stackelberg coordination model

In this section, we consider the manufacturer Stackelberg coordination model with lead-time incentive (CMSL), and design a revenue-sharing and cost-sharing contract to coordinate the optimal decisions of the assembler and the manufacturer. The assembler shares some crashing cost for the manufacturer. In addition, in order to reduce the assembler’s burden and optimize the price of prefabricated constructions, the manufacturer chooses to share the inventory cost of standard components with the assembler, with the assembler shares a certain amount of revenue with the manufacturer.

We assume that the revenue sharing ratio is \({\varphi }_{0}(0 < {\varphi }_{0} < 1)\); the inventory cost-sharing ratio is \({\vartheta }_{0}(0 < {\vartheta }_{0} < 1)\). The crashing cost-sharing ratio is \({\varepsilon }_{0}(0 < {\varepsilon }_{0} < 1)\), where the crashing cost assembler shared is \({\varepsilon }_{0}s({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }\), the crashing cost for the manufacturer is \((1-{\varepsilon }_{0})s({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }\), the inventory cost shared by the manufacturer is \({\vartheta }_{0}{hta}{p}^{-b}{t}^{-\lambda }\), the inventory cost of assembler is \((1-{\vartheta }_{0}){hta}{p}^{-b}{t}^{-\lambda }\). After sharing the revenue, the assembler’s income is \({\varphi }_{0}{pa}{p}^{-b}{t}^{-\lambda }\), and the manufacturer’s profit shared from the assembler is \((1-{\varphi }_{0}){pa}{p}^{-b}{t}^{-\lambda }\).

At this point, the decision problem faced by the assembler is

$${\pi }_{{\rm {A}}}^{{{\rm {CMSL}}}}\left(p\right)=\left({\varphi }_{0}p-\omega \right)a{p}^{-b}{t}^{-\lambda }-\left(1-{\vartheta }_{0}\right){hta}{p}^{-b}{t}^{-\lambda }-{\varepsilon }_{0}s({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }$$
(19)

The decision problem faced by the manufacturer is

$${\pi }_{{\rm {M}}}^{{{\rm {CMSL}}}}\left(\omega ,t\right)=\left(\omega -c\right)a{p}^{-b}{t}^{-\lambda }+\left(1-{\varphi }_{0}\right){pa}{p}^{-b}{t}^{-\lambda }-{\vartheta }_{0}{hta}{p}^{-b}{t}^{-\lambda }-(1-{\varepsilon }_{0})s({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }$$
(20)

When the supply chain system can distribute profits to the assembler and the manufacturer in any proportion, the prefabricated construction supply chain under decentralized decision is coordinated.

Proposition 13. We set δ0 ∊ (0,1], and when \(\left\{\begin{array}{c}{\varphi }_{0}p-\omega ={\delta }_{0}\left(p-c\right)\\ 1-{\vartheta }_{0}={\delta }_{0}\\ {\varepsilon }_{0}={\delta }_{0}\end{array}\right.\), the MSL model is coordinated.

The proof is in Appendix.

Proposition 13 shows that in CMSL model, when \(\left\{\begin{array}{c}{\varphi }_{0}p-\omega ={\delta }_{0}\left(p-c\right)\\ 1-{\vartheta }_{0}={\delta }_{0}\\ {\varepsilon }_{0}={\delta }_{0}\end{array}\right.\), under the combined action of revenue-sharing and cost-sharing contracts, the profit of prefabricated construction supply chain can be distributed to the assembler and manufacturer in any proportion. This avoids loss of supply chain profit optimization arising from each member’s pursuit of their own profits. According to the system profit distribution ratio \({\delta }_{0}\), the manufacturer determines the reasonable wholesale price of prefabricated components \(\omega\), and the manufacturer and assembler determine the sharing ratio \({\varphi }_{0}\), the stock cost-sharing ratio \({\vartheta }_{0}\) and the crashing cost-sharing ratio \({\varepsilon }_{0}\). In the prefabricated construction supply chain, the assembler and the manufacturer restrict each other, and make joint efforts to improve supply chain profits while simultaneously pursuing their own interests.

Vertical Nash coordination model

In this section, we consider the vertical Nash game coordination model with lead-time incentive (CNGL). Similar to the section “Manufacturer Stackelberg coordination model”, this section also designs a revenue-sharing and cost-sharing contract to coordinate the optimal decision of the assembler and the manufacturer.

We assume that the revenue sharing ratio is \({\varphi }_{1}(0 < {\varphi }_{1} < 1)\); the inventory cost-sharing ratio is \({\vartheta }_{1}(0 < {\vartheta }_{1} < 1)\). The multiplication function is used to represent the crashing cost shared by the assembler, where the cost-sharing ratio is \({\varepsilon }_{1}(0 < {\varepsilon }_{1} < 1)\). In this case, the crashing cost assembler shared is \({\varepsilon }_{1}s({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }\), the crashing cost for the manufacturer is \((1-{\varepsilon }_{1})s({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }\), the inventory cost shared by the manufacturer is \({\vartheta }_{1}{hta}{p}^{-b}{t}^{-\lambda }\), the inventory cost of assembler is \((1-{\vartheta }_{1}){hta}{p}^{-b}{t}^{-\lambda }\). After sharing the revenue, the assembler’s income is \({\varphi }_{1}{pa}{p}^{-b}{t}^{-\lambda }\), and the manufacturer’s profit shared from the assembler is \((1-{\varphi }_{1}){pa}{p}^{-b}{t}^{-\lambda }\).

At this point, the decision problem faced by the assembler is

$${\pi }_{A}^{{CNGL}}\left(p\right)=\left({\varphi }_{1}p-{\omega }_{l}\right)a{p}^{-b}{t}^{-\lambda }-\left(1-{\vartheta }_{1}\right){hta}{p}^{-b}{t}^{-\lambda }-{\varepsilon }_{1}s({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }$$
(21)

The decision problem faced by the manufacturer is

$${\pi }_{{\rm {M}}}^{{{\rm {CNGL}}}}\left(t\right)=\left({\omega }_{l}-c\right)a{p}^{-b}{t}^{-\lambda }+\left(1-{\varphi }_{1}\right){pa}{p}^{-b}{t}^{-\lambda }-{\vartheta }_{1}{hta}{p}^{-b}{t}^{-\lambda }-(1-{\varepsilon }_{1})s({t}_{1}-t)a{p}^{-b}{t}^{-\lambda }$$
(22)

When the supply chain system can distribute profits to the assembler and the manufacturer in any proportion after introducing the contract under centralized decision, the prefabricated construction supply chain under decentralized decision is coordinated.

Proposition 14. We set δ1 ∊ (0,1], and when \(\left\{\begin{array}{c}{\varphi }_{1}p-{\omega }_{l}={{\rm{\delta }}}_{1}\left(p-c\right)\\ 1-{\vartheta }_{1}={{\rm{\delta }}}_{1}\\ {\varepsilon }_{1}={{\rm{\delta }}}_{1}\end{array}\right.\), the NGL model is coordinated.

The proof is in Appendix.

Proposition 14 shows that in CNGL model, when \(\begin{array}{c}{\varphi }_{1}p-{\omega }_{l}={{\rm{\delta }}}_{1}\left(p-c\right)\\ 1-{\vartheta }_{1}={{\rm{\delta }}}_{1}\\ {\varepsilon }_{1}={{\rm{\delta }}}_{1}\end{array}\), the overall profit of supply chain under decentralized decision can achieve the supply chain profit under centralized decision. In this scenario, the supply chain achieves coordination. Similar to proposition 13, in this case, according to the system profit distribution ratio \({\delta }_{1}\), the manufacturer and assembler determine the sharing ratio \({\varphi }_{1}\), the inventory cost-sharing ratio \({\vartheta }_{1}\) and the crashing cost-sharing ratio \({\varepsilon }_{1}\).

Assembler Stackelberg coordination model

In this section, we consider the assembler Stackelberg coordination model with the lead-time incentive (CASL). In ASL model, the amount of crashing cost shared by the assembler is a decision variable. Therefore, the revenue-sharing and cost-sharing contract is no longer applicable here. In this section, we design a dynamic wholesale price contract to coordinate the ASL model. The contract is expressed as \(\omega \left(p,t\right)-c=\frac{\sigma }{D(p,t)}\), where \(\sigma\) is the coordination parameter. As a result, the manufacturer can encourage the assembler to adjust the price of prefabricated constructions, thereby lowering the wholesale price of prefabricated components. Substituting \(\omega \left(p,t\right)-c=\frac{\sigma }{D(p,t)}\) into Eqs. (10) and (11). Therefore, under the dynamic wholesale price contract, both parties face the following decision environment.

At this point, the decision problem faced by the assembler is

$${\pi }_{{\rm {A}}}^{{{\rm {CASL}}}}\left(p,\tau \right)=\left(p-c-{ht}-\tau ({t}_{1}-t)\right)a{p}^{-b}{t}^{-\lambda }-\sigma$$
(23)

The decision problem faced by the manufacturer is

$${\pi }_{{\rm {M}}}^{{{\rm {CASL}}}}\left(t\right)=\left(\tau -s\right)\left({t}_{1}-t\right)a{p}^{-b}{t}^{-\lambda }+\sigma$$
(24)

Thus, we have the optimal price of prefabricated constructions and the optimal producing time of non-standard components under CASL model.

\({p}^{{{\rm {CASL}}}}=\frac{b}{b-1}(c+\frac{\lambda h{t}_{1}}{\lambda -1})\)

\({t}^{{{\rm {CASL}}}}=\frac{\lambda {t}_{1}}{\lambda -1}\)

Under the dynamic wholesale price contract, the optimal profits of the assembler and the manufacturer are:

\({\pi }_{{\rm {A}}}^{{{\rm {CASL}}}}\left(\sigma \right)=\frac{a{(b-1)}^{b-2}{(\lambda -1)}^{\lambda +b-1}}{{b}^{b-1}{\lambda }^{\lambda }{{t}_{1}}^{\lambda }{(c\left(\lambda -1\right)+\lambda h{t}_{1})}^{b-1}}-\sigma\)

\({\pi }_{{\rm {M}}}^{{{\rm {CASL}}}}\left(\sigma \right)=\frac{{as}{t}_{1}{(b-1)}^{b}{(\lambda -1)}^{\lambda +b-1}}{{b}^{b}{\lambda }^{\lambda }{{t}_{1}}^{\lambda }{(c\left(\lambda -1\right)+\lambda h{t}_{1})}^{b}}+\sigma\)

The total profit of the supply chain is \({\pi }^{{{\rm {CASL}}}}={\pi }_{{\rm {A}}}^{{{\rm {CASL}}}}\left(\sigma \right)+{\pi }_{{\rm {M}}}^{{{\rm {CASL}}}}\left(\sigma \right)\).

\({\pi }^{{{\rm {CASL}}}}=\frac{{ab}{(b-1)}^{b-2}{(\lambda -1)}^{\lambda +b-1}(c\left(\lambda -1\right)+\lambda h{t}_{1})+{as}{t}_{1}{(b-1)}^{b}{(\lambda -1)}^{\lambda +b-1}}{{b}^{b}{\lambda }^{\lambda }{{t}_{1}}^{\lambda }{(c\left(\lambda -1\right)+\lambda h{t}_{1})}^{b}}\)

The proof of this part is basically the same as that in section “The assembler Stackelberg model” and we do not repeat it here.

Proposition 15. When \(\sigma \in \left[{\sigma }_{\min },\,{\sigma }_{\max }\right]\), the supply chain profit in the ASL model with dynamic wholesale price contract is realized the supply chain profit in GOL model. The supply chain is coordinated.

\({\sigma }_{\min }=\frac{{as}{t}_{1}{\left(b+\lambda -1\right)}^{b+\lambda }{\left(s-h\right)}^{\lambda }}{{b}^{b}{\lambda }^{\lambda }{\left(c+s{t}_{1}\right)}^{b+\lambda }}-\frac{{as}{\left(b+\lambda -1\right)}^{b+\lambda -1}{\left(s-h\right)}^{\lambda -1}}{{b}^{b}{\lambda }^{\lambda -1}{\left(c+s{t}_{1}\right)}^{b+\lambda -1}}+\frac{a{\left(b-1\right)}^{b-1}{\left(1-\lambda \right)}^{b+\lambda -3}({\omega }_{{\rm {l}}}-c)(3\lambda -2)}{{b}^{b-2}{\lambda }^{2\lambda }{{t}_{1}}^{\lambda }{(\left({\omega }_{{\rm {l}}}+{\lambda }^{2}h{t}_{1}-s{t}_{1}\right)\left(1-\lambda \right)+{\omega }_{{\rm {l}}}-c)}^{b-1}}\)

\({\sigma }_{\max }=\frac{a\left({bs}{t}_{1}-c\left(\lambda -1\right)\right){\left(s-h\right)}^{\lambda }}{{b}^{b}{\lambda }^{\lambda }{\left(c+s{t}_{1}\right)}^{b+\lambda }{\left(b+\lambda -1\right)}^{1-b-\lambda }}-\frac{a\lambda {\left(b+\lambda -1\right)}^{b+\lambda -1}{\left(s-h\right)}^{\lambda -1}}{{b}^{b}{\lambda }^{\lambda }{\left(c+s{t}_{1}\right)}^{b+\lambda -1}}-\frac{a{(b-1)}^{b-1}{(1-\lambda )}^{b+\lambda -1}{b}^{2-b}{\lambda }^{-2\lambda }{{t}_{1}}^{-\lambda }}{{(\left({\omega }_{{\rm {l}}}+{\lambda }^{2}h{t}_{1}-s{t}_{1}\right)\left(1-\lambda \right)+{\omega }_{{\rm {l}}}-c)}^{b-1}}\)

The proof is in Appendix.

Proposition 15 provides the range of \(\sigma\) to achieve the supply chain under ASL model coordination. Firstly, the value of \(\sigma\) ensures that the total profit of supply chain under decentralized decision can achieve the profit under centralized decision. Secondly, the profits of each member are guaranteed. However, while this section provides a range of \(\sigma\) values, the actual value of \(\sigma\) depends on the negotiating power of the manufacturer and assembler. For example, the lower the value of \(\sigma\), the higher the profit of the assembler. The assembler, as the leader of the supply chain, generally has stronger negotiating power, which drives the value of \(\sigma\) closer to \({\sigma }_{\min }\).

Numerical studies

In this section, numerical studies are performed based on the sensitivity analysis of two model parameters: self-price sensitivity of consumer (\(b\)) and self-time sensitivity of consumer (\(\lambda\)). It aims at comparing the optimal decisions and profits of each party under different scenarios. Based on correlative studies and satisfying all the aforementioned assumptions, we initially set \(\omega\)= 13, \(h\)= 0.8, \({t}_{1}\)= 10, \(a\)= 30,000, \(b\)= 1.5, \(\lambda\)= 0.67 and \(s\)= 2.1; where \(\omega\) refers to Zhai et al. (2016), \(h\) and \(s\) refer to Chen et al. (2017), while the remaining parameters are determined based on our models. To investigate the influence of \(\lambda\) and \(b\) on delivery time, price, and profit, we carefully selected 10 values within the ranges of \(\lambda \in [0.65,\,0.705]\) and \(b\in [1.45,\,1.56]\).

The influence of power structures

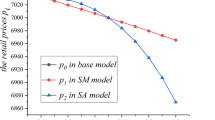
First, we investigate the effects of consumer time and price sensitivity (\(b\) and \(\lambda\)) on prefabricated construction price (\(p\)), construction delivery time (\(t\)), prefabricated component wholesale price (\(\omega\)), and the crashing cost shared by the assembler (\(\tau\)). Figure 1a–d, respectively, shows the impact of consumer time and price sensitivity on construction price and delivery time.

Fig. 1: Impact of consumer time and price sensitivity on construction price and delivery time.
figure 1

a Impact of b on p, b impact of b on t, c impact of λ on p, d impact of λ on t.

Full size image

It can be seen from Fig. 1a, c that when the assembler leads the supply chain, the price of prefabricated constructions is the highest, followed by the global optimal model and the vertical Nash game model. When the manufacturer leads the supply chain, the price is the lowest. Where the assembler leads the supply chain, he is inclined to keep construction prices higher in order to maximize profits. Where the manufacturer leads the supply chain, however, construction delivery times are longer and thus demand falls off. Therefore, the assembler has to reduce the construction price to attract enough consumers in order to ensure his profits. As can be seen from Fig. 1b and d, consumer price sensitivity has little influence on construction delivery time. However, in the vertical Nash and the assembler Stackelberg model, as the time sensitivity of consumers increases, the construction delivery time rises rapidly. It can be inferred that the manufacturer chooses to reduce the crashing cost in order to maintain profits rather than attract more consumers. However, with the introduction of the lead-time incentive, the supply chain led by the manufacturer becomes more beneficial to consumers.

Figure 2a–d, respectively, shows that where the assembler leads the supply chain, they alone can decide the crashing cost shared, being significantly lower than the initial value. Where the manufacturer leads the supply chain, they can decide the wholesale price of prefabricated components, with the wholesale price increasing significantly above the initial value. Therefore, when the assembler or the manufacturer leads the supply chain, they will be inclined to reduce the crashing cost shared by the assembler or increase the wholesale price of prefabricated components.

Fig. 2: Impact of consumer time and price sensitivity on wholesaling price and the amount of crashing cost.
figure 2

a Impact of b on ω, b impact of b on τ, c impact of λ on ω, d impact of λ on τ.

Full size image

Figure 3a, b shows the influence of \(b\) and \(\lambda\) on the total profit of supply chain in four models (MSL, NGL, ASL and GOL) respectively. Firstly, as consumers sensitivity to time and price increases, the assembler and the manufacturer are pressured to lowering prices or shortening delivery times, such that the total profit of the supply chain gradually decreases under each power structure. Secondly, where supply chain members jointly pursue profit maximization, the total profit of the supply chain in the GOL model will always be higher than that in a decentralized decision, proving proposition 12. Moreover, the ASL model is mostly more efficient than MSL and NGL models. The exception being when time sensitivity of consumers is high, in which case the total profit of the supply chain in the ASL model declines rapidly, while the profit changes in the MSL model remains relatively gentle. This is because in the MSL model, the manufacturer first decides the delivery time of the construction, and thus is able to adjust the wholesale price of the prefabricated components. Here, the increase in consumer time sensitivity has little impact on the supply chain. Similarly, it can be seen from Fig. 3a that with an increase of consumer price sensitivity, the profit curve of the supply chain led by the assembler is smoother.

Fig. 3: Impact of consumer time and price sensitivity on the total profit of supply chain in four models.
figure 3

a Impact of b on π b impact of λ on π.

Full size image

Figure 4a–d, respectively, shows the impact of consumer price and time sensitivity on the profits of the assembler and the manufacturer in the prefabricated construction supply chain.

Fig. 4: Impact of consumer price and time sensitivity on the profits of the assembler and the manufacturer.
figure 4

a Impact of b on πa, b impact of b on πm, c impact of λ on πa, d impact of λ on πm.

Full size image

When either the assembler or the manufacturer leads the supply chain, their specific profits increase significantly. This can be explained by the fact that when the assembler and the manufacturer act as supply chain leader, they can make decisions on the crashing cost shared by the assembler and the wholesale price of prefabricated components, while the introduction of a lead-time incentive gives them more leverage to improve their own profits. However, as shown in Fig. 4a–c, profits of both assembler and manufacturer gradually decline as consumers' sensitivity rises. In Fig. 4d, manufacturer's profits change more gently with an increase of consumers' time sensitivity. A similar conclusion can be drawn from Fig. 4c. With the increase of consumers time sensitivity, the assemblers’ profit decreases rapidly. Thus, it can be seen that the wholesale price of prefabricated components is the pivotal point in the game between assembler and manufacturer. Where the manufacturer leads the supply chain, a superior profit for the manufacturer can be guaranteed.

The influence of Lead-time incentive

In this section, we study the comparison of supply chain members and overall profits under three different power structures with/without lead-time incentive. Figure 5a–c shows the comparison results.

Fig. 5: Comparison of profits under three different power structures with/without lead-time incentive.
figure 5

a Impact of b on π(MS\MSL), b impact of b on π(NG\NGL), c impact of b on π(AS\ASL).

Full size image

In the three comparison figures in this section, the blue line represents the assembler, the manufacturer and the supply chain profit without Lead-time incentive, and the red line represents the profit of prefabricated enterprises and supply chain with Lead-time incentive. Firstly, by comparing the profits of the manufacturer with circular marks, it can be seen that the manufacturer’s profit has been significantly improved following the introduction of the lead-time incentive under three power structures. It can be seen that the introduction of the lead-time incentive can effectively share the crashing cost of the manufacturer. When the manufacturer leads the supply chain, his profit increases obviously, it is because of that he can decide the wholesale price of prefabricated components, which effectively wider the range of manufacture decision and improve his profit. Secondly, by comparing the profits of the assembler with triangle marks, an increase of consumer price sensitivity, results in a gentler profit curve of the assembler without lead-time incentive. But in taking the lead-time incentive into account, the profit of the assembler decreases rapidly with the increase of consumer time sensitivity. Therefore, where the consumers price sensitivity is low, the introduction of the lead-time incentive can improve assembler profit. When the consumers price sensitivity is high, the assembler is unable to share the crashing cost with the manufacturer, and thus the profit of the assembler plummets. Thirdly, by comparing the total profit of the supply chain with rectangle marks, it can be seen that when the consumer price sensitivity is low, the introduction of the lead-time incentive can effectively improve the overall profit of the supply chain. This is because the manufacturer’s profit changes little with an increase of consumer price sensitivity, whereas the assembler's profit is greatly impacted.

Conclusions and future research

This study incorporates manufacturer crashing strategy and delivery time incentives into the PCSC. The research shows that, firstly, the introduction of the lead-time incentive can increase the decision scope of supply chain members, resulting in profit optimization. Profits increase by allowing the assembler to decide the crashing cost shared in ASL model and by allowing the manufacturer to decide the wholesale price of prefabricated components in MSL model. Secondly, when supply chain participants fully cooperate in pursuit of supply chain profit, the supply chain profit of the global optimal model becomes higher than that under the three decentralized models. This finding lays the foundation for further supply chain coordination strategy research.

In the ASL model, the optimal crashing cost shared by the assembler is significantly lower than the default value. In the MSL model, the optimal wholesale price of prefabricated components is significantly higher than the default value. Therefore, under a decentralized decision, the assembler and the manufacturer erode each other’s profits as they attempt to improve their own profits. Similar conclusions can be found in the earlier discussed analysis of Jiang et al. (2023), although in that study the lead-time incentive mechanism is not considered. Additionally, the introduction of a lead-time incentive effectively improves the manufacturer’s profit, whereas, the profit of the assembler and supply chain remain dependent on the price sensitivity of consumers. Where consumer price sensitivity is low, profit of both the assembler and supply chain as a whole are optimized.

Further, by designing two revenue-sharing and cost-sharing models to coordinate the MSL and NGL models, as well as a dynamic wholesale price model to coordinate the ASL model, we find that in both the CMSL and CNGL models the two revenue-sharing and cost-sharing contracts allow supply chain profits to be distributed to supply chain members in any proportion. Under this scenario it is the party with the stronger negotiation position that will benefit. Simply, the assembler has the initiative to improve their profit while also maximizing the profit of the supply chain.

Based on the aforementioned research findings, this study proposes the following managerial recommendations for prefabricated construction enterprises operating under diverse power structures: (1) When enterprises make unilateral decisions, their profitability remains significantly low; therefore, collaborative decision between all parties is essential in order to collectively enhance profits. (2) When making decisions, enterprises should fully consider the impact of external factors, particularly the delivery time and price sensitivity of consumers. This is because as consumer sensitivity increases, both manufacturer and assembler must attract a sufficient number of consumers in order to sustain their profits. This is done by investing in crashing costs or reducing construction prices. Therefore, accurately assessing consumer sensitivity is crucial for maximizing profitability. (3) Regardless of the implementation of the lead-time incentive mechanism, both parties should strive to enhance their capabilities and status. The party with greater power will ultimately reap the highest profits. (4) The implementation of a lead-time incentive mechanism can effectively enhance manufacturers’ profits. However, the assembler should exercise caution in adopting any lead-time incentive mechanism, as its effectiveness in increasing profit relies on a combination of factors: high consumer sensitivity to time rather than price, and the assembler’s dominant position. (5) Manufacturer and assembler, as key entities in the PCSC, should actively embrace effective coordination contracts in order to enhance overall profitability and individual members’ profits.

Building upon this research, future studies will explore more comprehensive application scenarios. The current study focuses primarily on the PCSC involving manufacturers and assemblers. However, in the construction industry, supply chain participants may also include suppliers of prefabricated raw materials, transportation enterprises, and government bodies that promote prefabricated construction through subsidy policies. Thus, the inclusion of multi-stakeholders indicates the potential to expand the scope of future investigation from that of a two-tier supply chain to a multi-tier one. Moreover, some large projects are sold in batches. In such cases, the assembler’s ordering strategy, the inventory cost of standard components, and the manufacturer’s crashing strategy will change accordingly. Therefore, extending the research scope from a single period to multiple periods is another dimension worthy of investigation.

This study inevitably has certain limitations. Firstly, it focuses on analyzing the impact of lead-time incentive mechanisms on the profits and stability of the PCSC, as well as the role of dynamic wholesale price contracts and cost-revenue sharing contracts in supply chain coordination. However, to highlight the relationship between manufacturers and assemblers while simplifying the model as much as possible, this research only considers a two-echelon supply chain and does not account for a three-echelon supply chain. This limitation prevents the model from achieving an ideal state; therefore, future research could further refine the model based on these findings. Additionally, subsequent studies may explore other coordination contracts to enrich the theory and practice in this field.