Network externalities of the innovation network in China’s five urban agglomerations: based on “buzz-and-pipeline” theory

Abstract

In the era of the knowledge economy, innovation networks have emerged as crucial drivers in shaping urban economic development patterns. Network externalities represent a key mechanism for understanding the economic impact dynamics of innovation networks. This paper constructs a three-dimensional innovation network integrating knowledge, technology, and innovation. By applying social network analysis and GIS-based spatial analysis, it explores the spatiotemporal evolution of innovation networks in China’s five major urban agglomerations from 2011 to 2020. The dual-weight spatial econometric model is further employed to empirically examine the network externalities of intra- and inter-agglomeration innovation networks. The main findings are as follows: (1) From 2011 to 2020, intra-agglomeration networks displayed an uneven spatial distribution and a clear hierarchical structure. Inter-agglomeration networks evolved from a hub-and-spoke pattern to a diamond-shaped spatial structure. (2) Innovation networks generate significant externalities for urban economic development. The intra-agglomeration “buzz” effect produces stronger positive externalities, complementing the inter-agglomeration “pipeline” effect. Knowledge networks and technology networks interact, reinforcing these externalities. (3) Industrial upgrading moderates network externalities, but this effect remains confined to intra-agglomeration networks and has not yet overcome the inter-agglomeration threshold. (4) Network externalities vary across urban agglomerations and depend on the degree of network embeddedness, exhibiting clear heterogeneity. At the theoretical level, this paper constructs a multidimensional spatial model of urban innovation networks, integrating knowledge and technology flows. Drawing on “buzz-and-pipeline” theory, this paper proposes a framework that combines intra- and inter-agglomeration perspectives, offering new insights for the study of innovation network and network externalities.

Introduction

In the era of the knowledge economy, innovation serves as the endogenous driver of regional economic growth (Cui and Li, 2022). The global economy has experienced a profound transition from traditional production models to innovation-driven development. Innovation networks now occupy central roles in this transformation. Optimizing the foresight, strategic orientation, and systematic layout of basic research, along with rational resource allocation and spatial restructuring, can significantly enhance regional innovation capacity and provide a solid foundation for sustainable economic growth (Ma et al., 2020a). As key nodes in innovation networks, urban agglomerations serve not only as critical spatial carriers for promoting regional coordination and implementing innovation-driven strategies but also as essential platforms for enhancing regional innovation capacity and competitiveness (Luo et al., 2024). In the context of globalization, establishing competition-cooperation mechanisms, integrating regional comparative advantages and innovation resources, and optimizing spatial structures have become key to regional economic transformation. Through these approaches, urban agglomerations can generate nonlinear effects, where 1 + 1 + 1 > 3, injecting new vitality into the global innovation system and driving regional economic growth (Volgmann and Münter, 2022). Thus, constructing efficient innovation networks in urban agglomerations, optimizing regional comparative advantages, and enhancing the effectiveness of global innovation systems have become central issues in contemporary regional innovation studies.

From the “flow space” perspective, single-element flow cannot fully reveal the structural characteristics of regional innovation networks (Li and Phelps, 2018; Ma et al., 2020b). Research on innovation networks in urban agglomerations has also shifted from a one-dimensional approach to a multidimensional approach (Yue and Zhao, 2022). Since Marshall and Pigou proposed the externality concept, it has been widely applied in economic and geographical research (Alfred, 2013). Innovation network externalities can be understood as the indirect impact that innovation activities, through network connections and knowledge flow, have on surrounding cities or regions, extending beyond the boundaries of individual actors or organizations. These externalities encompass knowledge spillover effects and economic effects, which enhance regional innovation capacity and economic growth by facilitating technology diffusion, fostering collaborative cooperation, and optimizing resource allocation. Multidimensional innovation network externalities have become the key to and point of difficulty in current research. The “buzz-and-pipeline” model proposed by Bathelt et al. (2002) provides an important reference for understanding the multi-scale evolutionary pattern and mechanism of innovation networks. Therefore, the following questions need to be answered, both theoretically and empirically, to provide scientific guidance for exploring new ways to promote economic development from the perspective of innovation spatial structure optimization. The key research questions are as follows:

① How can a well-structured, hierarchical multidimensional innovation network be built based on knowledge flows and technology flows?

② Do network externalities and network superposition effects exist in a multidimensional innovation network? If they do, how do they influence urban economic development?

③ How does the intra-agglomeration “local buzz” interact with the inter-agglomeration “global pipeline”? What is the mechanism of this interaction?

Based on the “buzz-and-pipeline” model, we take the five urban agglomerations in China (the Beijing–Tianjin–Hebei region, the Yangtze River Delta, the Pearl River Delta, the middle reaches of the Yangtze River, and the Chengdu–Chongqing region) as examples and construct an innovation network for urban agglomerations using intercity co-paper publication data and co-patent application data. We explore the external economic effects of the innovation network from both the theoretical and empirical perspectives to clarify the mechanism and spatial characteristics of network externalities.

The key innovations of this study are as follows: (1) Regarding model innovation, we construct a spatial model of urban innovation networks with enhanced scientific rigor. By integrating co-paper publication data and co-patent application data, we develop a three-dimensional framework that captures both knowledge and technological flows. This approach overcomes the empirical limitations of gravity models and the one-dimensional nature of traditional data, enabling a more accurate representation of complex intercity innovation linkages. (2) Regarding mechanism innovation, grounded in the “buzz-and-pipeline” framework, this study examines the network externalities in innovation networks. We empirically assess their spatial spillover effects on regional economic development by integrating network and agglomeration externalities. Additionally, we explore the mechanisms and spatial heterogeneity of these spillovers within cyberspace. (3) Regarding methodological innovation. We extend the application of spatial econometric methods in network research. First, we introduce an innovation connection spatial matrix based on intercity linkages, replacing geographical proximity with network proximity to better capture spillover effects. Second, we pioneer a dual-weight spatial econometric model for comparative analysis of intra- and inter-agglomeration network externalities, providing a more comprehensive perspective on regional innovation dynamics.

The research framework is as follows (Fig. 1). The first section is the introduction. The second section conducts the literature review. The third section presents the theoretical mechanisms and research hypotheses. The fourth section describes the research design, including the study area, research methods, and data sources. The fifth section reveals the spatiotemporal evolutionary characteristics of the innovation network. The next section performs empirical research on the network externalities of the innovation network. The last section presents the research conclusions, suggestions and outlooks.

Fig. 1

Research framework.

Related works

Research on the mechanism of network effects

Scholars have examined network effects from two key perspectives: agglomeration externalities and network externalities. First, agglomeration externalities emphasize the spatial clustering of economic activities as a fundamental driver of regional economic development (Glaeser et al., 1992). In contexts with limited transportation and network connectivity, spatial spillover effects result mainly from the geographical concentration of economic activities. Agglomeration externalities capture the spatial benefits generated by such clustering (Capello, 2000). However, existing research has largely overlooked the role of spatial heterogeneity and spillover effects in shaping model estimation outcomes (Anselin and Griffith, 2010). Second, Camagni and Salone (1993) introduced the concept of “urban network externalities,” defining them as club goods embedded within networks. With advancements in urban transportation, industrial specialization, information and communication technologies, and cross-regional innovation collaboration, the networking of cities across spatial scales—including urban agglomerations, metropolitan areas, large cities, small and medium-sized cities, and small towns—has become increasingly pronounced (Huang et al., 2020; Yang et al., 2022). The role of urban networks and their cross-spatial spillover effects in economic growth is gaining importance (Lu and Mao, 2020). Current research on urban network externalities often centers on concepts such as the “borrowing scale” and the “agglomeration shadow” (Krugman, 1991). The interaction between agglomeration externalities and network externalities has attracted increasing attention, indicating a shift from a purely geographical perspective to a network-based approach (Van Meeteren et al., 2016). This transition does not imply a dichotomy between geographical space and network space. Instead, network externalities complement and extend agglomeration externalities. While agglomeration externalities stem from geographical proximity, urban network externalities emerge through network-driven interactions and competition. The interplay of these two forces drives complex spatial transformations in urban network environments (Li et al., 2023).

Research on the characteristics of innovation network construction and evolution

On the one hand, scholars often construct innovation networks from a single perspective. In terms of data, they rely primarily on a single dimension, such as patent collaboration, coauthored publications, or corporate investment, to build innovation networks (Dai et al., 2023; Ma et al., 2018a). Methodologically, social network analysis and gravity models are widely used to establish network structures (Ma et al., 2018b; Matthiessen et al., 2010). With respect to research content, existing studies focus mainly on network topology characteristics or the mechanisms of network evolution (Cao et al., 2021). On the other hand, with the rapid advancement of the new technological revolution, innovation activities are increasingly transcending geographical and factor-based constraints, evolving into multidimensional and complex systemic processes. As research on innovation network characterization moves beyond single-dimensional approaches, scholars are further exploring multidimensional and multi-level innovation networks. They integrate diverse data sources, including paper co-authorship, joint patent applications, and inter-regional technology transactions, to construct composite innovation indices. These efforts make it possible to analyze network structural characteristics and multidimensional proximity mechanisms (Dai et al., 2022; Lata et al., 2015; Wang et al., 2021).

Empirical study on the economic effects of innovation networks

With the increasing incorporation of social network analysis into innovation network research, scholars have increasingly focused on the relationships between the overall structural characteristics of networks—such as network density, node attributes, clustering patterns, and network group dynamics—and urban economic development (Scherngell and Hu, 2011; Si et al., 2020). Innovation networks play a significant role in enhancing the flow and sharing of innovative resources among network nodes. The flow of innovation factors contributes to improving urban total factor productivity and facilitates the spatial spillover of knowledge (Crespo and Vicente, 2016). In this regard, research offers important insights into how innovation networks can drive economic growth. With the application of “flow space” theory and “network externality” theory in innovation geography, the relationship between the flow of urban innovation factors and external economic effects has gained increasing attention. The integration of urban network externalities with agglomeration externalities is crucial for understanding how cities should integrate into networks to harness positive externalities (Huggins and Thompson, 2014). Scholars have also proposed mechanisms for promoting coordinated regional development through network externalities, considering aspects such as hyper-distance, decentralization, and shared features (Cao, 2019; Yao and Wu, 2022). Additionally, the impacts of network power and knowledge spillovers on economic efficiency have been examined from the perspective of network externalities (Dong et al., 2023; Oshan et al., 2020; Van Meeteren et al., 2016).

The literature has examined innovation networks from various perspectives, offering valuable theoretical insights for this study. However, several limitations remain: ① The analytical dimensions of innovation networks are relatively narrow. Research on innovation elements and network structures often focuses on a single dimension, and a comprehensive, multidimensional perspective is lacking. This limitation results in a fragmented understanding of China’s innovation landscape. ② The relationship between innovation networks and regional economies remains underexplored. Existing studies primarily emphasize the spatial structure and evolutionary mechanisms of urban innovation networks. However, research on how these networks influence economic development is relatively insufficient. ③ The external economic effects of innovation networks have not been thoroughly examined. Theoretical and empirical studies on the interplay and complementarity of multidimensional innovation networks are still lacking, leaving gaps in understanding their cumulative economic impact.

Theoretical mechanism and research hypotheses

Existence of network externalities in innovation networks

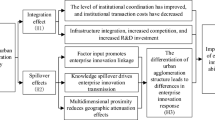
The network externalities of innovation networks are manifested primarily in knowledge spillover effects and economic effects. On the one hand, from the knowledge spillover perspective, innovation activities often involve informal, unconscious, and uncompensated knowledge flows (Cao et al., 2022). In an innovation network, knowledge creators cannot fully monopolize their knowledge. Network connections facilitate the diffusion, transfer, and sharing of knowledge across organizational boundaries, radiating to neighboring cities. In particular, network structural features such as triadic closure and structural holes play a key role in disseminating knowledge between different actors (Cortinovis and Van Oort, 2019), thus enhancing the overall knowledge flow within the innovation network. Through network connections, cities can overcome the limitations of existing knowledge systems, break innovation lock-ins, and achieve knowledge reorganization and technological breakthroughs (Cao et al., 2019). This knowledge flow not only promotes the spread of new technologies but also enables the recombination and optimization of existing knowledge between cities, thus improving innovation performance. On the other hand, from the economic effect perspective, network externalities promote the cross-city flow of innovation factors, which in turn affects regional economic growth. According to economic geography theory, a city’s stock attributes (such as its population size, capital scale, industrial structure, and innovation endowment) determine its functional position in the innovation network and influence the release of external economic effects (Cao et al., 2022). Under the influence of innovation networks, the flow of knowledge and technology not only enhances the innovation capacity of individual cities but also drives industrial upgrading and technological diffusion in neighboring cities (Oshan et al., 2020; Van Meeteren et al., 2016). Furthermore, the cross-city diffusion of tacit knowledge improves the overall innovation efficiency of urban agglomerations, accelerates the commercialization of innovation outcomes, and ultimately boosts regional economic growth (Bishop, 2012; Dong et al., 2023). In conclusion, network externalities expand the spatial scope of innovation diffusion through knowledge spillover effects and enhance the collaborative effects of intra-agglomeration factor flows through economic effects, ultimately influencing regional economic development.

Based on the above analysis, the following hypothesis is proposed:

H1: Network externalities exist in the innovation network of urban agglomerations. Under the influence of network externalities, urban production factors have an impact on the economic development of neighboring cities in the network.

The moderating effect of industrial structure transformation and upgrading

The real economy forms the foundation of regional innovation and sustainable development. Hence, the regional industrial structure plays a critical role in shaping innovation networks and their economic impacts (Innocenti et al., 2020). On the one hand, an advanced industrial structure fosters positive network externalities. The transformation and upgrading of the industrial structure enhance the innovation and the entrepreneurial environment, accelerate the aggregation of innovation resources, and facilitate the development of emerging industries. These factors collectively contribute to the formation of strong social and technological connections within a region, thus generating positive network externalities through improved regional linkages and economies of scale (Wang and Ma, 2017; Yin et al., 2022). On the other hand, an advanced industrial structure may also induce negative network externalities. Cities with higher-level industrial structures have advantages in acquiring innovation resources and efficiently integrating and controlling them. They are better positioned to access diverse and unique external knowledge, which allows them to dominate collaborative efforts and knowledge dissemination. As a result, through the strong siphon effect of their advanced industrial structures, these cities attract an overwhelming amount of resources, creating an “agglomeration shadow” that hinders the development of neighboring cities within the network. This phenomenon inevitably leads to negative network externalities (Mazzola et al., 2015; Yang et al., 2022).

Based on the above analysis, the following hypothesis is proposed:

H2: The transformation and upgrading of the industrial structure have a moderating effect on the release of network externalities in innovation networks. Cities with more advanced industrial structures experience stronger network externalities.

Effect differentiation of the “buzz-and-pipeline” model

The “local buzz and global pipeline” model illustrates how intra-agglomeration collaboration fosters localized knowledge spillovers, enhancing innovation dynamics, whereas inter-regional “pipelines” facilitate external knowledge acquisition and diffusion (Cao, 2019). Spatial proximity and functional connectivity enable network actors to exchange knowledge, technology, and information, optimizing resource allocation and regional innovation capacity (Cao et al., 2022; Zhao et al., 2022). Unlike industrial clusters, where innovation is constrained by localized interactions and cognitive lock-in, urban agglomerations transcend these limitations by integrating dense intra-regional knowledge flows with inter-regional linkages. This multi-nodal innovation system promotes cross-industry collaboration and knowledge recombination, driving technological convergence (Bathelt, 2007; Ren et al., 2023). Although pipelines provide access to external knowledge, they are limited by high transaction costs, a low frequency of interaction, and cognitive distance. In contrast, localized buzz, amplified by spatial proximity, fosters trust-based exchanges, frequent interactions, and shared cognitive frameworks, enabling rapid and efficient knowledge spillovers. This phenomenon results in denser innovation linkages, more efficient knowledge diffusion, and accelerated intra-innovation agglomeration (Cao et al., 2022). Thus, compared with inter-regional pipelines, intra-agglomeration “buzz” effects generate stronger positive network externalities, enhancing regional innovation capacity. Whether through knowledge spillovers or economic synergies, urban agglomerations act as key drivers of innovation and economic growth (Asheim et al., 2007; Bathelt et al., 2002). In conclusion, the “buzz-and-pipeline” model at the urban agglomeration scale transcends the spatial and cognitive limitations of industrial clusters, integrating localized knowledge networks with inter-regional innovation flows and thus reinforcing the role of urban agglomerations as central hubs in regional innovation systems.

Based on the above analysis, the following hypotheses are proposed:

H3a: Both intra-agglomeration “buzz” and inter-agglomeration “pipelines” generate significant network externalities.

H3b: Compared with inter-agglomeration network externalities, intra-agglomeration network externalities tend to be stronger and more positive.

The complementary effect of the “buzz-and-pipeline” model

“Buzz” and “pipelines” can function synergistically, and the interaction between intra-agglomeration “buzz” and inter-agglomeration “pipelines” contributes to urban economic growth (Wang et al., 2023). Intra-agglomeration buzz networks often risk innovation system lock-in due to the low variability of localized knowledge, leading to path dependence in regional economic development and reducing urban economic dynamism (Ma et al., 2024). In contrast, inter-agglomeration pipelines provide an open environment that enables cities to access essential knowledge resources for economic growth. First, inter-agglomeration pipelines attract highly heterogeneous innovation inputs, supplying cities with non-redundant knowledge that transcends existing skills and experiences. Second, they allow cities to acquire scarce, high-value knowledge from external sources, enhancing the completeness and comprehensiveness of urban knowledge stocks (Henn, 2012; Ren et al., 2023). This phenomenon fosters knowledge diversity, disrupts rigid innovation trajectories, and supports the commercialization of innovation outcomes (Cao et al., 2022). Thus, inter-agglomeration pipelines introduce new innovation perspectives, effectively driving urban economic development. Research highlights that the effects of innovation networks depend not only on localized knowledge accumulation but also on the inflow of external knowledge, where extra-regional technological relatedness can compensate for the limitations of intra-regional knowledge linkages (Chen and Wu, 2025). On this basis, intra-agglomeration buzz and inter-agglomeration pipelines are not independent but complementary mechanisms within regional innovation networks. Specifically, inter-agglomeration “pipeline” provides cities with diverse, extensive knowledge and information, whereas intra-agglomeration “buzz” fosters frequent knowledge exchange and absorption. This synergy enables cities to internalize and transform external knowledge, fostering a mutually reinforcing dynamic that enhances urban economic development capacity (Mao et al., 2023).

Based on the above analysis, the following hypothesis is proposed:

H4: The network externalities of intra-agglomeration “buzz” and inter-agglomeration “pipelines” exhibit complementary effects. Their synergy enhances the overall impact of innovation networks, creating a more effective driving force for urban economic development.

The interaction effect of “knowledge” and “technology” innovation networks

From the “flow space” perspective, innovation networks of different dimensions reflect the spatial dynamics of distinct innovation elements, potentially exhibiting interactive spatial correlations (Lyu et al., 2019). The flow of various innovation elements can be conceptualized as functional innovation networks within specific dimensions. Collectively, these networks form a broader urban innovation network, contributing to regional economic development (Lata et al., 2015). The knowledge network and technology network can be seen as distinct yet interrelated components of the urban innovation network. Therefore, analyzing the externalities of urban innovation networks requires a multidimensional perspective, rather than isolating the effects of individual functional networks. By integrating multiple dimensions, the network effect can achieve a synergistic outcome where 1 + 1 > 2 (Taylor et al., 2010). For example, logistics networks comprise various infrastructure networks that facilitate the movement of people, capital, and technology. The coordination of multidimensional logistics networks enhances population mobility, capital flows, and technological diffusion, while the integration of aviation and high-speed rail networks strengthens cross-regional investment linkages among enterprises (Ma et al., 2020c; Sheng et al., 2022). Similarly, innovation networks exhibit distinct functional relationships between different types of networks, generating interaction effects. The urban network structure derived from a single functional innovation network tends to be fragmented and unstable. In contrast, multidimensional innovation networks exhibit greater structural stability and self-organization, with stronger synergistic and complementary effects on the urban economic system.

Based on the above analysis, the following hypothesis is proposed:

H5: There is an interaction effect between the network externalities of the knowledge network and technology network. The interplay and synergy within this dual-layer network enhance the ability of cities to generate greater external economic effects through the network.

The mechanism of the network externalities in the urban agglomeration innovation network is shown in Fig. 2.

Fig. 2

Mechanism of network externality.

Research design

Study area

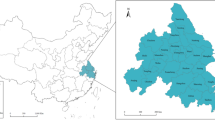
The objects of this study are the five major urban agglomerations in China, namely, the Beijing–Tianjin–Hebei region, the Yangtze River Delta, the Pearl River Delta, the middle reaches of the Yangtze River, and the Chengdu–Chongqing region, comprising a total of 95 cities (Fig. 3). However, due to data acquisition and zoning issues, Qianjiang, Xiantao, and Tianmen were excluded. Therefore, the actual scope of this study consists of 92 cities. The transformation trend of China’s urbanization strategy and the innovative development of the regional economy require close coordination with regional strategies such as the coordinated development of the Beijing–Tianjin–Hebei region, the integration of the Yangtze River Delta region, the Guangdong–Hong Kong–Macao Greater Bay Area, the Yangtze River Economic Belt, and the construction of the Chengdu–Chongqing dual-city economic circle.

Fig. 3: Study area.

The study area includes the five major urban agglomerations in China. a Beijing–Tianjin–Hebei. b Yangtze River Delta. c Pearl River Delta. d Middle reaches of the Yangtze River. e Chengdu–Chongqing.

Research methods

Innovation network construction

• (1) Three-dimensional innovation network construction

We construct a three-dimensional “knowledge–technology–innovation” network of urban agglomerations from a multidimensional innovation flow perspective, integrating paper cooperation and patent cooperation data (Dai et al., 2023; Ma et al., 2018a). Specifically, this study combines the knowledge flow and the technology flow to form a composite innovation flow, as illustrated in Fig. 4.

• A. Knowledge network

  The knowledge layer adopts an undirected symmetric matrix constructed from data on the collaborative publication of papers between cities. The network nodes are cities where different authors of the same paper are located. Network connectivity represents the relationship of the collaborative publication of papers among urban nodes.

  $${{PAP}}_{t}=\left(\begin{array}{cccc}0 & {P}_{12} & \cdots & {P}_{1n}\\ {P}_{21} & 0 & \cdots & {P}_{2n}\\ \vdots & \vdots & \vdots & \vdots \\ {P}_{n1} & {P}_{n2} & \cdots & 0\end{array}\right)$$

  (1)

  In the formula, ${{PAP}}_{t}$ represents the urban knowledge network matrix for year $t$. The diagonal data are 0, indicating the existence of intercity cooperation within the network and the absence of intracity cooperation. ${P}_{{nm}}$ represents the strength of paper collaboration between city $n$ and city $m$. $n$ is the total number of cities within the network.

• B. Technology network

  The technology layer adopts an undirected symmetric matrix constructed from intercity patent cooperation application data. The network nodes are cities where different applicants for the same patent are located. The network edge represents the joint patent application relationship between urban nodes.

  $${W}_{{PAT}}=\left(\begin{array}{cccc}0 & {T}_{12} & \cdots & {T}_{1n}\\ {T}_{21} & 0 & \cdots & {T}_{2n}\\ \vdots & \vdots & \vdots & \vdots \\ {T}_{n1} & {T}_{n2} & \cdots & 0\end{array}\right)$$

  (2)

  In the formula, ${{PAT}}_{t}$ represents the city technology network matrix for year $t$. The diagonal data are 0, indicating the existence of intercity cooperation within the network and the absence of intracity cooperation. ${T}_{{nm}}$ represents the strength of patent cooperation between city $n$ and city $m$. $n$ is the total number of cities within the network.

• C. Innovation network

Fig. 4: Construction of the innovation network in urban agglomerations.

The innovation network consists of three layers: knowledge layer, technology layer, and innovation layer.

The innovation layer is the aggregation of the knowledge layer and the technology layer. We use composite data such as patent data and paper data to represent urban innovation creation, with cities as network nodes and intercity collaborative innovation outputs as network edges. To construct an innovation network for urban agglomerations, two types of innovation element flow data are needed. However, the units and scales of the paper and patent data are different. Therefore, this paper chooses the maximum value standardization method to eliminate the impact of the data scale on the results. We use the weighted-sum method to obtain the comprehensive cooperation strength of intercity innovation, to eliminate the loss of actual information in gravity models (Dai et al., 2022). The formula is as follows:

$${I}_{{ij},t}={W}_{T}\times {PA}{T}_{{ij},t}+{W}_{P}\times {{PAP}}_{{ij},t}$$

(3)

In the formula, ${I}_{{ij},t}$ represents the strength of knowledge innovation cooperation between city $i$ and city$j$ in year ${\rm{t}}$; ${PA}{T}_{{ij}}$ and ${{PAP}}_{{ij}}$ represent the volume of intercity patent cooperation and paper cooperation, respectively; and ${W}_{T}$ and ${W}_{P}$ are the weights of patents and papers, respectively. We use the technique level assurance rate to correct the difficulty coefficient and to determine the weights to obtain the weights of papers and patents, which are ${W}_{P}=0.44$ and ${W}_{T}=0.56$, respectively.

Therefore, the urban innovation network matrix (${{INO}}_{t}$) is obtained as follows:

$$\begin{array}{l}{{INO}}_{t}=\left(\begin{array}{cccc}0 & {I}_{12} & \cdots & {I}_{1n}\\ {I}_{21} & 0 & \cdots & {I}_{2n}\\ \vdots & \vdots & \vdots & \vdots \\ {I}_{n1} & {I}_{n2} & \cdots & 0\end{array}\right)\\=\left(\begin{array}{cccc}0 & {T}_{12}{{\cdot }}{W}_{T}+{P}_{12}{{\cdot }}{W}_{P} & \cdots & {T}_{1n}{{\cdot }}{W}_{T}+{P}_{1n}{{\cdot }}{W}_{P}\\ {T}_{21}{{\cdot }}{W}_{T}+{P}_{21}{{\cdot }}{W}_{P} & 0 & \cdots & {T}_{2n}{{\cdot }}{W}_{T}+{P}_{2n}{{\cdot }}{W}_{P}\\ \vdots & \vdots & \vdots & \vdots \\ {T}_{n1}{{\cdot }}{W}_{T}+{P}_{n1}{{\cdot }}{W}_{P} & {T}_{n2}{{\cdot }}{W}_{T}+{P}_{n2}{{\cdot }}{W}_{P} & \cdots & 0\end{array}\right)\end{array}$$

(4)

• (2) Intra- and inter-urban agglomerations network construction

• A. Intra-urban agglomerations network

  The intra-urban agglomeration network reflects only the innovation collaboration within the urban agglomeration itself, with no collaboration across different urban agglomerations. The matrix is as follows:

  $${{INO}}_{t}^{a}=\left(\begin{array}{cccc}0 & {I}_{12}^{a} & \cdots & {I}_{1n}^{a}\\ {I}_{21}^{a} & 0 & \cdots & {I}_{2n}^{a}\\ \vdots & \vdots & \vdots & \vdots \\ {I}_{{ni}}^{a} & {I}_{n2}^{a} & \cdots & 0\end{array}\right)$$

  (5)
  $${{INO}}_{t}^{{within}}=\left(\begin{array}{cccc}{{INO}}_{t}^{1} & 0 & \cdots & 0\\ 0 & {{INO}}_{t}^{2} & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & {{INO}}_{t}^{u}\end{array}\right)$$

  (6)

  In the formula, ${{INO}}_{t}^{a}$ is the intra-agglomeration innovation cooperation matrix; ${{INO}}_{t}^{{within}}$ is the intra-agglomeration cooperation matrix of $u$ urban agglomerations; and $u$ is the number of urban agglomerations.

• B. Inter-urban agglomerations network

The inter-urban agglomeration network represents only the innovation cooperation relationships inter-agglomeration, with no innovation cooperation occurring intra-agglomeration. The matrix is as follows:

$${{INO}}_{t}^{{ab}}=\left(\begin{array}{cccc}0 & {I}_{12}^{{ab}} & \cdots & {I}_{1n}^{{ab}}\\ {I}_{21}^{{ab}} & 0 & \cdots & {I}_{2n}^{{ab}}\\ \vdots & \vdots & \vdots & \vdots \\ {I}_{{ni}}^{{ab}} & {I}_{n2}^{{ab}} & \cdots & 0\end{array}\right)$$

(7)

$${{INO}}_{t}^{{between}}=\left(\begin{array}{cccc}0 & {{INO}}_{t}^{12} & \cdots & {{INO}}_{t}^{1u}\\ {{INO}}_{t}^{21} & 0 & \cdots & {{INO}}_{t}^{2u}\\ \vdots & \vdots & \vdots & \vdots \\ {{INO}}_{t}^{u1} & {{INO}}_{t}^{u2} & \cdots & 0\end{array}\right)$$

(8)

In the formula, ${{INO}}_{t}^{{ab}}$ is the innovation cooperation matrix between urban agglomeration $a$ and $b$; ${{INO}}_{t}^{{between}}$ is the inter-agglomeration cooperation matrix of $u$ urban agglomerations; and $u$ is the number of urban agglomerations.

Social network analysis

Network embedding is an indicator that measures the tightness of connections and interactions between network nodes through embedded relationships. We use degree centrality to calculate it (Freeman, 1978; Wasserman and Faust, 1994), and the formula is as follows:

$${dgc}\left(i\right)=\frac{{\sum }_{j=1}^{n}{x}_{{ij}}}{n-1},i\;\ne\; j$$

(9)

In the formula, ${dgc}(i)$ represents the degree centrality of city $i$ in the network. ${x}_{i,j}$ represents the connection relationship between city $i$ and city $j$. When there is a cooperative innovation relationship between cities, the value is 1 and 0 otherwise. $n$ is the scale of the network nodes.

Spatial metrological inspection

• (1) Benchmark test model

  ① Spatial lag of X (SLX) model

  This study uses spatial econometric theory and methods to measure network externalities by estimating the spatial spillover effect (Boix and Trullén, 2007; Cheng and Su, 2021). As a starting point for research on spatial spillover effects, the SLX model, which has been demonstrated to be the most direct form of model used to investigate externalities, has been shown to be highly discriminative (Vega and Elhorst, 2015). On this basis, we choose the SLX model as the benchmark model to test the network externalities of the innovation network.

  We take urban agglomerations as the spatial geographical scale, noting that the innovation networks intra- and inter-agglomeration differ. Therefore, it is necessary to divide the production factors into intra- and inter-agglomeration. Therefore, we define the network correlation matrix intra- and inter-agglomeration as spatial weights, and we innovatively use a dual-weight spatial econometric model for estimation. We set up the following spatiotemporal two-way fixed effects dual-weight panel SLX model:

  $$\begin{array}{l}{Y}_{{it}}={\alpha }_{0}{\iota }_{N}+{\alpha }_{1}{W}_{\text{in}}{X}_{{it}}+{\alpha }_{2}{W}_{\text{out}}{X}_{{it}}+{\alpha }_{3}{X}_{{it}}\\\qquad\;+\,{\alpha }_{4}A{E}_{{it}}+{\alpha }_{5}{Z}_{{it}}+{\nu }_{i}+{\mu }_{t}+{\varepsilon }_{{it}}\end{array}$$

  (10)

  In the formula, $i$ represents the city; $t$ represents the year; the constant term vector ${\alpha }_{0}{\iota }_{N}$ is used to measure unobservable rates of technological progress, organizational operational efficiency, etc.; ${\alpha }_{1} \sim {\alpha }_{5}$ are variable coefficients; $Z$ is the set of control variables; ${\nu }_{i}$ represents individual fixed effects; ${\mu }_{t}$ represents time fixed effect; and ${\varepsilon }_{{it}}$ is the random perturbation term.

  ② Spatial Durbin model (SDM)

  To improve the robustness of the test results, this paper uses the SDM to conduct separate tests. The model is as follows:

  $$\begin{array}{l}{Y}_{{it}}={\beta }_{0}{\iota }_{N}+{\beta }_{1}{{W}_{\text{in}}Y}_{{it}}+{\beta }_{2}{{W}_{\text{out}}Y}_{{it}}+{\beta }_{3}{W}_{\text{in}}{X}_{{it}}\\\qquad\;+\;{\beta }_{4}{W}_{\text{out}}{X}_{{it}}+{\beta }_{5}{X}_{{it}}+{\beta }_{6}{Z}_{{it}}+{\beta }_{7}{W}_{\text{in}}{Z}_{{it}}\\\qquad\;+\;{\beta }_{8}{W}_{\text{out}}{Z}_{{it}}+{\nu }_{i}+{\mu }_{t}+{\varepsilon }_{{it}}\end{array}$$

  (11)

  In the formula, ${\beta }_{0}{\iota }_{N}$ is a vector of constant terms; ${\beta }_{1} \sim {\beta }_{8}$ are the coefficient vectors of the corresponding variables; and the rest of the terms have the same meaning as those above.

• (2) Moderating effect model

  To further examine the moderating effect of industrial transformation and upgrading (${{Istrh}}_{{it}}$) on the network externalities of the innovation network, we construct the following model:

  $$\begin{array}{l}{Y}_{{it}}={\omega }_{0}{\iota }_{N}+{\omega }_{1}{W}_{\text{in}}{X}_{{it}}+{\omega }_{2}{W}_{\text{out}}{X}_{{it}}+{\omega }_{3}{{Istrh}}_{{it}}\\\qquad\;+\;{\omega }_{4}{W}_{\text{in}}{X}_{{it}}\times {{Istrh}}_{{it}}+{\omega }_{5}{W}_{\text{out}}{X}_{{it}}\times {{Istrh}}_{{it}}\\\qquad\;+\;{\omega }_{6}{X}_{{it}}+{\omega }_{7}A{E}_{{it}}+{\omega }_{8}{Z}_{{it}}+{\nu }_{i}+{\mu }_{t}+{\varepsilon }_{{it}}\end{array}$$

  (12)

  In the formula, ${\omega }_{0}{\iota }_{N}$ is a vector of constant terms; ${\omega }_{1} \sim {\omega }_{8}$ are the coefficient vectors of the corresponding variables; and the rest of the terms have the same meaning as those above.

• (3) The complementary effect of “buzz-and-pipeline” model

  On the basis of the “buzz-and-pipeline” theory, the complementary and synergistic effects of the intra-agglomeration “buzz” and the inter-agglomeration “pipeline” are worth investigating. This section further introduces the interaction term of the core explanatory variables of intra- and inter-agglomeration to test the complementary effect of intra- and inter-agglomeration innovation networks.

  $$\begin{array}{l}{Y}_{{it}}={\theta }_{0}{\iota }_{N}+{\theta }_{1}{W}_{\text{in}}{X}_{{it}}+{\theta }_{2}{W}_{\text{out}}{X}_{{it}}+{\theta }_{3}{W}_{\text{in}}{X}_{{it}}\times {W}_{\text{out}}{X}_{{it}}\\\qquad\;+\;{\theta }_{4}{X}_{{it}}+{\theta }_{5}A{E}_{{it}}+{\theta }_{6}{Z}_{{it}}+{\nu }_{i}+{\mu }_{t}+{\varepsilon }_{{it}}\end{array}$$

  (13)

  In the formula, ${\theta }_{0}{\iota }_{N}$ is a vector of constant terms; ${\theta }_{1} \sim {\theta }_{6}$ are the coefficient vectors of the corresponding variables; and the rest of the terms have the same meaning as those above.

• (4) The interaction effect model of “knowledge” and “technology”

  The innovation network in this study is a multidimensional composite formed by the interaction between the knowledge network and the technology network. The complex interaction effects between different dimensional networks are worth exploring in depth. We introduce the interaction term of the core explanatory variable for testing:

  $$\begin{array}{l}{Y}_{{it}}={\gamma }_{0}{\iota }_{N}+{\gamma }_{1}{W}_{\text{in}}^{{tech}}{X}_{{it}}+{\gamma }_{2}{W}_{\text{out}}^{{tech}}{X}_{{it}}+{\gamma }_{3}{W}_{\text{in}}^{{basi}}{X}_{{it}}\\\qquad\;+\;{\gamma }_{4}{W}_{\text{out}}^{{basi}}{X}_{{it}}+{\gamma }_{5}{W}_{\text{in}}^{{tech}}{X}_{{it}}\times {W}_{\text{in}}^{{basi}}{X}_{{it}}+{\gamma }_{6}{W}_{\text{out}}^{{tech}}{X}_{{it}}\\\qquad\;\times\; {W}_{\text{out}}^{{basi}}{X}_{{it}}+{\gamma }_{7}{X}_{{it}}+{\gamma }_{8}A{E}_{{it}}+{\gamma }_{9}{Z}_{{it}}+{\nu }_{i}+{\mu }_{t}+{\varepsilon }_{{it}}\end{array}$$

  (14)

  In the formula, ${tech}$ and ${basi}$ represent the technology network and the knowledge network, respectively. The constant term vector is represented by ${\gamma }_{0}{\iota }_{N}$; ${\gamma }_{1} \sim {\gamma }_{9}$ are the coefficient vectors of the corresponding variables; and the rest of the terms have the same meaning as those above.

• (5) Variable definition

① Explained variable (Nilt)

The explained variable in this paper is the level of urban economic development, which is measured by nighttime light data (Uchida et al., 2024).

② Explanatory variables

The core explanatory variable of this article is ${WX}$, which is the network spatial lag term of the core production factor $X$ of the city and is used to represent the network externalities of neighboring cities. The network, $W$, is divided into the intra-agglomeration network ${W}_{{in}}$ and the inter-agglomeration network ${W}_{{out}}$. The core production factor ${X}_{i}$ can be divided into the capital factor $K$ and the human capital factor $L$, that is, ${X}_{i}=\left({K}_{i},{L}_{i}\right)$. Therefore, there are four core explanatory variables in this study: the network lag term ${W}_{{in}}K$ for the intra-agglomeration capital investment; the network lag term ${W}_{{in}}L$ for the intra-agglomeration human capital; the network lag term ${W}_{{out}}K$ for the inter-agglomeration capital investment; and the network lag term ${W}_{{out}}L$ for the inter-agglomeration human capital.

③ Control variables

• A. Agglomeration externalities

  Externalities refer to the influence of external factors on a subject. In economic geography, the mechanism and outcome of regional cooperation networks comprise two mutually coupled spatial economic processes: one comprises the agglomeration externalities formed by local resource aggregation, and the other comprises the network externalities driven by inter-regional cooperation networks. Therefore, to disentangle the economic effect of network externalities, we must control for agglomeration externalities.

  Referring to the relevant literature (Tan et al., 2022), we characterize the agglomeration externalities of urban innovation resources using two indicators: innovation diversity (Div) and innovation specialization (Spe).

  a. This article uses knowledge breadth to represent innovation diversity. Knowledge breadth refers to the scope of the knowledge domain of the innovation subject. Drawing on the methods of scholars (Akcigit et al., 2016), knowledge breadth is measured by the Herfindahl–Hirschman index (HHI) of invention patents and utility model patents using their IPC classification numbers. The calculation formula is as follows:

  $${{Pat}}_{{it}}=1-\sum {\alpha }^{2}$$

  (15)

  In the formula, ${{Pat}}_{{it}}$ represents the knowledge breadth of city $i$ in year $t$, and $\alpha$ is the proportion of each major group of patent classifications calculated according to the IPC classification number.

  b. The level of innovation specialization is related to the depth of knowledge accumulation, which generally refers to the degree of accumulation of professional knowledge and technology in a certain field. We use the location entropy of urban knowledge-based industries to measure the degree of knowledge specialization (Mi et al., 2022). According to the tertiary industry statistical category in the National Economic Industry Classification (GB/T4754-2002), urban knowledge-based industries include information transmission, the accounting services and software industry, the finance industry, the leasing and commercial services industry, scientific research, the technology services and geological exploration industry, and the education industry. The calculation formula is as follows:

  $${KL}{Q}_{{ij}}=\left(\frac{{{kc}}_{{ij}}}{{{kc}}_{i}}\right)/\left(\frac{{{kc}}_{j}}{{kc}}\right)$$

  (16)

  In the formula, ${KL}{Q}_{{ij}}$ represents the number of employees in urban knowledge-based industries; ${{kc}}_{i}$ represents the total number of employees in the city; ${{kc}}_{j}$ represents the number of employees in knowledge-based industries in all cities in China; and ${kc}$ represents the number of employees in all cities in China.

• B. Other control variables

Referring to the relevant literature (Cao, 2019; Ma et al., 2024), this article selects the following six control variables: ① The first is fiscal expenditure (Gov): Government fiscal expenditure can reflect the overall management level of the government over the economy and determine the effectiveness of economic development, and local fiscal general budget expenditure is used as the measurement. ② The second is human capital (L): Talent, especially high-quality talent, is a necessary support for economic development. The level of human capital is characterized by the total number of employees in society as a whole, measured as the sum of employees in urban units and private and individual employees at year-end. ③ The third is capital investment (K): Capital investment is an important factor of production in economic development and is characterized by the capital stock. The perpetual inventory method is used to calculate the capital stock of each city at constant prices. The formula is ${K}_{{it}}={K}_{{it}-1}(1-\delta )+{I}_{{it}}/{P}_{{it}}$. In the formula, ${I}_{{it}}$ is the total amount of fixed assets formed in the current year; $\delta$ is the depreciation rate (9.6%); and ${P}_{{it}}$ is the price index of fixed asset investment. To eliminate the impact of inflation, the fixed asset investment index of each province in the current year is used to convert the fixed asset investment of each city into fixed asset investment, with 2010 as the base period. ④ The fourth is openness to the outside world (Port): A close connection with the external market can enhance the stability of the industrial chain and have an impact on economic development. It is measured by the actual amount of foreign investment utilized in the current year and adjusted to 2010 constant prices based on the GDP deflator index. ⑤ The fifth is the industrial structure (Istr): Each industry contributes differently to economic development because of its own characteristics. The industrial structure is measured by the ratio of the value added of the tertiary industry to that of the secondary industry. ⑥ Finally, the sixth is educational level (Uni): Educational level affects the quality and sustainability of urban economic development, and a good educational environment is the foundation of economic development. It is expressed in terms of the number of college students per 10,000 people.

④ Moderating variable

We examine the moderating effect of industrial transformation and upgrading on innovation network externalities from the perspective of the advanced industrial structure (Yuan and Zhou, 2018). This variable reflects the degree of optimization of the industrial structure, that is, the degree of transformation from low value-added traditional structures to high value-added industrial structures. The formula is as follows:

$${{Istrh}}_{t}=\mathop{\sum }\limits_{i=1}^{3}\left({Y}_{i,t}/{Y}_{t}\times L{P}_{i,t}^{N}\right)$$

(17)

$$L{P}_{i,t}^{N}=\frac{\left(L{P}_{i,t}-L{P}_{{ib}}\right)}{\left(L{P}_{{if}}-L{P}_{{ib}}\right)}$$

(18)

In the formula, ${{Istrh}}_{t}$ is the level of the advanced industrial structure at time $t$. ${Y}_{i,t}$ is the output value of industry $i$ at time $t$. ${Y}_{t}$ is the total output value of the three industries at time $t$. $L{P}_{i,t}^{N}$ represents the standardized labor productivity of industry $i$ at time $t$. $L{P}_{i,t}$ is the labor productivity of industry $i$ at time $t$. $L{P}_{{ib}}$ and $L{P}_{{if}}$ are the labor productivity at the beginning and end of industrialization, respectively, which are calculated according to the standardization method of Chenery et al. (1986).

The descriptive statistics are shown in Table 1.

Table 1 Descriptive statistics.

Data sources and processing

The data used in this study are from the “China Urban Statistical Yearbook,” “China Science and Technology Statistical Yearbook,” “China High-Tech Industry Statistical Yearbook,” and “China Regional Innovation Capability Report” from 2011 to 2020, and they are supplemented by statistical bulletins and the yearbooks of various provinces, municipalities, and autonomous regions. The paper data are sourced from the WOS (Web of Science) Core Collection databases (SCI and SSCI). The patent data are sourced from the patent application data published on the website of the State Intellectual Property Office (SIPO). By matching the addresses of the paper author and patent applicant to their respective cities, we obtain a dataset of urban collaborative innovation. DMSP-OLS and NPP-VIIRS are two widely used nighttime light datasets sourced from the National Geophysical Data Center in the United States (https://www.ngdc.noaa.gov/eog/viirs/download_monthly.html). For some missing data, first, alternative data are found to fill in the missing values; then, linear interpolation is used to fill them in.

Spatiotemporal evolutionary characteristics of the network

Evolutionary characteristics of intra-agglomeration network

Figure 5 shows the spatial patterns of intra-agglomeration innovation networks. Over time, the innovation networks of the five major urban agglomerations have shown the characteristics of an increasing absolute degree of cities, increasing strength of intercity connections, and increasing network density. At the same time, because the evolution of innovation connections between cities is driven by network mechanisms such as hierarchical diffusion, priority attachment, and path dependence, urban innovation connections also present characteristics such as an uneven spatial distribution and distinct network levels.

Fig. 5: Evolutionary characteristics of intra-agglomeration network.

The figures show the evolutionary characteristics of the intra-agglomeration innovation network of China’s five major urban agglomerations in 2011 and 2020. a The intra-agglomeration innovation network in the Beijing–Tianjin–Hebei region. b The intra-agglomeration innovation network in the Yangtze River Delta. c The intra-agglomeration innovation network in the Pearl River Delta. d The intra-agglomeration innovation network in the middle reaches of the Yangtze River. e The intra-agglomeration innovation network in the Chengdu–Chongqing.

Specifically, as shown in Fig. 5a, the innovation network of the Beijing–Tianjin–Hebei region maintains a point–axis structure centered on Beijing. The density of innovation connections in the region decreases outwards from the core of the Beijing–Tianjin–Baoding–Shijiazhuang cluster, and the position of the core innovation corridor became more prominent in 2020, leading to a more pronounced imbalance in the spatial structure of the innovation network. As shown in Fig. 5b, the innovation network of the Yangtze River Delta maintains a “Z”-shaped corridor structure, with Hefei, Nanjing, Shanghai, Hangzhou, and Ningbo as its vertices. Among them, the innovation cooperation relationship between Shanghai and Nanjing is the closest. Figure 5c shows that the innovation network in the Pearl River Delta maintains a “Λ” structural feature along both sides of the Pearl River. In 2011, Guangzhou established innovation cooperation relationships with other cities within the Pearl River Delta. In 2020, all nine cities in the Pearl River Delta established complete innovation cooperation relationships with other cities within the cluster. However, the innovation cooperation between cities in eastern, western, and northern Guangdong is relatively loose. As shown in Fig. 5d, the innovation network in the middle reaches of the Yangtze River has shifted from a point–axis structure centered on Wuhan and Changsha to a “△”-shaped structure consisting of Wuhan, Changsha, and Nanchang. Innovation cooperation in the middle reaches of the Yangtze River is more limited to within provinces, with less cross-provincial innovation cooperation, and it is relatively concentrated between provincial capitals such as Wuhan, Changsha, and Nanchang, as well as direct cooperation between other cities and the three provincial capitals. The intensity of innovation cooperation between other cities is relatively small. As shown in Fig. 5e, the Chengdu–Chongqing innovation network exhibits a “”-shaped structural feature, with Chengdu as the core. From 2011 to 2020, innovation cooperation between Chengdu, Chongqing, and Mianyang became the core corridor for innovation flow within the group.

Evolutionary characteristics of inter-agglomeration network

The spatial pattern of inter-agglomeration innovation network from 2011 to 2020 is shown in Fig. 6. In connection density, the network presents a stable and compact development trend, and in connection structure, the network presents a transformation from an “axis–spoke” diffusion structure to a diamond-shaped spatial structure. In 2011, the inter-agglomeration network revealed the spatial structure of hub-and-spoke diffusion, with Beijing at its core. The innovation cooperation shows the obvious link characteristic of choosing the best approach. That is, high-intensity innovation cooperation basically forms between the core network and the edge cities in each urban agglomeration and shows an obvious “leapfrog” cooperation relationship. In 2020, the density of network connections significantly increased, presenting a distinct diamond-shaped spatial structure with Beijing, Shanghai, Shenzhen, and Chengdu as the vertices, and the network pattern became more stable. In terms of the scale of cooperation, Beijing remains the absolute core of the network. In addition to Beijing’s leading connections, cities such as Shanghai, Nanjing, Guangzhou, Shenzhen, Hangzhou, and Wuhan have gradually developed into key nodes of the network, and their leading role has significantly increased. Overall, there is a significant polarization phenomenon in the inter-agglomeration network; the distribution of innovation elements in the “flow space” is uneven; the threshold for urban status is relatively high; and the network power system is dominated by the network core cities represented by Beijing.

Fig. 6: Evolutionary characteristics of inter-agglomeration network.

The figures show the evolutionary characteristics of the inter-agglomeration innovation network of China’s five major urban agglomerations in 2011 and 2020. a The inter-agglomeration innovation network in 2011. b The inter-agglomeration innovation network in 2020.

Empirical results

Matrix processing results

Before testing network externalities, we need to discuss the standardization of the network matrix, that is, to determine whether to reconstruct the relationships of the local area network. The local averaging method balances the status and role of each node in the network through row standardization, whereas the local summation method enhances the advantages of the core nodes. We use the J test method (Lesage and Pace, 2009). If the J statistic in the model is significant, then the model is not suitable for the network matrix; otherwise, it is suitable. A comparison of the results of the J statistic under different network matrices reveals that the J statistic under the local averaging model of the knowledge network and the technology network is significant, whereas that under the local summation model is not significant, indicating that the local summation model is a more suitable matrix form. For the innovation network, the significance of the local averaging model is greater than that of the local summation model. Thus, we choose the local summation model for subsequent innovation network matrix processing.

Benchmark regression results

Table 2 presents the results of the network externality test for the SLX model. Regarding the intra-agglomeration network externalities, the coefficient of the network lag term for capital (${W}_{{in}}K$) in Model (1) is 28.435***, and is significant at the 1% level. The coefficient of the network lag term for human capital (${W}_{{in}}L$) is 2.439**, and is significant at the 5% level, indicating that the intra-agglomeration network exhibits significant network externalities. With respect to production factors, the connectivity and innovation cooperation within an urban agglomeration’s innovation network effectively promote synergistic, integration, and borrowing scale effects. Consequently, the network’s external spillover effects are activated, which significantly drives the economic development of neighboring cities in the network. Additionally, the coefficients of innovation diversity (Div) and innovation specialization (Spe) are both significant at the 1% level, suggesting that, when network externalities are considered, agglomeration externalities continue to have a significant positive impact on economic development. The presence of network externalities does not diminish the effect of agglomeration externalities. Regional competition within agglomerations may even enhance the impact of network externalities. As two distinct aspects of externality research, agglomeration and network externalities can have complementary functions.

Table 2 Benchmark inspection results.

From the perspective of the inter-agglomeration network externalities, the coefficients of the network lag terms for capital (${W}_{{out}}K$) and human capital (${W}_{{out}}L$) in Model (2) are −16.163* and 1.103**, respectively, and both are significant. These results indicate that the inter-agglomeration network has a significant negative externality effect on capital and a significant positive externality effect on human capital. One possible reason is that the innovation spillover accompanying capital is highly localized, which may stem from the specialization and regionalism of innovation itself, making it easier to form spillover effects in regions with similar knowledge backgrounds and resource conditions. At the same time, geographical distance may also affect the speed and scope of capital and knowledge flow, making the transfer of capital and knowledge more efficient and concentrated within a specific region. Therefore, long-distance cross-regional factor flow is more strongly controlled by the core cities of a region, resulting in a siphon effect under their agglomeration shadow, which hinders the development path of neighboring cities in the inter-agglomeration network and has a negative impact on their economic development. The test results confirm H1 and H3a.

On the basis of the intra- and inter-agglomeration network externalities, a comparison of Model (1) and Model (2) reveals that the intra-agglomeration capital has strong positive externalities. The coefficient of the intra-agglomeration human capital is larger and more significant, indicating that the intra-agglomeration innovation connections are more closely linked. Capital and human capital elements can generate strong externalities through the innovation network, thus promoting intra-agglomeration economic development. Model (3) further shows that when the inter-agglomeration production factors are controlled for, the production factors of intra-agglomeration still produce strong positive externalities. This indicates that, compared with the inter-agglomeration network, the intra-agglomeration network has stronger positive network externalities. On the basis of “buzz-and-pipeline” theory, the intra-agglomeration “buzz” can generate stronger external spillover effects through similar innovation structures and close trust relationships. Simultaneously, the inter-agglomeration “pipelines” strongly depend on “buzz,” and the release of the “pipeline” effect requires a sound “pipeline” system. This also confirms H3b.

Robustness test

Replacing the explained variable

We replace the total value of nighttime light with the mean value of nighttime light and actual GDP as the dependent variable for testing and conduct an auxiliary test of the benchmark regression results. The results of Models (1)–(3) in Table 3 indicate that when the explanatory variable is replaced with the mean value of nighttime light, both the intra-agglomeration capital and human capital elements have significant positive network externalities. The inter-agglomeration capital has significant negative externalities, whereas human capital has significant positive externalities. The capital and human capital intra- and inter-agglomeration in Models (4) and (5) exhibit significant network externalities, with the same direction of the effect as those in Models (1) and (2). In Model (6), although the coefficient of the influence of the intra-agglomeration capital and the inter-agglomeration human capital does not show statistical significance, the coefficient is positive. Therefore, when the explanatory variable is replaced, the intra-agglomeration capital and human capital, and the inter-agglomeration human capital, still exert positive network externality effects on urban economic development through innovation networks, but the inter-agglomeration capital has negative externalities. In summary, the innovation network has significant network externality effects on economic development. Compared with the inter-agglomeration network, the intra-agglomeration network has stronger network externalities for economic development. The test results further support H1 and H3.

Table 3 Robustness tests.

Modifying the sample period

The COVID-19 pandemic has significantly impacted China’s economic development since 2019. To eliminate the interference caused by the pandemic, the sample period is reduced to 2011–2018. The test results, presented in Table 3 (Models 7–9), show that for intra-agglomeration networks, the network externalities of production factors are significantly positive, with larger coefficients and stronger significance. The COVID-19 pandemic has had some effect on the external economic impacts of the network, further supporting H1. However, for inter-agglomeration networks, the impact is not significant. This result can be attributed to the relative underdevelopment of inter-agglomeration networks during the sample period, in which the network connections of inter-agglomeration networks are sparse, preventing the formation of effective network spillover effects. This finding indirectly confirms that during the early stages of network development, the inter-agglomeration “pipeline” is relatively weak, and the externalities are driven primarily by the intra-agglomeration “buzz.”

Replacing the inspection model

Considering that the economic development level between cities may be influenced by neighboring cities in the network, this section comprehensively considers the network dependence of the dependent and explanatory variables and adopts the spatial Durbin model (SDM) for enhanced robustness testing.

• (1) Global Moran’s I test results

  According to the global Moran’s I test results, the autocorrelation coefficients of innovation networks intra- and inter-agglomeration are all significant. Therefore, it is necessary to substitute the network dependency characteristics of the dependent variable into the model to re-examine network externalities.

• (2) SDM test results

In spatial econometric models with spatial dependence, the coefficients of explanatory variables cannot be directly interpreted as elastic (Zhang and Sun, 2022). Therefore, further analysis of the direct and indirect effects of the SDM test results is needed (Table 4). Among them, indirect effects refer to the impacts of urban production factors on other network-related cities within the innovation network, which are also the network externalities that we are concerned with. According to Models (1) and (2), when considering the innovation networks intra- and inter-agglomeration, the indirect effect of the intra-agglomeration capital is not significant, but the direction of the effect is positive (0.164); the indirect effect of the intra-agglomeration human capital is significantly positive (3.021**); the indirect effect of the inter-agglomeration capital is significantly negative (−2.784**); and the indirect effect of the inter-agglomeration human capital is significantly positive (2.033**). The results of Model (3) show that the indirect effect of capital is positive (0.222) when the dual-weight spatial econometric model, which considers the intra- and inter-agglomeration networks, is tested. The indirect effect of human capital is positive (0.582**). When the SDM is used, innovation networks still have significant network externality effects on the economic development of the five major urban agglomerations. This finding indicates that the conclusions drawn in this study are not dependent on the testing model and that the conclusions are robust, further verifying H1 and H3.

Table 4 SDM test results.

Moderating effect test

To avoid endogeneity issues when examining the moderating effects of industrial structure upgrading, it is necessary to exclude the industrial structure from the control variables. According to Table 5, the coefficient of the interaction term between industrial structure upgrading and the spatial lag term of production factors is significant within the urban agglomeration network but not significant in the inter-agglomeration network. This result indicates that the moderating effect of industrial structure upgrading is limited to the intra-agglomeration network and has not yet crossed the inter-agglomeration “threshold.” Specifically, the moderating effect of the intra-agglomeration capital is significantly negative (within: −4.792**, dual weight: −4.315*), indicating that the greater the urban industrial structure is, the stronger the siphon effect on the release of material capital. The upgrading of the urban industrial structure may force industrial transfer, causing neighboring cities to fall into an “agglomeration shadow zone,” thus hindering innovation spillovers and network externalities. For the intra-agglomeration human capital, the moderating effect of industrial structure upgrading is significantly positive (within: 4.824**, dual weight: 4.354*). H2 is verified. The upgrading of the industrial structure helps promote a fuller flow of talent and cooperation in the innovation process so that the positive externalities and spillover effects of human capital can be fully released and the sharing and transformation of innovation results can be more easily produced to improve the efficiency of regional innovation and strengthen the external economic effect of the innovation network.

Table 5 Moderating effect, complementary effect and interaction effect test results.

Complementary effect test of the “buzz-and-pipeline” model

The results from Models (4) and (5) in Table 5 show that, regardless of whether control variables are included, the coefficient for the capital interaction term is positive. After including the control variables, the coefficient becomes statistically significant (1.842*), whereas the coefficient for human capital is significantly negative (−1.285***, −1.152***). These results indicate a complementary effect between the intra-agglomeration “buzz” and the inter-agglomeration “pipeline” in driving urban economic development. This complementary effect is primarily observed in material capital, whereas human capital exhibits a substitution effect. The intra-agglomeration network is expected to generate stronger economic driving effects through the synergistic interaction of the intra-agglomeration “buzz” and the inter-agglomeration “pipelines.” Specifically, without the inter-agglomeration “pipeline” to provide non-redundant external knowledge for urban innovation entities, the high-intensity intra-agglomeration “buzz” can lead to the solidification of the local knowledge base. As a result, local innovation entities are restricted in initiating new innovations. In contrast, if the “buzz” is underdeveloped, the external knowledge from “pipelines” will also struggle to fully diffuse and integrate into the innovation system of urban agglomerations. However, it is also important to consider the competition between the “buzz” and “pipelines” for a city’s limited resources. Only with a reasonable distribution of resources can the beneficial interaction between “buzz” and “pipeline” be fully realized. The results support H4.

Interaction effect test of “knowledge” and “technology” innovation networks

In the interaction effect model, it is crucial to focus on the interaction coefficient of the core explanatory variable. If the coefficient is significantly positive, the two-layer network exhibits functional complementarity, enhancing network externalities. Conversely, if the coefficient is significantly negative, the two-layer network demonstrates functional substitution, which restrains network externalities. The interaction effect between the knowledge network and the technology network is shown in Table 5. Models (6) and (8) indicate that the multiplicative coefficient of the intra-agglomeration capital is positive and significant at the 1% level (intra: 2.912*, dual weight: 3.262***). Models (7) and (8) show that the cross-product of the inter-agglomeration capital is not significant (intra: −0.270, dual weight: 0.191). For material capital, leveraging the intra-agglomeration interaction effect between the knowledge network and the technology network is more conducive to releasing network spillover effects. Models (6)–(8) further demonstrate that the coefficients of the interaction term between human capital intra- and inter-agglomeration are significantly negative. This finding suggests that the interaction between the knowledge network and the technology network has substitution effects on the network spillover effects of human capital. One possible explanation lies in the competitive nature of the knowledge and technology networks with respect to innovative resources such as talent and information, their substitutability in industrial innovation paths, and the differences in knowledge dissemination and application. As a result, there may be a substitution effect between the two networks when driving economic growth. In the process of fostering the development of innovation networks, attention must be paid to the balance and coordination between knowledge and technology to better leverage their complementary synergistic effects. This finding supports H5.

Heterogeneity analysis

Node heterogeneity

In this section, the network embeddedness (degree centrality) of cities is grouped by the 50th percentile, and cities are divided into deeply embedded cities and non-deeply embedded cities. The network externalities of various urban clusters are tested via group regression. Models (1) and (2) in Table 6 indicate that the intra-agglomeration capital of deeply embedded cities exhibits significant positive network externalities; the intra-agglomeration human capital exhibits non-significant positive network externalities. The intra-agglomeration capital of non-deeply embedded cities exhibits non-significant positive network externalities; the intra-agglomeration human capital exhibits significant positive network externalities. For the inter-agglomeration network, the material capital and human capital elements of deeply embedded cities have non-significant negative network externalities; the material capital and human capital elements of non-deeply embedded cities are both positive network externalities. The positive network externalities of capital are significant, whereas human capital is not significant. Deeply embedded intra-agglomeration cities mainly exhibit knowledge spillover effects, whereas outside urban agglomerations, they mainly exhibit siphon effects. The conclusion confirms H3.

Table 6 Heterogeneity test results.

Heterogeneity of urban agglomerations

Table 6 reports the heterogeneous characteristics of network externalities in various urban agglomerations. According to Model (3), capital in the Beijing–Tianjin–Hebei region exhibits non-significant positive externalities within the urban agglomeration network, whereas externalities outside the urban agglomeration network are significantly positive. For human capital, the intra-agglomeration network has significant positive externalities, whereas the inter-agglomeration network has significant negative externalities. The network within the Beijing–Tianjin–Hebei urban agglomeration can help cities reshape their competitive advantages in collaborative innovation and share the benefits brought by network spillovers. This conclusion challenges the traditional view that administrative barriers and uneven resource allocation hinder collaborative innovation in the Beijing–Tianjin–Hebei region. Instead, it suggests that the intra-regional innovation network fosters the restructuring of urban competitive advantages through spillover effects. One possible explanation is that the intra-regional innovation network enhances regional competitiveness by facilitating efficient resource sharing and collaborative innovation. Moreover, it plays a crucial role in improving human capital efficiency, further reinforcing the positive externalities within the network (Chen and Xie, 2018; Zhou and Gu, 2022).

Model (4) indicates that the network externalities of capital and human capital within the Yangtze River Delta urban agglomeration are not significant, but the direction of the effect is negative. One possible reason is that the degree of knowledge integration in the Yangtze River Delta is relatively high. In the process of innovation cooperation, there is a trend of diminishing marginal returns, and the spillover effects of production factors within the group have entered a stage where marginal returns are negative. Therefore, close innovation connections can affect the contribution of production factors to economic development.

Model (5) indicates that capital has significant positive externalities within the Pearl River Delta urban agglomeration network, whereas the positive inter-agglomeration externalities are not significant. The network externalities of intra-agglomeration human capital are significantly negative, whereas the negative inter-agglomeration impact is not significant. The spillover effects of innovation activities in the Pearl River Delta remain limited to being within the urban agglomeration.

Model (6) indicates that the network externalities of production factors within the middle reaches of the Yangtze River are similar to those in the Pearl River Delta and that the network externalities of human capital are significantly negative. The innovation network in the middle reaches of the Yangtze River is in the development stage, with distinct hierarchical attributes and a trend of multi-center development, which will also have a siphon effect on talent within the group.

Model (7) shows that the intra-group and inter-group correlations of the Chengdu–Chongqing urban agglomeration are relatively sparse and that the network externalities are not significant. From the perspective of the influence direction, it exhibits negative intra-agglomeration network externalities and positive inter-agglomeration network externalities.

Conclusion and outlook

Conclusion

This paper examines the network externalities of intra- and inter-agglomeration innovation networks in China’s five major urban agglomerations based on the “buzz-and-pipeline” theory, using data from 2011 to 2020. The findings indicate the following:

• (1) At the theoretical level, we construct a multidimensional spatial model of urban agglomeration innovation networks by integrating knowledge and technology flows. By introducing a research perspective that combines intra-agglomeration and inter-agglomeration dynamics, it advances the understanding of innovation network effects and spatial spillovers, providing a novel theoretical framework for innovation network research.

• (2) The empirical test results show that intra-agglomeration networks exhibit significant positive externalities on regional economic development, with stronger intra-agglomeration effects. The circulation and sharing of intra-agglomeration innovation factors enhance knowledge spillovers and technology diffusion, fostering regional economic growth. Industrial upgrading moderates the intra-agglomeration externalities but has not yet surpassed the threshold in inter-agglomeration networks.

• (3) A complementary relationship exists between the intra-agglomeration “buzz” effect and the inter-agglomeration “pipeline” effect. In terms of physical capital, the intra-agglomeration innovation clustering and inter-agglomeration collaboration reinforce each other, boosting economic vitality. However, for human capital, the externalities of intra- and inter-agglomeration tend to be substitutive, meaning that local collaboration fulfills human capital needs, whereas inter-agglomeration cooperation provides access to external innovation resources.

• (4) The network externalities of innovation vary across different cities. At the urban agglomeration level, the Beijing‒Tianjin–Hebei innovation network facilitates knowledge spillovers and economic benefits through collaborative innovation. The Yangtze River Delta has reached a stage where the marginal return of intra-agglomeration factor spillovers has been negative. The Pearl River Delta still exhibits significant innovation spillover effects, but they remain confined within the agglomeration. Meanwhile, the Middle Yangtze River and Chengdu–Chongqing agglomerations have underdeveloped innovation networks, with weaker externalities. From the perspective of network embeddedness, cities deeply embedded in their intra-agglomeration networks benefit primarily from spillover effects, whereas those embedded in inter-agglomeration networks are more likely to experience siphoning effects.

Suggestions

On the basis of the research conclusions above, the following countermeasures and suggestions are proposed:

• (1) The evolution of the urban agglomeration innovation network should be strengthened. By leveraging the regional leadership effect of key nodes, we can strengthen the role of the “Beijing–Shanghai–Shenzhen–Chengdu” development axis. Doing so will enhance the radiation and coordination functions of the five major urban agglomerations—the Beijing–Tianjin–Hebei region, the Yangtze River Delta, the Pearl River Delta, the Chengdu–Chongqing region, and the middle reaches of the Yangtze River—as national innovation centers. At the same time, differentiated strategies should be implemented for the five major urban agglomerations. The Beijing‒Tianjin‒Hebei region should leverage Beijing’s position as a global innovation hub to promote collaborative innovation in knowledge-intensive industries. The Yangtze River Delta should strengthen Shanghai’s role as an international innovation source to promote the integration of R&D resources and institutional innovation. The Pearl River Delta should optimize innovation cooperation within the Guangdong–Hong Kong–Macao Greater Bay Area to improve the efficiency of technological transformation. The Chengdu–Chongqing region should rely on its regional industrial characteristics to strengthen collaborative innovation in intelligent manufacturing and new materials. The middle reaches of the Yangtze River should promote coordinated development between Wuhan, Changsha, and Hefei, optimizing the flow of regional innovation elements.

• (2) Network effects should be stimulated through multidimensional and multi-level urban connections. By overcoming the limitations of a single innovation element, we can upgrade the innovation network into a multi-level, multidimensional system, enhancing the interaction effects of knowledge flow, technology flow, talent flow, and capital flow. It is important to optimize the interaction between core cities and peripheral cities within urban agglomerations, facilitating the diffusion of innovation resources to secondary nodes and thus creating a gradient development model. Additionally, we should strengthen inter-level city linkages, constructing multi-directional innovation connections between large, medium, and small cities while preventing an over-concentration of resources.

• (3) The network effects intra- and inter-agglomeration should be released through “buzz” and “pipelines.” It is necessary to emphasize both cooperation intra- and inter-agglomeration and to give full play to the complementarity of the two modes of cooperation. The economic development effect of innovation networks can be realized through the cooperation of the intra-agglomeration “buzz” and the inter-agglomeration “pipelines.” For intra-agglomeration cities, more attention should be paid to the resource allocation strategy of the education and scientific research system to optimize the innovation relationships among city levels. With respect to inter-regional cities, more attention should be paid to the creation of a favorable environment to maintain a sound inter-regional innovation network.

Outlook

Notably, this study has several limitations. First, since its introduction, the “buzz-and-pipeline” theory has been widely applied in network research. However, as the formation mechanisms, spillover pathways, and externalities of innovation networks become increasingly complex, the applicability of this theory faces challenges. Future research could integrate perspectives from multilayer networks, AI-driven innovation diffusion, and digital platform embedding. Additionally, incorporating concepts such as “virtual pipelines,” “technological relatedness,” and “cognitive proximity” could expand the theoretical framework of the “buzz-and-pipeline” model, enhancing its relevance in the evolving innovation landscape (Chen and Wu, 2025; Wu et al., 2023). Second, this study focuses solely on China’s national-level urban agglomerations, and it excludes emerging growth poles and non-urban agglomeration regions. Future research could be expanded to a national or even global scale to explore the network characteristics and coordination mechanisms of innovation centers at different levels. Third, the current research is limited to city networks. Future studies could incorporate enterprises, industrial clusters, and science parks to examine how innovation networks interact with policy and investment networks, thus revealing the mechanisms of innovation resource allocation. Finally, this study relies primarily on patent and paper data. Future research could integrate alternative data sources, such as social networks, intellectual property transactions, and corporate mergers and acquisitions, to gain deeper insights into the cross-regional flow of innovation factors and their economic effects.