Abstract
This study explored the relationships among programming self-efficacy, learning strategies, and computational thinking on the basis of self-regulation theory. This study also investigated whether the cognitive styles moderated the structural relationships among the factors through the comparison between analytical and intuitive learners. The participants were 487 high school students enrolled in a computer programming course. Through partial least squares–structural equation modeling, this study confirmed that self-regulated learning strategies influenced computational thinking regardless of the cognitive styles. Programming self-efficacy also influenced self-regulated learning strategies. This study implied that self-efficacy is a prerequisite for self-regulated learning strategies for computer programming. However, the direct effects of programming self-efficacy on computational thinking were observed only in the intuitive students. Programming self-efficacy had an indirect impact on computational thinking through self-regulated learning strategies in analytical students. The self-regulated learning strategies, including metacognitive self-regulation and effort regulation, should be facilitated to improve the computational thinking of analytical students. In addition, this study suggested offering tailored instruction to cater to students with different cognitive styles, ultimately enhancing the effectiveness of computational education and positive programming behavior.
Similar content being viewed by others
Introduction
With the growing integration of artificial intelligence into various aspects of life and learning, computational thinking education, which is closely related to computer science, is receiving increasing attention from scholars and educators. Computational thinking involves a series of thinking processes using computers and computational concepts to solve different types of problems (Wing, 2008). Considering computational thinking remains an ill-defined and developing structure in psychological terms, building its jurisprudential network is necessary to ensure its growth and integration (Román-González et al., 2018). Guggemos (2021) also claimed that in-depth analysis of computational thinking’s correlation with other variables can contribute to its development and understanding. Despite the availability of studies on computational thinking, few discuss the individual characteristics factors related to computational thinking. Studying the factors that directly and indirectly affect computational thinking can improve research on the development of individuals’ computational thinking. Furthermore, such findings can inform curriculum improvement aimed at cultivating computational thinking.
Compared with external factors, internal factors are more critical because they are implicit in nature and difficult to observe (Zhang et al., 2023). Among internal individual characteristics, students’ self-efficacy for computer programming has been widely discussed as a determining factor affecting learning outcomes and thinking skill development. Various strategies and activities have been integrated into programming learning to promote the success of computational thinking education (Li et al., 2023). Despite these efforts, most students lack sufficient skills and confidence in computer programming. When learning programming, students use a rich set of domain specific and universal cognitive and metacognitive strategies, akin to those studied by self-regulated learning researchers (Kong & Liu, 2023). Students with good self-regulated abilities often use metacognitive and resource management strategies in programming; with this advantage in learning, they can perform well (Sholihah & Firdaus, 2023). Moreover, computational thinking is considered a cognitive process regulated by metacognitive practices (Allsop, 2019). Thus, among learning strategies, metacognitive self-regulation, including planning, monitoring, and regulating activities, should receive much attention in computational thinking education. In addition, effort regulation strategies reflect the commitment of learners to planning in the face of difficulties and can regulate the sustained use of learning strategies (Pintrich, et al., 1991). Lack of self-efficacy and self-regulated learning strategies alongside autonomy may lead to negative consequences, such as procrastination (Heo et al., 2022). However, supporting students to develop self-regulated learning with self-efficacy is particularly challenging in the context of computer programming, which demands extra attention to self-regulation in the learning process.
The self-efficacy of students can have both direct and indirect effects on their learning process and ability development through self-regulated learning processes (Bandura, 1992). Although educators emphasize the complexity of students’ acquisition of computational thinking (Chen et al., 2023), limited research pays attention to the intermediary learning processes (e.g., metacognitive self-regulation and effort regulation) between students’ personal beliefs about programming and disposition to computational thinking. Moreover, students with different cognitive styles benefit from distinct learning environments and strategies. Their cognitive styles affect their strategy adoption, thinking development, and learning outcome to varying degrees (Aciang et al., 2023). Although many studies have demonstrated the effects of self-regulation on learning performance, its effects on the computational thinking of students with different cognitive styles remain unclear. Some studies have focused on learning achievements, teaching styles, and learning methods, but few have considered cognitive styles within the deeper personality structures of learners (Theodoropoulos et al., 2017). Therefore, this study aims to provide evidence on which variables are related to and contributing to the development of computational thinking and whether the effect is consistent across students with different cognitive styles.
To address this gap in computational thinking and programming education, this study aims to take a self-regulated perspective to explore how students’ programming self-efficacy and cognitive styles affect computational thinking. First, this study investigates the effects of programming self-efficacy and learning strategies (metacognitive self-regulation and effort regulation) as self-regulated behavior on computational thinking. Second, this study examines the extent to which cognitive styles moderate the effects of programming self-efficacy and self-regulated learning strategies on computational thinking. This study answers the following two research questions:
RQ1. What are the effects of programming self-efficacy and self-regulated learning strategies on computational thinking?
RQ2. Do the cognitive styles of students moderate the effects of programming self-efficacy and self-regulated learning strategies on computational thinking?
Literature review
Computational thinking, programming self-efficacy, and cognitive styles
Definition and history of computational thinking
Wing (2006, p. 33) regarded computational thinking as a fundamental skill facilitated by computers and their widespread applications; it “involves solving problems, designing systems, and understanding human behavior, by drawing on the concepts fundamental to computer science.” Computational thinking gradually attracted the attention of researchers, and different interpretations of its definition emerged, which can be broadly divided into three perspectives. The first perspective closely links computational thinking to programming. For example, Brennan and Resnick (2012) introduced a computational thinking framework centered on computational concepts, practices, and perspectives, which was inspired by the Scratch programming environment. The second perspective emphasizes computational thinking as a set of higher-order thinking skills, including creativity, critical thinking, problem solving, cooperative thinking, and others (e.g., International Society for Technology in Education, 2015; Mannila et al., 2014). The third perspective focuses on process, explaining that computational thinking is a cognitive process that involves abstraction, decomposition, algorithmic thinking, representation, generalization, and evaluation (e.g., Li et al., 2023; Selby & Woollard, 2013). In line with these conventional definitions, computational thinking is not just a cognitive process but also a skill integral to the learning process, supporting students in problem-solving (Chen et al., 2023).
Learners with computational thinking are great at analyzing new information and handling new problems, thereby improving their problem-solving abilities. With the rapid development of artificial intelligence, the convergence of human cognitive abilities, robots, and computer programming underscores computational thinking as an essential skill in modern society (Lin & Mubarok, 2024). Substantial efforts have been made to improve learners’ computational thinking (e.g., Chen et al., 2023; Chiang et al., 2022; Li et al., 2023). Despite studies on the acquisition of computational thinking in education and training contexts, the relationships between computational thinking and the factors for its effective acquisition during computer programming remain under-explored (Lee et al., 2023; Şen, 2023). Furthermore, identifying predictors of computational thinking must be prioritized when providing meaningful computational thinking training for educators and institutions to cultivate high-quality digital talents (Durak & Saritepeci, 2018). In this context, identifying variables that directly and indirectly affect computational thinking during computer programming can contribute to the experimental research on the development of learners’ computational thinking. The findings can inform the improvement of computer science courses aimed at cultivating computational thinking. From this perspective, this study focuses on the effect of various factors during computer programming on the level of computational thinking.
Effect of programming self-efficacy on computational thinking
Self-efficacy plays a significant role in determining learning performance and achievement; it refers to the “beliefs in one’s capabilities to organize and execute the courses of action required to produce given attainments” (Bandura, 1997, p. 3). When individuals with high self-efficacy set goals for themselves, they tend to be patient when facing challenges, because they are clearly aware of the relationship between their gains and efforts (Lee et al., 2023). Programming self-efficacy mainly involves the computational perspective of students, representing their understanding and evaluation of their ability to use programming knowledge and skills in solving computational problems (Kong, 2017; Román-González et al., 2019). Determining and evaluating the programming self-efficacy of students enables them to gauge their performance in programming learning (Cigdem, 2015). Based on the theory of self-efficacy, learners with high self-efficacy tend to be goal oriented, strive to regulate, persist in learning, and execute tasks, thereby attaining success and competence (Bandura, 1992). In summary, students’ programming self-efficacy, a self-judgment of their effective programming learning, may have a strong positive impact on their acquisition of computational thinking.
Numerous empirical studies have also supported this inference, many of which have shown a significant relationship between the programming self-efficacy level of students and the development of their computational thinking ability. For instance, Chiang et al. (2022) applied cluster analysis to classify elementary school students who received STEM online education based on their self-efficacy from high to low. They found that students with high self-efficacy perform better in computational thinking and task value than students with low self-efficacy. Another research on talented and gifted secondary school students has discovered a positive and medium correlation between their programming self-efficacy and computational thinking (Avcu & Ayverdi, 2020). The programming self-efficacy of students with norm-typical level also has a significant impact on their computational thinking performance (Yildiz-Durak et al., 2019). In addition, Martin and Rimm-Kaufman (2015) proposed that students who have positive and relatively high self-efficacy are likely to be encouraged to engage in classroom tasks in terms of motivation, behavior, and cognition. Nonetheless, no research explores whether the relationships between students’ programming self-efficacy and computational thinking are influenced by other cognitive and behavioral factors of the programming process and the predictive status among them. Therefore, an in-depth analysis of the mechanisms by which programming self-efficacy influences computational thinking is necessary and beneficial.
Cognitive styles as a moderator for programming
Individuals’ cognitive styles can influence their information processing, including identifying problems, searching and interpreting information, and generating thoughts, and play a significant role in the development of computational thinking (Yen & Liao, 2019). Several studies have emphasized the importance of considering learners’ cognitive characteristics, such as cognitive styles, when researching technology-related educational matters (Aciang et al., 2023; Gu et al., 2022). Personal cognitive styles remain relatively constant, or at least they are less susceptible to being influenced over time and situation. Cognitive styles refer to differences in individual preferences for information organization, process, and representation, which can usually be manifested in perception, thinking, decision making, learning, and problem solving (Yilmaz, 2021). Cognitive style is explained from different dimensions. The present study used the cognitive style dimensions proposed by Allinson and Hayes (1996) to classify intuitive learners and analytical learners. Intuitive learners, driven by their right brain, favor random exploration methods based on sensation and adopt a global perspective for immediate judgment. They prefer to view problems comprehensively from a holistic perspective (Aciang et al., 2023). By contrast, analytical learners, led by the left brain, tend to make corresponding strategies based on psychological reasoning and attention to details (Kickul et al., 2009). They prefer structured methods to solve problems and are more adaptable to situations that require step-by-step analysis.
Differences in cognitive styles among learners significantly affect their learning outcome, perception, problem solving, and decision making (Theodoropoulos et al., 2017). For instance, in a study on robot classrooms for a Taiwanese secondary school, analytical students have significantly higher academic performance and cognitive engagement than intuitive students, but their mental load was lower than that of intuitive students (Aciang et al., 2023). Papert (1980) defined computational thinking as a procedural thinking process for designing and executing computer programs. This definition implies that learners’ cognitive styles and powerful thinking may impact their learning and thinking ways (Lai et al., 2023). In programming education, students with different cognitive styles may exhibit varied learning outcomes, problem-solving strategies, and learning behavior (Yen & Liao, 2019). Durak and Saritepeci (2018) pointed out that improving computational thinking skills becomes easy and sustainable by considering the cognitive styles of students in instructional design. Overall, understanding the effect of cognitive styles on the development of computational thinking and learning strategies in programming can provide important implications for educators, researchers, and developers.
Self-regulated learning and successful programming learning
Self-regulated learning in programming
Bandura (1992) proposed that self-efficacy can influence achievement by affecting the self-regulation of cognitive, motivational, emotional, and decision-making processes, such as seeking assistance and managing effort. Zimmerman (2000, p. 14) defined self-regulated learning as “self-generated thoughts, feelings, and actions that are planned and cyclically adapted to the attainment of personal goals.” The self-regulation of cognition and behavior can be achieved through students’ learning strategies (Ramírez Echeverry et al., 2018). As the foundation of self-regulated learning, these learning strategies, including metacognitive and resource management strategies (Pintrich et al., 1991), refer to psychological operations or activities carried out to facilitate learning tasks (Ramírez Echeverry et al., 2018). With the expansion of programming education to non-major students, many programming courses have adopted a self-regulated learning mode. Therefore, in computer programming classrooms, more exploration should also be conducted on students’ self-regulated learning strategies.
The problem-solving process in computer programming involves multiple processes similar to self-regulated learning stages, from planning to evaluation (Kong & Liu, 2023). Students who participate in self-regulated learning can self-monitor their learning, seek help from appropriate sources, strategically select tasks they feel capable of completing, and actively adapt to challenges while following feedback (Zimmerman & Schunk, 2011). When programming, it is important for learners to first understand the problem, identify potential solution processes, and acquire necessary knowledge. This initial stage is similar to the planning or pre-thinking stage of self-regulated learning. Learners should also possess the ability to troubleshoot coding errors by understanding the underlying issues and identifying solutions. This problem-solving process aligns with the monitoring or performance stage of self-regulated learning. Throughout programming, learners should assess their potential solutions, similar to the evaluation or self-reflection stage of self-regulated learning (Shin & Song, 2022). Studies on how to improve students’ programming performance and computational thinking abilities by supporting their self-regulated learning have already been conducted (e.g., Gao et al., 2023; Lee et al., 2018). As such, if students can apply more metacognitive and resource management strategies in their programming learning, they are likely to excel and attain a higher quality of computational thinking development. Similarly, students with advanced levels of computational thinking may be more capable of using self-regulated learning strategies.
Self-regulated learning and computational thinking
Students with good self-regulated learning skills are great at setting goals and managing learning and can effectively and efficiently self-monitor, organize, and evaluate their own learning (Sholihah & Firdaus, 2023). They continuously adjust strategies based on monitoring results during the learning process, ultimately forming the optimal solutions (Hong et al., 2021). These skills correspond to important components of computational thinking, including abstraction, algorithms, and evaluation (Sholihah & Firdaus, 2023). In addition, Myers (2021) focused on the intersection of self-regulated learning and computational thinking and summarized that the connection between them can support the development of citizens in preparation for the 21st century. The definition of computational thinking in computer science education supports this statement; it strengthens the importance of cognitive processes that promote computational thinking education, such as self-regulation (Gerosa et al., 2021).
Some empirical studies have also revealed the relationship between self-regulated learning and computational thinking. For example, a study on how students solve trigonometric problems through self-regulated learning has shown that students who exhibit high levels of self-regulated learning are capable of completing three to four indicators of computational thinking. Those with moderate self-regulated learning can complete one to three indicators, while students with low levels of self-regulated learning can manage at most one indicator (Sholihah & Firdaus, 2023). Liu et al. (2021) analyzed experimental data from sixth-grade students in Taiwan. They found that programming self-regulation is an important variable in predicting problem-solving ability, and computational thinking is positively correlated with problem-solving ability. They also concluded that personal traits, such as learning style and self-regulation ability, can help learners enhance their computational thinking. Moreover, a cross-sectional study on Chinese children has shown a positive correlation between their self-regulation and computational thinking, and children’s self-regulated learning fully mediates the relationship between their sequencing ability and computational thinking (Gao et al., 2023). However, direct evidence suggesting a connection between self-regulated learning strategies and computational thinking is little. Little is also known about the underlying mechanisms between these cognitive abilities.
Previous studies have explained how self-regulation mediates the relationship between various variables. Individuals need self-regulation skills to set long-term plan goals, implement strategies, manage time, prepare for potential events, and persist in tasks when facing failure (Baumeister & Vohs, 2003). Self-regulation, therefore, resembles a psychological mechanism associated with positive outcomes (Morosanova, 2013), capable of altering the relationship between two correlated factors in favor of positive outcomes. Cognitive styles, programming self-efficacy, and self-regulated learning strategies are important predictive factors for successful programming learning, and the most important outcome of programming learning is the improvement of learners’ computational thinking level. Considering these two facts, this study was conducted to understand whether programming self-efficacy, cognitive style, and self-regulated learning strategies are related to computational thinking and explore the possible mediating role of self-regulated learning strategies on the relationship between programming self-efficacy and computational thinking.
Research model and hypothesis
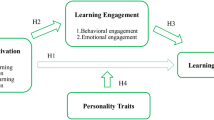
Collectively, educational theories and empirical findings from the previously reviewed studies suggest the hypothesized mediation model of self-regulated learning strategies on the relationship between programming self-efficacy and computational thinking. The hypothesized model is depicted in Fig. 1, and all hypotheses guiding the research questions are listed below.
H1. Programming self-efficacy is positively related to metacognitive regulation strategies.
H2. Programming self-efficacy is positively related to effort regulation strategies.
H3. Programming self-efficacy is positively related to computational thinking.
H4. Metacognitive regulation strategies are positively related to computational thinking.
H5. Effort regulation strategies are positively related to computational thinking.
H6. Cognitive styles moderate the effects of programming self-efficacy and self-regulated learning strategies on computational thinking.
Learners with a higher sense of self-efficacy are better at regulating effort and executing tasks during the learning process, achieving excellent achievements (Bandura, 1992). Self-efficacy can significantly positively predict the use of learning strategies, including metacognitive regulation, monitoring, self-setting goals, effort regulation, and time management (Cho & Shen 2013; Heo et al., 2022; Wolters & Hussain, 2015). Furthermore, in robot programming, Baek et al. (2019) found that second-grade students’ self-efficacy, learning preferences, and intrinsic motivation significantly affect their coding achievement and computational thinking. They concluded that self-efficacy is an important predictor of computational thinking. By analyzing a survey they conducted on 106 middle school students, Avcu and Ayverdi (2020) found a positive correlation between programming self-efficacy and computational thinking. The programming self-efficacy of gifted students is an important predictor of computational thinking and explains 31.5% of the total variance in computational thinking. Given previous research findings, this study hypothesizes that programming self-efficacy positively affects self-regulated learning strategies, including metacognitive self-regulation and effort regulation, as well as computational thinking (H1, H2, and H3).
A survey on online software education for elementary school students has shown that participants’ self-regulated learning and GRIT significantly predict computational thinking, with the explanatory power reaching 87% of the total (Lee et al., 2018). Similarly, Gao et al. (2023) revealed that self-regulation is significantly positively associated with computational thinking. If children have a higher level of self-regulation, they tend to perform better in computational thinking tasks. In addition, according to Allsop (2019), computational thinking is a cognitive process regulated by individual metacognition. As such, metacognitive self-regulation is considered to significantly affect computational thinking. Moreover, previous studies have found that students who use high-level metacognitive and resource management strategies in computer programming learning exhibit significantly higher programming performance than those who use low-level strategies (Bergin et al., 2005). Effort regulation in resource management strategies is a form of self-management that refers to students controlling their efforts and attention when facing uninteresting tasks (Heo et al., 2022). This approach is crucial for the sustained use of metacognitive self-regulation strategies and academic success (Pintrich et al., 1991). Furthermore, a fundamental assumption of the self-regulated learning framework lies in its pivotal mediating role, bridging personal factors, including self-efficacy, with learning outcomes across diverse fields (Pintrich, 2004). Based on previous research findings related to self-regulated learning in computer programming, this study hypothesizes that metacognitive self-regulation and effort regulation positively affect computational thinking (H4 and H5).
Cognitive styles, as another personal characteristic factor in this study, represent an important predictor of learner interest, perseverance, and positive performance in tasks (Luse et al., 2013). They influence students’ preferences in how they process information and approach tasks (Chen & Tseng, 2021). When learners with varying cognitive styles are in the same learning environment, their perception and processing of information may differ (Aciang et al., 2023). Previous studies have discovered the significant relationships between cognitive styles and programming-related skills (Catherine, 1995; Cunha & Greathead, 2007). In addition, Sırakaya et al. (2020) found that STEM attitudes and thinking styles (holistic or analytical) significantly affect computational thinking skills, with an explanatory variance of 43%. Most previous studies have focused on investigating the direct effect of cognitive styles on individual cognition and behavior of learners. The effect of cognitive styles on computer programming processes and outcomes must be investigated from different perspectives. Therefore, this study hypothesizes that cognitive styles may moderate the relationships between variables related to computer programming, such as programming self-efficacy, computational thinking, and self-regulated learning strategies in the computer programming process (H6).
Methods
Context and participants
As mentioned earlier, the key stages of self-regulated learning for learners correspond to the process of using computer programming for problem solving. Although the activities in the programming course in this study were not intentionally designed to promote certain types of self-regulated learning strategies, students have ample opportunities to apply these strategies to programming learning. In addition, during the review courses, this study further provided scaffolding to better support students in using computer programming to solve problems autonomously, as shown in Fig. 2. Students first needed to analyze programming problems, that is, pre-design and plan. This section adopted question-prompted scaffolding, and students need to answer two questions: “What are the key requirements of the problem to be solved? What programming knowledges are needed?” Subsequently, students designed programming algorithms and implemented them using Python programming. The software IDLE (Python 3.10) was provided to students; it supports providing feedback after running code, facilitating self-monitoring by students. To support students in their self-reflection on algorithms, they were provided with an evaluation scale consisting of three dimensions (i.e., coding completeness, normativity, and conciseness). The rating scale was divided into three levels for each dimension, and each level provided specific explanations for students to understand.
A total of 487 participants were recruited from two high schools in northern China, including 216 boys and 271 girls. Their average age was 15.6 years old. They had the same information technology education background and learned Python programming for two semesters. Before the experiment, we conducted an online survey on their cognitive styles and then identified them as either intuitive or analytical learners. Other data were also collected using online electronic surveys, achieving a response rate of 94.4% (distributed: 516, returned: 487).
Measures and instruments
Two data collection instruments were used to measure the theoretical model in this study. The measurement scales are outlined below, along with references, item counts, and the Cronbach’s alphas for the latent variables.
The cognitive styles measurement employed the Cognitive Style Index (CSI) questionnaire developed by Allinson and Hayes (1996). This instrument is both psychometrically robust and convenient for research purposes. Comprising 38 items, the questionnaire utilized a true-uncertain-false trichotomous response format. Each “true” response was assigned 2 points, “uncertain” received 1 point, and “false” garnered 0 point, yielding a maximum score of 76 points. A reverse scoring approach was applied to 17 items, where a “true” response indicated an analytical orientation. A higher overall score on the CSI reflects a more analytical and less intuitive cognitive style. Scores equal to or below the mean or median were categorized as “intuitive style,” whereas those surpassing the mean were classified as “analytical style.” The CSI was widely used in many studies and has shown satisfactory internal consistency reliability (Cronbach’s alpha = 0.84–0.92). In this study, the Cronbach’s alpha for the measurement reached 0.97. Participants could complete the task within 10 min.
For another instrument, based on self-regulated learning theory and existing scales used in related studies, we initially set up a questionnaire consisting of 23 items and three factors, namely, programming self-efficacy, self-regulated learning strategies, and computational thinking. We adopted the 5-point Likert scale ranging from 1 (strongly disagree) to 5 (strongly agree) to measure all items in the questionnaire. Among these factors, programming self-efficacy was measured by six items, which were from the programming attitude scale developed in the study of Sun et al. (2022) with junior high school students. The programming efficacy dimension of this questionnaire was based on expectancy theory model and applicable to the computer programming context. Its Cronbach’s reliability value was 0.94. The measurement for the self-regulated learning strategies of students was divided into two dimensions: metacognitive regulation strategies (eight items), and effort regulation strategies (four items). As a widely used instrument in self-regulated learning assessment, the Motivated Strategies for Learning Questionnaire (MSLQ; Pintrich et al., 1991) with satisfactory internal consistency (Cronbach’s α = 0.69–0.79) was adopted to measure students’ learning strategies in this study. To maintain consistency with the items in other dimensions of the scale, we changed the 7-point Likert items used in the original MSLQ to a 5-point Likert items. Given that the MSLQ instrument aims to measure university students’ use of self-regulated learning strategies, most of the items had to be adjusted to fit the research subjects and programming context in the present study. For example, in the effort regulation dimension of learning strategies, the item “Even when course materials are dull and uninteresting, I manage to keep working until I finish” was revised to “Even when programming is dull and uninteresting, I manage to keep working until I finish.” The computational thinking measurement included five items. These items were adapted from the Computational Thinking Scale (CTS; Tsai et al., 2021), which had a Cronbach’s reliability estimate of 0.91. The self-reported scale was rooted in the problem-solving process definition of computational thinking and independent of any programming contexts. CTS was designed to assess the computational thinking dispositions of young children, so only a few items were adopted for the present study to measure high school students’ computational thinking in a computer programming environment. For example, the item “I usually think about the relations between different problems” was applicable to the object of this study.
Data analysis
This study used the statistical software IBM SPSS (version 23.0) and SmartPLS (version 3.0) to analyze the collected data. The specific steps are as follows:
First, to clarify the factors of the original scale with 24 items, exploratory factor analysis (EFA) was performed using IBM SPSS 23.0. By Stevens’ (1996) criterion, 195 cases were used to perform EFA. The results are shown in supplementary information. After eliminating items with factor loadings below 0.50, the final scale consisted of 23 remaining items.
Second, confirmatory factor analysis (CFA) was conducted to evaluate the construct validity and discriminant validity of programming self-efficacy, metacognitive self-regulation strategies, effort regulation strategies, and computational thinking. In addition, we calculated item loadings, average variance extracted (AVE), and composite reliability (CR) to estimate the convergent validity. The validity and reliability of the measurement model were assessed by estimating the values of composite reliability and average variance explained. Additionally, discriminant validity was evaluated through Pearson’s correlation analysis among all factors.
Third, to answer RQ1, this study performed the partial least squares–structural equation modeling (PLS–SEM) analysis using maximum likelihood estimation to test the first five hypotheses. This analysis focuses on making predictions and was appropriate for a small sample size (Hair et al., 2011). In addition, PLS–SEM was considered appropriate for this research because the proposed model was supported by theoretical knowledge that was still in the developmental stage. We performed bootstrap estimation with 5,000 samples using bias-corrected percentile method and presented the results at the 95% confidence level (Cheung, 2007). To answer RQ2, multi-group analysis in SEM was performed to examine the moderation effects of cognitive styles (i.e., intuitive vs. analytical students) on the effects of programming self-efficacy and self-regulated learning strategies on computational thinking.
Results
Reliability and validity
The outer model consisted of four variables, namely, programming self-efficacy (PS), metacognitive self-regulation (MS), effort regulation (ER), and computational thinking (CT). For the reliability and validity of the measurement model, outer loadings, Cronbach’s alpha, rho-A, CR, and AVE values were examined. As shown in Table 1, the outer loadings of all items were 0.72–0.87 and sufficiently high on their corresponding constructs. Moreover, the Cronbach’s alpha values ranged between 0.86 and 0.91, surpassing the 0.7 threshold for ensuring internal consistency (Fornell & Larcker, 1981). Construct reliability values ranged between 0.90 and 0.93, meeting the reliability standard (Nunnally & Bernstein, 1994). The rho-A values for all constructs (0.86–0.91) also exceeded the suggested value of 0.70 (Hair et al., 2011). In addition, AVE values all surpassed 0.56, surpassing the threshold of 0.50 (Bagozzi et al., 1991). Accordingly, meeting all the recommended criteria indicates sufficient evidence of the item's reliability, internal consistency, and convergent validity of the measurement model.
To assess discriminant validity, we used Fornell and Larcker’s criteria (1981) to determine how much a concept and its indicators differed from another concept and its indicators. As their criteria suggested, the correlations shared between items in any two constructs and the square root of the average variance of constructs should be compared. In Table 2, the values of inter-construct correlations were below in the same column, and the values of square root of average variance were shown in bold font and parentheses on the diagonals. For each construct, the correlation coefficients with other constructs were lower than all square root of the AVE values, showing the discriminant validity of the measurement.
Hypothesis testing
The path coefficients among the latent variables were assessed for statistical significance. The findings regarding the first five hypotheses of the two groups, intuitive students (N = 153) and analytical students (N = 139), were compared.
The results concerning intuitive students are depicted in Fig. 3. All five hypotheses were accepted at p < 0.001 and p < 0.01. Programming self-efficacy had a positive significant effect on metacognitive self-regulation (β = 0.55, t = 8.97), effort regulation (β = 0.62, t = 13.32), and computational thinking (β = 0.20, t = 3.39); thus, H1, H2, and H3 were supported. In addition, self-regulated learning strategies including metacognitive self-regulation (β = 0.27, t = 3.68) and effort regulation (β = 0.50, t = 6.41), had positive influences on computational thinking; consequently, H4 and H5 were also supported. The variances explained in the sub-sample consisting of intuitive students were 30.2% for metacognitive self-regulation, 37.8% for effort regulation, and 71.4% for computational thinking.
The hypothesis testing results reported differences between the intuitive and analytical students. Compared with the intuitive students, only four hypotheses were accepted with analytical students at p < 0.001 and p < 0.05 (Fig. 4). Programming self-efficacy significantly affected metacognitive self-regulation (β = 0.54, t = 8.68) and effort regulation (β = 0.36, t = 3.92) and computational thinking; as a result, H1 and H2 were supported. Furthermore, the effects of metacognitive self-regulation (β = 0.15, t = 2.30) and effort regulation (β = 0.55, t = 5.88) on computational thinking were statistically significant; therefore, H4 and H5 were supported. However, no significant relationship between programming self-efficacy and computational thinking was found; hence, H3 was not supported. In the sub-sample consisting of analytical students, 29.0% variance in metacognitive self-regulation, 12.4% in effort regulation, and 44.5% in computational thinking were explained.
The direct and indirect effects of each variable in the two groups were shown in Table 3. For the hypothesis testing, the direct effects of programming self-efficacy on computational thinking were not found in the analytical group. However, the indirect effects of programming self-efficacy on computational thinking through metacognitive self-regulation and effort regulation were statistically significant at p < 0.001.
Multi-group analysis
To test the moderating effects of cognitive styles on the effects of programming self-efficacy and learning strategies on computational thinking, multi-group analysis (MGA) was performed to examine whether the differences were significant for the two groups (i.e., intuitive students and analytical students). The MGA results are shown in Table 4. For total effects and total indirect effects (i.e., PS→CT), significant differences were found for intuitive and analytical students. Moreover, significant differences were observed between the two groups for PS→ER in direct effects. By contrast, the differences were not significant for the effects of self-regulated learning strategies on computational in the two groups. Accordingly, the relationship between programming self-efficacy and computational thinking was moderated by students’ cognitive styles; H6 was partially supported.
Discussion
Discussion for findings
Educational research on predicting students’ computational thinking has generated practical significance that guides teaching designs in programming education. This study explored the effects of programming self-efficacy and learning strategies on computational thinking from a self-regulated learning perspective. It also investigated if this relationship was moderated by students’ cognitive styles by comparing the intuitive and analytical students.
The findings indicate that programming self-efficacy positively affects self-regulated learning strategies, including metacognitive self-regulation and effort regulation, for both intuitive and analytical groups. This result is consistent with previous research findings about the effect of programming self-efficacy on metacognitive self-regulation learning strategies (Wolters & Hussain, 2015). Previous studies have concluded that learners with higher beliefs in task interest and utility value are more inclined to employ strategies for monitoring and controlling their cognitive process (Bergin et al., 2005). In addition, the results of Heo et al. (2022) are further reinforced by our research, which demonstrates the impact of programming self-efficacy on effort regulation. Self-efficacy emphasizes the importance of the individual’s perceived belief in their ability to organize and execute something, which can lead to engagement or disengagement from an activity or action (Bandura, 1992). According to Bandura (1997), individuals with a high level of self-efficacy view difficult tasks as challenges to face, set challenging goals for themselves, and maintain a firm commitment to achieving these goals. When encountering obstacles, they quickly regain their confidence and only increase the necessary effort to participate in the learning process. This behavior resonates with learning computer programming. For example, students who classify themselves as having high self-efficacy in computer programming are willing to participate in programming learning, work hard when faced with difficult programming tasks, and adjust their learning strategies in a timely manner to achieve pre-set goals during this process (Román-González et al., 2018). Therefore, the present study verified the impact of programming self-efficacy on learning strategies as self-regulated behavior.
The findings of this study also confirm the direct and indirect effects of programming self-efficacy on the computational thinking of students with different cognitive styles. This conclusion confirms the findings of the previous studies (Avcu & Ayverdi, 2020; Baek et al., 2019; Yildiz-Durak et al., 2019). In the present study, programming self-efficacy is only directly related to computational thinking in intuitive students. Aciang et al. (2023) explained that people with high intuition tend to focus on the present and the specific information obtained from their perceptions and often pay attention to patterns when collecting information. Generally, programming tasks are pattern based, and intuitive students tend to perform well based on cognitive style expectations. However, the direct effects of programming self-efficacy on computational thinking are not observed in the analytical students. Instead, in the analytical group, programming self-efficacy indirectly affects computational thinking through self-regulated learning strategies. Intuitive learners who focus on current perception make decisions based on emotions and rely on their belief in their ability to accomplish something (Gorla, 2015). By contrast, analytical learners who are good at thinking and analyzing often use logical reasoning processes to draw conclusions (Theodoropoulos et al., 2017). Even if they have a high sense of programming self-efficacy, they need to adjust their cognitive strategies to achieve better learning achievements and improve their computational thinking abilities.
In terms of self-regulated learning strategies, the effects of metacognitive self-regulation and effort regulation on computational thinking are found in both groups. This result is consistent with the findings that students who use high levels of self-regulated learning strategies perform statistically better than students with lower levels of these strategies (e.g., Bergin et al., 2005; Gao et al., 2023). The execution of computer programming tasks involves the learning of complex concepts that require cognitive efforts, whether it is in class learning or after class practice. For this reason, self-regulated learning strategies have become crucial in computer programming. Additionally, this study recognized the indirect effects of programming self-efficacy on computational thinking through self-regulated learning strategies, including effort regulation and metacognitive self-regulation. This finding supports Heo et al.’s (2023) and Zhang et al.’s (2023) results that self-efficacy indirectly affects cognitive outcomes through self-regulated learning strategies.
Last, this study used MGA to examine whether students’ cognitive styles moderate the effects of programming self-efficacy and self-regulated learning strategies on computational thinking. Statistical differences exist between the intuitive and analytical students, specifically, the effects of programming self-efficacy on effort regulation and computational thinking, which align with the research findings of Chen and Tseng (2021) and Sırakaya et al. (2020). Variables, such as programming self-efficacy, metacognitive self-regulation, or effort regulation, affect computational thinking, and the effects may differ given learners’ cognitive styles. Therefore, educators and scholars should apply tailored instructional strategies and provide distinct support for students with different cognitive styles.
Implications
Unlike previous research on computer programming education, this study expands the focus of programming education beyond computational thinking training to include programming efficacy and self-regulated learning. It also identifies the relationships between the cognitive styles of learners and the key elements of the programming learning process. In addition, this study provides insights for educators and researchers who are committed to helping students achieve success in programming learning.
First, this study confirms that programming self-efficacy has a significant positive effect on students’ self-regulated learning strategies and computational thinking. When students have a high sense of self-efficacy in programming, they believe that they can complete programming tasks and are likely to achieve positive learning outcomes (Lee et al., 2023). Teaching design should consider promoting high programming self-efficacy of students engaged in computer programming, perhaps by making them believe they can complete tasks that are considered difficult. Teachers can provide students with suitable scaffolding to support their problem-solving in programming, such as guiding their thinking and providing positive feedback. In addition, the difficulty of programming tasks should gradually increase to adapt to student skill development and prevent any negative effect on programming self-efficacy.
Second, this study provides theoretical evidence for the relationship between self-regulated learning in computer programming and computational thinking. The results indicate that metacognitive self-regulation strategies and effort regulation strategies have significant positive effects on students’ computational thinking. Teachers should take corresponding actions to encourage learners to engage in these self-regulation processes and promote their computational thinking. For example, metacognitive practice includes planning, evaluation, and monitoring, which can be seen as regulating the triggering and execution control of cognitive activities (Allsop, 2019). Therefore, providing learners with continuous and timely feedback can facilitate self-monitoring of learning progress and performance and set appropriate learning goals for subsequent tasks (Şen, 2023). Educators can model these self-regulated learning strategies for students in a programming environment or guide them to learn how to use these strategies independently during programming.
Third, this study confirms that when explaining the effect of students’ programming self-efficacy on computational thinking from a self-regulation perspective, their cognitive style must be considered. Although this study does not find a direct relationship between programming self-efficacy and computational thinking among analytical students, this relationship is mediated by self-regulated learning strategies. Analytical students with programming confidence can improve their computational thinking performance by understanding how to effectively use metacognitive self-regulation and effort regulation strategies. Compared with intuitive learners, analytical learners have more confidence in evaluating, planning, and coordinating resources, but they lack confidence in discovering and identifying new opportunities (Aciang et al., 2023). Hence, educators can design targeted programming activities based on the cognitive style of students to provide easy and sustainable learning of computational thinking.
Conclusion
This study aims to understand how students’ programming self-efficacy directly affects their computational thinking and indirectly affects it through self-regulated learning strategies. Based on the analysis results of path analysis and MGA, all six hypotheses proposed in this study are well supported. Programming self-efficacy and self-regulated learning strategies are the main predictors of computational thinking, but no direct relationship is found between programming self-efficacy and computational thinking for analytical students. The results of path analysis also reveal that programming self-efficacy affects self-regulated learning strategies. An additional important finding is the moderation effect of students’ cognitive styles on the relationships among these constructs. The positive findings of this preliminary investigation are beneficial for studying the factors that affect computational thinking and programming success and provide recommendations for further research.
This study also has limitations. First, the sample size of this study is relatively small and only from China. Comrey and Lee (2013) concluded that a relatively small sample size of SEM analysis may lower accuracy in parameter estimation. With a broader sample size, additional evidence can be gathered to further support the findings and further generalize these conclusions across different countries and cultures. Another limitation of this study is that the measures only involve self-reporting. However, self-reported data may be disrupted by external influences such as social pressure and personal beliefs (Chan, 2009). Utilizing multiple sources of data and other types of measures, including observations, interviews, and think-aloud protocols, may help further explain the nature of the relationships among programming self-efficacy, self-regulated learning, and computational thinking.
Despite these limitations, the results of this study provide insights into this important topic. This study emphasizes the deepest layers of individual thinking, namely, the cognitive styles and self-efficacy of learners, and focuses on self-regulated learning involved in the programming process. Previous studies have focused mainly on what students gain from computer programming (e.g., programming performance or skill improvement), whereas our study focuses on how students gain. In the future, the theoretical framework elucidated in this study holds promise to serve as a strong basis for predicting or elucidating student performance in computer programming. It also offers novel perspectives on the evolution of computational thinking in related instruction.
Data availability
Data will be made available on request.
References
Aciang I-S, Hwang G-J, Chen C-H (2023) Decision-guided chatbots and cognitive styles in interdisciplinary learning. Comput Educ 201:104812. https://doi.org/10.1016/j.compedu.2023.104812
Allinson CW, Hayes J (1996) The cognitive style index: a measure of intuition-analysis for organizational research. J Manag Stud 33(1):119–135. https://doi.org/10.1111/j.1467-6486.1996.tb00801.x
Allsop Y (2019) Assessing computational thinking process using a multiple evaluation approach. Int J Child Comput Interact 19:30–55. https://doi.org/10.1016/j.ijcci.2018.10.004
Avcu YE, Ayverdi L (2020) Examination of the computer programming self-efficacy’s prediction towards the computational thinking skills of the gifted and talented students. Int J Educ Methodol 6(2):259–270. https://doi.org/10.12973/ijem.6.2.259
Baek Y, Yang DZ, Fan YB (2019) Understanding second grader’s computational thinking skills in robotics through their individual traits. Inf Discov Deliv 47(4):218–228. https://doi.org/10.1108/idd-09-2019-0065
Bagozzi RP, Yi Y, Phillips LW (1991) Assessing construct validity in organizational research. Adm Sci Q 36(3):421–458. https://doi.org/10.2307/2393203
Bandura A (1997) Self-efficacy: the exercise of control. New York: Freeman
Bandura A (1992) Exercise of personal agency through the self-efficacy mechanism. In R Schwarzer (Ed.), Self-efficacy: Thought control of action (pp 3–38) Hemisphere Publishing Corp
Baumeister RF, Vohs KD (2003) Self-regulation and the executive function of the self. In MR Leary & JP Tangney (Eds), Handbook of self and identity (pp 197–217). The Guilford Press
Bergin S, Reilly R, Traynor D (2005) Examining the role of self-regulated learning on introductory programming performance. In Proceedings of the First International Workshop on Computing Education Research (pp 81–86). New York, NY: Association for Computing Machinery. https://doi.org/10.1145/1089786.1089794
Brennan K, Resnick M (2012) New frameworks for studying and assessing the development of computational thinking. In Proceedings of the 2012 Annual Meeting of the American Educational Research Association (pp 13–17). Vancouver, Canada
Catherine B-C (1995) Cognitive style, personality, and computer programming. Comput Hum Behav 11(2):241–260. https://doi.org/10.1016/0747-5632(94)00034-F
Chan D (2009) So why ask me? Are self-report data really that bad? In CE Lance, & RJ Vandenberg (Eds.), Statistical and methodological myths and urban legends: Doctrine, verity and fable in the organizational and social sciences (pp 311-338). New York: Routledge
Chen C-H, Liu T-K, Huang K (2023) Scaffolding vocational high school students’ computational thinking with cognitive and meta-cognitive prompts in learning about programmable logic controllers. J Res Technol Educ 55(3):527–544. https://doi.org/10.1080/15391523.2021.1983894
Chen SY, Tseng YF (2021) The impacts of scaffolding e-assessment English learning: a cognitive style perspective. Comput Assist Lang Learn 34(8):1105–1127. https://doi.org/10.1080/09588221.2019.1661853
Cheung MWL (2007) Comparison of approaches to constructing confidence intervals for mediating effects using structural equation models. Struct Equ Modeling A Multidiscip J 14(2):227–246. https://doi.org/10.1080/10705510709336745
Chiang F-K, Zhang Y, Zhu D, Shang X, Jiang Z (2022) The influence of online STEM education camps on students’ self-efficacy, computational thinking, and task value. J Sci Educ Technol 31:461–472. https://doi.org/10.1007/s10956-022-09967-y
Cho M-H, Shen D (2013) Self-regulation in online learning. Distance Educ 34(3):290–301. https://doi.org/10.1080/01587919.2013.835770
Cigdem H (2015) How does self-regulation affect computer-programming achievement in a blended context? Contemp Educ Technol 6(1):19–37. https://doi.org/10.30935/cedtech/6137
Comrey AL, Lee HB (2013) A first course in factor analysis. Psychology Press
Cunha AD, Greathead D (2007) Does personality matter? An analysis of code review ability. Commun ACM 50:109–112. https://doi.org/10.1111/10.1145/1230819.1241672
Durak H-Y, Karaoglan Yilmaz FG, Yilmaz R (2019) Computational thinking, programming self-efficacy, problem solving and experiences in the programming process conducted with robotic activities. Contemp Educ Technol 10(2):173–197. https://doi.org/10.30935/cet.554493
Durak HY, Saritepeci M (2018) Analysis of the relation between computational thinking skills and various variables with the structural equation model. Comput Educ 116:191–202. https://doi.org/10.1016/j.compedu.2017.09.004
Fornell C, Larcker D (1981) Structural equation models with unobservable variables and measurement error: algebra and statistics. J Mark Res 18(3):382–388. https://doi.org/10.2307/3150980
Gao H, Yang W, Jiang Y (2023) Computational thinking in early childhood is underpinned by sequencing ability and self-regulation: a cross-sectional study. Educ Inf Technol 28(4):14747–14765. https://doi.org/10.1007/s10639-023-11787-5
Gerosa A, Koleszar V, Tejera G, Gómez-Sena L, Carboni A (2021) Cognitive abilities and computational thinking at age 5: Evidence for associations to sequencing and symbolic number comparison. Comput Educ Open 2:100043. https://doi.org/10.1016/j.caeo.2021.100043
Gorla N (2015) The role of cognitive style in the comprehension of systems analysis tools. In Proceedings of 21st IRF International Conference (pp 76-79). India: Chennai
Gu X, Tan Y, Wu X, Cai Z, Lai Q, Cheng M, Zhao Q (2022) Active versus passive strategy in online creativity training: How to best promote creativity of students with different cognitive styles? Think Skills Creat 44:101021. https://doi.org/10.1016/j.tsc.2022.101021
Guggemos J (2021) On the predictors of computational thinking and its growth at the high-school level. Comput Educ 161:104060. https://doi.org/10.1016/j.compedu.2020.104060
Hair JF, Ringle CM, Sarstedt M (2011) PLS-SEM: Indeed a silver bullet. J Mark Theory Pract 19(2):139–152. https://doi.org/10.2753/MTP1069-6679190202
Heo H, Bonk CJ, Doo MY (2022) Influences of depression, self-efficacy, and resource management on learning engagement in blended learning during COVID-19. Internet High Educ 54:100856. https://doi.org/10.1016/j.iheduc.2022.100856
Hong JC, Lee YF, Ye JH (2021) Procrastination predicts online self-regulated learning and online learning ineffectiveness during the coronavirus lockdown. Personal Individ Differ 174:110673. https://doi.org/10.1016/j.paid.2021.110673
International Society for Technology in Education. (2015). Computational thinking leadership toolkit first edition. Retrieved from https://cdn.iste.org/www-root/2020-10/ISTE_CT_Leadership_Toolkit_booklet.pdf
Kickul J, Gundry LK, Barbosa SD, Whitcanack L (2009) Intuition versus analysis? Testing differential models of cognitive style on entrepreneurial self-efficacy and the new venture creation process. Entrep Theory Pract 33(2):439–453. https://doi.org/10.1111/j.1540-6520.2009.002
Kong SC (2017) Development and validation of a programming self-efficacy scale for senior primary school learners. In SC Kong, J Sheldon, & KY Li (Eds.), In Proceedings of the International Conference on Computational Thinking Education (pp 97–102). The Education University of Hong Kong
Kong SC, Liu B (2023) Supporting the self-regulated learning of primary school students with a performance-based assessment platform for programming education. J Educ Comput Res 61(5):977–1007. https://doi.org/10.1177/07356331221143832
Lai X, Ye J, Wong GKW (2023) Effectiveness of collaboration in developing computational thinking skills: a systematic review of social cognitive factors. J Comput Assist Learn 39(5):1418–1435. https://doi.org/10.1111/jcal.12845
Lee J, Chae Y, Lee M (2018) Predictability of elementary students’ self-regulated learning, grit and parents support on computational thinking and learning satisfaction in online software education. J Korean Assoc Inf Educ 22(6):689–699. https://doi.org/10.14352/jkaie.2018.22.6.689
Lee SW-Y, Liang J-C, Hsu C-Y, sai M-J (2023). Students’ beliefs about computer programming predict their computational thinking and computer programming self-efficacy. Interact Learn Environ, online. https://doi.org/10.1080/10494820.2023.2194929
Li Q, Jiang Q, Liang J-C, Xiong W, Liang Y, Zhao W (2023) Effects of interactive unplugged programming activities on computational thinking skills and student engagement in elementary education. Educ Inf Technol 28(9):12293–12318. https://doi.org/10.1007/s10639-023-11634-7
Lin C-J, Mubarok H (2024) Promoting young learners’ computational thinking with AI-based robots and the ICAP model in blended learning contexts. Interact Learn Environ online. https://doi.org/10.1080/10494820.2024.2308101
Liu YC, Huang TH, Sung CL (2021) The determinants of impact of personal traits on computational thinking with programming instruction. Interact Learn Environ 31(8):4835–4849. https://doi.org/10.1080/10494820.2021.1983610
Luse A, McElroy JC, Townsend AM, DeMarie S (2013) Personality and cognitive style as predictors of preference for working in virtual teams. Comput Hum Behav 29(4):1825–1832. https://doi.org/10.1016/j.chb.2013.02.007
Mannila L, Dagiene V, Demo B, Grgurina N, Mirolo C, Rolandsson L, et al. (2014) Computational thinking in K-9 education. In Proceedings of the working group reports of the 2014 on innovation & technology in computer science education conference, ITiCSE-WGR 2014 (pp 1e29). New York: ACM
Martin DP, Rimm-Kaufman SE (2015) Do student self-efficacy and teacher-student interaction quality contribute to emotional and social engagement in fifth grade math. J Sch Psychol 53(5):359–373. https://doi.org/10.1016/j.jsp.2015.07.001
Morosanova VI (2013) Self-regulation and personality. Procedia-Soc Behav Sci 86:452–457. https://doi.org/10.1016/j.sbspro.2013.08.596
Myers EK (2021) The role of executive function and self-regulation in the development of computational thinking. In M Bers (Ed.), Teaching computational thinking and coding to young children (pp 64-83). IGI Global
Nunnally JC, Bernstein IH (1994) Psychometric theory (3rd ed). McGraw-Hill
Papert S (1980) Mindstorms: Children, computers, and powerful ideas (1, 2nd ed). Basic Books
Pintrich PR (2004) A conceptual framework for assessing motivation and self-regulated learning in college students. Educ Psychol Rev 16(4):385–407. https://doi.org/10.1007/s10648-004-0006-x
Pintrich PR, Smith DAF, Garcia T, Mckeachie WJA (1991) A manual for the use of the motivated strategies for learning questionnaire (MSLQ)
Ramírez Echeverry JJ, Rosales-Castro LF, Restrepo-Calle F, González FA (2018) Self-regulated learning in a computer programming course. IEEE Rev Iberoam de Tecnol del Aprendiz 13(2):75–83. https://doi.org/10.1109/RITA.2018.2831758
Román-González M, Moreno-León J, Robles G (2019) Combining assessment tools for a comprehensive evaluation of computational thinking interventions. In SC Kong, & H Abelson (Eds.), Computational thinking education (pp 79–98). Springer Open Access
Román-González M, Pérez-González J-C, Moreno-León J, Robles G (2018) Extending the nomological network of computational thinking with non-cognitive factors. Comput Hum Behav 80:441–459. https://doi.org/10.1016/j.chb.2017.09.030
Selby CC, Woollard J (2013) Computational thinking: The developing definition. In Presented at the 18th Annual Conference on Innovation and Technology in Computer Science Education. Canterbury, England: University of Kent
Şen Ş (2023) Relations between preservice teachers’ self-efficacy, computational thinking skills and metacognitive self-regulation. Eur J Psychol Educ 38:1251–1269. https://doi.org/10.1007/s10212-022-00651-8
Shin Y, Song D (2022) The effects of self-regulated learning support on learners’ task performance and cognitive load in computer programing. J Educ Comput Res 60(6):1490–1513. https://doi.org/10.1177/07356331211052632
Sholihah U, Firdaus AI (2023) Student’s computational thinking ability in solving trigonometry problems in the review of self-regulated learning. Jurnal Penelitian Pendidikan IPA, 9(2), 626-633. https://doi.org/10.29303/jppipa.v9i2.2821Stevens, J (1996). Applied multivariate statistics for the social science (3rd ed.). Lawrence Erbaum
Sun L, Hu L, Zhou D (2022) Programming attitudes predict computational thinking: Analysis of differences in gender and programming experience. Comput Educ 181:104457. https://doi.org/10.1016/j.compedu.2022.104457
Sırakaya M, Alsancak Sırakaya D, Korkmaz Ö (2020) The impact of STEM attitude and thinking style on computational thinking determined via structural equation modeling. J Sci Educ Technol 29:561–572. https://doi.org/10.1007/s10956-020-09836-6
Theodoropoulos A, Antoniou A, Lepouras G (2017) How do different cognitive styles affect learning programming? Insights from a game-based approach in Greek schools. ACM Trans Comput Educ 17(1):1–25. https://doi.org/10.1145/2940330
Tsai M-J, Liang J-C, Hsu C-Y (2021) The computational thinking scale for computer literacy education. J Educ Comput Res 59(4):579–602. https://doi.org/10.1177/0735633120972356
Wing JM (2006) Computational thinking. Commun ACM 49(3):33–35
Wing JM (2008) Computational thinking and thinking about computing. Philos Trans R Soc A Math Phys Eng Sci 366(1881):3717–3725
Wolters CA, Hussain M (2015) Investigating grit and its relations with college students’ self-regulated learning and academic achievement. Metacognit Learn 10:293–311. https://doi.org/10.1007/s11409-014-9128-9
Yen JC, Liao WC (2019) Effects of cognitive styles on computational thinking and gaming behavior in an educational board game. Int J Learn Technol Learn Environ 2(2):1–10. https://doi.org/10.52731/ijltle.v2.i2.477
Yilmaz O (2021) Cognitive styles and religion. Curr Opin Psychol 40:150–154. https://doi.org/10.1016/j.copsyc.2020.09.014
Zhang Z, Maeda Y, Newby T, Cheng Z, Xu Q (2023) The effect of preservice teachers’ ICT integration self-efficacy beliefs on their ICT competencies: The mediating role of online self-regulated learning strategies. Comput Educ 193:104673. https://doi.org/10.1016/j.compedu.2022.104673
Zimmerman BJ (2000) Attaining self-regulation: a social cognitive perspective. In Boekaerts, M, Pintrich, PR, & Zeidner, M (Eds.), Handbook of self-regulation (pp. 13-39). SanDiego, CA: Academic Press
Zimmerman BJ, Schunk DH (Eds), (2011). Handbook of self-regulation of learning and performance. Routledge
Acknowledgements
This study was also supported by the National Natural Science Foundation of China (Project Approval # 62077012, # 62307021).
Author information
Authors and Affiliations
Contributions
Qi Li: Methodology, Data Curation, Formal Analysis, Visualization, Writing—Original Draft; Qiang Jiang: Conceptualization, Writing—Review and Editing, Resources, Supervision; Jyh-Chong Liang: Methodology, Writing—Review and Editing; Weiyan Xiong: Writing—Review and Editing; Wei Zhao: Resources, Supervision.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethical approval
This study complies with ethical standards and guidelines outlined in the Declaration of Helsinki. Because of the observational nature of the study, also in the absence of any involvement of therapeutic medication, according to the decision made by the Ethics Committee of Northeast Normal University on 2nd March 2023, this questionnaire-based study does not require ethical approval.
Informed consent
All aspects of this study were conducted voluntarily by participants and with the approval of their parents. Between 27th March 2023 and 10th December 2023, all participants and their parents signed informed consent forms. In addition, they were informed that personal information would be hidden during the research. They were also free to withdraw from the research at any time.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Li, Q., Jiang, Q., Liang, JC. et al. Roles of programming self-efficacy, cognitive styles, and self-regulated learning strategies on computational thinking in computer programming. Humanit Soc Sci Commun 12, 1412 (2025). https://doi.org/10.1057/s41599-025-05686-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-025-05686-y