Heavy rains from tropical cyclones (TCs) significantly impact coastal areas, causing severe urban flooding and transportation disruptions1,2,3,4,5,6,7,8. The Tropical Rainfall Measuring Mission (TRMM)–Multi-satellite Precipitation Analysis (TMPA) has provided data for the past 20 years, showing an 8% increase in the annual average TC rain rate (RR) within the total rainfall area (a radius of ~500 km from the center of the TC eye)9,10. Despite advancements in forecasting the track and intensity of TCs11,12, the accuracy of predicting their RRs has not significantly improved. In particular, it is challenging to predict the rapid change in average TC RRs within a short period, such as 24-h.

Currently, numerous scholars9,10,13,14 have investigated the interannual trends of average TC RRs in recent years and their potential contributing factors. Two well-established satellite-based products, the TMPA15,16 and the Integrated Multi-satellitE Retrievals for Global Precipitation Measurement (IMERG)17,18, are widely used to estimate TC RRs. A recent study9 reported a 24% decrease in the annual average TC RRs within the inner-core (a radius of ~125 km from the center of the TC eye) due to increasing atmospheric stability (AS). It is also identified a strong positive relationship between TC total rainfall area RRs and translation speeds19. Lin et al.20 proposed that the rainfall area of a TC is influenced by relative sea surface temperatures (SSTs), whereas the absolute SST is linked to increases in the TC RR. However, little attention has been given to the temporal stability of the TC rainfall (amplitude of change in average RR over a 24-h period) in previous studies using observational datasets. It is widely recognized that the study of the intensification rate of TC intensity (amplitude of change in TC intensity over a 24-h period) is crucial for predicting rapid intensification and improving preparedness for wind-induced disasters in coastal areas21,22,23,24,25,26,27,28,29,30,31,32. Similarly, the temporal stability of the global TC RR should be considered. In particular, a rapid change in the average TC RR within a short timeframe indicates a sudden surge (or plummeting) in total rainfall within the TC rainfall area, which is crucial for TC rainfall forecasting.

Using the satellite-based observational rainfall dataset and the reanalysis dataset (see “Methods” and Supplementary Table 1), we calculate changes in TC 24-h RRs to quantify the temporal stability of TC precipitation over the past two decades. We conclude that RRs in the TC total rainfall area may become increasingly easier to maintain at higher levels.

Results

Narrowing in annual TC 24-h RR changes

Considering that the TC total rainfall is calculated by multiplying the average RR and the TC total rainfall area (Supplementary Fig. 1), although the average RR value in the TC total rainfall area is small (usually 1–3 mm h–1)9,10,15,19, its slight change in a short timeframe may still indicates a substantial change in the TC total precipitation over that period.

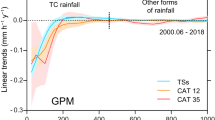
Here, we seek to understand the global interannual trend in TC 24-h RR changes. Although the distribution of global TC 24-h RR changes in the IMERG is wider than that in the TMPA between 2001 and 2019 (Supplementary Fig. 2), both observational datasets show similar patterns in S-shaped curves (see Fig. 1 and “Methods”). For the TMPA data, the results for the TC total rainfall area indicate statistically significant trends (P value < 0.05) across all quantiles, except for those between the 35th and 55th quantiles. The 5th percentile exhibits the highest trend, showing an increase of ~0.21 ± 0.08 mm h–1 per decade, while the 95th percentile displays the lowest trend, with a decrease of approximately –0.16 ± 0.07 mm h–1 per decade (Fig. 1a). Notably, the lower percentiles exhibited positive slopes, while the higher percentiles showed negative slopes, indicating a gradual narrowing in the distribution of TC 24-h RR changes (Supplementary Fig. 3). In simpler terms, the number of TCs exhibits high RR volatility decreases. The inner-core and rainband areas demonstrate similar trends, with the inner-core area exhibiting the highest slope amplitude, ranging from 1.51 ± 0.35 to –1.37 ± 0.41 mm h–1 per decade, and a high level of confidence (Fig. 1b). However, the confidence level associated with the IMERG slope for each quantile is relatively low, despite its large magnitude. Nevertheless, the annual trends of the 5th and 95th percentiles are statistically significant (P value < 0.05) for both the TMPA and IMERG (Fig. 1c).

Fig. 1: Regression slopes of the quantiles for global TC 24-h RR changes during the period 2001–2019. Slopes are shown for the TMPA (blue) and the IMERG (red).
figure 1

a TC total rainfall area, b Inner-core, and c Rainband area. The dots represent the slopes derived from least squares regression of the 24-h RR change as a function of year for each quantile from 0.05 to 0.95 at intervals of 0.05 (see “Methods”). The shaded area indicates the two-sided 95% confidence intervals. The solid dots indicate statistical significance at the 95% confidence level, and the hollow dots indicate nonsignificance.

Full size image

Decrease in rapid changes of annual TC 24-h RR

The events of rapid decrease (RD) and rapid increase (RI) of TC RR both reflect the two extremes of TC 24-h RR change (see “Methods” and Supplementary Table 2). Next, we utilize both RI and RD events in the average TC RR to describe rapid changes in TC 24-h RR. Both the TMPA (1998–2019) and IMERG (2001–2020) show statistically significant (P value < 0.05) and consistent decreasing trends in the annual RR RI and RD ratios in the total rainfall area, inner-core area, and rainband area of TCs (see Fig. 2 and Supplementary Fig. 4), thereby increasing confidence in our results. Specifically, according to the TMPA data, the TC inner-core exhibited the highest slope, with rates of –2.78 ± 0.6% per decade for RI and –3.02 ± 0.53% per decade for RD (Fig. 2b). This is followed by the total rainfall area, which has slopes of –1.74 ± 0.57% per decade for RI and –2.23 ± 0.55% per decade for RD (Fig. 2a). These findings align with the narrowed distribution of global TC 24-h RR changes shown in Fig. 1 and Supplementary Fig. 3. In general, the declining trend of TC RR RD is steeper than that of RI. Given the RD event of TC RR is not conducive to maintaining a higher TC rainfall level, the interannual trend in the temporal stability of TC RRs is now clear. In the context of a significant increase in the annual average RRs of the TC total rainfall area over the past two decades9,10, RRs in the total rainfall area of TCs may increasingly become easier to maintain at higher levels without decreasing.

Fig. 2: Global interannual trends of the TC RR RI (blue) and RD (red) ratios based on the TMPA dataset (1998–2019).
figure 2

a TC total rainfall area, b Inner-core, and c Rainband area. The shaded areas indicate the two-sided 95% intervals of the slopes, and the dashed line represents the linear regressions.

Full size image

Furthermore, we investigate possible modifications to the definitions of RI and RD for RRs in the TC total rainfall area using the TMPA data. We examine variations in the time interval lengths at which RR changes occur (Supplementary Fig. 5a, b, see “Methods”) and apply different percentile criteria (Supplementary Fig. 5c–g). Remarkably, all of these modifications consistently demonstrate a statistically significant decreasing trend in the annual TC RR RI and RD ratios. This affirms the robustness of the results based on the proposed criteria for the TC RR RI and RD thresholds in this study (see “Methods”).

Previous studies revealed a decline in annual TC frequency under global warming33,34. When the RI and RD ratios of RRs are successively replaced with the average frequency of RR RI (RD) events per TC (Supplementary Fig. 6a–c) and the count of RR RI (RD) events (Supplementary Fig. 6d–f), the interannual trends continue to exhibit statistically significant decreases. This finding implies that the decreasing trend in the global annual TC RR RI and RD ratios may not be attributed to interannual trends in TC lifetime and frequency.

To proceed, we turn our attention to the global spatial distribution of interannual trends in TC RR RI and RD events based on the TMPA dataset (Fig. 3). Significant decreases in RI and RD events are observed in most offshore regions of the major ocean basins, particularly around Madagascar, the East China Sea, and Central America. The decreasing trend in RD events is more pronounced than that of RI events in these areas. A similar pattern can be observed in the corresponding IMERG results (Supplementary Fig. 7), which confirms the robustness of our findings.

Fig. 3: Global spatial distribution of linear trends in annual RR RI and RD counts of the TC total rainfall area based on the TMPA dataset (1998–2019).
figure 3

a TC RR RI events and b TC RR RD events. The 22-year linear trend is calculated for each 2.5° × 2.5° latitude–longitude grid. The black dots denote values statistically significant at the 95% confidence level. Data smoothing using a three-point smoother is performed for better display clarity.

Full size image

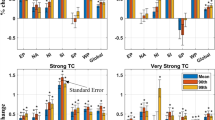
The corresponding statistical data based on the TMPA dataset for interannual trends in TC RR RI and RD ratios in various regions can be found in Supplementary Table 3. Overall, the trend slope in the Northern Hemisphere (–2.06 ± 0.93% per decade for RI and –2.50 ± 0.72% per decade for RD) exceeds that in the Southern Hemisphere (–1.58 ± 0.78% per decade for RI and –2.02 ± 1.28% per decade for RD). The trend slope of the RI ratio in the latitudinal range of 5–20° (–1.92 ± 0.63% per decade) is greater than that in the range of 20–35° (–1.24 ± 0.90% per decade). Notably, when dividing the global region into an offshore region (including landfall cases) and an open ocean region using a 400 km offshore distance based on Li et al.’s method31, the trend slope of the RD ratio in the offshore region (–2.87 ± 0.77% per decade) is significantly greater than that in the open ocean region (–1.77 ± 0.67% per decade), indicating a potential for continued heavy rainfall along the coast. Statistically significant decreasing trends are observed in all ocean basins, with the exception of the Eastern North Pacific, South Pacific, and Northern Indian Ocean. The lack of a trend in these regions may be attributed to the limited sample size.

Convective rainfalls dominate the TC RR rapid change

To analyze the mechanism behind the rapid change in the average RR of the TC total rainfall area, we divide the 24-h RR change in each TC total rainfall area into convective RR change and stratiform RR35 change samples (see “Methods”). Figure 4a, b illustrates the global interannual trends in the convective and stratiform RR RI and RD ratios, respectively, within the TC total rainfall area using the TMPA data from 1998 to 2019. The annual RR RI and RD ratios of average convective rain in the TC total rainfall area display statistically significant decreasing trends (–2.00 ± 0.64% per decade for RI and –2.18 ± 0.5% per decade for RD), which is consistent with the findings for the average RR (Fig. 2a). The trends of the annual RI and RD ratios of average stratiform RRs in the TC total rainfall area are not statistically significant (P value = 0.135 for RI and P value = 0.749 for RD). Importantly, when excluding the samples corresponding to convective RR RI and RD events from Fig. 2a, the decreasing trends nearly disappear. Specifically, the linear fitting slopes decrease to –0.14 ± 0.13% per decade (RI) and –0.25 ± 0.26% per decade (RD), respectively (Fig. 4c). However, excluding the samples corresponding to stratiform RR RI and RD events from Fig. 2a has a minimal impact on the trend of the annual TC RR RI and RD ratios (Fig. 4d). Put another way, the interannual trend of the 24-h average RR rapid change in the TC total rainfall area is primarily influenced by convective rain.

Fig. 4: Global interannual trends of the RR RI (blue) and RD (red) ratios of the TC total rainfall area based on the TMPA dataset (1998–2019).
figure 4

a TC Convective RR, b TC stratiform RR, c TC average RR excluding convective RR RI (RD) cases, and d TC average RR excluding stratiform RR RI (RD) cases. The shaded areas indicate the two-sided 95% intervals of the slopes, and the dashed line represents the linear regressions.

Full size image

Potential links to global warming

Now we seek to understand the potential links between the interannual trends of rapid changes in convective rain within the TC total rainfall area and global warming. Research by Guzman and Jiang10 indicates that global warming triggers an increase in the precipitable water reserves of TCs. Silvers et al.36 revealed that rising SSTs weaken large-scale tropical circulations, decrease the convective anvil cloud fraction, and increase AS. Based on the Weather Research and Forecasting model, Tu et al.9 observed that increased AS suppresses the ascent of vapor in TCs, hindering the increase of TC convective rainfall. Using data from the fifth-generation European Centre for Medium-Range Weather Forecasts atmospheric reanalysis (EAR5) (1998–2019) and the TMPA (1998–2019), we collect data on regional Hadley circulation, total column water vapor (TCWV) (see “Methods”), and TC convective RR RI and RD events across the five ocean basins, averaged from peak TC seasons, within the latitudinal range of 35°S–35°N. This data allows us to calculate the meridional distribution of interannual trends (Supplementary Fig. 8). The region of intensified ascending airflow is concentrated between 5°S and 5°N, indicating a contraction of tropical convection (Supplementary Fig. 8a). This finding aligns closely with Zhang’s results34 based on climate models. The statistically significant weakening of ascending airflow primarily occurs around 10°S and 10°N, creating conditions that suppress convection in those regions (Supplementary Fig. 8a). The statistically significant increase in annual average TCWV mainly occurs in the latitudinal range of 10–20°N, resulting in a higher precipitation reserve in this range (Supplementary Fig. 8b). Coincidentally, the meridional distribution of TC convective RR rapid change trends indicates that the most significant decrease occurs within this latitudinal range.

Next, we turn our attention to the interannual trends within the latitudinal range of 5–20° in the Western North Pacific, Eastern North Pacific, North Atlantic, South Indian Ocean, and South Pacific (Fig. 5). Note that there is a strong correlation coefficient of 0.93 between increasing SST and TCWV, as well as a correlation coefficient of 0.89 between increasing SST and AS in the latitudinal range of 5–20° (Supplementary Fig. 9). On the one hand, the statistically significant trends in AS from 1998 to 2019 highlight regions of weakened vertical convection (Fig. 5a–e), particularly at 10–20°N in the Western North Pacific, Eastern North Pacific, and North Atlantic, as well as at 10–15°S in the South Indian Ocean and South Pacific. In these areas, TC convective RR RI events decrease relatively significantly. On the other hand, peaks in statistically significant TCWV trends during the same period are clearly identified at 10–15°N in the Western North Pacific (Fig. 5f), 15–20°N in the Eastern North Pacific (Fig. 5g), and 10–20°S in the South Indian Ocean (Fig. 5i). In these regions, TC convective RR RD events also decrease noticeably. We conclude that the temporal stability of TC convective RR at low latitudes is enhanced by the synergistic effects of increased AS and TCWV. Consequently, the annual TC RR RI and RD ratios significantly decreased within the latitudinal range of 5–20° during the period from 1998 to 2019, exhibiting slopes of –1.92 ± 0.63% per decade and –2.17 ± 0.76% per decade, respectively (Supplementary Table 3). Figure 6 depicts a comprehensive schematic of the physical mechanisms illustrating the increasing temporal stability of TC RR in an environment characterized by rising SST within the latitudinal range of 5–20°.

Fig. 5: Meridional distribution of interannual trends in (a–e) atmospheric stability (AS, unit: K) and (f–j) total column water vapor (TCWV, unit: kg m-2) over individual ocean basins (1998–2019).
figure 5

a, f Western North Pacific (WNP): 100°E–180°, July–October; b, g Eastern North Pacific (ENP): 180–90°W, July–September; c, h North Atlantic (NA): 90–10°W, August–October; d, i South Indian Ocean (SIO): 30–130°E, January–March; and e, j South Pacific (SP): 130°E–120°W, January–March. The trends of environment variables (solid lines), averaged over peak TC seasons and smoothed using a three-point smoother, are restricted to a latitudinal range of 5–20° at 2.5° intervals, based on the ERA5 dataset. Solid dots indicate statistical significance at the 95% confidence level, while hollow dots represent nonsignificance. The histogram indicates the interannual trends of TC convective RR RI (red bar) and RD (blue bar) events during peak TC seasons. These trends are calculated across 5° latitudinal bins using the TMPA dataset. The error bars in the histogram indicate the standard error of the linear trend in each 5° latitudinal bin.

Full size image
Fig. 6: Schematic diagrams of the increasing TC RR temporal stability in a warming environment.
figure 6

a The early-stage situation. b The current situation. The legends of the colored arrows are listed in the lower panel of this figure, HC indicates Hadley cell.

Full size image

Discussion

This study reveals that the temporal stability of TC rainfall within the latitudinal range of 5–20° has significantly increased over the past two decades. However, the reason behind the decrease in the TC RR RI ratio within the latitudinal range of 20–35° remains uncertain. Tu et al.19 demonstrated a clear positive correlation between the average RR of the TC total rainfall area and the translation speed of TCs. If the TC translation speed increases rapidly within a 24-h period, the net inflow of the TC in the lower troposphere increases, and the TC’s convergent upward motion is enhanced, which contributes to a RI in the TC RR. Kossin37 proposed a global slowdown in the annual average translation speed of TCs over the past ~70 years, although other scholars38 have questioned the validity of this trend in the last two decades. The prevailing consensus is that the annual average translation speed of TCs decreases at latitudes between 20° and 35° due to global warming39,40. This means that the annual ratio of factors conducive to the TC RR RI is decreasing. Therefore, we propose that the decrease in the annual TC RR RI ratio within this latitudinal range may be linked to the average speed at which TCs move in that region.

By analyzing the samples of 24-h changes in global TC translation speed from the International Best Track Archive for Climate Stewardship (IBTrACS) dataset (1998–2019) at various percentiles, we observe that the average 24-h RR change in the TC total rainfall area is significantly positive in the 95–100th percentile bin (Supplementary Fig. 10c). Additionally, within the latitudinal range of 20–35°, the annual average 24-h change in TC translation speed decreases significantly in the 95–100th percentile bin (Supplementary Fig. 10d, e, we define the samples of this bin as events that indicate a rapid increase in TC translation speed). These findings align with the results of Yamaguchi et al.39. Evidently, the trend in high TC 24-h translation speed changes within the latitudinal range of 20–35° may contribute to the decreasing trend in the TC RR RI ratio in this region. This is further supported by the fact that removing the TC RR RI events corresponding to the 95–100th percentiles of TC 24-h translation speed changes from the total RR RI samples in the latitudinal range of 20–35° reduces the trend slope by ~36% (Supplementary Fig. 10f). We conclude that, with the poleward shift trend of TC formation locations41,42,43, this effect may become more prominent in the future. A flow chart summarizing the possible linkages is provided in Fig. 7.

Fig. 7: Flow chart of a possible linkage between anthropogenic global warming and recent increasing global TC RR temporal stability.
figure 7

The uncolored box indicates a weak factor.

Full size image

Other factors, such as TC intensity and vertical wind shear44,45, may also influence the temporal stability of TC rainfall. Mei et al.46 suggested that TCs with higher intensities tend to move at a faster pace. Nevertheless, this conclusion may not hold true within a 24-h period. For example, in the 95th to 100th percentile range of TC 24-h translation speed changes, the average reaches its peak positive value of 14.1 knots (Supplementary Fig. 10a), while the average change in TC intensity over the same period is significantly negative at –7.4 knots (Supplementary Fig. 10b). This phenomenon can be attributed to an increase in vertical wind shear within the TC during that time. Thus, the influence of TC 24-h translation speed rapid increases on the RR RI within the latitudinal range of 20–35° can be discussed without considering the corresponding TC intensity. In the future, understanding the intrinsic relationship between TC intensity and TC RR rapid changes will be crucial.

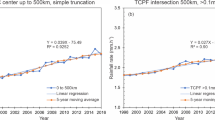
The annual average standard deviation of the average RR in the total rainfall area of TCs shows a statistically significant decrease (Supplementary Fig. 11). In the context of a significant increase in annual average TC RRs over the past two decades, this declining trend does not indicate a reduction in the threat posed by TC rainfall. The increasing temporal stability of global TC heavy rainfall will undoubtedly pose an additional threat to land, especially as the locations of a TC’s lifetime maximum intensity migrate toward the coast47. All of these factors should be considered collectively in future efforts to enhance TC catastrophe preparedness.

The findings of this study have significant implications for forecasting rapid changes in TC rainfall. However, due to limited data availability, the future trajectory of the interannual trend in the temporal stability of TC rainfall remains uncertain. Given the complexity of the processes involved, there is no conclusive evidence regarding how global Hadley circulation, AS, and TCWV may further change in a continuously warming environment. Therefore, future climate models, including reanalysis and forecasting, may require higher temporal and spatial resolutions to account for the impacts of these factors. Furthermore, incorporating modern in-situ observational data—such as from manned aircraft48, dropsondes, buoys, and 3D LiDAR—can significantly improve the accuracy of TC RR models.

Methods

Data

Historical records of TCs, including their location, intensity, and translation speed, are obtained from the International Best Track Archive for Climate Stewardship (IBTrACS, v4r00)49. Only TCs with wind speeds of at least 35 knots are considered. The corresponding rainfall data are derived from two sources: the TRMM Multi-satellite Precipitation Analysis (TMPA) 3B42 V750 and the IMERG Final Precipitation L3 Half Hourly 0.1° × 0.1° V0651 datasets. For the purpose of comparison, a 3-h temporal resolution is used as the standard, and rainfall data with different resolutions from IMERG are excluded. The TRMM satellite, which operated from January 1998 to October 2014, provided precipitation data until it is replaced by the IMERG products. The National Aeronautics and Space Administration continued to generate TMPA quantitative precipitation estimates until December 201916, when the IMERG retrieval algorithm is implemented. This algorithm is also used to extend the IMERG dataset using TRMM raw data back to June 200018, ensuring a complete overlap period between the two datasets from 2001 to 2019. The parameters from the monthly ERA5 dataset52 are used to analyze environment variables, such as SST, dry static atmospheric stability (AS), total column water vapor (TCWV) and Hadley circulation. AS, as defined by Sharmila and Walsh43, is the potential temperature difference between two vertical layers: θ300−θ900. All the data are standardized to UTC time (00:00, 03:00, 06:00, 09:00, 12:00, 15:00, 18:00, and 21:00) for consistency. Supplementary Table 1 provides a detailed overview of the data used in this study.

TC-related RR

RR refers to the amount of precipitation that falls over a unit area within a designated time period. For TCs, the RR is typically measured as the average RR within a specified search radius around the TC eye center53,54:

$${R}_{t}=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{m}{P}_{i}$$
(1)

where \({R}_{t}\) is the average RR of the defined TC rainfall area at time t; \({P}_{i}\) is the RR per pixel, mm h–1; and \(n\) is the total number of pixels (including rainy and non-rain pixels) in the defined TC rainfall area. In general, m is equal to n. The radius of the TC rainfall area varies depending on the ocean basin and intensity category (tropical storm: 35–63 knots, category 1 to 2: 64–95 knots, and category 3 to 5: ≥96 knots). The boundary of the inner-core area is determined by the position of the maximum gradient in the radial average RR9, while the region beyond the inner-core is referred to as the rainband area. Additional details can be found in Supplementary Fig. 1.

In TC convective rain-related analyses, the rainfall pixels in the TC total rainfall area are categorized into two types: convective and stratiform. A convective rainfall pixel is defined as having an RR of ≥5 mm h–1, while a stratiform rainfall pixel is defined as having an RR of ≤4 mm h–1 35. Note, that pixels with RRs in the range of 4–5 mm h–1 usually have a mix of convective and stratiform rains with a sample size of less than 5%9, so these pixels are not included in the analysis. When calculating \({R}_{t}\) for a specific type (convective RR or stratiform RR) within the TC total rainfall area, m represents the number of corresponding pixels. Consequently, one convective RR sample and one stratiform RR sample can be separated from one sample representing an average RR in the TC total rainfall area.

TC 24-h RR change

The TC 24-h RR change is defined as the change amplitude of the average TC RR every 24-h period. We calculate TC 24-h RR changes to quantify the temporal stability of TC precipitation.

$${\Delta R}_{t}={R}_{t+24h}-{R}_{t}$$
(2)

where \({R}_{t}\) and \({R}_{t+24h}\) are the average TC RRs corresponding to time t and t + 24 h, respectively. Note that, with individual exceptions due to the TC intensity difference within 24 h (the respective radii need to be determined according to Supplementary Fig. 1), the calculated radii for \({R}_{t}\) and \({R}_{t+24h}\) are always the same. The initial point for each 24-h RR change is selected as the representative location for that case. In addition, we modify the time intervals sequentially from 24 h to 12 h (Supplementary Fig. 5b) and then to 6 h (Supplementary Fig. 5a) to examine the effects of the diurnal cycles.

In this study, each TC 24-h RR change is treated as an event. Figure S2 displays the global probability density plots obtained from the TMPA and IMERG 24-h RR changes within the TC total rainfall area from 2001 to 2019. A logarithm transformation is applied to illustrate the differences in the tails of the distributions. The sample of TC 24-h RR changes is ranked from smallest to largest each year, and quantile regression is employed to calculate the slope of every five quantiles between the 0.05 and 0.95 quantiles for each year. As shown in Fig. 1, these slopes, which vary with quantiles, are plotted as an S-shaped curve.

The TC RR RI and RD Thresholds

In accordance with the defined criteria for the RI threshold of TC intensity22,23,27,32, we initially determine the thresholds of TC RR RD and RI using the 5th and 95th percentiles of the global TC 24-h RR change samples from the corresponding dataset, respectively. The RD threshold indicates that 5% of the 24-h RR changes within each dataset do not exceed this value, thereby defining the TC RR RD events. Similarly, the RI threshold indicates that 5% of the 24-h RR changes within each dataset is not lower than this value, thereby defining the TC RR RI events. Supplementary Table 2 provides a summary of the TC RR RD and RI thresholds for the total rainfall area, inner-core area, and rainband area within various specified regions based on the TMPA dataset (1998–2019). In this study, we utilize the global RR RD and RI thresholds in the defined TC rainfall area. The TC RR RI (RD) ratio is defined as the ratio of TC 24-h RR changes equal to or greater (lower) than the RR RI (RD) threshold to the total count of TC 24-h RR changes. The global TMPA RI thresholds for the convective and stratiform RR samples are 1.10 mm h–1 and 0.33 mm h–1, respectively; the global TMPA RD thresholds for the convective and stratiform RR samples are –1.21 mm h–1 and –0.46 mm h–1, respectively (Fig. 4).

Statistical information

Simple linear regression is conducted to analyze the interannual trends in TC 24-h RR changes, TC RR RI and RD events, SST, AS, TCWV, and TC 24-h translation speed changes (as depicted in Figs. 1 to 3, Supplementary Figs. 3 to 11, and Supplementary Table 3). These diagrams include shaded areas representing the two-sided 95% confidence intervals. The significance of the linear trends is assessed using a two-tailed t-test, with P-values below 0.05, indicating that the slope estimate is statistically significant. In addition, the coefficients of determination (R²) are calculated to quantitatively assess the strength of these trends.

Discretization of TC translation speed

Given that the distribution of TC translation speeds closely approximates integer differences, dividing the transition speeds by quantiles presents challenges. To address this, a Monte Carlo technique is employed to introduce random noise into TC translation speeds. The translation speed of each TC is adjusted by adding a random number drawn from a normal distribution with a mean of 0 and a variance of 1 × 10–6. This approach ensures that TC translation speed can be discretized within an acceptable error range, allowing for the division of the data into intervals of five percentiles without significantly altering the overall distribution trend (refer to Supplementary Fig. 10a–c).