Introduction

El Niño‒Southern Oscillation (ENSO) is one of the dominant interannual variabilities that significantly impacts tropical cyclone (TC) activities in the western North Pacific (WNP)1,2. Considerable spatiotemporal differences exist among individual ENSO events, often referred to as ENSO diversity or complexity3. ENSO spatial diversity, which is based on different sea surface temperature (SST) anomaly centers (central and eastern Pacific warming or cooling), has been documented to have significant impacts on TC activity4,5,6,7,8,9,10.

In addition to spatial diversity, there are significant differences in the temporal cycle of ENSO. According to the linear ENSO theory, both El Niño and La Niña events typically develop in late boreal spring–summer, peak in boreal winter, and then decay in the following year. However, individual observed ENSO events show a distinct temporal evolution during the decaying phase11,12,13. Many La Niña events tend to persist through the following summer and re-intensify into another La Niña event in the subsequent winter14,15,16,17, instead of transforming into an El Niño or a neutral state. In some cases, La Niña events can even last for three consecutive years, as seen in the 2020–2022 La Niña. In contrast, El Niño events are more likely to decay rapidly and transition into La Niña phases, although some multi-year El Niño events exist, such as the 2014‒2016 event18. Therefore, a La Niña event may follow an El Niño, a La Niña, or a norm event.

Numerous studies have investigated the distinct impacts of varying El Niño transition speeds on the regional climate and weather during the decaying year19,20,21,22. Additionally, these studies explored the effects on TC activity, including the genesis location and position of TC rapid intensification23,24,25,26. Multi-year La Niña events affect the global climate differently from single-year La Niña events16,18,27,28. It has been noted that, compared to single-year La Niña events, multi-year La Niña events can trigger prolonged extreme disasters, such as longer periods of drought or wetness29. However, few studies have investigated the influence of different La Niña evolution phases on TC activity over the WNP30.

Previous studies have investigated TC activity mainly in the decaying summer of El Niño and La Niña events, focusing primarily on the delayed impacts of the preceding ENSO states31,32. A question arises as to whether TC activity in boreal autumn (September–October–November [SON]) during the developing phase of La Niña could be modulated by the delayed impacts of the preceding ENSO phases. Under future global warming scenarios, multi-year ENSO events, especially multi-year La Niña events, may occur more frequently, suggesting an increase in the persistent La Niña phase29. In this study, we classify three types of La Niña developing phases based on their preceding ENSO states: cyclic La Niña (transitioning from El Niño to La Niña), multi-year La Niña (the persistent phase), and episodic La Niña (developing from a neutral state). We investigate the differing impacts of these La Niña types on TC activity. Measuring the potential for TC genesis involves assessing various environmental factors that influence TC development. One widely used method is the calculation of the Genesis Potential Index (GPI) which integrates four key environmental factors—vertical wind shear, relative humidity, absolute vorticity, and sea surface temperature—into a single dimensionless index33. The GPI has been extensively used to quantify the relation between TC genesis and environmental conditions under different climate variabilities (e.g., ENSO7,34, Madden–Julian Oscillation35,36). Therefore, this study adopts the GPI to examine the relative contributions of each favorable environmental factor to differences in TC genesis across three types of La Niña transitions.

Results

Variations in TC genesis frequency during different types of La Niña developing phases

From 1950 to 2022, a centered 30-year base period is used to calculate anomalies and eliminate the global warming trend. An El Niño (La Niña) is defined as a 3-month running average of Niño 3.4 sea surface temperature anomalies (SSTa) exceeding +0.5 °C (−0.5 °C) for at least five consecutive seasons. Twenty-three La Niña events are identified and classified into three types of La Niña evolution. The temporal evolutions of these La Niña events, starting from the preceding year, are shown in Supplementary Fig. S1. Among the 23 La Niña events, nine are cyclic (1964, 1970, 1973, 1983, 1988, 1998, 2005, 2007, 2010), three are episodic (1954, 2017, 2020), and 11 are multi-year La Niña events (1954–1955*, 1970–1971*, 1973–1974*–1975*, 1983–1984*, 1998–1999*–2000*, 2007–2008*, 2010–2011*, 2020–2021*–2022*), where the asterisk (*) denotes the multi-year events studied, including their second or third years. TCs over the WNP are mainly active in boreal summer (June–July–August [JJA]) and autumn (SON). Since the anomaly of Niño 3.4 index remained neutral during JJA in several La Niña events, while it exceeded –0.5 °C during SON for all La Niña events, this study focuses on the differences in TC activity associated with La Niña during SON.

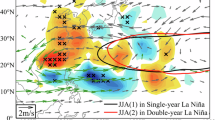
Figure 1 displays the TC genesis location and GPI anomalies in the WNP for different types of La Niña. Some TCs form near the coast; however, as shown in Supplementary Tables S1–3 and Supplementary Fig. S2, these TCs not only display high intensities but also tend to have long durations. Given their significant impacts on coastal regions, they are therefore included in the analysis of this study. Across all three types of La Niña events, a consistent characteristic is observed: TC genesis predominantly clusters near the western region of the WNP, exhibiting a distinct pattern from El Niño events and corroborating earlier research findings4. The GPI anomalies during all La Niña events clearly exhibit a northwest‒southeast pattern, with particularly negative values in the southeastern quadrant of the WNP (0°–20°N, 150°E–180°) and positive values west of 150°E (Fig. 1a). For cyclic, multi-year and episodic La Niña events, GPI anomalies display a northwest‒southeast pattern, with most TC genesis locations occurring within regions of positive GPI anomalies.

Fig. 1: Characteristics of TC genesis and GPI anomalies in the WNP and SCS during different types of La Niña events.
figure 1

Composites of TC genesis positions (black dots) and GPI anomalies (shading, 1/°C) for a all La Niña years, b cyclic La Niña, c multi-year La Niña, and d episodic La Niña in autumn (SON) during their developing phases. White stippling indicates the significance of composite anomalies at the 95% confidence level. e Annual TC genesis frequency (1/°C) over WNP (0°–30°N, 99°E–180°), and SCS (0°–23°N, 99°–121°E) for all La Niña, cyclic La Niña, multi-year La Niña, and episodic La Niña events in SON during their developing phases, respectively. The GPI anomalies and TC genesis frequency are normalized by the absolute value of SST anomalies averaged over Niño 3.4. The red asterisk “*” above the bar denotes that the frequency is different from that of other La Niña evolution types at the 90% confidence level. The purple and green rectangles in (a–d) represent the WNP and SCS region analyzed in this study.

Full size image

The TC distribution patterns in Fig. 1b–d reveal that the number of TCs and the values of GPI anomalies show obvious differences in the SCS among the three types of La Niña events. The number of TCs in the WNP (0°–30°N, 99°E–180°) and SCS (0°–23°N, 99°–121°E) is calculated separately (Fig. 1e). The characteristics of TC genesis east of the Philippines (EOP, 0°–30°N, 121°E–180°) closely resemble those observed in the WNP (Supplementary Fig. S3); therefore, no further discussion of EOP TCs will be provided in the following text. In the whole WNP, the annual frequency of TC genesis is 13.5 during cyclic La Niña events, which is higher than that during multi-year and episodic La Niña events (12.2 and 11.4, respectively, Fig. 1e). Furthermore, the distribution of TC genesis locations indicates that the variation in the number of TCs in the SCS may primarily account for the discrepancy in TC counts across the entire region among the three types of La Niña events (Fig. 1).

During cyclic La Niña events, the annual mean number of TCs generated in the SCS is approximately 2.6 times greater than that in the other two types of La Niña events (Fig. 1e), with the differences being significant at the 90% confidence level. In term of the GPI distribution, the significantly largest GPI anomalies are also observed in the SCS during cyclic La Niña (Fig. 1b), indicating that TC genesis numbers may respond differently to different types of La Niña events in the SCS compared to the broader WNP region. While previous research has indicated a significant increase in TC activity in the SCS during La Niña events, the impacts of different types of La Niña evolution have not been extensively differentiated37,38. This study emphasized that, only during cyclic La Niña events, did TC genesis in the SCS significantly increase compared with that during the other two types of La Niña events, whereas TC frequency did not significantly differ between the other two types of La Niña events (Fig. 1e). The GPI anomalies and TC genesis frequency analyzed above are normalized by the absolute value of SST anomalies averaged over Niño 3.4 to eliminate the influences of different ENSO intensities. Additionally, the impacts of the three evolution types of El Niño events on TC genesis in the WNP and SCS do not show significant differences compared to that during La Niña events (Supplementary Figs. S4 and S5).

Large-scale atmospheric circulations influencing SCS TC genesis among three types of La Niña events

The GPI connects the genesis frequency and location of TCs to the large-scale environmental conditions that prompt TC formation. Given the significant differences in GPI anomalies observed in the SCS among the three types of La Niña events, the quantitative contribution of each component of the GPI in the SCS is estimated individually on the basis of a linear approximation method39, which has been used in several studies40,41. In all three types of La Niña evolution, relative humidity serves as the primary contributor, indicating that a significant increase in relative humidity leads to a substantial increase in GPI in the SCS (Fig. 2). Previous studies have highlighted the crucial role of relative humidity in TC variability during La Niña phases37,38, which supports the results obtained in this study. In particular, among the three types of La Niña evolution, relative humidity has pronounced effects during cyclic La Niña events, contributing significantly more than the other two types of La Niña events at the 90% confidence level. Absolute vorticity and potential intensity exert weak impacts on GPI changes, and vertical wind shear displays a weakly negative contribution to GPI anomalies during cyclic La Niña events. In multi-year La Niña events, relative humidity contributes mostly to GPI anomalies as well as to cyclic and episodic La Niña events, whereas the impacts of the other three environmental factors are negligible. In contrast, the contributions of relative humidity, absolute vorticity, potential intensity and vertical wind shear are comparable, and the positive roles of the first three could be offset by those of vertical wind shear during episodic La Niña.

Fig. 2: The relative contributions of each favorable environmental factor to the differences in GPI anomalies in the SCS across three types of La Niña transitions.
figure 2

Contributions of each term on the right-hand side of Eq. (1) to GPI anomalies in the SCS for cyclic La Niña, multi-year La Niña, and episodic La Niña in SON during the developing phase. The four terms include \({\alpha }_{1}\delta Term1\) (red bar, 1/°C; \(Term1={|{10}^{5}{\eta }_{850}|}^{3/2}\)), \({\alpha }_{2}\delta Term2\) (orange bar, 1/°C; \(Term2={|1+0.1Vshear|}^{-2}\)), \({\alpha }_{3}\delta Term3\) (sky-blue bar, 1/°C; \(Term3={|\frac{H}{50}|}^{3}\)), and \({\alpha }_{4}\delta Term4\) (blue bar, 1/°C; \(Term4={|\frac{{V}_{pot}}{70}|}^{3}\)). The coefficients \({\alpha }_{1}\), \({\alpha }_{2}\), \({\alpha }_{3}\) and \({\alpha }_{4}\) are constant and their details are provided in Eq. (5) in the Methods section. These four terms are normalized by the absolute value of SST anomalies averaged over Niño 3.4.

Full size image

According to the above diagnostic analysis based on GPI, the SCS GPI anomalies during boreal autumn mainly stem from the relative humidity term, and then how the relative humidity in the SCS changes during the three types of La Niña events is investigated. The vertical integral of the water vapor flux from 1000 to 700 hPa and its divergence are shown in Fig. 3a–c. It is evident that during cyclic La Niña and multi-year La Niña events, the enhanced water vapor fluxes converge over the SCS and the Maritime Continent. These convergences are especially stronger and more significant during cyclic La Niña events. Abnormal westerly moisture transport from the Indian Ocean is the strongest during cyclic La Niña events, whereas abnormal easterly moisture from the Pacific is comparable among all three types of events. From the pressure‒longitude distribution of relative humidity anomalies averaged over 0°–23°N, we observed a significant increase in moisture convergence at approximately 100°–125°E (Fig. 3d). This convergence is associated with notable upwelling motion, which results in a marked increase in mid-level relative humidity during cyclic La Niña. In contrast, the anomalies of westerly moisture transport from the Indian Ocean are very weak during the other two types of La Niña events (Fig. 3b, c, e, f). Such different water vapor flux patterns are associated with regional large-scale circulations. It is clear that during the SON of cyclic La Niña, an anomalous cyclone is located in the SCS (Fig. 3g), favorable for water vapor convergence here and significantly different from the other two types of La Niña events (Fig. 3h, i).

Fig. 3: Key large-scale oceanic and atmospheric factors inducing differences in TC genesis across three types of La Niña transitions.
figure 3

Composite anomalies of (a–c) the vertical integral of water vapor flux (vectors; kg m−1 s−1) and its divergence (shading; 10−6 kg m−2 s−1) from the surface to 700 hPa, d–f pressure‒longitude cross sections of relative humidity (shading; %), zonal divergent wind (vector; m/s), and vertical velocity (vector; 10−2 Pa s−1) averaged along 0°–23°N, and g–i SST anomalies (°C) and 850 hPa wind anomalies (vectors; m/s) in SON during the developing phase for cyclic La Niña (left column), multi-year La Niña (middle column), and episodic La Niña (right column), respectively. The white dots and black vectors indicate the significance of composite anomalies at the 95% confidence level. The red rectangles (0°–23°N, 109°–121°E) in (a–c) and (g–i) highlight the SCS region analyzed in this study.

Full size image

Possible mechanisms related to anomalous environmental factors

From the evolution of tropical SSTa and lower-level winds during the three types of La Niña events, the anomalous SCS cyclone in boreal autumn is accompanied by beneath significant warm SSTa during cyclic La Niña events (Fig. 3g and Supplementary Fig. S6). The distribution of SSTa during SON among the three types of La Niña events reveals significant distinctions in the Indo-Pacific warm pool region (25°S–20°N, 90°–150°E; Fig. 3g–i). Specifically, in the case of cyclic La Niña events, the SSTa appears relatively warm in this area compared with the other two types of La Niña events. According to the classic Matsuno‒Gill response42,43, the warmer SSTa is responsible for a pair of cyclonic (anticyclonic) circulations along the equator on the western (eastern) side of the heat source in the cyclic La Niña (Supplementary Fig. S6d). Therefore, a hypothesis is proposed that these warm SSTa potentially serve as triggers for the anomalous cyclonic circulation observed over the SCS.

To verify the above hypothesis, a control run and four sensitivity experiments are conducted using CAM4, the details of which are shown in the Methods section. From the La Niña-Exp, the negative SSTa in the central and eastern Pacific can induce an anticyclone in the WNP (Fig. 4a, e). The differences between the Warm pool-Exp and La Niña-Exp results show flow field patterns that closely resemble the observed circulation, revealing a cyclonic circulation over the SCS and westerly anomalies in the tropical Indian Ocean (Fig. 4b, f). These findings underscore the substantial influence of warmer SSTa within the Indo-Pacific warm pool in triggering these distinctive circulation anomalies.

Fig. 4: SST anomalies added for three sensitivity experiments and wind field anomalies based on the outputs.
figure 4

a La Niña-Exp is conducted by adding observed cold SST anomalies over the central-eastern Pacific (25°S–25°N, 150°E–70°W). The other three sensitivity experiments, b Warm Pool-Exp, c Indian Ocean-Exp, and d Philippine Sea-Exp, involve adding observed warm SST anomalies over three key regions (Warm Pool: 25°S–20°N, 90°–150°E; Southeastern Indian Ocean: 0°–20°N, 120°–150°E; Philippine Sea: 25°S–0°, 90°–120°E) to the SON climatology-averaged SST (shading; °C), with observed cold SST anomalies also added over the central‒eastern Pacific (25°S–25°N, 150°E–70°W) in each experiment. The differences in wind field anomalies (m/s) in SON are shown between e La Niña-Exp and the control experiment, and f–h Warm Pool-Exp, Indian Ocean-Exp, Philippine Sea-Exp and La Niña-Exp, respectively. The green vectors indicate composite anomalies that are significant at the 95% confidence level.

Full size image

During the cyclic La Niña, the evolution of the observed warm SSTa in the southeastern Indian Ocean and the Philippine Sea exhibits distinct features (Supplementary Figs. S6a–d). Warm SSTa in the southeastern Indian Ocean persist from winter during the mature phases of El Niño to SON during the developing phase of La Niña. In contrast, SSTa in the eastern Philippine Sea warm up from JJA. To investigate the potential influence of warm SSTa in these subregions on SCS circulation anomalies, two additional sensitivity experiments (Indian Ocean-Exp and Philippine Sea-Exp) are conducted. In the Indian Ocean-Exp, the warm SSTa added in the southeastern Indian Ocean drive a cyclonic circulation in the southeastern Indian Ocean, potentially facilitating the transport of water vapor from the Indian Ocean to the WNP in the Southern Hemisphere (Fig. 4c, g). Furthermore, the alignment of the circulation anomalies in the Philippine Sea-Exp with those from the observations suggests that warm SSTa in the Philippine Sea could be the primary factor inducing such large-scale circulation anomalies (Fig. 4d, h), conducive to favorable conditions for TC genesis in the SCS.

The aforementioned results underscore the important role of sustained SST warming east of the Philippine Sea in causing a pronounced anomalous cyclone in SON over the SCS during the cyclic La Niña. This SST warms up during the decaying summer of El Niño (Supplementary Fig. S6c) owing to cloud-radiative feedback caused by a robust anticyclone over the Philippine Sea44. This anomalous anticyclone suppresses local convection and reduces rainfall, leading to diminished cloud cover and enhanced solar radiation within the region44. The persistence of this robust anticyclone has been documented to be closely related to the preceding winter El Niño and maintained through three distinct mechanisms.

Firstly, warming in the equatorial east‒central Pacific, coupled with negative SST anomalies in the western Pacific, potentially triggers an anomalous Philippine Sea anticyclone by suppressing convective heating in the mature phases of El Niño, persisting into the decaying summer45. Secondly, the preceding El Niño could induce simultaneous SST warming in the Indian Ocean and tropical North Pacific through the atmospheric bridge (Supplementary Fig. S6c). Then the warm SSTa in the Indian Ocean serves as a capacitor and excites the eastward propagating Kelvin wave, which aids in sustaining the presence of an anticyclone over the WNP46. Additionally, North tropical Atlantic (NTA) warming could sustain the WNP anticyclone through subtropical wave trains12,47,48,49 and Kelvin waves50. Diabatic heating from positive SST anomalies over the NTA triggers cyclonic circulation in the subtropical northeastern Pacific and anticyclonic circulation in the WNP, which is referred to as a subtropical wave train (Supplementary Fig. S6c). This response is driven by a Gill-type Rossby response and wind-evaporation-SST feedback. Tropospheric temperature, represented by the geopotential height (gpm) anomaly difference between 200 and 850 hPa51, shows a Kelvin wave wedge penetrating into the WNP during JJA of cyclic La Niña (Supplementary Fig. S7c). This effect, combined with relaying influence from the Indian ocean, exerts a remote impact on the anticyclone in the WNP52. On the other hand, summertime SST cooling in the equatorial east‒central Pacific may also sustain the WNP anticyclone through the Rossby response53.

In the JJA of multi-year La Niña, the Philippine Sea is affected by an anomalous cyclonic circulation, potentially due to the greater contribution of cold SSTs from the Indian Ocean. In contrast, during JJA of episodic La Niña events, the warmest SST anomalies in the North Atlantic and cooling in the tropical Atlantic counteract the effects on WNP circulation. Additionally, there is minimal influence from the weakest cooling in the equatorial central and eastern Pacific, as well as the Indian Ocean. Together, these factors contribute to the formation of a weak WNP anticyclone (Supplementary Fig. S6k).

Discussion

This study investigates whether TC activity in boreal autumn during the developing phase of La Niña could be modulated by the delayed impacts of preceding ENSO phases. Specifically, we focus on the effects of three evolution types of La Niña (cyclic La Niña, multi-year La Niña, and episodic La Niña) on TC activity over the WNP. The occurrence of TCs in the entire WNP during La Niña events is higher compared to other periods, primarily due to significant differences in the SCS, as indicated by anomalies in the GPI. During cyclic La Niña events, the TC frequency in the SCS is nearly three times greater than that in the other two La Niña evolution types, corresponding to GPI anomalies in the SCS. Analysis of the four components of the GPI reveals significantly greater positive contributions from relative humidity, primarily fostering increased TC genesis in the SCS during the cyclic La Niña transition, in contrast with the lesser impacts on the other two La Niña evolution types. Specifically, the significant increase in relative humidity during El Niño to La Niña events can be traced back to enhanced moisture transport from the Indian Ocean and water vapor convergence in the SCS. These atmospheric conditions are linked to anomalously warm SSTa in the Philippine Sea during SON. Both local air‒sea interactions and remote forcings from warmer SST in the tropical North Atlantic Ocean and Indian Ocean, triggered by the preceding El Niño event, contribute to the increased autumn SST in the Philippine Sea.

This study presents the distinct variability in autumn SCS TCs during diverse La Niña evolution phases, providing a statistical foundation for comprehending the relationship between SCS TCs and La Niña events. Our findings indicate that relative humidity significantly impacts SCS TC formation, particularly during cyclic La Niña events, thereby improving early predictions and informing mitigation strategies for regions vulnerable to TCs. However, one limitation of this study is that the CAM4 model primarily simulates the environmental conditions affecting TCs rather than the TCs themselves. Future research should address this limitation by incorporating high-resolution models capable of simulating TC formation, which would provide greater insight into the interaction between environmental variables and TC development.

This study addresses a critical gap in the literature by examining the impact of different ENSO evolution types on TC genesis, considering various preceding ENSO states. While most existing research has primarily focused on the decay rates of ENSO events23,54,55, our analysis reveals no significant differences in TC activity among the three types of El Niño evolution. This finding highlights the necessity of shifting focus to the various transitions of La Niña, which have a substantial influence on TC genesis. By investigating the effects of different La Niña transitions, we aim to enhance the understanding of how varying ENSO states affect TC activity. This research offers valuable insights for future studies and practical applications in weather forecasting and disaster preparedness.

Methods

Observational data and identification of TC and ENSO events

In this study, 6-hourly TC best track data is obtained from the China Meteorological Administration (CMA)56, and only TCs with maximum sustained wind speeds greater than 34 knots are considered. The monthly mean atmospheric variables (wind speed, relative humidity and absolute vorticity) are obtained from the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis v5 (ERA5) with 1°\(\times\)1° grid57. The monthly mean SST data are provided by the Met Office Hadley Centre Sea Ice and SST dataset (HadISST)58, with a horizontal resolution of 1°\(\times\)1°. Composite analyses are conducted in this study, with statistical significance assessed via a two-tailed Student’s t-test. According to the definition provided by the National Oceanic and Atmospheric Administration (NOAA) Climate Prediction Center (CPC), an El Niño (La Niña) event is determined on the basis of the 3-month running mean of the Niño 3.4 index, which represents the SSTa averaged over the Niño 3.4 region (5°S–5°N, 170°–120°W)59,60. An El Niño event occurs when Niño 3.4 index is greater than +0.5 °C, while a La Niña event is defined when the index is less than –0.5 °C for more than five consecutive seasons (https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php). To eliminate the global warming trend, a centered 30-year base period, as adopted by the CPC, is used to calculate the anomalies.

The genesis potential index

The genesis potential index proposed by Emanuel and Nolan (2004)33 is calculated to investigate the role of environmental factors, which is defined as

$$GPI=\begin{array}{cccc}\underbrace{{\left|{10}^{5}{\eta }_{850}\right|}^{3/2}}_{{\rm{Term}}1} & \underbrace{{|1+0.1Vshear|}^{-2}}_{{\rm{Term2}}} & \underbrace{{\left|\frac{H}{50}\right|}^{3}}_{{\rm{Term3}}} & \underbrace{{\left|\frac{{V}_{pot}}{70}\right|}^{3}}_{{\rm{Term4}}}\end{array}$$
(1)

where \(\eta\) represents the absolute vorticity \(({s}^{-1})\) at 850 hPa, H represents the relative humidity at 600 hPa (%), \({V}_{{shear}}\) represents the vertical wind shear (m/s) between 850 hPa and 200 hPa, and \({V}_{{pot}}\) represents the potential intensity (PI, m/s)61, which is defined as

$${V}_{pot}^{2}=\frac{{C}_{k}}{{C}_{D}}\frac{{T}_{s}}{{C}_{D}}(CAP{E}^{\ast }-CAP{E}^{b})$$
(2)

where \({C}_{k}\) represents the exchange coefficients associated with enthalpy, \({C}_{D}\) denotes the drag coefficient, \({T}_{s}\) is the sea surface temperature and \({T}_{0}\) is the mean outflow temperature. CAPE is calculated by the vertically integrated buoyant energy between the level from which the parcel is initially lifted (\({z}_{i}\)) and the level of neutral buoyancy (LNB). Following Emanuel62, CAPE is calculated as follows

$$CAPE={\int }_{{\!\!z}_{i}}^{LNB}g\frac{T-\bar{T}}{\bar{T}}dz={\int }_{{\!\!p}_{n}}^{{p}_{i}}g\frac{T-\bar{T}}{\bar{T}}dp$$
(3)

where \({z}_{i}\) is the parcel’s initial height, \({p}_{i}\) is the initial pressure, and pn is the pressure at the LNB. T represents parcel’s temperature at the initial height, and \(\bar{T}\) represents the sounding temperature (T in K). The quantity \({{CAPE}}^{* }\) represents the saturation CAPE at the radius of maximum wind, defined as the distance from the TC center to the region of maximum wind speed, which extends from the sea surface (initially lifted level) to the LNB. Here, \({p}_{i}\) represents sea level pressure, whereas \({{CAPE}}^{b}\) is calculated for the parcel in the ambient region, which is located outside of eyewall. The initial lifting for \({{CAPE}}^{b}\) is approximated from the boundary layer, estimated to be approximately 500–600 hPa63.

A linear decomposition method are adopted to calculate the contribution of each factor39, and the contribution of each factor can be calculated as follows

$$\delta GPI={\alpha }_{1}\delta Term1+{\alpha }_{2}\delta Term2+{\alpha }_{3}\delta Term3+{\alpha }_{4}\delta Term4$$
(4)

where \({\alpha }_{1}\), \({\alpha }_{2}\), \({\alpha }_{3}\), and \({\alpha }_{4}\) are assumed to be constant coefficients and expressed as follows:

$$\left\{\begin{array}{c}{{\alpha }}_{{1}}{=}\overline{{Term2}}\times \overline{{Term3}}\times \overline{{Term4}}\\ {{\alpha }}_{{2}}{=}\overline{{Term1}}\times \overline{{Term3}}\times \overline{{Term4}}\\ {{\alpha }}_{{3}}{=}\overline{{Term1}}\times \overline{{Term2}}\times \overline{{Term4}}\\ {{\alpha }}_{{4}}{=}\overline{{Term1}}\times \overline{{Term2}}\times \overline{{Term3}}\end{array}\right.$$
(5)

where \(\delta\) denotes the composite anomaly with respect to climatology in each of the three La Niña evolution types and an overbar denotes the climatology. For the first term \(({\alpha }_{1}\delta Term1)\) on the right, \(\delta Term1\) means the anomalies of Term1 \(({|{1}{{0}}^{{5}}{{\eta }}_{{850}}|}^{{3}{/}{2}})\) compared to climatology, and \(\overline{{Term2}}\) \(({|1+0.1Vshear|}^{-2})\), \(\overline{{Term3}}\) \(({|\frac{H}{50}|}^{3})\) and \(\overline{{Term4}}\) \(({|\frac{{{V}}_{{pot}}}{70}|}^{3})\) in \({\alpha }_{1}\) means the climatology mean of each term, respectively. Consequently, the first term on the right-hand side represents the contribution of vertical wind shear to TC genesis. The explanation for the other three items on the right is similar.

Vertically integrated water vapor flux and its divergence

The transport and convergence of water vapor can affect the genesis and activity of TCs. To analyze the effects of water vapor distribution anomalies on TC activity, two variables, the vertically integrated moisture flux (VIMF) and its divergence (VIMFD), are used in this study. VIMF and VIFMD are defined as follows64:

$$VIMF=\frac{1}{g}{\int }_{{\!\!p}_{t}}^{{p}_{s}}q(u,v)dp$$
(6)
$$VIMFD=\frac{1}{g}{\int }_{{\!\!p}_{t}}^{{p}_{s}}q\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)dp$$
(7)

where q is the absolute humidity, g = 9.8 m/\({s}^{2}\) is the acceleration of gravity, p is the atmospheric pressure, and u and v denote the zonal and meridional wind velocities, respectively. Li et al.65 noted that the water vapor in the WNP is mainly concentrated below 700 hPa and that the mean sea surface pressure is close to 1000 hPa. Therefore, the upper layer pressure (Pt) for integration is chosen to be 700 hPa, and the surface layer pressure (Ps) is chosen to be 1000 hPa.

Model experiment

The Community Atmosphere Model version 4 (CAM4)66, used as the atmosphere component of Community Earth System Model version 1 (CESM1), is employed to assess the impact of large environmental factors on TC activity during three distinct types of La Niña. In this study, we selected the typical grid f19_g16, which features a 1.9° × 2.5° resolution for the atmosphere and land, and a gx1v6 grid for the ocean and ice. The f19 component refers to a finite volume grid with approximately 2-degree spacing, while g16 indicates a displaced pole grid with a 1-degree resolution. There are 26 vertical layers extending from the surface to the top. Further details on this resolution can be found in the CESM user guide at https://www2.cesm.ucar.edu/models/cesm1.0/cesm/.

A control run and four sensitivity experiments are conducted. The control run is forced by the climatological mean SST and integrated for 32 years, with the last 30 years used to calculate the climatology. All four sensitivity experiments involve adding negative SON-averaged SSTa in the east-central Pacific (25°S–25°N, 150°E–70°W) to the climatological mean SST to verify their influence on circulation anomalies. In the first sensitivity experiment, only the negative SSTa are added (La Niña-Exp, Fig. 4a). In the Warm pool experiment (Warm pool-Exp), warm SSTa in the Indo-Pacific warm pool region (25°S–20°N, 90°–150°E) are added alongside the negative SSTa (Fig. 4b). The Indian Ocean experiment (Indian ocean-exp) include warm SSTa in the southeastern Indian Ocean (25°S–0°, 90°–120°E) in addition to the negative SSTa (Fig. 4c). In the Philippine Sea experiment (Philippine Sea-exp), SSTa in the east of the Philippine Sea (0°–20°N, 125°–150°E) are added with the negative SSTa (Fig. 4d). Each sensitivity experiment is integrated for 32 years, with the last 30 years used to calculate the climatology.