Introduction

Snowpack over the mountains of the western United States provides runoff as it gradually melts over the warm season, filling reservoirs and providing water to ~ 100 million people1,2. Snowpack and the delayed release of snowmelt serves as a natural reservoir, alleviating elevated demands during the spring and summer time when decreases in seasonal precipitation occur3. This snowmelt comprises 53% of runoff4 and 75% of total western US water supply over the region5. Almost all snow stations across the western US show declines in April 1st snow water equivalent (SWE) over recent decades6,7,8. The losses are significant at about a third of stations9, but natural variability has likely prevented significant trends from emerging at the others10. Under high emissions scenarios, near-zero snowpack is possible over broad regions by end-of-century11,12,13. This has major implications for not just water resources, but also surface radiative properties14 and fire risk via decreased soil moisture15.

In addition to snowpack, the cumulative annual snowfall is another critical metric to project because it quantifies the total potential runoff from snowmelt. Under 21st-Century warming, a substantial portion of snowfall is expected to be converted to rain16. This will make the water profoundly more difficult to capture and increase flood risk, given that rain-induced runoff comes in short bursts, i.e., immediately following the storms in which it falls. Snowfall integrated over the region has already decreased by 10-20%17.

Previous studies have projected snowfall loss over the region, either by statistically downscaling global climate model (GCM) projections, or by running a regional climate model (RCM) in a future climate. Generally, more extreme projections are made with RCMs18,19 than statistical downscaling18,20, although methodical differences make study intercomparisons challenging. RCM projections are advantageous because, unlike statistical downscaling, they represent the physical mechanisms connecting large-scale to local climate change. The North America Coordinated Regional Climate Downscaling Experiment (NA-CORDEX;21) consists of 9 Coupled Model Intercomparison Project Phase 5 (CMIP5) GCMs downscaled over North America at 25-km grid spacing, under various forcing scenarios. But its resolution allows a limited representation of the complex terrain of the western U.S. and its rain/snow partitioning. Higher-resolution efforts have been performed, but for individual GCMs, given the associated extreme computational cost18,22,23,24, or for multiple GCMs but over a domain limited to the Los Angeles region25. However, recently, a novel dataset was generated, known as the Western United States Dynamically Downscaled Dataset (WUS-D3;26,27). WUS-D3 consists of the Shared Socioeconomic Pathway (SSP) 3-7.0 projections from 14 CMIP6 GCMs dynamically downscaled with the Weather Research and Forecasting (WRF) model over the western U.S at 9-km grid spacing (Fig. S1). The driving GCMs were bias-corrected to reanalyses prior to their downscaling, meaning that the 14 RCM projections are all based on the same observationally constrained historical base state.

Despite this advance in the projection of future snow, large uncertainty remains in the WUS-D3 projections because they are forced by GCMs with wildly different futures. In particular, climate sensitivity, the degrees of warming resulting from a doubling of CO2 concentrations, ranges in CMIP6 from 1.8–5.628. GCMs also vary substantially in the geographical distribution of warming trends29. Moreover, changes in total precipitation may offset or exacerbate the warming-induced losses. Averaged across GCMs, there is wetting over the north of the western U.S. and drying over the south30,31,32. But the specific partition line between wetting and drying, as well as the magnitudes therein, vary substantially. This precipitation uncertainty reflects differences in model physics and hence differences in forced changes, but also depends on natural variability.

In this study, to account for the uncertainty in temperature and precipitation changes in GCMs, we quantify the sensitivity of western U.S. snowfall losses to these larger-scale changes projected by GCMs. In this way, we quantify the snow loss that will result from a given amount of large-scale warming, and from a given magnitude of regional wetting/drying. We apply a hybrid downscaling model to determine the amount of RCM-simulated snowfall loss as a function of GCM-simulated temperature and precipitation changes. The existence of a large ensemble of RCM projections is critical for this purpose because multiple projections are needed to robustly infer the relationship between large-scale climate change and local snow losses. Moreover, because the RCM projections constitute a small minority of the full CMIP6 ensemble, we apply our hybrid downscaling model to the broader ensemble, under multiple emissions scenarios. We thus derive the full spread of western U.S. snowfall projections based on three scenarios (SSP3-7.0, SSP2-4.5, and SSP1-2.6) of CMIP6.

Results

Representation of historical snowfall

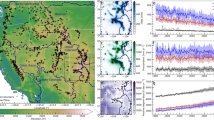
The historical (1980–2014) annual snowfall over the western U.S. ranges from ~100 mm (rain-water equivalent) over the plains to ~1000 mm over major mountain ranges in the multi-model mean (MMM) of downscaled GCMs (WRF–CMIP6; Fig. 1b). The MMM snowfall is in close agreement with the equivalent dynamically downscaled reanalysis dataset (WRF–ERA5; Fig. 1a), as expected given the mean-state bias correction performed prior to dynamical downscaling. However, prior work has shown that WRF–ERA5 underestimates historical spring SWE by 33% across the Sierra Nevada and overestimates spring SWE by 10% across the Middle Rockies compared to SNOTEL sites33.

Fig. 1: Historical multi-model mean and uncertainty in annual snowfall.
figure 1

a WRF–ERA5; (b) and (c) WRF–CMIP6 multi-model mean and standard deviation, respectively; (d) volumetric annual snowfall integrated over the given EPA ecoregions, based on gridded values. Bars, boxes, and whiskers represent the multi-model mean, ±1 standard deviation, and the full model spread, respectively. The dot beside each boxplot shows the WRF–ERA5 value.

Full size image

Viewed as totals over mountain ranges, annual volumetric snowfall ranges from 17 ± 1.6 km3 over the Wasatch–Uinta to 55 ± 3.2 km3 over the Middle Rockies (Fig. 1d). (The mountain ranges shown constitute almost the entirety of the area that receives significant snowfall; cf. Fig. 1a.) The units here reflect the total runoff that is potentially available from snowmelt annually, although generally 20–30% of snowfall sublimates34. For context, the capacity of Lake Mead, the largest reservoir in the U.S., is ~ 35 km3, which is close to the mean volumetric snowfall across ranges. Given that Lake Mead provides water to ~ 20 million people, as well as for agriculture throughout the Southwest, these totals indicate the massive dependence of western U.S. water resources on annual snowfall over its mountain ranges.

Subtle disagreements within WRF–CMIP6 arise from synoptic variability in GCMs. The contrasting representations of synoptic variability over the Northeast Pacific and impacts on California precipitation within CMIP6 were illustrated by 35. These disagreements are visible in the local standard deviation across the ensemble (Fig. 1c) and in the spreads in range totals (Fig. 1d) based on the historical period. Thus, although the mean states of prognostic variables of each GCM are bias corrected to the same reanalysis, the probability distribution functions of those variables still differ within the ensemble. Reassuringly though, the disagreements within WRF–CMIP6 are small. (The standard deviation is generally about one tenth of the ensemble mean, both at individual grid cells and in range totals). For most ranges, the WRF–ERA5 totals are near the middle of the historical WRF–CMIP6 spread (Fig. 1d).

Contributions of temperature and precipitation to end-of-century snowfall losses

Next, we assess future changes in snowfall across the western US. As expected, annual snowfall universally decreases throughout the western U.S. by end-of-century (Fig. 2a). The MMM of WRF–CMIP6 projects on the order of 50 mm yr−1 loss over the plains and on the order of 200 mm yr−1 loss over major mountain ranges. Integrated over mountain ranges, this entails volumetric losses in the MMM ranging from 6 km3 over the Wasatch–Uinta to 14 km3 over the Cascades (Fig. 2g). However, the WRF–CMIP6 simulations exhibit substantial inter-model variability in snowfall loss across mountainous terrain (exceeding 100 mm yr−1 in places; Fig. 2d). This leads to large uncertainty in total volumetric snowfall losses over various mountain ranges (e.g., 11 ± 3 km3 over the Sierra Nevada, 14 ± 3 km3 over the Cascades, 10 ± 3 km3 over the North Cascades,13 ± 4 km3 over the Middle Rockies, and 12 ± 4 km3 over the Southern Rockies; Fig. 2g).

Fig. 2: End-of-century absolute snowfall losses, and contributions of temperature and precipitation.
figure 2

a, d Change of snowfall; (b, e) contribution of the change in ratio of precipitation falling as snow; (c, f) contribution of the change in total precipitation; top row: multi-model mean; second row: standard deviation; (g) ecoregion-integrated volumetric absolute snowfall loss, based on gridded values. Bars, boxes, and whiskers represent the multi-model mean, ±1 standard deviation, and the full model spread, respectively.

Full size image

To identify the atmospheric drivers of these snowfall losses and the model uncertainty therein, we perform a simple decomposition:

$$S=R* P$$
(1)

where S is annual snowfall, P is annual precipitation, and R is the fraction of precipitation falling as snow. This enables us to decompose future losses as follows:

$$\Delta S\approx P\Delta R+R\Delta P$$
(2)

where the first term represents snow loss due to the decreasing fraction of precipitation falling as snow (i.e., the impact of warming), and the second term represents snow loss or gain due to changes in total precipitation. This approximation neglects a second-order term, ΔRΔP, which is small (Fig. S2).

The warming term, PΔR, is almost identical to the total snowfall loss in the MMM (Fig. 2b). And in the MMM the precipitation term, RΔP, is of relatively small magnitude everywhere (Fig. 2c). However, the uncertainty in PΔR generally does not account for all the uncertainty in ΔS (Fig. 2d, e). This is particularly evident over the Sierra Nevada where uncertainty in RΔP (0 ± 4 km3) is greater than of PΔR (–11 ± 2 km3; Fig. 2f), and thus, the uncertainty in ΔS is greater than that due to warming alone. By contrast, the Southern Rockies are noteworthy in that most of the downscaled GCMs project drying, so that the spread in ΔS (–12 ± 4 km3) is shifted down from that of PΔR (–10 ± 4 km3). Meanwhile, in the northwest of the domain, the uncertainty from precipitation is small relative to total uncertainty. Thus, over the Cascades, North Cascades, and Northern Rockies, the uncertainty from the warming term is almost identical to that of ΔS. Note that the breakdown of uncertainty is not linear, so that the uncertainty of the two terms does not sum to that of ΔS. However, a linear decomposition of the model spread is performed later.

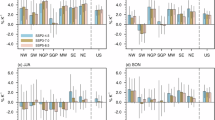
Viewed as fractional losses, the losses are more uniform across the western U.S. than suggested by the absolute values (Fig. 3a, g). However, a pronounced zonal gradient of fractional ΔS exists in the MMM (Fig. 3a). Near the west coast in excess of 50% snow is lost by end of century, while farther inland losses are around 25%. Viewed as range totals, this means that the North Cascades, Cascades, Sierra Nevada, and Northern Rockies lose 51 ± 12%, 57 ± 12%, 46 ± 11%, and 49 ± 12%, respectively (Fig. 3g). And, contrastingly, the Middle Rockies, Wasatch–Uinta, and Southern Rockies lose 24 ± 8%, 35 ± 9%, and 28 ± 8%, respectively. These MMM fractional losses are similar to those reported in previous studies18,19,20,36.

Fig. 3: End-of-century fractional snowfall losses, and contributions of temperature and precipitation.
figure 3

As Fig. 2, but showing fractional changes. Grid cells are masked that have <100 mm yr−1 historical snowfall in the multi-model mean. But these grid cells still contribute to the ecoregion totals. a, d Change of fractional snowfall; (b, e) contribution of the change in ratio of precipitation falling as snow; (c, f) contribution of the change in total precipitation; top row: multimodelmean; second row: standard deviation; (g) ecoregion-integrated fractional snowfall loss, based on gridded values. Bars, boxes, and whiskers represent the multi-model mean, ±1 standard deviation, and the full model spread, respectively.

Full size image

As with the absolute values, the warming term is almost precisely equal to ΔS in the MMM, viewed as grid cell values (Fig. 3a, b) and range totals (Fig. 3g). However, like the absolute values, the spread in the precipitation term (Fig. 3f) alters the spread in fractional snow losses, particularly over the southern states. This reflects GCM disagreements in the location of the transition zone between subtropical drying and mid-latitude wetting (Fig. S3).

Elevation dependence of snowfall losses

A more detailed impression of the geographical variation in snowfall loss is facilitated by a breakdown by elevation (Fig. 4). Figure 4a shows the fraction of volumetric snowfall loss predicted in each elevation bracket, over each mountain range as well as over the full western U.S. As expected, a greater fraction of snowfall will be lost at lower elevations. Over the western U.S., 42 ± 9%, 42 ± 10%, 31 ± 8%, and 23 ± 8% will be lost below 1 km, between 1–2 km, between 2–3 km, and above 3 km, respectively, under SSP3-7.0. And for individual mountain ranges the contrast is greater. For example, in the Sierra Nevada, 83 ± 10%, 61 ± 10%, 42 ± 11%, and 25 ± 13% will be lost in the same elevation brackets. This analysis highlights that losses will be largest near the west coast and below 2-km elevation, and smallest further inland and at high elevations (e.g., 17 ± 8% above 3 km in the Middle Rockies.

Fig. 4: Elevation dependence of end-of-century western-U.S. snowfall losses.
figure 4

a Volumetric snowfall loss within the given elevation brackets of the given ecoregions, plus the entire western U.S., expressed as a percentage of the historical value. b The percentage of each ecoregion’s total volumetric snowfall loss that is in each elevation bracket, i.e., the four values for each ecoregion sum to 100%. The percentages are calculated for each downscaled GCM and then the distributions are plotted for each ecoregion and elevation bracket. Bars, boxes, and whiskers represent the multi-model mean, ± 1 standard deviation, and the full model spread, respectively. Some elevation brackets are missing from some ecoregions, indicating that there are no relevant grid cells with > 0 historical snowfall.

Full size image

However, the above analysis does not indicate the contributions that each elevation bracket makes to the total losses, which is shown in Fig. 4b. In this metric, the different downscaled GCMs are in much closer agreement. Over the western U.S., the majority of losses will be between 1–2-km elevation (59 ± 2%), with the losses below 1 km (18 ± 1%) and between 2–3 km (21 ± 2%) of secondary importance. And the losses above 3 km are negligible in the total losses (2 ± 1%). The Southern Rockies are a notable exception in this regard, in that 31 ± 3% of losses are above 3 km. The breakdowns in Fig. 4b are mostly a reflection of the elevations at which the most snow falls historically in each mountain range (Fig. S4). But, lower elevations contribute more to future losses than to the historical climatology. For example, in the Sierra Nevada the 1–2-km and 2–3-km brackets contribute 32 ± 2% and 54 ± 1% of historical snowfall, but 43 ± 5% and 48 ± 3% of future losses.

Building a hybrid downscaling model for snowfall loss

The large spread in ΔS throughout the western U.S. (mean ± stdev) motivates us to further understand that uncertainty in terms of the driving GCMs. It is reasonable to assume that the RCM projections with the greatest losses due to the PΔR term are those driven by GCMs with the greatest warming. Meanwhile, we hypothesize that the RCM projections where the warming-induced losses are offset/exacerbated by the RΔP term are those driven by GCMs with regional increases/decreases of cool-season precipitation.

We thus propose the following hybrid downscaling model for changes in fractional snowfall using information from all 14 RCM/GCM pairs at each grid cell:

$${(\Delta S/S)}_{{\rm{RCM}}}\approx \alpha \Delta {T}_{{\rm{GCM}}}+\beta {(\Delta P/P)}_{{\rm{GCM}}}$$
(3)

Here, (ΔP/P)GCM is based on the cold season (November–April; NDJFMA), given that cold-season precipitation drives snowfall and the GCM-projected warm-season precipitation trends over the western U.S. are highly different to those in the cold season26. However, using ΔTGCM over the cold season, perhaps surprisingly, leads to a poorer performance of the regression model than annual-mean ΔTGCM (Fig. S5). This reflects that, counterintuitively, annual-mean ΔTGCM is a significantly better predictor than cold-season ΔTGCM of cold-season ΔTRCM (Fig. S6). We believe that this reflects snow-albedo feedback (SAF), which in the GCMs is maximized in different locations to the RCM, due to the poor representation of topography. Historical GCM temperature biases are also a factor here; for example a cold-biased GCM has more historical snowpack and thus in some locations greater SAF in the future, amplifying warming. But, the GCM spread in ΔT that is attributable to historical temperature bias has no bearing on the RCM spread in ΔS, given that all GCMs were bias-corrected prior to downscaling. Therefore, to minimize this effect we use annual-mean ΔTGCM in Eq. (3), given that most of the western U.S. is snow-free outside of the cold season.

Crucially, ΔTGCM and (ΔP/P)GCM are both local. This requires the GCM Deltas to be interpolated to the RCM grid, so that broadly speaking, a GCM Delta applies to all RCM grid cells within the given GCM grid cell. The local regression is particularly important for (ΔP/P)GCM. But it also improves the performance of the regression model for ΔTGCM, instead of using global-mean warming (Fig. S7). It is also crucial that the regression is conditioned on a zero intercept, i.e., snow loss must be zero if there is no temperature or precipitation change. The error in Eq. (3) can be reduced by including an intercept, but this is unphysical and represents over-fitting.

This decomposition is similar to ref. 37 who expressed 1 April SWE observations over the western U.S. as a multi-linear regression against temperature and precipitation over the precedent cold season. That study performed the regression to understand the roles of temperature and precipitation in determining observed SWE trends over 1960–2002. In this study, by contrast, we apply a similar framework to understand the sensitivity of RCM-simulated end-of-century snowfall losses to GCM boundary conditions. Thus, the novelty here is that the RCM is needed to convert the varying GCM projections of temperature and precipitation into high-resolution snow losses. For this reason, the regression coefficients can only be reliably derived (and validated) with a large ensemble of dynamically downscaled GCM projections.

The combination of ΔTGCM and (ΔP/P)GCM generally explains more than 75% of the variance in RCM snow projections across the western U.S. (Fig. 5a). In particular, the northwest of the domain generally sees at least 85% of variance explained. The explained variance is lower over the interior states, particularly Wyoming, below 30% in some areas. This is consistent with37, who found the combination of temperature and precipitation to be less predictive of observed SWE trends further inland than near the west coast. These regions correspond very closely to those in which a non-negligible portion of annual snow falls outside of NDJFMA (Fig. S8); hence, using (ΔP/P)GCM in NDJFMA as a predictor leads to error. Thus, in a leave-one-out validation of Eq. (3), there is a domain-mean absolute error of 6.7% snowfall loss (Fig. S9, which is small but not negligible compared to a domain-mean 38.1% snowfall loss.

Fig. 5: A multi-linear regression model predicting RCM snowfall loss from GCM temperature and precipitation change.
figure 5

Eq (3) is applied at each grid cell by least-squares multi-linear regression. a Explained variance from the regression model, calculated as 1 − σ2(LHS − RHS)/σ2(LHS), where LHS and RHS are the left-hand and right-hand sides of Eq. (3); (b) as (a) but based on a single linear regression model with ΔTGCM as the sole predictor, i.e., setting β = 0 in Eq. (3); (c) a−b; (d, e) the sensitivity of (ΔS/S)RCM to ΔTGCM and (ΔP/P)GCM, respectively, based on the multi-linear regression, i.e., α and β in Eq. (3). Grid cells are masked that have < 100 mm yr−1 historical snowfall in the multi-model mean.

Full size image

The imperfect performance of the regression model throughout the domain may arise from issues including:

  • the SAF issue noted previously;

  • topographic heterogeneity in the RCM that is not represented by the GCMs, such that the mesoscale and orographic distributions of ΔT and ΔP in the RCM are not predictable from ΔT and ΔP in the GCM;

  • winter precipitation trends of opposite sign to those in spring/fall, such that the mean NDJFMA trend masks relevant trends in subsets of the cool season.

We retain annual ΔTGCM and NDJFMA (ΔP/P)GCM as our predictors for the sake of simplicity of the regression model and generality of results. But we note that improved predictions could be achieved, e.g., by adjusting the period of the year upon which predictions are made, based on each grid cell’s snow season.

Notably, the variance explained by warming alone (i.e., applying Eq. (3) with β = 0) is less than that of the multi-linear regression (Fig. 5b). Thus, the variance explained by precipitation changes, although near-universally lower than that of warming, is not negligible in some areas (Fig. 5c). Large areas see more than 20% variance explained by (ΔP/P)GCM, particularly where there is large uncertainty in the precipitation contribution to RCM snowfall loss (cf. Fig. 3f).

Based on the multi-linear regression, the western U.S. sees sensitivities of 1.8–22.8% snow loss per degree warming, with a domain mean of 9.1% K−1 (Fig. 5d). The sensitivity is largest, more than 15% K−1, near the west coast, over the western slopes of the Sierra Nevada and Cascades, consistent with Fig. 4. Sensitivity decreases from west to east, and from north to south, with the high Rockies experiencing around 5% K−1. This is consistent with projections from statistical downscaling of GCMs, a variable resolution GCM, and PGW experiments18,19,20, and with observations37. This map largely reflects historical winter temperatures, with high sensitivity where temperatures are close to freezing and low sensitivity where they are considerably colder (Fig. S10). One exception to the prevailing west/east contrast is the southeastern Sierra Nevada, which has low sensitivity, given that it has the highest elevation within the domain, and thus precipitation falls at lower temperatures.

By contrast, precipitation sensitivities are relatively uniform throughout the region. Most of the domain sees ~ 0.5% snow gain/loss in the RCM per 1% of precipitation gain/loss in the GCM. This discrepancy reflects that more of the increased/decreased precipitation falls as rain than in the historical rain-to-snow ratio. But there are small areas at the highest elevations where the relationship is roughly one-to-one.

Extrapolating snowfall loss to the full CMIP6 ensemble

The regression coefficients derived in the previous section allow us to apply the hybrid downscaling model to the full CMIP6 ensemble, i.e., including GCMs that have not been dynamically downscaled. A further benefit of this approach is that it allows us to extrapolate snow projections to emissions scenarios other than the SSP3-7.0 scenario used to drive the RCM simulations. Thus, we apply Eq. (3), with the α and β coefficients derived in Fig. 5d, e, to all available GCMs under SSP3-7.0, as well as the lower emissions SSP2-4.5 and SSP1-2.6.

It is important first to understand the spread in ΔTGCM and (ΔP/P)GCM over the RCM domain across CMIP6 (Fig. S11). Based on 34 GCMs, the MMM warming over the western U.S. is 3.6 K under SSP3-7.0, 2.7 K under SSP2-4.5, and 1.8 K under SSP1-2.6, with corresponding inter-model standard deviations of 0.90 K, 0.74 K, and 0.70 K. Precipitation projections exhibit the well-documented pattern of wetting/drying over the northern/southern parts of the region30,31,32, with greater wetting and drying under higher-emissions scenarios. And, as for temperature, uncertainty is greater under higher-emissions scenarios (domain-mean inter-model standard deviations of 11.5%, 9.7%, and 8.5% under SSP3-7.0, SSP2-4.5, and SSP1-2.6).

Applying Eq. (3) to the larger CMIP6 ensemble of 34 GCMs, we derive mean projections and uncertainty in snowfall loss over the western U.S., under the three scenarios (Fig. 6). Under SSP3-7.0, the total volumetric loss over the western U.S. is 34 ± 8% or 84 ± 16 km3 (Fig. 6g). And across the domain, the local loss varies from 9% to 73% in the MMM (Fig. 6a), while the local standard deviation is generally about a fifth of the local MMM (Fig. 6d). In terms of range totals, the contrast between the western and eastern parts of the region is clear: the North Cascades, Cascades, Sierra Nevada, and Northern Rockies lose 45 ± 13%, 49 ± 14%, 40 ± 11%, and 44 ± 12%, while the Middle Rockies, Wasatch–Uinta, and Southern Rockies lose 22 ± 5%, 31 ± 7%, and 25 ± 6%. These uncertainty ranges are shifted upward (i.e., less snow loss) by 3–8% from the WRF simulated losses in the 14-GCM downscaled ensemble (cf. Fig. 3g). This reflects that warming over the western U.S. in the full CMIP6 ensemble mean is about half a degree less than in the sub-ensemble (Fig. S12). This result underscores the importance of extrapolating the results to the broader ensemble.

Fig. 6: Projections of snowfall loss over western U.S. extrapolated to full CMIP6 ensemble under three scenarios.
figure 6

(ΔS/S)RCM is estimated based on Eq. (3), using the coefficients derived in Fig. 5d, e and the GCM deltas in Fig. S11. a–c Multi-model mean; (d–f) standard deviation; left column: SSP3-7.0; middle column: SSP2-4.5; right column: SSP1-2.6; (g) ecoregion-integrated and western-U.S.-integrated fractional volumetric snowfall loss, based on regression at each grid cell. Bars, boxes, and whiskers represent the multi-model mean, ±1 standard deviation, and the full model spread, respectively. Grid cells are masked that have <100 mm yr−1 historical snowfall in the multi-model mean. But these grid cells still contribute to the ecoregion and western U.S. totals.

Full size image

The societal benefit of lowering emissions is highlighted by the equivalent projections under SSP2-4.5 and SSP1-2.6 (Fig. 6b, c, g). Unlike SSP3-7.0, in which emissions double by end-of-century, in SSP2-4.5 emissions hover around current levels before starting to fall by mid-century, while in SSP1-2.6 emissions reach net-zero by late century38. The total volumetric loss over the western U.S. is reduced to 25 ± 6% and 17 ± 6% under SSP2-4.5 and SSP1-2.6. And across the domain the local MMM loss varies from 7% to 60% under SSP2-4.5, and from 5% to 44% under SSP1-2.6. However, the model spread for these scenarios (Fig. 6e, f) is larger, relative to the MMM, than under SSP3-7.0. This reflects the greater influence of internal variability on end-of-century changes under weaker greenhouse-gas forcing. The range-total losses are reduced by about a third for SSP2-4.5 relative to SSP3-7.0, and by half for SSP1-2.6 (Fig. 6g). For example, under SSP1-2.6, quoting the same ranges: the North Cascades, Cascades, Sierra Nevada, and Northern Rockies lose 23 ± 10%, 25 ± 10%, 19 ± 8%, and 21 ± 9%, while the Middle Rockies, Wasatch–Uinta, and Southern Rockies lose 10 ± 4%, 14 ± 5%, and 11 ± 5%. These statistics illustrate that under lower emissions scenarios, in particular SSP1-2.6, and particularly in the interior states, snow losses could be kept to levels that are likely to be much more manageable throughout the western U.S.

Discussion

Although previous studies have produced RCM projections of snowfall losses over the western U.S., the crucial advance made in this study is that now we can express these losses as a function of large-scale warming and wetting/drying. Large uncertainty remains in both of these aspects of climate change. Specifically, averaged over the western U.S. under SSP3-7.0, the inter-model standard deviations of annual-mean ΔTGCM and cold-season (ΔP/P)GCM are 0.90 K and 11.5%. The spatial patterns of (ΔP/P)GCM vary drastically across GCMs to the extent that, other than wetting over the Northern/Middle Rockies, there is not a single mountain range where the sign of the change is consistent (Fig. S3). Our multi-model mean projections are consistent with those based on other RCM simulations or statistical downscaling of GCMs under high emissions scenarios4,18,19,20,36. Specifically, losses of over 50% are projected over the Cascades and Sierra Nevada by end-of-century, but only about 25% over the Rockies. However, for stakeholders and policymakers to receive actionable projections, it is critical to communicate the uncertainty in projections and express its sensitivity to both temperature and precipitation. This also informs stakeholders of expected snow loss under worst-case scenarios in which warming and drying are both at the high ends of the GCM-ensemble spreads.

We argue that the conclusions of this study can only be reliably reached via a diverse ensemble of dynamically downscaled GCM projections, such as we have presented. This argument is twofold. First, a diverse ensemble is needed to connect the GCM to RCM changes robustly. This is illustrated in Fig. S13 in which the regression coefficients in Eq. (3) are progressively calculated with an increasing number of GCMs. (The ΔTGCM coefficients converge on those in Fig. 5 at about 4 GCMs, while the (ΔP/P)GCM coefficients converge at about 10 GCMs.) This illustrates the unique power of WUS-D3, with 14 downscaled GCMs, with regards to precipitation sensitivity. Second, RCMs are needed because statistical downscaling is unable to represent the mesoscale, convective, and orographic processes connecting large- to local-scale climate change, and thus estimates lower snow losses than RCMs18. Issues also arise in statistical downscaling due to bias correction against observation-derived gridded products based on poor station coverage in parts of the western U.S., limiting the ability to train a statistical model39.

Our results are based on a 9-km downscaling over the western U.S. One may question whether this grid spacing is sufficient to represent the complex terrain of the region adequately, and in particular represent the rain/snow partitioning over the relevant mountain ranges. To address this issue, we utilize a 3-km downscaling of the 9-km domain over a reduced domain of California (Fig. S1). 3-km downscaling was performed for 5 of the 14 GCMs. Thus, in Fig. S14 we compare the fractional snowfall losses over the Sierra Nevada and southern Cascades between the 9-km and 3-km domains, as derived in Fig. 3, just based on those 5 downscaled GCMs. As expected, finer detail is resolved in the 3-km domain, more clearly representing individual catchments. However, there is no fundamental difference between the two domains in the regional structure of losses over the Sierra Nevada, nor in the contributions of temperature or precipitation. Specifically, the 9 km (3 km) domains predict that the Sierra Nevada loses 47 ± 4% (45 ± 4%) snowfall, while temperature alone causes 45 ± 8% (45 ± 8%) loss, and precipitation alone causes 3 ± 14% loss (2 ± 15% gain). Thus, although better able to project losses in individual catchments, the 3-km domain does not highlight any shortcomings in the 9-km results, when viewed at the spatial scale at which our results are analyzed. This comparison between the two domains over California lends confidence to the 9-km projections over the wider western U.S. domain presented throughout this manuscript.

It is important to distinguish between the loss of snowfall, quantified in this study, and that of SWE (i.e., snowpack). We argue that the decrease in total annual snowfall is equally important to project as SWE because it represents the total amount of runoff that could result from snowmelt. SWE decreases at a greater rate than snowfall because it also reflects the rate and timing of snowmelt, and thus declines therein do not necessarily represent net losses. For context, we compare annual snowfall losses to those of various SWE metrics (Fig. S15): in the MMM, averaged over grid cells that receive > 100 mm y−1 snowfall, snowfall decreases by 38%; by contrast, the equivalent losses of SWE are 43% (annual-maximum, ΔSWEmax), 63% (annual mean; ΔSWEmean), and 68% (April 1st; ΔSWE1 Apr). And the local ΔSWEmax and ΔSWEmean are almost perfectly correlated with ΔS. This means that ΔTGCM and (ΔP/P)GCM are equally as predictive of ΔSWERCM as for ΔSRCM. In other words, the multi-linear regression model derived for snowfall loss in Fig. 5 can also be viewed as one for SWE losses, but with the coefficients rescaled. However, ΔSWE1 Apr is only highly correlated with ΔS at the highest elevations, meaning that changes in the duration of the snow season at lower elevations prevent a one-to-one relationship with snowfall. Thus, a regression model for changes to SWE on a specific date would be more complex, which we do not attempt in this study.

Although most of the projected snowfall losses will be replaced by increased rainfall, this would decrease water availability during the snowmelt season when western U.S. water demand is high and precipitation is low. This is exemplified by the fact that historically 53% of runoff and 75% of water supply in the western U.S. come from snowmelt, despite only 37% of precipitation falling as snow4,5. In addition, reductions in snowfall can require reductions in reservoir freshwater storage due to the risk of winter-season floods that will increasingly be driven by shorter and more intense rainfall-driven runoff40. Thus, the method employed here is applicable to other regions with complex terrain and a significant fraction of runoff coming from snowmelt. The sensitivity of snowfall/SWE loss in other regions to GCM signals will depend on the mesoscale, orographic, and convective-scale meteorological processes that define the local hydroclimate. With increasing computational capacity and the increasing efficacy of machine-learning methods, deriving this sensitivity in other regions will become increasingly feasible. Thus, the threat to water resources in regions around the world dependent on snowmelt may be elucidated, as made possible in this study, so that adaptation measures, infrastructure and mitigation may be planned accordingly.

Methods

WUS-D3

All 14 bias-corrected dynamically downscaled GCM projections from WUS-D327 were used (Table S1). These experiments are otherwise-equivalent to the same experiments without bias correction of the driving GCMs26. Note that additional downscaled GCMs have been added to the bias-corrected dataset (incorporated in the current study) since the publication of27. All GCMs were downscaled with the Weather Research and Forecasting (WRF) Model Version 4.1.341. The simulations span 1980–2100 with the historical forcings up to 2014 and SSP3-7.038 thereafter. WRF was driven by the GCM boundary conditions with a 45-km parent domain over the Northeast Pacific and most of North America, and a 9-km nested domain, whose results are presented in this study, over the western U.S. (with some buffering). Our results are calculated from the 1980–2014 and 2066–2100 means for the historical and future climates, respectively. See ref. 33 for the full domains and details of the WRF configuration. We also used the equivalent model setup (WRF–ERA5;33) driven by the European Centre for Medium-Range Weather Forecasts (ECMWF)’s European Reanalysis Version 5 (ERA5;42) for comparison to the GCM-driven simulations in Fig. 1.

In addition to the 9-km results, we also present results from a 3-km domain over California, including parts of Oregon, Nevada, and Arizona (Fig. S1). These 3-km simulations were added to WUS-D3 since the publication of ref. 27, and have not been published until now. They were performed using the 9-km output as initial and boundary conditions, over the same period (1980–2100). The 3-km domain was configured exactly as the 9-km domain, except without convective parameterization, following common practices. The 3-km downscaling was performed for 5 of the 14 GCMs for which the 9-km downscaling was performed (Table S1).

Bias correction of the GCM boundary conditions was applied to surface pressure and temperature, mean sea-level pressure, and SSTs, as well as to three-dimensional temperature, geopotential height, specific humidity, and zonal and meridional winds. The bias correction of each variable and calendar month was computed by the difference in 1980–2014 climatology between the respective GCM and ERA5. This technique preserves the long-term trend, resulting in the large differences in future snowfall between downscaled GCMs shown throughout the manuscript. See ref. 27 for more details of the bias-correction methodology. For the current study, the bias correction is critical because the decomposition in Eq. (2) includes historical R and P. If using non-bias-corrected GCMs, then the disagreements in historical R and P would also have to be included in the decomposition presented in Fig. 2. However, the bias correction preserves the variability of the raw GCM data, resulting in the small differences in historical snowfall climatology between downscaled experiments (Fig. 1). To account for these small disagreements, the regression model that we build (Eq. 3) is based on fractional decreases of snowfall.

Calculating snowfall losses

Our results are presented as grid-point values and mountain-range totals. The grid cell values are taken directly from the 9-km WRF grid. The range totals are calculated by integrating the annual snowfall over a 9km-by-9km grid cell, then summing all grid cells within the given Environmental Protection Agency (EPA) ecoregion, giving units of km3 yr−1. In some figures this process is repeated over the entire domain, to give the western U.S. total. And, in Fig. 4, this process is further refined for individual elevation brackets within each ecoregion. In this way, the ecoregions covering more area have a tendency to have greater totals. And within each ecoregion, elevation brackets that cover more surface area of the ecoregion have a tendency to have greater totals.

This process is repeated for each downscaled GCM and then the boxplots are constructed based on the model spread. To calculate fractional changes to range totals (Figs. 3, 6), the historical and future climatologies are integrated over the range individually, then the fractional change is calculated from these two values. Each downscaled GCM’s fractional change is based on its own historical value. Calculating fractional changes using the multi-model mean historical value for each downscaled GCM makes very little difference, given the small differences in historical values between GCMs (Fig. 1).

Computing the hybrid downscaling model

The hybrid downscaling model (Eq. 3) was built at each grid cell based on least-squares error. T and P represent surface air temperature and total precipitation. The GCM deltas were computed from the full calendar year (ΔTGCM) and from NDJFMA (ΔP/P)GCM, based on the same two periods as for the RCM deltas (1980–2014 and 2066–2100). The GCM deltas were calculated from the same variant as that used to dynamically downscale the relevant GCM (Table S1) and bilinearly interpolated to the WRF grid in order to compute the regression.

The variance explained by ΔTGCM in Fig. 5b is based on the otherwise-equivalent single-linear regression model for ΔTGCM. But, the variance explained by (ΔP/P)GCM in Fig. 5c is calculated as the residual between Fig. 5a and b. This approach is motivated by the far greater correlation between ΔTGCM and (ΔS/S)RCM than between (ΔP/P)GCM and (ΔS/S)RCM over almost all of the domain (not shown). Thus, (ΔP/P)GCM is deemed a second-order predictor. If calculating a single-linear regression model based on (ΔP/P)GCM, over-fitting occurs, i.e., the model tries to attribute variance to (ΔP/P)GCM that is really attributable to ΔTGCM.

The statistically downscaled projections from the larger CMIP6 ensemble (Fig. 6) are achieved by computing Eq. (3) with the α and β coefficients derived from the 14 dynamically downscaled simulations (Fig. 5). These coefficients are applied to all 34 GCMs (Table S2) for which monthly data of both surface temperature and precipitation were archived under each of the historical, SSP3-7.0, SSP2-4.5, and SSP1-2.6 experiments. For the GCMs that were not dynamically downscaled, the r1i1p1f1 variant was used unless unavailable (Table S2). To calculate the fractional state and fractional western U.S. losses in Fig. 6, the fractional loss at each grid cell was weighted by the MMM historical snow in the dynamically downscaled ensemble (Fig. 1b), then averaged over the given state/western U.S. This is because there is no historical snowfall to use as a baseline for the non-dynamically downscaled GCMs.