Introduction

The terrestrial carbon and water cycles are fundamental components of the Earth’s biosphere and climate system1, deeply intertwined through processes like photosynthesis and evapotranspiration (ET) that mediate the exchange of energy, carbon, and water between the land surface and the atmosphere2,3,4,5. Gross primary production (GPP), a key measure of carbon fixation by plants, is intricately linked to ET via leaf stomata, the process through which water is transferred to the atmosphere via evaporation and plant transpiration6,7,8. The strength of the correlation between GPP and ET, known as carbon-water coupling (CWC), serves as a critical indicator of how well carbon uptake and water use are synchronized and what are the conditions of eco-hydrological balances in ecosystems6,9,10. Understanding the dynamics of CWC is crucial because it directly influences land-atmosphere feedbacks through changing eco-hydrological dynamics that govern atmospheric moisture, surface cooling, and precipitation patterns.

A strong CWC signifies an ecosystem’s ability to efficiently sequester carbon while maintaining balanced water fluxes through evapotranspiration11. This, in turn, promotes surface cooling and enhances atmospheric moisture, which can stimulate precipitation and contribute to climate regulation on both local and regional scales12,13,14. Conversely, a weakening of CWC of an originally tightly coupled GPP-ET ecosystem—a decoupling of these interconnected processes—signals that ecosystems are losing their capacity to balance carbon and water cycling effectively (i.e., ecosystems are losing their eco-hydrological balances)15,16. This decoupling leads to reduced evapotranspiration, less surface cooling, and diminished atmospheric moisture, exacerbating the effects of climate change. As environmental changes continue, predicting how CWC will evolve becomes increasingly complex. Despite its importance, the dynamics of CWC have been rarely explored, and understanding its evolution in response to climate change is essential for predicting future ecohydrological outcomes and their implications for global water availability17,18,19, food security20, and climate regulation21,22.

Existing research has primarily focused on water use efficiency (WUE), a measure of the trade-off between carbon gain and water loss, and how it is influenced by rising atmospheric CO₂, soil moisture, and vapor pressure deficits3,4,8,23. While WUE trends have been widely studied, particularly in relation to increasing CO₂ concentrations and their impact on ecosystem water relations, the broader question of how CWC itself evolves over time remains underexplored. Some studies suggest that vegetation growth is increasingly constrained by water availability24,25,26, with soil moisture dependence intensifying at continental scales27. However, there is little consensus on how the synchronization between the carbon and water cycles—CWC—may evolve as global environmental changes accelerate.

Here, by leveraging long-term in-situ measurements, remote sensing observations, and land surface model simulations, we elucidate the spatial and temporal dynamics of the GPP-ET coupling strength across the extratropical Northern Hemispheric (NH) ecosystems and identify the primary drivers of the trends. We focused on NH ecosystems because they play a crucial role in shaping long-term trends in global net carbon uptake28. These ecosystems are particularly vulnerable to the impacts of a warming climate29, making their analysis essential for understanding broader ecological responses and informing climate adaptation strategies. First, we investigated the spatiotemporal patterns of GPP-ET coupling using two independent GPP-ET datasets: one based on ground-based eddy covariance (EC) tower observations, referred to as the EC GPP-ET, and the other derived from satellite data, termed the RS GPP-ET. Second, we utilized satellite-derived leaf area index (LAI), enhanced vegetation index (EVI), and solar-induced fluorescence (SIF) as proxies of GPP to provide additional evidence of CWC changes. Third, we employed simulations from land surface models to assess whether these models could accurately capture the observed trends of the GPP-ET coupling strength. Our findings offer new insights into future climate dynamics and strategies for ecosystem management.

Results

Evidence from long term in-situ measurements

To investigate the changes in the GPP and ET coupling, we used FLUXNET and calculated the correlation between GPP and ET across the NH ecosystems (see Fig. 6 for FLUXNET sites). As shown in Fig. 1a, the mean correlation coefficients between GPP and ET were consistently positive, with the highest value of 0.48 and the lowest value of 0.33. Using the 5-year moving correlation analysis, we found a significant decreasing trend in the CWC strength, with a decline rate of −0.013 per year (R2 = 0.62, p < 0.01). This indicates that the coupling strength between GPP and ET weakened from 2001 to 2014. Among the 80 sites, 59% (47 sites) exhibited decreasing trends, while 41% (33 sites) showed increasing trends. Despite large across-site variations, the mean EC GPP-ET correlation decreased by 21% from the initial five-year period of this century—2001–2005 (0.48) to the last five-year period—2010–2014 (0.38) (Fig. 1b).

Fig. 1: Evolution of CWC strength during the 2001–2014 calculated from 80 EC sites.
figure 1

a Time series of EC GPP-ET correlation calculated using 5-year moving window. Numbers in each point indicate the number of sites involved in calculating the EC GPP-ET correlation within each 5 years. The gray line in each dot indicates the deviations among the sites. The inserted barplot indicates the site count showing decreasing (orange: Dec) and increasing (blue: Inc) trends in EC GPP-ET correlation. b Comparison of CWC strength between the first 5 years (2001-2005) and the last 5 years (2010-2014).

Full size image

We further investigated the CWC strength across different ecosystem types (Table 1). We found a consistent trend in EC GPP-ET correlation across all the NH ecosystems. Specifically, the strongest GPP-ET correlation (0.95) was found in woody savanna, which showed a decline trend of −0.0017/year. The lowest GPP-ET correlation (0.27) was found in evergreen needle-leaf forest and cropland, and they showed relatively high decline rates of −0.0443/year and −0.0197/year, respectively. In contrast, ecosystems such as evergreen broadleaf forests and wetlands exhibited strong GPP-ET correlations (0.61) but different rates of decline (−0.109/year and −0.093/year, respectively). The mixed forests and grasslands had moderate correlations of 0.29 and 0.52, with declining trends of −0.0261/year and −0.0007/year, indicating a varied response across different ecosystems. These findings suggest that while the overall CWC strength decreased, the rate and magnitude of this decline varied obviously among ecosystem types.

Table 1 Trends of EC GPP-ET correlation (2001–2014) derived from EC tower GPP and ET data for different ecosystem types
Full size table

Evidence from satellite-derived data products

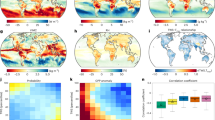
To gain further insights into the relationship between GPP and ET across the whole NH, we analyzed the spatiotemporal evolution of the CWC strength using four sets of remote sensing GPP data (CMG, EC-LUE, MODIS, and PML) and three sets of ET data (GLEAM, MODIS, and PML) (Fig. 2). As depicted in Fig. 2, the RS GPP-ET correlations derived from the 12 data combinations across the NH were almost all significantly positive, with an average correlation coefficient of 0.69 (p < 0.01). These positive correlations were also confirmed by the individual data combinations (Supplementary Fig. 1). However, it should be noted that relatively large areas showed negative correlation between GPP and ET when the EC-LUE GPP product was used. Widespread significant declines in the RS GPP-ET correlation were found, particularly in high-latitude and mid-to-low-latitude areas of the NH (Fig. 2b). 18.9% of the NH exhibited significant (p < 0.05) decreasing trends in RS GPP-ET correlation, while 13.2% showed increasing trends. The spatial distribution of the trend remained evident across different combinations of GPP and ET data (Supplementary Fig. 2). When looking at the time series of RS GPP-ET correlation using 5-year moving window, we found the ensemble mean value of GPP-ET correlation showed a significant decreasing trend (−0.005/year, p = 0.000). This decreasing trend was also confirmed when using 10-year moving correlation analysis (Supplementary Fig. 3). All different data combinations also exhibited varying degrees of decline in the GPP-ET correlation (Fig. 2g), indicating a weakening CWC strength during the study period. In total, the mean RS GPP-ET correlation decreased from 0.46 to 0.41 (decreased by 11%) from the first 5 years to the last, which is lower than that of EC site observation (Supplementary Fig. 4). To further investigate whether the changes in GPP-ET are robust across different ecosystems, we further explored the magnitude and variations of GPP-ET in various ecosystems (Supplementary Table 1). Consistent with the observations, RS GPP-ET correlations were all positive across different ecosystems. In contrast, we observed an increasing correlation between RS GPP-ET in the DBF, CRO, and CSH ecosystems over the past years, which may be influenced by the sample size and duration of the study. However, other ecosystems exhibited a decreasing trend consistent with EC tower observations. To further explore whether this trend persists over a longer timescale (1982−2018), we also utilized some supplementary data (GPP datasets from GLASS and REC-LUE and ET datasets from Gleam and TerraClimate) and employed 5-year, 10-year, and 15-year moving windows to detect the evolution of GPP-ET correlation. We found that regardless of the moving average used, their ensemble averages consistently exhibited a significant declining trend (Supplementary Fig. 5).

Fig. 2: Spatiotemporal patterns of carbon-water correlation (2001-2018).
figure 2

a Spatial distribution of GPP-ET correlation. Rmean indicates the average of RS GPP-ET correlation values based on the 12 data combinations, with statistical significance marked by ** at p < 0.01. b Spatial trends in RS GPP-ET correlation over the study period. Dot-shaded areas represent regions with significant trends (p < 0.05). The pie chart indicates the proportion of significant (p < 0.05) positive (green) and negative (orange) trends in GPP-ET correlation. c Aggregated mean values of trends along latitudinal gradients, with gray-shaded areas showing the standard deviation among the 12 data combinations. d Spatial distribution of correlation between vegetation indices (EVI, NDVI, LAI, and SIF) and ET. Rmean indicates the spatial average of GPP-ET correlation values, with statistical significance marked by ** at p < 0.01. e Spatial trends in the correlation between vegetation indices (EVI, NDVI, LAI, and SIF) and ET over the study period. Dot-shaded areas represent regions with significant trends (p < 0.05). The pie chart indicates the proportion of significant (p < 0.05) positive (green) and negative (orange) trends. Gray areas indicate non-significant change portions. f Aggregated mean values of trends along latitudinal gradients, with gray-shaded areas showing the standard deviation among the 12 data combinations. g, h Temporal evolution of correlations of RS GPP-ET (g) and vegetation indices and ET (h) from 2001 to 2018, analyzed using a 5-year moving window. The black line represents the ensemble mean of the 12 data combinations, while the gray dashed lines denote individual combinations of remote sensing data.

Full size image

To further validate the changes in the GPP-ET correlation, we employed satellite-derived EVI, NDVI, LAI, and SIF as proxies for GPP to examine the CWC strength (Fig. 2d). We found that these GPP proxies positively correlated with ET across almost the whole NH with an average correlation of 0.35 (p < 0.01). When looking at the individual combinations, we found that all GPP proxies (LAI, NDVI, EVI, and SIF) exhibited significant positive correlations with ET, although they displayed considerable spatial variability. For example, large areas in high-latitude regions showed a negative NDVI-ET correlation (Supplementary Fig. 6). In comparison, the trends in the correlation between GPP proxies and ET showed relatively greater spatial consistency over the study period, with significant declines in the correlation across large areas in the high-latitude regions, particularly in the North America (Supplementary Fig. 7). In total, 18.7% of the total areas showed significant (p < 0.05) decreasing CWC strength, while 13.6% showed increasing trends, which were similar to that of gridded GPP-ET correlation. The aggregated latitude pattern showed that the trend of correlation between GPP proxies and ET was almost all negative, except for the regions between 43.5°N and 47°N and regions around 73.5°N. The CWC strength showed a significant decreasing tendency (−0.0034/year, p < 0.01), which was also confirmed by the individual combinations of the satellite-derived GPP proxies and ET products (Fig. 2h and Supplementary Fig. 7). Overall, similar to EC tower observations, the satellite-derived GPP data and proxies, along with satellite-derived ET data indicate that the CWC strength decreased during 2001-2018.

Carbon-water coupling based on process-based model simulations

We further analyzed the spatiotemporal patterns in the CWC strength using simulations from 13 different global vegetation models within the TRENDY ensemble (see Methods). These models, driven by observed climate fields, varying CO₂ concentrations, and land use changes (S3), provided the real predictions of GPP and ET for the period from 2001 to 2018. This approach allows us to compare trends in carbon-water coupling in TRENDY models with results from EC and RS observations. Despite structural differences, most models (with the exception of CABLE-POP and IBIS) produced similar spatial patterns in the correlation coefficients between GPP and ET (Supplementary Fig. 8). The modeled GPP-ET correlation to a large extent, matched those derived from satellite data (Fig. 2a). The models simulated significant (p < 0.05) positive correlations between GPP and ET across most of the NH, except for the CABLE-POP and IBIS models, which yielded negative values in high-latitude regions.

Over the past 19 years, the geographic patterns of GPP-ET correlation trends varied substantially among models (Supplementary Fig. 9). When aggregated to the entire study region, only seven models captured the negative trend in the GPP-ET correlation (Fig. 3). The ensemble of the models showed almost no trends in GPP-ET correlation during the study period. Only two models, CABLE-POP and CLM5.0, exhibited significant negative trends (p < 0.05). In contrast, six other models showed positive trends in GPP-ET correlation. Notably, the IBIS and ISBA-CTRIP models demonstrated significant increasing trends (p < 0.01 and p < 0.05, respectively) (Fig. 3b). This discrepancy arises because these models (Supplementary Fig. 9) produced smaller areas with decreasing GPP-ET correlation trends compared to satellite observations (Fig. 2). These findings highlight a divergence between model simulations and satellite observations, indicating that most land surface models fail to accurately capture the observed decline in the GPP-ET correlation.

Fig. 3: Temporal evolution of correlations of GPP-ET derived from Trendy models.
figure 3

a Times series of GPP-ET correlation calculated using 5-years moving windows. Black line indicates the ensemble mean of the 13 models, and the gray dashed lines indicate the time series of GPP-ET of each Trendy model. b Trend of GPP-ET correlation during the study period. ** and * denote the significant levels at p < 0.01 and p < 0.05, respectively.

Full size image

Attribution

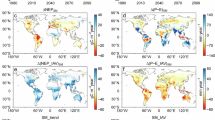
Finally, we evaluated the influence of climate factors (i.e., air temperature, precipitation, and solar radiation) and atmospheric CO2 concentration on the dynamics of CWC strength using two different methods: the partial correlation (PC) analysis and the Lindeman, Merenda, and Gold (LMG) method (Fig. 4). We based our attribution analysis on satellite-derived GPP and ET data as they accurately captured the CWC and its trends during the study period shown by the EC tower data. The PC analysis revealed that atmospheric CO2 accounted for one-third (33.1% in total, and 16.7% of them are statistically significant) of the variability in CWC strength. Air temperature, precipitation, and solar radiation contributed similarly and explained 23.7%, 22.0%, and 21.3% of the variability, respectively (Fig. 4a). From the magnitude perspective, CO2 contributed mostly to the decreasing GPP-ET correlation, followed by air temperature, solar radiation, and precipitation. Spatially, the influence of CO2, precipitation, and solar radiation extended across almost the entire NH, while the impact of temperature was primarily concentrated in high-latitude regions (e.g., the Northern Europe). The spatial patterns identified using the LMG method closely mirrored those observed in the PC analysis, with increased atmospheric CO2 identified as the primary driver in 35.0% (20.4% of them are statistically significant) of the total areas, and similarly, air temperature, precipitation, and solar radiation had comparable influences on CWC changes (Fig. 4b). To further confirm the contribution to CWC changes, we also employed a machine learning approach (random forest) to identify the dominant factors. The results showed that CO₂ changes controlled 51.7% of the area, with 24% having a significant impact, while the remaining influence was attributed to temperature, solar radiation, and precipitation changes (supplementary Fig. 10). In summary, the variations in CWC strength over the past two decades were primarily driven by increased atmospheric CO2 concentration.

Fig. 4: Control factors of carbon-water coupling during 2001-2018.
figure 4

a Control factors of carbon-water coupling derived using partial correlation analysis (PC). b Control factors of carbon-water coupling derived using LMG analysis. Tables indicate the proportions of controlled areas by each factor. SR, Pre, and Temp indicate the solar radiation, precipitation, and air temperature. Dot-shaded areas represent regions with significant trends (p < 0.05). In the pie chart, the outer ring represents the total controlled area, while the inner ring indicates the proportion of the significantly controlled area.

Full size image

Discussion

In this study, we observed a significant decline in CWC strength across the NH over the past two decades, identified through EC tower observations and remote sensing data. This weakening CWC suggests a shift in the ecohydrological coupling, with broad implications for ecosystem and hydrological functioning30. Understanding the mechanisms driving this decline is crucial not only for improving our predictive models but also for projecting the broader ecological and hydrological impacts. Our findings indicate that the primary driver of the decline in CWC strength is the increasing concentration of atmospheric CO2, which affects GPP and ET in ways that weaken their correlation31,32. The direct impact of elevated CO2 on ecosystems is twofold: it enhances photosynthesis, thereby increasing GPP, while simultaneously reducing stomatal conductance, leading to a decrease in ET17,33. The reduction in stomatal conductance is a physiological response of plants to elevated CO2, and conserves water by limiting the loss of water vapor through stomata34,35,36. However, this response also disrupts the tight coupling between carbon uptake and water loss, as the enhanced carbon fixation does not translate proportionately into increased water use. In addition to the physiological responses of vegetation to elevated CO2, the radiative effects may also play an important role in downregulating the coupling strength19,37. For example, increased precipitation caused by the elevated CO2 may alleviate the water stress of ecosystems, and the decrease of GPP will not necessarily be linked to decrease of ET6. As a result, the GPP-ET relationship weakens, leading to a decline in CWC (see coupling mechanism diagram presented in Supplementary Fig. 11). Other factors, including changes in temperature, precipitation, and solar radiation, further influence the CWC strength by altering plant physiology and water availability.

Climate factors such as temperature, solar radiation, and precipitation also contribute to the observed decline in CWC. Temperature is a key driver of both GPP and ET, influencing photosynthetic rates and VPD, which regulates transpiration. Rising temperatures can exacerbate water stress26, particularly in arid and semi-arid regions, leading to further coupling of GPP-ET. In contrast, in temperate regions, warmer temperatures might extend the growing season, leading to complex, region-specific responses in CWC38 (Fig. 4). Solar radiation, which drives photosynthesis, can also influence CWC. Changes in radiation, whether due to cloud cover, atmospheric aerosols, or shifts in the Earth’s energy balance, can alter the CWC by affecting the amount of energy available for photosynthesis and ET. For example, changes in solar radiation may have significantly contributed to increased water constraints on vegetation in the NH over the past few decades26. Changes in the intensity, frequency, and seasonal distribution of precipitation can significantly impact both GPP and ET39. In regions with increasing precipitation, the enhanced water availability may decrease the GPP-ET correlation, whereas in regions experiencing declining rainfall, water stress could further enhance the coupling7. In addition to the climatic factors, disturbances (e.g., deforestation, wildfire) could also contribute to the decline of CWC, which can be a good subject in future research30. To examine whether the dominant factors consistently influence correlation dynamics throughout the study period, we employed a moving window method to analyze the evolving area fractions controlled by CO2, precipitation, solar radiation, and air temperature (Supplementary Fig. 12). Overall, CO2 has maintained a dominant controlling effect throughout the study, with its influence gradually increasing. As CO2 levels are projected to continue rising in the future, the relationship between GPP and ET may become increasingly uncertain.

Since similar environmental and physiological processes influence both CWC and WUE, our results also have divergent implications for WUE dynamics. If GPP and ET are becoming less synchronized, it indicates that external drivers such as rising CO₂ levels and climate variability are altering the balance between carbon assimilation and water fluxes. In particular, rising atmospheric CO₂ enhances photosynthesis while reducing stomatal conductance, which can increase WUE at the leaf level23. However, at the ecosystem scale, this effect may be offset by increased evaporative demand due to warming and increased VPD4, changes in precipitation patterns, and vegetation structural adjustments8, leading to spatially variable WUE responses. To better understand these interactions, future studies should investigate the extent to which the observed CWC decline translates into changes in WUE at different spatial and temporal scales. The observed decoupling trend of carbon and water fluxes has significant implications for the functioning of ecosystems and their ability to provide critical services such as carbon sequestration and water regulation40,41. The decline in carbon-water coupling suggests that the carbon and water cycles are becoming increasingly decoupled, which may signify that the ecosystems are reshaping their eco-hydrological balances under the elevated CO234. This coupling could also alter the feedback loops that regulate climate-vegetation interactions14. This trend could reduce the ability of ecosystems to buffer climate change through carbon sequestration, as the efficiency of water use becomes more variable and less predictable. Such a shift would have profound implications for climate change mitigation strategies that rely on the carbon sink function of terrestrial ecosystems42. The weakening CWC also disrupts land-atmosphere feedbacks, which regulate the exchange of water, carbon, and energy between ecosystems and the atmosphere. A strong correlation between GPP and ET ensures that as ecosystems take up more carbon through photosynthesis, they also transpire more water, helping to cool the land surface and moisten the atmosphere9,12,43. This cooling and increased atmospheric moisture can enhance cloud formation and precipitation, providing critical feedback that stabilizes ecosystems and regulates local and regional climates, especially in regions prone to extreme weather events like droughts and heatwaves44. When ecosystems become less synchronized in their carbon and water cycles (weakening CWC strength), they lose their ability to regulate local climates through evaporative cooling and precipitation recycling45. This makes ecosystems more vulnerable to extreme climate events, such as prolonged droughts and heatwaves, which can further stress vegetation and reduce productivity46. Reduced moisture recycling, caused by the weakening CWC, exacerbates drought conditions, creating a negative feedback loop that further weakens the CWC, intensifies ecosystem stress, and reducing water availability39. In summary, with changing CWC strength, relying on natural ecosystems to achieve carbon neutrality goals is becoming increasingly uncertain.

Land surface models exhibited substantial discrepancies from in situ and satellite-derived observations in depicting the trend of the CWC strength. While most models captured the correlation between GPP and ET, many land surface models included in the TRENDY project have failed to adequately replicate the correlation trend (Supplementary Fig. 9). We further explored the reasons underlying the failure of these models to capture the correlation trend (Fig. 5). Our findings reveal that the majority of the models, with the exception of VISIT-NIES, underestimated the negative influence of CO2 on the trend of GPP-ET correlation, and even predicted a positive effect of CO2 on this correlation trend. This discrepancy stands in stark contrast to remote sensing observations (Fig. 4). Such inaccuracies may stem from the utilization of diverse stomatal conductance equations across the TRENDY models, which results in varied vegetation responses to CO2 and subsequently leads to different predictions of GPP-ET coupling and its trend47. The representation of stomatal conductance (gs) in land surface models plays a critical role in simulating the interactions between carbon and water fluxes. Most models employ variations of the Ball-Berry (BB) or Medlyn (M) or Leuning approach11,48,49, these approaches link gs to GPP, CO₂ concentration, and relative humidity (RH). The BB model, which expresses gs as (GPP × RH)/CO₂, results in complex interactions under rising CO₂ levels: while increased CO₂ enhances photosynthesis, it simultaneously reduces gs, leading to a partial suppression of transpiration and total ET. This formulation suggests that in arid regions, where soil moisture limitations constrain GPP responses to CO₂ fertilization, the decoupling between GPP and ET may be more pronounced4. In contrast, in humid environments where water is more available, both GPP and ET may increase in a more synchronized manner, leading to weaker decoupling8. Therefore, the development of a universal and accurate stomatal conductance model is essential to improve the simulation of vegetation responses to CO2 effects in climate models50. Moreover, more than half of the models (seven out of a total of 13) predicted positive effects of climate change on GPP-ET correlation trends, underscoring the need for more accurate projections of vegetation responses to climate change within these models. Currently, these model limitations hamper our ability to make accurate predictions about the impacts of future climate change on carbon and water dynamics, and by extension, on the global climate system itself. This underscores the urgent need for land surface models to more accurately capture the spatial and temporal dynamics of carbon-water coupling. It is essential to incorporate more sophisticated representations of the physiological responses of plants to elevated CO2, as well as the complex feedbacks between carbon, water, and other environmental factors like temperature, solar radiation, and precipitation51,52. Strengthening these aspects of the models will likely enable better understanding of how ecological and hydrological processes interact and how these interactions influence and are influenced by climate change. In addition, while we have analyzed trends in CWC across different ecosystem types, a more direct comparison based on moisture limitation would provide additional insights into the spatial variations of GPP-ET decoupling1. Future studies should explicitly quantify trends as a function of moisture availability, for example, by examining relationships with soil moisture indices or aridity metrics, to better assess how different gs formulations influence model predictions of carbon-water interactions.

Fig. 5
figure 5

Attributions of GPP-ET correlation trend using the 13 models from TRENDY project.

Full size image

While our results reveal a general decline in CWC across the Northern Hemisphere, discrepancies exist between site-level EC observations and RS-derived estimates. Specifically, our comparison (Supplementary Fig. 13) indicates that only 56.3% of EC sites exhibit trends consistent with RS-based ensemble estimates, while the remaining sites show inconsistencies. These discrepancies likely stem from multiple sources of uncertainty inherent in both datasets. First, EC-based measurements provide high-temporal-resolution, site-specific observations that capture local environmental variations, whereas RS-derived estimates represent spatially aggregated values that smooth out small-scale heterogeneity53. Differences in land cover, vegetation structure, and microclimate conditions surrounding EC towers may not be adequately represented in RS products, leading to potential mismatches in CWC trends. Second, uncertainties in RS retrieval algorithms, sensor limitations, and data processing techniques can introduce biases. Factors such as cloud cover, atmospheric correction errors, and variations in satellite overpass times may contribute to discrepancies between EC and RS-based estimates54,55. Third, the number and spatial distribution of EC sites used in this study are limited, which may contribute to the relatively low proportion of sites showing agreement with RS-based trends. The EC sites included in our analysis are mainly located in Europe and central North America, while other regions, especially arid and semi-arid ecosystems, are underrepresented. This uneven distribution may affect the overall consistency between EC and RS datasets. Despite these limitations, the general consistency observed in more than half of the EC sites with RS estimates supports the robustness of our findings.

In conclusion, we show that CWC strength in northern ecosystems has declined, driven primarily by rising CO₂ levels, with contributions from other climatic factors. This decoupling trend may indicate that the ecosystems in the Northern Hemisphere are reshaping their eco-hydrological balances due to the elevated CO₂ levels. The failure of most land surface models to capture this trend highlights an urgent need for enhanced modeling approaches that incorporate the decoupling effects of CO₂ and the complex interplay of climate variables. As atmospheric CO₂ continues to rise, refining these models is critical for improving climate projections and developing strategies to mitigate the impacts of climate change on terrestrial ecosystems.

Materials and methods

Study area and flux data

Our study focused on the NH extratropical terrestrial ecosystems (≥23.5°N, Fig. 6). We first collected GPP and ET data from 80 sites in the global eddy covariance flux database FLUXNET201556. These data were detrended for the growing season (April to October) during the corresponding period. We then conducted an interannual variability correlation analysis. Temporal dynamics of the GPP-ET correlation (Pearson’s correlation coefficients) were analyzed using a 5-year moving window. Note that FLUXNET’s GPP and ET data are only available until 2014, so we analyzed the 5-year moving correlation between EC GPP-ET for the period 2001-2014, yielding a total of 10 time points. We applied specific criteria for data selection, including a continuous time length of over six years and high-quality gap-filling within each year. This ensured that we could analyze the 5-year moving correlation of EC GPP-ET. Overall, we obtained data from 26 sites with recording lengths between 6 and 8 years, 25 sites with recording lengths between 9 and 11 years, and 29 sites with recording lengths of more than 12 years (Fig. 6). These 80 sites encompass various land cover types: 23 evergreen needle-leaf forests (ENFs), 13 deciduous broadleaf forests (DBFs), 2 evergreen broadleaf forests (EBFs), 14 grasslands (GRAs), 11 croplands, 6 open shrublands (OSHs), 5 wetlands (WETs), 3 mixed forests (MFs), 2 woody savannas (WSAs), and 1 closed shrubland (CSH). GPP and latent heat flux (LE) data were collected from these sites, and LE measurements converted to ET. GPP was calculated from the net ecosystem exchange (NEE) measurements using the nighttime partitioning approach.

Fig. 6: EC tower sites collected from different ecosystems in the Northern Hemisphere.
figure 6

The inserted barplot indicates the EC tower numbers in each year gap.

Full size image

Satellite-derived data

We utilized four satellite-derived GPP datasets and three satellite-derived ET datasets to investigate changes in the RS GPP-ET coupling over the past 19 years. The GPP datasets include estimates from the EC-LUE model (EC-LUE GPP)57, VPM model (VPM GPP)58, MODIS (MODIS GPP)59, and PML model (PML GPP)60. The EC-LUE model is an approach that integrates eddy covariance observations with the concept of light use efficiency to estimate gross primary productivity in terrestrial ecosystems. The input data for this model include air temperature, dew point temperature, and photosynthetically active radiation, which are derived from NASA’s global atmospheric reanalysis dataset, MERRA-2. Additionally, land cover data are obtained from the MODIS sensors aboard the Terra and Aqua satellites, while LAI is sourced from the GLASS dataset, which is a fusion of AVHRR (1981–2000) and MODIS (2000–present) data and relies on MODIS sensors. The VPM model incorporates vegetation characteristics and meteorological data to estimate photosynthesis rates and productivity. VPM primarily relies on MODIS remote sensing data (MOD09A1 C6: EVI and LSWI, MYD11A2 C6: Nighttime LST and MCD12Q1 C51: Land cover type), NCEP Reanalysis meteorological data (for air temperature and photosynthetically active radiation estimation), and static vegetation data from Earth Stat and ISLSCP (for spatial distribution of C4 crops and grasslands). MODIS GPP is derived from MODIS observations, analyzing vegetation indices, solar radiation, and temperature to provide consistent GPP estimates across different regions. The PML utilizes meteorological forcing data from GLDAS-2.1, including precipitation, air temperature, vapor pressure, shortwave downward radiation, longwave downward radiation, and wind speed. Monthly atmospheric CO₂ concentrations are sourced from NOAA’s global average oceanic surface data. Remote sensing inputs are derived from MODIS Collection 6 products, including LAI from MCD15A3H.006, albedo from MCD43A3.006, and surface emissivity from MOD11A2.006.

In addition to GPP data, we also used satellite-derived leaf area index (LAI), enhanced vegetation index (EVI), normalized difference vegetation index (NDVI), and solar-induced fluorescence (SIF) to examine the carbon-water coupling. The vegetation data comprises MODIS EVI, MODIS LAI, MODIS NDVI61, and SIF62. EVI enhances vegetation monitoring in high biomass areas by correcting atmospheric and soil background effects. LAI measures the total leaf area per unit ground area. NDVI estimates vegetation health and density by measuring the difference between near-infrared and red light reflectance. SIF, an energy flux emitted by vegetation canopies during photosynthesis, correlates strongly with GPP and is widely used as a proxy of GPP63. The SIF data are derived from the global OCO-2-based SIF product, GOSIF62.

ET data were obtained from three sources: MODIS64, PML60, and GLEAM65. The MODIS ET data, computed using the MOD16 algorithm, integrates remote sensing information with land surface models. The PML ET data combines the Penman-Monteith equation with the Leuning photosynthesis model to estimate ET. The GLEAM ET data utilizes remotely sensed soil moisture, vegetation, and surface temperature data, along with meteorological inputs, to provide comprehensive ET estimates. Prior to our analysis, all datasets were bilinearly resampled to a spatial resolution of 0.25 degrees. We used four sets of GPP/vegetation index data combined with three sets of ET data to explore the CWC relationship and its evolution patterns, resulting in a total of 12 carbon-water coupling changes under each indicator during the study period of 2001−2018.

Land surface model simulations

In this study, we utilized GPP and ET outputs from 13 process-based ecosystem models: CABLE_POP, CLASSIC, CLM5.0, DLEM, IBIS, ISBA_CTRIP, JSBACH, JULES, LPJ_GUESS, ORCHIDEE, VISIT_NIES, and VISIT. These models adhered to the protocol established by the historical climate carbon cycle model intercomparison project (TRENDY V12)66. Each model was initialized from its pre-industrial equilibrium, set at the beginning of the 1900s, and run through to 2020 under three distinct scenarios. In this study, we employed the S3 scenario, which represents real-world conditions where models are driven by observed historical climate variations, rising CO2 concentrations, and land use changes. All models provided estimates for both GPP and ET. To facilitate comparison with satellite observations, we bilinearly resampled the GPP and ET outputs to a spatial resolution of 0.25°.

Moving correlation analysis

This study focused on the correlation between interannual variations in carbon and water across the Northern Hemisphere (NH) extratropical regions from 2001 to 2018. The GPP, NDVI, LAI, SIF, and ET were aggregated based on growing season values, defined as April through October, following previous definitions26,28. To quantify the spatiotemporal changes in carbon-water coupling evolution over the past two decades, we applied a 5-year moving window for each grid cell, indexing the results to the middle year. For instance, the GPP-ET correlation for 2003 represented the correlation over the period from 2001 to 2005. This 5-year moving window approach ensured that sufficient time series points were available to reflect correlation fluctuations. Within each calculation period, data were detrended to accurately determine the correlation between interannual variations. After calculating the 5-year moving window correlation, the non-parametric Theil-Sen slope estimator67,68 was employed to conduct the trend analysis. The significance (p < 0.05) of these trends was assessed using the Mann–Kendall test69,70.

Attribution analysis

The contributions of climate factors (mean annual air temperature, precipitation, and shortwave solar radiation (SR)) and atmospheric CO2 to the observed trends of carbon-water coupling changes were assessed using two methods. A linear regression model was developed using GPP-ET correlation as a function of mean growing season air temperature, precipitation, SR, and growing season CO2 in each 5-year moving window for each grid cell. The most important factor driving correlation dynamics was determined according to the absolute partial correlation (PC) coefficients of each factor32. To evaluate the robustness of the attribution analysis based on regression models, we also used Lindeman, Merenda, and Gold (LMG) relative importance algorithm to test the relative importance of each factor in driving correlation changes. LMG attribution analysis is a method used to assess the relative importance of multiple predictors in explaining a response variable. It decomposes the total variance explained by a set of variables into contributions from each variable and calculates these contributions based on the average contribution of each predictor when it is included in different model combinations71. This method was implemented in R using the “relaimpo” package.