Multidecadal variability of the ENSO early-winter teleconnection to Europe and implications for seasonal forecasting

Abstract

The impacts of El Niño-Southern Oscillation (ENSO) on the North Atlantic and European sector (NAE) climate are season-dependent and, in some cases, not linear and/or not stationary. Previous studies have found multidecadal variability in ENSO teleconnections to NAE in certain seasons, relating it to changes in the background state. However, the stationarity of the teleconnection and its surface impacts in Europe during early winter remain largely unexplored, a gap intended to be addressed in this study. The observational analysis reveals changes in the teleconnection impacts and mechanisms over recent decades. These changes have strong implications for the assessment of seasonal predictability, hence the performance of the SEAS5 seasonal prediction model is analysed. While SEAS5 does not accurately capture the observed non-stationarity, it displays pronounced multidecadal changes in forecast skill. This implies the emergence of windows of opportunity for seasonal forecasting, where predictability may be higher than initially expected.

Introduction

El Niño-Southern Oscillation (ENSO) is the leading mode of global climate variability at interannual timescales. Through its tropical and extratropical teleconnections, ENSO can influence the climate of numerous regions worldwide^1,2, highlighting its role as the main source of seasonal predictability. Studying the impacts of ENSO on the North Atlantic and European sector (NAE) poses a major challenge since this region features strong internal variability, which makes it difficult to isolate the ENSO-forced signal^3,4. Even so, numerous studies have shown that ENSO exerts a significant influence on the NAE climate, though this influence is highly complex: it exhibits strong seasonal variability^5,6, depends on the intensity and spatial distribution of sea-surface temperature (SST) anomalies in the ENSO region^7,8 and is, in some cases, not linear^9,10, not symmetric^11,12, and not stationary¹³.

In the case of the boreal winter season, previous studies have found that the ENSO teleconnection to NAE is remarkably different between early winter (November-December; ND) and late winter (January-February; JF)^14,15. This shift of the ENSO teleconnection in mid-winter is not exclusive to the NAE region, as it has also been reported to occur over the North Pacific and East Asia^16,17,18. For the NAE region, much of the literature has focused on the late-winter teleconnection, when the ENSO signal in NAE appears to be stronger and more robust. It projects onto the North Atlantic Oscillation (NAO), with the positive (negative) phase being more likely in La Niña (El Niño) years^6,9. The relevant mechanisms to the ENSO-NAE late winter teleconnection include tropospheric and stratospheric pathways. On the one hand, the tropospheric pathway in late winter is mainly characterised by the horizontal propagation of stationary Rossby waves triggered by anomalous convection over the central tropical Pacific^19,20, and downstream propagation of eddy energy from the North Pacific into the North Atlantic^21,22. On the other hand, the stratospheric pathway involves changes in the upward propagation of Rossby waves into the stratosphere, which affects the strength of the stratospheric polar vortex. These alterations of the vortex subsequently exert a downward influence on the troposphere, thereby affecting the atmospheric circulation in the North Atlantic^23,24. While the early-winter teleconnection has received comparatively less attention, significant progress has been made over the last few years in the understanding of its impacts on the North Atlantic large-scale circulation and the mechanisms involved. In early winter, studies have shown that ENSO affects the second mode of atmospheric circulation variability in the North Atlantic, namely the East Atlantic Pattern (EAP), such that a +EAP (−EAP) is favoured in El Niño (La Niña) years^14,15,25. Regarding the mechanisms, the tropospheric pathway to NAE is characterised by Rossby wave propagation from different source regions, such as the tropical Pacific Ocean. Additionally, through its interbasin interactions, ENSO-related sources can be found over the Gulf of Mexico-Caribbean Sea^10,14, as well as over the tropical Atlantic⁹. Besides, the Indian Ocean dipole, which is partly driven by ENSO, also serves as a relevant source of Rossby waves that reach the NAE region^26,27,28, thus modulating the ENSO impact on NAE. Conversely, the stratospheric pathway does not play a significant role in early winter^14,24. As outlined above, the impacts and mechanisms of the ENSO early-winter teleconnection to NAE are notably different from those of late winter.

Nevertheless, it is worth pointing out that ENSO teleconnections to extratropical regions, including NAE, can exhibit multidecadal variability (i.e., non-stationary teleconnections)^13,29. The observed multidecadal variability of these teleconnections may stem from well-known physical processes, which mainly involve changes in the background state (or climatology) of sea-surface temperature (SST) and upper-level flow³⁰. The differences in the SST background state can affect the ENSO-associated convective precipitation patterns, thereby modifying the location and/or activity of the different sources of Rossby waves. In addition, the climatological upper-level flow plays a central role in the propagation of these Rossby waves by determining the regions through which they can propagate, as well as their path^20,31. Hence, changes in the climatological upper-level flow can notably impact the tropospheric pathways of the ENSO teleconnections. These shifts in the background states of SST and upper-level flow can be associated with well-known low-frequency modes of variability of the climate system, such as the Atlantic Multidecadal Variability (AMV) or the Pacific Decadal Oscillation (PDO). Furthermore, these background states may change in response to increasing greenhouse forcing, and indeed several ENSO teleconnections are expected to change in a warmer climate^32,33,34. Nevertheless, observed non-stationarity of ENSO teleconnections may not respond to specific physical processes, but may simply show up as a result of stochastic, low-frequency noise³⁵.

Despite the valuable insights gained from recent studies, there are still relevant aspects of the ENSO early-winter teleconnection to NAE that remain unclear. In particular, whether this teleconnection is stationary or exhibits multidecadal variability remains largely unexplored. Some studies have found a non-stationary link between ENSO and the climate in NAE, relating it to changes in the PDO regime through the autumn and winter seasons^36,37, while others describe a link with the AMV in spring and summer^37,38. Moreover, a recent study based on reanalysis data identified a strengthening of the link between ENSO and the EAP in early winter after the late 1990s³⁹. However, whether this shift just corresponds to an isolated fluctuation or is the manifestation of a non-stationary teleconnection is still uncertain. Furthermore, it is also pertinent to investigate how the changes in the North Atlantic circulation associated with ENSO have impacted the European surface climate (i.e., surface air temperature and precipitation). Previous studies on the impacts of the early-winter teleconnection to NAE have mainly focused on the atmospheric circulation in the North Atlantic, while the impacts on the European surface climate have received considerably less attention.

An additional issue regarding the early-winter teleconnection to NAE is that many state-of-the-art dynamical seasonal prediction models significantly underestimate the magnitude of its impacts and show considerable signal-to-noise errors^40,41,42. This problem has been widely reported for seasonal forecasts in the boreal winter season^43,44. Despite this issue, operational seasonal forecasting systems exhibit moderate (and statistically significant) forecast skill in the prediction of the EAP in early winter^25,42. ENSO plays a key role as the main source of predictability at seasonal timescales in many regions worldwide, and hence an accurate representation of its teleconnections is of central importance in seasonal prediction models. Thus, if a change in the ENSO teleconnection is identified in the observations, it is important to assess whether that change is accurately reproduced within the seasonal forecasting models. Given the relevance of ENSO teleconnections to the skill of seasonal forecasts, it is feasible to expect that any significant change in the teleconnection in the observations and/or within the model may result in substantial changes in the forecast skill. Hence, analysing the teleconnection from a non-stationary perspective in these models is necessary to understand how the skill of seasonal forecasts may have changed due to the changes in the ENSO teleconnection. In this sense, it is vital to identify periods with a robust teleconnection in the observations which, to some extent, is successfully reproduced within the models. These periods offer windows of opportunity for seasonal forecasting, as they feature enhanced skill in the models.

Hence, given the current limited understanding of its possible multidecadal variability, studying the ENSO early-winter teleconnection to NAE, within a non-stationary framework, is necessary. In addition, it is important to evaluate how operational seasonal prediction models reproduce the observed teleconnection and its changes, and how the forecast skill is affected by these changes. Thus, the main objectives of this work are to assess these two main issues. In the first part of the paper, we use reanalysis and observational datasets in order to assess the stationarity of the ENSO early winter teleconnection to the North Atlantic, and its impacts on the European surface climate. In the second part, we aim to evaluate the performance of a seasonal prediction model, used operationally, in reproducing the observed impacts of the teleconnection. The analysis within the model is also conducted within a non-stationary framework, seeking to identify potential changes in the forecast skill resulting from the multidecadal variability of the teleconnection.

Results

Firstly, the analysis of the ENSO early-winter teleconnection to NAE is carried out using observational and reanalysis datasets. The main objective here is to describe the multidecadal changes in the teleconnection and its impacts on European surface climate.

Multidecadal variability of the ENSO early-winter teleconnection to the North Atlantic

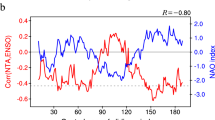
We begin by analysing the teleconnection between ENSO and the EAP using different observationally-derived datasets that span the 20th century, in order to determine whether it differs across decades (Fig. 1). A robust non-stationary relationship emerges in all the datasets. The correlation between the Niño 3.4 index and the East Atlantic index (EA, see Methods) is positive and statistically significant in most of the second half of the 20th century (solid lines), with a decrease in the correlation between the late 1970s and the late 1990s. In contrast, no significant correlation is found in the first half of the century, where the correlation coefficient approaches zero or even becomes negative. In order to gain insight into possible modulations of the teleconnection, and following previous studies, we compare the moving correlations with low-frequency modes of variability of the ocean (dashed lines). These include the low-frequency PDO, AMV and global SST anomalies standardised indices (see Methods). Even though the examination of the physical mechanisms underlying the multidecadal variability of the teleconnection is not within the scope of this work, we note that several changes in the teleconnection appear to occur almost concurrently with changes in the ocean mean state. In particular, from the 1960s–1970s, we note that the ENSO-EAP relationship and the PDO index tend to evolve in opposite phases, such that the negative PDO phase features a positive, statistically significant correlation between the Niño 3.4 index and the EA index, while the positive PDO phase features comparatively lower, and generally not statistically significant correlation values. In previous decades, however, the multidecadal variability of the teleconnection cannot be readily explained by one of these modes individually. This could possibly reflect that the teleconnection pattern depends on some complex combination of these modes of variability of the ocean. In addition, it is possible that global warming, represented by the upward trend in the globally-averaged SST anomalies, is affecting the teleconnection pattern in the recent decades.

Fig. 1: Non-stationarity of the link between ENSO and the EAP in early winter.

21-year running correlation between the Niño 3.4 index and the EA index in early winter, using mean sea-level pressure (MSLP) data from different reanalysis products (solid lines, left axis). The dots indicate that the correlation is statistically significant at the 95% significance level. The low-frequency component (21-year running mean) of the PDO, AMV, and global (45° S - 60° N) SST indices are shown with dashed lines in the right axis. SST data from the HadISST database are used.

From this point on, the study will focus on the teleconnection from the 1950s, as the number of surface and, especially, upper-air observations is substantially higher in the second half of the 20th century, which reduces the uncertainties in the gridded reanalysis and observational datasets^45,46. This study period, though shorter, is sufficient for the objectives of the study, as it features periods with positive, significant correlation between ENSO and the EAP, and a period in which the correlation is lower and, in general, not statistically significant. As noted before, these changes appear to occur almost concurrently with the changes in the PDO regime, such that in the period with positive PDO, the ENSO-EAP relationship is weaker, while it is found to be stronger in the negative PDO phase (Fig. 2a).

Fig. 2: The changing ENSO early-winter teleconnection to the North Atlantic and Europe.

a Time series of the low-frequency component of the PDO index (dashed line), and moving correlation between the Niño 3.4 index and the EA index in ND (solid line). b Regression map of ND SST anomalies (shading; °C) and ND Z200 (isolines; dgpm) onto ND Niño 3.4 index during P1 (1950–1975; top), P2 (1976–1996; middle) and P3 (1997-2022; bottom). For the SST field, only values at the 90% confidence level or higher are shown. For the Z200 field, values at the 90% confidence level or higher are shown with solid lines. Otherwise, dashed lines are shown. c Time series of the ND Niño 3.4 index. Blue bars show La Niña events (Niño 3.4 ≤ −0.5 std), while El Niño events (Niño 3.4 ≥ +0.5 std) are shown with red bars. Bars in grey represent neutral ENSO events (−0.5 std < Niño 3.4 < +0.5 std).

In order to describe these changes in the ENSO early-winter teleconnection over the last decades, different study periods are defined, and the teleconnection is analysed separately in each of them. Based on the previous observation, and building on previous studies that suggested a modulation of the ENSO teleconnection to Europe by the PDO through the autumn and winter seasons, we take into account the interdecadal changes in the Pacific Ocean mean state and the PDO regime. The decadal component of the PDO index shows three regimes throughout the study period 1950–2022 (Fig. 2a, dashed line). A negative PDO regime was present until the mid-1970s, closely matching the well-documented 1976 climate regime shift in the Pacific Ocean^47,48. An additional shift in the PDO regime took place in the late 1990s, associated to another climate shift in the Pacific^49,50 and changes in the Pacific tropical convection^51,52. These shifts set the limits of the different study periods employed in the analysis of the teleconnection. Nevertheless, it is worth stressing that demonstrating the influence of the PDO in the teleconnection is not within the scope of this paper. Instead, our aim here is to describe the changes in the observed teleconnection, which appear to be associated with changes in the PDO regime in the last decades.

Most of the ENSO events that occurred from the 1950s until the mid-1970s (hereafter period P1) were of weak to moderate intensity (Fig. 2c). From the mid-1970s until the late 1990s (hereafter P2), when the low-frequency PDO index was positive (Fig. 2c, dashed line), ENSO events showed enhanced variability. There was a prevalence of El Niño events, with strong El Niño (Niño 3.4 > 1.5 std) and strong La Niña (Niño 3.4 < −1.5 std) events being more frequent than in P1. Finally, the period from the late 1990s (hereafter P3) features a prevalence of La Niña events, together with the outstanding El Niño events in 1997 and 2015, when the Niño 3.4 index reached +3.2 and +3.4 std, respectively. The periods analysed also exhibit changes in ENSO properties, such as its spatial pattern and intensity, as shown in the regression map of ND SST anomalies onto the ND Niño 3.4 index (Fig. 2b, shading). The period P1 displays a prevalence of eastern ENSO events, since the largest SST anomalies are located over the eastern equatorial Pacific (close to 110° W). These anomalies appear together with weaker SST anomalies of the same sign over the Indian Ocean. However, during P2, the largest regression values appear over the central equatorial Pacific, while SST anomalies are weaker in the eastern equatorial Pacific (over the Niño 1.2 region) and in the Indian Ocean. The SST anomalies over the ENSO region are constrained closer to the equator than in P1, suggesting that the dynamics of ENSO events were driven by equatorial processes, such as thermocline feedbacks. Finally, the largest regression values in P3 are located over the central-eastern equatorial Pacific, similarly to P1, and SST anomalies in the Indian Ocean are stronger than in P2.

Overall, these changes in the ocean background state, together with changes in the ENSO-associated SST anomalies, could feasibly lead to changes in the extratropical teleconnections of ENSO. Indeed, the analysis of the 200-hPa geopotential height (Z200) anomalies reveals that the early-winter atmospheric circulation response in NAE to ENSO has undergone considerable changes at multidecadal timescales. The shape and orientation of the wave train emanating from the equatorial Pacific that reaches the Euro-Atlantic sector show important changes between the defined periods. In P1, the response of the North Atlantic circulation to ENSO is most prominent to the south of Iceland and Greenland, with negative anomalies in the Z200 regression field. To its south, there is a positive Z200 anomaly centre over the subtropical North Atlantic. This setup, which supports westerly winds aloft directed towards western Europe, resembles the EAP. This is verified by the significant correlation values between the ND Niño 3.4 index and the EA index in P1 (Fig. 2a, solid line). However, in P2, the Z200 field pattern shows a shift to the north of the centre of negative anomalies in the North Atlantic, which is now located in Greenland-Iceland, in a pattern that resembles the positive phase of the NAO. In turn, no significant correlation between the ND Niño 3.4 index and EA is observed. However, the Z200 anomalies over the North Atlantic are generally lower in magnitude and less significant, as compared to P1. Lastly, in P3, a significant strengthening of the Z200 response to ENSO is identified in the North Atlantic. The centre of negative Z200 anomalies shifts again back to the south, with positive Z200 anomalies in southern Europe and Scandinavia. This pattern again resembles more the EAP, rather than the NAO, and the correlation between the Niño 3.4 and EA is again statistically significant. The difference of correlations between ND Niño 3.4 and EA, between the +PDO and the -PDO periods, is marginally statistically significant (pval = 0.1). However, the difference of the Z200 regression patterns (Fig. S1) clearly reveals the southward shift of the centre of negative anomalies in the North Atlantic in the negative PDO phase. In order to assess whether this difference could be arising from sampling uncertainties in the observations, a bootstrap resampling was performed, revealing that the differences in the teleconnection patterns are very unlikely to be explained by sampling uncertainties (hatched regions in Fig. S1). This fact suggests that these changes in the teleconnection may be rooted in physical processes, which could be associated with changes in the PDO regime. Additionally, even though we focused on the Z200 field over NAE, significant differences between the three periods appear in other extratropical regions, particularly over the Aleutians. Differences are also visible regarding the Gill response in the equatorial Pacific, which are suggestive of changes in the ENSO-associated convection patterns and may modify the location and intensity of the sources of wave activity that propagate towards the extratropics.

In a similar way to the Z200 field, the relationship between ENSO and the surface atmospheric fields, namely mean sea-level pressure (MSLP), surface air temperature (T2m) and total accumulated precipitation in ND, show important variations between the three periods defined (Fig. 3). In order to allow for the possibility of a non-symmetric response to ENSO, separate composites are calculated for El Niño and La Niña events in each of the three periods.

Fig. 3: Changes in the ENSO impact on the North Atlantic and European surface climate.

Composites for La Niña years (a, c, e) and El Niño years (b, d, f) of anomalies of MSLP (isolines; hPa), T2m (shading; °C) and total accumulated precipitation (coloured dots; mm) in ND during P1 (a, b), P2 (c, d) and P3 (e, f). For T2m and precipitation, only values at the 90% confidence level or higher are shown. For the MSLP field, values at the 90% confidence level or higher are represented with solid lines. Otherwise, dashed lines are shown. The size of the sample (n) used for each composite is shown above the corresponding composite.

In P1, the main MSLP response to ENSO is found to the west-southwest of the British Isles, with positive anomalies for La Niña and negative for El Niño. The position of this centre of MSLP anomalies agrees more with an EAP than the NAO (Fig. 3a, b). Moreover, the MSLP anomalies are considerably stronger in the El Niño composite. This could be due to a non-symmetric teleconnection, but also could arise from sampling uncertainty, since the La Niña composite features a larger sample size (10 years) than the El Niño one (7 years). Nevertheless, by performing a bootstrap resampling (see details in Methods), it is found that the MSLP response is indeed stronger for El Niño than for La Niña (pval = 0.09), suggesting the possibility of a non-symmetric teleconnection. The very weak MSLP response in La Niña in P1 leads to marginal impacts on precipitation, mainly in southern Iberia and parts of central Europe. For El Niño events, significant positive precipitation anomalies appear in the southwest of Europe, including most of Iberia, parts of France and the south of the British Isles. Additionally, positive precipitation anomalies appear in northern Fennoscandia. These anomalies can be explained by the advection of moist maritime air due to the position of the low-pressure systems. On the contrary, negative precipitation anomalies appear in parts of central Europe. While the impacts on precipitation are stronger, the impacts on temperature remain marginal for El Niño events in this period.

However, the largest MSLP response in P2 appears further north than in P1 (close to Iceland) and exhibits a more zonal orientation. This pattern resembles the NAO more than the EAP, in its positive phase for El Niño and negative phase for La Niña events (Fig. 3c, d). The centre of MSLP anomalies is stronger in La Niña than in El Niño, but this difference may be explained by sampling uncertainty. Unlike in the previous period, the impacts on T2m are significant over a large swathe of central-northeastern Europe, with particularly strong T2m anomalies over Fennoscandia, where they reach up to −1.5 °C for La Niña and +1.5 °C for El Niño events. The MSLP gradient present in NAE in La Niña events sets up a northerly flow that advects colder air masses into this part of Europe. Since these air masses advected from polar latitudes generally feature a limited moisture content, negative precipitation anomalies are favoured over some areas of Scandinavia and western Europe. In El Niño events, the +NAO MSLP pattern contributes to the advection of mild and moist air from the Atlantic to central-northern Europe, resulting in positive T2m anomalies. Positive precipitation anomalies are favoured in areas of Scandinavia and the British Isles.

Lastly, in P3, the main centre of MSLP anomalies associated with ENSO shifts back to the south (Fig. 3e, f), in a similar way as the Z200 field (Fig. 2b, isolines). Instead of the NAO, this MSLP pattern closely resembles the EAP, with the response in El Niño being significantly stronger than in La Niña (pval = 0.05). La Niña years are associated with a positive MSLP anomaly to the west of Ireland, which contributes to a northerly flow in western Europe, supporting colder than average conditions in southern Europe. This air flow leads to weaker-than-average westerly winds over western Europe, explaining the below-normal precipitation amounts in early winter in parts of the British Isles and Iberia. For El Niño, the MSLP anomaly is stronger, leading to the opposite response in temperature and precipitation. The position of the low-pressure anomaly favours the advection of moist and mild air from the Atlantic Ocean into western Europe, contributing to above-average temperatures in the southwest, where anomalies reach up to +1 °C. Besides, positive precipitation anomalies in early winter are associated to El Niño events in most of the Iberian Peninsula and the British Isles, as well as in several other parts of southwestern Europe.

Note that, even though P1 and P3 show somewhat similar large-scale North Atlantic circulation patterns in response to ENSO (in terms of MSLP and Z200), the surface impacts are not the same, particularly for T2m. In order to find a plausible explanation for this, we analysed the regressions of 850 hPa temperature (T850) and 850 hPa geopotential height (Z850) anomalies onto the ND Niño 3.4 index (Fig. S2). In P1, the area of negative Z850 anomalies to the west of the British Isles is somewhat tilted towards the southeast, while in P3 it is tilted towards the northeast. This change in the orientation of the Z850 anomalies implies that, for El Niño events, the air flow arriving at southwestern Europe comes from lower latitudes of the Atlantic in P3. Conversely, for La Niña events, the air flow comes from latitudes further north. Additionally, the SST in southwestern Europe is warmer for El Niño in P3 than in P1 (Fig. S3b). As a result, the air mass that is advected in southwestern Europe has higher T850 in El Niño and colder T850 in La Niña in P3 as compared to P1, probably explaining the stronger T2m anomalies in P3. Note also that the MSLP response in P3 is stronger for both El Niño and La Niña, which may result in a stronger advection of air masses into SWEU. On the contrary, the weaker advection in P1, particularly in La Niña, may lead to impacts in T2m and precipitation that are not statistically significant.

Regarding the T2m anomalies associated with ENSO, it is worth pointing out that Arctic sea ice anomalies are linked to ENSO^53,54,55, and these anomalies can exert significant impacts on the Eurasian climate by altering the atmospheric circulation. However, this influence is mainly found in late winter^56,57, whereas it is weak and lacks statistical significance in early winter⁵⁸. Hence, we consider that Arctic sea ice is not playing a relevant role in the T2m anomalies associated with ENSO found here, which appear to be mainly driven by the circulation anomalies induced by ENSO.

Impact of ENSO on early-winter temperature variability in Europe

Thus far, we have shown that ENSO is associated with significant atmospheric circulation anomalies over the North Atlantic in early winter, which results in significant correlation with precipitation and, especially, T2m. Furthermore, it is really worth highlighting that these impacts have apparently undergone notable changes throughout the last decades, supporting the hypothesis of a non-stationary teleconnection in ND. Since the surface impacts are more widespread for T2m than for precipitation, we now aim to understand the relevance of these impacts on European T2m. In particular, we aim to address the question: Are the impacts of the teleconnection relevant to the T2m variability of Europe? We therefore begin by estimating how much of the ND T2m variability in Europe is associated with ENSO. To this purpose, the leading mode of ND T2m variability is calculated separately for the southwestern Europe [10° W-15° E, 30° N-50° N] (SWEU) and northeastern Europe [3° W-50° E, 55° N-70° N] (NEEU) domains, by means of a principal component analysis (PCA)⁵⁹. The domains are shown with a red box in Fig. 4a and a green box in Fig. 4b, respectively. The PCA is performed separately for both regions due to their distinct climatological features and variability: NEEU shows cooler temperatures and a much higher variability compared with SWEU (Fig. S4). As a result of the PCA, the leading empirical orthogonal functions (EOF) together with their principal components (PC) are obtained. The results of the PCA show that the early-winter temperature variability of NEEU and SWEU is generally independent of each other, and thus confirm the convenience of performing the PCA separately. The leading EOF pattern in NEEU associates higher values of T2m anomalies than in SWEU in the three periods, denoting the higher variability that seasonal-mean temperatures show during ND in this region. Once the leading PC are obtained for both regions and for the three study periods, we correlate them to the ND Niño 3.4 index (values in grey boxes).

Fig. 4: Changes in temperature variability over Europe and their relation to ENSO.

Leading EOFs of early-winter temperature in NEEU (a, c, e) and SWEU (b, d, f), presented in the form of linear regression maps, together with their respective PCs time-series, for the periods P1 (a, b), P2 (c, d), and P3 (e, f). Only values significant at the 90% confidence level are shown in the EOFs. The percentage of the total variance (fvar) explained by each mode is indicated above the corresponding PC time series. In addition, the Pearson correlation coefficient (r) and its p-value (pval) between the PC and the ND Niño 3.4 index are displayed in the lower-right box on the PC time series.

In P1, the first mode in NEEU (Fig. 4a) consists of same-sign anomalies affecting almost the whole NEEU domain, being more intense to the north. This mode is not significantly correlated to ENSO. The leading mode in SWEU is also a monopole pattern of T2m anomalies (Fig. 4b) that does not show significant correlation with ENSO. In P2, however, we showed that ENSO is associated with significant ND T2m anomalies over most of central and northern Europe (Fig. 3c, d). Indeed, the ND Niño 3.4 index has positive (r = 0.60) and statistically significant correlation (pval = 0.024) with the first mode of temperature variability in NEEU, which explains up to 70.6 % of the total ND T2m variability (Fig. 4c). Comparing the ND Niño 3.4 index (dotted purple line in Fig. 4c) with the first principal component of early-winter temperature (blue line in Fig. 4c), warm anomalies in NEEU in P2 usually occur during El Niño events, whereas negative temperature anomalies are usually present during La Niña events, a result that could be observed in the composites in Fig. 3c, d. Also note how the spatial pattern of T2m anomalies associated with this mode is spatially wider than in P1, affecting other European regions outside the NEEU domain. As for SWEU in P2, its leading mode of ND T2m variability is not significantly correlated with ENSO. Finally, in P3, the results of the composite plots showed that ENSO is related to T2m over southern and western Europe (Fig. 3e, f). This relation is relevant to the T2m variability of SWEU, as its leading EOF explains up to 82.2% of the total ND T2m variability and shows significant positive correlation to the ND Niño 3.4 index (r = 0.58, pval = 0.012). Thus, since the late 1990s, positive early-winter temperature anomalies in SWEU tend to occur during El Niño events and negative anomalies during La Niña events (blue and dotted purple lines in Fig. 4f). Conversely, the leading mode in NEEU has no correlation with ENSO in P3. Note the larger spatial extension of the T2m anomalies associated with each mode, with EOF1 in NEEU also associating T2m anomalies outside the NEEU domain and the same holds for the SWEU domain. In fact, unlike in P1 and P2, the leading PCs of NEEU and SWEU are significantly correlated in P3 (r = 0.41, pval = 0.04).

These results show that the impacts of the ENSO teleconnection are quite relevant to the seasonal ND T2m variability over Europe, since it affects the leading mode of variability of the region that is affected by the teleconnection (NEEU in P2 and SWEU in P3).

Teleconnection mechanisms

It has been found how ENSO is significantly related with the ND T2m variability of NEEU in P2 and SWEU in P3, while in P1 the impacts on T2m are marginal. However, why does ENSO lead to such distinct impacts on T2m between these periods? To answer this question, we explore the mechanisms driving the response of the North Atlantic atmospheric circulation to ENSO in each of the periods. In order to identify the tropospheric mechanisms of this early-winter extratropical teleconnection, the source and direction of wave energy propagation at 200 hPa, described by the wave activity flux (WAF), is analysed together with the Rossby wave source (RWS)⁶⁰. In particular, the term of the RWS representing the advection of mean absolute vorticity by the anomalous divergent wind is evaluated. This term is referred to as tropical RWS (see Methods), and is frequently employed in the assessment of tropical-extratropical teleconnections⁶¹. Stratospheric pathways are not considered in this analysis, since they are active in late winter rather than in early winter^14,24. Considering that the response of the NAE atmospheric circulation to ENSO appears not to be equally strong for El Niño and for La Niña and not stationary, separate composites of the WAF are calculated for El Niño and La Niña events in the different periods.

In P1, the main tropical RWS anomalies associated with ENSO are found over East Asia, around 20-40° N, 120° W, the central tropical Pacific, as well as over the Gulf of Mexico and Caribbean Sea (Fig. 5a, b). However, no wave energy from any of these sources reaches the North Atlantic region in the La Niña composite, except possibly for a weak influence from the Gulf of Mexico and Caribbean Sea, explaining the very weak impacts on the North Atlantic atmospheric circulation. Conversely, the propagation of wave energy in the North Atlantic is stronger in the P1 El Niño composite, as shown by the larger magnitude of the WAF vectors in this region. According to the WAF vectors and Z200 field, it is possible that the EAP in the North Atlantic is favoured by some wave propagation from the eastern tropical Pacific, and from the subtropical North Atlantic. On the contrary, the wave train that originates over Eastern Asia does not make it into North America and therefore does not appear to contribute to the observed Z200 signal in the North Atlantic, as shown by the WAF vectors.

Fig. 5: Tropospheric mechanisms of the early-winter ENSO teleconnection to NAE.

Composites for La Niña (a, c, e) and El Niño (b, d, f) of ND Z200 anomalies (contour lines; dgpm) and wave activity flux (WAF; see Methods) (vectors; m²s⁻²). The anomalous Rossby wave source (RWS) term corresponding to the advection of absolute vorticity by the anomalous divergent wind at 200 hPa is shown with shading, only in the regions where it is significant at the 95% significance level. Results are plotted for the periods a, b P1, c, d P2 and e, f P3.

In P2, the regions with anomalous tropical RWS are broadly similar to P1. In the La Niña composite, the -NAO pattern appears to be mainly contributed by a Rossby wave train triggered from eastern North America, from where the WAF vectors that reach the northern centre of the NAO emanate. This is probably favoured by the anomalous RWS over North America and the Caribbean Sea, related to the Gulf of Mexico-Caribbean Sea wave source^10,14. Again, there does not appear to be any significant influence in the North Atlantic from the Indian Ocean or East Asia, as suggested by the WAF vectors in the La Niña composite. In the case of El Niño events in P2, however, the +NAO signal in the North Atlantic is favoured by the propagation of Rossby waves from the tropical Pacific and from East Asia. The WAF vectors indicate that stationary Rossby waves emanate from two regions in the tropical Pacific Ocean: one near 150° W and another one near 120° W. Unlike in the La Niña case, the influence from the East Asia wave source is clear in the El Niño composite. In this way, the Rossby wave energy associated with this source propagates northeastward, reaching North America. From there, it appears to interfere with the wave propagation from the tropical Pacific sources, finally reaching the North Atlantic region. Therefore, it is likely that combined effect from the tropical Pacific and East Asia wave trains lead to the +NAO signal in the North Atlantic in the El Niño events in P2. Hence, unlike in P1, the sources over the Pacific Ocean and East Asia appear to exert a clear influence on the Z200 signal in the North Atlantic in P2.

Conversely, the contribution from the East Asian wave source to the NAE atmospheric circulation associated with ENSO is notably weaker in La Niña events in P3 (Fig. 5e). Even though a wave train emanates from there, it tilts southward and does not make it further east through North America. Instead, the positive Z200 anomaly in the North Atlantic (which resembles the negative phase of the EAP) seems to be explained by the propagation of wave energy from the eastern tropical Pacific and the Gulf of Mexico-Caribbean Sea area. The El Niño composite in P3 (Fig. 5f), however, reveals a strong Rossby wave train from East Asia, which reaches western North America. The associated wave energy then weakens and heads to the south, where it converges and probably interferes with strong wave energy coming from the eastern tropical Pacific Ocean. The wave energy continues to propagate eastward and then curves when reaching the North Atlantic. Furthermore, the wave pattern featured on the Z200 anomaly field in the North Atlantic, with a positive centre close to (30° N, 60° W), and the associated WAF vectors, resembles the pattern of wave propagation coming from the Caribbean and tropical Atlantic found in previous studies^10,14. In fact, a remarkable strengthening of the anomalous RWS is observed over this region with respect to the previous periods. This signal is not so clear for La Niña events in P3, since no significant Z200 anomalies close to (30° N, 60° W) are found and the magnitude of the tropical RWS is weaker, suggesting that the enhanced influence from the Gulf of Mexico and Caribbean Sea precipitation dipole after the late 1990s³⁹ principally occurs in El Niño years. In summary, in El Niño events in P3, the combined effect of wave energy originating from the eastern tropical Pacific, the Caribbean-tropical Atlantic and, to a lesser extent, the Eastern Asia sources likely explains the observed +EAP signal in the North Atlantic.

Overall, for the periods analysed, we identify sources of wave energy over the Pacific Ocean, East Asia, and the Caribbean Sea and the tropical North Atlantic region. These are the source regions that have been identified in the literature for the ENSO early winter teleconnection to NAE^14,28. However, the influence from the East Asia wave train in the North Atlantic atmospheric circulation response to ENSO is clear in El Niño composites in P2 and P3, but not so in La Niña. Furthermore, the source over the eastern tropical Pacific Ocean (near 120° W) generally shows stronger activity in the El Niño composites, and the influence from the wave energy coming from the Caribbean Sea and the tropical Atlantic is clearer in P3, primarily in El Niño events. Thus, the relative activity shown by these wave source regions and the particular way in which their associated wave trains propagate towards the extratropics and interact with each other, ultimately determine the observed impacts of ENSO on the atmospheric circulation in the North Atlantic. A possible explanation for the different propagation patterns of the wave trains will be explored in the Discussion.

Oceanic sources of predictability of early-winter temperature in Europe

Given that ENSO exerts an important influence on the European ND T2m variability in the last decades, we next aim to gain insight into the ND T2m predictability that could be attained from the tropical SST anomalies. Specifically, predictability is analysed for the leading mode of ND T2m variability in NEEU for P2 and in SWEU for P3, since it was shown that these modes are significantly correlated to ENSO. To analyse the predictability, the regression of the SST anomalies onto the corresponding PC is computed. This is done for the contemporaneous (October-November-December; Fig.6c), one season-lag (July-August-September; Fig. 6b) and two-seasons lag (April-May-June; Fig. 6a) SST anomalies.

Fig. 6: Oceanic sources of early-winter temperature predictability in Europe.

Upper panel: regression map of SST anomalies in a AMJ, b JAS and c OND onto the leading principal component of ND T2m variability for NEEU in P2. Lower panel: regression map of SST anomalies in d AMJ, e JAS and f OND onto the leading principal component of ND T2m variability for SWEU in P3. Only values at the 90% significance level or higher are shown.

The leading mode of ND T2m variability in NEEU is significantly correlated to the ND Niño 3.4 index in P2, but the regression of the SST anomalies in April-May-June onto the PC1 time series does not show any significant values in the tropics (Fig. 6a, top), indicating that this mode lacks predictability from the SST in these months. However, when the July-August-September SST anomalies are employed, significant warm anomalies emerge in the central equatorial Pacific (Fig. 6b, top), which intensify and extend to the eastern equatorial Pacific in the late-autumn and early-winter, with the largest regression coefficients located over the central equatorial Pacific (Fig. 6c, top). This result suggests that developing ENSO events, particularly those with an onset over the central Pacific, have an influence on the ND PC1 of T2m in NEEU, with predictability starting during the summer.

As for the regression onto the leading PC for SWEU in P3 (Fig. 6a, bottom), a negative SST anomaly signal is present over the tropical and subtropical North Atlantic in April-May-June, with an El Niño signal emerging throughout the summer months (Fig. 6b, bottom). Unlike in the case of NEEU, the SST anomalies extend both through the central and eastern equatorial Pacific, with the strongest regression values located in the eastern equatorial Pacific. These anomalies intensify as the late-autumn and early-winter seasons progress, with the strongest SST anomalies located over the central-eastern equatorial Pacific. Hence, in P3, the ND PC1 of T2m in SWEU has predictability coming from the ENSO region and this predictability starts to appear in the summer, with developing eastern-based ENSO events supporting the positive phase of the PC1 (i.e., warm ND T2m anomalies) for El Niño events and the negative phase (i.e., cold ND T2m anomalies) for La Niña events. However, it is worth pointing out that significant negative SST anomalies are present over the tropical and subtropical North Atlantic before the boreal summer, especially in P3. These anomalies, of opposite sign to the ones present over the ENSO region, have been linked to the onset of ENSO events⁶². Thus, the tropical and subtropical North Atlantic SST could also serve as a source of predictability, with longer lead times than ENSO.

A relevant question that still needs to be addressed is whether the oceanic sources of predictability of ND T2m, identified using observational and reanalysis datasets, are accurately captured by the state-of-the-art dynamical seasonal prediction models. For this to hold, a successful reproduction of the teleconnection is essential. Thus, in the following analysis, we evaluate the SEAS5 dynamical seasonal prediction model from the European Centre for Medium-Range Weather Forecasts (ECMWF)⁶³ (see Methods). The choice of SEAS5 over other operational seasonal forecasting systems mainly resides in its long period of retrospective forecasts (or hindcasts), which starts in 1981. Given that the teleconnection under analysis exhibits non-stationarity, having a sufficiently long hindcast period is essential. Thus, the 42-year period in the model allows us to assess how the model reproduces the observed non-stationarity of the teleconnection and the potential impacts of the non-stationarity on the forecast skill. Our analysis in SEAS5 is first conducted for P3, since it is the only period that is fully covered by the model hindcast, and features a robust teleconnection to the EAP in the observations.

SEAS5 early-winter temperature skill in P3

From the previous analysis, using observational and reanalysis datasets, a significant impact of ENSO on ND T2m in SWEU was found in P3. When examining the SEAS5 model, the prediction of ND T2m from the ensemble mean exhibits significant skill in several European regions, but particularly over SWEU (Fig. 7, top panel). Moderate skill is found as early as in the August initialisation (Fig. 7a), with values of the anomaly correlation coefficient (ACC) between 0.4 and 0.6 over parts of the Iberian Peninsula, France and Fennoscandia. Skill then decreases for the forecasts initialised in September (Fig. 7b) in Iberia, meanwhile significant positive ACC values of 0.4–0.6 extend over central-western Europe. The spatial pattern of skill for predicting early-winter T2m anomalies remains very similar in the October initialisation, but with overall slightly lower values in central-western Europe and slightly higher ones in parts of Iberia (Fig. 7c). Thus, although the model’s ability to accurately predict ND T2m anomalies varies depending on the initialisation, it is reasonably good (ACC 0.4-0.6) in parts of SWEU in P3. This moderate skill is very likely associated with the skill in the prediction of the EAP in early-winter seasonal forecasts^25,40.

Fig. 7: SEAS5 skill for early-winter temperature.

Forecast skill, expressed in terms of the anomaly correlation coefficient (ACC) between the SEAS5 ensemble mean and the E-OBS database early-winter T2m anomalies for the period P3 and for the a August, b September and c October initialisations. Hatching represents areas where the skill is significant at the 95% confidence level. Regression maps of the ND SST anomaly onto the SWEU ND PC1 for SEAS5 d August, e September and f October initialisations. Only values at the 90% significance level or higher are shown.

To confirm that SEAS5 skill in SWEU in P3 comes from ENSO, we perform a PCA on the ND T2m anomalies over the SWEU domain. Areas not over land were not considered so that the domain matches exactly the one used in the observational database (E-OBS). The model’s EOF1 consists of the same-sign anomalies throughout the domain, with a similar spatial pattern as E-OBS and overall weaker amplitude, especially with increasing forecast lead time, due to it being an ensemble mean (Fig. S5). In order to identify the SST anomaly pattern associated with EOF1, linear regressions onto the model’s PC1 are computed, obtaining the patterns shown in Fig. 7b. Despite some differences among the initialisations, the common feature is that the highest linear regression coefficients are found over the equatorial Pacific, with stronger SST anomalies in the September initialisation. Positive SST anomalies also appear over the Indian Ocean. Hence, in SEAS5, ND T2m variability in SWEU is partly driven by ENSO and the IOD, which contribute to skill for predicting ND T2m in SWEU. Comparing the regression patterns in SEAS5 with those obtained using observational datasets (Fig. S6), the spatial distribution of tropical SST anomalies is fairly similar. In the light of these results, SEAS5 appears to be reproducing the teleconnection between ENSO and ND T2m in SWEU in P3 remarkably well.

Late 1990s teleconnection shift in SEAS5

As found in the observational analysis, the ENSO early-winter teleconnection to NAE underwent a notable shift in the late 1990s, with the impacts on European T2m being remarkably different before and after the late 1990s (see Fig. 3). Considering that a significant part of the skill in seasonal forecasts results from an accurate representation of the ENSO teleconnections, it is worth examining whether the change in the observed early-winter teleconnection has had an impact on the skill of SEAS5 forecasts. To address this, we first need to evaluate how the pattern of ENSO impacts in SEAS5 resembles that from observations. This needs to be done separately for the periods P2 (ENSO-NAO teleconnection, with impacts on T2m over NEEU) and for P3 (ENSO-EAP teleconnection, with impacts on T2m over SWEU). The relatively long hindcast period, plus the 25-member ensemble realisations in SEAS5, allows us to explore this with sufficient robustness. To this purpose, the regression of ND T2m anomalies onto the ND Niño 3.4 index is computed for the periods 1981-1996 (which is the subset of period P2 included in SEAS5) and P3, in observations and in SEAS5 October initialisation. To allow a more straightforward comparison between the model and observations, the observed ND Niño 3.4 index used in this analysis is calculated in the same way as in SEAS5, which implies using only ND data for the common period 1981-2022. Additionally, ND T2m anomalies in observations are now calculated using data for the period 1981-2022. In the model, regressions are calculated by concatenating the data from the 25 ensemble members.

In 1981-1996, the impacts of ENSO on ND T2m in the observations are mainly focused over central-northeastern Europe (Fig. 8a, top), with regression values close to +1° C. However, the pattern in SEAS5 is notably different and apparently the model fails to reproduce the observed pattern. The model only captures significant T2m anomalies mainly in parts of SWEU, and with a comparatively very weak magnitude (Fig. 8b). Nevertheless, one could well consider that the differences between the model and the observations may stem from sampling uncertainty or internal variability, due to the much smaller sample size in the observations. The sample size of the observations is n = 16 (16 years), whereas the sample used for the regression in SEAS5 has size n = 400 (16 years x 25 ensemble members). Thus, in order to evaluate the sampling uncertainty and internal variability when comparing models and observations, we generate sampled realisations in SEAS5 by randomly selecting one ensemble member for each year of initialisation. This procedure is repeated 1000 times to construct a set of 1000 sampled realisations in the model, which are all equally plausible. In each of these, the regression of ND T2m anomalies onto the Niño 3.4 index is computed, thereby yielding a set of 1000 plausible teleconnection patterns within the model. The distribution of the possible teleconnection impacts in the model is shown in the histogram in Fig. 8c, corresponding to the spatially-averaged regression coefficient over NEEU (where the strongest impacts are found in the observations). Ideally, the observed pattern (vertical red line) should fall somewhere in the range of these possible model outcomes. However, it falls in the right tail of the distribution, suggesting that it is very unlikely that the differences between SEAS5 and the observations arise from sampling errors or internal variability. Strikingly, the model displays moderate skill in this period over northern Europe, in parts where the teleconnection is not successfully reproduced (Fig. 8d). It is thus feasible to consider that ND T2m forecast skill in this period over the cited regions is not coming from ENSO. In the late 1990s, the teleconnection underwent a pronounced shift, and the strongest impacts on T2m in observations are found in SWEU thereafter (Fig. 8e). The spatial pattern of teleconnection impacts in SEAS5 is certainly better reproduced in this period, with statistically significant positive T2m anomalies also found in SWEU, although again with a notably weaker magnitude than in observations (Fig. 8f). Analysing the distribution of plausible teleconnections in SEAS5 in this period over SWEU (Fig. 8g), we find that, while positive values are prevalent, the observation lies in the far right tail of the distribution, nearly ruling out the possibility that sampling or internal variability are mainly explaining these differences. As a consequence of the more accurate reproduction of the teleconnection pattern in the model in P3, forecast skill is significantly enhanced over parts affected by the teleconnection, in SWEU (Fig. 8h). Similar results hold for the August and September initialisations (Figs. S7 and S8, respectively), where significant changes in the modelled teleconnection and in the regions with higher forecast skill are also found. Thus, a very remarkable result here is that forecast skill may vary in time as a result of changes in the teleconnection and how the teleconnection is simulated in the model. For this reason, thorough consideration needs to be taken in the assessment of forecast skill and their sources in seasonal prediction models, in particular to avoid mixing different signals, which will be discussed later.

Fig. 8: ENSO early-winter teleconnection in SEAS5 October initialisation.

Linear regression coefficients of ND T2m anomaly onto ND Niño 3.4 index in the a, e E-OBS observational database and b, f SEAS5 (member-concatenated) October initialisation. Only values at the 90% significance level or higher are shown. c, g Normalised histogram showing the distribution of spatially-averaged regression coefficients over c NEEU and d SWEU in the set of 1000 SEAS5 plausible realisations. The vertical red line shows the E-OBS value. d, h SEAS5 ACC for predicting ND T2m anomaly in the October initialisation. Hatching represents significant skill at the 95% confidence level. Results are shown for the periods 1981–1996 (top row) and P3 (1997–2022; bottom row). The NEEU and SWEU are shown with a red box in a and a green box in e, respectively.

As shown, the magnitude of the impacts of ENSO on T2m are significantly underestimated in SEAS5, and the spatial pattern is not well reproduced in 1981-1996. This could be explained by too weak ENSO-induced circulation anomalies in the North Atlantic in SEAS5, and possibly to a failure to reproduce the observed ENSO-induced NAO pattern in 1981-1996. To test this, we compare the regression maps of MSLP anomalies onto the Niño 3.4 index between SEAS5 and ERA5 shown in Fig. 9. In 1981-1996, the MSLP anomalies associated with ENSO show a pattern that resembles the NAO in ERA5 (Fig. 9a). In contrast, the pattern in SEAS5 shows very weak MSLP anomalies, with the centre of negative anomalies further south and with a less zonal orientation than in ERA5 (Fig. 9b). However, valuable insights can be gained when analysing the set of 1000 plausible realisations. Most of these sampled realisations underestimate the strength of the observed NAO pattern, and its resulting impacts on T2m in NEEU (Fig. 9c). However, those realisations that exhibit a stronger NAO pattern, closer to ERA5, generally show stronger ENSO impacts on T2m in NEEU (r = 0.74, pval < 0.001). This result confirms that the SEAS5 failure to reproduce the impacts of ENSO on T2m over NEEU in 1981-1996 is likely explained by its failure to reproduce the NAO pattern associated with ENSO in this period. Moreover, those realisations that more accurately represent the impacts of ENSO on SLP and T2m generally exhibit higher forecast skill of T2m (r = 0.78, pval < 0.001), confirming the central role of the ENSO teleconnection on the skill of seasonal forecasts. In 1997-2022, the MSLP pattern closely resembles an EAP in ERA5 (Fig. 9d). The spatial pattern of MSLP anomalies in SEAS5, especially regarding the position of the negative centre of MSLP anomalies to the west of the British Isles, is better reproduced in this period, although again with a significant underestimation of the magnitude of the anomalies (Fig. 9e). There are virtually no realisations showing the observed magnitude of MSLP anomalies to the west of the British Isles, and consequently the observed magnitude of T2m anomalies in SWEU (Fig. 9f), suggesting that the model-observations discrepancies are unlikely to be explained by sampling uncertainty and/or internal variability. Once again, we note that those realisations yielding a stronger EAP, closer to ERA5, generally show stronger impacts of ENSO on T2m in SWEU (r = −0.72, pval < 0.001), which subsequently tend to exhibit higher prediction skill for ND T2m over SWEU (r = 0.59, pval < 0.001). Overall, these results suggest that a more accurate representation of the impacts of ENSO on the North Atlantic atmospheric circulation could substantially enhance seasonal forecast skill of the surface climate in parts of Europe.

Fig. 9: Underestimation of the ENSO teleconnection to NAE in SEAS5.

Regression map of MSLP anomalies onto the Niño 3.4 index in a, d ERA5 and (b, e) SEAS5 October initialisation (member-concatenated). c Scatter plot of the NAO index, defined as the spatial average of the regression values over the blue box minus the regression values over the red box in a, and the spatial average of the regression of T2m anomalies onto the Niño 3.4 index over NEEU, for all the SEAS5 plausible realisations. The colour of the dots represents the ACC of the T2m over NEEU. f Scatter plots of the EA index, computed as the spatial average of the regression values over the purple box in d, and the spatial average of the regression of T2m anomalies onto the Niño 3.4 index in SWEU, for all the SEAS5 plausible realisations. The colour of the dots represents the ACC of the T2m over SWEU. The green star in (c) and (f) represents the observations. Results are shown for the periods (a, b, c) 1981-1996 and (d, e, f) 1997-2022.

Discussion

In the present study, the ENSO early-winter teleconnection to NAE has been analysed within a non-stationary framework, seeking for a better assessment of seasonal predictability.

Our results suggest that the ENSO early-winter teleconnection to the North Atlantic exhibits notable non-stationary features. Previous studies showed that, in early winter, ENSO is associated with the EAP in the North Atlantic^14,15. However, by analysing this relationship in different 20th century reanalysis and observational datasets, it was found that it was very weak in the first half of the 20th century, while it underwent a considerable strengthening and became statistically significant from the 1950-1960s, with a weakening between the late 1970s and the late 1990s. In order to avoid uncertainties in the observational datasets related to the limited number of observations earlier in the 20th century, we focused on the multidecadal variability of the teleconnection in the period 1950-2022. Throughout this period, different impacts of ENSO on the North Atlantic atmospheric circulation were found, with a NAO pattern between the late 1970s and the late 1990s, and an EAP between the 1950s and late 1970s, and from the late 1990s. Through a bootstrap resampling, we showed that these differences in the teleconnection patterns between the periods are very unlikely to be explained by sampling uncertainties. Moreover, these different impacts of ENSO on the North Atlantic atmospheric circulation have resulted in distinct impacts of ENSO on the surface European climate. The propagation of stationary Rossby waves from several source regions contributes to the observed ENSO signal over the North Atlantic, including India and East Asia, the tropical Pacific Ocean and the Caribbean-tropical Atlantic region, in agreement with previous studies^14,64. However, the observed contributions from the India-East Asia region and the Pacific Ocean are generally larger in El Niño than in La Niña, and the influence of the Caribbean and tropical Atlantic region is enhanced in P3³⁹, particularly in El Niño events. These changes in the tropospheric pathways of the teleconnection suggest that the observed non-stationarity has indeed a physical origin, and is not mainly explained as a result of stochastic noise.

Even though this study did not aim to examine the physical processes underlying the multidecadal variability of the teleconnection, it is acknowledged as an important subject for future research. In particular, from the 1950s–1960s, we note that the ENSO teleconnection patterns differ during the different PDO phases, but the possible role of the PDO in the ENSO-NAE teleconnection in early winter needs to be investigated. The mechanism we hypothesise to explain the observed multidecadal variability of the teleconnection in the last decades is that the different Pacific Ocean background states, related to changes in the PDO regime, can lead to changes in the properties of ENSO^65,66 and in the upper-level flow⁶⁷, modifying the sources of tropospheric Rossby wave trains and their propagation towards the extratropics. This ultimately results in different impacts of ENSO on NAE³⁸. Our observational analyses appear to support this hypothesis, since the patterns of stationary Rossby wave propagation to NAE exhibit differences between the periods considered (Fig. 5). The differences in the propagation of the wave energy could be explained by significant differences in the climatological upper-level flow (Fig. S9d), particularly over East Asia and the Pacific Ocean, where wave sources exist. However, this hypothesis regarding a possible modulation from the PDO needs to be tested, and is intended to be examined in future work by designing and running sensitivity experiments, which would allow to properly isolate the effects of the PDO.

Nevertheless, it should be noted that this hypothesis does not necessarily imply that the teleconnection will be exactly the same under periods with the same PDO phase. As an example, both P1 and P3 feature a -PDO regime, but the ENSO impact on the North Atlantic atmospheric circulation is slightly different (e.g., Figs. S2, S3). This suggests that, apart from the PDO, other agents may also be playing a role in shaping up the teleconnection pattern. Taking into account that several ENSO teleconnections are expected to change under a warmer climate^32,33,34, and the remarkable warming of global SST in P3 with respect to P1 (Fig. 1), it is feasible to consider that global warming could, to some extent, explain the differences in the teleconnection between P1 and P3. Moreover, P3 shows significant changes in the upper-level flow with respect to P1 over several regions (Fig. S9b), which could explain some of the differences found in the tropospheric pathways of the teleconnection between P1 and P3 (Fig. 5). Furthermore, the role of the AMV also needs to be explored. In a similar way to the PDO, the AMV can excite an atmospheric Rossby wave train^68,69,70 that can impact the background state. In fact, the AMO has been shown to affect ENSO teleconnections to Europe, though mainly in spring and summer^37,38. In this sense, long pre-industrial control simulations from CMIP6 models could be used to confirm the non-stationarity of the teleconnection and better understand the roles of the PDO and/or AMV. Moreover, analysis of Pacific and Atlantic Pacemaker experiments would allow a better understanding of the mechanisms underlying the multidecadal variability of the teleconnection. Particularly, targeted sensitivity experiments, in which the effects of each of these potential drivers (PDO, AMV, global warming) can be properly isolated, would provide a very robust framework to disentangle their relative roles and therefore to better understand the non-stationarity of the teleconnection. Overall, this underscores that there is still a substantial amount of work required to fully understand the multidecadal variability of the ENSO early-winter teleconnection to NAE.

Besides, the results from this study have relevant implications for the assessment of early-winter seasonal predictability in Europe. SST anomalies over the ENSO region in the summer serve as predictors of the leading mode of ND T2m variability in southwestern Europe in P3. SEAS5, a state-of-the-art dynamical seasonal prediction model, accurately captures this source of predictability. However, significant discrepancies emerged when comparing the impacts of the ENSO teleconnection in the model with those of the observations. While SEAS5 reasonably captures the spatial pattern of the impacts of the teleconnection after the late 1990s (ENSO-EAP teleconnection) (Figs. 8f, 9e), it failed to reproduce the observed NAO pattern before the late 1990s (Fig. 9b) and its resulting impacts on T2m over Europe (Fig. 8b). In addition, for both periods, the magnitude of the ENSO-associated anomalies in NAE is significantly weaker than in the observations. These results entail significant consequences for the skill of its seasonal forecasts. In particular, the regions with higher forecast skill of ND T2m before and after the late 1990s vary substantially (Fig. 8d,h). This result implies that assessing the skill of a seasonal prediction model using the entire hindcast period might be masking potential sources of skill, which are more clearly revealed during certain periods. Certainly, using all the hindcast years gives a more statistically robust assessment of the skill. However, we showed that in the case of early winter, this may be problematic, as it would involve the mixing of two periods (P2 and P3) with distinct teleconnection patterns and forecast skill. Overall, this would yield a weaker and somewhat unrealistic picture of the model’s performance. We therefore recommend avoiding this mixing of signals when it comes to evaluating the skill of operational seasonal forecasts. It is worth noting that the aforementioned changes in skill probably could not have been identified without a long hindcast period.

One may well consider that the weaker teleconnection impacts in the SEAS5 model compared to the observations found in Fig. 8 reside in the much larger sample size in the model. However, constructing 1000 sampled realisations allowed us to obtain a set of 1000 plausible teleconnection patterns within the model, which provides a more robust framework to assess the model’s performance. We showed that the observations fall as an outlier, in the far tail of the model distribution. This is shown to occur both in P2 and in P3, highlighting that the impacts of the teleconnection within the model are systematically too weak, and very unlikely to be attributable to sampling uncertainty in the observations or to internal variability. This also suggests that the too weak teleconnection patterns in state-of-the-art seasonal models reported in recent works^25,40,41 come down to deficiencies in accurately reproducing certain aspects of the teleconnection in both periods.

The sources of model deficiencies that contribute to the underestimation of the ENSO impacts on NAE in early winter are only beginning to be understood and warrant further investigation in the future. Particularly, how the models reproduce the tropical convection patterns, the sources of Rossby wave propagation, and the jet stream configuration are fundamental aspects to analyse when it comes to extratropical teleconnections. Recent works have identified deficiencies involving missing eddy-feedback^41,71 and jet biases in the North Atlantic⁴². Identifying and fixing these deficiencies for future model versions is key to turn the potential predictability found in the observations into actual predictability in the real-time seasonal forecasts from dynamical models. Our results indeed suggest that these models can notably benefit from a more realistic representation of the ENSO teleconnection, yielding substantially more accurate seasonal forecasts (Fig. 9c, f). This would ultimately improve the quality of climate services provided to end users.

Methods

Definition of indices

The Niño indices describe the SST variability over different regions of the tropical Pacific and are frequently used to describe the strength and variability of ENSO events. In this study, we use the standardised Niño 3.4 index, which is representative of both the central and eastern equatorial Pacific and captures the two main ENSO flavours. It is defined as the area average of linearly detrended SST anomalies (relative to the period 1950-2022) in the region 170° W-120° W, 5° S-5° N. ND SST anomaly data are used for the computation of this index, and thus we refer to it as the ND Niño 3.4 index. In SEAS5, anomalies are calculated relative to the period 1981–2022. Years in which the ND Niño 3.4 index ≥ 0.5 std are classified as El Niño, whereas those having ND Niño 3.4 ≤ −0.5 std are classified as La Niña years.

The Pacific Decadal Oscillation (PDO) is defined as the leading EOF of SST anomaly variability in the extratropical North Pacific Ocean (120° E-100° W, 20° N-70° N). The associated principal component is referred to as the PDO Index⁷².

The Atlantic Multidecadal Variability (AMV) index is defined as the area-averaged detrended low-pass filtered SST anomalies in the North Atlantic north of the equator (80° W-0°, 0° -60° N)⁷³.

The global SST index, used as an indicator of the global warming trend in the SST, is calculated from yearly-averaged global SST anomalies, excluding the area northward of 60° N and southward of 45° S⁷⁴.

The East Atlantic index (EA) is defined as the principal component time series associated with the second empirical orthogonal function (EOF) of sea-level pressure anomalies in the North Atlantic region (90° W-40° E, 20° N-80° N). The EA index is standardised.

Observational and reanalysis datasets

The E-OBS dataset⁷⁵ v28.0e from the European Climate Assessment & Dataset is employed in this study to analyse atmospheric surface fields in Europe. This dataset provides daily mean surface air temperature and total precipitation data based on in-situ observations, interpolated to a regular 0.25° horizontal resolution grid, spanning the period 1950-2022. It consists of an ensemble product with 100 members, and we herein make use of the ensemble mean as a best estimate of the observed fields. For atmospheric fields on pressure levels, the European Centre for Medium Range Weather Forecasts (ECMWF) fifth generation reanalysis, ERA5, is utilised⁷⁶. Monthly-averaged data are retrieved from the Copernicus Climate Data Store (CDS) on a regular 0.25° horizontal resolution grid. As for sea-surface temperature (SST) data, the Met Office Hadley Centre’s sea ice and sea-surface temperature dataset, HadISST1, is employed⁷⁷. It provides monthly averaged SST data based on observations since the late 19th century, interpolated to a regular grid with 1° horizontal resolution.

In order to analyse the ENSO-EAP relationship throughout the 20th century, different 20th-century reanalysis and observational datasets are employed. These include JRA-3Q reanalysis, from the Japan Meteorological Agency (JMA)⁷⁸, CERA-20C reanalysis from ECMWF⁴⁵, 20CRv3 reanalysis from the National Oceanic and Atmospheric Administration (NOAA)⁷⁹, the Cooperative Institute for Research in Environmental Sciences (CIRES), and the U.S. Department of Energy (DOE), and the HadSLP gridded observational dataset from the Met Office Hadley Centre⁸⁰.

Data pre-processing

For observational, reanalysis and model data, different temporal aggregations are calculated as needed. The study focuses on early-winter, thus the aggregation used most frequently here is November-December (ND) for most of the fields, although several 3-month means are additionally calculated for SST data. Then, anomalies are calculated for each aggregation by removing their corresponding climatological average of the study period 1950-2022. In order to avoid the influence of long-term trends associated with global warming, the linear trend is removed. Additionally, a Butterworth high-pass filter⁸¹, with a cutoff frequency of 7 years⁻¹ is applied to the data, in order to amplify the high-frequency variability related to the ENSO phenomenon.

Analysis of teleconnection impacts

The influence of ENSO on the climate variability of NAE is assessed by means of a linear regression analysis between the El Niño index and the anomalous field (e.g., T2m, MSLP, Z200...). This analysis is performed point by point throughout the entire grid, and the results are displayed in the form of regression maps, in which the regression coefficient of the linear fit is shown for each of the grid points. Since the El Niño index is standardised, these maps represent how the spatial structure of the anomalies of the field changes per standard deviation of the index.

Analysis of tropospheric pathways

The wave activity Flux (WAF) is calculated in order to diagnose the propagation of stationary tropospheric Rossby wave activity. Takaya and Nakamura derived the zonal and meridional components of the WAF vector for quasigeostrophic eddies on a zonally varying basic flow in spherical coordinates⁸²:

$$W=\frac{p\cos \varphi }{2| U| }\left(\begin{array}{r}\frac{U}{{a}^{2}{\cos }^{2}\varphi }\left[{\left(\frac{\partial {\psi }^{{\prime} }}{\partial \lambda }\right)}^{2}-{\psi }^{{\prime} }\frac{{\partial }^{2}{\psi }^{{\prime} }}{\partial {\lambda }^{2}}\right]+\frac{V}{{a}^{2}\cos \varphi }\left[\frac{\partial {\psi }^{{\prime} }}{\partial \lambda }\frac{\partial {\psi }^{{\prime} }}{\partial \varphi }-{\psi }^{{\prime} }\frac{{\partial }^{2}{\psi }^{{\prime} }}{\partial \lambda \partial \varphi }\right]\\ \frac{U}{{a}^{2}\cos \varphi }\left[\frac{\partial {\psi }^{{\prime} }}{\partial \lambda }\frac{\partial {\psi }^{{\prime} }}{\partial \varphi }-{\psi }^{{\prime} }\frac{{\partial }^{2}{\psi }^{{\prime} }}{\partial \lambda \partial \varphi }\right]+\frac{V}{{a}^{2}}\left[{\left(\frac{\partial {\psi }^{{\prime} }}{\partial \varphi }\right)}^{2}-{\psi }^{{\prime} }\frac{{\partial }^{2}{\psi }^{{\prime} }}{\partial {\varphi }^{2}}\right]\end{array}\right)$$

(1)

where φ and λ are the latitude and longitude, p is the pressure normalised by 1000 hPa, a is the Earth’s radius, ∣U∣, U and V represent the climatological (or basic state) magnitude of the horizontal wind, zonal and meridional component of the wind, respectively, and ${\psi }^{{\prime} }$ represents the geostrophic streamfunction anomaly or perturbation. The WAF defined this way is a horizontal vector, and its direction is parallel to the local group velocity of the stationary Rossby wave packet. Since φ tends to 0 as we approach the equator, the WAF is only computed and shown for latitudes higher than 20°.

The Rossby wave source (RWS) is derived from the barotropic vorticity equation in pressure coordinates⁶⁰. In its linear form, the Rossby wave source anomaly ($RWS^{\prime}$) is defined as⁶¹:

$$RW{S}^{{\prime} }=-{\vec{{v}_{\chi }}}^{{\prime} }\cdot \nabla \overline{\zeta }-\overline{\zeta }\nabla \cdot {\vec{{v}_{\chi }}}^{{\prime} },$$

(2)

where $\overrightarrow{{v}_{\chi }}$ is the divergent component of the horizontal wind vector and ζ the absolute vorticity. The overbars and primes denote the climatological mean and perturbation components, respectively. The first term on the right-hand side of Eq. (2) represents the advection of mean absolute vorticity by the anomalous divergent wind. This term, referred to as tropical Rossby wave source, is used in this paper when analysing the tropospheric pathways of the teleconnection, given its main contribution in the excitation of Rossby wave trains in ENSO extratropical teleconnections.

Model data

SEAS5 is the latest generation of ECMWF’s seasonal forecasting system, and has been producing real-time seasonal forecasts since November 2017⁶³. The system includes a global coupled ocean-atmosphere general circulation model. The ocean model is the Nucleus for European Modelling of the Ocean (NEMO) version 3.4.1, with 0.25° ORCA grid resolution and 75 vertical levels. The Louvain-la-Neuve sea ice model (LIM2)⁸³ is also included in the system. The atmospheric component is the ECMWF Integrated Forecasting System (IFS) version 43r1, with the spectral horizontal resolution being T319, 91 vertical levels and with the model top at 0.01 hPa. Forecasts are initialised on the first day of each month and reach up to 7 months lead time. In order to assess the model biases, SEAS5 includes a re-forecast period from 1981 to 2016, while the real-time forecast period is from 2017 onwards. The re-forecasts consist of a 25-member ensemble, with the ocean and sea ice initial conditions being provided by the ECMWF Ocean ReAnalysis System 5 (ORAS5) and the atmospheric initial conditions coming from the ERA-Interim reanalysis⁸⁴, while the real-time forecasts have a larger ensemble size (51 members), with ECMWF ocean analysis system OCEAN5⁸⁵ and ECMWF operational analyses providing the initial conditions for the ocean and sea ice, and for the atmosphere, respectively. For the analysis carried out in this study, the August, September, and October initialisations are used. Since the model’s ability to reproduce the teleconnection is assessed for early-winter (ND), a minimum forecast lead time of 1 month is imposed to avoid the influence of the atmosphere's initial conditions in the forecast of ND; thus, the November initialisation is not considered. Moreover, the re-forecasts are used together with the real-time forecasts, which allows us to assess the model’s performance during the period 1981–2022. Since the ensemble size is different for re-forecasts (25) and real-time forecasts (51), 25 members are used when combining both, except for the August initialisation, in which the re-forecast ensemble includes 51 members, and therefore, the 51 members are used. As in the observational and reanalysis datasets, the linear trend has been removed from the model’s fields to filter out the influence of global warming trends.

Statistical significance

The statistical significance of results was estimated by means of a bootstrap resampling with 1000 permutations⁵⁹.

In Fig. 3, it is found that for the three periods that the sample with a smaller size (El Niño sample vs. la Niña sample) features a weaker MSLP field response. To test whether the weaker response is a result of a non-symmetric teleconnection or simply due to sampling uncertainty, a bootstrap resampling is performed as follows: for each period, we identify the area with the strongest MSLP response. This area is denoted as A. For P1 and P3 A is west of the British Isles, whereas in P2 it is over Iceland. Then, from the larger sample (La Niña in P1 and P3, and El Niño in P2), we construct 10,000 sub-samples by randomly selecting n elements, with n being the size of the smaller sample (El Niño in P1 and P3, and La Niña in P2). In each of the sub-samples, we compute the area-average of MSLP anomalies over A. The obtained values are then compared with the area-average of MSLP anomalies in the smaller sample. The percentage of sub-samples yielding a value larger than or equal to the observed one is used as an estimation of the p-value. For example, in P1, 10,000 sub-samples of n = 7 are created from the La Niña sample. When computing the area-average of the MSLP anomalies over A in each of these sub-samples, it is found that only 3% of the sub-samples have a MSLP response that is stronger than that of the El Niño sample. This would render p val = 0.03. However, since this test is carried out 3 times (one time for each period), the corresponding p-values have to be multiplied by 3, and hence in this case pval = 0.09.