Introduction

The definition of monsoon systems has evolved with time. Initially, monsoons were understood as resulting from simple thermal contrasts between continental masses and the neighbouring oceanic basins1,2. From this perspective, increasing monsoon rainfall intensity was expected to correlate with the strength of monsoon flows advected from the ocean. However, observations contradict this assumption: the thermal contrast that drives monsoon circulation is typically strongest at the onset of the monsoon season, whereas monsoon fluxes peak later, when rainfall and cloud cover have already cooled the landmass, thereby reducing the thermal contrast3. Another shortcoming of this definition becomes evident when it is applied to the projected impacts of global warming on specific monsoon systems. For instance, climate model projections indicate that, although land-sea thermal contrasts–key drivers of monsoon onset–are expected to intensify over the North American monsoon region under global warming, the associated monsoonal circulation and precipitation are projected to weaken4.

This traditional definition also frames monsoons as predominantly regional phenomena, thereby excluding subcomponents of the monsoon system that may be influenced by extratropical or even global factors5. This complexity of physical processes underpinning monsoon systems may, in part, explain the failure of climate models participating in the Coupled Model Intercomparison Projects (CMIPs) to capture the drought sequences that affected the Sahel during the 1970s and 1980s6,7. To address these limitations, a novel theory–known as the energy-budget framework–has recently been developed4. This energy-based perspective posits that continental monsoon subsystems and the intertropical convergence zone (ITCZ) are components of a single, energetically direct planetary circulation that links terrestrial and oceanic precipitation8, exhibiting synchronized seasonal variability at multiple time scales9. The theory is supported by observation showing that regions of peak monsoon precipitation, characterized by intense convective activity, coincide with centers of upper-tropospheric divergence that diverge energy away from deep convection zones.

The global perspective on monsoons advocated by the energy-budget framework provides a clear path toward improving their predictability. In this study, we adopt this global approach by proposing a novel index that captures the variability and changes of the West African Sahel monsoon (roughly within 10°–20°N and 16°W–17°E) at both intraseasonal and interannual time-scales (see “Methods” for definitions). While continental monsoons are components of a larger global system, we argue that a monsoon index that reconciles both its regional and global features is more suitable for predictive and projection purposes. We hypothesize that such an index should not only capture the local and regional mechanisms governing the Sahel monsoon (e.g., low-level westerlies [LLWs], African easterly jet [AEJ], tropical easterly jet [TEJ]10, and the West African westerly jet [WAWJ]11) but also incorporate signals from large-scale teleconnections such as the El Niño-Southern Oscillation (ENSO)12 and the Atlantic Meridional Mode (AMM)13. Our findings may be useful to operational climate forecasting centres, as improved predictive capability could enhance forecast reliability and inform early warning systems. Although numerous prior studies14,15,16,17,18 have proposed indices for monitoring the evolution of the West African Monsoon (WAM), most, if not all, are based on atmospheric fields averaged over the region. While such indices are effective for nowcasting, as they provide information on very short-term time scales, they are limited for medium- and long-term forecasts. Indices based solely on local or regional climate fail to capture remote anomalies that induce profound changes in the global energy balance, whose regional or local footprints may only emerge after short or long lag periods. For instance, among other processes, the positive phase of the South Atlantic Ocean Dipole (SAOD) is associated with positive precipitation anomalies along the Guinean coast19. It typically leads Sahelian monsoon rainfall by about 1–3 months, due to its influence on the meridional sea surface temperature (SST) gradient and subsequent modulation of the West African monsoon circulation20,21. In contrast, its positive northeast pole (NEP), which encompasses the Atlantic Niño region (ATL3), modulates the interannual variability of Sahelian rainfall, often leading by 1–2 months through changes in equatorial Atlantic SST that influence the position of the ITCZ22. Similarly, El Niño (La Niña) events–characterized by warm (cool) SST anomalies in the tropical Pacific (e.g., Niño3.4 region)–typically lead the West African monsoon season by 2 to 6 months, and are known to suppress (enhance) rainfall over the Sahel via atmospheric teleconnections that alter the Walker and Hadley circulations23. The positive phase of the Atlantic Meridional Mode (AMM), usually developing in boreal spring, also precedes the Sahel rainy season by about 2 to 3 months, and tends to induce positive rainfall anomalies over the region by reinforcing the northward displacement of the ITCZ and strengthening the monsoon flows24.

The climate variables from which such an index should be derived must ensure that large-scale teleconnections are adequately captured to reflect the closure of the energy balance. This requirement limits the choice to either SST or sea level pressure (SLP), both of which are known to modulate Sahelian precipitation and associated systems25,26. As is well known, the SST and SLP are to some extent interrelated–cool SST poles induce oceanic high-pressure systems, which in turn influence atmospheric circulation and energy distribution–although other processes, such as oceanic and atmospheric waves, may also affect SST and SLP patterns27.

In this work, we use SLP as a proxy to develop the new global Sahel Monsoon Ocean-Pressure Index (SMOPI, see “Methods”). SLP effectively represents prevailing meteorological conditions in the Sahel26. One advantage of constructing SMOPI using SLP is that one of the SLP regions used in the index formulation aligns closely with the Sahel area, ensuring that local atmospheric conditions are directly incorporated and enhancing the index’s representativeness and reliability as an indicator of Sahel monsoon intensity. We demonstrate that SMOPI effectively integrates regional drivers and large-scale teleconnections associated with the dominant mode of Sahelian rainfall variability. Furthermore, SMOPI is effectively able to portray both regional and global features of the Sahelian monsoon, accurately reflecting the temporal dynamics of historical precipitation and lending support to the global monsoon concept5. While developed for the Sahel, SMOPI framework is conceptually transferable to other monsoon systems such as the Indian, East Asian, or South American monsoons, where rainfall is also controlled regionally and remotely28,29.

Results

The Sahelian rainfall and remote SLP boxes’ relationship

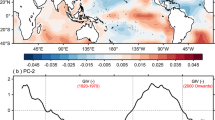
The first objective is to identify remote oceanic or continental regions that exhibit significant teleconnections with Sahel rainfall. Thus, by analysing the linear (Pearson) and non-linear (distance) correlations between area-averaged Sahel precipitation and mean SLP globally (Figs. 1a–d and S1–S2, respectively), one continental region and four oceanic basins emerge as areas where the absolute correlation values are strongest and statistically significant (p < 0.01). The continental region (SLP1 thereafter), which includes the Sahel itself (extending further eastward up to around 37°E), shows a strong positive correlation with SLP. Three of the four oceanic basins exhibit positive correlations with Sahel rainfall: the first is located in the southwestern tropical Atlantic Ocean (SLP2 thereafter), the second is near the southern Indian Ocean subtropical high (SLP3 thereafter), and the third covers almost the whole tropical Pacific Ocean (SLP4 thereafter). On the contrary, the oceanic basin located in the northeastern tropical Atlantic Ocean (SLP5 thereafter) displays a strong negative and statistically significant correlation with rainfall in the Sahel. The geographical coordinates of the five SLP domains are listed in Table S1. SLP1 and SLP4 are low-pressure regions, whereas SLP2, SLP3 and SLP5 are high-pressure regions, respectively. The spatial arrangement of identified continental and oceanic regions shows evidence that the zonal (i.e., east-west) and meridional (i.e., south-north) pressure gradients that shape the monsoon large-scale circulation are considered5. The linear regression-based analysis (p < 0.01) shows a spatial pattern that is almost identical to that of the correlation in terms of both distribution and sign of the precipitation-SLP teleconnection (Fig. 1e, f). The two reanalyses, JRA55 (Fig. 1a, e) and ERA5 (Fig. 1b, f), consistently exhibit very similar locations of SLP boxes and extent of associations.

Fig. 1: Detection of continental regions and oceanic basins used to define the SMOPI.
figure 1

a–d Spatial distribution of the correlation between area-averaged precipitation over the Sahel and global mean sea level pressure (SLP). Only statistically significant correlation values (p < 0.01) based on a two-sided Student’s t-test are shown. The datasets used are the JRA-55 reanalysis (a), ERA5 (b), MPI-ESM1-2-LR (c) and the ensemble mean of 29 CMIP6 models (hereafter CMIP6) (d). Black rectangles (SLP boxes) indicate areas of maximum and statistically significant correlation values used to compute the SMOPI. The red rectangle denotes the Sahel. e–h Same as (a–d), but for the linear regression between area-averaged precipitation over the Sahel and global mean SLP.

Full size image

In addition to reanalysis, we computed SMOPI using historical simulations from 29 CMIP6 models. This extension serves multiple purposes. First, it allows robust evaluation of the index’s stability and applicability across a wide range of climate model configurations. Second, it enables comparison between observed (reanalysis-based) and simulated atmospheric pressure patterns, highlighting systematic model biases in representing key pressure regions that influence Sahel monsoon variability. Furthermore, by using CMIP6 data, we evaluated the index’s potential as a diagnostic tool in future climate scenarios, enhancing its relevance for long-term climate monitoring and impact studies. Overall, including CMIP6 simulations reinforces the generalizability of SMOPI and provides critical insights into the realism and diversity of modelled monsoon dynamics. The spatial location of SLP boxes and the sign of teleconnections are also manifested in MPI-ESM1-2-LR (shown as an example), although with smaller positive values (Fig. 1c, g). The ensemble mean of the 29 CMIP6 models (CMIP6, thereafter; Fig. 1d, h) and most of the individual models (Figs. S3, S4) capture the spatial distribution of the correlation and regression, and, hence, the location of the continental region and oceanic basins along with the sign of the correlation and regression. CMIP6, however, overestimates the magnitude of teleconnections, which is presumably associated with its failure to mimic the past variability of the Sahel rainfall6,7. This assumption is further explored in the next sections. Indeed, CMIP6 fails to capture the temporal evolution of the first principal component (PC1) of rainfall in the Sahel, which shows a decline up to the 1980s, followed by a recovery from the 1990s onward (Fig. S5a). Instead, CMIP6 modelled a moderately steady growth in the rainfall PC1, whose temporal evolution is only moderately correlated (0.53* ≤ r ≤ 0.62*) against observations (CRU, UDEL, and GPCC Fig. S5b). Is SMOPI able to report such a failure? This question is addressed in the following sections. Moreover, interestingly, the ERA5 reanalysis too does not capture the leading mode of historical Sahel rainfall interannual variability, showing the weakest (and statistically insignificant) correlation (r ≤ 0.25) when compared to the three observational datasets, although it performs fairly well on the intraseasonal timescale (r ≥ 0.59*, Fig. S5c). In contrast, the Japanese 55-year reanalysis (JRA-55) accurately reproduces the PC1 of Sahelian rainfall both for the year-to-year (r ≥ 0.76*, see Fig. S5b) and month-to-month (r ≥ 0.67*, see Fig. S5c) variability. Therefore, JRA-55 is used as the reference reanalysis in the remainder of the study.

In the Sahel, the year-to-year evolution of rainfall PC1 is strongly and significantly correlated with the seasonal mean rainfall in each dataset (r ≥ 0.98*), except for JRA-55 (r = 0.61*), where the correlation remains moderate but still statistically significant (see Fig. S5a). The percentage of total variance explained by PC1 is 7.3 times greater than that of PC2 in CRU (PC1/PC2 = 74.4%/10.2%), 3.3 times in JRA55 (54.8%/16.8%), 7.7 times in ERA5 (66.9.4%/8.7%), and 9.98 times in CMIP6 (87.8%/8.8%). This implies that the region’s climate variability is close to the climatology, even when including the modulating effect of the external forcing factors. This sustains the assertion that a Sahel rainfall index should remain efficient both when the Sahel climate is regionally forced and when remote drivers of the Sahel’s climate systems are at play. The reliability of SMOPI will therefore be assessed relative to rainfall PC1 rather than the climatology, to avoid noise that may result from other, less relevant modes of variability. Unlike simple smoothing, the use of PC1 allows for an objective extraction of the dominant, spatially coherent rainfall signal and facilitates consistent comparison across observational datasets and climate models.

Reconciling the Sahel monsoon rainfall and SMOPI

Once the SLP boxes that underpin the Sahel monsoon rainfall variability are identified, SMOPI is calculated using Eqs. 1–3 (see “Methods”). In the present section, we examine the strength and sign of the relationships between, on the one hand, SMOPI and Sahel rainfall, and between individual SLP boxes and Sahel rainfall. On the other hand, we investigate the nature of the interactions amongst different SLP boxes themselves, and explore whether such counteracting effects lead to amplification or attenuation effects on the Sahel rainfall. The overarching relationships are summarized into a heatmap plot (Fig. 2). The Pearson correlations (Fig. 2a-d) and distance correlations (Fig. 2e-h) yield consistent results, indicating a predominance of linear relationships –or negligible nonlinear effects– between SMOPI/SLP boxes and Sahel monsoon rainfall. Additionally, these findings primarily suggest that interactions between the SLP boxes are also largely linear. Specifically, at the subseasonal time scale, \({I}_{{SMOPI}}\) is positively correlated (p < 0.01) with rainfall PC1 for JRA55 (r = 0.75*), ERA5 (r = 0.64*), MPI-ESM1-2-LR (r = 0.66*) and for CMIP6 (r = 0.63*). On the other hand, the correlation for the interannual variability of \({I}_{{SMOPI}}\) and PC1 rainfall (Fig. S6) displays strong, positive values for JRA-55 (r = 0.75*), MPI-ESM1-2-LR (r = 0.61*), and CMIP6 (0.93*) but a negative one for ERA5 (r = -0.40). As aforementioned, this inconsistency is primarily attributed to ERA5’s failure to capture the dominant mode of Sahelian precipitation interannual variability (Fig. S5a,b), given that its \({I}_{{SMOPI}}\) closely resembles that of JRA-55 (r = 0.97*, p < 0.01). Most individual CMIP6 models show positive correlations between rainfall PC1 and SMOPI (Fig. S7). Results similar to the above ones emerge when regressing SMOPI onto the Sahel PC1 rainfall (Fig. S8).

Fig. 2: The Sahel monsoon rainfall and SMOPI relationship.
figure 2

Heatmap of Pearson correlation (a–d) and Distance correlation (e–h) between Sahel monsoon rainfall first principal component (PC1 Rainfall) and SMOPI for subseasonal variability. Correlations between high- and low-pressure systems over the continental region and oceanic basins (SLP boxes), and both Sahel monsoon rainfall and SMOPI, are also shown, for (a, e) JRA55, (b, f) ERA5, (c, g) MPI-ESM1-2-LR and (d, h) CMIP6. Additionally, intercorrelations among the five SLP boxes highlight the neutralizing or amplifying effects among the physical processes associated with pressure systems, leading to amplified or attenuated rainfall. In each box, the top number indicates the correlation value, and the bottom number is the p-value.

Full size image

As previously noted, the SLP1-4 boxes show a positive and significant correlation with rainfall PC1, whereas the SLP5 does the reverse, consistent across all datasets. Figure 2 unveils that at the intraseasonal time scale, \({I}_{{SMOPI}}\) is positively and significantly correlated (moderately) with SLP1-4 boxes, while concomitantly, it is negatively and significantly correlated (strongly) with SLP5. A coherent signal has not emerged at the interannual scale (Fig. S6), as each dataset exhibits a distinct configuration of interlinkages between \({I}_{{SMOPI}}\) and SLP1–4. This is potentially linked to the diversity in the years of occurrence of large-scale teleconnections across datasets30, which either originate from or influence the different SLP basins, as will be demonstrated later in this study. In contrast, the relationship between \({I}_{{SMOPI}}\) and SLP5 consistently shows a coherent signal characterized by a strong negative and significant correlation. This suggests a vital footprint of SLP5 in shaping the strength of \({I}_{{SMOPI}}\). Furthermore, the correlation between the various SLP1-4 boxes is always positive, although sometimes almost non-existent and not significant. However, SLP3 and SLP4 boxes show weak negative interactions with the SLP5 box. This indicates potentially conflicting, though not systematic, effects between the southern Indian Ocean subtropical high and the north tropical Atlantic high, and between the central Pacific low and the north tropical Atlantic high. For instance, a weakening of the Indian Ocean subtropical high may coincide with a strengthening of the North Tropical Atlantic high, driven by Indian Ocean warming that feeds back to cool the subpolar North Atlantic through teleconnections mediated by surface wind anomalies31. Alternatively, the Atlantic Meridional Overturning Circulation (AMOC) mediates by modulating the tropical hydrological cycle and enhancing Atlantic salinity. Over short timescales, an intensified AMOC subsequently drives increased northward ocean heat transport, leading to warming in the northern Atlantic32.

In general, the aforementioned results highlight that no single SLP region alone can reproduce the level of correlation with Sahel monsoon rainfall achieved by SMOPI. For instance, while some individual boxes, such as SLP1 or SLP4, show moderate correlations (up to r = 0.56), SMOPI consistently reaches higher values (r ≥ 0.63) across reanalyses and models. This supports the idea that SMOPI effectively combines complementary and sometimes opposing signals from multiple regions, rather than relying on a dominant SLP region. The interdependencies shown in Fig. 2, rather than being redundant, reflect physically distinct mechanisms that the index integrates through its formulation. This design explains its superior skill compared to individual SLP regions and supports its use as a synthetic and efficient diagnostic index of Sahel rainfall variability.

The SMOPI reliably captures past Sahel rainfall variability

We have previously established a robust statistical relationship between SMOPI and precipitation in the Sahel. However, it remains an open question whether SMOPI temporal dynamics reflect those of the leading mode of Sahelian precipitation, a question that is crucial for assessing the reliability and informative value of SMOPI. Figure 3 evidences the efficiency of SMOPI. Indeed, SMOPI properly reports the dry spells of the 1970s-1980s and the precipitation recovery since the 1990s onward (Fig. 3a). Additionally, as aforementioned, SMOPI is strongly correlated with rainfall PC1, and closely mirrors its temporal evolution (except for ERA5, as justified above; see Fig. 3b). Notably, the similarity between rainfall PC1 and SMOPI is nearly perfect for CMIP6, suggesting that SMOPI informs the models’ failure to reproduce historical Sahel rainfall variability accurately. This result highlights important implications, as it points to SMOPI-underlying processes as potential contributors to CMIPs’ precipitation biases33, sources of uncertainties in model future projections33 and underlying mechanisms of historical droughts experienced in the Sahel34,35,36. It is worth noting that the prolonged drought of the 1970s and 1980s in the Sahel may have also been partially driven by anthropogenic aerosol forcing, particularly sulfate aerosols over the North Atlantic. Several studies37,38,39 have linked aerosol-induced SST cooling to reduced moisture transport toward the Sahel. The inability of some CMIP6 models to reproduce the observed drought may in part reflect uncertainties or omissions in their aerosol forcing representation. More encouragingly, at the intraseasonal timescale, SMOPI exhibits a strong correlation with Sahelian precipitation (Fig. 3c) and shows a strong regression pattern across nearly all the Sahel (Fig. 3d). These relationships are also evident for most of the 29 individual CMIP6 models (Figs. S9 and S10). The spatial extent of the association diminishes at the interannual scale for JRA55 and MPI-ESM1-2-LR, and, as expected, is absent for ERA5, while it remains unchanged for CMIP6 (Fig. S11). However, at this timescale, unlike the CMIP6 ensemble mean, most of the 29 individual models display a reduced spatial extent of the relationships (Figs. S12 and S13). While these results support the fact that SMOPI tracks the temporal dynamics of precipitation in the Sahel relative to the time scale under consideration, it remains to be determined whether the strength of \({I}_{{SMOPI}}\) reflects the magnitude and patterns of the physical processes, both regional and global, that underpin Sahelian monsoon precipitation.

Fig. 3: The SMOPI definition and links with the leading mode of the Sahel rainfall variability.
figure 3

a 5-year smoothed of the temporal evolutions of the SMOPI intensity over the period 1965-2014, from JRA55 (blue), ERA5 (green), MPI-ESM1-2-LR (purple) and CMIP6 (red). The results from the 29 CMIP6 models are also shown (thin red curves). Shaded bands represent the mean ±1 standard deviation for each dataset, except for CMIP6, where the band indicates the inter-model spread. Half-regression lines are shown for the two main rainfall sequences of the Sahel study period: the drying phase (1965-1985) and the rainfall recovery phase (1986-2014). b The SMOPI intensity (solid lines) and PC1 rainfall anomalies (dashed lines) are superimposed, along with their respective uncertainty ranges. r-values represent the correlation between the SMOPI intensity and PC1 rainfall anomalies. The asterisk (*) marks statistical significance (p < 0.01) based on a two-sided Student’s t-test. Spatial distribution of correlation coefficients (c) and regression slope (d) between the SMOPI intensity and the Sahel PC1 rainfall anomalies at subseasonal time scale, from JRA55, ERA5, MPI-ESM1-2-LR and CMIP6. Only statistically significant values (p < 0.01) are shown.

Full size image

The SMOPI tracks regional mechanisms underlying Sahelian monsoon rainfall

We employed composite analysis to investigate whether variations in the strength of SMOPI are associated with changes in physical processes underpinning Sahelian rainfall. Similarly, we do not rule out the possibility that SMOPI may uncover other factors underlying Sahelian monsoon rainfall that have hitherto been poorly understood or elucidated. For each dataset, we selected years of anomalously weak SMOPI, i.e., with \({I}_{{SMOPI}} < -0.5\) to construct a weak (negative) composite and years of anomalously strong SMOPI, i.e., with \({I}_{{SMOPI}} > +0.5\) to construct a strong (positive) composite (see Table S2), in which we subtracted the long-term (1965-2014) climatology. This threshold corresponds to moderate anomalies, assuming a standard normal distribution of the index. It represents a balance between statistical robustness–by ensuring a sufficient sample size for composite analysis–and physical relevance, as it captures years with notable monsoonal anomalies without being limited to extreme events. This approach is consistent with previous studies using similar thresholds for standardized climate indices such as ENSO40 or NAO41 phases. For the CMIP6 ensemble mean, results are shown as the mean of the strong and weak composite years identified for each ensemble member separately. As seen in Fig. 3, the fact that the weak phases of SMOPI predominantly fall in the 1970s-1980s and the strong phases in the 2000s is purely coincidental and reflects the underlying rainfall dynamics of the Sahel during this historical period. This temporal distribution emerges naturally from the intrinsic variability of the index over 1965-2014, and not from any deliberate selection of decades. Over this period, the SMOPI approximates a normal distribution. We acknowledge, however, that the distribution and the resulting composites could vary if computed over a different period with distinct rainfall regimes. In general, the outcomes highlight that when SMOPI is weak, the Sahel experiences reduced precipitation (Fig. 4a, c, e, g). Conversely, when SMOPI is strong, the Sahel experiences increased precipitation (Fig. 4b, d, f, h). This result is consistent across all datasets, including most of the individual CMIP6 models (Figs. S14 and S15).

Fig. 4: Sahelian monsoon rainfall responses to anomalous weak and strong SMOPI.
figure 4

a–h Composite anomalies–defined as dry years (weak SMOP) minus 1965-2014 climatology (first line) and wet years (strong SMOPI) minus 1965-2014 climatology (second line)– of Sahelian monsoon rainfall are displayed for JRA55 (a, b), ERA5 (c, d), MPI-ESM1-2-LR (e, f) and CMIP6 (g, h). i–p Same as in (a–h), but for the standardized anomaly of the vertically integrated (1000-100 hPa) moisture flux convergence.

Full size image

Subsequently, the environmental dynamical conditions supporting the observed changes in precipitation patterns are investigated. We first examined the composite anomaly patterns of the total column (1000–100 hPa) vertically integrated moisture flux convergence (VIMFC). Consistent with the precipitation composites, the decline in rainfall observed during years with abnormally weak SMOPI is associated with enhanced divergence of moisture flux, indicating a drying of the atmospheric column (Fig. 4i, k, m, o). Conversely, years characterized by an abnormally strong SMOPI exhibit increased moisture convergence across most of the Sahel, inducing a moistening of the air column (Fig. 4j, l, n, p). Most of the individual CMIP6 models show consistent results as well (Figs. S16 and S17). Subsequently, we checked whether the regional organization in the vertical profile of the convective system of the Sahel monsoon rainfall explains the pattern of the VIMFC associated with each composite (Fig. 5). Three key regional features of the Sahel monsoon rainfall system are explored: the low-level monsoon flows42, the mid-tropospheric AEJ and the upper-layer TEJ10,43. All datasets consistently agree on the role of the TEJ and the AEJ in modulating dry and wet conditions over the Sahel, in line with existing literature10,42. Indeed, wet years are marked by a strong TEJ, whereas dry years exhibit a weakened TEJ43. Additionally, during wet years, the AEJ intensifies near the northern boundary of the Sahel but weakens toward the southern edge, suggesting enhanced moisture retention in the region that triggers and maintains squall lines and Mesoscale Convective Systems (MSCs44). In contrast, during dry years, the AEJ is weaker at the northern entrance but stronger at the southern boundary, potentially indicating reduced moisture advection from the Mediterranean into the Sahel and, conversely, increased outflows that deplete regional moisture44,45.

Fig. 5: The SMOPI effectively tracks regional features of the Sahelian monsoon rainfall.
figure 5

Composite standardized anomalies–defined as dry years (weak SMOPI) minus climatology (first column) and wet years (strong SMOPI) minus climatology (second column)– of the zonal wind component (u-wind) are shown for JRA55 (a, b), ERA5 (c, d), MPI-ESM1-2-LR (e, f) and CMIP6 (g, h). Three key features of Sahel monsoon rainfall variability are consistently identified across datasets, although with different strength: the monsoon flows (blue), African Easterly Jet (AEJ, red) and Tropical Easterly Jet (TEJ, green). Contour lines denote the corresponding mean composite and highlight the vertical structure of the organized convective system.

Full size image

Conflicting results, however, emerge among datasets regarding the way monsoon flows are connected to wet and dry conditions in the Sahel. The two reanalysis datasets show opposite configurations, with JRA55 featuring anomalous enhanced (reduced) monsoon flows during dry (wet) years (Fig. 5a, b), while ERA5 does the reverse (Fig. 5c, d). For MPI-ESM1-2-LR, the monsoon flows are anomalously weakened for both positive and negative composites (Fig. 5e, f). Finally, CMIP6 exhibits anomalous weak (strong) monsoon flows during dry (wet) years (Fig. 5g, h). At first glance, the monsoon flows are not, therefore, the factor that differentiates between dry and wet years or at least, the imprint of the monsoon flow strength is not at the forefront in shaping wet or dry conditions in the Sahel. Instead, the AEJ and TEJ are identified as playing that role. This result is endorsed by earlier work by Shekhar and Boos46. These authors established that the Saharan shallow meridional circulation (SMC) is often weaker and polewardly displaced during wet years. This feature reduces mid-level dry air advection, favoring the development of deep convection and, in turn, the monsoon flow, leading to increased rainfall. In dry years, the SMC strengthens and moves towards the equator. This position facilitates the movement of warm, dry mid-altitude air towards the Sahel, thereby suppressing convection. Although not all datasets agree on the role of the SMC, the results based on our reference reanalysis (JRA-55) are consistent with the findings of Shekhar and Boos46, showing a weakening (strengthening) and northward (equatorward) shift of the SMC during strong (weak) SMOPI years. This agreement supports the reliability of the SMOPI-based composites and confirms SMOPI as a physically meaningful index sensitive to real-world monsoon dynamics.

Models do not consistently agree on which configurations of the TEJ and AEJ correspond to dry (Fig. S18) or wet (Fig. S19) conditions. At times, certain models simulate the wet-phase configuration during dry composite years, and conversely. Nevertheless, most models generally succeed in reproducing the characteristic monsoon flow patterns associated with each composite. However, as previously discussed, monsoon fluxes are not the primary determinant of wet or dry conditions in the Sahel. An accurate representation of monsoon flows alone, though necessary, is insufficient, which partly explains the persistent difficulty in capturing precipitation variability over the region. Advancing CMIP6 models in the Sahel should therefore prioritize the improvement of AEJ and TEJ.

SMOPI on the trail of remote teleconnections of the Sahel monsoon rainfall

Examining the climatology of the composites also unravels the involvement of remote teleconnections, some of which are consistent with the responses observed in regional features such as the TEJ. It is not unlikely that the observed AEJ patterns in both composites are also influenced by these large-scale forcings, given the recently highlighted interlinkages between the AEJ and the TEJ through the Lagrangian coherent structures47. To shed light on which global teleconnections of Sahel monsoon rainfall are depicted by the SMOPI, and whether consistent regional responses occur as previously noted, global SST patterns are also explored during phases of strong and weak SMOPI, as shown in Fig. 6. Signals from eight remote teleconnections emerge (Fig. 6a–d).

Fig. 6: The SMOPI effectively captures large-scale teleconnection patterns associated with Sahelian monsoon rainfall.
figure 6

Composite anomalies–defined as dry years (weak SMOPI) minus climatology (first column) and wet years (strong SMOPI) minus climatology (second column)– of global sea surface temperatures are presented for JRA55 (a), ERA5 (b), MPI-ESM1-2-LR (c) and CMIP6 (d). Eight large-scale forcing factors of Sahel monsoon rainfall variability are consistently uncovered across datasets, albeit with varying strength and imprint: the Atlantic Meridional Mode (AMM), Niño3.4, South Atlantic Ocean Dipole (SAOD), the Atlantic Niño (ATL3), Niño3, Niño4 and Niño1 + 2. The signal of the Indian Ocean Dipole (IOD) is also detected, but exclusively in the MPI-ESM1-2-LR model.

Full size image

The first four are ENSO, with El Niño conditions (including Niño3.4, Niño3, Niño4, and Niño1 + 2) associated with dry years, and La Niña conditions associated with wet years, consistent with previous studies48,49,50,51. ENSO forces the monsoon via the Walker and regional Hadley-like circulation, whereby El Niño events lead to a weakening of the TEJ, whereas La Niña events strengthen it. This modulation is mediated by surface temperature gradients across the Pacific and Indian Oceans, as well as between the Tibetan Plateau and the Indian subcontinent23,52,53,54. The fifth teleconnection is SAOD, consisting of a warm northeast and cool southwest of the South Atlantic Ocean (SAO). Its positive phase is observed in the wet composites, while the negative phase appears in the dry composite, aligning with former findings by Nnamchi et al.19. The sixth teleconnection is the Atlantic Niño (ATL3), embedded within the northeastern part of the SAO, which is the SAOD’s northeastern pole. Its negative phase is associated with dry years, whereas the positive phase corresponds to wet years. One might be surprised by the polarity of the ATL3 signal, given that its typical influence on the West African monsoon involves inducing positive (negative) precipitation anomalies over the Guinean Coast and negative (positive) anomalies over the Sahel. However, this is not a contradiction. That conventional response merely reflects the dominant mode of the teleconnection pathway. Indeed, the work of Ward55 demonstrated that, among 93 years analyzed, 36 exhibited homogeneous rainfall anomalies of the same sign, either positive or negative, across both the Guinean Coast and the Sahel. Therefore, the ATL3 phase polarity revealed by the SMOPI in this study is consistent with the fact that the SLP boxes used to construct the SMOPI were identified based on Sahelian rainfall anomalies. In other words, the SMOPI only reveals the ATL3 mode, which homogeneously forces precipitation in the Guinea Coast and Sahel. While the SAOD primarily influences precipitation over the Guinea Coast, the ATL3 is also linked to interannual rainfall variability over the Sahel19. Nnamchi et al.19 argued that during the positive phase of the SAOD, the southwestern pole acts as a moisture source toward the northeastern pole, inducing strong moisture convergence and convection over the Guinea Coast, a process known as the Lindzen–Nigam mechanism56. During positive rainfall anomalies over the Guinea Coast, ATL3 warming reduces the land–ocean thermal contrast, limiting the extent of inland moisture penetration and enhancing moisture accumulation and convection near the coast57. Nicholson and Webster58 showed that the same condition in the Sahel is linked to the inertial instability driven by the land–ocean pressure gradient and low-level westerlies that shift the AEJ northwestward, enhancing ascent over the Sahel and subsidence over the Guinea Coast.

The seventh teleconnection is the AMM, the leading source of coupled ocean-atmosphere variability in the Atlantic Ocean, also referred to as the tropical Atlantic SST dipole59. Its positive phase–characterized by warmer SSTs in the northern tropical Atlantic and cooler SSTs in the south–emerges during strong SMOPI years, whereas its negative phase–cooler in the north and warmer in the south–corresponds to weak SMOPI years, consistent with previous findings13,60. During a positive AMM phase, intensified trade winds in the warmer northern pole and weakened winds in the cooler southern pole reinforce the SST gradient, shifting the ITCZ northward and thereby promoting positive rainfall anomalies over the Sahel61,62.

The strength of these first seven signals varies across datasets, including the 29 individual CMIP6 models (Figs. S20 and S21), and largely depends on the magnitude and polarity of the respective SST poles constituting each index. The last signal (eighth) appears in the tropical Indian Ocean and follows two configurations reported in the literature. One involves warming of the tropical Indian Ocean during wet years, seen only in the two reanalyses (Fig. 6a, b). In this case, warmer SSTs alter the Asian monsoon overturning circulation, which feeds back as descent over North Africa, enhancing Sahelian precipitation45. The second is the Indian Ocean Dipole (IOD), captured by MPI-ESM1-2-LR and CMIP6 (Fig. 6c, d) and some individual CMIP6 models (Figs. S20 and S21). Zhang and Han63 showed that during a positive IOD, enhanced rainfall over the western tropical Indian Ocean weakens trade winds toward the tropical Atlantic, leading to warm SSTs that trigger the Atlantic Niño, which subsequently affects Sahelian rainfall.

In summary, Fig. 7a–d reveals that the AMM signal is predominant within the SMOPI at the intraseasonal timescale, with statistically significant correlations (p < 0.01) of r = 0.84* for JRA55, 0.86* for ERA5, 0.70* for MPI-ESM1-2-LR, and 0.79* for the CMIP6 ensemble. This finding is further corroborated by the striking similarity in the temporal evolution of the AMM and the SMOPI at the interannual timescale (Figs. 7k, m, S22). Next come the El Niño signals from the Pacific (Niño3.4, Niño3, Niño4, and Niño1 + 2) and the Atlantic (ATL3), which exhibit moderate, negative, and statistically significant correlations, along with upward trends in their temporal evolution (Fig. 7e–h). There is no clear consensus regarding the imprints of the SAOD and IOD on the SMOPI across the different datasets, although their signals appear to be the weakest. While JRA55 and MPI-ESM1-2-LR (Fig. 7a, c) indicate a negative correlation between the IOD and the SMOPI, ERA5 and CMIP6 (Fig. 7b, d) show the opposite, highlighting a potential source of uncertainty in observed and projected Sahelian precipitation.

Fig. 7: Extent and sign of teleconnections within SMOPI at intraseasonal timescale.
figure 7

a–d Heatmaps of Pearson correlation coefficients between large-scale climate teleconnections and SMOPI. The relationship between each teleconnection index and the Sahelian rainfall first principal component (PC1 Rainfall) is also shown to assess the consistency of SMOPI with established rainfall dynamics (i.e., except IOD, positive association with SMOPI leads to positive association with PC1 rainfall and vice versa). Results are presented for (a) JRA55, (b) ERA5, (c) MPI-ESM1-2-LR, and (d) the CMIP6 multi-model ensemble. e–l Temporal evolution of all teleconnection indices, displayed across datasets–JRA55 (blue), ERA5 (green), MPI-ESM1-2-LR (purple), and CMIP6 (red). (m) Temporal evolution of the newly developed SMOPI. (n) Temporal evolution of the first principal component of Sahelian rainfall (PC1 Rainfall).

Full size image

Discussion

We introduced a new synthetic index, the SMOPI, designed to monitor the temporal evolution and intensity of Sahelian precipitation. A key strength of SMOPI lies in the SLP boxes used for this purpose, one of which is located directly over the Sahel, ensuring that local meteorological conditions are explicitly incorporated into the SMOPI structure. The others reflect remote, dynamically coherent pressure centres. As such, SMOPI does not only reflect large-scale remote influences but also captures local dynamical signals tied to surface pressure anomalies within the region itself. This combination enhances the diagnostic power of the index and supports its relevance for real-time applications, such as nowcasting or early-warning systems for rainfall anomalies in the Sahel. At first sight, the informative value of SMOPI appears to vary with the time scale considered. In this work, we found SMOPI to be more effective at intraseasonal than interannual timescales, although it remains fairly effective at both timescales. SMOPI proves to be a robust and inclusive index, as it is capable of revealing both regional mechanisms and large-scale teleconnections that underpin Sahelian monsoon rainfall. As such, it offers novel opportunities for climate modelling, particularly for the evaluation of climate models and benchmarking by providing insights into monsoon variability. Furthermore, by exposing the misrepresentation of historical Sahel droughts in CMIP6 simulations, SMOPI provides insights into model deficiencies that could inform future improvements.

As with any climate index, the SMOPI construction rests on a number of assumptions that merit careful consideration. First, the selection of SLP regions is based on documented teleconnection pathways, but remains sensitive to the input dataset and reference period. Second, the regions involved may reflect overlapping modes of variability; for instance, the SAOD, ATL3, and AMM all influence the tropical Atlantic sector through different but sometimes correlated mechanisms, raising the possibility of partial redundancy. Lastly, the index’s performance depends on the quality of the underlying data, particularly in reanalysis products. While JRA-55 serves as a reliable reference, the lower performance of ERA5 despite its SLP similarity illustrates the importance of precipitation representation when evaluating coupled indices like SMOPI.

Our findings also lay the groundwork for further research. Remote forcing factors do not influence the Sahelian monsoon in the same way, and their simultaneous occurrence can either amplify or dampen rainfall. Future studies should aim to disentangle and quantify the contributions of individual drivers to the SMOPI signal and clarify the physical mechanisms through which they modulate rainfall. Although SMOPI demonstrates a strong diagnostic capacity to reproduce observed variations in Sahelian monsoon rainfall, its use in operational forecasting systems has not yet been evaluated. We therefore emphasize that SMOPI currently holds potential as a prediction tool, but further testing with dedicated forecast systems is required to establish its predictive skill. In particular, assessing its lead-lag relationships with known precursors and developing probabilistic forecasting approaches will be essential to evaluate its suitability for real-time and operational applications. For long-term projections, investigating SMOPI’s evolution under various greenhouse gas scenarios will help anticipate future Sahelian monsoon responses. Unlike many conventional indices based on fixed SST patterns (e.g., ATL3, AMM, SAOD) or monsoon flow metrics (e.g., WASMI17), SMOPI is constructed from sea level pressure fields statistically linked to Sahel rainfall. This approach enables a more dynamic and dataset-flexible diagnostic that captures both regional and remote drivers in a unified framework. While we do not present a full side-by-side performance comparison in terms of lead time or forecast skill, future studies should assess SMOPI’s added value in prediction systems alongside existing indices. Although SMOPI was deliberately constructed as a pressure-only index to maximize generalizability and comparability across datasets, future studies could investigate whether integrating SLP with additional variables, such as SST, mid-level winds, or humidity, might further improve its diagnostic or predictive skill, particularly in operational forecasting contexts.

Finally, although SMOPI was developed for the Sahel, its underlying methodology, linking regional precipitation to coherent SLP patterns, is hypothetically transferable to other monsoon regions, such as South Asia, East Asia, and South America, where precipitation variability is also shaped by regional dynamics and remote teleconnections28,29. By identifying region-specific SLP structures statistically connected to rainfall, SMOPI-like frameworks could serve as a unified template for global monsoon diagnostics, model evaluation, and climate risk assessments.

Methods

The reference reanalysis dataset utilized in this study is the Japanese 55-year Reanalysis (JRA-5564) with a spatial resolution of 1.25° × 1.25°. JRA-55 was chosen over the higher-resolution fifth-generation European Centre for Medium-Range Weather Forecasts (ECMWF) atmospheric reanalysis (ERA565), which has a finer grid spacing of 0.25° × 0.25°, due to its superior portrayal of the dominant mode (i.e., the first principal component PC1) of rainfall variability in the Sahel (Fig. S5a). This assertion is based on a comparison of both reanalysis datasets against three observational datasets: the Climatic Research Unit gridded Time Series (CRU TS4.0866) observational dataset, which has a resolution of 0.5° × 0.5° and covers the period 1901–2023, the University of Delaware Terrestrial precipitation version 5.01 (UDEL67 on a 0.5° × 0.5° grid from 1901 to 2017, and the Global Precipitation Climatology Center version 8 (GPCC68) with a 1° × 1° grid for 1891-2019 (Fig. S5a, b).

Additionally, the analysis includes 29 Coupled Model Intercomparison Projects phase 6 models69 and their multi-model ensemble mean (CMIP6, thereafter) from the first realization (‘r1i1p1f1’; Table S3). As previously noted, CMIP models failed to reproduce the severe Sahel droughts of the 1970s and 1980s6,7 (Fig. S5a, b). Including them in the analysis allows assessing whether the proposed index can accurately report this shortcoming. Specifically, examining the consistency between SMOPI and precipitation patterns simulated by CMIP6 tests the index’s effectiveness in capturing Sahelian precipitation variability within a broader global context. To achieve this, the study period extends from 1965 to 2014, i.e. 50 years, ensuring coverage of both the prolonged drought episodes (1970s–1980s) and the subsequent rainfall recovery phase (1990s–onward) in the Sahel. Limiting the study period to 2014 is also contingent on the availability of CMIP6 historical data. All datasets have been remapped onto a common 2.81° × 2.81° grid to align with the lowest resolution among the models. While this may reduce spatial gradients in regions like the Sahel, the SMOPI construction relies on regional SLP box averages, which are less affected by resolution loss. Comparisons between the native and regridded datasets confirmed that the key correlation structures underlying SMOPI remained consistent.

During the summer monsoon season, June-September (JJAS), subtracting the tropical mean SLP (30°S–30°N, 180°W–180°E) from the global SLP reveals the spatial distribution of oceanic high-pressure regions (Figs. S23 and S24). Some of these high-pressure systems directly influence the WAM system. For instance, the South Atlantic High (SAH) plays a crucial role in regulating the availability of monsoon flow over the Gulf of Guinea. Masses of moist air advection originating from the SAH, initially southeasterly, are deflected by the Coriolis force, turning into southwesterlies over the Gulf of Guinea. Similarly, the North Atlantic High (NAH) is associated with strong monsoon rainfall and positive phases of the North Atlantic Oscillation (NAO70). Other high-pressure centres exert an indirect modulatory effect. Mascarene High (MH) is a notable example, which sustains the Indian monsoon system71. In turn, the Indian and West African monsoons share a common upper-tropospheric circulation component, the TEJ, whose intensity in each sector depends on region-specific factors43.

Building on these observations, we explore the relationship between SLP over oceanic basins and Sahelian rainfall. To achieve this, we employed three statistical metrics: the Pearson correlation coefficient, the distance correlation, and linear regression. First, we used the Pearson correlation coefficient, which is commonly applied to identify linear relationships between two normally distributed variables. This analysis allowed us to highlight the oceanic basins that exhibit strong and statistically significant (based on a two-tailed Student’s t-test with a significance level of p < 0.01) teleconnections with the Sahel and to determine the direction of these relationships. However, since the Pearson correlation is limited to detecting linear dependencies, it may overlook nonlinear interactions, potentially leading to inaccuracies in identifying the most relevant oceanic basins. To address this limitation, we further employed the distance correlation, a more comprehensive metric capable of capturing both linear and nonlinear relationships, to assess the sensitivity of our results based on Pearson correlation. Finally, recognizing that correlation does not imply causality, we applied linear regression coefficients to reinforce the robustness of our findings.

Based on the sign (positive or negative) of the relationship between each oceanic or continental basin and Sahel precipitation72, the SMOPI is defined by the following equation:

$${SMOPI}=\frac{1}{4}({\beta }_{1}{{SLP}}_{1}+{\beta }_{2}{{SLP}}_{2}+{\beta }_{3}{{SLP}}_{3}+{\beta }_{4}{{SLP}}_{4})-{\beta }_{5}{{SLP}}_{5}$$
(1)

where SLP1, SLP2, SLP3, SLP4, and SLP5 denote area-averaged SLP over the respective identified oceanic or continental basins shown in Fig. 1. The associated coefficients \({\beta }_{k}\)(with k = 1, 2, 3, 4, 5) serve as weights for each SLP region, reflecting the geometric shape of their respective grids and approximating their real contribution to the strength of SMOPI. These coefficients are calculated as area-weighted averages of SLP using the following equation:

$${\beta }_{k}=\frac{{\varSigma }_{i,j}{X}_{i,j}\cos ({\phi }_{i})}{{\varSigma }_{i,j}\cos ({\phi }_{i})}{\rm{with\; k}}=(\mathrm{1,2,3,4,5})$$
(2)

where X(i,j) denotes the SLP field, i indexes latitudes, j longitudes and \(\cos ({\phi }_{i})\) is the weight associated with the latitude \({\phi }_{i}\). The coefficients \(\beta\) are then used to multiply the corresponding SLP box in the SMOPI formula. The weighting coefficients \({\beta }_{k}\) are determined over the entire analysis period (1965-2014). They reflect the spatial and temporal variability of the SLP within each box and are therefore inherently dependent on the dataset and analysis period. As such, the \({\beta }_{k}\) values are not universal constants, but vary depending on the magnitude and structure of the SLP variability across datasets and time windows. This sensitivity emphasizes that for prediction or forecasting applications, the coefficients should be derived from the dataset used, thus ensuring consistency between the SMOPI and the variability of the data source. It is worth noting that SLP boxes are chosen so that they include the position of the maximum or minimum correlations. This makes the SMOPI less sensitive to the size of SLP boxes. The intensity of SMOPI (\({I}_{{SMOPI}}\)) is defined as the standardized anomaly of SMOPI, given by the equation:

$${I}_{{SMOPI}}=\frac{{SMOPI}-\overline{{SMOPI}}}{{\sigma }_{{SMOPI}}}$$
(3)

where \(\overline{{SMOPI}}\) designates the long-term mean of SMOPI, and \({\sigma }_{{SMOPI}}\) represents its standard deviation. As defined, the SMOPI can be used across different scales, from subseasonal to multidacaldal.

To examine how \({I}_{{SMOPI}}\) informs the Sahel monsoon rainfall intensity, we constructed composites based on years of strong (positive) and weak (negative) \({I}_{{SMOPI}}\), respectively. Specifically, positive composites correspond to years when \({I}_{{SMOPI}} > +0.5\), while negative composites are defined for years when \({I}_{{SMOPI}} < -0.5\). The features of key regional and remote drivers of the Sahel monsoon rainfall system are then examined during each composite phase. This helps identify whether \({I}_{{SMOPI}}\) effectively reflects hydrodynamic conditions conducive to wetting or drying in the Sahel. The effects of the SMOPI’s strength are explored by analyzing its (1) interannual and (2) intra-seasonal interannual variability of the JJAS season. In this article, the first case will be referred to simply as interannual variability, while the second case will be referred to as intra-seasonal variability. The interannual variability refers to year-to-year changes in JJAS-averaged SMOPI values (one value per year), while intra-seasonal or subseasonal variability refers to month-to-month fluctuations within the JJAS season, using the monthly values of SMOPI for June, July, August, and September across all years. We believe that examining the interannual variability of the SMOPI can reveal changes in the Sahel’s climate variability, especially in the context of global warming. Understanding these interannual variations is crucial for improving the accuracy of long-term climate projections, which can be beneficial to early warning systems and climate adaptation strategies. On the other hand, exploring intra-seasonal variability allows for a more detailed understanding of the shorter-term, within-season variations in the SMOPI. This is particularly important for operational forecasting and early warning systems that focus on seasonal weather patterns. By investigating these shorter-term fluctuations, one can, for instance, predict the onset and intensity of the monsoon more accurately, which has significant implications for e.g. agricultural planning, water management, and disaster preparedness in the Sahel region. Together, these two approaches provide complementary perspectives on the role of the SMOPI in shaping both the short-term and long-term climate dynamics of the Sahel. Each approach has its own unique contribution to enhancing climate projections, improving forecasting models, and ultimately strengthening early warning systems to better respond to the impacts of climate change.