Introduction

The first seminal works reporting single photon emission in transition metal dichalcogenides (TMDs)1,2,3,4,5 have stimulated an explosion of research activities aimed at investigating the possibility to use quantum emitters (QEs) in TMDs for ultra-compact quantum photonics6,7. Compared to other established solid-state-based quantum-light sources, such as semiconductor quantum dots, QEs in TMDs have the clear advantage of being relatively simple and cheap to fabricate, and their spatial position across the substrate can be controlled with high precision8,9,10,11,12. In addition, well-established processing techniques developed for conventional semiconductors can also be exported to TMDs so as to achieve, for example, coupling of QEs with nanophotonic cavities or tuning of QE emission properties via external perturbations13,14,15,16,17,18,19. Yet, QEs in TMDs still need to prove their real potential for quantum photonics: even though single photon emission in TMDs can be routinely observed, the low photon indistinguishability20 and coherence time21 are limiting factors. Even the generation of entangled photons—a possibility suggested by recent works but hampered by the presence of a sizeable exciton fine structure splitting—has still to be demonstrated22,23. Therefore, it is quite clear that additional research activities aimed at understanding the origin and the fundamental properties of QEs in TMDs, as well as at developing novel source-engineering methods, are paramount.

The formation of QEs in TMDs has been observed in WSe2, WS2, MoS2, and MoTe2, using a variety of methods8,10,12,24,25. Most of them make use of static strain-gradients that switch on exciton funnelling towards localized potential wells where single photon emission takes place. Whether strain alone is sufficient to create these potential wells, or it needs the aid of defects to enable the formation of localized intervalley-bound states, is still a question of theoretical debate26,27,28. From the experimental side, on the other hand, strain gradients that allow for the formation of QEs are usually obtained upon transferring thin TMD crystals fabricated via mechanical exfoliation on textured substrates featuring nanopillars, metal nanostructures, nano-indentations, and nanobubbles8,29,30,31,32 to mention a few. Recent experiments using an atomic force microscopy (AFM) tip have also shown that it is possible to attain tight control over the strain profile, and the deterministic writing of QEs in TMDs has become a reality29. However, in all these schemes, the strain configuration is usually frozen. This leads to QEs whose emission properties are fixed by the local degree of bending of the monolayer (ML), i.e., by the local strain configuration that has enabled their formation. Moreover, different QEs feature dissimilar emission properties (including energy, intensity, and polarization) due to different local strain configurations at the QE location. This is clearly not ideal for several advanced quantum photonic applications, which instead require photonic states with the same properties. Previous attempts to strain tuning of TMDs have indeed demonstrated the possibility to attain dynamic control over the exciton emission energy and polarization angle13,33,34. However, considering the key role of strain, a natural question arises: can strain be used to dynamically control the brightness of QEs in TMDs?

In this work, we demonstrate experimentally and theoretically an important aspect that has been overlooked in previous works due to the lack of suitable technological platforms: the possibility of using dynamic strain fields to control the distribution of excitons among individual QEs. This is achieved via a novel device featuring piezoelectric pillars onto which a WSe2 ML is transferred. Specifically, we show that the application of a voltage to the device allows us to tune not only the energy but also the brightness of QEs in TMDs. Numerical simulations combined with drift-diffusion equations show that the experimental findings can be explained by a strain-induced reconfigurable potential landscape with localized potential wells, whose confining energy can be modified to change the QEs being populated by the photo-generated carriers.

Results

Site-controlled and energy-tunable quantum emitters on piezoelectric pillars

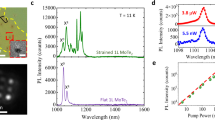
The working principle of the hybrid 2D-semiconductor-piezoelectric device used in this work is illustrated in Fig. 1a: it consists of a gold-coated (001)-[Pb(Mg1/3Nb2/3)O3]0.72-[PbTiO3]0.28 (PMN-PT) piezoelectric plate with a WSe2 ML attached to it by Van der Waals forces (see “Methods”). The top side of the piezoelectric plate is electrically grounded, whereas a voltage is applied on the bottom side: an induced vertical electric field (Fp) along the poling direction of the PMN-PT produces an out-of-plane (strain along the z-direction) and an in-plane (strain in the x-y direction) deformation of the plate, which is then transferred to the attached ML. The amplitude and polarity of the applied voltage control the magnitude and the compressive/tensile nature of the strain field, respectively14,33. It is well known that a voltage applied to the piezoelectric actuator induces a modification of the strain status of the semiconductor nanomaterial attached to it. This has been confirmed in the past, not only using optical spectroscopy35 but also via direct X-ray experiments36. To induce the static deformations of the ML at predefined positions, i.e., the formation of site-controlled QEs8, an array of piezoelectric pillars is fabricated by focused ion beam (FIB) (see “Methods”). The diameter (height) of the pillars is about 1.4 μm (115 nm), and they are arranged across the substrate in a square pattern. Figure 1b shows an optical microscopy picture of the device for a pitch distance between pillars of 5 μm. We highlight that, besides inducing the formation of QEs in the ML, the piezoelectric pillars can deform themselves to dynamically reconfigure the strain state of the attached ML. Figure 1c shows the AFM image from one of the pillars covered with the ML, which results in being firmly attached to the surface of the piezoelectric plate. Interestingly for what will be discussed in the following, nanometer-sized protuberances (height~10 nm and diameter ~50–100 nm) are formed along a corona over the pillars’ edges. This is ascribed to ML bending at imperfections formed during the device fabrication and is likely to be responsible for the formation of QEs, as explained below. These protuberances are an integral part of the piezoelectric pillar and deform with it while applying the electric field Fp (see Supplementary Note 12 for further details).

Fig. 1: The hybrid 2D-semiconductor-piezoelectric device.
figure 1

a Sketch of the device consisting of a PMN-PT piezoelectric plate featuring pillars over which a WSe2 ML is transferred. The top and bottom surfaces of the plate are gold-coated. The application of a voltage (electric field Fp along the poling direction) through an AlN chip-carrier produces the out-of-plane (ε⊥) and in-plane (ε||) deformation of the piezoelectric plate, which is eventually transferred to the attached ML. b Optical-microscopy image of a WSe2 ML (transparent brownish region delimited by a dashed white line) transferred on top of the piezoelectric pillars. c 3D AFM picture of a representative piezoelectric pillar (height~115 nm and diameter~1400 nm) covered by a WSe2 ML. d Micro-PL map of a WSe2 ML transferred on top of piezoelectric pillars taken on the region highlighted by the point-dashed black box in (b). The maximum intensity of the PL spectrum is reported for each pixel and normalized to the absolute maximum recorded over the entire map. Dashed white circles highlight the position of the four pillars. e Micro-PL spectra recorded outside (orange line) and at the edge (dark-cyan line) of a pillar. The emission energy of the WSe2 ML 2D-neutral-exciton is indicated with a blue vertical line. f Second-order autocorrelation measurement obtained on a single QE. The single photon emission nature is confirmed by the low value g2(0) = 0.21(3). The orange solid line shows the fit to the experimental data55, while the dashed orange one is the single-photon limit.

Full size image

To investigate the formation of site-controlled QEs, we performed spatially resolved micro-photoluminescence (PL) measurements at 5 K (see “Methods”). Figure 1d shows the PL intensity map as obtained by detecting light in the spectral window 710–780 nm and taking the maximum value of the PL spectrum while scanning the excitation laser spot in steps of about 110 nm around four pillars. Local PL intensity maxima attributed to the radiative recombination of localized excitons are found on top of the pillars, specifically around the corona. Despite these lines are related to exciton or multiexciton complexes (such as trions, biexcitons, etc.), we generally refer to them as localized excitons. We also note that the contribution of the 2D neutral free exciton (expected at around 1.74 eV, see Fig. 1e) is negligible for the excitation power used in the experiments. Representative micro-PL spectra acquired outside and at the edge of a pillar are shown in Fig. 1e. In the latter, a relatively sharp (full width at half maximum of ~370 µeV) emission line is observed in the spectral range where QEs in WSe2 usually appear3,5. To demonstrate that these isolated lines act as single photon sources, we spectrally filter one of them and perform second-order photon-correlation measurements g(2)(τ) using a standard Hanbury–Brown and Twiss set-up. As shown in Fig. 1f, pronounced photon antibunching is observed, with values at zero-time delay as low as g(2)(0) = 0.21 ± 0.03. We repeated the experiments for several emitters and observed similar results, thus unequivocally demonstrating that these recombination centers act as nonclassical light sources. We attribute the origin of these QEs to the static strain gradients that drive the photo-generated excitons into potential wells forming at the border of the top part of the pillars, specifically at the protuberances visible in the AFM image of Fig. 1c31. It is important to mention that our results agree with previously reported studies that use pillars of similar size and aspect ratio8. However, here the pillars are made from a piezoelectric material that can deform its shape and thus enable dynamic studies of the optical properties of the QEs.

To investigate the type of strain introduced by the piezoelectric pillar, we first perform finite-element-method (FEM) numerical simulations of a PMN-PT plate featuring pillars on top (no ML attached) as a function of the electric field Fp applied along the poling direction. We stress that the protuberances at the pillars’ rim (see Fig. 1c) are not considered in these simulations, but they will be the focus of the next section. Figure 2a shows the hydrostatic in-plane strain \({\varepsilon }_{{xx}}+{\varepsilon }_{{yy}}\) map for Fp = 15 kV/cm. A nonuniform strain distribution is observed on top of the pillar, with compressive strain values varying from about −0.25% at the center to about −0.1% towards the edges, where strain-relaxation is at play. Since most of the QEs occur at the edges, the dynamic strain we induce is in the order of 0.1%, which prevents us from large changes in the oscillator strength (see Supplementary Note 8). The out-of-plane strain \({\varepsilon }_{{zz}}\) is also slightly compressive, as shown in Fig. 2b together with the morphological changes of the pillar upon the application of different Fp. These changes can be ascribed to an enhanced electric field at the edge (in analogy with a “tip effect”), or to a competing deformation of the sides (which move laterally) and the top part (which moves upward/downward), resulting in a nontrivial deformation at the corners.

Fig. 2: Strain effects on the QE emission energy.
figure 2

a Numerical FEM simulation of the in-plane hydrostatic strain \({\varepsilon }_{{xx}}+{\varepsilon }_{{yy}}\) as obtained in a piezoelectric (001)-PMN-PT plate with pillars and for an applied electric field Fp = 15 kV/cm. b Profile of the pillar along the Z-X directions and as a function of the electric field applied to the piezoelectric plate. The insert shows the FEM simulation of the out-of-plane strain \({\varepsilon }_{{zz}}\) for Fp = 15 kV/cm. c In-plane hydrostatic strain \({\varepsilon }_{{xx}}+{\varepsilon }_{{yy}}\) taken from numerical simulations as a function of Fp. The different lines correspond to the strain measured at the different points highlighted with letters in (a). d Shift of the energy of QEs located at different positions on top of the piezoelectric pillar as a function of Fp. The different colored points correspond to different QEs. The solid lines are linear fits to the experimental data. The insert shows the histogram of the energy-shift rate of all the QEs investigated in this work.

Full size image

Taking into account that a compressive/tensile strain introduces an increase/decrease of the WSe2 band-gap, we expect a blueshift of all the QE emission lines when we apply positive voltages, which is exactly what we observe experimentally, as shown in Fig. 2d. The spread in the energy shift rates can be justified with the FEM simulations, which returned values that depend on the specific location across the pillar (see Fig. 2c for the points highlighted with letters in Fig. 2a, and Supplementary Note 10 for a detailed discussion). We measure shift rates up to 0.3 meV cm/kV, with differences of up to one order of magnitude for distinct QEs (see the insert of Fig. 2d). Before proceeding further, we would like to emphasize the relevance of this result: first, in stark contrast to previous works focusing on naturally occurring wrinkles on piezoelectric actuators (without pillars)15, we always observe that the energy shift follows the sign of the Fp. This is readily explained by the simulations shown in Fig. 2a, which, in combination with Fig. 2c, d, also suggests that the ML closely follows the pillar shape. Second, we highlight that the energy shift is fully reversible (see Supplementary Note 1) and, when we use both positive and negative Fp, we can observe energy variations up to 8 meV (see Supplementary Fig. 2.3h). These features of the device are the key to obtain the following main result of our work.

Strain-induced redistribution of excitons among localized quantum emitters

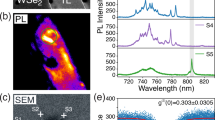
We now investigate the evolution of the PL intensity with Fp to understand whether strain can be used to control the population of QEs in TMDs. Figure 3a illustrates a series of spectra collected while varying Fp in the range 0–15–0 kV/cm. Two emitters, labeled as QE1 and QE2, exhibit an interesting behavior: while Fp increases, the maximum PL intensity of QE1 (QE2) decreases (increases). This feature is clearly visible in Fig. 3b, which depicts the two spectra at 0 and 15 kV/cm. The intensity of QE1 drops to a factor 0.6 of its initial value at 15 kV/cm, while QE2 increases by a factor 3. Additionally, these intensity modulations are reversible. Figure 3c, d shows the maximum PL intensity in the spectral range of QE1 and QE2, respectively, as a function of Fp. The blue and red dots, which correspond to the forward and backward ramps, overlap, suggesting the reversibility of the QEs’ brightening/darkening.

Fig. 3: Strain-induced variation of QEs’ intensity.
figure 3

a Color-map of the maximum PL intensity as a function of the external electric field Fp. The spectra are collected on a pillar while a back-and-forth scan of Fp from 0 to 15 kV/cm is performed. b PL spectra at 0 and 15 kV/cm. A QE1 (QE2) darkening (brightening) is observed at 15 kV/cm. c–d Maximum PL intensity as a function of Fp for both QE1 and QE2, respectively. The intensity of the two emitters shows two main features: (i) while QE1 decreases for increasing Fp, QE2 increases, and (ii) the intensity of both QEs goes back to the initial value, suggesting that the process is reversible.

Full size image

To substantiate these findings, we systematically investigate the evolution of the PL intensity with Fp over one specific pillar—pillar 2 in Fig. 1d—(see Fig. 4a), but very similar results were observed in the other three pillars (see Supplementary Note 2). Figure 4e shows five PL spectra collected from −10 to 30 kV/cm in steps of 10 kV/cm collected from the white spot in Fig. 4a. Stark changes are observed. Besides the systematic energy shift discussed in the previous section, we find that QEs strongly change their intensity, some even disappearing. These changes are particularly apparent for the two emission lines indicated by QE2 and QE3 in Fig. 4e. As we are dealing with intensity measurements, particular care must be devoted to the alignment and stability of the collection optics. We must exclude, for example, drifts of the sample with respect to the objective collecting light while the pillar is expanding/contracting. We adopt several preventive measures to verify this is not the case in our experiments. First, we utilize an experimental set-up in which the objective is held at a low temperature and in a vacuum inside the cryostat, together with the sample. This ensures long-term stability, and we can collect light from the same QE for days without the need to re-adjust the sample position. Second, we record PL maps (like the one shown in Fig. 4a) for each applied Fp and we find that the panchromatic integrated intensity—as obtained by integrating the entire PL spectrum over all the pixels inside the region of interest (Zone 1 and Zone 2, determined as the dashed green and purple ellipses in Fig. 4a)—remains almost constant (see data points in Fig. 4f, where the standard deviation over all the data is below 5%). This clearly indicates that the number of detected photogenerated excitons does not vary with Fp and that no misalignment of the collection optics is affecting our experiments. Third, we performed a careful analysis to demonstrate that blinking at a short time scale does not affect the estimation of the QE intensities (see Supplementary Note 3), which we can provide with about 15% uncertainty. Finally, to exclude unequivocally that the intensity changes are related to sample drifts, we perform multi-Gaussian fits of the PL spectrum recorded in each position of the spatial map. Then we record the intensity of the light emitted by the single QE, namely the intensity of the Gaussian peak of a given energy, in each position over the whole 2D map and for each specific Fp. This procedure, which follows the one reported in ref. 37 and which we called hyperspectral maps, leaves us with new maps in which we can single out the emission area of each specific QE, which corresponds to the area of the device where each specific QE generates photons. We then combine the individual maps of each QE for each Fp, as shown in Fig. 4b–d for QE1 (1.644 eV at Fp = 0), QE2 (1.691 eV at Fp = 0), and QE3 (1.672 eV at Fp = 0) acquired at Fp = −10,10, and 30 kV/cm. Each map of individual QEs is separately normalized to its maximum along the electric field sweep. We note that the size of these areas is determined by the exciton diffusion length and the diffraction limit, about 300 nm for the optics and laser used in this work (see “Methods”). We emphasize that, although we cannot determine the exact position of the emitters due to their close proximity, it is possible to distinguish them by their optical emission energy in the PL spectra. For further considerations about the strain effects on the QEs’ position, see Supplementary Note 4. With these maps at hand, we can extract both the total integrated intensity from a single QE (Fig. 4g), as well as the energy shifts of each QE (Fig. 4f) for each value of Fp. It is evident that QE2 (QE3) dramatically increases (decreases) in intensity with Fp, while QE1 remains almost constant. Similar intensity changes are observed for other QEs visible in the spectra shown in Fig. 4e (note that it is not always possible to follow their complete evolution with Fp, as some lines merge with others). Yet, these measurements show that piezoelectric-induced strain can modify the intensity of each emission line dynamically. Remarkably, the intensity of QE3 drops from several thousand counts to just a few tens, approaching the noise level of our detection system, for applied electric fields above 20 kV/cm. It is also worth noticing that no clear correlation between the energy shift and the rate at which the PL intensity changes is observed. Besides lines that change intensity in a nonlinear fashion but at a constant energy-shift rate, we also found QEs with similar energy-shift rates (like QE2 and QE3) but featuring opposite intensity changes.

Fig. 4: Exciton redistribution among localized QEs.
figure 4

a Spatially resolved micro-PL map of pillar #2 shown in Fig. 1d). b Spatially resolved micro-PL map of light emitted by QE1, QE2, and QE3 for Fp = −10 kV/cm. The maps are extracted separately from a hyperspectral map of PL spectra and making multi-Gaussian fits of the single PL spectrum in each pixel to identify the intensity of the light emitted by the single QE in each position of the whole 2D map. Each map of an individual QE is separately normalized to its maximum along the electric field sweep. The white area corresponds to regions where the QE’s intensity is smaller than 10% of its maximum. c The same as (b) for Fp = 10 kV/cm. d The same as (b) for Fp = 30 kV/cm. e Micro-PL spectra recorded at the position marked by the white spot in (a). The spectra show the evolution from −10 kV/cm to 30 kV/cm. The orange dots highlight the QE3 expected position, showing the emitter’s disappearance. The dashed orange and red arrows guide eyes to follow QE2 and QE3. f Integrated area of the panchromatic PL spectrum as a function of Fp in different regions over the pillar. Brown dots refer to the total pillar area, while the green and purple dots refer to the two ellipses shown with the same color in (a), labelled as Zone 1 and Zone 2, respectively. We estimated an error of 10% from an analysis of integrated PL vs time, and reported it for three points as an example. g Normalized integrated area of the PL intensity of the three QEs studied in (b–d) as a function of Fp. The uncertainty in the intensities is estimated to be around 15%, as discussed in supplementary, Note 3. h Energy shifts of the three QEs studied in (b–d) as a function of Fp. The solid lines are linear fits to the experimental data, while m stands for the energy shift rate.

Full size image

At first sight, there can be different explanations for this phenomenon. For instance, one may argue that the band bending ensuing the application of Fp can lead to a change of the exciton dipole moment and, possibly, a separation of electrons and holes that decreases the emission intensity and favors the appearance of charged exciton complexes38. Another possible explanation—in the well-established intervalley-defect-exciton picture28—is that strain modifies the coupling between weakly localized exciton states and strongly localized defect levels. Furthermore, strain could also affect the electron-hole exchange interaction due to a modification of the intervalley scattering rates39. Both effects should indeed lead to a change in the oscillator strength of the transitions. However, two important points need to be noticed here: First, the strain values delivered by our actuator are on the order of 0.1–0.3% and should lead to a relatively small change in the oscillator strength of the QE transitions13,28 (see Supplementary Note 8 for further details). Second and most importantly, the overall integrated intensity of the light emitted by the QEs over all their extent remains constant. This is true not only for the whole pillar but also for spatial regions that have a size comparable to the exciton diffusion length, as shown in Fig. 4f for the green and purple ellipses in Fig. 4a. Thus, the fact that the QEs change intensity while the overall PL intensity from the region of interest remains constant strongly suggests that the induced strain is regulating the distribution of the photogenerated excitons among the different QEs without changing their actual number (i.e., we can exclude strong nonradiative contributions).

Discussion

At this point, a rather simple and intuitive physical picture emerges: The QEs originate from localized potential wells (local band-gap minima) of a disordered potential landscape, similar to the case of random alloys40. Their populations, directly linked to their PL emission intensity, are related to the way excitons funnel and thermalize toward the potential-landscape minima, which are in turn determined by the local deformation of the ML right after the fabrication process, i.e., by the static strain field. Instead, the dynamic strain delivered by the piezoelectric pillar modifies the relative heights of different potential wells and the way photo-generated excitons distribute among the different QEs while keeping their overall number constant. The exciton distribution changes at each applied Fp, and the QE PL intensity modifies accordingly. Note that each PL map is performed after the potential landscape has been modified by the applied dynamic strain. Once the new potential profile is established, photo-generated excitons are funnelled accordingly, resulting in an exciton redistribution driven by diffusion within the strain-modulated potential landscape. To verify the correctness of this suggestive hypothesis, we perform theoretical calculations that combine drift-diffusion equations with the strain profile obtained by numerical FEM simulations, as described in the following.

We use the excitonic drift-diffusion equations considering a potential landscape \(u\left(\vec{r}\right)\) which changes as a function of the position \(r\) across the pillar. For a nonuniform density of excitons \(n\left(\vec{r}\right)\), the equilibrium state condition for exciton diffusion \(\vec{{J}_{d}}\) = \(D\nabla n\left(\vec{r}\right)\) and drift current \(\vec{{J}_{\mu }}=\mu n\left(\vec{r}\right)\nabla u\left(\vec{r}\right)\) is described by the following differential equation41,42,43:

$$\nabla \left(\vec{{J}_{d}}\right)+\,\nabla \left(\vec{{J}_{\mu }}\right)-\frac{n(\vec{r})}{\tau }-{n}^{2}\left(\vec{r}\right){R}_{A}+S\left(\vec{r}\right)=0,$$
(1)

where D is the diffusion coefficient, µ = \(\frac{D}{{K}_{B}T}\) is the mobility that depends on temperature, τ is the exciton lifetime, and RA is the Auger recombination rate that we assume to be negligible with respect to the radiative recombination rate due to the low power excitation used during the experiment44 (see Supplementary Note 9 for further details). S(r) is the exciton generation source, i.e., our excitation laser, which, according to the experimental conditions, we assume to have a Gaussian profile S(r) = \(\frac{{I}_{0}}{2\pi {\sigma }^{2}}{e}^{-\frac{{r}^{2}}{2{\sigma }^{2}}}\) with maximum intensity \({I}_{0}\) and σ is the beam width radius. In Eq. 1, the terms that dynamically drive the change in the exciton density are the diffusion and the drift terms. The generation and recombination terms are mainly responsible for exciton density in steady-state conditions, with the latter also partially responsible for the size of the potential landscape experienced by the exciton through diffusion length \(l=\sqrt{D* \tau }\). On the other hand, the ratio between the diffusion coefficient and the mobility, which is basically related to the temperature, sets two different regimes: (i) the diffusive regime in which most of the excitons spread over the whole area—a condition that is usually achieved at elevated temperatures; (ii) at low temperature the drift regime rules the diffusion of excitons, which move towards the minima of the potential landscape. Since the experiments are performed at low temperatures (4 K), we can safely assume that the simulations are mainly concerned with the drift regime

To calculate the exciton distribution \(n\left(r\right)\), we first need to evaluate the potential landscape \(u\left(r\right)\) upon the application of Fp, which is obtained by FEM simulations of the strain status of the piezoelectric pillar (see methods and Supplementary Note 7). More specifically, we first calculate the hydrostatic strain distribution map (\({\varepsilon }_{{xx}}\,\)+ \({\varepsilon }_{{yy}}\)) and then obtain the bandgap energy variation with respect to the one corresponding to the unstrained ML via (see Supplementary Note 6):

$${E}_{g}({eV})\simeq {E}_{{go}}-0.0638{\varepsilon }_{{xx}}-0.0636{\varepsilon }_{{yy}},$$
(2)

where \({E}_{{go}}\) is the “unstrained” bandgap energy45,46. Note that the contribution of \({\varepsilon }_{{zz}}\) is found to be negligible and is therefore neglected in the calculation.

In this step of our theoretical approach, there are a few points that need to be discussed: First, we now consider the geometrical protuberances at the pillar rim that simulate the disordered profile (visible in the AFM map of Fig. 1c), leading to the formation of the different QEs. Second, we highlight that it is extremely difficult to experimentally evaluate the initial static strain configuration (or pre-strain) at the QE location with the desired accuracy, as it results right after mechanical exfoliation. This would require optical spectroscopy techniques with sub-diffraction-limited resolution at low temperature, compatible with the application of high voltages, and with sufficient stability and throughput to enable intensity measurements with high accuracy. Thus, we can evaluate only the dynamic changes of \(u\left(r\right)\) induced by Fp, i.e., by the strain fields induced by the piezoelectric actuator. This is not a problem per se, but our model requires the initial height of the potential well leading to the QE formation as input. Considering that the QEs are formed at the geometrical protuberances along the periphery of the pillar (see Fig. 1c) and that the emission energy is approximately equal to the local bandgap value of the ML at these positions, the height of the potential wells can be indirectly estimated via Eq. (2) and assuming the induced strains by the protuberances \({\varepsilon }_{{tot}}\) = \({\varepsilon }_{{yy}}+{\varepsilon }_{{xx}}\). More specifically, using the spread in emission energy of the different QEs (which varies in a range from 0.04 to 0.1 eV with respect to the unstrained ML emission energy of the 2D-exciton, about 1.75 eV) Eq. (2) shows that the pre-strain in the ML at the QEs positions ranges from about 0.3–0.7% (we did not consider quantum confinement effects in our model, as the withdrawn conclusions are qualitatively similar).

These pre-strain values are thus randomly assigned to the different protuberances, whose geometries have been included in the FEM simulations according to the results of AFM measurements (see Supplementary Note 7 for more details). Since it is reasonable that the ML closely follows the piezoelectric substrate, we assume it feels the same strain as Fp varies. Finally, we note that the pillar structure is not pivotal in redistributing excitons between QEs. Indeed, the pillar initially deforms the ML leading to a bandgap gradient in the ML from the bottom (higher) to top (lower) (see Supplementary Note 8), and thus a net exciton funnelling towards the top of the pillar where they recombine at QEs positions (see Fig. 1d). We therefore limit our study to the diffusion of excitons between QEs placed along a circle mimicking the geometrical distribution of the protuberances on the pillar rim.

With u(r) at hand, we can now solve the drift-diffusion Eq. (1) and map the exciton distribution n(r) across the whole potential landscape, a procedure repeated at Fp = 50 kV/cm and 25 kV/cm. The left half of Fig. 5a shows the results for n(r) at Fp = 50 kV/cm. To reproduce our experimental settings, we performed a convolution between n(r) and a point spread function (PSF) with 250 nm FWHM to match the typical spatial extent of our QEs (as measured after spectrally isolating the different emission lines, see Fig. 4b–d and Supplementary Figs. 2.1–3). The right half of Fig. 5a shows the results of the convolution. The PSF enlarges the peaks in n(r) (corresponding to the protuberances), resulting in a profile which is similar to what was observed experimentally (as reported in Fig. 1d, for example). Figure 5b depicts the difference between the exciton densities n(r) at Fp = 50 and 25 kV/cm after the PSF convolution. We observe stark changes: some protuberances collect more/fewer excitons at the expense/in favor of others while the overall number of excitons across the profile remains constant—in perfect qualitative agreement with our experimental results. To obtain further insight into this effect, we show in Fig. 5c, d the values of the band gap variation and n(r), without PSF convolution, calculated along a circular corona parallel to the white arrow reported in Fig. 5a for both the values of Fp. It is apparent that the potential wells whose height/depth increases more with compressive strain gain excitons at the expense of nearby wells, as indicated by the black arrows in Fig. 5d. However, we emphasize that the relative height of the potential wells is not the only relevant parameter, but also the relative distance among the different protuberances plays a role in the exciton diffusion (see discussion in Supplementary Note 11). Moreover, focusing on just a few protuberances (see Fig. 5e), we can clearly observe cases in which each of them gains/loses excitons at a different rate, a behavior that we also observe experimentally (see Supplementary Notes2 and 5). We want to highlight that we are not claiming that the exciton redistribution occurs between individual emitters. Even if this picture is suggestive, it is unlikely to happen because of the complex potential landscape, in which several QEs can collect excitons from a region having a size roughly equal to the exciton diffusion length. Therefore, the exciton redistribution likely occurs rather among many different QEs that are about 1 µm apart from each other.

Fig. 5: Simulation of exciton redistribution among localized QEs.
figure 5

a Exciton density distribution at Fp = 50 kV/cm with and without convolution with the point-spread function (PSF). The 250 nm PSF reproduces the effect of the collection optics. The result without convolution is the left portion of the image. The white arrow indicates the arc of circumference along which band gap variation and exciton density (without convolution) are extracted to build up (c). The white rectangle highlights the region selected for (d), where both defects gaining and losing excitons occur. b Variation of the exciton density distribution, obtained by subtracting the exciton density at Fp = 25 and 50 kV/cm after the PSF convolution. c Band-gap energy variation and d exciton density as recorded along the white arrow in (a) for Fp = 50 kV/cm and Fp = 25 kV/cm. For clarity, the black dashed line shows the energy shift obtained for Fp = 50 kV/cm red-shifted by 6.9 meV. e Schematics of the 3D exciton density for the five protuberances highlighted by the white box in (a) at Fp = 25 and 50 kV/cm after a Gaussian smoothing. The three central protuberances gain excitons while the two later ones lose carriers.

Full size image

In summary, our results show that the strain fields delivered by piezoelectric pillars allow the energy and the intensity of light emitted by QEs in TMDs MLs to be actively controlled. The experimental findings are explained by a strain-induced modification of a disordered potential landscape, which enables a redistribution of the excitons among different QEs. It is worth emphasizing that we can explain the experimental findings without invoking a strain-induced modification of the coupling between the monolayer exciton states and the localized defect states. In fact, the change in the oscillator strength of the optical transitions is supposed to be small for the strain values (about 0.1–0.3%) investigated in this work. Yet, devices that enable full control over the strain tensor in TMDs with a magnitude as large as 1% are available47, and we envision the development of integrated quantum photonic devices to control the flow of excitons among distinct and interconnected QEs in TMDs, and eventually, to switch them on and off on demand. Moreover, our device concept could be used to improve the brightness of single-photon sources in 2D materials and opens the path towards their exploitation in quantum communication applications48.

Methods

Sample fabrication

The piezoelectric pillars were fabricated on top of a 200-µm-thick PMN-PT piezoelectric plate by a FIB. The patterning of the piezoelectric substrates was performed using a cross-beam FIB/SEM microscope. The Ga+ Ion column was used for this purpose under an acceleration voltage of 30 kV with a current probe of 84 pA. Binary image-based masks for the definition of the circular pillar arrays have been created with an image pixel size of 5 nm in total areas of 18 × 18 μm2. Pillars with a diameter of 1400 nm were patterned. The milling rate was previously calibrated by creating cross-sectional cuts in the sample leading to total exposure times per 18 × 18 μm2 areas of 533 s for steps around 100 nm. Afterwards, both sides of the patterned piezoelectric plate were coated by electron-beam and thermal evaporation with a Cr(5 nm)/Au(40 nm) bilayer for electrical contact. The WSe2 ML was obtained by mechanical exfoliation on PDMS stamps and transferred on top of the gold-coated piezoelectric nanopillars by using the dry transfer technique49. A positive voltage was used for the poling of the piezoelectric plate, meaning that positive/negative voltages introduce an in-plane compressive/tensile strain field on its surface. A sketch of a complete device is shown in Fig. 1a. In particular, the strain fields are introduced on the attached ML by applying voltages on the bottom side of the piezoelectric plate while the top side is grounded.

Photoluminescence

A continuous-wave He-Ne laser emitting at 633 nm is used as an excitation laser source for the µ-PL experiment. The laser passes through a beam splitter, which reflects 10% of the laser light, and then it is sent through a periscope inside a He-closed-cycle cryostat equipped with an objective with 0.81 numerical aperture. The sample is mounted on an x-y-z piezoelectric stage and is electrically connected to an outer voltage supplier via high-voltage vacuum feedthroughs. The PL emitted by the sample is then collected by the same objective in a back-scattering geometry, and the collimated beam is spatially filtered via a single-mode optical fiber. A long pass filter filters out the laser at the spectrometer entrance, which is 750 mm long and equipped with a 300 g/mm diffraction grating. At the outport of the spectrometer, a liquid nitrogen-cooled CCD acquires the PL signals. The sample is mounted underneath the objective (kept fixed) and moved with nanopositioners in steps of about 110 nm. In this way, a PL spectrum is taken from every single pixel of the 2D map. The time correlation measurements are performed using a Hanbury–Brown and Twiss setup consisting of a beam splitter and two avalanche photodiodes (time resolution of about 400 ps) connected to correlation electronics.

Numerical simulations by finite element method (FEM)

The in-plane hydrostatic strain field (\({\varepsilon }_{{xx}}\) + \({\varepsilon }_{{yy}}\)) distribution on PMN-PT piezoelectric 5 × 5 mm2 plates—(001) orientation—is simulated by FEM using the commercially available software COMSOL Multiphysics. A 3D pillar model is built with a geometry inspired by AFM measurements. We placed different ellipsoids to model the nanometer-sized protuberances (which lead to the formation of QEs) along the pillar rim. The voltage is applied on the bottom side of the piezoelectric plate, inducing an out-of-plane electric field across the thickness of the piezoelectric plate, [001] direction, which is varied from 25 to 50 kV/cm. The top side of the piezoelectric plate is set to ground. The gluing effect of the device to a chip carrier (obtained using silver paint in the experiments) is simulated by including an isotropic solid material (“soft block”) under the piezoelectric substrate with a small Young modulus (about 500 Pa). The latter value has been checked in a separate work by direct comparison with experiments where the PL shift versus measured strain values have been analyzed36. The bottom boundary of the “soft block” is fixed. See Supplementary Note 7 for further information about the geometrical design and specific values for the elastic and piezoelectric tensor used for the PMN-PT plate.

Drift-diffusion model (DDE)

The drift-diffusion Eq. (1) is solved using the commercially available software COMSOL Multiphysics through the coefficient form PDE module. The details of the model can be found elsewhere41,42,43. We set the exciton density equal to zero at the borders, defined by a circle centered on the pillar’s center and radius equal to four times the pillar’s radius (2.8 µm). Our boundary conditions are realistic as, on the borders, the distance from potential minima is much greater than the diffusion length of the carriers (200/300 nm). To follow the experimental procedure, we illuminate a point of the potential landscape with the Gaussian laser source S(r), and we then run the drift-diffusion simulation to calculate n(r). We iterate the procedure scanning the laser source origin in steps of 200 nm over a square grid with an edge equal to 2 µm, and we then sum all the obtained n(r), convolving their weights with a Gaussian point spread function with 250 nm FWHM. The parameters used in the simulations are the ones reported in the following. D = 0.6 cm2/s, τ = 1.1 ns, T = 10 K, FWHMLaser = \(2* \sqrt{2{{ln}}\,{{ln}}\,\left(2\right)\,}*\sigma\) = 0.5 µm. Reported values of diffusion coefficients for excitons in monolayer TMDC range from D = 0.1 cm2/s to D = 10 cm2/s50. For the lifetime value, we chose a lifetime of the same order of magnitude as we measured in QEs in our sample, see Supplementary Note S9. It is worth mentioning that we run simulations with different lifetime values, spanning from ten ps to 10 ns. Since lifetime rules mainly the number of excitons, and partially the potential landscape felt by the excitons, only changes in the exciton density absolute numbers were observed.

Energy band-gap calculation in strained WSe2 monolayers

To calculate the dependence of the bandgap on the strain fields introduced by the piezoelectric device, we performed ab-initio simulations on strained WSe2 monolayers with the Quantum ESPRESSO package51. We used ultrasoft pseudopotentials52 and the GGA approximation with the PBE parametrization53 to treat exchange and correlation. A plane-wave energy cutoff of 55 Ry and a 7 × 7 k-point grid on the xy plane are used in the calculations. The coordinates were relaxed until all forces were smaller than 10−3 Ry/Bohr. The resulting band structure without strain has a direct bandgap of 1.53 eV. Notice that although the absolute value of the bandgap given by GGA is usually underestimated, the relative evolution with strain can be adequately captured54. Consequently, the actual strain field value can be calculated by introducing an offset. Next, we calculated the evolution of the bandgap change (ΔE) as a function of uniaxial \({\varepsilon }_{{xx}}\) and \({\varepsilon }_{{yy}}\) components of the strain fields (note that the \({\varepsilon }_{{zz}}\) component is found to be negligible). Such evolutions are roughly linear, and by interpolating them, it is possible to obtain the following expression (ΔE in eV and strain in %): ΔE(\({\varepsilon }_{{xx}}\), \({\varepsilon }_{{yy}}\)) = −0.0638364⋅\({\varepsilon }_{{xx}}\) − 0.0636273\(\cdot {\varepsilon }_{{yy}}\), where we have taken as the coordinate at the origin the average of the coordinates at the origin of both uniaxial interpolations. Using this formula, it is possible to reproduce the band-gap differences for arbitrary strain values with reasonable precision. The graph of the interpolation can be found in Supplementary Note 6.