Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

A unified realization of electrical quantities from the quantum International System of Units

Nature Electronics volume 8, pages 663–671 (2025)Cite this article

Subjects

Abstract

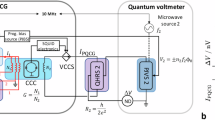
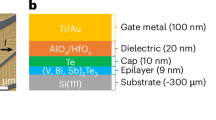
In the revised International System of Units (SI), the ohm and the volt are realized from the von Klitzing constant and the Josephson constant, and a practical realization of the ampere is possible by applying Ohm’s law directly to the quantum Hall and Josephson effects. As a result, it is possible to create an instrument capable of realizing all three primary electrical units, but the development of such a system remains challenging. Here we report a unified realization of the volt, ohm and ampere by integrating a quantum anomalous Hall resistor (QAHR) and a programmable Josephson voltage standard (PJVS) in a single cryostat. Our system has a quantum voltage output that ranges from 0.24 mV to 6.5 mV with combined relative uncertainties down to 3 μV V−1. The QAHR provides a realization of the ohm at zero magnetic field with uncertainties near 1 μΩ Ω−1. We use the QAHR to convert a longitudinal current to a quantized Hall voltage and then directly compare that against the PJVS to realize the ampere. We determine currents in the range of 9.33–252 nA, and our lowest uncertainty is 4.3 μA A−1 at 83.9 nA. For other current values, a systematic error that ranges from −10 μA A−1 to −30 μA A−1 is present due to the imperfect isolation of the PJVS microwave bias.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Illustration of a current measurement with the unified system.
Fig. 2: Validation of QAHR quantization.
Fig. 3: Direct realization of the ampere and contextualization.
Fig. 4: Time dependence of indirect realizations of the ampere and of QAHR longitudinal resistivity ρxx.

Similar content being viewed by others

Data availability

Data that support the findings of this study are included as Supplementary Information. Raw data files (for example, CCC output files) are available from the corresponding authors upon reasonable request. Source data are provided with this paper.

References

  1. Mills, I. M., Mohr, P. J., Quinn, T. J., Taylor, B. N. & Williams, E. R. Redefinition of the kilogram: a decision whose time has come. Metrologia 42, 71–80 (2005).

    Article  Google Scholar 

  2. Milton, M. J., Davis, R. & Fletcher, N. Towards a new SI: a review of progress made since 2011. Metrologia 51, R21 (2014).

    Article  Google Scholar 

  3. Davis, R. An introduction to the revised international system of units (si). IEEE Instrum. Meas. Mag. 22, 4–8 (2019).

    Article  Google Scholar 

  4. Poirier, W., Djordjevic, S., Schopfer, F. & Thévenot, O. The ampere and the electrical units in the quantum era. C. R. Phys. 20, 92–128 (2019).

    Article  Google Scholar 

  5. Taylor, B. & Witt, T. New international electrical reference standards based on the Josephson and quantum Hall effects. Metrologia 26, 47–62 (1989).

    Article  Google Scholar 

  6. Jeckelmann, B. & Jeanneret, B. The quantum Hall effect as an electrical resistance standard. Rep. Prog. Phys. 64, 1603–1655 (2001).

    Article  Google Scholar 

  7. Tzalenchuk, A. et al. Towards a quantum resistance standard based on epitaxial graphene. Nat. Nanotechnol. 5, 186–189 (2010).

    Article  Google Scholar 

  8. Schopfer, F. & Poirier, W. Quantum resistance standard accuracy close to the zero-dissipation state. J. Appl. Phys. 114, 064508 (2013).

    Article  Google Scholar 

  9. Ribeiro-Palau, R. et al. Quantum hall resistance standard in graphene devices under relaxed experimental conditions. Nat. Nanotechnol. 10, 965–971 (2015).

    Article  Google Scholar 

  10. Rigosi, A. F. & Elmquist, R. E. The quantum Hall effect in the era of the new SI. Semicond. Sci. Technol. 34, 093004 (2019).

    Article  Google Scholar 

  11. Bloch, F. Josephson effect in a superconducting ring. Phys. Rev. B 2, 109–121 (1970).

    Article  Google Scholar 

  12. Fulton, T. A. Implications of solid-state corrections to the Josephson voltage-frequency relation. Phys. Rev. B 7, 981–982 (1973).

    Article  Google Scholar 

  13. Clothier, W., Sloggett, G., Bairnsfather, H., Currey, M. & Benjamin, D. A determination of the volt. Metrologia 26, 9–46 (1989).

    Article  Google Scholar 

  14. Tiesinga, E., Mohr, P. J., Newell, D. B. & Taylor, B. N. CODATA recommended values of the fundamental physical constants: 2018. Rev. Mod. Phys. 93, 025010 (2021).

    Article  Google Scholar 

  15. Keller, M. W. Current status of the quantum metrology triangle. Metrologia 45, 102–109 (2008).

    Article  MathSciNet  Google Scholar 

  16. Scherer, H. & Camarota, B. Quantum metrology triangle experiments: a status review. Meas. Sci. Technol. 23, 124010 (2012).

    Article  Google Scholar 

  17. Hohls, F. et al. Semiconductor quantized voltage source. Phys. Rev. Lett. 109, 056802 (2012).

    Article  Google Scholar 

  18. Brun-Picard, J., Djordjevic, S., Leprat, D., Schopfer, F. & Poirier, W. Practical quantum realization of the ampere from the elementary charge. Phys. Rev. X 6, 041051 (2016).

    Google Scholar 

  19. Djordjevic, S., Behr, R. & Poirier, W. A primary quantum current standard based on the Josephson and the quantum Hall effects. Nat. Commun. 16, 1447 (2025).

    Article  Google Scholar 

  20. Sullivan, D. & Dziuba, R. F. Low temperature direct current comparators. Rev. Sci. Instrum. 45, 517–519 (1974).

    Article  Google Scholar 

  21. Williams, J. Cryogenic current comparators and their application to electrical metrology. IET Sci. Meas. Technol. 5, 211–224 (2011).

    Article  Google Scholar 

  22. Chae, D.-H., Kim, M.-S., Kim, W.-S., Oe, T. & Kaneko, N.-H. Quantum mechanical current-to-voltage conversion with quantum Hall resistance array. Metrologia 57, 025004 (2020).

    Article  Google Scholar 

  23. Chae, D.-H., Kim, M.-S., Oe, T. & Kaneko, N.-H. Series connection of quantum Hall resistance array and programmable Josephson voltage standard for current generation at one microampere. Metrologia 59, 065011 (2022).

    Article  Google Scholar 

  24. Chen, Y. et al. Massive Dirac fermion on the surface of a magnetically doped topological insulator. Science 329, 659–662 (2010).

    Article  Google Scholar 

  25. Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).

    Article  Google Scholar 

  26. Checkelsky, J. G., Ye, J., Onose, Y., Iwasa, Y. & Tokura, Y. Dirac-fermion-mediated ferromagnetism in a topological insulator. Nat. Phys. 8, 729–733 (2012).

    Article  Google Scholar 

  27. Fox, E. J. et al. Part-per-million quantization and current-induced breakdown of the quantum anomalous Hall effect. Phys. Rev. B 98, 075145 (2018).

    Article  Google Scholar 

  28. Götz, M. et al. Precision measurement of the quantized anomalous Hall resistance at zero magnetic field. Appl. Phys. Lett. 112, 072102 (2018).

    Article  Google Scholar 

  29. Rodenbach, L. K. et al. Metrological assessment of quantum anomalous Hall properties. Phys. Rev. Appl. 18, 034008 (2022).

    Article  Google Scholar 

  30. Okazaki, Y. et al. Quantum anomalous Hall effect with a permanent magnet defines a quantum resistance standard. Nat. Phys. 18, 25–29 (2022).

    Article  Google Scholar 

  31. Patel, D. K. et al. A zero external magnetic field quantum standard of resistance at the 10−9 level. Nat. Electron. 7, 1111–1116 (2024).

    Article  Google Scholar 

  32. Stewart, W. Current-voltage characteristics of Josephson junctions. Appl. Phys. Lett. 12, 277–280 (1968).

    Article  Google Scholar 

  33. Kautz, R. L. Design and operation of series-array Josephson voltage standards. In Proc. International School of Physics ‘Enrico Fermi’, Course CX, 27 June–7 July, 1989 (eds Crovini, L. & Quinn, T. J.) 259–296 (Eslevier, 1992).

  34. Kautz, R. L. Shapiro steps in large-area metallic-barrier Josephson junctions. J. Appl. Phys. 78, 5811–5819 (1995).

    Article  Google Scholar 

  35. Rosen, I. T. et al. Measured potential profile in a quantum anomalous Hall system suggests bulk-dominated current flow. Phys. Rev. Lett. 129, 246602 (2022).

    Article  Google Scholar 

  36. Lippertz, G. et al. Current-induced breakdown of the quantum anomalous Hall effect. Phys. Rev. B 106, 045419 (2022).

    Article  Google Scholar 

  37. Gotz, M. et al. Improved cryogenic current comparator setup with digital current sources. IEEE Trans. Instrum. Meas. 58, 1176–1182 (2009).

    Article  Google Scholar 

  38. Drung, D. et al. Improving the stability of cryogenic current comparator setups. Supercond. Sci. Technol. 22, 114004 (2009).

    Article  Google Scholar 

  39. Drung, D., Götz, M., Pesel, E., Barthelmess, H. J. & Hinnrichs, C. Aspects of application and calibration of a binary compensation unit for cryogenic current comparator setups. IEEE Trans. Instrum. Meas. 62, 2820–2827 (2013).

    Article  Google Scholar 

  40. Mise en Pratique for the Definition of the Ampere and Other Electrical Units (BIPM, 2019); www.bipm.org/documents/20126/41489676/SI-App2-ampere.pdf/0987a90e-051b-dd7f-827d-3f7b32751a61

  41. BIPM et al. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. JCGM 100:2008 (JCGM, 2008); www.bipm.org/documents/20126/2071204/JCGM_100_2008_E.pdf

  42. Calibration and measurement capabilities electricity and magnetism: DC current (low and intermediate values). BIPM www.bipm.org/kcdb/ (2023).

  43. Keller, M. W., Zimmerman, N. M. & Eichenberger, A. L. Uncertainty budget for the NIST electron counting capacitance standard, ECCS-1. Metrologia 44, 505–512 (2007).

    Article  Google Scholar 

  44. Camarota, B. et al. Electron counting capacitance standard with an improved five-junction R-pump. Metrologia 49, 8–14 (2011).

    Article  Google Scholar 

  45. Giblin, S. et al. Towards a quantum representation of the ampere using single electron pumps. Nat. Commun. 3, 930 (2012).

    Article  Google Scholar 

  46. Stein, F. et al. Validation of a quantized-current source with 0.2 ppm uncertainty. Appl. Phys. Lett. 107, 103501 (2015).

    Article  Google Scholar 

  47. Bae, M.-H. et al. Precision measurement of single-electron current with quantized Hall array resistance and Josephson voltage. Metrologia 57, 065025 (2020).

    Article  Google Scholar 

  48. Stein, F. et al. Robustness of single-electron pumps at sub-ppm current accuracy level. Metrologia 54, S1–S8 (2016).

    Article  Google Scholar 

  49. Yamahata, G., Giblin, S. P., Kataoka, M., Karasawa, T. & Fujiwara, A. Gigahertz single-electron pumping in silicon with an accuracy better than 9.2 parts in 107. Appl. Phys. Lett. 109, 013101 (2016).

    Article  Google Scholar 

  50. Zhao, R. et al. Thermal-error regime in high-accuracy gigahertz single-electron pumping. Phys. Rev. Appl. 8, 044021 (2017).

    Article  Google Scholar 

  51. Giblin, S., Yamahata, G., Fujiwara, A. & Kataoka, M. Precision measurement of an electron pump at 2 GHz; the frontier of small DC current metrology. Metrologia 60, 055001 (2023).

    Article  Google Scholar 

  52. Bestwick, A. et al. Precise quantization of the anomalous Hall effect near zero magnetic field. Phys. Rev. Lett. 114, 187201 (2015).

    Article  Google Scholar 

  53. White, M. et al. Direct implementation of a frequency-programmable Josephson voltage standard to provide an SI traceable optical power scale. Metrologia 61, 045002 (2024).

    Article  Google Scholar 

  54. Fox, A. E., Dresselhaus, P. D., Rüfenacht, A., Sanders, A. & Benz, S. P. Junction yield analysis for 10 V programmable Josephson voltage standard devices. IEEE Trans. Appl. Supercond. 25, 1–5 (2014).

    Article  Google Scholar 

  55. Fox, A. E., Butler, G., Thompson, M., Dresselhaus, P. D. & Benz, S. P. Induced current effects in Josephson voltage standard circuits. IEEE Trans. Appl. Supercond. 29, 1–8 (2019).

    Article  Google Scholar 

  56. Rodenbach, L. K. et al. Bulk dissipation in the quantum anomalous Hall effect. APL Mater. 9, 081116 (2021).

    Article  Google Scholar 

Download references

Acknowledgements

We thank T. Mai, F. Fei, G. J. Fitzpatrick and E. C. Benck for assistance with the NIST internal review process. We also thank I. T. Rosen and M. A. Kastner for enlightening discussions throughout this work. L.K.R., M.P.A. and D.G.-G. were supported by the Air Force Office of Scientific Research (AFOSR) Multidisciplinary Research Program of the University Research Initiative (MURI) under grant no. FA9550-21-1-0429. At the initiation of the project, L.K.R., M.P.A. and D.G.-G. were supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, under contract no. DE-AC02-76SF00515 and the Gordon and Betty Moore Foundation through grant no. GBMF9460. P.Z., L.T. and K.L.W. acknowledge support from the National Science Foundation (NSF) under the Accelerating Interdisciplinary Frontiers in Quantum Sciences and Technologies (grant no. 2125924, NRT-QISE) and Quantum Devices with Majorana Fermions in High-Quality Three-Dimensional Topological Insulator Heterostructure (grant no. 1936383, QII-TAQS) programmes. P.Z., L.T. and K.L.W. were also supported by the Army Research Office MURI under grant nos. W911NF16-1-0472 and W911NF-19-S-0008. Commercial equipment, instruments and materials are identified in this paper to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology or the US government, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose. Work presented herein was performed, for a subset of the authors, as part of their official duties for the US government. Funding is hence appropriated by the US Congress directly. Part of this work was performed at nano@stanford, supported by the National Science Foundation under grant no. ECCS-2026822.

Author information

Author notes

  1. These authors contributed equally: Linsey K. Rodenbach, Jason M. Underwood.

Authors and Affiliations

  1. Department of Physics, Stanford University, Stanford, CA, USA

    Linsey K. Rodenbach & David Goldhaber-Gordon

  2. Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA, USA

    Linsey K. Rodenbach, Molly P. Andersen & David Goldhaber-Gordon

  3. Physical Measurement Laboratory, National Institute of Standards and Technology (NIST), Gaithersburg, MD, USA

    Jason M. Underwood, Ngoc Thanh Mai Tran, Alireza R. Panna, Zachary S. Barcikowski, Shamith U. Payagala, Dean G. Jarrett, Randolph E. Elmquist, David B. Newell & Albert F. Rigosi

  4. Joint Quantum Institute, University of Maryland, College Park, MD, USA

    Ngoc Thanh Mai Tran & Zachary S. Barcikowski

  5. Department of Materials Science and Engineering, Stanford University, Stanford, CA, USA

    Molly P. Andersen

  6. Department of Electrical and Computer Engineering, University of California, Los Angeles, Los Angeles, CA, USA

    Peng Zhang, Lixuan Tai & Kang L. Wang

Authors
  1. Linsey K. Rodenbach
    View author publications

    Search author on:PubMed Google Scholar

  2. Jason M. Underwood
    View author publications

    Search author on:PubMed Google Scholar

  3. Ngoc Thanh Mai Tran
    View author publications

    Search author on:PubMed Google Scholar

  4. Alireza R. Panna
    View author publications

    Search author on:PubMed Google Scholar

  5. Molly P. Andersen
    View author publications

    Search author on:PubMed Google Scholar

  6. Zachary S. Barcikowski
    View author publications

    Search author on:PubMed Google Scholar

  7. Shamith U. Payagala
    View author publications

    Search author on:PubMed Google Scholar

  8. Peng Zhang
    View author publications

    Search author on:PubMed Google Scholar

  9. Lixuan Tai
    View author publications

    Search author on:PubMed Google Scholar

  10. Kang L. Wang
    View author publications

    Search author on:PubMed Google Scholar

  11. Dean G. Jarrett
    View author publications

    Search author on:PubMed Google Scholar

  12. Randolph E. Elmquist
    View author publications

    Search author on:PubMed Google Scholar

  13. David B. Newell
    View author publications

    Search author on:PubMed Google Scholar

  14. Albert F. Rigosi
    View author publications

    Search author on:PubMed Google Scholar

  15. David Goldhaber-Gordon
    View author publications

    Search author on:PubMed Google Scholar

Contributions

L.K.R., J.M.U., D.B.N., A.F.R. and D.G.-G. conceived and designed the experiments. L.K.R., J.M.U., N.T.M.T., A.R.P., M.P.A. and Z.S.B. performed the experiments. L.K.R., J.M.U., N.T.M.T., A.R.P., Z.S.B. and D.G.-G., analysed the data. P.Z., L.T. and K.L.W. contributed MTI thin film materials. L.K.R. and M.P.A. fabricated and qualified QAH devices. L.K.R., J.M.U., N.T.M.T., A.R.P., S.U.P., D.G.J, R.E.E., D.B.N., A.F.R. and D.G.-G. contributed specialized hardware and expertise to support metrology experiments. L.K.R. and J.M.U. wrote the paper. N.T.M.T., A.R.P., M.P.A., Z.S.B., A.F.R. and D.G.-G. reviewed and provided input on the paper.

Corresponding authors

Correspondence to Jason M. Underwood or David Goldhaber-Gordon.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Electronics thanks Stephen Giblin, Michael Hilke and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Longitudinal resistivity as a function of top gate voltage.

Shown are measurements of QAHR longitudinal resistivity, ρxx, versus top gate voltage Vgate, performed with the CCC’s nanovoltmeter. First, Vgate was quickly swept toward negative voltages (blue circles, integration time τ = 10 s). Vgate was next brought back to zero and then swept toward positive voltages (orange squares, τ = 10 s). Each symbol represents an average of 30 observations per measurement. The time between measurements (symbols) was approximately 7 minutes. The curved arrows are intended as guides to the eye and show the sweep direction. Finally, Vgate was slowly swept over a narrow range (green crosses, τ = 60 s). For the narrow sweep, each symbol represents an average of 10 observations and the time between measurements was 12 minutes. The local minimum in ρxx seen near Vgate = 0 V indicates that the native Fermi level is well positioned near the center of the magnetic exchange gap. The mixing chamber temperature over the course of these sweeps (lasting about two hours total) only decreased by 0.2 mK. The decrease in ρxx near Vgate = 0 with each sweep suggests that either ρxx is strongly sensitive to temperature or that thermalization occurs over very long timescales.

Source data

Extended Data Fig. 2 Characterization of QAHR quantization in the presence of microwave leakage.

Deviation of the Hall resistance from quantization, δRyx/RK = (Ryx − RK)/RK, was measured as a function of bias current I and PJVS microwave bias. The impact of the microwave leakage varied with the microwave frequency f. For f = 0 (blue circles, microwave bias disabled), each symbol represents the average of at least three measurements, each based on at least 30 observations. For other frequencies only one measurement (again, based on at least 30 observations) was performed for each current. Error bars show the Type A (statistical) uncertainty. Note that the uncertainty for some points may be smaller than the symbol. For the f ≠ 0 measurements, the PJVS microwave excitation was active (input power P = 1 mW), but the PJVS output voltage was zero. The frequencies fn in the legend are as follows: f0 = 9.701 GHz (orange crosses), f1 = 18.00 GHz (yellow squares), and f2 = 14.00 GHz (violet diamonds).

Source data

Extended Data Fig. 3 Example raw measurement data of Vnull.

Shown are raw Vnull data taken for I = 83.9 nA. (a) 800 individual measurements of Vraw,null over several polarity reversal cycles are shown as red dots. Each raw measurement was acquired using a 60 s integration time. The triangular symbols show \({V}_{{\rm{null}}}^{+}\) (\({V}_{{\rm{null}}}^{-}\)), the average value of the raw null voltage readings for the positive (negative) portion of a polarity reversal cycle. (b) The 18 measurements of Vdiff calculated from the data in (a) via Eq. (4) are shown as cross-symbols. The solid green line is Vnull – the average of the 18 Vdiff values. The dashed line shows the corresponding null voltage expected from the indirect realization of the ampere, \({V}_{{\rm{null}},{\rm{expected}}}={I}_{\rm{indirect}}{R}_{K}-Nf{K}_{J}^{-1}\). (c) An expanded view of the two trendlines shown in (b).

Source data

Supplementary information

Supplementary Information

Supplementary discussion, Figs. 1–8 and Tables 1–3.

Supplementary Data 1

Source data for main article results.

Source data

Source Data Figs. 2–4

Tabular data in Excel format.

Source Data Extended Data Figs. 1 and 2

Tabular data in Excel format.

Source Data Extended Data Fig. 3

Tabular data in Excel format, sheets 1 and 2.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rodenbach, L.K., Underwood, J.M., Tran, N.T.M. et al. A unified realization of electrical quantities from the quantum International System of Units. Nat Electron 8, 663–671 (2025). https://doi.org/10.1038/s41928-025-01421-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41928-025-01421-2

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing