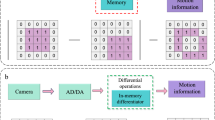
Abstract
Developing artificial intelligence systems that are capable of learning at the edge of a network requires both energy-efficient inference and learning. However, current memory technology cannot provide the necessary combination of high endurance, low programming energy and non-destructive read processes. Here we report a unified memory stack that functions as a memristor as well as a ferroelectric capacitor. Memristors are ideal for inference but have limited endurance and high programming energy; ferroelectric capacitors are ideal for learning, but their destructive read process makes them unsuitable for inference. Our memory stack uses a silicon-doped hafnium oxide and titanium scavenging layer that are integrated into the back end of line of a complementary metal–oxide–semiconductor process. With this approach, we fabricate an 18,432-device hybrid array (consisting of 16,384 ferroelectric capacitors and 2,048 memristors) with on-chip complementary metal–oxide–semiconductor periphery circuits. Each weight is associated with an analogue value stored as conductance levels in the memristors and a high-precision hidden value stored as a signed integer in the ferroelectric capacitors. Weight transfers between the different memory technologies occur without a formal digital-to-analogue converter. We use the array to validate an on-chip learning solution that, without batching, performs competitively with floating-point-precision software models across several benchmarks.
Similar content being viewed by others
Main
The use of artificial intelligence (AI) in edge devices requires the AI tasks to be performed with minimal energy consumption. This has driven research into in- or near-memory computation, but such devices mainly focus on inference and lack on-chip training capabilities. Yet, for personalized applications in user-specific environments—such as autonomous driving, smart manufacturing and medicine—adaptive on-chip local training and fine-tuning of neural network parameters are essential1,2. Performing both inference and learning at the edge creates conflicting requirements for the memory of edge devices3: training requires the high-precision iteration of multiple parameters, so the memory must have high write endurance, low programming energy and fast operation; however, inference (using an already trained neural network with pre-stored parameters) requires memory with high read endurance and resilience to read disturbances for data handling.
Memristors are memory devices that use the formation and dissolution of conductive filaments to alter their resistance state4. Programming operations require precise current values to define resistance states, which affects the programming power and write endurance. By contrast, reading operations require only a low-voltage, short pulse to determine the resistance values. Memristors, therefore, have virtually unlimited read endurance, making them ideal for inference. In addition, memristor-based architectures can leverage in-memory computing to minimize data movement to greatly reduce energy consumption1,2,5,6,7,8,9,10. However, the limited write endurance and high programming energy make them poorly suited for on-chip training, necessitating off-chip training and pre-programming for specific tasks11.
Ferroelectric capacitors (FeCAPs) record information using the polarization of ferroelectric dipoles that are manipulated by an external electric field12. The ultralow displacement current required for polarization reversal offers exceptional programming endurance and negligible energy consumption, making FeCAPs highly suitable for training13,14. However, the polarization state must be reprogrammed after each read operation, thereby linking read endurance to write endurance. This poses challenges for inference applications.
One approach to the challenge of training at the edge is to combine memristors with accurate digital static random-access memory, which can be made using standard transistors15. However, in advanced complementary metal–oxide–semiconductor (CMOS) nodes, static random-access memory has a considerable area footprint, which can limit the amount of memory available for learning systems at the edge. Additionally, static random-access memory is a volatile memory and is, therefore, unsuitable for lifelong training, which requires non-volatile storage solutions for weights. Another solution is the integration of a hybrid memory (HM) architecture that incorporates diverse memory types. For example, a fully analogue solution based on a synaptic unit cell combining non-volatile phase change memory (PCM) with conventional CMOS-based capacitors (the PCM array was fabricated and the CMOS capacitors were simulated) has been explored16. However, such solutions lack scalability because of the large footprint of the capacitors required to store high-resolution weights.
Three-dimensional (3D) monolithic integration of memristors for in-memory computing, ternary content-addressable memory arrays and buffers have been demonstrated using one-kilo-devices to facilitate one-shot learning17. An approach based on an 8 × 3 array of ferroelectric field-effect transistors with molybdenum disulfide channels that allows the decoupling of training and inference operations has also been developed18. Nevertheless, these systems have issues related to material compatibility, high thermal budgets during fabrication and high cost of co-integration of different memory technologies on the same die, as well as more complex device structures requiring new masks and process steps.
In this Article, we report a single memory stack based on silicon-doped hafnium oxide that can be used to fabricate both memristors and FeCAPs in the same back-end-of-line (BEOL) process. All devices are initially FeCAPs and can be transformed into memristors through a single electrical forming operation (Fig. 1a), creating a network of FeCAPs and memristors on the same chip. Unlike 3D monolithic approaches, this integration requires no additional masks, thereby simplifying manufacturing by combining both technologies into a unified memory stack19,20. We use the approach to fabricate a hybrid FeCAP/memristor memory circuit in 130-nm-node CMOS technology, comprising 16,384 FeCAP devices connected to 2,048 memristor devices, along with associated CMOS peripheral circuits.
a, Same BEOL-integrated metal–ferroelectric–metal stack (cross-section tilted scanning electron microscopy view with a focused ion beam), can be used as either FeCAP (P–E hysteresis loops) or, after a forming operation, as memristor (butterfly shaped current–voltage curve). Details of the electrical characterization procedure are provided in the Methods. b, High-level description of the training procedures for off-chip (left) and on-chip (right) implementations. For on-chip inference, only pre-programmed memristors are required to store the analogue weights. For on-chip training, each weight is associated with an analogue value—used for the inference—that is stored in memristors, and a higher-precision hidden value—for use only during training—that is stored in FeCAPs. c, Schematic of the proposed training strategy leveraging our unified memory technology.
We illustrate the potential of our technology for on-chip learning at the edge using a dedicated technique inspired by quantized neural networks21. In this circuit, each weight is associated with an analogue value stored as conductance levels in the memristors and a high-precision hidden value stored as a signed 10-bit integer in the FeCAPs (Fig. 1b). The multiply-and-accumulate operations, critical for forward and backward data propagation to train an artificial neural network (ANN), as well as for inference, are performed in situ using the memristor devices in the analogue domain. The high-precision FeCAP memory is updated on receiving each new input, whereas the memristor analogue weights are only periodically updated during weight transfer operations, to record the sign and the three most significant bits (MSBs) stored in the FeCAPs (Fig. 1c).
We experimentally characterize the digital-to-analogue transfer of the MSB hidden values stored in the FeCAPs to the memristor analogue weight stored as a conductance value in our hybrid array. Using these measurements for calibration, we conduct system-level simulations across several benchmarks. Our results demonstrate competitive accuracy compared with software-based floating-point precision models, as well as meeting hardware constraints related to endurance (this work follows a previous report of ours in which we showed the results of a simpler training technique that used memristors only in the binary mode and did not show FeCAP-to-memristor digital-to-analogue transfer22).
Metal–ferroelectric–metal stack as FeCAP and memristor
Among the memory types suitable for integration into advanced commercial processes, filamentary memristors have been extensively studied for analogue in-memory neural network inference7,8,23. In parallel, FeCAPs have shown promise for non-volatile, high-density embedded dynamic random-access memory applications for AI workloads13. Here we produced a hybrid FeCAP/memristor memory and developed the associated programming strategy to combine the strengths of both approaches.
We developed a metal–ferroelectric–metal capacitor that functions as both filamentary memristor and FeCAP, depending on the initialization process applied, that is, forming or wake up, respectively. We integrated a 10-nm ferroelectric silicon-doped hafnium oxide (HfO2) film with a titanium (Ti) scavenging layer into the BEOL process of 130-nm foundry CMOS. This combination leverages silicon-doped HfO2 typically used for FeCAPs and the Ti scavenging layer usually used in memristors. Figure 2a shows the crystallization of the HfO2 film, along with the top and bottom electrodes. The Ti layer serves a dual purpose: enhancing the ferroelectric properties for higher remanent polarization in the FeCAP24, and increasing the oxygen vacancy concentration to promote conductive filament formation for memristor operation25. Details about the process used to fabricate the unified memory stack are provided in the Methods.
a, High-resolution transmission electron microscopy cross-section showing 10-nm Si:HfO2 film crystallization. b, Raw distributions of zero and one states in a 16-kilo-device FeCAP array (based on 1T–1C cells) (3 V–2 µs reading and programming pulses). c, Polarization-switching energy as a function of pulse duration and amplitude. d, Median memory window as a function of cycling, for programming conditions A and B defined in b. e, Raw distributions of zero and one states in 16-kilo-device FeCAP arrays, measured after 107 endurance cycles, for programming conditions A and B. f, Average memristor conductance and standard deviation at 1σ with increasing programming currents. g, Experimental conductance distributions with eight levels programmed per cell. h, High-conductance state (HCS) and low-conductance state (LCS) distributions measured for the of 16-kilo-device memristor array after several SET–RESET cycling phases.
We first fabricated 16,384-device FeCAP arrays (based on one transistor–one capacitor (1T–1C) cells) and 16,384-device memristor arrays (based on one transistor–one memristor (1T–1R) cells) on the same wafer using the metal–ferroelectric–metal memory stack, testing the two arrays separately. To function as FeCAPs, the hafnium oxide devices require a one-time wake-up process through repeated ferroelectric switching to stabilize their response26. Subsequently, FeCAPs function as binary memories: they can be programmed to the polarization ‘zero’ state by applying a positive pulse to the top electrode (source line) or to the polarization ‘one’ state by applying a positive pulse to the bit line (BL). The read process is destructive, performed by attempting to program a zero and measuring the subsequent BL voltage. Figure 2b shows the distribution of the BL voltage in the zero and one states for the 16,384 devices of the array at the end of the wake-up process (that is, after 1,000 programming cycles). This voltage is measured by ramping up the reference voltage (Vref) of the on-chip sense amplifier. The median memory window, defined as the separation between median Vref values for zero and one states, is 360 mV, with a worst-case memory window of 120 mV.
Figure 2c shows the programming energy required to switch one bit as a function of pulse duration for various programming voltages (Methods). Two programming conditions A and B are highlighted (Supplementary Note 1). Condition B is the most energy efficient, achieving switching energies below 200 fJ bit−1. To assess the write endurance, we performed repeated SET–RESET operations. Figure 2d indicates that the median memory window remains positive for both programming conditions over 107 cycles. Condition A had a consistently higher median memory window than condition B, but the distribution of zero and one states after 107 cycles reveals bit failures with programming condition A. This result aligns with the general correlation between programming window and endurance capabilities for several memory technologies, that is, a high programming window can be achieved with higher current/voltage programming conditions, but generally at the cost of endurance capabilities27. Therefore, hereafter, we adopted programming condition B.
To be used as memristors, hafnium oxide devices must undergo a one-off forming process creating a conductive filament of oxygen vacancies between the device’s top and bottom electrodes. For this process, we applied an adaptive pulse train (6 V, 300 µs) to the top electrode of each device whereas grounding the bottom electrode, until a target resistance of 50 kΩ was achieved. The device can then be switched between the low- and high-conductance states by applying negative or positive voltages, respectively, to the top electrode. When programming to the high-conductance state, the access transistor limits the programming current to a compliance value, which determines the final conductance (Fig. 2f). This mechanism allows memristors to function as analogue multilevel memory stores. However, the resolution of the memristor is limited by stochastic effects inherent to its switching mechanism: Fig. 2g shows the distribution of the 16,384 memristors following programming at eight conductance levels (the programming conditions are summarized in Supplementary Note 2). Figure 2h shows the results of write endurance tests, estimating the SET–RESET cycling endurance to be 105 cycles, which is two orders of magnitude less than when using the device as an FeCAP.
In contrast to other HfO2-based devices that may revert from a memristive to a ferroelectric regime under strong RESET pulses28,29, no such reversion is observed in our technology. The thin Ti scavenging layer at the top electrode restricts filament dissolution, preventing a ‘deep RESET’ to the pristine insulator state. This ensures that once filamentary conduction is formed, it remains stable throughout the operating conditions.
Hybrid FeCAP/memristor memory circuit
After testing the memristor and FeCAP arrays separately, we fabricated and tested a hybrid array comprising 128 vertical transfer lines, each with 128 FeCAPs and 16 memristors (Fig. 3a). Our circuit also incorporated on-chip CMOS components such as registers to address each memristor and FeCAP device, drivers to program the devices, sense amplifiers for the FeCAP devices and a timing block for automatic pulse generation for the FeCAP array. An optical micrograph of the circuit is shown in Fig. 3b. The basic building block of the hybrid FeCAP/memristor array is the synapse circuit depicted in Fig. 3c. This circuit comprises an ensemble of one transistor–one FeCAP (1T–1C) cells, where the BL of each cell is directly connected to the gates of the selection transistors of two 1T–1R cells. This circuit is used as part of a vertical transfer line: we activate the right numbers of FeCAPs and memristors in a vertical transfer line using the word lines (WLs) of the device’s access transistors.
a, Array-level organization of the hybrid memories and peripheral circuit. b, Optical micrograph of the fabricated array. c, Schematic of the hybrid FeCAP/memristor memory circuit. d, To account for the significance of the MSBs during the data transfer process, the MSBs are implemented using capacitors with distinct areas: four times the minimum area, twice the minimum area and minimum area, respectively, for the first, second and third MSBs. e, Average voltage measurements after loading the transfer line (TL), and reading a zero or a one as a function of the capacitor area, with standard deviation at 1σ.
This sub-circuit allows direct digital-to-analogue data transfer from the FeCAP cells to the two memristors without requiring intermediate circuits. The hidden weights used during training are stored in FeCAPs in a sign-and-magnitude 10-bit integer format, using one bit for the sign and nine bits for the magnitude. We refer to the first three magnitude bits as the MSBs and the last six as the least significant bits (LSBs). The sign-and-magnitude representation, rather than the more conventional two’s complement representation, facilitates data transfer operations. The analogue weight used for forward and backward propagation steps, as well as inference, is stored in two memristor cells in a differential configuration, allowing both positive and negative values to be stored.
The parallel reading of the selected FeCAP elements within the transfer line involves loading the parasitic capacitance of the transfer line to an analogue voltage, which is proportional to the sum of ones stored in the selected 1T–1C cells. This FeCAP-data-dependent voltage is used as the gate voltage of the selected 1T–1R cells. Therefore, it defines the compliance current during the memristor programming operation, effectively defining the programmed devices’ conductance (Fig. 2f).
Data transfer from high-precision hidden weights to analogue memristors is done in two steps. First, the sign-bit cell is read to determine which of the two 1T–1R cell needs to be programmed. Second, the three MSB FeCAP cells are read in parallel, loading the transfer line’s capacitance with a voltage that corresponds to the stored data. This voltage (VTL) sets the compliance current in the 1T–1R cell. A voltage pulse is applied to the to-be-programmed memristor source line (SLRe), whereas the memristor bit line (BLRe) is grounded. This process eliminates the need for symmetrical, linear updates of memristor values, allowing for RESET and SET operations with compliance current determined by the FeCAPs’ stored values. Details are provided in Supplementary Note 3.
To account for the relative significance of MSBs, capacitors with different areas are used: four times, twice and the minimum area for the first, second and third MSBs, respectively (Fig. 3d). This choice results in near-linear spacing between the VTL values for different bit combinations (Supplementary Note 4). An HM with distinct capacitor sizes for the three MSBs is implemented by connecting a 1T–4C, 1T–2C and 1T–1C to the same transfer line, all with minimum-sized capacitors (Fig. 3d). Capacitors for the sign bit and six LSBs are minimum sized, as they do not participate in the analogue transfer.
We validated the direct transfer from digital words (FeCAPs) to analogue conductance values (memristors) using our fabricated hybrid array. Figure 3e shows the transfer-line voltage measured when reading a zero or a one for one to four capacitors connected in parallel. The transfer-line voltage follows the equivalent areas, defined as the area of a single capacitor multiplied by the number of capacitors read in parallel and the state stored in the capacitor, that is, zero or one. This curve confirms that capacitors with varied sizes can be exploited to reflect the significance of MSBs.
Finally, Fig. 4 presents the measured data for the digital-to-analogue transfer of the sign (green) and the three MSBs (blue) from the FeCAP to the two memristor cells. We measured the difference in conductance between the two memristors encoding the positive weight (G+) and negative weight (G−) for all possible sign and MSB combinations. The integer values from –7 to 7, plus zero (represented by two combinations), stored in the FeCAPs were successfully transferred as 15 distinct differential conductance levels. The electrical characterization details of the transfer procedure are provided in the Methods.
Training at the edge
We assessed the performance and power consumption of the proposed FeCAP/memristor memory circuit for on-chip training and transfer learning using hardware-aware simulation validated by our extensive statistical measurements (Fig. 4). The core idea behind our approach is that although the analogue precision of memristors suffices for inference, it falls short for learning, which requires small, progressive weight adjustments. Inspired by quantized neural networks21, we adopted a hybrid approach: forward and backward passes use low-precision weights stored in analogue memristors, whereas updates are done using higher-precision FeCAPs. Memristors are periodically reprogrammed based on the MSBs stored in FeCAPs, ensuring efficient and accurate learning.
We implemented this approach in a three-layer fully connected neural network for the Modified National Institute of Standards and Technology database (MNIST) digit classification task (Fig. 5a and Methods). Figure 5b depicts the on-chip training procedure using stochastic gradient descent. For each training sample, neuron activations are calculated by feed-forward matrix–vector multiplication between the analogue weights (memristors) and the previous layer’s activations. Errors at the output layer are back-propagated to evaluate loss gradients and update hidden weights. The hidden weight update matrix, ΔWh, is multiplied by a binary mask M that dictates which weights to update in the FeCAPs. Mask elements follow a Bernoulli distribution with a given probability p. This stochastic update, loosely inspired by biophoton emission and propagation in the brain30, enhances convergence. No momentum is used to minimize the hardware costs. Hidden weights (10-bit integers in FeCAPs) are updated for each sample, whereas analogue weights (memristors) are updated every k inputs via the digital-to-analogue procedure. Further details are provided in the Methods. Details on the data flow of operations during training are presented in Supplementary Note 11.
a, Diagram showing the fully connected three-layer neural network used for the on-chip training on the MNIST digit classification task. b, Representation of the on-chip training procedure based on the stochastic gradient descent algorithm. The FeCAP array used to store the hidden weights is stochastically updated with input of each new image, whereas the memristor array used to store the analogue weights is updated after input of every k images. c, Accuracy after ten training epochs as a function of the k parameter. The dot plots represent ten individual data points from separate training runs. The inset shows the mean accuracy values with the corresponding minimum and maximum ranges. d, Number of memristor and FeCAP programming operations at the end of one training round as a function of k. e, Total programming energy for memristors, and FeCAPs at the end of one training round as a function of k. We assumed a programming energy of 1 pJ and 100 fJ for a single memristor and FeCAP, respectively47,48. f, MNIST classification, Fashion-MNIST classification and ECG detection accuracies obtained with the FP and our proposed training strategy based on HM in both ideal memory case (w/o Var) and with artificially induced errors in the transfer operation due to device variability (w/ Var). For the MNIST dataset, we also include a case in which the network was trained with ten-image mini-batches, with batch normalization (Methods). The bar chart represents the mean value, and the dot plots show the corresponding individual data points (n = 5).
We evaluated the accuracy, total programming energy and number of programming operations for FeCAP and memristor devices at the end of training for the MNIST task against the parameter number of inputs before updating the analogue weights k. Figure 5c shows that the test accuracy remains stable for k values up to 100 but drops for larger values. Decreasing k increases the number of both memristor and FeCAP programming operations (Fig. 5d), which increases the energy consumption (Fig. 5e). With k values lower than ten, the number of required memristor programming operations also exceeds the endurance of memristors. For k values greater than 50, the memristor programming energy drops below that of an FeCAP, stabilizing between 20 nJ and 30 nJ. Thus, the programming energy is dominated by hidden weight updates rather than the transfer operations. At k = 100, the method achieves 96.7% accuracy with approximately 38 nJ of total energy consumption, representing a 38-fold reduction with no loss of accuracy with regard to k = 1. The number of programming operations remains 17 times below the memristor endurance limit and 75 times below the FeCAP limit. Therefore, we used k = 100 for further analysis.
We also assessed robustness to memory errors. Figure 5f compares the accuracy for MNIST, Fashion-MNIST and electrocardiogram (ECG) detection tasks using classical ANN (full precision (FP)) and our HM approach, with and without induced transfer errors due to device variability. Device variability was estimated from the characterization of electrical transfer (Fig. 4). Details on the architectures and hyperparameters for the Fashion-MNIST and ECG tasks are provided in the Methods. Training with FP weights yields the highest accuracy. For all three datasets, the HM approach with hidden weight quantization reduces accuracy by approximately one percentage point, and induced transfer errors by approximately one additional percentage point. Further details on mitigating overlapping conductance distributions—including an optional iterative programming scheme and its cost–benefit analysis—are presented in Supplementary Note 10.
All these simulations were performed with ‘online’ training, that is, updating the hidden weights after each training sample presentation. Figure 5f also shows that using mini-batch training with batch normalization (Fig. 5f) would improve accuracy and resilience to transfer errors, with only a 0.8 percentage point loss on MNIST between FP and HM with errors. However, this approach limits continuous on-chip learning due to the memory costs for storing activation values and batch normalization parameters.
Finally, we evaluated our approach on more challenging transfer learning tasks using the edge-friendly MobileNet-V2 neural network as a base feature extractor. First, we pre-trained MobileNet-V2 on CIFAR-100, then froze its convolutional layers and added a newly initialized fully connected layer, which we trained online on CIFAR-10 (Fig. 6a,b). We also considered harder scenarios: pre-training MobileNet-V2 on ImageNet and then transferring to various specialized datasets (Oxford-IIIT Pet31, Oxford Flowers 102 (ref. 32), Caltech Birds33 and Stanford Cars34).
a, Schematic showing the transfer learning strategy with initial MobileNet-V2 architecture pre-trained on a base dataset using a quantization-aware training strategy to obtain a fixed quantized feature extractor (QFE). b, The MobileNet-V2 quantized feature extractor was used in conjunction with a newly initialized classifier for transfer learning of the pre-trained model toa new dataset. The proposed HM-based training strategy was used to train the classifier. c, Test accuracies on the five evaluated datasets for different classifier (C) configurations, varying in precision (32-bit floating point or 4-bit) and training strategy (offline or HM-online). The bar chart represents the mean value, and the dot plots show the corresponding individual data points (n = 10).
Figure 6c compares three settings in these five scenarios: a purely software baseline using 32-bit floating-point weights with mini-batch training; a purely software 4-bit classifier (still trained with mini-batches); and our hardware online approach, incorporating device-level variability during FeCAP-to-memristor transfer operations. In all five scenarios, quantizing the classifier to four bits did not greatly impact accuracy. By contrast, our purely online method showed a moderate drop (1.2 percentage points on CIFAR-100/CIFAR-10, and 1.8–7.3 percentage points on the ImageNet-based tasks). The amount of accuracy loss is directly correlated with the difficulty of the transferred task. As detailed in Supplementary Note 12, most of this drop stems from the lack of mini-batch updates, rather than from FeCAP-to-memristor transfer variability. More sophisticated on-chip training strategies could further reduce this accuracy gap. Note that the mean number of FeCAP-to-memristor transfer operations to achieve final accuracy ranges from 2,740 (for Oxford Flowers 102) and 4,550 (for CIFAR-10), well below the memristor endurance limit. The number of FeCAP programming operations per device, approximately 512 times more, also remains well below the FeCAP endurance limit.
Conclusion
We have reported a simple and energy-efficient HM technology for the on-chip training of ANNs that incorporates FeCAPs and memristors within the BEOL of foundry CMOS. Combining these two technologies into a unified memory stack simplifies the integration process using the same number of masks as a traditional integration scheme with a single type of memory. The data-disruptive nature of reading FeCAP devices makes them inefficient for inference once training is complete and causes read endurance to be limited by the write endurance, thereby restricting the useful lifetime of trained devices. In comparison, a full memristor implementation would benefit from the read stability of conductance states and energy-efficient in-memory computing, but their low write endurance and high programming energy are incompatible with training. Even with a small dataset, the number of programming operations for one training round can exceed the endurance limit of the memristor devices in the proposed stack (for example, the number of write operations for the k = 1 case of the MNIST dataset is around 1.2 × 106; Fig. 5d,e).
Our approach leverages the high programming endurance and low programming energy of FeCAPs, and the near-infinite read endurance and analogue nature of memristors. FeCAP devices store high-precision hidden weights that undergo frequent programming operations during training, whereas memristor devices store analogue weights that are read during inference and training but only periodically updated. We fabricated a circuit containing 16,384 FeCAP devices and 2,048 memristors. CMOS periphery circuits were used to transfer the trained hidden weights stored in a digital format in the FeCAP devices to equivalent analogue conductance values stored in the memristor devices, thereby eliminating the need for digital-to-analogue converters. The ANN was trained using a stochastic gradient descent algorithm. On the basis of measurements of the transfer circuits, the results obtained across several edge benchmarks are competitive with those achieved by floating-point precision software models, without the endurance limitations associated with hardware constraints. We observed month-long stability of the memristor states (Supplementary Note 9). In the situation of lifelong learning, our hybrid approach naturally leverages the robust retention of FeCAPs, as any weight transfer corrects any drift in the memristor conductance levels. Such weight transfers might also be performed for the sole purpose of compensating any memristor drift.
A major cost of our approach is the need for FeCAPs with distinct areas or multiple capacitors per bit to store the MSBs of the hidden weights. This allows for the transfer and conversion of digital data into multilevel analogue conductance values without requiring dedicated digital-to-analogue converters. The number of MSBs requiring large capacitors is determined by the maximum number of analogue conductance levels that can be reliably programmed in the memristor devices. Our technology can store a maximum of eight distinct analogue levels, corresponding to three bits, or four bits per weight when including the sign. This is a good compromise: 4 bits is a typical weight resolution in highly quantized neural networks, providing high accuracy even on advanced AI tasks35. Note that in our results with MobileNet-v2 neural networks, only the last fully connected layer of MobileNet-v2 undergoes HM training, which is common in transfer learning scenarios in which pre-trained convolutional features remain fixed. This strategy greatly reduces the memory footprint and computations on resource-constrained edge devices and still yields competitive accuracy. Our framework could be applied to earlier layers or other architectures, like ResNet or transformers, but doing so would increase the hardware overhead and memory demands (including requiring higher precision for the FeCAP weights).
Optimizing the unified memory stack to function as both ferroelectric memory and memristor was crucial. In particular, the thickness and oxygen-vacancy profile of the Si-doped HfO2 layer was optimized by adjusting the deposition parameters and through interface design. To ensure the crystallization of the film in the ferroelectric orthorhombic phase and maintain an annealing temperature compatible with the BEOL, the Si-doped HfO2 cannot be scaled to less than 10 nm (ref. 36). However, memristors typically have a thinner optimal thickness to reduce the forming voltage. For this reason, we adopted a thickness of exactly 10 nm for our devices. An optimized oxygen-vacancy concentration can enhance ferroelectricity by stabilizing the orthorhombic phase and reduce the forming voltage, but vacancies must be carefully managed to avoid promoting non-ferroelectric phases (further details of how 1% silicon doping optimally balances ferroelectric polarization and filament formation are provided in Supplementary Note 8).
When integrating our devices into industrial processes, we anticipate our devices will be laterally scaled to increase memory density. Such scaling would be expected to reduce the number of interface defects and provide higher endurance for the FeCAPs37, without affecting memristor behaviour, as it relies on filament formation. Switching to more advanced materials, such as hafnium zirconium oxide, could further enhance the endurance of FeCAPs. Enhanced endurance can pave the way for training end-to-end deep neural networks, beyond fine-tuning situations. Another direction of future research would be to create an all-ferroelectric unified memory by replacing our filamentary memristors with ferroelectric tunnel junctions (FTJs). This could benefit from the high resistance and low programming currents of FTJs. However, FTJs generally require different material stacks and very thin barriers (<5 nm) that complicate co-integration with FeCAPs. Furthermore, the programming mechanism for multiple conductance states in FTJs does not align with our analogue transfer circuit, which relies on a proportionate programming current defined by the FeCAP’s stored value.
Another way to enhance scalability would be to use high-aspect-ratio 3D FeCAPs13,38,39 (Supplementary Note 5 shows the feasibility of integrating 3D capacitors with distinct equivalent areas on the same selector transistor for more compact MSB hardware implementation). Our technology holds potential for other forms of on-chip learning, particularly continuous, adaptive learning. Hidden weights in binarized and quantized neural networks have been shown to function as metaplastic variables, and modifying their training techniques can mitigate forgetting40,41. Thus, our HM circuit, which harnesses two memory technologies for the non-volatile storage of hidden and analogue weights, could naturally enable continuous on-chip training for adaptive and lifelong learning applications.
Methods
Hysteresis loops in FeCAP and butterfly shaped switching curves in memristors
Figure 1a shows five polarization–electric field (P–E) hysteresis loops measured using the positive-up–negative-down (PUND) technique at ±3 V–10 kHz on 550-nm-diameter capacitors after a wake-up phase of 104 triangular pulses at ±3 V–10 kHz. The P–E plot is obtained by averaging the measured displacement current of 1,000 capacitors.
Figure 1a also shows five quasi-static current–voltage curves for the SET and RESET operations of a 1T–1R device. For the SET operation, the WL of the access transistor was set to 1 V, the BL was grounded, and the top electrode was swept between 0 V and 2.6 V in 50-mV steps. For the RESET operation, the WL of the access transistor was set to 4.5 V, the top electrode was grounded, and the BL was swept between 0 V and 1.45 V in 50-mV steps. SET operations were always preceded by RESET ones. Before cycling, the 1T–1R device underwent forming, during which the WL of the access transistor was set to 1.05 V, the BL was grounded, and the top electrode was swept between 0 V and 5.2 V in 50-mV steps.
FeCAP and memristor technologies and circuits
The circuits described in the ‘Results’ section use a hybrid industrial/academic process. They were fabricated using a 130-nm CMOS foundry process with four metal layers. The unified memory, based on ferroelectric Si-doped hafnium oxide and enabling the fabrication of memristor and FeCAP, was fabricated on tungsten vias on top of metal layer four. The unified memory stack consists of a 150-nm-thick titanium nitride (TiN) bottom electrode, a 10-nm-thick Si-doped HfO2 ferroelectric layer, a 4-nm-thick Ti scavenging layer and a 100-nm-thick TiN top electrode. TiN electrodes were deposited by physical vapour deposition at 350 °C. The HfO2 layer was deposited by atomic layer deposition at 300 °C, with HfCl4 and H2O as the precursors. The oxide film was then doped with silicon by ion implantation to achieve a 1% Si mean concentration. The Ti scavenging layer was deposited by physical vapour deposition at the top electrode interface, with no air break between the Ti and TiN top electrode. The resulting stack was etched to define square capacitors with 600-nm sides. Capacitors were then encapsulated by SiN and SiO2 deposited at 400 °C, followed by a planarization step before via opening and metal five deposition at 450 °C. A specific thermal annealing step was performed at the end of process at a BEOL-compatible temperature.
FeCAP arrays, used to evaluate the memory performance of the proposed unified memory stack functioning as a binary ferroelectric device (Fig. 2b–e), include shift registers to address distinct lines, control circuits for the shift registers, line drivers to connect the addressed lines to an external voltage and sense amplifiers for data readout. A clocked latch sense amplifier is used to compare the BL voltage to an external reference voltage during read operations. The digital peripheral circuitry is supplied with 4.8 V. A 660-nm-wide minimum-length selector transistor is serially connected to the designed capacitor.
Memristor arrays, used to evaluate the performance of the proposed unified memory stack as an analogue memory (Fig. 2f–h), include line decoders and drivers to connect the addressed lines to an external voltage. The digital peripheral circuitry is supplied with 4.8 V. A 3.5-μm-wide minimum-length selector transistor is serially connected to the designed resistor.
The main blocks of the HM array are detailed in Fig. 3c. The digital peripheral circuitry of the HM array is supplied with 4.8 V. A 1-μm-wide minimum-length selector transistor is serially connected to the memristors, and a 500-nm-wide minimum-length access transistor is used for the FeCAPs. Pulse generation and current measurements are performed outside the test scribes by the characterization setup. Optionally, a timing block can be used for standard pulse generation in the FeCAP and HM arrays.
Programming energy estimation of FeCAPs
The programming energy of the ferroelectric memory cell reported in Fig. 2c has been evaluated as
where PR is the remanent polarization, S is the capacitor area, MW0σ is the median memory window, CD is the dielectric capacitance, CBL is the BL parasitic capacitance and Vprog is the programming voltage. Thus, the switching energy is obtained from the experimentally measured median memory window for the various programming conditions and the estimated capacitance values. For the median memory window extraction, we measured the distributions of the zero and one states with analogous writing and reading pulses for each pulse amplitude–duration combination. We estimated the dielectric capacitance for the memory element as \({C}_{{\rm{D}}}={\epsilon }_{0}{\epsilon }_{{\rm{r}}}\frac{S}{d}=9.5\,{{\rm{fF}}}\), with ϵr = 29.7, and the BL parasitic capacitance as CBL = 188 fF (ref. 42).
Electrical characterization setups
PUND measurements on FeCAPs and quasi-static characterization of memristors were performed using signals generated by a Keysight B1530 waveform generator/fast measurement unit module and analysed by a Keysight B1500A semiconductor parameter analyser, which is controlled by a Python-coded interface (Python 3.12).
The same setup was used to characterize the FeCAP arrays. The Keysight B1530 module was connected to a custom-made printed circuit board with a co-integrated Arduino microcontroller for signal and instruction management.
To program and read the memristor arrays, voltage pulses were produced externally using a RIFLE NplusT engineering test system. This system is equipped with a 100-MHz arbitrary waveform generator and a C++-programmable computer. The computer controlled the pulses generated by the arbitrary waveform generator, which were applied to the memristor arrays.
The HM array was characterized via external power supplies (Rohde & Schwarz HMP4040 and Keysight E3631A), a pulse pattern generator (Anritsu MP1763C), an arbitrary waveform generator (Tektronix AFG1062) and a digital multimeter (Keysight 34470A). The instruments were managed by a Python interface, and communication with the computer occurs via GPIB connections. All signals were connected to our 200-mm wafer through a 25-pin probe card, interfacing with 25 metal pads.
Weight transfer electrical characterization
For the weight transfer characterization shown in Fig. 4, we used the manufactured HM array to transfer data from seven minimum-sized 1T–1C cells, corresponding to the three MSBs of the hidden weight, to one 1T–1R cell. The first MSB is represented by 4T–4C cells, the second by 2T–2C cells, and the third by the 1T–1C cell. This is equivalent to the transfer from three 1T–1C cells with sizes 4Smin, 2Smin and Smin, respectively (Supplementary Note 6).
Before each transfer operation, the memristor device is RESET to a low-conductance state, and the data to transfer is written into the seven FeCAPs. The TL is then precharged to 0 V. During the transfer operation, the source lines of the seven FeCAP devices are pulsed with a 3.5 V–10 µs pulse, the WLs are set to 4.8 V and the BL is floating. At the same time, a 2.3 V–10 µs pulse is applied to the memristor source line. The memristor BL is set to –0.9 V. This negative voltage setting for the memristor was necessary to obtain a gate–source voltage (Vgs) suitable for the resistive random-access memory’s selector transistor during the transfer operation. Nevertheless, an accurate co-design of the BL parasitic capacitance, material stack and device geometry could eliminate the need to set any bias voltage on the memristor’s bottom electrode, simplifying the transfer procedure. Finally, the memristor’s conductance is externally read with 400-mV-voltage pulses.
Note that in our design, a complete synapse uses two memristors and 14 FeCAPs (one for sign, four for the first MSB, two for the second MSB, and one for the last MSB and each LSB), meaning that in a transfer line, only 112 out of the 128 FeCAPS are used.
Neural network simulations
A three-layer fully connected neural network was trained to address the MNIST dataset43. Here 60,000 images were used for each training epoch, and the MNIST test set of 10,000 images was used for validation. The network has one input layer with 784 neurons, two hidden layers with 200 and 100 neurons each, and one output layer with 10 neurons. The inputs are greyscale images with values from 0 to 255, normalized between –1 and 1. For the online training simulations (details in Supplementary Note 7 and Supplementary Algorithms 1–4), each hidden layer undergoes layer normalization44 (where scale- and shift-trainable parameters γ and β are set to one and zero, respectively), followed by rectified linear unit activation. The activation function of the output layer is a softmax function, preceded by layer normalization. The ANN with hybrid memories was trained for ten epochs, with a learning rate of 0.1. The calculated hidden weight update matrix is multiplied by a binary mask M that dictates whether a hidden weight should be updated or not. Each element of the mask is independently drawn for each example during training, following a Bernoulli distribution with a given probability of 20%. For FP floating-point hidden weight simulations, the same update strategy and hyperparameter values were used. For the mini-batch training simulations (details in Supplementary Note 7 and Supplementary Algorithms 2–5), the normalization layer was replaced by a batch normalization layer (γ and β are set to one and zero, respectively). The same hyperparameters are used as in the online training case. The mini-batch size is 10 and the number of training epochs is increased to 100.
A four-layer fully connected neural network architecture was used for the Fashion-MNIST dataset45 with 784–200–100–100–10 neurons. As in the previous case, the inputs are greyscale images with values from 0 to 255, normalized between –1 and 1. Again, 60,000 images were used for each training epoch, and a test set of 10,000 images was used for validation. The network was trained for ten epochs at a learning rate of 0.1 and a hidden weight update probability of 10%. The same hyperparameters were used for the FP floating-point hidden weight simulations.
For the ECG binary detection task, a fully connected neural network with one hidden layer of 200 neurons was used. No normalization layers were added. A rectified linear unit activation function was used for the hidden layer, and a sigmoid activation function was used for the output neuron. Data from the MIT–BIH Arrhythmia database46 were used for this study. The dataset consists of half-hour dual-channel ECG recordings from 48 subjects. Individual heartbeats were extracted from each recording, forming 700-ms time series centred on the R-wave peak. Using the fft function from NumPy, a frequency spectrum was generated for each time series. The ten lowest-frequency components were selected from each channel, resulting in 20 features characterizing each heartbeat as a static data point. Heartbeats were categorized as either normal and healthy (‘N’ label) or exhibiting signs of arrhythmia (‘L’, ‘R’, ‘e’, ‘j’, ‘A’, ‘a’, ‘J’, ‘S’, ‘V’, ‘E’, ‘F’, ‘/’, ‘f’ and ‘Q’ labels). A subset of 20,000 data points (10,000 healthy and 10,000 unhealthy heartbeats) was randomly sampled from 47 subjects for model training. Subsequently, models were tested using data points from a previously unseen subject (patient 208). The network was trained for ten epochs, with a learning rate of 0.3 and an update probability of 20%. For the floating-point hidden weight simulations, the same hyperparameters were used.
The parameters in the HM circuit consist of FeCAP and memristor devices, which are not as precise as their 32-bit floating-point counterparts. Therefore, to emulate the training when using the HM operation, we set the representation of our hidden and analogue weights to 10-bit and 4-bit integers, respectively, to match the proposed HM circuit. The hidden weights are stored in ten binary FeCAP cells, and the analogue weights are stored in two memristor cells with eight conductance values each. During inference, we truncate the 10-bit values to their 4-bit approximations (Supplementary Algorithm 3 and Supplementary Note 7), thereby mimicking the operation applied during the proposed digital-to-analogue transfer procedure in our unified memory. Furthermore, memristors and FeCAPs suffer from other types of non-ideality such as device-to-device and cycle-to-cycle variabilities. The method by which we account for these device non-idealities and their impact on the transfer operation is described below and in Supplementary Note 7 and Supplementary Algorithm 4.
Hardware-aware neural network simulations
The statistical electrical characterization of the transfer operation on the HM circuit was used to account for the device non-idealities in the hardware-aware neural network simulations. We approximated our 10-bit hidden weights (Wh) to their 4-bit version (Wa) each time a transfer operation was performed. For each analogue weight, we sampled a random number from a normal distribution with average value μW equal to the corresponding Wa value and standard deviation σW. The profile of the analogue weight is based on the statistical characterization of our HM circuit (Fig. 4). The detailed simulated procedure is described below.
We modelled the conductance of a memristor device in the differential pair as a random variable with normal probability distribution:
where σG is the conductance standard deviation, μG is the average conductance of a transferred level and X is a standard normal random variable. Moreover, we considered a linear relationship between the mapped conductance and the weight value:
where μG,max and μG,min are the average conductance values of the corresponding average maximum (Wa,max) and minimum (Wa,min) transferred weights in absolute value, respectively. By equating the first member of equations (3) and (2), we get
For three MSBs, Wa,max = 7 and Wa,min = 0. Therefore,
The analogue weight values are sampled from a normal distribution with standard deviation 7σG/(μG,max − μG,min) and average value 7(μG − μG,min)/(μG,max − μG,min). The average conductance for each transferred value is obtained experimentally from the characterization in Fig. 4. In particular the average conductance values for the eight levels are μG,min = μG,0 = 1.4 µS, μG,1 = 11.9 µS, μG,2 = 36.5 µS, μG,3 = 58.3 µS, μG,4 = 73.9 µS, μG,5 = 85.5 µS, μG,6 = 95.9 µS and μG,max = μG,7 = 103.9 µS. For each level, we consider a constant standard deviation equal to the average of the standard deviations of the eight levels, that is, σG = 8.7 µS. Consequently, the σW parameter is
Since two separate memristors are used to encode either positive or negative weights, no sign error can occur during the transfer operation. This approach was also implemented in our hardware-aware simulations. The same hyperparameters mentioned above for each dataset were used for the hardware-aware simulations.
Number of memristor and FeCAP programming operations and programming energy evaluation
To estimate the number of programming operations and the corresponding programming energy in FeCAPs and memristors during training (Fig. 5d,e), we followed this procedure. We counted the number of updates for each hidden weight, taking into account the probabilistic weight update scheme. The number of operations on FeCAPs was defined as twice the maximum number of hidden weight updates, because each time the weight is read, it has to be rewritten. Moreover, for each transfer operation, each FeCAP incurs four additional programming operations: reading and rewriting data to save it in another FeCAP cell for further reloading, and then actually transferring (reading) and reloading (writing) the weight.
For the memristors, the number of operations is defined by the parameter k, that is, the number of inputs after which the weights are transferred from FeCAPs to memristors. For each transfer operation, each memristor requires two programming operations: one for resetting the device and one to write the analogue weight.
The programming energy consumption of the two arrays is evaluated by multiplying the number of programming operations by the estimated switching energy for FeCAPs and memristors. We set the programming energy for FeCAP and memristor operations to 100 fJ and 1 pJ (refs. 47,48), respectively.
Transfer learning simulations
Two separate MobileNet-V2 neural network architectures49 were pre-trained on CIFAR-100 (ref. 50) and ImageNet51 to obtain weight-quantized models (4b/INT) using the learned step size quantization method52. The images contained in the CIFAR-100 dataset were resized to 128 × 128 pixels before being fed to the network. The images in the ImageNet dataset were randomly resized between 240 pixels and 480 pixels in their smaller dimension, and then a random crop of 224 × 224 pixels was extracted and fed to the network for learning. The hyperparameters used during this step were as follows: batch size 128 (for CIFAR-100) or 64 (for ImageNet), 500 epochs (for CIFAR-100) or 200 epochs (for ImageNet), Adam optimizer, learning rate of 10−4 and weight decay of 10−5. The FP model achieved a top-1 test accuracy of 79.5% on the CIFAR-100 dataset, whereas the quantized model achieved a top-1 test accuracy of 77.4%; on ImageNet, the FP model achieved a top-1 precision of 69.92%, whereas the quantized model achieved a top-1 accuracy of 68.3%.
We then started from a MobileNet-V2 feature extractor obtained previously and added a newly initialized classifier on top. During this step, the feature extractor was fixed and only the classifier parameters were updated. We used the feature extractor pre-trained on CIFAR-100 to perform transfer learning on CIFAR-10, and the network pre-trained on ImageNet for all other considered datasets. During this phase, every dataset was augmented with the horizontal flip of every image; thus, these datasets used in our experiments contain twice as many images as the original datasets. The images from the datasets were resized to 128 pixels (for CIFAR-10) or 224 pixels (for other datasets) before being fed into the network. For every presented result, the training procedure consists of a tenfold cross-validation scheme: we randomly split the dataset into ten subsets, making sure that an image and its horizontal-flip counterpart could not lie in the training and validation set, respectively; then, we iteratively selected a subset as the validation set and nine others as the training set, and used the validation set to determine when the training should stop; we finally report the tenfold mean and standard deviation of the top-1 accuracy. For the offline transfer learning simulations (Fig. 6c, Offline), a standard optimizer (Adam), batch size of 128, learning rate of 10−4 and learned step size quantization of the inference weights (4b/INT) were used. For the online transfer learning with the HM training strategy developed (Fig. 6c, HM-online), the hidden weights were updated for each training sample with an update probability of 1. The inference weights were updated after 512 new inputs and the learning rate was set to 10−1 with a learning rate decay of 0.1.
Data availability
Some preliminary results from this study have been reported in ref. 22. The MNIST43, Fashion-MNIST45, MIT–BIH ECG46, CIFAR-10 and CIFAR-100 (ref. 50), ImageNet51, Stanford Cars34, Caltech Birds33, Oxford-IIIT Pet31 and Oxford Flowers 102 (ref. 32) datasets are publicly accessible. All other measured data are freely available from the corresponding authors upon request.
Code availability
All software programs used in the presentation of the Article are available from the corresponding authors upon request.
References
Zhang, W. et al. Edge learning using a fully integrated neuro-inspired memristor chip. Science 381, 1205–1211 (2023).
Bianchi, S. et al. A self-adaptive hardware with resistive switching synapses for experience-based neurocomputing. Nat. Commun. 14, 1565 (2023).
Zhang, W. et al. Neuro-inspired computing chips. Nat. Electron. 3, 371–382 (2020).
Wong, H.-S. P. et al. Metal-oxide RRAM. Proc. IEEE 100, 1951–1970 (2012).
Le Gallo, M. et al. A 64-core mixed-signal in-memory compute chip based on phase-change memory for deep neural network inference. Nat. Electron. 6, 680–693 (2023).
Ambrogio, S. et al. An analog-AI chip for energy-efficient speech recognition and transcription. Nature 620, 768–775 (2023).
Wan, W. et al. A compute-in-memory chip based on resistive random-access memory. Nature 608, 504–512 (2022).
Yao, P. et al. Fully hardware-implemented memristor convolutional neural network. Nature 577, 641–646 (2020).
Ielmini, D. & Wong, H.-S. P. In-memory computing with resistive switching devices. Nat. Electron. 1, 333–343 (2018).
Prezioso, M. et al. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 521, 61–64 (2015).
Rasch, M. J. et al. Hardware-aware training for large-scale and diverse deep learning inference workloads using in-memory computing-based accelerators. Nat. Commun. 14, 5282 (2023).
Böscke, T. S., Müller, J., Bräuhaus, D., Schröder, U. & Böttger, U. Ferroelectricity in hafnium oxide thin films. Appl. Phys. Lett. 99, 102903 (2011).
Ramaswamy, N. et al. NVDRAM: a 32Gb dual layer 3D stacked non-volatile ferroelectric memory with near-DRAM performance for demanding AI workloads. In Proc. 2023 IEEE International Electron Devices Meeting (IEDM) 1–4 (IEEE, 2023).
Luo, Y., Luo, Y.-C. & Yu, S. A FeRAM-based volatile/non-volatile dual-mode buffer memory for deep neural network training. In Proc. 2021 Design, Automation and Test in Europe Conference and Exhibition (DATE) 1871–1876 (2021).
Wen, T.-H. et al. Fusion of memristor and digital compute-in-memory processing for energy-efficient edge computing. Science 384, 325–332 (2024).
Ambrogio, S. et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 558, 60–67 (2018).
Li, Y. et al. Monolithic three-dimensional integration of RRAM-based hybrid memory architecture for one-shot learning. Nat. Commun. 14, 7140 (2023).
Ning, H. et al. An in-memory computing architecture based on a duplex two-dimensional material structure for in situ machine learning. Nat. Nanotechnol. 18, 493–500 (2023).
Max, B., Pešić, M., Slesazeck, S. & Mikolajick, T. Interplay between ferroelectric and resistive switching in doped crystalline HfO2. J. Appl. Phys. 123, 134102 (2018).
Knabe, J., Berg, F., Goß, K. T., Boettger, U. & Dittmann, R. Dual-mode operation of epitaxial Hf0.5Zr0.5O2: ferroelectric and filamentary-type resistive switching. Phys. Status Solidi A 221, 2300409 (2023).
Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R. & Bengio, Y. Quantized neural networks: training neural networks with low precision weights and activations. J. Mach. Learn. Res. 18, 6869–6898 (2017).
Martemucci, M. et al. Hybrid FeRAM/RRAM synaptic circuit enabling on-chip inference and learning at the edge. In Proc. 2023 IEEE International Electron Devices Meeting (IEDM) 1–4 (IEEE, 2023).
Esmanhotto, E. et al. Experimental demonstration of multilevel resistive random access memory programming for up to two months stable neural networks inference accuracy. Adv. Intell. Syst. 4, 2200145 (2022).
Barrett, N. et al. Oxygen vacancy engineering in Si-doped, HfO2 ferroelectric capacitors using Ti oxygen scavenging layers. Appl. Phys. Lett. 125, 043502 (2024).
Lee, J. et al. Role of oxygen vacancies in ferroelectric or resistive switching hafnium oxide. Nano Converg. 10, 55 (2023).
Lederer, M. et al. On the origin of wake-up and antiferroelectric-like behavior in ferroelectric hafnium oxide. Phys. Status Solidi RRL 15, 2100086 (2021).
Grossi, A. et al. Resistive RAM endurance: array-level characterization and correction techniques targeting deep learning applications. IEEE Trans. Electron Devices 66, 1281–1288 (2019).
Jiang, P. et al. Freely switching between ferroelectric and resistive switching in Hf0.5Zr0.5O2 films and its application on high accuracy on-chip deep neural networks. Sci. China Inf. Sci. 66, 122409 (2023).
Long, X., Tan, H., Sánchez, F., Fina, I. & Fontcuberta, J. Ferroelectric electroresistance after a breakdown in epitaxial Hf0.5Zr0.5O2 tunnel junctions. ACS Appl. Electron. Mater. 5, 740–747 (2023).
Zarkeshian, P., Kergan, T., Ghobadi, R., Nicola, W. & Simon, C. Photons guided by axons may enable backpropagation-based learning in the brain. Sci. Rep. 12, 20720 (2022).
Parkhi, O. M., Vedaldi, A., Zisserman, A. & Jawahar, C. V. Cats and dogs. In Proc. 2012 IEEE Conference on Computer Vision and Pattern Recognition 3498–3505 (IEEE, 2012).
Nilsback, M.-E. & Zisserman, A. Automated flower classification over a large number of classes. In 2008 Sixth Indian Conference on Computer Vision, Graphics & Image Processing 722–729 (IEEE, 2008).
Wah, C., Branson, S., Welinder, P., Perona, P. & Belongie, S. Caltech-UCSD Birds 200. Report No. CNS-TR-2011-001 (California Institute of Technology, 2011).
Krause, J., Stark, M., Deng, J. & Fei-Fei, L. 3D object representations for fine-grained categorization. In 2013 IEEE International Conference on Computer Vision Workshops 554–561 (IEEE, 2013).
Zhuang, B., Shen, C., Tan, M., Liu, L. & Reid, I. Towards effective low-bitwidth convolutional neural networks. In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 7920–7928 (IEEE Computer Society, 2018).
Grenouillet, L. et al. Reliability assessment of hafnia-based ferroelectric devices and arrays for memory and AI applications (Invited). In Proc. 2023 IEEE International Reliability Physics Symposium (IRPS) 1–8 (IEEE, 2023).
Alcala, R. et al. BEOL integrated ferroelectric HfO2-based capacitors for FeRAM: extrapolation of reliability performance to use conditions. IEEE J. Electron Devices Soc. 10, 907–912 (2022).
Grenouillet, L. et al. A highly reliable 1.8 V 1 Mb Hf0.5Zr0.5O2-based 1T1C FeRAM array with 3-D capacitors. In Proc. 2023 IEEE International Electron Devices Meeting (IEDM) 1–4 (IEEE, 2023).
Haratipour, N. et al. Hafnia-based FeRAM: a path toward ultra-high density for next-generation high-speed embedded memory. In Proc. 2022 International Electron Devices Meeting (IEDM) 6.7.1–6.7.4 (IEEE, 2022).
Laborieux, A., Ernoult, M., Hirtzlin, T. & Querlioz, D. Synaptic metaplasticity in binarized neural networks. Nat. Commun. 12, 2549 (2021).
D’Agostino, S. et al. Synaptic metaplasticity with multi-level memristive devices. In Proc. 5th IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS) 1–5 (IEEE, 2023).
Laguerre, J. et al. Memory window in Si:HfO2 FeRAM arrays: performance improvement and extrapolation at advanced nodes. In Proc. 2023 IEEE International Memory Workshop (IMW) 1–4 (IEEE, 2023).
Deng, L. The MNIST database of handwritten digit images for machine learning research. IEEE Signal Process. Mag. 29, 141–142 (2012).
Ba, J. L., Kiros, J. R. & Hinton, G. E. Layer normalization. Preprint at https://arxiv.org/abs/1607.06450 (2016).
Xiao, H., Rasul, K. & Vollgraf, R. Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms. Preprint at https://arxiv.org/abs/1708.07747 (2017).
Moody, G. B. & Mark, R. G. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 20, 45–50 (2001).
Lanza, M. et al. Memristive technologies for data storage, computation, encryption, and radio-frequency communication. Science 376, eabj9979 (2022).
Molas, G. & Nowak, E. Advances in emerging memory technologies: from data storage to artificial intelligence. Appl. Sci. 11, 11254 (2021).
Sandler, M., Howard, A. G., Zhu, M., Zhmoginov, A. & Chen, L.-C. Inverted residuals and linear bottlenecks: mobile networks for classification, detection and segmentation. In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition 4510–4520 (2018).
Krizhevsky, A. & Hinton, G. Learning multiple layers of features from tiny images. Univ. of Toronto https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (2009).
Deng, J. et al. ImageNet: a large-scale hierarchical image database. In Proc. 2009 IEEE Conference on Computer Vision and Pattern Recognition 248–255 (IEEE, 2009).
Esser, S. K., McKinstry, J. L., Bablani, D., Appuswamy, R. & Modha, D. S. Learned step size quantization. Preprint at https://arxiv.org/abs/1902.08153 (2019).
Martemucci, M., Rummens, F., Vianello, E. & Hirtzlin, T. Hybrid FeRAM/OxRAM data storage circuit. US patent US2024/0135979 A1 (2024).
Acknowledgements
We acknowledge funding support from the European Research Council (consolidator grant DIVERSE: 101043854, to E.V.) and through a France 2030 government grant (ANR-22-PEEL-0010, to D.Q. and E.V.). A large language model (OpenAI GPT-4o) was used to assist with style and grammar revisions in certain sections of the manuscript.
Author information
Authors and Affiliations
Contributions
M.M., F.R., T.H. and E.V. developed the hybrid synapse concept. M.M. designed and laid out the FeCAP/memristor memory test chip, under the supervision of F.R. and S.S. M.M. and S.M. performed the characterization of the FeCAP and memristors arrays. O.G. and M.M. performed the characterization of the hybrid FeCAP/memristor circuit. L.G. and C.C. led the fabrication of the test chips using the unified ferroelectric/memristive memory technology. M.M. developed the hardware-aware training of the hybrid FeCAP/memristor memory circuit for the MNIST, Fashion-MNIST and ECG benchmarks under the supervision of F.R., A.F.V. and D.Q. Y.M. developed the hardware-aware transfer learning of the hybrid FeCAP/memristor memory circuit. E.V., D.Q. and M.M. wrote the initial version of the manuscript. E.V. directed the work. All authors participated in the data analysis, discussed the results and co-edited the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The HM implementation is protected under US patent number US2024/0135979 A1, published on 25 April 2024 (ref. 53). M.M., F.R., E.V. and T.H. are named inventors of this patent. The other authors declare no competing interests.
Peer review
Peer review information
Nature Electronics thanks Dashan Shang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Notes 1–12, Figs. 1–10, Algorithms 1–5 and Table 1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Martemucci, M., Rummens, F., Malot, Y. et al. A ferroelectric–memristor memory for both training and inference. Nat Electron (2025). https://doi.org/10.1038/s41928-025-01454-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41928-025-01454-7