Spatiotemporal modeling quantifies cellular contributions to uptake of Aspergillus fumigatus in the human lung

Abstract

The human lung is confronted daily with thousands of microbial invaders reaching the lower respiratory tract. An efficient response by the resident type 1 and type 2 alveolar epithelial cells (AECs) and alveolar macrophages (AMs) cells during the early hours of innate immunity is a prerequisite to maintain a non-inflammatory state, but foremost to rapidly remove harmful substances. One such human-pathogenic invader is the opportunistic fungus Aspergillus fumigatus. If the spherical conidia are not cleared in time, they swell reaching approximately twice of their initial size and germinate to develop hyphae around six hours post-infection. This process of morphological change is crucial as it enables the pathogen to invade the alveolar epithelium and to reach the bloodstream, but also makes it conspicuous for the immune system. During this process, conidia are first in contact with AECs then with migrating AMs, both attempting to internalize and clear the fungus. However, the relative contribution of AMs and AECs to uptake of A. fumigatus remains an open question, especially the capabilities of the barely investigated type 1 AECs. In this study, we present a bottom-up modeling approach to incorporate experimental data on the dynamic increase of the conidial diameter and A. fumigatus uptake by AECs and AMs in a hybrid agent-based model (hABM) for the to-scale simulation of virtual infection scenarios in the human alveolus. By screening a wide range of parameters, we found that type 1 AECs, which cover approximately 95% of the alveolar surface, are likely to have a greater impact on uptake than type 2 AECs. Moreover, the majority of infection scenarios across the regime of tested parameters were cleared through uptake by AMs, whereas the contribution to conidial uptake by AECs was observed to be limited, indicating that their crucial support might mostly consist in mediating chemokine secretion for AM recruitment. Regardless, as the first host cell being confronted with A. fumigatus conidia, our results evidence the large potential impact of type 1 AECs antimicrobial activities, underlining the requirement of increasing experimental efforts on this alveolar constituent.

Introduction

The innate immune system constitutes the first line of defense in the protection of the human body against invading microbes. Due to the continuous inhalation of particles by humans, the immune system is permanently challenged to rapidly remove harmful microbes from the lungs to maintain a non-inflammatory and healthy state¹. Alveolar epithelial cells (AECs) line the lung alveoli and thus act as a physical barrier to noxious particles, making them important players in immune defense by preventing microbes from entering the bloodstream^2,3. The relatively large and flat type 1 AECs make up about 95% of the alveolar surface^4,5, although they are outnumbered by the smaller surfactant-producing type 2 AECs that cover only about 5%⁶. Inhaled microbes reaching the lower respiratory tract encounter AECs that – besides functioning as physical barriers – are also able to internalize and kill invading microbes^7,8,9. In addition, AECs secrete cytokines and chemokines that may recruit alveolar macrophages (AMs), which are the professional phagocytes resident in lung alveoli^8,10,11. AMs patrol the alveolar surface in numbers that vary dynamically around twelve cells per alveolus^12,13 to detect and clear harmful particles within hours post-infection^14,15,16. However, it is still not understood what the relative contribution of AMs and AECs is in the uptake of particles to prevent respiratory diseases^17,18.

One such respiratory threat is due to the ubiquitous mold Aspergillus fumigatus^19,20. This opportunistic pathogen is often diagnosed too late and – since treatment options are limited – is associated with mortality rates up to 90% in immunocompromised patients^19,21,22. Consequently, A. fumigatus is one of four human-pathogenic fungi that belong to the Critical Priority Group according to the recently updated rating by the World Health Organization (WHO)^23,24,25. Humans inhale several hundred A. fumigatus conidia per day²⁶ and these, due to their small size ( ~ 2-3 µm diameter), reach the alveoli in the lower respiratory tract^20,27. If able to evade the innate immune response, conidia pose a substantial risk for immunocompromised patients^28,29. Due to the large number of alveoli in the human lung (~ 500 million), no more than one conidium per alveolus can be expected on statistical grounds^13,30. The spherical conidium will adhere to AECs and, after roughly two hours, will start to swell reaching up to twice its initial diameter³¹. At around six hours post-infection, germination of the conidium begins with the formation of hyphae, which are able to damage the alveolar epithelium and penetrate the lung tissue to enter blood vessels leading to clotting or dissemination via the bloodstream^32,33. The innate immune response to inhaled A. fumigatus conidia is mediated by both AECs and AMs³⁴ via recognition, uptake, and clearance of their internalized cargoes^{35,36,37,38,39,40}, but the relative contribution of these cells to conidial removal from the alveolus in the early hours is a subject of ongoing discussions⁴¹. In addition, the differences between type 1 and type 2 AECs in terms of their phagocytic capabilities are barely explored, as the experimental data on type 1 AECs is sparse because of their difficult cell cultivation and rare established in vitro protocols⁴².

Understanding the underlying mechanisms of the complex interplay between A. fumigatus conidia and the early innate immune system is crucial to improving diagnosis and treatment. To investigate this, wet-lab experiments can be combined with mathematical analyses representing the heart of systems biology^43,44. In this multidisciplinary approach, computational models are used to simulate complex biological systems that are calibrated to experimental data allowing millions of virtual experiments to be conducted⁴⁵. The mathematical description of systems can be realized by ordinary differential equations (ODEs) or partial differential equations (PDEs), state-based models or agent-based models, and game theory^{46,47,48,49,50,45,51,52,53,54}. Agent-based models are computationally expensive but can account for stochastic systems with inhomogeneous properties, e.g., to investigate microbial infections in whole-blood^55,56 or modeling receptor-ligand binding kinetics at the single cell level⁵⁷. In the past, we developed a hybrid agent-based model of a human alveolus (hABM), which was applied in earlier studies to explore the impact of AM numbers¹³, investigate the function of pores of Kohn⁵⁸, compare the immune response in the murine and human alveoli³⁰, as well as quantify the impact of chemokine secretion on fungal clearance^59,60.

In the present study, we investigated the early immune response against A. fumigatus in the human lung and, specifically how type 1 and type 2 AECs and AMs contribute to fungal clearance. Based on newly evaluated experimental data from Bertuzzi et al.^35,36 and in line with previous experimental findings^37,61,62 indicating a more efficient uptake of swollen conidia, we developed a conidial growth model linking conidial uptake by AECs and AMs to conidial swelling and integrated it into the previously developed hABM^{13,30,58,59,60}. We ran millions of stochastic computer simulations and predicted the A. fumigatus uptake contributions by type 1 and type 2 AECs and AMs during the first hours post-infection. Assuming that conidial swelling also determines the pathogen recognition as such and the subsequent onset of chemokine secretion by AECs, we investigated fungal clearance for shifted onsets of chemokine secretion. Also, we screened over reduced and increased AM numbers simulating compromised and primed early immune states. Our simulations suggest that, in the majority of infection scenarios, fungal clearance is dominated by phagocytosis due to AMs, while uptake by AECs decisively depends on whether the conidium is confronted with type 1 or type 2 AECs. To analyze the large amount of simulation outcomes further, we fitted a surrogate infection model¹³ enabling the prediction of requisite uptake rates of host cells for timely fungal clearance. In summary, we present a bottom-up modeling approach based on experimental data that links conidial swelling to its recognition and uptake and investigates the relative contribution of conidial uptake by AMs and AECs. Ultimately, our study highlights the importance of AMs for innate immunity but also reveals the relatively unexplored role of type 1 AECs as the host cell with the greatest potential leverage for fungal clearance in the early hours.

Results

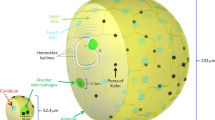
We studied the relative contributions of alveolar epithelial cells (AECs) and alveolar macrophages (AMs) to the early immune response against A. fumigatus pursuing the bottom-up approach shown in Fig. 1. First, to link fungal uptake with conidial swelling in time, we fitted a Verhulst ODE model to the dynamically increasing conidial diameter based on re-analyzed experimental data from in vitro infection assays of type 2 AECs with A. fumigatus conidia^35,36. This enabled us to formulate a Malthus ODE model for the time-dependent uptake rate that is increasing as a result of the increasing contact area between the conidium and the host cell. We fitted this time-dependent uptake rate of type 2 AECs to the above-mentioned infection assays^35,36 (see Fig. 1A–C). Next, we extended this mechanism to uptake by type 1 AECs and AMs and implemented these new features into our previously developed hybrid agent-based model (hABM)^{13,30,58,59,60} for the human alveolus. To explore the relative contributions of AECs and AMs to the uptake of A. fumigatus conidia, we ran millions of virtual infection scenarios with the hABM for the fitted uptake rate of type 2 AECs and screened over uptake rates for type 1 AECs and AMs (see Fig. 1D–F). In addition, we tested chemokine secretion onsets that are delayed by their dependence of conidial swelling with time, which affects the migration behavior of AMs, as well as the dynamic change in AM numbers within the alveolus. The mathematical details are explained in Methods in Extended hybrid agent-based model of the human alveolus, while Supplementary Video S1 illustrates the composition of the hABM and Supplementary Video S2 shows exemplary simulations of the hABM for the uptake by AMs, type 1 AECs, and type 2 AECs. Lastly, we trained a surrogate infection model (SIM), established in our previous study¹³, to interpolate the hABM simulation outcomes across the vast parameter space. The SIM enabled us to predict the relative uptake contributions of type 1 and type 2 AECs as well as AMs, allowing us to identify favorable parameter regimes for efficient clearance of A. fumigatus conidia from the human alveolus (see Fig. 1G). Based on our findings, we suggest new experimental efforts on type 1 AECs, as in almost all cases they are first exposed to A. fumigatus conidia and thus have the greatest impact in vivo.

Fig. 1: Bottom-up approach to model the immune response against A. fumigatus lung infection.

A–C Based on experimental phagocytosis assays between A. fumigatus conidia and type 2 AECs (A), we fitted a Verhulst ODE model to the increase of conidial diameter (B), and an extended Malthus ODE model to uptake indexes resulting in an increasing chance of uptake from non-swelling to swelling conidia. The dotted arrow denotes the transition from a resting to a swelling conidium that is taken up with a higher probability (C). D–F Including the fitted ODEs into a previously developed hybrid agent-based model (hABM) of one human alveolus, we were able to simulate millions of virtual infection scenarios. The hABM comprises one alveolus as a ¾ sphere consisting of type 1 AECs (yellow) and type 2 AECs (light blue). The entrance ring (dark blue) and pores of Kohn (PoK) (black) are the boundaries of the system (see Supplementary Video S1). The migration of AMs (green) is directed by the chemokine signal (white isolines) to locate the A. fumigatus conidia (red). The conidium can be taken up by AMs, type 1 and type 2 AECs, as demonstrated in the Supplementary Video S2. G By training a surrogate infection model (SIM) on the hABM output, we were able to predict uptake indexes by AMs and AECs for an interpolated parameter space.

Dynamics of conidial swelling is captured by the Verhulst ODE model

Conidia of A. fumigatus undergo swelling before the onset of hyphal growth that occurs around six hours post-infection. To study this early phase of infection, we exploited our experimental data obtained from infection assays of type 2 AECs and A. fumigatus^35,36. We re-analyzed the image data (see Methods in Experimental Data) and extracted the conidial diameter over time. Figure 2A shows that the Verhulst ODE model (dashed dark blue line) can be accurately fitted to the time-dependent conidial diameter (light blue points) reaching the lowest mean squared error (${MSE}$) with ${MSE}=0.5979$ compared to further baseline models (see Methods in Modeling the swelling of A. fumigatus conidia by a Verhulst ODE model, Supplementary Results 1.1 and Supplementary Figs. S1A, B, and fitted parameters in Supplementary Table S1). The model’s sensitivity was investigated in Supplementary Results 1.2 where also the bootstrap method is described which was used to create the 95% confidence bands in Fig. 2. At the time $t=0\,\min$, the conidial diameter is on average about $2.8{\mu m}$, swells over time reaching the exponential growth phase between times $t=60\,\min$ to $t=120\,\min$ and saturating with a diameter of about $4.6{\mu m}$ between times $t=240\,\min$ to $t=300\,\min$.

Fig. 2: Modeling the conidial swelling and size-dependent uptake by type 2 AECs.

A The Verhulst ODE model (blue dashed lined) exhibits the experimental conidial diameter in µm (blue points, mean values as big blue points) in the first 12 h. The blue shaded area represents the 95% confidence bands of the model prediction. B The Verhulst ODE model as the relative increase in area compared to $t=0\,\min$ (blue dashed lined). The dark red dots represent the conidial size at $t=0\,\min$ and the red dots represent the swollen conidial part over time. C The extended Malthus ODE model (dark red dashed line) fitting the experimental size-dependent conidial uptake by type 2 AECs (red points, mean values as big red points). The orange dashed line represents the normal Malthus ODE model. The red shaded area represents the 95% confidence bands of the model prediction. D The extended Malthus ODE to model the theoretical uptake index for different uptake rates ${r}_{{up}0}$. Different opacity values for different values of ${r}_{{up}0}$ for more (blue dotted lines) or less (green dotted lines) efficient uptake than type 2 AECs.

Fitting the parameters of the Verhulst ODE model enabled us to retrieve the relative increase in the conidial area, which is shown by the dashed dark blue line in Fig. 2B. Starting from an area of $100 \%$ (denoted as a dark red point) in the resting state at time $t=0\,\min$, we predict that the area increases to $103 \%$ at time $t=60\,\min$, and further to $127 \%$, $213 \%$ and $274 \%$ (denoted as red rings surrounding the red point) at times $t=120\,\min$, $t=180\,\min$ and $t=300\,\min$, respectively. We denoted this percental surface area increase as a function of time, $S(t)$, with $S\left(t=0\,h\right)=1.0$ and $S\left(t\ge 5h\right)=2.74$, e.g., 274% (see Fig. 2B and Methods in Modeling the swelling of A. fumigatus conidia by a Verhulst ODE model). As shown in Supplementary Fig. S1, the Verhulst ODE model can fit the temporal conidial diameter increase also for different experimental in vitro settings (see Methods in Experimental Data, Supplementary Results 1.1 and Supplementary Table S1), which underlines its general applicability to conidial diameter increase.

Malthus ODE model proposes conidial uptake to depend on time-dependent swelling

Exploring the mechanism of conidial uptake by type 2 AECs, we re-considered the experimental data from the infection assays^35,36 that are displayed as the uptake index (red points) as a function of time in Fig. 2C. The uptake index corresponds to the percentage of conidia that are taken up based on the encountered conidia as a function of time post-infection and yielded mean values of $15.5 \%$ at $t=120\,\min$, $40.5 \%$ at $t=240\,\min$ and $62.2 \%$ at $t=360\,\min$. To model the uptake dynamics, we derived and fitted a Malthus ODE model based on the assumption of a constant uptake rate ${r}_{c-{up}}$ between conidium and type 2 AEC (see Methods in Modeling the uptake of conidia via an extended Malthus ODE model and Supplementary Results 1.3). However, as can be seen in Fig. 2C (orange dotted line), the fitted Malthus ODE does not reflect the dynamics of the mean values accurately for all experimentally measured time points. Next, we linked the Verhulst ODE model, which was fitted in the previous section for the dynamics of the conidial diameter and subsequent increasing surface area $S\left(t\right),$ to the uptake rate by type 2 AECs. The resulting extended Malthus ODE model is based on a time-dependent uptake rate governed by the conidial diameter (see Methods in Modeling the uptake of conidia via an extended Malthus ODE model. To test the overfitting and robustness of this derived extended Malthus ODE, cross-validation and sensitivity analysis was performed before the model was fitted to all data points exhibiting a lower ${MSE}=0.098$ compared to ${MSE}=0.101$ of the normal Malthus ODE (see Supplementary Results 1.2 and Supplementary Table S2). The optimal parameter was found to be ${{r}_{{up}0}^{{AEC}2}:= r}_{{up}}^{{AEC}2}(t=0)=0.00137\,{m}{{in}}^{-1}$ resulting in a time-dependent uptake parameter, ${r}_{{up}}^{{AEC}2}\left(t\right)={r}_{{up}0}^{{AEC}2}\cdot S(t)$ as shown by the dark red dashed curve in Fig. 2C. The confidence interval of the parameter ${r}_{{up}0}^{{AEC}2}$ was investigated in Supplementary Results 1.2. As can be seen in Fig. 2B, the time-dependent uptake rate ${r}_{{up}}^{{AEC}2}(t)$ reaches its maximum of approximately 274% of its initial value after 5 h, meaning ${r}_{{up}}^{{AEC}2}\left(t=5h\right)=0.00137\,{m}{{in}}^{-1}\cdot 2.74=0.00375\,{m}{{in}}^{-1}$, that is when the contact area increases saturates.

The fitted extended Malthus ODE links the increasing contact area between the conidium and the type 2 AEC to an increasing uptake rate of the type 2 AECs. This correlation has also been indicated previously for other host cells^37,61,62. Therefore, we use the extended Malthus ODE to model the uptake index of AMs ($U{I}_{{AM}}$), and type 1 AECs ($U{I}_{{AEC}1}$) with their respective uptake rates ${r}_{{up}0}^{{AM}}(t)$ and ${r}_{{up}0}^{{AEC}1}(t)$. Note that all uptake indexes $U{I}_{{HC}}$ (or ${UI}$ by HC) refer to the relative uptake indexes of a host cell (HC), calculated over the number of conidia that can be reached by the respective HC (see Methods in Input parameter and output measures for the extended hABM). The computed uptake indexes with the extended Malthus ODE can be seen in Fig. 2D for varying uptake rates. As elaborated in Supplementary Results 1.4, these are very accurate for stationary AECs that have permanent contact with the conidium but represent an upper limit for AMs that, prior to uptake, must migrate toward the conidium.

Uptake by type 1 AECs dominates the total uptake in the absence of AMs

In order to investigate the relative contributions of AECs and AMs to A. fumigatus uptake, we extended the hABM (see Methods in Extended hybrid agent-based model of the human alveolus) by implementing mechanisms simulating conidial swelling (Verhulst ODE model; see Methods in Modeling the swelling of A. fumigatus conidia by a Verhulst ODE model) and size-dependent conidial uptake by type 1 and type 2 AECs as well as AMs (Malthus ODE model; Methods in Modeling the uptake of conidia via an extended Malthus ODE model). At first, we considered a scenario where only type 1 and type 2 AECs are present, $i.e.$ we simulated the immune response in the human alveolus in the absence of AMs resembling a compromised immune status¹⁷. We used the fitted uptake rate ${r}_{{up}0}^{{AEC}2}=0.00137\,{m}{{in}}^{-1}$ for type 2 AECs and varied the uptake rate ${r}_{{up}0}^{{AEC}1}$ for type 1 AECs (see Table 1) based on a conducted literature search (see Supplementary Results 1.5 and Supplementary Table S3).

Table 1 The parameter ranges for the virtual experiments with the hABM

As shown by the light blue curve in Fig. 3A, the relative uptake by type 2 AECs (based on the total number of conidia confronted with type 2 AECs) reaches about $62 \%$ at time $t=360\,\min$ regardless of type 1 AEC uptake rates ${r}_{{up}}^{{AEC}1}(t)$, as stationary type 1 and type 2 AECs do not compete over the conidium. Also, the extended Malthus ODE model (dashed dark red curve) is completely in line with the stochastic simulations for type 2 AEC uptake (light blue curve) as AECs are stationary and in direct contact with the conidium revealing the consistency of our simulation results with the analytical calculation. As shown in Fig. 3A, for time-dependent uptake rates of type 1 AECs ${r}_{{up}}^{{AEC}1}\left(t\right)={r}_{{up}0}^{{AEC}1}\cdot S(t),$ for ${r}_{{up}0}^{{AEC}1}\in \{{0.000137,0.000685,0.00274}\}$ in $m{{in}}^{-1}$, corresponding to $0.1\cdot {r}_{{up}}^{{AEC}2}(t)$, $0.5\cdot {r}_{{up}}^{{AEC}2}(t)$ and $2\cdot {r}_{{up}}^{{AEC}2}(t)$, (shown in dotted, dashed, and solid lines), respectively, we find that the overall uptake indexes of $11 \%$, $38 \%$, or $84 \%$ (orange lines) at six hours post-infection are entirely dominated by the relative uptake of the type 1 AECs (green lines). The reason for this somewhat non-intuitive result becomes clear from Fig. 3B, where we show that the total alveolar surface is mostly covered by type 1 AECs, such that the conidium will most likely (95.76%) be confronted with type 1 AECs rather than type 2 AECs. Thus, the uptake capacity of AECs mainly depends on type 1 AECs, simply because type 2 AECs will be rarely confronted with conidia (< 5%). In the absence of AMs, there is no cell movement and spatial impact which is why the results shown in Fig. 3A from the stochastic simulations confirm the analytical calculation (see Fig. 2D). Under conditions resembling a compromised immune status, we conclude that in the context of our stochastic model simulations (i), the uptake is entirely dominated by type 1 AECs and (ii) the uptake by AECs alone will not be sufficient to keep the alveolus free from conidia before fungal germination starts.

Fig. 3: Simulation results of the extended hABM.

A The hABM simulations results without AMs. The light blue line shows the relative uptake by type 2 AECs matching the analytical solution from the extended Malthus ODE Model (dark red dotted). The green curves show the relative uptake by type 1 AECs, and the orange lines show the overall uptake by AECs. Different line styles denote different values of ${r}_{{up}0}^{{AEC}1}$. B The spatial distribution of conidia being confronted with type 1 or type 2 AECs averaged over all hABM simulations. C–F The blue lines denote the uptake by AMs, and the green lines denote the uptake by type 1 and type 2 AECs combined. The orange lines denote the overall uptake. The corresponding parameter combination is written at the top. In (C), different line styles denote different values of ${r}_{{up}0}^{{AM}}$. In (D) different line styles denote varied delayed chemokine secretion ${t}_{{s}_{{AEC}}}$ scenarios. In (E) different line styles denote different AM numbers ${n}_{{AM}}$. In (F) different line styles denote different values of ${r}_{{up}0}^{{AEC}1}$. In (A, C–F) error bars represent the 95% confidence interval as obtained from the standard error of independent Bernoulli trials.

Uptake by AMs exceeds the total uptake by AECs

Next, simulating virtual infection scenarios that resemble the immunocompetent status, we included AMs to compare their relative contribution to fungal clearance in the human alveolus. Using the extended hABM, stochastic simulations were performed for varied uptake rates for type 1 AECs, ${r}_{{up}0}^{{AEC}1}$, and AMs, ${r}_{{up}0}^{{AM}}$, and the fitted uptake rate for type 2 AECs, ${r}_{{up}0}^{{AEC}2}=0.00137{m}{{in}}^{-1}$. In addition, we screened over values for delayed onset of chemokine secretion ${t}_{{s}_{{AEC}}}$ by AECs as well as varied AM numbers ${n}_{{AM}}$. A detailed description of the screened parameters and their ranges, especially about shifted ranges for uptake by AECs versus uptake by AMs, is provided in the Methods in Input parameter and output measures for the extended hABM, Table 1 and the conducted literature search in Supplementary Results 1.5 and Supplementary Tables S3, S4. The hABM simulation results for an immunocompetent status are displayed in Fig. 3C–F, where we focused on the uptake indexes at six hours before fungal germination.

As can be seen in Fig. 3C, with an uptake of $88 \%$ and $70 \%$ (blue solid and dashed lines), AMs dominate the total uptake of conidia for type 1 AEC uptake rates ${r}_{{up}}^{{AEC}1}\left(t\right)$ with ${r}_{{up}0}^{{AEC}1}=0.000685\,{m}{{in}}^{-1}$ (orange solid and dashed lines). In these scenarios for AM uptake rates ${r}_{{up}}^{{AM}}\left(t\right)$ with ${r}_{{up}0}^{{AM}}=0.068\,{m}{{in}}^{-1}$ and ${r}_{{up}0}^{{AM}}=0.014\,{m}{{in}}^{-1}$, AECs reach uptake indexes of about $12 \%$ (green solid line) and $23 \%$ (green dashed line), respectively. In both cases (dashed and solid lines), the impact of AMs increases rapidly with time as soon as chemokines are secreted starting from time ${t}_{{s}_{{AEC}}}=60\,\min$. The impact of the secretion onset ${t}_{{s}_{{AEC}}}$ can be seen in Fig. 3D in more detail; the later the onset of chemokine secretion is the longer AMs move randomly, with a clear reduction in the relative uptake by AMs (blue solid and dashed lines) at six hours post-infection. In this case for ${r}_{{up}0}^{{AM}}=0.274\,{m}{{in}}^{-1}$, ${r}_{{up}0}^{{AEC}1}=0.00274\,{m}{{in}}^{-1}$, implying that the uptake rate of AMs is 100 times higher than that of type 1 AECs, the relative contribution of AECs rises from $38 \%$ to $49 \%$ when the secretion of chemokines starts relatively late at ${t}_{{s}_{{AEC}}}=180\,\min$ instead of ${t}_{{s}_{{AEC}}}=120\,\min$, such that the relative uptake by AMs drops from $62 \%$ to $51 \%$. As shown in Fig. 3E, a low AM uptake rate ${r}_{{up}}^{{AM}}(t)$ with ${r}_{{up}0}^{{AM}}=0.00137{m}{{in}}^{-1}$ cannot be compensated by immediate chemokine secretion or high AM numbers (blue solid line) while the overall uptake does not reach more than 80% (orange solid line). In Fig. 3F, we consider the rather unrealistic scenario of an extremely high uptake rate of type 1 AECs with ${r}_{{up}0}^{{AEC}1}=5\cdot {r}_{{up}0}^{{AEC}2}=0.068\,{m}{{in}}^{-1},$ being five times higher than the fitted uptake rate of type 2 AECs, which would make AECs the main player in uptake with a 75% contribution. In summary, the simulation results indicate that AMs clear the majority of A. fumigatus in most parameter regimes while AECs can compensate to a certain extent but remain important for guidance through chemokine signaling.

Surrogate model reflects fungal infection dynamics and assesses model sensitivity

To fully exploit the hABM simulation data, we previously established a surrogate infection model (SIM) based on a Multilayer Perceptron (MLP)¹³ and fitted it to the simulation data by the hABM as described in Methods in the surrogate infection model using a multilayer perceptron. The SIM-enabled us to interpolate between all simulated values of the large input parameter space accurately and predicted uptake indexes of AECs $(U{I}_{{AEC}})$ and AMs $(U{I}_{{AM}})$, described in Methods in input parameter and output measures for the extended hABM, for a specific time point that are otherwise computed by time-intensive hABM simulations.

We applied the SIM to perform a global sensitivity analysis of the hABM using the Sobol sensitivity analysis⁶³ to assess the influence of the input parameter (${r}_{{up}0}^{{AEC}1},$ ${r}_{{up}0}^{{AM}},$ ${t}_{{s}_{{AEC}}},$ ${n}_{{AM}}$) on the uptake indexes $U{I}_{{AEC}}$ and $U{I}_{{AM}}$ at the timepoint $t=6h$. As shown in Fig. 4A, the uptake rate ${r}_{{up}0}^{{AEC}1}$ of type 1 AECs has the largest impact in first-order (green bar) with a Sobol index of 0.7 and total-order (green striped bar) with a Sobol index of 0.75 on the uptake index of AECs $U{I}_{{AEC}}$. The remaining parameters have low impacts with Sobol indexes below 0.2. In comparison, the uptake index of AMs $U{I}_{{AM}}$ is most influenced by their uptake rate ${r}_{{up}0}^{{AM}}$ (see Fig. 4B), even though not as dominant with a Sobol index of 0.42 (first-order, blue bar) and 0.48 (total-order, blue striped bar). For the uptake by AMs, $U{I}_{{AM}}$, also the uptake rate ${r}_{{up}0}^{{AEC}1}$ and the number of AMs ${n}_{{AM}}$ play a non-negligible role with Sobol indexes between 0.2 and 0.3. The impact on both uptake indexes by the delay of chemokine secretion ${t}_{{s}_{{AEC}}}$ is the lowest with Sobol indexes below 0.1. In all cases, the total-order measures are higher than the first-order measures indicating a highly non-linear and complex system. Our analysis underlines the importance of the uptake rates of AECs and AMs.

Fig. 4: Sobol sensitivity analysis of the hABM with the SIM.

A Relative impact of the input parameters on the uptake index of AECs $U{I}_{{AEC}}$ in the hABM is denoted with the Sobol index. B Relative impact of the input parameters on the uptake index of AMs $U{I}_{{AM}}$ in the hABM denoted with the Sobol index.

AMs are indispensable for the clearance of A. fumigatus in the human alveolus

Using the outputs $U{I}_{{AEC}}$, $U{I}_{{AM}}$ of the SIM, we evaluated several measures to gain insights about the infection dynamics in the hABM: i) the difference between $U{I}_{{AEC}}$ and $U{I}_{{AM}}$ to assess which cell type contributes more to conidial uptake (uptake comparison $({UC})$), (ii) the total uptake index $({UI})$, which we defined as the sum of $U{I}_{{AEC}}$ and $U{I}_{{AM}}$ (see Methods in Input parameter and output measures for the extended hABM) and (iii) relative uptake contributions for AECs, $U{I}_{{AEC}}/(U{I}_{{AEC}}+U{I}_{{AM}})$, and for AMs, $U{I}_{{AM}}/(U{I}_{{AEC}}+U{I}_{{AM}})$ (see Methods in Input parameter and output measures for the extended hABM and The surrogate infection model using a multilayer perceptron).

In Fig. 5, we present the SIM predictions for an average AM number of ${n}_{{AM}}=12$. With an immediate (left plots), as well as delayed onset of chemokine secretion (${t}_{{s}_{{AEC}}}=90\,\min$) (middle plots), AMs clear the infection in the majority of scenarios reaching high values of ${UI}=100 \%$ (see Fig. 5A left and middle plot). Upon late chemokine secretion, starting at ${t}_{{s}_{{AEC}}}=180\,\min$ (right plot in Fig. 5A), the AECs’ relative contribution increases, denoted by the increased green area, but concurrently worsen overall uptake of ${UI} < 95 \%$ for ${r}_{{up}0}^{{AM}} < 0.037\,{m}{{in}}^{-1}$ (right plot Fig. 5B). In Fig. 6, SIM predictions are shown for AM numbers ranging from low (${n}_{{AM}}=4$, left plots) and average (${n}_{{AM}}=12$, middle plots) to high (${n}_{{AM}}=28$, right plots) and for the onset of chemokine secretion at ${t}_{{s}_{{AEC}}}=60\,\min$. For reduced AM numbers ${n}_{{AM}}=4$, AECs can support, but only high uptake rates ${r}_{{up}}^{{AM}}\left(t\right),$ ${r}_{{up}}^{{AEC}1}(t)$ with ${r}_{{up}0}^{{AM}} > 0.19\,{m}{{in}}^{-1}$ and ${r}_{{up}0}^{{AEC}1} > 0.0013\,{m}{{in}}^{-1}$ (right upper corner in Fig. 6A and Fig. 6B left plots) were found to be sufficient to reach high values ${UI}=100 \%$. For high AM numbers of ${n}_{{AM}}=28$, AM uptake rates ${r}_{{up}}^{{AM}}\left(t\right)$ with ${r}_{{up}0}^{{AM}} > 0.01\,{m}{{in}}^{-1}$ were sufficient for AMs to surpass the uptake contribution by AECs (blue area in Fig. 6B right plot) and simultaneously reach a high overall clearance of ${UI}=100 \%$ (yellow area in Fig. 6A right plot). For all scenarios in Figs. 5, 6, we found that, for low uptake rates with ${r}_{{up}0}^{{AM}} < 0.0068\,{m}{{in}}^{-1}\approx 5\cdot$ ${r}_{{up}0}^{{AEC}2}$ for AMs, even high uptake rates with ${r}_{{up}0}^{{AEC}1}=0.0027\,{m}{{in}}^{-1}\approx 2\cdot$ ${r}_{{up}0}^{{AEC}2}$ for type 1 AECs, being twice as high as the uptake rate by type 2 AECs, was not sufficient to reach ${UI}=100 \%$ the screened regime of parameters. Ultimately, in Fig. 7, we consider the uptake rates of AMs ${r}_{{up}0}^{{AM}}\in [{\mathrm{0.037,0.19}}]$ in $m{{in}}^{-1}$ (the second rows in each plot in Figs. 4 and 5) and compare the relative uptake contributions of AECs (green curves) and AMs (blue curves). We can see that for an immediate chemokine secretion, AECs do not reach more than 20% contribution (Fig. 7A left), while this goes up to more than 30% if chemokine secretion starts late ${t}_{{s}_{{AEC}}}=120\,\min$ (Fig. 7A right), in case we assume ${r}_{{up}0}^{{AEC}1}={r}_{{up}0}^{{AEC}2}$. For low and high AM numbers in the exemplary combinations in Fig. 7B, the contribution of AECs does not become more than 40%. This underlines the importance of uptake by AMs as the professional resident phagocytes, and that this cannot be compensated by early onsets of chemokine secretion, high AM numbers, or increased uptake rates by type 1 AECs.

Fig. 5: Predictions with the SIM for varying onsets of chemokine secretion.

A, B Uptake comparisons and indexes at the onset of germination at $t=360\,\min$. All plots denote on the x-axis the time-dependent uptake rate ${r}_{{up}}^{{AEC}1}\left(t\right)={r}_{{up}0}^{{AEC}1}\cdot S\left(t\right)$ for varying ${r}_{{up}0}^{{AEC}1}$ for type 1 AECs and on the y-axis the time-dependent uptake rate ${r}_{{up}}^{{AM}}\left(t\right)={r}_{{up}0}^{{AM}}\cdot S(t)$ for varying ${r}_{{up}0}^{{AM}}$. The plots are displayed for low ${t}_{{s}_{{AEC}}}=0\,\min ,$ medium ${t}_{{s}_{{AEC}}}=90\,\min$ and high ${t}_{{s}_{{AEC}}}=180\,\min$ onsets of chemokine secretion for an average AM number of ${n}_{{AM}}=12$. Predicted ${UI}$ and ${UC}$ values are rounded to integers dividable by five for better visibility of ${UI}$ and ${UC}$ structures. A The color-coded uptake comparison ${UC}$ denotes in green (positive values) that AECs take up more conidia and in blue (negative values) that AMs take up more conidia. B The color-coded uptake index ${UI}$ denoting in blue a low and in yellow a high overall uptake index of 100% by AMs and AECs combined.

Fig. 6: Predictions with the SIM for varying AM numbers.

A, B Uptake comparisons and indexes at the onset of germination at $t=360\,\min$. All plots denote on the x-axis the time-dependent uptake rate ${r}_{{up}}^{{AEC}1}\left(t\right)={r}_{{up}0}^{{AEC}1}\cdot S\left(t\right)$ for varying ${r}_{{up}0}^{{AEC}1}$ type 1 AECs and on the y-axis the time-dependent uptake rate ${r}_{{up}}^{{AM}}\left(t\right)={r}_{{up}0}^{{AM}}\left(t=0\right)\cdot S(t)$ for varying ${r}_{{up}0}^{{AM}}.$ The plots are displayed for low (${n}_{{AM}}=4$), average (${n}_{{AM}}=12$), and high $({n}_{{AM}}=28)$ AM numbers and onsets of chemokine secretion at ${t}_{{s}_{{AEC}}}=60\,\min$. Predicted ${UI}$ and ${UC}$ values are rounded to integers dividable by five for better visibility of ${UI}$ and ${UC}$ structures. A The color-coded uptake comparison ${UC}$ denotes in green (positive values) that AECs take up more conidia and in blue (negative values) that AMs take up more conidia. B The color-coded uptake index ${UI}$ denoting in blue a low and in yellow a high overall uptake index of 100% by AMs and AECs combined.

Fig. 7: Predictions with the SIM for the clearance contributions of the hABM.

A, B Uptake contribution of AMs compared to AECs (y-axis) given on the x-axis the time-dependent uptake rate ${r}_{{up}}^{{AEC}1}\left(t\right)={r}_{{up}0}^{{AEC}1}\cdot S\left(t\right)$ for varying ${r}_{{up}0}^{{AEC}1}$ for type 1 AECs. Different opacities of the blue and green curves stand for high (dark) down to low (bright) values of the time-dependent uptake rate ${r}_{{up}}^{{AM}}\left(t\right)={r}_{{up}0}^{{AM}}\cdot S\left(t\right)$ for varying ${r}_{{up}0}^{{AM}}$ AMs. The blue curves denote the relative uptake contribution by AMs, and the green curves denote the relative uptake contribution by type 1 and type 2 AECs combined. The values are normalized, such the sum of two curves for the same value of ${r}_{{up}0}^{{AM}}$ adds up to 100. A Predictions for ${n}_{{AM}}=12$ ${t}_{{s}_{{AEC}}}=0\,\min$ (left) and ${t}_{{s}_{{AEC}}}=120\,\min$ (right). B Predictions for low AM numbers and early onset of chemokine secretion ${n}_{{AM}}=4,$ ${t}_{{s}_{{AEC}}}=0\,\min$ (left) and for high AM numbers and late onset of chemokine secretion ${n}_{{AM}}=28$, ${t}_{{s}_{{AEC}}}=120\,\min$.

Discussion

In this study, we investigated the relative contributions of alveolar epithelial cells (AECs) and alveolar macrophages (AMs) in the internalization of swelling A. fumigatus conidia during the first hours post-infection. Based on recently performed in vitro experiments^35,36 on the uptake of conidia by type 2 AECs, we were able to fit a Verhulst ODE model to conidial diameter data and coupled the dynamics of swelling with an extended Malthus ODE model. We fitted the system of ODEs to the size-dependent uptake of conidia by type 2 AECs hypothesizing that swelling increases the observed uptake probability during the first six hours (see Fig. 1A–C and Fig. 2). We extended this mechanism to uptake by type 1 AECs and AMs and studied the dynamics with computer simulations using a previously developed hybrid agent-based model (hABM)^{13,30,58,59,60} for the human alveolus (see Fig. 1D–F and Fig. 3). Using the hABM, we ran millions of stochastic virtual experiments to simulate the first hours of immune response in the human lung against A. fumigatus conidia and screened over various uptake rates of type 1 AECs and AMs, delayed onsets of chemokine secretion, induced by a swelling conidium, as well as the impact of varying AM numbers. Using the hABM simulations results, we trained a surrogate infection model (SIM) to interpolate the parameter space, assessed the sensitivity of the hABM (see Fig. 4), and predicted the uptake proportions of AECs compared to AMs and the overall clearance of A. fumigatus conidia (see Fig. 1G and Figs. 5, 6 and 7).

We fitted a Verhulst ODE model to the diameter of swelling conidia over time exhibiting a logistic growth curve saturating at around a diameter of $4.6{\mu m}$ or area increase $274 \%$ in comparison to $t=0\,\min$. As these dynamics can depend on the strain of A. fumigatus (here: A1160⁺), the growth medium or the underlying cells (here: immortalized A549 cells, used as a model for human type 2 AECs), we also fitted the Verhulst ODE model to two other experimental settings resulting in comparable parameter settings (see Supplementary Table S1) which shows a general logistic increase of conidial surface area during the first hours post-infection. In all cases, we found the exponential growth phase to start approximately at around one hour, until it slows down after three hours and saturates after approximately four to five hours. The lung provides a warm and humid environment offering ideal growth conditions. These are mimicked in the utilized in vitro data retrieved from experiments on type 2 AECs, which lets us expect a comparable development of A. fumigatus in the lung. Based on the conidial diameter increase, we fitted a second model – an extended Malthus ODE model – to simulate the uptake of conidia by type 2 AECs, as constant uptake rates do not reflect temporal uptake indexes, which is why we coupled the mechanism with the swelling-induced increased contact area between conidia and host cell. This is because once the conidium starts to swell as part of the germination process, the melanin layer in the cell wall undergoes structural changes leading to an increased number of exposed pathogen-associated molecular patterns (PAMPs). Consequently, the increased contact area between conidia and host cell makes conidia more accessible for pattern recognition receptors (PRRs) such as Toll-like receptors (TLRs) and C-type lectin receptors (CLRs). The binding of PAMPs to PRRs triggers immune reactions and makes the conidia susceptible to being recognized and internalized by host cells. Therefore, the increased diameter can be seen as an implicit measure for the number of PAMP-PRR bindings on the conidial surface. The fact that swollen conidia are taken up faster by AMs and AECs than resting conidia is well-known^37,62 and supports our modeling approach that incorporates the increasing contact area driving the increase of uptake rates as a function of time, a proposed mechanism that is yet to be tested experimentally. Moreover, it is speculated that AECs do not necessarily start to secret chemokines at first contact, but that this is a delayed process during the first hours post-infection^45,64,65. We assume that the underlying AEC is required to recognize a substantial change in the number of visible PAMPs on a conidium becoming apparent with the increasing size of conidial swelling. Once a threshold of PAMP-PRR is reached, intracellular pathways of the AEC become sufficiently activated to induce the secretion of pro-inflammatory cytokines and chemokines. In our simulations, the various thresholds of the number of visible PAMPs that trigger the chemokine secretion are modeled by the delayed chemokine secretion onset ${t}_{{s}_{{AEC}}}$. Since the size of the conidium does not increase remarkably anymore after four hours, we assume that the melanin layer is largely dissolved with the number of visible PAMPs saturating around this time. Thus, the cascade of innate immune response is activated before, which is evidenced by experiments where various cytokines could already be measured at four hours post-infection⁶⁶. Based on these experimental findings, we assumed the most probable period for the onset of chemokine secretion to be between one and two hours, and not later than three hours, corresponding to the time window when the conidial diameter increase enters the exponential phase. Future studies should focus on extending the simulations beyond six hours post-infection, where germination of conidia will start. Simulating the germination process as a function of time will enable quantifying the conditions under which conidia will be able to cross the valley of death. This is the time span between the start of conidial swelling and the onset of germination, where the probability of conidial detection is increased due to the expression of PAMPs by the conidia and the chemotactic guidance of AMs. We expect that the valley of death will be crossed by those conidia that relatively quickly swell, germinate, and develop hyphae that cannot be phagocytosed by AMs but require the recruitment of neutrophils to the alveolus⁴⁶.

We included the described ODE models into a previously developed hABM^{13,30,58,59,60}. We used this model of one human alveolus with fitted (type 2 AECs) and screened uptake rates (type 1 AECs and AMs) to simulate virtual infection scenarios in the human lung (see Fig. 1D–F and Supplementary Videos S1, S2). However, at first, we simulated scenarios for a compromised system in the absence of AMs. It was recognized that even for a high type 1 AEC uptake rate ${r}_{{up}}^{{AEC}1}\left(t\right)$ with ${r}_{{up}0}^{{AEC}1}=0.00274\,{m}{{in}}^{-1}$, which is twice as high as for type 2 AECs, the overall uptake by type 1 and type 2 AECs combined, does not reach sufficient uptake indexes of more than 90% at six hours post-infection, so it would be unable to completely prevent fungal germination. Furthermore, the overall uptake is mainly dominated by type 1 AECs because they cover around 95% of the lung surface as also confirmed in the to-scale extended hABM. This means that, even though type 2 AECs outnumber type 1 AECs, they are barely confronted with microbial invaders, which makes their direct role in fungal clearance minor. However, in vitro experiments are typically conducted with type 2 AECs due to established protocols and cultivation, which are then used to estimate uptake rates also for type 1 AECs. This can lead to a strong under- or overestimation of the general role of AECs, e.g., in case type 1 AECs take up significantly more or less than type 2 AECs. Because of this gap in the data, we suggest increasing experimental efforts for studies with type 1 AECs, as they can have a large positive or negative leverage for infection clearance.

We also used the hABM to run immunocompetent infection scenarios with the fitted uptake rate for type 2 AECs and varied the uptake rates of type 1 AECs and AMs. Moreover, we screened over a delayed onset of chemokine secretion by AECs and varying AM numbers, both impacting the uptake efficiency of AMs. The simulation results showed that AMs can unfold their full proficiencies through initiated chemotactic migration, the moment the AMs sense the chemokine gradient, which lets the uptake indexes increase steeply. AECs have a supportive role when the efficiency of AM uptake is reduced but can usually not compensate to reach high overall uptake indexes ${UI}=100 \%$. For an average AM number ${n}_{{AM}}=12$, AMs dominate the majority of cleared infection scenarios. Thus, even though their accumulated surface area covers only about 3% of the alveolar surface, the impact of AMs is compensated by their ability to migrate in the alveolus. However, this necessary detection process by AMs leads to a deviation between the expected AM uptake indexes by the extended Malthus ODE and the uptake indexes retrieved by the hABM simulations. As a result, we assume that estimating AM uptake rates from experimental studies for the hABM in the same way as for AEC uptake rates leads to an underestimation, as uptake by AMs in the hABM is a process of conidial detection and uptake itself, in contrast to uptake by AECs whose detection time is zero (see Supplementary Results 1.4 and Supplementary Fig. S3). Interestingly, as we observed in the spatiotemporal hABM simulations, the conidium can be confronted with more than one AM at the same time, which multiplies their chance of uptake by AMs. On the contrary, only one AEC at a time can be in contact with the conidium, because the AECs are stationary cells forming the cellular wall of the alveoli. As we have shown previously, we expect AMs to be able to clear the infection for low infection doses in most cases, only for high infection doses or low AM activity neutrophils are recruited to the site of infection⁴⁶ to reduce the risk of unwanted host cell damage due to a high inflammation⁶⁷.

Lastly, we trained a SIM on the hABM simulation results to assess the sensitivity of the hABM and to interpolate the input parameter space allowing us to conduct a fast and accurate analysis of the uptake comparison and the uptake index. Since the healthy human lung is generally not at risk of A. fumigatus infections, we can narrow down the parameter space to regimes for which the predicted uptake indexes reach ${UI}=100 \% .$ The conidial uptake is dominated by AMs in these parameter regimes, except for rare cases where the uptake rates of type 1 AECs exceed the fitted uptake rate of type 2 AECs by factors that are at least two-fold higher. However, the exact uptake rates of AMs are difficult to determine experimentally since it is not a simple measure of alive conidia at a certain time point but depends on experimental conditions such as the cell density or environment. In addition, these measurements are mostly global, while the uptake rates in our agent-based approach work locally per immune cell. This matter was further analyzed in Supplementary Results 1.4 and Supplementary Fig. S3 elaborating how uptake indexes measured in our hABM simulations are connected to actual local uptake rates per cell. Based on this analysis, we expect that experimentally measured uptake rates are a lower bound for time-dependent uptake rates of AMs. Together with the broad literature search that we conducted (see Supplementary Results 1.5 and Supplementary Table S3), we attempt to predict the parameter ranges for uptake rates: Wasylnka et al.⁶⁸ reported that 98% conidia were killed by AMs in mice at 6 hours post-infection, which leads to an estimated uptake rate of ${r}_{{up}0}^{{AM}}\gg 0.0056{m}{{in}}^{-1}$. Apart from the neglected detection time, only the killed conidia were measured, but since the percentage of taken-up conidia is higher than the percentage of killed conidia, the true uptake rate is expected to be higher. From Philippe et al.⁶¹, we derive an uptake rate measured at $t=240\,\min$ which translates to increased ${r}_{{up}0}^{{AM}}\gg 0.0061\,{m}{{in}}^{-1}$ because of not measured AM migration time. Based on the exact experimental conditions, these actual uptake rates can be higher by at least one order of magnitude due to necessary AM migration and conidial detection time (see Supplementary Results 1.4 and Supplementary Fig. S3), which let us expect AM uptake rates approximately at least at ${r}_{{up}}^{{AM}}\left(t\right) > 0.05$ ${\min }^{-1}$. Regarding the uptake rates of stationary AECs, there is less uncertainty between experimentally derived uptake rates and model uptake rates since there is immediate contact between the conidium and the host cell. However, measurements of uptakes by AECs type 2 human cells of type A549 still vary. Keizer et al.⁶⁹ measured 75% to 81% taken up after 4 hours across different strains leading to an AEC type 2 uptake rate of up to ${r}_{{up}0}^{{AEC}2}=0.0044\,{m}{{in}}^{-1}$, which were the highest values we could find. It also indicates transferability between isolates⁷⁰. On the contrary, for one of these isolates (ATCC46645), Seidel et al.⁷¹ found only 30% of conidia taken up after 6 h reaching only ${r}_{{up}0}^{{AEC}2}=0.0005\,{m}{{in}}^{-1}$. In the same study, it was reported that AECs have difficulties to kill conidia efficiently and could rather be used by A. fumigatus as an immune evasion pathway, which would once more emphasize the necessity of effective AMs regarding uptake and killing. In total, as there is no data on type 1 AECs and based on experimental type 2 studies, we expect uptake rates of AECs type 1 and type 2 not to be higher than ${r}_{{up}}^{{AEC}1}\left(t\right) < 0.005\,{m}{{in}}^{-1}$. Together with the hABM simulations for competent AMs (sufficient uptake, numbers, and signaling), an uptake contribution of AECs lower than 30% is indicated. However, in case of surprisingly high (or low) uptake rates of type 1 AECs, the uptake contribution can go steeply up (or down) because the contribution of AECs during fungal clearance by phagocytosis is dominated by type 1 AECs which is why determining the uptake rate by type 1 AECs is crucial. This is also indicated by our sensitivity analysis with the uptake rate of type 1 AECs exhibiting the highest Sobol indexes. Available studies on the uptake of nanoparticles by type 1 AECs were conducted⁷², but insights are difficult to transfer to much larger A. fumigatus conidia. In conclusion, studies in vivo and in vitro generally show that uptake rates of AMs are higher than uptake rates of AECs, as expected for professional phagocytes (see Supplementary Table S3), but based on available data, their actual values can only be narrowed down, since they depend on cell types, A. fumigatus strains, and general experimental conditions. To tackle the above-mentioned gap in the data about conidial response to type 1 AECs, but also validating predicted uptake rates of AMs and AECs for different conditions by our modeling approach, more experimental efforts are necessary in the form of combined phagocytosis assays measuring the proportion of taken up conidia over time. To study these cross-cellular systems, advanced in vitro methods for example organ-on-chips models^73,74,75 are suitable as they also model complex cell-to-cell interactions in a realistic system, e.g., whether AECs take up less in the presence of AMs or when neutrophils migrate to the site of infection, mimicking the in vivo situation but keeping the variables under control.

In summary, our virtual infection modeling approach consisting of a system of ODEs fitted to experimental data and an established hABM of one human alveolus, proposes a size-dependent uptake mechanism of A. fumigatus conidia that remains to be experimentally tested. Using predictive modeling, we narrowed down the ranges for unknown uptake parameters as well as for the onset of chemokine secretion by AECs in the context of the hABM. Based on these in silico findings that need to be tested in vitro as a subsequent step, our simulations suggest that AMs are the dominant player in clearing the lung from A. fumigatus conidia, while AECs can contribute to a minor extent with potential leverage, largely depending on type 1 AEC uptake rates. However, an important role for AECs also lies in their function to early secrete chemokines and direct AMs more efficiently toward the conidia. Additionally, based on our spatiotemporal simulations, and a broad analysis of available literature, we also suggest increasing efforts in studying type 1 AECs. They cover around 95% of the pulmonary surface area and are constantly confronted with not only conidia but all types of microbial invaders. Uncovering the functionality of type 1 AECs and their differences from type 2 AECs will be crucial for filling the gaps in our understanding of early pulmonary innate immunity.

Methods

Experimental data

The experimental data at the base of this work was derived from newly generated germination data (Supplementary Fig. 1A) and in vitro infections presented in Bertuzzi et al.^35,36 (Figs. 1B and 2B). There, germination of A1160⁺ conidia (Rizzetto et al., 2013) was evaluated in 24-well plate format with 1.05 × 10⁵ conidia/cm² (4 × 10⁵ conidia/mL) in supplemented DMEM (10% fetal bovine serum (FBS), 1% penicillin/streptomycin cocktail) at 37 °C, 5% CO₂ every hour for 16 h. Cell area (µm²) and shape (aspect ratio) were quantified using a custom ImageJ algorithm (Ortiz et al., (In preparation, see Supplementary Results 1.1) across three replicate wells and over 1000 cells per replicate. For in vitro infection experiments, 200 µl of a 10⁶ spore/ml suspension of the A. fumigatus strain A1160^+/tdtT (genetically modified to constitutively express the red fluorescent protein tdTomato). The data of Bertuzzi et al.^35,36 was initially used for infections of the human pulmonary carcinoma epithelial cell line A549 (American type culture collection, CCL-185) at a MOI 0.5 (with 10⁵ AECs in a > 90% confluent monolayers). The infected cells were incubated at 37 °C, 5% CO₂ for the indicated hours, when single-cell analyses of the uptake of tdTomato-expressing Af strains via differential fluorescent staining with the chitin-binding cell-impermeant dye Calcofluor White by cultured AECs were performed as described in Bertuzzi & Howell, 2021⁷⁶. After identification of A. fumigatus-AEC interaction events using the IDEAS® software, for each time-point of infection (30 min, 2, 4 and 6 h post-infection), fungal area (µm²) and shape (aspect ratio) of internalized and adherent A. fumigatus A1160^+,tdtT AECs (n = 10–160 for each time-point, 2 biological replicates) were measured using Image J version 1.53c.

Modeling the swelling of A. fumigatus conidia by a Verhulst ODE model

To mechanistically model conidial swelling in terms of the conidial diameter ${Diam}$ in $\mu m$, we assumed that the conidial diameter consists of a constant initial diameter (${Dia}{m}_{{rest}}$), representing the size of a resting conidium, and a part that increases due to conidial swelling (${Dia}{m}_{{swell}}(t)$). The time-dependent diameter of the conidium is given by ${Diam}\left(t\right)={Dia}{m}_{{rest}}\left(t\right)+{Dia}{m}_{{swell}}(t)$, where we modeled the swelling part ${Dia}{m}_{{swell}}$ using a Verhulst ODE model, which represents a logistic growth model:

$$\frac{d\left[{Dia}{m}_{{swell}}\right]}{{dt}} = {r}_{{swell}}\cdot \left[{Dia}{m}_{{swell}}\right]\left(1-\frac{\left[{Dia}{m}_{{swell}}\right]}{{C}_{{swell}}}\right),\, \\ {Dia}{m}_{{swell}}\left(t=0\right)={D}_{{swell}}^{0}$$

(1)

with swelling rate ${r}_{{swell}}$, the carrying capacity ${C}_{{swell}}$ in $\mu m$ as well as the swelling diameter ${D}_{{swell}}^{0}$ in $\mu m$ at time $t=0\,\min$. The constant resting part is represented by one parameter ${Dia}{m}_{{rest}}\left(t\right)={D}_{{rest}}^{0}$ with $d\left[{Dia}{m}_{{rest}}\right]/{dt}=0$. Therefore, we have $d\left[{Diam}\right]/{dt}=d\left[{Dia}{m}_{{swell}}\right]/{dt}$. The analytical solution of ${Diam}(t)$ is given as:

$$Diam(t;{\Theta }_{diam})=\frac{{C}_{swell}}{{D}_{swell}^{0}+({C}_{swell}-{D}_{swell}^{0}){e}^{-{r}_{swell}\cdot t}}{D}_{swell}^{0}+{D}_{rest}^{0}$$

(2)

with the diameter at $t=0$ referring to the size of the conidium when it enters the alveolus: ${Diam}\left(t=0\right)={D}_{{swell}}^{0}+{D}_{{rest}}^{0}$. We fitted the model parameters ${\Theta }_{{diam}}=({r}_{{swell}},{C}_{{swell}},{D}_{{swell}}^{0},{D}_{{rest}}^{0})$ by minimizing the mean squared error (MSE):

$$MS{E}_{diam}({\Theta }_{diam})=\frac{1}{N} {\sum }_{i=0\ldots N}{(Diam({t}_{i};{\Theta }_{diam})-Dia{m}_{data}(i))}^{2}$$

(3)

The data points ${Dia}{m}_{{data}}\left(i\right)$ exhibits all $i=1,\ldots ,N$ data points. For the main manuscript, these were extracted for aspect ratios larger than 0.8 from the previous work on in vitro infection assays⁷⁶ described in the previous Methods in Experimental Data. The fitted curve ${Diam}(t)$ can be seen in Fig. 2A, and the fitted parameters can be found in Supplementary Table S1. Also, it shows the parameter of the model fit for two further experimental settings: (i) described in the previous section (see Supplementary Fig. S1C), and ii) extracted from Alonso et al.,³¹ (Supplementary Fig. S1D). We performed the parameter estimation using the package SciPy.optimize⁷⁷ of the SciPy 1.13.0 library in Python 3.10.

Modeling the uptake of conidia via an extended Malthus ODE model

In our approach, we assumed permanent contact between AECs and conidia. We model the uptake of conidia by type 2 AECs with an uptake rate ${r}_{{up}}^{{AEC}2}$, which corresponds to an uptake probability ${p}_{{up}}^{{AEC}2}$ per time step. Based on the confrontation assays with type 2 AECs³⁵, which can be seen in Fig. 2C, we concluded that the uptake rate ${r}_{{up}}^{{AEC}2}$ is increasing with time by the surface area increase over time $S\left(t\right)$. Here, $S(t)$ denotes the time-dependent mechanism that causes the increase in the uptake rate ${r}_{{up}}^{{AEC}2}$ and by that the decrease in the number of free conidia ${FreeCon}$. Thus, we modeled the population of free conidia ${FreeCon}$ with ${FreeCon}\left(t=0\right)=1.0$ (an initial population of 100%) with a Malthus ODE model (representing an exponential growth model) extended by the mechanism $S$:

$$\frac{d\left[{FreeCon}\right]}{{dt}}={-\left[{FreeCon}\right]\cdot r}_{{up}0}^{{AEC}2}\cdot S(t)$$

(4)

A more detailed derivation of the extended Malthus ODE model from the normal Malthus ODE model is presented in Supplementary Results 1.4. We denote the uptake rate as ${{r}_{{up}}^{{AEC}2}\left(t\right):= r}_{{up}0}^{{AEC}2}\cdot S\left(t\right)$ that depends on the surface area increase over time $S(t)$ and the parameter ${r}_{{up}0}^{{AEC}2}:= {r}_{{up}}^{{AEC}2}(t=0)$, representing the uptake rate at $t=0$. We assume half the surface area of the conidium (modeled as a sphere) is in permanent contact with one type 2 AEC and $S(t)$ to be describing the contact area over time relative to $t=0\,\min$:

$$S\left(t\right)=\frac{2\pi {\left(\frac{{Diam}\left(t\right)}{2}\right)}^{2}}{2\pi {\left(\frac{{Diam}\left(t=0\right)}{2}\right)}^{2}}={\left(\frac{{Diam}\left(t\right)}{{Diam}(t=0)}\right)}^{2}={\left(\frac{\left[{Diam}\right]+{D}_{{rest}}^{0}}{{D}_{{swell}}^{0}+{D}_{{rest}}^{0}}\right)}^{2}$$

(5)

By representing $S(t)$ in by the means of $[{Diam}]$, the term becomes time-independent and can be included in Eq. (5) as shown in Eq. (6). The resulting system of ODEs, including Eqs. (1), (4), and (5) models the population of free conidia ${FreeCon}$, linked to the conidial swelling and subsequent increasing contact area between conidia host cell (HC). Based on ${FreeCon}$, we can model the opposite conidia population, the percentage of conidia that was taken up by the respective host cells (HCs), e.g., type 1 or type 2 AECs or AMs, denoted as the uptake index ${UI}$. This is the actual model that we fit and is described by the $U{I}_{{HC}}$ ODE Model as $U{I}_{{HC}}\left(t\right)=1-{FreeCon}(t)$. Minimizing the mean squared error ${MSE}$, as conducted in Methods Section, Eq. (3), of the extended Malthus ODE model to the data from infection assays with type 2 AECs, we were able to fit the model output to the data (see Fig. 2C and Supplementary Table S2). In addition, a cross-validation was conducted to validate the model’s robustness and compare it to the normal Malthus ODE, as seen in Supplementary Results 1.2.

Extended hybrid agent-based model of the human alveolus

The previously developed virtual infection model of one human alveolus is a hybrid agent-based model (hABM) and was used in numerous studies to assess a to-scale infection scenario between the early immune reaction and the pathogenic fungus A. fumigatus^{13,30,58,59,60}. The hABM reproduces the anatomical and physiological spatiotemporal characteristics of one of the approximately 500 million human alveoli as a ¾ sphere on a cellular and molecular level. It encompasses both type 1 and type 2 AECs, along with pores of Kohn (PoKs) that facilitate air pressure, and cell and molecule exchange between neighboring alveoli. In the model, the proportional surface coverage of type 1 (~ 95%) and type 2 (~ 5%) AECs is reflected through lung cell counts and alveolar measures taken from Stone et al. (1992)¹² calculated down to one alveolus. Thus, the initial condition for one stochastic simulation is given by the random placement of one conidium on type 1 or type 2 AEC and randomly placed type 2 AECs, PoKs, and AMs. After a concealment time of the conidium, the underlying AEC starts to secret chemokines to attract the resident alveolar macrophages (AM). The AM follows the chemokine gradient through a biased persistent random walk, exhibiting chemotactic migration (see Supplementary Videos S1 and S2). This is based on the previously introduced diffusion of chemokines (Pollmächer et al.⁵⁹) that takes place on the inner surface of the alveolus which is modeled by partial differential equations and solved with the Euler scheme on discrete grid points (see Supplementary Video S1) approximating the 3/4 sphere of the alveolus^59,78. For the chemokine secretion, the optimal configuration of secretion rate ${s}_{{AEC}}$ and diffusion coefficient $D$, of ${s}_{{AEC}}/D=2.1\times {10}^{3}\mu {m}^{-2}$, with $D=20{\mu }{m}^{2}/\min$ was applied, as found previously¹³. Further parameters were set to values extracted from literature or were screened in previous publications to which we refer here^{13,30,58,59,60}. Each infection scenario is simulated for ${t}_{\max }=8h$ with a time step of $\Delta t=0.1\,\min$. Because of the amount of data per timestep, we write an output (the data points) only every 30 min. It is important to note that we consider the first six hours of infection before the moment when germination and hyphal growth are expected to set in.

In the current study, we extended the hABM to incorporate the uptake of conidia by AECs and AMs. While in previous studies, the detection time was studied, i.e. the first time point until an AM touched the conidium (compare with “Infection Score”), we here study the uptake time by AECs and AMs. For this, we fitted and implemented a time-dependent uptake mechanism (see Methods in Modeling the uptake of conidia via an extended Malthus ODE model), namely the uptake rate ${r}_{{up}}^{{HC}}\left(t\right)={r}_{{up}0}^{{HC}}\cdot S(t)$ with ${r}_{{up}0}^{{HC}}:= {r}_{{up}0}^{{HC}}(t=0)$ of the of the respective HC for all HCs including type 1 and type 2 AECs and AMs described by a system of ODEs and included it in the hABM:

$$\frac{d\left[{FreeCon}\right]}{{dt}} = {-\left[{FreeCon}\right]\cdot r}_{{up}0}^{{HC}}\cdot {\left(\frac{\left[{Diam}\right]+{D}_{{rest}}^{0}}{{D}_{{swell}}^{0}+{D}_{{rest}}^{0}}\right)}^{2},\, \\ {FreeCon}\left(t=0\right)=1.0$$

(6)

$$\frac{d\left[{Diam}\right]}{{dt}} = {r}_{{swell}}\cdot \left[{Dia}{m}_{{swell}}\right]\left(1-\frac{\left[{Dia}{m}_{{swell}}\right]}{{C}_{{swell}}}\right),\, \\ {Dia}{m}_{{swell}}\left(t=0\right)={D}_{{swell}}^{0}$$

(7)

The presented ODE of increasing diameter is simultaneously solved, within each hABM simulation, using the Euler method⁷⁸ with the same time step of $\Delta t=0.1\,\min$ while the uptake is decided by the time-dependent (or diameter-dependent) uptake rates ${r}_{{up}}^{{HC}}(t)={r}_{{up}0}^{{HC}}\cdot S(t)$, translating into the uptake probability ${p}_{{up}}^{{HC}}\left(t\right)={r}_{{up}}^{{HC}}\left(t\right)\cdot \Delta t$ per time step, applied in the event of contact between HC and conidium. The values for ${r}_{{up}0}^{{AEC}1}$ and ${r}_{{up}0}^{{AM}}$ were screened while the ${r}_{{up}0}^{{AEC}2}=0.00137{m}{{in}}^{-1}$ was fitted (see Methods in Modeling the uptake of conidia via an extended Malthus ODE model).

Input parameter and output measures for the extended hABM

To cover realistic infection scenarios, we screened over uptake rates of type 1 AECs ${r}_{{up}0}^{{AEC}1}$ in the approximate regions of the fitted uptake rate of type 2 AECs. Moreover, we screened over up to 730-fold higher parameter regimes for uptake rates of AMs ${r}_{{up}0}^{{AM}}$ compared to the fitted uptake rate of type 2 AECs ${r}_{{up}0}^{{AEC}2}$, because AECs are significantly less able to take up A. fumigatus than AMs, as indicated in in vivo and in vitro studies (see Supplementary Table S3).In addition, this exceeded values for the parameter regime of the AM uptake rates is supported by results provided in Supplementary Results 1.4 where we showed that estimated uptake rates of AMs from literature tend to be underestimated compared to uptake rates of AECs, due to a neglected AM migration time towards the conidium, in contrast to stationary AECs. Also, we screened over delayed onsets of chemokine secretion ${t}_{{s}_{{AEC}}}$ by AEC. Depending on the timely recognition of a conidium by AECs on their surface, chemokines are released to attract AMs leading to chemotactic movements and directed immune responses⁶⁴. We hypothesized that the onset of chemokine secretion may depend on the state of conidial swelling during the first hours post-infection (see Supplementary Table S4). Consequently, we simulated infection scenarios assuming that the secretion of chemokines is triggered by a minor ($3 \%$ after $t=60\,\min$), medium ($27 \%$ after $t=120\,\min$), or substantial ($\ge 113 \%$ after $t\ge 180\,\min$) swelling state of the conidium (see Fig. 2B). In addition, we also varied AM numbers and considered a low $({n}_{{AM}}=4)$, average $({n}_{{AM}}=12)$, and increased $({n}_{{AM}}=28)$ presence of these immune cells¹³ simulating different states of the immune system.

As an output, we measure the proportion of simulations in which the conidium was taken up by (i) type 1 AECs, (ii) type 2 AECs, or (iii) AM after a time $t$. We call this measure the relative uptake index, denoted as $U{I}_{{HC}}\in [{\mathrm{0,1}}]$. In this regard, it is important to distinguish between the relative uptake index $U{I}_{{HC}}$ that is calculated over the conidia that can be reached by the respective host cell and the absolute uptake index $U{I}_{{HC}}^{* } = {w}_{{HC}}U{I}_{{HC}}$ for a weight ${w}_{{HC}}\in [{\mathrm{0,1}}]$, that is calculated over all conidia. The weight ${w}_{{HC}}$ describes the proportion of conidia that can be reached by the respective host cell and is used to derive the absolute uptake index from the relative uptake index. If the host cell can reach all conidia, e.g., AMs or AECs (type 1 & type 2), meaning ${w}_{{HC}}=1.0$, then the relative uptake index is equal to the absolute uptake index, $U{I}_{{HC}}^{* }=U{I}_{{HC}}$. As combined measures, we consider the combined uptake by type 1 and type 2 AECs $(U{I}_{{AEC}})$, the overall or total uptake index $({UI})$, and the uptake comparison (${UC}$), denoting whether AMs or AECs take up more conidia. The weights ${w}_{{AEC}}={w}_{1}+{w}_{2}=1.0,{w}_{{AM}}=1.0$, they are calculated as:

$$U{I}_{{AEC}} = {w}_{1}U{I}_{{AEC}1}+{w}_{2}U{I}_{{AEC}2},\,{UI}={w}_{{AEC}}U{I}_{{AEC}}+{w}_{{AM}}U{I}_{{AM}},\, \\ {UC} = {w}_{{AEC}}U{I}_{{AEC}}-{w}_{{AM}}U{I}_{{AM}}$$

(8)

To obtain the relative uptake contribution normalized to the overall uptake indexes (which can be lower than 100%), we calculate the uptake contribution per cell type as $U{I}_{{AEC}}/{UI}$ for AECs and $U{I}_{{AM}}/{UI}$ for AMs. To calculate error bars for each parameter configuration, we ran 10,000 simulations to guarantee statistical stability with 95% confidence intervals of ${CI}=U{I}_{{HC}}+/-1.96\cdot \sqrt{U{I}_{{HC}}\left(100-U{I}_{{HC}}\right)/{n}_{{HC}}}$, as obtained from the standard error of ${n}_{{HC}}$ independent Bernoulli trials, while ${n}_{{HC}}$ is the number of simulations accounting for the respective $U{I}_{{HC}}$. Overall parameter configurations, we ran about 10 million computer simulations (see Table 1). The hABM was implemented and extended in modern C + +, and its code base is provided in the available code section. The stochastic simulations of our vectorized and highly parallelized hABM were conducted on an AMD EPYC 7742 64-core processor. One data point which is averaged from 10,000 simulations, took up to one hour. Using several machines with multiple processors, the total computation time for all simulations was around one month.

The surrogate infection model using a multilayer perceptron

In order to analyze the simulated parameter space systematically, we trained a surrogate infection model (SIM), which resembles the SIM in our previous study, which was referred to as MLP¹³. Here, we fitted a feedforward multi-layer perceptron (MLP), which is a fully connected artificial neural network, on output values of the hABM to interpolate the parameter space without running the cost-intensive 10,000 hABM simulations per parameter configuration. The SIM allowed reducing computational costs for stochastic simulations via the hABM, while accurately predicting hABM simulation outcomes. Among other machine learning approaches, we chose the MLP for the SIM because it can be directly adapted to a changing number of input and output variables. In this case, the model $SIM:{{{{\mathbb{R}}}}}^{5}\to {[0,1]}^{2}$ consists of five input variables $({r}_{{up}0}^{{AEC}1},{r}_{{up}0}^{{AM}},{t}_{{s}_{{AEC}}},{n}_{{AM}},t)$ and two output variables $(U{I}_{{AEC}},U{I}_{{AM}})$ whereby $U{I}_{{AEC}}\in \left[{\mathrm{0,1}}\right]$ summarizes the uptake proportion by type 1 and type 2 AECs together and $U{I}_{{AM}}\in [{\mathrm{0,1}}]$ the uptake proportion by AMs. With these two outputs, the main measurements of uptake comparison (${UC}=U{I}_{{AEC}}-U{I}_{{AM}}$) and uptake index $({UI}=U{I}_{{AEC}}+{UI\_AM})$ could be straightforwardly computed. We implemented the MLP with two hidden layers (21 and 11 neurons) and a logistic activation function. We fitted the SIM with a mean squared error of ${MSE}={2.63\cdot 10}^{-5}$ (see Methods in Modeling the swelling of A. fumigatus conidia by a Verhulst ODE model) as a cost function. For the implementation of the MLP as a SIM and its optimization, we utilized the package PyTorch 1.13 in Python 3.10⁷⁹, which is provided in the available code.

Statistics and reproducibility

The results presented are reproducible within the statistic uncertainties using the given code⁸⁰ and data⁸¹ resources (see also code and data availability statement) and description of the models in the Methods. To reproduce the in silico simulation results with the hABM, the code can be downloaded, compiled, and run for the given parameter configurations in Table 1. With this, the provided raw data and resulting Fig. 3 can be reproduced. The error bars in Fig. 3 represent the 95% confidence interval of the stochastic computer simulations resulting from 10,000 simulations per parameter combination. The fit of the deterministic Verhulst ODE (diameter) and (extended) Malthus ODE (uptake) models shown in Fig. 2 can be reproduced using the provided code and the provided experimental data. The uncertainty bands shown in Fig. 2 represent the 95% confidence interval of the model predictions and were computed via a bootstrap method (see Supplementary Results 1.2). The surrogate infection model can be retrained and evaluated using the provided code enabling the reproduction of Figs. 5–7. The individual models were fit to (i) the experimental data, i.e., the ODE models, and (ii) the simulated data, i.e., the SIM, using the MSE as cost-function and the package SciPy.optimize⁷⁷ and the package PyTorch 1.13 in Python 3.10⁷⁹ respectively, that is also provided in the available code.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.