Introduction

Protein structure prediction is an important problem in biophysics and computational biology, which has been extensively studied in the past few decades. The progress of structure prediction methods has been monitored by biannual events of community-wide assessment, the Critical Assessment of Protein Structure Prediction (CASP) for over twenty years1. Various types of methods have been developed over years, such as coarse-grained model-based methods2,3,4,5, and machine learning approaches, particularly deep learning6,7,8,9. CASP14 witnessed a breakthrough by AlphaFold2 (AF2)10, which achieved an accuracy that is close to experimental resolution for many targets and analyzed its performance11. Since the release of AF2, it has been used for many practical applications in biology12, including for molecular replacement in X-ray crystallography13, structure modeling for cryo-electron microscopy (cryo-EM) maps14,15,16, and structure-based drug design17,18. The use of AF2 models is further facilitated by the AlphaFold Database19 which now holds structure models of over 200 million proteins. AF2 has made a substantial impact on many areas of biology and biotechnology.

Although AF2 yields accurate structure models in many cases, it still has several limitations. Firstly, for proteins with multiple domains, AF2 typically builds the individual domain structures correctly but often fails to capture the relative orientations of the domains. In some proteins, domains are connected by a linker, which is meant to be flexible. In such cases, predicting a different domain orientation from the corresponding Protein Data Bank (PDB)20 entry is not necessarily incorrect; however, it becomes a problem when the predicted model shows inconsistencies with experimental density data21, Nuclear Magnetic Resonance (NMR), or cryo-EM maps. Similarly, AF2 often predicts long unstructured loops, which may be intrinsically disordered regions of the protein, but they are in a particular conformation in cryo-EM maps and need to be correctly predicted to fit accurately.

Another noted limitation of AF2 is that it is designed to predict a static conformation given an input sequence22,23. However, a protein may have two or more viable conformations that correspond to different functional or physical states responding to various conditions, such as interactions with other molecules and environmental conditions24,25. G protein-coupled receptors (GPCRs) are a representative example of proteins which have two conformations that correspond to active and inactive states26. The development of protocols for generating multiple biologically relevant conformations is a focus in the post-AF2 era, and various ideas have been implemented until now22. Approaches include manipulation on multiple sequence alignments (MSAs) via subsampling27,28,29, clustering30, or amino acid replacements31, and deep generative models32,33,34.

Practical and feasible approaches to address the aforementioned limitations include incorporating constraints, such as distance information between amino acid residues, derived from experimental data. AlphaLink35 converts distance restraints from cross-linking mass spectrometry (XL-MS) into 128 distogram bins, integrates those into pair representations, and fine-tunes AF2 with recycling updates for coupling maximizing synergy between MSAs and crosslinks to produce distance-driven protein structure predictions. Similarly, RASP36 uses NMR NOESY peak intensity restraints as contact information between amino acid pairs to enhance AF2 predictions. RASP considers distance restraints as additional edge information, embedding them into four distinct types of contacts that are incorporated into MSA, pair representations, IPA attention weight matrix and atom coordinates separately. These two approaches are effective for handling experimental data; however, they have two limitations: first, a large number of distance restraints are required for accurate predictions, typically more than 10, otherwise, on some cases, their performances are even worse than AF2. Second, the methods are designed for building a single conformation and not for generating multiple conformations.

Here, we propose Distance-AF, a deep learning-based approach that builds upon AF2 by incorporating additional information of distances between amino acids. We expect distance constraints to be derived from experimental data, such as crosslinking, cryo-EM maps, NMR measurements, or known residue–residue interactions. Constraints may also originate from biological hypotheses proposed by users. Based on these inputs, Distance-AF will generate structure models that users can analyze to evaluate their hypotheses. We built the method upon AF2 instead of AlphaFold3 (AF3)37, which was released more recently, because AF3 uses diffusion model as the network architecture for generating structures which incorporate a random procedure in the algorithm. On the other hand, AF2 is a supervised learning-based method and is more suitable for the overfitting regime to provided distance constraints, which is the core of the idea of Distance-AF. In contrast to the approaches taken by Alphalink and RASP, Distance-AF implements distance constraints as an additional term in the loss function within the structure module of AF2. This term is iteratively optimized in harmony with other loss terms from AF2 to ensure that individual domains follow protein-like geometry and are correctly folded while satisfying the distance constraints. This approach eliminates the need for a pre-training stage, thereby avoiding the substantial computational resources required. With this design without pre-training enables Distance-AF to exhibit flexibility in predicting diverse protein structures even with a limited number of constraints that are insufficient for the other methods. Moreover, Distance-AF is simple yet effective for iteration processes.

We first show that Distance-AF is able to effectively modify domain orientation as guided by provided distance constraints to obtain correct overall conformation. The benchmark study we conducted showed that Distance-AF performs a large deformation of protein structures, often by a root-mean square deviation (RMSD) of over 10 Å, by moving domains to satisfy a few distance constraints provided. We also tested its sensitivity with rough distance constraints biased varying up to 5 Å that demonstrating Distance-AF is robust and keeps high accuracy even with approximate distances. Additionally, we demonstrate that Distance-AF is useful in building structural models that fit experimental data: Distance-AF successfully constructed the conformation of multi-domain proteins that fit a cryo-EM map from AF2 models that were globally incorrect. We also show that Distance-AF was able to generate alternative conformations of GPCRs in different functional states from a small number of distance constraints between transmembrane helices. Finally, Distance-AF successfully generates an ensemble of conformations of proteins based on constraints provided by NMR.

Results

Overview of Distance-AF

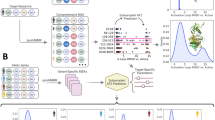
Distance-AF builds on the AF210 network architecture to predict protein structures while incorporating distance constraints. This method is effective when AF2 does not build a predicted structure that agrees with known domain arrangements. Users can input a few distance constraints between specified domains, which are integrated into the loss function of AF2, and the structure is iteratively updated until the specified distances are satisfied. The code and example files as well as instruction are provided in the GitHub repository, https://github.com/kiharalab/Distance-AF. In the Method section, we provided brief instructions. Figure 1a illustrates the framework of Distance-AF.

Fig. 1: Overall framework of Distance-AF.
figure 1

a The network consists of two modules. The first module is Evoformer from AF2, which takes the protein sequence as input and computes the single representation and the pair representation. The second part, the structure module, is modified from AF2, where the distance constraints between residues, which is another input information, is considered and used to in loss optimization through an iterative process. This fine-tuning process continues until the loss converges. b Learning curves of four loss functions for the first 1000 iterations. An AF2 model for PDB: 6P66 of chain A is used in this example, which had an RMSD of 20.65 Å to the native. The structure has two domains. The first domain ranges from residues 5 to 253, and the second domain is from residues 261 to 471. We used six distance constraints, between specific residue pairs (30, 378), (71, 290), (132, 333), (166, 310), (178, 406), and (251, 463). Six time steps, 0, 100, 255, 400, 600, and 1000 are highlighted. c The structure of the six steps, shown in panel b, final predicted and native structures, are visualized. The final structure has an RMSD of 4.27 Å.

Full size image

Distance-AF consists of two modules. The first module is Evoformer, the same one as used in AF2. Evoformer takes a MSA constructed from a query protein sequence as well as a matrix that contains pairwise residue information that is constructed from the MSA embedding, and computes a MSA embedding and a pair embedding through iterative optimization between the two embeddings to ensure they have consistent information10. To construct an MSA for a query protein, similar sequences were searched on the Uniref30 database38. Then, a single sequence embedding, which corresponds to the query sequence, is extracted from the MSA embedding and passed to the structural module together with the pairwise embedding and the user-specified residue-pair distance constraints as additional input information. A residue-pair distance is defined by the Euclidean distance between Cα atoms of two residues taken from two domains, which need to be moved to achieve a desired global conformation of the target protein. As we examined later, about 6 constraints are sufficient to move domains into desired positions.

Distance-AF employs an overfitting mechanism, iteratively updating network parameters until the predicted structure satisfies the given distance constraints. Thus, the network was not pretrained on a training set; rather it starts with the same weights as the original AF2. This iterative process allows the model to fine-tune the coordinates, enforcing them to follow the provided distance information, which is provided in the form of a distance loss that is combined with other loss terms (Fig. 1a). More concretely, Distance-AF constructs structure models in the following steps in the structural module. First, the structure module operates invariant transformation to predict the 3D coordinates of heavy atoms of the target protein using the single and pair representations from the Evoformer module. For the predicted structure, a loss function called the distance-constraint loss is then computed, which measures the divergence between distances in the predicted structure and user-provided distances of pairs of Cα atoms:

$${L}_{{dis}}=\frac{1}{N}{\sum }_{i=1}^{N}{({d}_{i}-{d}_{i}^{{\prime} })}^{2}$$
(1)

where \({d}_{i}\) is the specified distance constraints on the ith pair of Cα atoms, \({d}_{i}^{{\prime} }\) is measured distance in the predicted structure for the corresponding Cα atom pair; and \(N\) is the number of distance constraints. This distance-constraint loss is combined with the intra-domain FAPE loss10 (Supplementary Fig. 1), the angle loss, and the violation terms into the total loss as defined in Eq. 2. These loss terms are illustrated in Supplementary Fig. 2. As shown, the weight for the distance-constraint loss is changed according to the level of satisfaction with the loss:

$$L=\left\{\begin{array}{c}1.0* {L}_{{dis}}+\,{L}_{{fape}}+\,{L}_{{angle}}+{L}_{{vio}} \, \, {L}_{{dis}} > 10 \hfill \\ {2.0* L}_{{dis}}+\,{L}_{{fape}}+\,{L}_{{angle}}+{L}_{{vio}} \, \, 5 < \,{L}_{{dis}} < 10 \hfill \\ \begin{array}{c}{4.0* L}_{{dis}}+\,{L}_{{fape}}+\,{L}_{{angle}}+{L}_{{vio}} \, \, 1 < \,{L}_{{dis}} < 5 \hfill \\ 1.0* {L}_{{dis}}+10* \,{L}_{{fape}}+\,{L}_{{angle}}+{L}_{{vio}} \, \, {L}_{{dis}} < 1\end{array}\end{array}\right.$$
(2)

where the first term, \({L}_{{dis}}\), is defined in Eq. 1. The second component, \({L}_{{fape}}\), is the intra-domain FAPE loss, a penalty term for the pair-wise frame-aligned point error of residues within individual domains defined by users. This term is to prevent the local structure of domains from being destroyed by lowering \({L}_{{dis}}\). The third and fourth loss terms are angle and violation loss, the same terms as AF2. \({L}_{{angle}}\) penalizes the deviation of predicted backbone torsion angles and dihedral angles at sidechain. \({L}_{{vio}}\) penalizes unidealized bond lengths, peptide bond angles and atom clashes that are inconsistent with physical properties10. In Distance-AF, as the true structure of a target protein is unknown, we take the original structure predicted by AF2 as the reference against which intra-domain FAPE, angle, and violation loss are computed.

As shown in Eq. 2, the entire framework is optimized via the integrated loss with a dynamic reweighting mechanism to tune the global gradients depending on the level of satisfaction of \({L}_{{dis}}\). This design is needed to balance between \({L}_{{dis}}\) and the other terms because minimizing \({L}_{{dis}}\) will distort the initial structure from AF2, which will increase the other loss. At the beginning of the iteration, when \({L}_{{dis}}\) is large, its weight is set to a small value to avoid distorting the local structures of individual domains. As the iteration progresses, the weight of \({L}_{{dis}}\) is increased to guide the domains toward their correct relative positions. Once the domains are nearly correctly positioned, the weight of \({L}_{{dis}}\) is reduced again to refine and restore any local structural distortions introduced during the domain adjustment process. The weight values were determined from observation of the behavior of intermediate model conformations in a very early stage of the development of this method using a couple of targets used at that time. As described, Distance-AF employs an over-fitting process to satisfy user-provided distance constraints by iterative optimization procedure. By default, structure optimization under Eq. 2 is performed for up to 30,000 iterations. This number was chosen based on the observation that large proteins (e.g., those with more than 1000 residues) are sufficiently optimized by this number of iterations. Usually we terminated a run much earlier as the convergence of the loss function is observed. Optimization should continue until the overall loss function (Eq. 2), and in particular the distance loss (Eq. 1), has saturated. After the optimization, we reported the resulting modeling accuracy values, RMSD and TM-score39, GDT-TS40, and GDT-HA40 using the software TM-score39 and PyMOL41.

In Fig. 1b, c, we show an example of the iterative structural deformation by Distance-AF. This is a predicted structure from chain A of XPB-Bax1 complex (PDB ID: 6P66), which has two domains (residue 5-253 and 261-471). In this example, RMSD improved from 20.65 Å to 4.27 Å by applying Distance-AF in comparison with the native structure (PDB ID: 6P66). Figure 1b shows four loss functions separately, the distance loss, the FAPE loss, the angle loss, and the violation loss. In Fig. 1c actual structures at key steps are visualized. At time 0 (Fig. 1c), the two domains were predicted correctly by AF2, however the relative orientation of the two individual domains are largely different from the native structure (shown on the right of Fig. 1c). The distance loss is at its maximum, but the FAPE is minimum as it is a fresh output from AF2. But this improvement came at the cost of a noticeable increase in the FAPE loss. At the beginning of the iteration, the violation loss sharply spiked indicating that atom clashes occurred and quickly relaxed. The FAPE loss kept rising because the overall structure was distorted from the starting conformation. Iteration 255 corresponds to a peak in the FAPE and angle losses and a convergence point for the distance loss, indicating that the distance constraints are nearly satisfied, but local structures are compromised. This can be seen in the structure; the domains are almost at their correct relative position, while helices in the smaller domain is distorted. Iterations 400 and 600 represent intermediate stages during the convergence of the FAPE, angle, and violation losses, signifying that Distance-AF is actively involved in the recovery of local structures while maintaining stability in the distance loss. At Iteration 1000, all four loss functions are almost converged, indicating an accurate predicted structure is produced in terms of overall conformation. At this point, helices of the smaller domain were also recovered.

Performance on improvement over incorrect AF2 models

We first tested Distance-AF on 25 incorrect structure models constructed by AF2. These models were selected from the AlphaFold Database19 with the following criteria: First, we selected entries in the AlphaFold Database that have corresponding entries in PDB by the date of March 15th, 2023. From them, we selected AF2 models which have an RMSD over 10 Å to the corresponding PDB structures with a resolution of 3.0 Å or better that were determined by X-ray crystallography or cryo-electron microscopy and have an average pLDDT of 0.75 or higher. The corresponding PDB entries for an AFDB entry was identified by first examining the correspondence of PDB entries for the UniProt ID of the AFDB entry. We also performed sequence alignment to ensure that the PDB entry covers more than 80% of the AFDB entry.

Subsequently, we examined whether a protein model is likely to contain two or more domains by clustering residues based on the Predicted Aligned Error (PAE) provided by AFDB, which reflects the uncertainty in the distances between residue pairs in the model. Typically, in multi-domain protein models, residues within the same domain exhibit low PAE values, whereas residue pairs across different domains show high PAE values. To identify such domain-specific patterns, we performed clustering using the PAE matrix while varying the number of clusters. After each clustering, we checked whether any residue pairs belonging to different clusters had PAE values below 3 Å. If four or more such pairs were observed, suggesting that the corresponding domains should be merged, we reduced the number of clusters and repeated the clustering process. From the resulting clusters, we first excluded residues with a pLDDT score below 70. Then, if a cluster contained 50 or more remaining residues, it was considered a domain. Only proteins with two or more such domains were retained for subsequent visual inspection.

Additionally, AFDB models and their corresponding PDB entries were visually inspected using PyMOL. Entries were excluded if they contained long disordered regions (approximately >30 residues), gaps in the PDB structure, or were complexed with other chains that appeared critical for determining the conformation. Models were also excluded if they lacked clear domain structures, exhibited domain swapping, or contained local domain regions that were entirely incorrect. A domain structure was considered incorrect if the RMSD of the region exceeded 2.0 Å. Thus, the 25 selected targets have a high confidence (pLDDT) but globally incorrect orientations of domains. The length of proteins in the dataset varied from 138 to 830. The 25 targets are listed in Supplementary Data 1. These 25 targets are non-redundant; each pair has less than 25% sequence identity between them (Supplementary Fig. 3). For each target, six distance constraints that connect two domains of the protein were applied in Distance-AF. Constraints were selected so that residues involved in the constraints were spread in each domain and initial distances in the AF2 model deviate largely from the correct distance. We show the benchmarking results in Fig. 2a.

Fig. 2: Modeling performance of Distance-AF.
figure 2

The dataset of 25 targets was used. a comparison of Distance-AF(D-AF) against AF2 (blue circles), Rosetta (orange squares), and AlphaLink (green triangles) in terms of four metrics, RMSD, TM-Score, GDT-TS, and GDT-HA. b Modeling results with perturbated distance constraints. For a set of six distance constraints used for a target, the distance was perturbated randomly between ±5.0 Å for 10 times. Thus, 10 (perturbations) x 25 (models) =250 model results were plotted. Resulting models were evaluated in the four metrics relative to the average perturbation. c The model quality in the four metrics are shown with a different number of distance constraints. Four targets were used, 1MKMA, 2Z99A, 5HXYA, and 5KECA.The number of constraints used were 0, 1, 2, 3, 4, 6 (our default setting; shown in crosses), 10, 14, 18, 22, 26, and 30.

Full size image

Figure 2 summarizes modeling results by Distance-AF. Individual results are provided in Supplementary Data 2. We compared with three methods, the original AF2, Rosetta42,43, and AlphaLink35. To run Rosetta and AlphaLink, the same set of distance constraints were applied (Methods). Models were evaluated using four metrics, the RMSD, TM-Score39, GDT-TS40 and GDT-HA40. The higher the better for the latter three metrics. The data in Fig. 2a–c, are provided in Supplementary Data 2, 3, 4, respectively.

When compared to AF2 models, apparently Distance-AF built more accurate models than AF2 for all 25 targets. Distance-AF reduced RMSD of models on average by 11.75 Å. 18 out of 25 targets had an RMSD under 5 Å while all 25 targets by AF2 had an RMSD larger than 10 Å. Regarding TM-score, Distance-AF yielded an average TM-score of 0.834 compared to 0.622 by AF2. For other two metrics, Distance-AF/AF2 demonstrate average scores of 0.751/0.594 on GDT-TS, 0.598/0.522 on GDT-HA, respectively.

Figure 2a presents comparisons with Rosetta and AlphaLink, respectively. Distance-AF outperformed both in the four key metrics across most of the targets. The average RMSD values for Distance-AF, Rosetta, and AlphaLink were 4.22 Å, 6.40 Å, and 14.29 Å, respectively. In terms of TM-Score, Rosetta and AlphaLink achieved 0.728 and 0.644, respectively, which were significantly lower than Distance-AF’s 0.834. The improvement of AlphaLink over AF2 was observed to be marginal.

In Fig. 2b, we perturbated the distances in the constraints and examined how the inaccurate constraints affected the modeling results. From the same six constraints, 10 constraint sets were generated by perturbating each distance by up to 5.0 Å. The modeling results with these perturbated constraints were plotted relative to the average perturbation. Apparently, a correlation between the average perturbation and the accuracy of the models was observed. The Pearson’s correlation of the average perturbation distance and RMSD, TM-Score, GDT_TS, and GDT_HA, was 0.262, −0.277, −0.311, and −0.303, respectively. Although a weak correlation was generally observed, the modeling results demonstrated robustness. For example, 62.8% of the models remained within an RMSD of 6.0 Å, retaining the correct overall fold, even when the average perturbation was up to 2.0 Å. Similarly, in terms of TM-Score, 44% of models had scores above 0.8 for average perturbation up to 2.0 Å. Interestingly, there are about 22% of the cases when perturbations even made more accurate models. Upon closer examination, we observed that such improvements happen when perturbed constraints, particularly for longer distances, allow a domain to optimize its relative orientation or escape a local minimum during convergence. In Fig. 2c, we conducted an additional ablation study using four randomly selected targets (1MKM Chain A, 2Z99 Chain A, 5HXY Chain A, and 5KEC Chain A). We varied the number of constraints from 0 (equivalent to the vanilla AlphaFold2) to 30. For each constraint setting, we randomly added or removed constraints to achieve the desired number. We observed that the models became more accurate as the number of constraints increased. The accuracy values nearly plateaued when four to six constraints were used, with minimal improvements beyond six constraints.

Note that these 25 targets are difficult to correctly fold with AF337 as well as AlphaFold2(AF2)-Conformations28 (Supplementary Fig. V). AF2-Conformations generated 130 different conformations by using different subsamples from the input multiple sequence alignment. AF3 and AF2-Conformations did not make much improvement over AF2 in most of the targets. Distance-AF performed substantially better than AF3 and AF2-Conformations.

Distance-AF models have slightly higher Molprobity scores44 and atom clash scores (Supplementary Fig. 5) but the values are in a similar range as that are observed in experimental structures in PDB. This is partly because the loss function includes the violation loss (Eq. 2), which is used in AF2 to avoid unphysical stereochemistry of proteins. Applying structure relaxation by molecular dynamics (MD) further improves Molprobity and atom clash scores (Supplementary Fig. 5) to the level that is better than the starting AF2 models. Applying MD only changes RMSD by 0.01 Å (from 4.11 to 4.12 Å) on average (Supplementary Data 2).

Examples of models built by Distance-AF

In this section, we discuss six illustrative examples of models generated by Distance-AF. The first example (Fig. 3a) is the model of the fibrillarin–Nop5p complex45 (PDB ID: 1NT2, chain ID: B). This 258-amino-acid protein consists of two domains: the N-terminal domain, which features a long α-helix (on the right side of the figure), and the C-terminal domain, which contains six helices. AF2 placed the N-terminal domain in an incorrect relative position (cyan), resulting in an RMSD of 11.83 Å. Correcting the N-terminal domain required a hinge motion at the linker between the two domains, a task that Distance-AF handled straightforwardly with proper constraints. After applying Distance-AF, the RMSD was reduced to 2.28 Å.

Fig. 3: Six examples of models built by AF2 and D-AF.
figure 3

Detailed evaluation results are available in Supplementary Data 1 and 2. For each example, three structures are shown: the native structure (green), the superimposed model by AF2 (cyan) to native(green), and the superimposed model by D-AF (magenta) to native(green); a The Nop5p subunit of fibrillarin/Nop5p complex (PDB: 1NT2, chain: B, 258 amino acids). AF2 RMSD: 11.83 Å, D-AF RMSD: 2.28 Å. b CbnR subunit from a LysR family transcriptional regulator (PDB:1IXC, chain:A, 295 amino acids). AF2 RMSD: 16.33 Å, D-AF RMSD: 1.96 Å. c The LarsR protein of LasR-Aqs1 complex from Pseudomonas aeruginosa (PDB: 6V7W, chain: B, 239 amino acids). AF2 RMSD: 18.69 Å, D-AF RMSD: 2.18 Å. d Single MgsA protomer with three domains of the E. coli MgsA protein (PDB: 3PVS, chain: A, 447 amino acids), AF2 RMSD: 17.63 Å, D-AF RMSD: 3.07 Å. e The Raf1 subunit from assembly of RuBisCO (PDB: 6KKN, chain: A, 376 amino acids), AF2 RMSD: 17.90 Å, D-AF RMSD: 5.42 Å; f A protein of two tandem RNA recognition motifs of Human antigen R (PDB: 4EGL, chain: A, 177 amino acids), AF2 RMSD: 13.73 Å, D-AF RMSD: 7.83 Å.

Full size image

The next example is a model of the LysR-type transcriptional regulator (LTTR) protein46 (PDB ID: 1IXC, chain ID: A) (Fig. 3b). AF2 positioned the 294-residue CbnR subunit in an incorrect orientation (the cyan domain on the left), with nearly a 90° deviation from the correct orientation relative to the long linker helix. Similar to the first example, correcting this required a large hinge motion between domains. Distance-AF successfully performed this adjustment, reducing the RMSD from 16.33 Å to 1.96 Å.

Figure 3c is a model for the transcriptional regulator LasR protein47, composed of 239 amino acids (PDB ID: 6V7W, chain ID: B). This protein has an N-terminal ligand-binding domain, characterized by an α-β-α sandwich structure, connected with a smaller DNA-binding α-helical domain. In the correct conformation, the interface of these two domains forms a ligand (3-oxo-C12-HSL) binding pocket. The linker between the two domains has 13 residues. AF2 placed the DNA-binding domain in a wrong orientation; the two domains even do not have any physical (cyan). Correcting the orientation needed rotation of the DNA-binding domain almost 180°, which is successfully achieved by D-AF. The overall RMSD improved from 18.69 Å to 2.18 Å by D-AF.

The next example in Fig. 3d also needed a large motion with rotation of a domain for correcting an AF2 model. This is maintenance of genome stability protein A (MgsA)48 of Escherichia coli, which is 446 residue long (PDB ID: 3PVS, chain ID: A). It has an N-terminal ATP-binding domain (residues approximately up to 165), an α-β class structure shown around the top middle of the figure. This is followed by two domains: a large α-helical lid domain (residues ~166–247) and a C-terminal tetramerization domain (residues ~251–446), both shown on the left side of the figure. AF2 placed these two domains completely opposite the ATP-binding domain (cyan), resulting in a large RMSD of 17.63 Å. However, D-AF accurately repositioned these two domains to the opposite side with an about 180° flip, reducing the RMSD to 3.07 Å.

Figure 3e provides an example where the model by D-AF had an imperfect rotation angle of a domain. The protein shown is the RuBisCO accumulation factor Raf1 from Anabaena sp. PCC 712049, which has two distinct domains: an N-terminal α-helical domain (Raf1α, residues 1–197) and a C-terminal β-sheet domain (Raf1β, residues 221–347) (PDB ID: 6KKN, chain ID: A). These domains are connected by a long linker of 23 residues, spanning ~60.9 Å. This domain arrangement is crucial for the protein’s function, as two Raf1β domains must be swapped between two copies of the protein to pack against each other. As shown in the figure, AF2 misplaced the Raf1β domain (cyan). While D-AF managed to position it closer to the correct location, there was a slight error in its rotational orientation, resulting in an RMSD of 5.42 Å.

The final example (Fig. 3f) features an ELAV-like protein with two tandem RNA recognition domains50(PDB ID: 4EGL, chain ID: A). AF2 incorrectly positioned the second domain (cyan), as shown in the bottom left of the figure. D-AF managed to adjust the domain closer to its correct spatial position, with a partial rotation toward the correct orientation (magenta); however, further rotation is needed for optimal alignment with the native structure. The RMSD was reduced from 13.73 Å to 7.83 Å, reflecting the improvement in orientation, though the domain’s positioning remains suboptimal.

In summary, D-AF successfully repositioned domains by satisfying distance constraints without distorting the individual domain structures. The method performs particularly well when only hinge motion is required. However, finding the correct domain orientation was occasionally less successful when rotational adjustments were involved.

Modeling disordered tails

In this section, we present more extreme cases in which a terminal region of target proteins, connected by a disordered region, is misplaced in the AF2 models (Fig. 4). In these cases, the disordered region is not even crystallized due to its excessive flexibility. Individual data is provided in Supplementary Data 5.

Fig. 4: Four examples of correcting a terminal region of a structure connected by a disordered region.
figure 4

For each example, three structures are shown: the native structure (green), the superimposed model by AF2 (cyan) to native (green), and the superimposed model by D-AF (magenta) to native (green). Arrows indicate the position of the terminal region that was revised by D-AF. Six constraints were used for distance-AF input. The domain information is in Supplementary Data 5. a The hypoxic regulator of sterol synthesis Nro1 from Schizosaccharomyces pombe (PDB: 3MSV, chain: A, 393 amino acids). AF2 RMSD: 12.9 Å, D-AF RMSD: 2.3 Å. b FERM domain of focal adhesion kinase from Gallus gallus (PDB: 3ZDT, chain: A, 377 amino acids). AF2 RMSD: 5.0 Å, D-AF RMSD: 1.7 Å. c C-terminal domain of Ribosomal RNA-processing protein 5 from Saccharomyces cerevisiae (PDB: 5NLG, chain: A, 314 amino acids). AF2 RMSD: 9.6 Å, D-AF RMSD: 1.6 Å. d Serine protease domain from Ryegrass mottle virus (PDB: 6FF0, chain: A, 275 amino acids). AF2 RMSD: 10.6 Å, D-AF RMSD: 3.4 Å.

Full size image

The first example (Fig. 4a) is a 393-residue protein (PDB: 3MSV) that has an N-terminal helix (residues 13–33; indicated by arrows in the figure) which is largely misplaced by AF2 (cyan). In the AF2 model, the helix is positioned at the top right of the figure, with minimal residue contacts with the main body of the structure. D-AF successfully relocated the helix to the correct position, reducing the RMSD from 12.9 Å to 2.3 Å. The second example (Fig. 4b) features a long disordered region at its C-terminus, where the tail segment (residues 368–373) interacts with the central region of the protein. AF2 placed the tail in a completely isolated location (on the left side of the figure), whereas D-AF correctly positioned it at the binding site. The protein in the next example (Fig. 4c) has a horseshoe-like conformation that consists of multiple short helices. The first helix (res: 1–11) is largely misplaced to the left bottom in the figure. D-AF successfully moved it to its correct binding site, reducing the RMSD from 9.6 Å to 1.6 Å. In the final example (Fig. 4d), the C-terminal tail (residues 256–265), initially placed on the left side of the structure by AF2 (cyan), was relocated to the opposite side by D-AF (magenta). These examples demonstrate that D-AF is also effective in correcting disordered tail regions, even when large structural rearrangements are required.

Application to structure fitting in cryo-EM maps

Next, we applied Distance-AF for protein structure fitting to cryo-EM maps. In structure modeling for a cryo-EM map, it is common to fit predicted models by AF2 to the map density15,51,52,53. However, the predicted conformation often does not match the density, even when individual domains are correctly predicted. In such cases, manual adjustment of domain positions is required. In Fig. 5, we show four examples of modeling improvement by using Distance-AF. These targets are selected from the DAQ-Score database54, which contains structure models built from cryo-EM and deposited to PDB. The map resolution ranges from 2.5 to 5 Å, and the structures show sufficient overlap and cross-correlation coefficient with the map. The DAQ score55 indicates that the structures do not have modeling errors. However, the AF2-predicted model exhibits a large discrepancy, with an RMSD of over 8 Å. As shown in the left panel of each example, AF2 models have individual domain structures essentially correct but one of the domains are largely displaced even to outside of the maps. Distance-AF moved the displaced domain successfully to the correct region in the map resulting in substantially improved alignment with the cryo-EM density. The data of Fig. 5 are provided in Supplementary Data 6.

Fig. 5: Examples of structure fitting for cryo-EM maps with Distance-AF For each example in a row, the left panel shows the native structure in PDB (green) superimposed with a AF2 model (cyan).
figure 5

The map is shown in gray. Middle, the Distance-AF model using six distance constraints (magenta) superimposed with the native (green). Right, the Distance-AF model using three distance constraints (orange) superimposed with the native (green). a The structure of human pyruvate carboxylase in apo state (PDB:7WTA, chain: A) derived from a cryo-EM map (EMD-32773) of a 3.9 Å resolution. RMSD: AF2 model, 8.32 Å; Distance-AF model with six constraints, D-AF(6), 2.64 Å; Distance-AF model with three constraints, D-AF(3), 3.14 Å. b A cryo-EM structure of elongation factor 2 from thermophilic eukaryotic 80S ribosome protein (PDB: 7OLD, chain: C); EMD-12977 at a 3.0 Å resolution. RMSD: AF2 model, 11.12 Å; D-AF(6), 3.30 Å; D-AF(3), 4.81 Å. c The structure of subunit RecB from DNA binding protein of RecBCD enzyme (PDB: 8B1R, chain: B) from a cryo-EM map of 3.2 Å resolution (EMD-15803). RMSD: AF2, 10.4 Å; D-AF(6), at 3.46 Å; D-AF(3), 4.78 Å. d The structure of intermediate capsid viral protein 6 (VP6) of rotavirus (PDB:1QHD, chain: A) from a map EMD-1461 with resolution of 3.8 Å. RMSD: AF2, 8.02 Å; D-AF(6), 3.25 Å; D-AF(3), 6.76 Å.

Full size image

The first example (Fig. 5a) is the human pyruvate carboxylase protein in apo state (PDB: 7WTA, chain A), which consists of two distinct domains connected by a long loop of 82 residues. The AF2 model folded the loop in a way that the small domain was placed close to the larger domain, resulting in a high RMSD of 8.32 Å. With six constraints, Distance-AF positioned the small domain almost correctly, with only a minor rotational shift (RMSD: 2.64 Å). Under three constraints achieved nearly the same accuracy, although with a slightly larger rotational shift of the small domain (RMSD: 3.14 Å). The next example (Fig. 5b) is elongation factor 2 from thermophilic eukaryotic 80S ribosome protein (PDB: 7OLD, chain: C), which consists of two similarly sized domains of 359 and 455 residues. Upon superimposing the AF2 model with the native structure, we observed that one domain was translated and rotated away from its correct orientation. Using six and three constraints, Distance-AF significantly improved the model, reducing the RMSD from 11.12 Å to 3.30 Å and 4.81 Å, respectively. Figure 5c shows models of the subunit RecB from DNA binding protein of RecBCD enzyme (PDB: 8B1R, chain: B). The smaller domain of nuclease activity connected by a long 35 residue loop was not in the right orientation, but that was almost corrected by the constraints. The final example (Fig. 5d) is intermediate capsid viral protein of rotavirus (PDB: 1QHD, chain A). In the AF2 model, a β-sandwich domain, shown as the lower half in the figure, flipped outside of the map. With six distance constraints, the domain was corrected in the right direction, achieving an RMSD of 3.25 Å. Using three constraints resulted in a slightly larger rotational shift, increasing the RMSD slightly, but the domain’s position was still essentially correct.

Overall, these examples demonstrate that Distance-AF can improve the fit of AF models by incorporating a small number of distance constraints, which can be derived from examining the maps or other sources.

Application to local structural modification

GPCRs represent one of the largest protein families in the human genome and constitute a major class of drug targets, accounting for 36% of all FDA-approved drug targets56. GPCRs undergo conformational changes to transmit signals across the cell membrane, and accurately modeling their multiple conformational states is crucial for drug development and for understanding their functional mechanisms57,58. Here, we demonstrate that Distance-AF can model functional conformations of GPCRs starting from a different functional state by applying local conformational changes between them. We selected two pairs of active and inactive states of GPCR from the GPCRdb59 database (Fig. 6). These pairs were selected because the structures of both active and inactive states are available, and the structures of the two states have an RMSD over 2 Å measured on the seven transmembrane helices. In this experiment, Distance-AF is aimed to adjust one or two helices exhibiting the greatest deviation from the target structure. The overall RMSD is then calculated across all seven helices to evaluate the performance. The data are provided in Supplementary Data 7. In Fig. 6a, we demonstrate the transition from the active state (PDB ID: 6OYA, chain ID: R) to the inactive state (PDB ID: 3C9L, chain ID: A) of bovine rhodopsin protein using Distance-AF. With Distance-AF, the sixth helix that is the main difference between the conformations of the two states (highlighted in the dashed box), was pulled toward the inactive form (green). As shown, the resulting helix conformation (magenta) agreed better to the inactive form than the active form (cyan). The RMSD computed on the seven helices (helix RMSD) improved from 3.30 Å to 3.03 Å by Distance-AF. The second example (Fig. 6b) is the opposite case, from inactive (PDB ID: 7BVQ, chain ID: A) to active state of the beta-adrenergic receptor protein (PDB ID: 7BTS, chain ID: A) where the fifth and sixth helices in the inactive conformation (cyan) were pulled toward the active position (green). In this case, the pulled helices moved toward the active conformation (magenta), certainly reduced the helix RMSD from 2.55 Å to 2.07 Å but did not have a perfect overlap to the target.

Fig. 6: Local conformational change to GPCRs.
figure 6

a Rhodopsin protein active (PDB: 6OYA, chain: R), inactive form (PDB: 3C9L, chain: A). In the parentheses, the average Ca distances of the 6th helix that are pulled by Distance-AF from the active form helix (cyan) to inactive form (green) toward the target inactive form are shown. Distance constraints applied are provided in Supplementary Data 7. b Beta-adrenergic receptor protein, active (PDB: 7BTS, chain: A), inactive (PDB: 7BVQ, chain: A). Distance-AF pulled the 5th and 6th helices of the inactive form (cyan) toward the active position (green). The structure in magenta is the resulting model by Distance-AF. c Rhodopsin, active form (6OYA-R). From the AF2 model that has an average Ca distances of 2.06 Å (cyan) at the 6th helix, it was pulled towards the correct active form (green). The structure in magenta is the result of applying Distance-AF. d Beta-adrenergic receptor protein, PDB ID: 7BTSA). The 5th helix in the AF2 model (cyan) was pulled toward the target crystal structure (green), which yielded the conformation in magenta.

Full size image

Additionally, two examples are shown in Fig. 6c, d where an incorrect helix in an AF2 model was pulled toward the correct position. In Fig. 6c, the AF2 model for the active state of rhodopsin protein (6OYA-R) had a transmembrane helix deviated (cyan) from the correct position (green). Distance-AF moved the helix to the conformation (magenta) that has almost perfect overlap with the target. In the last example (Fig. 6d), Distance-AF moved two helices (cyan) towards the right conformation (green), making the helices almost the right conformation as the target (green) from 3.34 Å to 2.89 Å, but the deviation comes from the loop and the helix conformations are substantially improved. In all the cases, Distance-AF made natural modification to the target helix orientation, not violating protein-like overall conformations. The improvement of helix RMSD values of the helical regions was not large, decreasing from 3.34 Å to 2.89 Å; however, the deviation originates primarily from the loop regions, while the helical conformations show substantial improvement. In all cases, Distance-AF introduced natural modifications to the target helix orientation without disrupting the overall protein-like conformations. Moreover, the movement of Distance-AF is so effective and successful on no more than two helices that has generalized RMSD improvement on seven helices.

Application to generating protein ensembles

In this application, we generated protein conformational ensembles using Distance-AF, unlike previous sections where we generated single conformations with Distance-AF. We selected two proteins from the Protein Ensemble Database60, whose structures were determined by NMR and have over 20 conformations in their PDB entries, where conformation changes of the models happened across their two structural domains. The first protein is skeletal muscle troponin C (PDB ID: 1TNW) and the second one is the HIV-1 capsid protein (PDB ID: 2M8P). For each of these two proteins, we defined two domains and derived six distance constraints between residues across the two domains. To generate diverse ensembles, we introduced different distance constraints to a generated AF2 model at various iterative stages with random ordering. Distances used are provided in Supplementary Data 8. We generated seven conformations for each protein. The data shown in Fig. 7 are provided in Supplementary Data 9 and 10.

Fig. 7: Performance of Distance-AF on NMR protein ensembles.
figure 7

a Left, conformational ensemble of troponin C (PDB ID: 1TNW), seven representatives of clusters from 20 conformations in the PDB entry are shown. The clusters were generated with an RMSD cutoff of 5.0 Å. right, conformational ensemble of HIV-1 capsid protein (PDB ID: 2M8P). seven representatives form 100 conformations are shown. b GDT-TS distributions of two domains of the proteins are shown. Blue, GDT-TS of all pairs of conformations in the PDB entry; orange, domain pairs of conformations generated by Distance-AF. The domains of the two proteins are manually determined. 1TNW, domain 1: residue 1 to 91; domain 2: 96 to 162. 2M8P, domain 1: 1 to 145; domain 2: 160 to 220. c The standard deviation of main-chain dihedral angles (phi, psi angles) along amino acid numbers of the native (dashed blue) and the generated conformations by Distance-AF (orange) on target 1TNW, the unit is in degree. Left: standard deviation curves on phi angles, right: standard deviation curves on psi angles. The regions specified by red dotted lines are the linker regions. d The standard deviation of main-chain dihedral angles (phi, psi angles) along amino acid numbers of the native (dashed blue) and the generated conformations by Distance-AF (orange) on target 2M8P, the unit is in degree. Left: standard deviation curves on phi angles, right: standard deviation curves on psi angles. The regions specified by red dotted lines are the linker regions. For c and d, the distance constraints were sampled from the N-terminal and the C-terminal domains outside of these linker regions.

Full size image

Figure 7a visualizes the ensemble structures of troponin C (left) and HIV-1 capsid protein (right). The conformation ensemble in magenta are the NMR-derived structures, which shows in seven different clusters with RMSD diverse from each other over 5 Å, while the ensemble in a different color for each chain was generated by Distance-AF. For troponin C, Distance-AF successfully captured the conformational variability of the protein by predicting the bottom domain into five clusters, which align closely with the broad range of native states observed in the native conformations. Similarly, for the HIV-1 capsid protein, seven different clusters are displayed from native conformations with pairwise RMSD difference above 5 Å, the conformations generated by Distance-AF correspond to approximately four diverse clusters that reflect the NMR ensemble.

In Fig. 7b, we computed GDT-TS score40 of pairs of domains to demonstrate that the predicted ensembles by Distance-AF maintain high structural integrity and folding pattern while diverse in different conformations. GDT-TS is an average of the weighted fraction of residues in two structures that are within 1, 2, 4, 8 Å when the structures are superimposed. It ranges from 0 to 1 with 1 indicating a perfect match of the two structures compared. As shown, domains from the NMR ensembles as well as those generated by Distance-AF have all 0.65 or higher GDT-TS, indicating that the domain structures are kept almost the same.

Figure 7c shows the standard deviation of dihedral angles (left: phi, right: psi) computed across multiple conformations along the residue positions of troponin C. The blue dashed lines represent the native structures, while the orange lines correspond to the ensembles generated by Distance-AF. The residues in the linker region, which connects two domains, are highlighted between two vertical red dotted lines. A large standard deviation of angles was observed at the linker region in both NMR ensemble and structures generated by Distance-AF. There are other standard deviation peaks, but they correspond to long loop regions that connect helices, which do not have stable structure. Figure 7d is for HIV-1 capsid protein. For the NMR ensemble, a single peak of the standard deviation was observed at the linker region. This peak is also observed for the ensemble by Distance-AF. There were some other smaller peaks, which turned out to correspond to the residues that were involved in the distance constraints.

The results in Fig. 7b, c and 7d show that Distance-AF is able to generate diverse conformational ensembles while preserving the quality and compactness of intra-domain structures.

Discussion

We developed Distance-AF, a deep learning method that leverages the AF2 framework while integrating distance constraints to ensure the predicted structures align with the provided distance information. While AF generally makes reasonable predictions, practical scenarios often reveal cases where domain or local structure orientations in the model do not align with specific experimental data or biological knowledge. This mismatch does not necessarily indicate an error in AF’s prediction; rather, the target protein may naturally exhibit flexibility in a linker region, and AF may have accurately predicted a plausible structure with a particular domain orientation that coincidentally conflicts with experimental data. However, correcting domain orientation in such models is challenging, as AF does not allow users to specify distance constraints during its prediction process.

In Distance-AF, user-provided distance constraints are incorporated into the loss function, which is iteratively optimized to achieve conformations that align with the specified distances. Compared to existing methods35,36 that retrain the neural network to handle distance constraints, this approach is the key innovation, which offers several significant advantages: Distance-AF is independent of a specific training set. Therefore, the development did not need substantial computational resources that would be required for full training of the network. Additionally, it facilitates an intuitive, conformational adjustment from the initial structure model to the refined model that satisfies the desired distance constraints. Distance-AF showed substantial improvement of the modeling accuracy in terms of RMSD and TM-score over the AF2, Rosetta, and AlphaLink.

Applications of Distance-AF include refining predicted structural models using provided distance constraints, fitting structures to cryo-EM maps, modeling different functional states, and generating structural ensembles. The distance information used by Distance-AF does not need to come from experimental data; hypothetical distances can also be provided. This allows users to visualize how applying specific constraints may alter the overall structure and to assess whether the proposed distances are structurally feasible. Notably, Distance-AF ensures that the overall structure is modified naturally while satisfying the specified distances, as AF2 inherently understands the principles of natural protein conformations.

Distance-AF works best when specified distance constraints are between two structured domains and linear move of domains are required to reach the target conformation. The modeling results are in principle affected by the accuracy of the provided distance constraints, but as shown in Fig. 2b, the results were reasonably robust to perturbations of the distances. In the current implementation, provided distance constraints are considered as a whole by the sum of the distance difference in a current structure (Eq. 1). Instead, we plan to give a weight to each distance to allow prioritizing some of the distances over others, depending on the importance or confidence. Modeling is challenging if pulling domains cause severe atom clashes or substantial rotation is needed for achieving the target conformation. Also, satisfying distance constraints between multiple many domains could be challenging, although we have not tested it yet.

We plan to extend Distance-AF to support protein multimers and incorporate additional types of constraints, such as main-chain and side-chain angles, atomic distances within binding pockets to accommodate ligand interactions, and the generation of ensembles for disordered proteins that maintain core structures and key residue distances.

Methods

Structure modeling with constraints as an overfitting problem

Distance-AF is built on AlphaFold2 (AF2) and uses the same network weights as AF2. Unlike conventional supervised learning methods, it is not pretrained on a separate training dataset. Instead, Distance-AF introduces distance constraints (Eq. 1), which is implemented as an intra-domain FAPE loss, as described in this section. This distance constraint loss is incorporated alongside the standard loss terms used in AF2 (see Eq. 2) and is minimized iteratively during the modeling process (Fig. 1). In this framework, the target structure is effectively “overfit” to the loss function that includes the distance constraints.

Intra-domain FAPE loss

Supplementary Fig. 1 shows the pseudo code for computing the intra-domain FAPE loss. This is the Lfape in Eq. 2. The computation requires 3 types of information. (1) \({{domain}}_{1}\), \({{domain}}_{2}\):residue index of each domain, specified as input; (2) \({\vec{x}}_{{pred}}\), \({\vec{x}}_{{initial}}\): predicted and initial frames; (3) \({T}_{{pred}}\), \({T}_{{initial}}\): Rigid transformation from frames to coordinates. First, the predicted and initial frames are aligned and converted to coordinates in a common origin, referred to as local coordinates (steps 1–3). Next, the frame-aligned point error for every pair is calculated (step 4). Finally, based on the definition of domain-wise residues, errors on residue pairs across separate domains are masked to zero, while those related to residues within the same domain are retained and averaged (steps 5–7).

Settings of computation

The network depth of structure module is set to 8. The learning rate is 0.001 using the Adam optimizer with \({\beta }_{1}=0.9\) and \({\beta }_{2}=0.99\), controlling the exponential decay rate for the moving average of the first-order moment (mean) and second-order moment (variance) of the gradients. L2 regularization is implemented by built-in weight decay in Adam optimizer, and we use drop-out rate = 0.1 in structure module. By default, we use up to 30,000 iterations to accommodate large targets that usually require more iterations to converge.

The computation time for Distance-AF is largely dependent on the length of the protein sequence and the number of iterations. For a target sequence of up to 500 amino acids with up to 30,000 iterations, Distance-AF can complete the process within less than an hour to a few hours. We have optimized the Distance-AF framework to efficiently utilize GPU memory during the loss backward stage. With a GPU having 24GB of memory, it is possible to run any target sequence of up to 1500 residues. In Supplementary Table 1, we provided the times needed and GPU memory of example cases with different protein lengths in comparison with AF2 and Rosetta.

Running Distance-AF

Distance-AF optimizes an AF2 model to satisfy user-provided distance constraints. Users are expected to obtain such distance information from experiments, such as crosslinking, NMR, or by fitting the current structure model to an EM map, from literature, or from some ideas by the users based on their expert knowledge of the protein they want to model. Distance-AF is a tool to make the structure with the provided distance constraints, which can be visualized and examined by the users to confirm or design biological hypotheses.

Distance-AF codes and example files are available at https://github.com/kiharalab/Distance-AF. Example files are provided in the folder, Example/1IXCA/. Distance constraints are provided in a text file (in the example file, it is dist_constraint.txt). In the file, for each line residue pairs and the distance between them are provided. The Usage section of the GitHub top page provides step to step guide: As Distance-AF improves over structure models of AF2, first users need to run AF2 and obtain the embedding file. Then, run distance-AF in a command line:

python3 Distance_AF.py [--target_file=TARGET_FILE] [--emd_file=EMD_FILE] [--dist_info=DIST_INFO] [--window_info=WINDOW_INFO] [--initial_pdb=INITIAL_PDB]

with these options and other parameters, where --target_file is to provide the path to the directory of the files, --emd_file is to specify the embedding file from AF2, --dist_info is to provide the distance constraint file, --window_info provides the domain information, and --initial_pdb is the starting structure file which will be optimized by Distance-AF. For more details, please see the GitHub repository.

Running existing methods

We compared Distance-AF to vanilla AF210, Rosetta42,43, and AlphaLink35. The predicted structures by AF2 were downloaded from the AF2 Database on 03/15/2023.

We ran Rosetta 3.13, downloaded from the official website of RosettaCommons42,43. Considering that Rosetta uses a Monte Carlo approach, we ran Rosetta 10 times for each target and choose the structure with the lowest Rosetta energy score. We used 0.1 as the weight parameter for distance constraints, because 0.1 gave the most accurate results on several targets among five values, 0.01, 0.1, 1.0 (default), 5.0, and 10.0 we tested. The command and options we used to run Rosetta is as follows:

/apps/rosetta/w2021.38/main/source/bin/relax.static.linuxgccrelease -s initial.pdb -constraints:cst_file dist_constraint.cst -out:nstruct 10 -out:path:all output_dir -constraints:cst_weight 0.1 -score:weights ref2015_cst -relax:script /apps/rosetta/w2021.38/main/source/src/apps/public/relax_w_allatom_cst/always_constrained_relax_script

To run AlphaLink we followed the instruction at https://github.com/lhatsk/AlphaLink. Considering that some of the distance constraints exceeded 10 Å, we employed the AlphaLink model that accepts longer constraints named as finetuning_model_5_ptm_distogram.pt. The restraint CSV file was prepared using the exactly the same distance constraints applied to Distance-AF. The command used to run AlphaLink was as follows:

python predict_with_crosslinks.py 1IXCA.fasta restraint_distributions.csv --distograms --use_precomputed_alignments 1IXCA/msas/ --checkpoint_path AlphaLink_model/finetuning_model_5_ptm_distogram.pt --uniref90_database_path uniref90.fasta --mgnify_database_path mgy_clusters.fa --pdb70_database_path pdb70/pdb70 --uniclust30_database_path uniclust30_2018_08/uniclust30_2018_08 --jackhmmer_binary_path $CONDA_PREFIX/bin/jackhmmer --hhblits_binary_path $CONDA_PREFIX/bin/hhblits --hhsearch_binary_path $CONDA_PREFIX/bin/hhsearch --kalign_binary_path $CONDA_PREFIX/bin/kalign

Statistics and reproducibility

We used Python version 3.8.0 to compute Pearson correlation with p-value < 0.01. The data we used in this work is from 2 public databases, RCSB and AlphaFold database, with details elaborated in Results section. Source data underlying all figures are provided in Supplementary Data files and Supplementary Information. Our open source code can be run to reproduce all results in this work.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.