Introduction

Graph representation learning for molecules has gained significant attention in drug discovery and materials science, as it effectively encapsulates molecular structures and enables the effective investigation of structure-activity relationships1,2,3,4,5,6. In this paradigm, atoms are treated as nodes and chemical bonds as edges, effectively encapsulating the connectivities that define molecular behavior. However, it poses significant challenges due to intricate relationships among molecules and the limited chemical knowledge utilized during training.

Contrastive Learning (CL) is often employed to study relationships among molecules. The primary focus within the domain of CL applied to molecular graphs centers on 2D–2D graphs comparisons. Noteworthy representative examples: InfoGraph7 maximizes the mutual information between the representations of the graph and its substructures to guide the molecular representation learning; GraphCL8, MoCL9, and MolCLR10 employ graph augmentation techniques to construct positive pairs; MoLR11 establishes positive pairs with reactant-product relationships. In addition to 2D-2D graph CL, there are also noteworthy efforts exploring 2D–3D and 3D–3D CL in the field. 3DGCL12 is 3D–3D CL model, establishing positive pairs with conformers from the same molecules. GraphMVP13, GeomGCL14, and 3D Informax15 propose 2D–3D view CL approaches. To conclude, 2D–2D and 3D–3D comparisons are intra-modality CL, as only one graph encoder is employed in these studies. However, these approaches often focus on the motif and graph levels, leaving atom-level CL less explored. For example, consider Thalidomide: while the (R)- and (S)-enantiomers share the same topological graph and differ only at a single chiral center, their biological activities are drastically different-the (R)-enantiomer is effective in treating morning sickness, whereas the (S)-enantiomer causes severe birth defects. In other words, the (R)- and (S)-enantiomers are similar in terms of topological structure but dissimilar in terms of biological activities. Thus, a more sophisticated approach is required to tackle these scenarios. A potential solution would be to use continuous metrics within a multi-view space, enabling a more comprehensive understanding of these complex molecular relationships.

There are multiple approaches for such similarity learning. One approach among them is instance-wise discrimination, which involves directly assessing the similarity between instances based on their latent representations or features.16. Naive instance-wise discrimination relies on pairwise similarity, leading to the development of contrastive loss17. Although there are improved loss functions such as triplet loss18, quadruplet loss19, lifted structure loss20, N-pairs loss21, and angular loss22, these methods still fall short in thoroughly capturing relationships among multiple instances simultaneously23. To address this limitation, a joint multi-similarity loss has been proposed, incorporating pair weighting for each pair to enhance instance-wise discrimination23,24. However, these pair weightings require the manual categorization of negative and positive pairs, as distinct weights are assigned to losses based on their categories. In this case, we can borrow the idea of relational learning (RL)25 from computer vision by using different augmented views of the same instance tasks to similar features, while allowing for some variability. This approach captures the essential characteristics of the instance in a continuous scale, promoting relative consistency across the views without requiring them to be identical. By doing so, it enhances the model’s ability to generalize and recognize underlying patterns in the data.

Besides, in order to enable a multi-view analysis from diverse sources is essential for improving molecule analysis, we can apply the multi-modality fusion26,27,28,29,30,31,32. It combines diverse heterogeneous data (e.g., text, images, graph) to create a more comprehensive understanding of complex scenarios. This approach leverages the strengths of each modality, potentially improving performance in tasks like sentiment analysis or medical diagnosis. While challenging to implement due to the need to align different data streams, successful fusion can provide insights beyond what’s possible with single modalities, advancing AI and data-driven decision-making. In particular, the way to fuse different modalities should also depends on the dominace of each unimodality30. However, when it comes to multimodal learning for molecules, we often encounter data availability and incompleteness issues. This raises a critical question: how can multimodal information be effectively leveraged for molecular property reasoning when such data are absent in downstream tasks? Recent studies have demonstrated the effectiveness of pretraining molecular graph neural networks (GNNs) by integrating additional knowledge sources10,33,34,35. Building on this foundation, a promising solution is to pretrain multiple replicas of molecular GNNs, with each replica dedicated to learning from a specific modality. This approach allows downstream tasks to benefit from multimodal data that is not accessible during fine-tuning, ultimately improving representation learning.

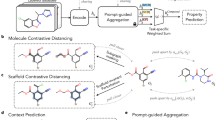
Facing these challenges and opportunities, we propose multimodal fusion (MMF) with relational learning (MMFRL) for molecular property prediction as shown in Fig. 1, a framework features RL and MMF. RL utilizes a continuous relation metric to evaluate relationships among instances in the feature space36,37. Our major contribution comprises three aspects: Conceptually: We introduce a modified relational learning (MRL) metric for molecular graph representation that offers a more comprehensive and continuous perspective on inter-instance relations, effectively capturing both localized and global relationships among instances. Methodologically: Our proposed modified relational metric captures complex relationships by converting pairwise self-similarity into relative similarity, which evaluates how the similarity between two elements compares to the similarity of other pairs in the dataset. In addition, we integrate these metrics into a fused multimodal representation, which has the potential to enhance performance, allowing downstream tasks to leverage modalities that are not directly accessible during fine-tuning. Empirically: MMFRL excels in various downstream tasks for Molecular Property Predictions. Last but not least, we demonstrate the explainability of the learned representations through two post-hoc analysis. Notably, we explore minimum positive subgraphs (MPS) and maximum common subgraphs to gain insights for further drug molecule design.

Results

The effectiveness of pre-training

We first illustrate the impact of pre-training initialization on performance on DMPNN38. As shown in Table 1, the average performance of pre-trained models outperform the non-pre-trained model in all tasks except for Clintox. The results of various downstream tasks indicate that different tasks may prefer different modalities. Notably, the model pre-trained with the NMR modality achieves the highest performance across three classification tasks. Similarly, the model pre-trained with the Image modality excels in three tasks, two of which are regression tasks related to solubility, aligning with findings from prior literature35. Additionally, the model pre-trained with the Fingerprint Modality method achieves the best performance in two tasks, including MUV, which has the largest dataset.

Table 1 Study on the performances of MMFRLUnimodality
Full size table

Overall performance of MMFRL

As shown in Tables 2 and 3, MMFRL demonstrates superior performance compared to all baseline models and the average performance of DMPNN pretrained with extra modalities across all 11 tasks evaluated in MoleculeNet. Results in Supplementary Information Table D.2 and D.3 demonstrates our great performance compared to the baseline models on the directory of useful decoys: enhanced (Dud-E)39 and LIT-PCBA40 datasets. This robust performance highlights the effectiveness of our approach in leveraging multimodal data. In particular, while individual models pre-trained on other modalities for Clintox fail to outperform the NoPre-training model, the fusion of these pre-trained models leads to improved performance. Besides, apart from Tox21 and Sider, the fusion models significantly enhance overall performance. In particular, the intermediate fusion model stands out by achieving the highest scores in seven distinct tasks, showcasing its ability to effectively combine features at a mid-level abstraction. The late fusion model achieves the top performance in two tasks. These results underscore the advantages of utilizing various fusion strategies in multimodal learning, further validating the efficacy of the MMFRL framework.

Table 2 Overall performances (ROC-AUC) on classification downstream tasks
Full size table
Table 3 Overall performances (RMSE) on regression downstream tasks. The best results are denoted in bold, and the second-best are indicated with underlining
Full size table

Analysis of the fusion effect

General comparison among various ways of fusions

Early fusion is employed during the pretraining phase and is easy to implement, as it aggregates information from different modalities directly. However, its primary limitation lies in the necessity for predefined weights assigned to each modality. These weights may not accurately reflect the relevance of each modality for the specific downstream tasks, potentially leading to suboptimal performance.

Intermediate fusion is able to capture the interaction between modalities early in the fine-tuning process, allowing for a more dynamic integration of information. This method can be particularly beneficial when different modalities provide complementary information that enhances overall performance. If the modalities effectively compensate for one another’s strengths and weaknesses, intermediate fusion may emerge as the most effective approach.

In contrast, Late fusion enables each modality to be explored independently, maximizing the potential of individual modalities without interference from others. This separation allows for a thorough examination of each modality’s contribution. When certain modalities dominate the performance metrics, Late fusion can maximize on these strengths, ensuring that the most impactful information is utilized effectively. This approach is especially useful in scenarios where the dominance of specific modalities can be leveraged to enhance overall model performance.

In addition, we conduct an ablation study to evaluate the performance of our proposed loss functions against two traditional CL losses-contrastive loss and triplet loss-in the context of intermediate fusion. The experimental results as shown in Supplementary Information Table D.1 demonstrate that our proposed methods outperform the baseline approaches across the majority of tasks in the MoleculeNet dataset, thereby highlighting the superiority of our approach.

Explainability of learnt representations

To demonstrate the interpretability of learnt representations of fusion, we present post-hoc analysis for two tasks, ESOL and Lipo, as demonstration. The results showcase that learnt representations can capture task-specific patterns and offer valuable insights for molecular design.

ESOL with intermediate fusion. As presented in Table 3, the intermediate fusion method 5.3.2 exhibits superior performance on the ESOL regression task for predicting solubility. To further analyze this performance, we employed t-SNE to reduce the dimensionality of the molecule embeddings from 300 to 2, resulting in a heatmap visualized in Fig. 2. The embeddings derived from individual modalities prior to fusion do not display a clear pattern, showing no smooth transition from low to high solubility. In contrast, the embeddings by intermediate fusion reveal a distinct and smooth transition in solubility values: molecules with similar solubility cluster together, forming a gradient that extends from the bottom left (indicating lower solubility) to the upper center (representing higher solubility). This trend underscores the effectiveness of the intermediate fusion approach in accurately capturing the quantitative structure-activity relationships for aqueous solubility.

Fig. 1: Multimodal fusion with relational learning for molecular property prediction (MMFRL).
figure 1

This figure shows our proposed idea about how to transfer the knowledge from other modalities and use fusion to improve the performance further. Unlike the general contrastive learning framework shown in Supplementary Information Figure 1, MMFRL doesn’t need to define positive or negative pairs and is capable of learning continuous ordering from target similarity. In Early fusion, a single Initialized GNN is created by combining all modality information during pretraining. In Intermediate and Late Fusion, each modality has its own initialized GNN.

Full size image
Fig. 2: T-SNE visualization depicting the ESOL molecule embeddings for intermediate fusion in Section 5.3.2 alongside molecules within the highlighted region.
figure 2

Each point in the heatmap corresponds to the embeddings of respective molecules in ESOL, with color indicating solubility levels. Red denotes higher solubility, while blue indicates lower solubility. The embeddings derived from individual modalities prior to fusion do not display a clear pattern; the embeddings by intermediate fusion form a gradient that extends from the bottom left (indicating lower solubility) to the upper center (representing higher solubility).

Full size image

Additionally, we examined the similarity between the respective embeddings prior to intermediate fusion and the resulting fused embedding, as depicted in Fig. 3. Our analysis indicates that the embeddings from each modality exhibit low similarity with the intermediate-fused representation. This observation suggests that the modalities complement each other, collectively enhancing the resulting representation of the intermediate-fused embedding.

Fig. 3: This figure shows the distribution of similarities between each modality and the intermediate fusion embedding for ESOL.
figure 3

In both cosine similarity and dot product, the embeddings from each modality exhibit low similarity with the intermediate-fused representation.

Full size image

Lipo with late fusion. As detailed in Table 3, the Late Fusion method (described in Section 5.3.3) demonstrates superior performance on the Lipo regression task for predicting solubility in fats, oils, lipids, and non-polar solvents. According to Equation (11), the final prediction is determined by the respective coefficients (wi) and predictions (pi) from each modality.

In Fig. 4, we present the distribution of values for the coefficients, predictions, and their products for each modality. Notably, the simplified molecular input line entry system (SMILES) and Image modalities display a wide range of values, highlighting their potential to significantly influence the final predictions. This observation aligns with the strong performance achieved when pretraining using either of these two modalities, as shown in Table 1. In contrast, the NMRPeak values display a narrower range, indicating its role as a modifier for finer adjustments in the predictions. Furthermore, we observe that the contributions from NMRSpectrum and Fingerprint modalities are minimal, with their corresponding values approaching zero. This outcome highlights the advantages of the Late Fusion approach in effectively identifying and leveraging dominant modalities, thereby optimizing the overall predictive performance.

Fig. 4: Lipo late fusion contribution analysis reveals that the three primary contributors are SMILES, image, and NMRpeak.
figure 4

In contrast, NMRspectrum and fingerprint exhibit negligible contributions.

Full size image

Substructure analysis with BACE. We explore the binding potential of positive inhibitor molecules targeting BACE and their associated key functional substructures, referred to as MPS. To identify MPS, we employ a Monte Carlo Tree Search (MCTS) approach integrated into our BACE classification model, as implemented in RationalRL41. MCTS, being an iterative process, allows us to evaluate each candidate substructure for its binding potential with our model. Following the determination of MPSs, we categorize the original positive BACE molecules based on their respective MPSs. By computing the binding potential difference between the original molecule and its MPS, we can identify structural features that contribute to changes in binding affinity as shown in Fig. 5.

Fig. 5: The left sub-figure is the boxplot of the binding difference for the respective groups of molecules by the top eight most frequent minimum positive subgraph.
figure 5

The right sub-Figure showsthe detail strucutre of the 5th MPS.

Full size image

In the case of the MPS 5 group, the binding score is heavily influenced by steric effects. The top three high-performing designs (5a-5c) all feature a flexible and compact alkylated pyrazole structure (colored green), which likely facilitates better accommodation within the binding pocket. In contrast, the three lowest-performing designs (5n-5p) incorporate a more rigid and bulky (trifluoromethoxy)benzene moiety (colored red), which may introduce steric hindrance and reduce binding efficiency. Additionally, the pyrazole ring contains two nitrogen atoms, offering more potential for hydrogen bonding interactions with the target protein, whereas the (trifluoromethoxy)benzene group has only one oxygen atom, limiting its capacity for such interactions. This comparison highlights the importance of both molecular flexibility and functional group composition in optimizing binding affinity.

Sensitivity Analysis

Choosing the most effective fusion strategy can be empirical. However, our results presented in Table 2, 3, and Supplementary Information Table D.1, D.2, and D.3 provide strong evidence that our lightweight fusion strategy (early, intermediate, and late fusion) outperforms existing approaches in the literature. To guide the selection among these strategies, our intuition is as follows: if a modality is highly relevant to the downstream task, earlier fusion is likely to be more effective; otherwise, later fusion may be preferable.

To test this hypothesis, we performed a retrospective analysis to assess the sensitivity of downstream tasks to different fusion strategies. Since early fusion embeddings often lack the flexibility to adapt to individual samples, we excluded them from this analysis. Instead, we used pretrained encoders to extract embeddings for each modality and performed a simple linear regression between the embeddings and task labels. We then computed the Pearson correlation between the predicted values and the ground truth as a measure of each modality’s relevance.

For each dataset, we recorded the highest correlation across all modalities as the “Top 1" score. We then concatenated the embeddings from all modalities and repeated the regression analysis. The improvement in correlation is reported as the “Pearson Gain." A higher Pearson Gain suggests that earlier fusion of multiple modalities is more beneficial. As shown in Table 4, datasets where intermediate fusion performs best generally exhibit higher Pearson Gain compared to late fusion, supporting our intuition. However, for ESOL and FreeSolv, the correlation from a single modality is already high, making them less suitable for this analysis.

Table 4 Person correlation of different modalities and chosen fusion strategies across datasets
Full size table

Conclusion

In summary, we introduce a RL metric for molecular graph representation that enhances the understanding of inter-instance relationships by capturing both local and global contexts. Our method transforms pairwise self-similarity into relative similarity through a weighting function, allowing for complex relational insights. This metric is integrated into a multimodal representation, improving performance by utilizing modalities not directly accessible during fine-tuning. Empirical results show that our approach, MMFRL, excels in various molecular property prediction tasks. We also demonstrate a detailed study about the explainability of the learned representations, offering valuable insights for drug molecule design. Despite these accomplishments, further exploration is needed to achieve more effective integration of graph- and node-level similarities. Looking ahead, we are enthusiastic about the prospect of applying our model to additional fields, such as social science, thereby broadening its applicability and impact.

Dataset

Selected modalities for target similarity calculation

The following modalities are used for target similarity calculation. For details on training the corresponding encoders to obtain fixed embeddings for these modalities, please refer to Supplementary Information Section C.

Fingerprint

Fingerprints are binary vectors that represent molecular structures, capturing the presence or absence of particular substructures, fragments, or chemical features within a molecule. In particular, we utilize Morgan fingerprints, which are based on the extended-connectivity fingerprints (ECFP) method introduced by Rogers and Hahn42. Specifically, we generate fingerprints using AllChem.GetMorganFingerprintAsBitVect(mol, 2), which corresponds to ECFP4 (radius = 2). Because ECFP4 is one of the most effective and interpretable molecular representations43.

Simplified molecular input line entry system (SMILES)

SMILES offers a compact textual representation of chemical structures.

Nuclear magnetic resonance (NMR)

NMR spectroscopy provides detailed insights into the chemical environment of atoms within a molecule44. By analyzing the interactions of atomic nuclei with an applied magnetic field, NMR can reveal information about the structure, dynamics, and interactions of molecules, including the connectivity of atoms, functional groups, and conformational changes. In our experiments, NMRspectrum provides the information about the overal information of molecule while NMRpeak provides the information about the individual atoms in the molecule.

Image

Images (e.g., 2D chemical structures) provide a visual representation of molecular structures.

All of the similarity calculation from the modalities above are listed in Supplementary Information C.

Pre-training

NMRShiftDB-245 is a comprehensive database dedicated to nuclear magnetic resonance (NMR) chemical shift data, providing researchers with an extensive collection of expert-annotated NMR data for various organic compounds with molecular structures (SMILES) (Accessed June 2023). There are around 25,000 molecules used for pre-training and no overlap with downstream task datasets.

Downstream tasks

For Downstream tasks, our model was trained on 11 drug discovery-related benchmarks sourced from MoleculeNet46. Eight of these benchmarks were designated for classification downstream tasks, including BBBP, BACE, SIDER, CLINTOX, HIV, MUV, TOX21, and ToxCast, while three were allocated for regression tasks, namely ESOL, Freesolv, and Lipo. The datasets were divided into train/validation/test sets using a ratio of 80%:10%:10%, accomplished through the scaffold splitter47 from Chemprop38,48, like previous works. The scaffold splitter categorizes molecular data based on substructures, ensuring diverse structures in each set. Molecules are partitioned into bins, with those exceeding half of the test set size assigned to training, promoting scaffold diversity in validation and test sets. Remaining bins are randomly allocated until reaching the desired set sizes, creating multiple scaffold splits for comprehensive evaluation.

The DUD-E dataset39 is a widely used benchmark for virtual screening, containing 102 protein targets, thousands of active compounds, and carefully selected decoys that resemble actives in physico-chemical properties but differ topologically. In contrast, Low-Throughput Informatics-Targeted PubChem BioAssay (LIT-PCBA)40 offers a more realistic and challenging benchmark, derived from real experimental assays across 15 targets, with no artificial decoys and inherent data noise and imbalance. Together, they represent two ends of the spectrum in virtual screening evaluation-DUD-E with idealized conditions, and LIT-PCBA with real-world complexity. For the fine-tuning setting, We follow the same split and test approach as49 for DUD-E and50 for LIT-PCBA.

Methods

We first explain the preliminaries, and then our proposed modified metric in RL to facilitate smooth alignment between the graph and referred unimodality. Then, we introduce approaches for integrating multimodalities at different stages of the learning process.

Molecular representation with DMPNN

The message passing neural network (MPNN)51 is a GNN model that processes an undirected graph G with node (atom) features xv and edge (chemical bond) features evw. It operates through two distinct phases: a message passing phase, facilitating information transmission across the molecule to construct a neural representation, and a readout phase, utilizing the final representation to make predictions regarding properties of interest. The primary distinction between DMPNN and a generic MPNN lies in the message passing phase. While MPNN uses messages associated with nodes, DMPNN crucially differs by employing messages associated with directed edges38. This design choice is motivated by the necessity to prevent totters52, eliminating messages passed along paths of the form v1v2…vn, where vi = vi+2 for some i, thereby eliminating unnecessary loops in the message passing trajectory.

MRL in pretraining

Original Relation Learning25 ensures that different augmented views of the same instance from computer vision tasks share similar features, while allowing for some variability. Suppose zi is the original embedding for the i-th instance. Then \({{{{\bf{z}}}}}_{{{{\bf{i}}}}}^{1}\) is the embedding of first augmented view for zi, and \({{{{\bf{z}}}}}_{{{{\bf{i}}}}}^{2}\) is the embedding of second augmented view for zi. In this case, the loss of RL is formulated as following:

$${s}_{ik}^{1}=\frac{{{\mathbb{1}}}_{i\ne k}\cdot \exp ({{{{\bf{z}}}}}_{{{{\bf{i}}}}}^{1}\cdot {{{{\bf{z}}}}}_{{{{\bf{k}}}}}^{2}/\tau )}{{\sum }_{j = 1}^{N}{{\mathbb{1}}}_{i\ne j}\cdot \exp ({{{{\bf{z}}}}}_{{{{\bf{i}}}}}^{1}\cdot {{{{\bf{z}}}}}_{{{{{\bf{j}}}}}^{2}}/\tau )}$$
$${s}_{ik}^{2}=\frac{{{\mathbb{1}}}_{i\ne k}\cdot \exp ({{{{\bf{z}}}}}_{{{{\bf{i}}}}}^{2}\cdot {{{{\bf{z}}}}}_{{{{\bf{k}}}}}^{2}/{\tau }_{m})}{{\sum }_{j = 1}^{N}{{\mathbb{1}}}_{i\ne j}\cdot \exp ({{{{\bf{z}}}}}_{{{{\bf{i}}}}}^{2}\cdot {{{{\bf{z}}}}}_{{{{\bf{j}}}}}^{2}/{\tau }_{m})}$$
$${L}_{RL}=-\frac{1}{N}\mathop{\sum }_{i=1}^{N}\mathop{\sum }_{k=1\atop k\ne i}^{N}{s}_{ik}^{2}\log ({s}_{ik}^{1}).$$

We propose a modified relational metric by adapting the softmax function as a pairwise weighting mechanism. Let \(| {{{\mathcal{S}}}}|\) denote the size of the instance set. The variable si,j represents the learned similarity where zi is the embedding to be trained. On the other hand, \({t}_{i,j}^{R}\) defines the target similarity that captures the relationship between the pair of instances in the given space or modality R, where \({{{{\bf{z}}}}}_{{{{\bf{i}}}}}^{R}\) is a fixed embedding. The detailed formulation for the loss of MRL is provided below:

$${s}_{i,j}=\frac{\exp (sim({{{{\bf{z}}}}}_{{{{\bf{i}}}}},{{{{\bf{z}}}}}_{{{{\bf{j}}}}}))}{{\sum }_{k = 1}^{| {{{\mathcal{S}}}}| }\exp (sim({{{{\bf{z}}}}}_{{{{\bf{i}}}}},{{{{\bf{z}}}}}_{{{{\bf{k}}}}}))}$$
(1)
$${t}_{i,j}^{R}=\frac{\exp (sim({{{{\bf{z}}}}}_{{{{\bf{i}}}}}^{{{{\bf{R}}}}},{{{{\bf{z}}}}}_{{{{\bf{j}}}}}^{{{{\bf{R}}}}}))}{{\sum }_{j = 1}^{| {{{\mathcal{S}}}}| }\exp (sim({{{{\bf{z}}}}}_{{{{\bf{i}}}}}^{{{{\bf{R}}}}},{{{{\bf{z}}}}}_{{{{{\bf{k}}}}}^{{{{\bf{R}}}}}}))}$$
(2)
$${L}_{MRL}=-\frac{1}{| {{{\mathcal{S}}}}| }\mathop{\sum }_{i=1}^{| {{{\mathcal{S}}}}| }\mathop{\sum }_{j=1}^{| {{{\mathcal{S}}}}| }{t}_{i,j}^{R}\log ({s}_{i,j}).$$
(3)

Notably, unlike other similarity learning approaches23,24, our method does not rely on the categorization of negative and positive pairs for the pair weighting function. Additionally, our use of the softmax function ensures that the generalized target similarity ti,j adheres to the principles of convergence, which results in better ranking consistency between the graph modality and the auxiliary modality, compared with the original Relational Study, as follows:

Theorem 5.3

(Convergence of MRL Metric)

Let \({{{\mathcal{S}}}}\) be a set of instances with size of \(| {{{\mathcal{S}}}}|\), and let \({{{\mathcal{P}}}}\) represent the learnable latent representations of instances in \({{{\mathcal{S}}}}\) such that \(| {{{\mathcal{P}}}}| =| {{{\mathcal{S}}}}|\). For any two instances \(i,j\in {{{\mathcal{S}}}}\), their respective latent representations are denoted by \({{{{\mathcal{P}}}}}_{i}\) and \({{{{\mathcal{P}}}}}_{j}\). Let ti,j represent the target similarity between instances i and j in a given domain, and let di,j be the similarity between \({{{{\mathcal{P}}}}}_{i}\) and \({{{{\mathcal{P}}}}}_{j}\) in the latent space. If ti,j is non-negative and {ti,j} satisfies the constraint \({\sum }_{j = 1}^{| {{{\mathcal{S}}}}| }{t}_{i,j}=1\), consider the loss function for an instance i defined as follows:

$$L(i)=-\mathop{\sum }_{j=1}^{| {{{\mathcal{S}}}}| }{t}_{i,j}\log \left(\frac{{e}^{{d}_{i,j}}}{{\sum }_{k = 1}^{| {{{\mathcal{S}}}}| }{e}^{{d}_{i,k}}}\right)$$
(4)

then when it reaches ideal optimum, the relationship between ti,j and di,j satisfies:

$${softmax} \, ({d}_{i,j})={t}_{i,j}$$
(5)

For detailed proof, please refer to Supplementary Information Section A.

Fusion of multi-modality information in downstream tasks

During pre-training, the encoders are initialized with parameters derived from distinct reference modalities. A critical question that arises is how to effectively utilize these pre-trained models during the fine-tuning stage to improve performance on downstream tasks.

Early stage: multimodal multi-similarity

With a set of known target similarity {tR} from various modalities, we can transform themto multimodal space through a fusion function. There are numerous potential designs of the fusion function. For simplicity, we take linear combination as a demonstration. The multimodal generalized multi-similarity \({t}_{i,j}^{M}\) between ith and jth objects can be defined as follows:

$${t}_{i,j}^{M}=fusion(\{{t}^{R}\})$$
(6)
$$=\sum {w}_{R}\cdot {t}_{i,j}^{R}$$
(7)

where \({t}_{i,j}^{R}\) represents the target similarity between ith and jth instance in unimodal space R, wR is the pre-defined weights for the corresponding modal, and ∑wR = 1. Then we can make \({t}_{i,j}={t}_{i,j}^{R}\) in equation (3). Such that, it still satisfy the requirement of convergence (See proof in Supplementary Information Section A). In this case, the learnt similarity during pretraining will be aligned with this new combined target similarity.

Intermediate stage: embedding concatenation and fusion

Intermediate fusion integrates features from various modalities after their individual encoding processes and prior to the decoding/readout stage. Let f1, f2, …, fn represent the feature vectors obtained from these different modalities. The resulting fused feature vector can be defined as follows:

$${{{{\bf{f}}}}}_{{{{\rm{fused}}}}}={\mbox{MLP}}({\mbox{concat}}\,({{{{\bf{f}}}}}_{1},{{{{\bf{f}}}}}_{2},\ldots ,{{{{\bf{f}}}}}_{n}))$$
(8)

Where concat represents concatenation of the feature vectors. The fused features are then fed into a later readout function or decoder for downstrean tasks prediction or classification. The multi-layer perceptron is used to reduce the dimension to be the same as fi.’

Late stage: decision-level

Late fusion (or decision-level fusion) combines the outputs of models trained on different modalities after they have been processed independently. Each modality is first processed separately, and its predictions are combined at a later stage.

Let p1, p2, …, pn be the predictions (e.g., probabilities) from different modalities. The final prediction pfinal can be computed using a weighted sum mechanism:

$${w}_{i}={T}_{i}({{{{\bf{f}}}}}_{i})$$
(9)
$${p}_{i}={{\mbox{readout}}}_{i}({{{{\bf{f}}}}}_{i})$$
(10)
$${p}_{{{{\rm{final}}}}}=\mathop{\sum }_{i=1}^{n}{w}_{i}{p}_{i}$$
(11)

Where wi are the weights assigned to each modality’s prediction, and they can be adjusted based on the importance of each modality. In particular, wi is tunable during the learning process for respective downsteak tasks.