Structural and physical investigation of ordered BaO-deficient Ba₃PuO₆

Abstract

Ternary actinide compounds allow for a range of oxidation states and a rich but often not well-known chemistry. Here, a BaO-deficient plutonium-containing perovskite with a composition close to Ba₃PuO₆ has been obtained via solid state synthesis. The compound was characterised using X-Ray Diffraction from room temperature up to 1473 K, revealing two phase transitions and ordered Ba-deficiency. X-ray Absorption Spectroscopy was performed at the Pu L₃- and M₅-edges. The XANES spectrum at the Pu L₃-edge and the XANES in high-energy resolution mode at the Pu M₅-edge both indicate a Pu(VI) oxidation state. Despite the rather complex crystallographic unit cell, Extended X-ray Absorption Fine Structure (EXAFS) spectroscopy at the Pu L₃-edge yields Pu-O distances of 2.01(1) and 2.4(3) Å. The low-temperature heat capacity of Ba_2.875PuO_5.875 was measured between 5 and 270 K. The heat capacity and standard entropy at 298.15 K were found to be C_p = (251 ± 8) J⋅K⁻¹⋅mol⁻¹ and ${S}_{m}^{0}=(318\pm 8)\,{{\rm{J}}} \! \cdot \! {{{\rm{K}}}}^{-1} \cdot {{{\rm{mol}}}}^{-1}$, respectively. The magnetic susceptibility was measured from 2 to 320 K and shows a temperature-independent paramagnetism, consistent with the hexavalent oxidation state of Pu. This article reports the first extended low-temperature heat capacity curve and a temperature-dependent magnetic susceptibility measurement in a [Rn]5f² Pu-based system.

Introduction

The actinide elements (An) at the bottom of the periodic table allow for a wide range of oxidation states and a concomitant rich chemistry. Throughout the actinide group, the 5f electron-shell is gradually filled, but the exact nature of the electronic occupation of the valence shells remains a matter of debate, especially for the transuranium elements like plutonium (Pu). In recent years, a surprising feature was reported for the well-known material PuO₂: Tobin and Wu obtained a [Rn]5f⁵ occupation using a N_4,5 branching ratio analysis,¹ which is however contrary to the [Rn]5f⁴ occupancy that Bagus, Schacherl and Vitova reported². In a very recent study by Bajaj, Ramanantoanina et al., a clear distinction was made between 5f⁴ open shell electrons that do not participate in bonding and 5f electrons transferred from O to Pu, which do participate in covalent Pu-O interaction³. Another surprising case is the long-range magnetic order in the perovskite compounds BaPuO₃ and SrPuO₃ below 164(1) and 76(1) K, respectively⁴, that one would not expect for a [Rn]5f⁴ system without unpaired electrons. Moreover, although the shortest Pu-Pu distance is smaller than 4.5 Å, the transition temperature is high⁵. Systematic studies into the solid state chemistry of systems of Pu-O with alkali (Li, Na, K, Rb, Cs) or alkaline-earth (Be, Mg, Ca, Sr, Ba) metals are very rare and often date back to the last century, except for Na-Pu-O^6,7,8. The Na-Pu(VI)-O phases that were reported therein are claimed to be impossible in a recent DFT study because calculations predict Pu(V) is the maximum physical oxidation state in solid state actinide compounds⁹.

As evidenced by the cited cases BaPuO₃ and SrPuO₃, alkaline-earth actinide oxides crystallise in perovskite phases. In addition to these compounds, BaAn^IVO₃ with An = Th, Pa, U, Np, Am, Cm and Cf have been studied experimentally by at least one technique^10,11,12,13. More rare double perovskites with barium and actinides have been reported to exist: Ba₃PaO_5.5¹⁰ and Ba₃An^{V I}O₆ with An = U, Np, Pu^14,15, but the understanding of any of these compounds is rather poor and the literature raises questions starting very basically at the stoichiometry of the compounds. A generalised overview of the phases reported in the Ba-An-O system^{14,15,16,17,18,19,20,21} was made with respect to the Ba/An ratio and the average formal oxidation state, and is shown in Fig. 1, in which the perovskite-related phases are presented by open squares.

Fig. 1: Non-exhaustive overview of reported phases in the Ba-An-O systems^{14,15,16,17,18,19,20,21}.

The phases are organised based on their Ba/An ratio and the average formal An oxidation state. Note that not all An (mainly U, Np, Pu) crystallise in all depicted stoichiometries. The dotted lines are guides for the eye.

The plutonium-containing double perovskite Ba₃PuO₆ was synthesised and reported for the first time by Keller in 1962¹⁴. The compound was synthesised by heating BaO₂ and PuO₂ in a 3:1 ratio in oxygen-flow at 1423 and 1523 K. Keller found the dark brown Ba₃PuO₆ to have a cubic structure ($Fm\bar{3}m$) with cell parameter a = 8.844(6) Å and Pu-O distances of 2.211 Å. The Pu(VI) oxidation state was derived from the absorption spectrum in 1 N HCl, where only ${{{\rm{PuO}}}}_{2}^{2+}$(aq.) was found. In experiments of equimolar ratio BaO₂ and PuO₂ in oxygen flow, Ba₃PuO₆ and PuO₂ were found up to 1073 K, above which Keller proposed the ordered perovskite-structure ${{\rm{Ba}}}({{{\rm{Pu}}}}_{{{\rm{x}}}}^{4+},{{{\rm{Pu}}}}_{0.5(1-{{\rm{x}}})}^{6+},{{{\rm{Ba}}}}_{0.5(1-{{\rm{x}}})}){{{\rm{O}}}}_{3}$ to form based on a non-linear trend in lattice parameter. Next to this dark brown Ba₃PuO₆, Keller tried to produce a Pu(V)-based Ba-Pu-O compound. For a deep black reaction mixture of Ba₃PuO₆, PuO₂ and 3 BaO in Ar-flow at 1273–1473 K, he found again ${{\rm{Ba}}}({{{\rm{Pu}}}}_{{{\rm{x}}}}^{4+},{{{\rm{Pu}}}}_{0.5(1-{{\rm{x}}})}^{6+},{{{\rm{Ba}}}}_{0.5(1-{{\rm{x}}})}){{{\rm{O}}}}_{3}$. Absorption spectrometry in 0.5 N HCl showed only Pu⁴⁺ and ${{{\rm{PuO}}}}_{2}^{2+}$(aq.) and he concluded the constitution to be Ba₃PuO_5.5. Gens et al. reported the standard enthalpy of formation at 298.15 K of Ba₃PuO₆, but unlike Keller, they did not find an ideal perovskite-type structure²². They prepared Ba₃PuO₆ from a BaCO₃ and PuO₂ mixture which was heat-treated at 900, 1000, 1100 and 1200 K with intermittent grinding. They also described that the thermal history of PuO₂ dictates the reactivity towards BaO and they used slow temperature increases to avoid Ba loss. Four successful syntheses gave identical diffraction patterns, that indicated a distorted perovskite structure and Pu was found to be hexavalent by spectrophotometry. Ba₃PuO₆ stock from Argonne National Laboratory is mentioned as Pu(VI) stock for X-ray absorption experiments in some studies^23,24, but data on this stock are not available in open literature to our knowledge.

Investigations on the uranium-containing double perovskite compound Ba₃UO₆ showed an analogous development: a first indication of an ordered perovskite-type structure^25,26 was later indexed in space groups of lower symmetry. Rietveld indexed all lines but three to a rather small tetragonal cell²⁷. Kemmler-Sack and Seemann reported a much larger rhombohedral cell for Ba₃UO₆.²⁸ Griffiths, Kemmler-Sack and Treiber reported that (next to triclinic Ba₃UO₆), a tetragonal BaO-deficient phase is formed, viz. Ba_2.875UO_5.875^16,17,18. Rietvelds solution is listed in the Pearsons Crystal Database as similar to Ba_2.875UO_5.875. De Blieck et al. used electron diffraction to determine the lattice of Ba₃UO₆²⁹. They interpreted the structure to be a 531 oriented superlattice.

Thus, Ba₃PuO₆ in particular and the Ba-Pu-O system in general deserve attention and the solid state chemistry of the Ba-U-O system may serve as a more investigated analogy. Three main hypotheses can be formulated after studying the literature about the perovskite-related structures in the Ba-An-O systems: First, the BaO-deficient phase Ba_2.875AnO_5.875 should be understood as a stoichiometric compound or as a member of solid solutions on the pseudo-binary BaO-AnO₃ axis, i.e. as a (end-)member of a purely An(VI)-solid solution series. More precisely, a solid solution Ba_3−xAnO_6−x exists with a maximum x = 0.125. Second, the perovskite phases are related via the pseudo-binary system BaAnO₃–Ba_1+yAnO_3+x–Ba₃AnO₆, i.e. with increasing average formal oxidation state of the actinide ion, following the dotted line in Fig. 1^14,21. The conjecture by Keller from 1964 that an ordered perovskite structure exists of composition ${{\rm{Ba}}}({{{\rm{Pu}}}}_{{{\rm{x}}}}^{4+},{{{\rm{Pu}}}}_{0.5(1-{{\rm{x}}})}^{6+},{{{\rm{Ba}}}}_{0.5\left(1-{{\rm{x}}}\right.}){{{\rm{O}}}}_{3}$ is an equivalent proposal¹⁴ to the proposal of Cordfunke et al., although according to the latter, uranium oxidises via U(V) to U(VI), while Keller proposes a mixture between Pu(IV) and Pu(VI)^14,21. Third, the actual chemistry is given by a ternary phase field enclosed by (at least) BaAnO₃−Ba₃AnO₆−Ba_2.875AnO_5.875.

The crystallography of Ba₃PuO₆ needs to be revisited in light of the complexity found in the Ba-U-O system^21,28, while the recent findings for nominally 5f⁴ PuO₂ and BaPuO₃ raise the question on the nature of the nominally closed-shell (no unpaired electrons) [Rn]5f² Ba₃PuO₆ compound as well^1,4. The goal of this work is to unravel the chemistry and the related impact on the physical properties of Ba₃PuO₆, but we find particularly its BaO-deficient related phase, and report on crystal structure, oxidation state, Pu-coordination and electronic structure, thermal expansion, low-temperature heat capacity, standard entropy and magnetic susceptibility. The analysis will follow the paradigm for this class of materials as set out in Fig. 1. Figure 1 implies that proper analysis needs to account for the (average) formal An oxidation state and for the Ba/An ratio. Once these properties are established, physical and thermodynamic properties of well-defined compounds can be studied.

Results and discussion

The results and discussion are organised in line with the paradigm set out in Fig. 1. After a short description of the synthesis, the average Pu formal oxidation state investigations using X-ray Absorption Spectroscopy are presented. Next, the results that led to the Ba/Pu quantification and crystal structure (XRD, EXAFS) are described. Last, study of various physical and thermodynamic properties (thermal expansion, low-temperature heat capacity, magnetic susceptibility) is discussed.

The black reaction mixture of synthesis 1 did not change colour upon the subsequent thermal treatments. A gradual mass loss was observed, as is expected with the loss of CO₂ from the reactant BaCO₃. The diffraction pattern collected after the heat treatment at 900 K, showed peaks that could be attributed to BaCO₃ and PuO₂. After the heat treatment at 1000 K, a new phase was found on the diffraction pattern. BaCO₃ is still partially visible, but disappeared after the heat treatment at 1100 K. At 1100, 1200 and 1270 K, the diffraction patterns showed the new phase and the reagents were not visible any more. The black reaction mixture of synthesis 2 did not change colour. As noted in the introduction, Keller reported a dark brown colour for Ba₃PuO₆ obtained in oxygen flow, and a deep black colour for the decomposition product Ba₃PuO_5.5 in Ar-flow¹⁴. The thermogravic-differential thermal analysis (TG-DTA) result on a reaction mixture of 3BaCO₃ and PuO₂ in air is shown and discussed in the SI.

To study the average Pu oxidation state, X-ray absorption spectra at the Pu L₃ and M₅-edge were recorded. The recorded X-ray Absorption Near Edge Structure (XANES) spectrum at the Pu L₃-edge of Ba_2.875PuO_5.875 is shown in Fig. 2. The edge threshold is compared to PuO₂ measured at the same beamline³⁰. A shift towards higher energy with respect to PuO₂ measured at the same beamline is clearly observed while the white line aligns well with Na₄Pu(VI)O₅ collected at ROBL as shown in Fig. 2 as well. This indicates a solid state Pu(VI) compound, contradicting claims from theory that Pu(V) is the highest possible oxidation state for solid state samples⁹, as was also found by Pidchenko et al. on ${{{\rm{K}}}}_{4}{{{\rm{PuO}}}}_{2}{({{{\rm{CO}}}}_{3})}_{3}$³¹. The white line is rather broad and an additional shoulder-like feature in between the edge-position and the primary white line is visible. Comparison with solid state uranate and neptunate species shows that the shoulder is common for ‘-ate’ geometry and solid state samples tend to give a broad white line^{8,32,33,34,35}. Moreover, the calculated Pu L₃-edge spectra of Ba_2.875PuO_5.875 and BaPuO₃ (space group Pnma) using FDMNES are shown in Fig. 2, and a similar shoulder-like feature is visible at the low-energy side of the white line. The calculated near-edge structure is very similar to the experimentally observed spectrum, underpinning the proposed structural model.

Fig. 2: Pu L₃-edge spectra of Ba_2.875PuO_5.875.

The XAS spectrum collected at the INE beamline of the KIT Light Source is compared to PuO₂ measured at the same beamline³⁰, FDMNES calculations (calc.) of Ba_2.875PuO_5.875 and BaPuO₃, and Pu(IV) and Pu(VI) spectra from literature⁸.

The high-resolution XANES spectrum collected around the Pu M₅-edge in scattering angle of 142° relative to the incident beam is shown in Fig. 3, together with a PuO₂ reference sample measured in the same geometry. A shift in the peak position of the sample compared to PuO₂ is clearly visible, indicating a higher oxidation state than the starting material of the reaction. To the best of our knowledge, no Pu(VI) M₅ plutonate spectrum of a solid state sample has been reported before; compared to aqueous plutonyl species, the peak reported here for Ba_2.875PuO_5.875 starts at the same energy, but the spectral feature labelled A is a bit broader³⁶. The energy shift between A and B spectral features is with almost 4 eV similar to aqueous species. The Pu M₅-edge and L₃-edge spectra both indicate a pure Pu(VI) character for Ba_2.875PuO_5.875, supporting the first scenario formulated in the introduction (vide supra). The herein reported material should thus be understood as a stoichiometric compound Ba_2.875PuO_5.875 or as an end member on the BaO-An(VI)O₃ axis. If the actual stoichiometry would be a member of the line BaAnO₃-Ba₃AnO₆ in Fig. 1, like in scenario 2, the true compound would be ${{{\rm{Ba}}}}_{2}({{{\rm{Pu}}}}_{0.0625}^{4+},{{{\rm{Pu}}}}_{0.9375}^{6+},{{{\rm{Ba}}}}_{0.875}){{{\rm{O}}}}_{5.8125}$ or ${{{\rm{Ba}}}}_{2}({{{\rm{Pu}}}}_{0.125}^{5+},{{{\rm{Pu}}}}_{0.875}^{6+},{{{\rm{Ba}}}}_{0.875}){{{\rm{O}}}}_{5.8125}$, meaning 6.25% Pu(IV) or 12.5% Pu(V) in the crystal structure instead of Pu(VI) only. The HR-XANES at the M₅-edge excludes scenario 2, as mixed oxidation states of over 5% should be clearly discernible. As scenario 3 includes scenario 1, it can neither be excluded nor confirmed and further analysis of the Ba/Pu ratio has to be undertaken.

Fig. 3: Pu M₅-edge spectrum of Ba_2.875PuO_5.875.

The recorded HR-XANES spectrum is compared to the PuO₂ spectrum measured in the same geometry. Both spectra are measured at the ACT station of the CAT-ACT beamline, KIT Light Source.

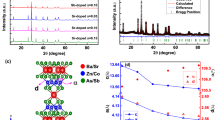
The X-ray diffraction pattern obtained after the last heat treatment at 1273 K of synthesis 1 is shown in Fig. S.1. The split main diffraction peak and the presence of multiple other minor peaks indicates that the cubic symmetry reported by Keller for Ba₃PuO₆¹⁴, will not be able to explain the diffraction pattern found in this work. Gens et al.²² reported a table with visually estimated relative intensities on a scale from 1 to 10, meaning all peaks with a relative intensity higher than 5% in our work should be compared. The early models proposed by Keller¹⁴ and Gens et al.²² consisted in a cubic cell corresponding to a 32-fold superstructure of the perovskite, but the latter authors mentioned peaks that cannot be indexed by this model. In spite of slight discrepancies in Bragg position and intensity ascribable to the experimental conditions (Fig. S.2 in Supplementary Note 1), these peaks were also observed in the present work, along with some extra peaks. Given all reagents reacted to a product that is stable in the temperature window 1000–1270 K, it can be concluded that a pure product was formed that is the same or close to the material Gens et al. obtained. However, in-depth structural characterisation of the material is required to explain all peaks in the obtained diffraction pattern. As mentioned in the introduction, the crystal structure of Ba₃UO₆ initially proposed to be cubic was later assigned lower symmetry. As a starting point to elucidate the crystal structure of the material obtained in this work, it was found, however, that all peaks could be matched using the tetragonal model of Treiber et al.¹⁸ for BaO-deficient Ba₃UO₆ in space group I4/mmm (139). Compared to the archetype perovskite structure ABO₃ in Kröger-Vink notation, this model can be written as $({{{\rm{Ba}}}}_{{{\rm{A}}}}^{{{\rm{x}}}})({{{\rm{Pu}}}}_{{{\rm{B}}}\,8/16}^{{{\boldsymbol{\cdot }}}{{\boldsymbol{\cdot }}}}\,{{{\rm{Ba}}}}_{{{\rm{B}}}\,7/16}^{{\prime}{\prime}}\,{{{\rm{Va}}}}_{{{\rm{B}}}\,1/16}^{{{\prime}{\prime}} {{\prime}{\prime}} })({{{\rm{O}}}}_{{{\rm{O}}}\,47/16}^{{{\rm{x}}}}\,{{{\rm{Va}}}}_{{{\rm{O}}}\,1/16}^{{{\boldsymbol{\cdot }}}{{\boldsymbol{\cdot }}}{}})$. In this model, the cation vacancies (Va) are located in the ${{{\rm{Ba}}}}_{{{\rm{B}}}}^{{\prime}{\prime}}$-sublattice, while the anion vacancies are statistically distributed over the O_O sites. The Ba4 atoms shifted position by 0.55 Å towards the holes, while the U2 and U3 atoms moved respectively 0.17 and 0.26 Å in the direction of the holes¹⁸. Cell parameters for the obtained Pu-material could be successfully derived by a LeBail fit using the U-model in space group I4/mmm, but an initial Rietveld attempt to refine all atomic distances resulted in unrealistic bond distances and, in particular, the low weight of the oxygen atoms compared to Pu and Ba resulted in high uncertainty on their positions. The model by Treiber et al. poses two problems that need clarification. First, the Ba:Pu ratio does not match our weighed target stoichiometry. Second, no discrimination between unit cells with the same reflection conditions was made using the LeBail fit. The absence of reflection conditions matches with the archetype space group I4/mmm, but also with numerous hemihedral tetragonal groups. Group-subgroup relationships via octahedral tilting were analysed for ordered double perovskites by Howard, Kennedy and Woodward in 2003³⁷. In their Fig. 1, the only space group next to I4/mmm is I4/m, in which the loss of the vertical mirrors is due to geared rotations of the corner-connected octahedra along the four-fold axes. The resulting bending of the M-O-M linkages in the (001) planes is correlated to the inter-cations distances. Other types of group-subgroup relationships were found, but none strictly cover the current structure type^38,39,40.

XRD data were collected up to 1473 K with the aim to get more insight in possible phase transitions and the thermal expansion of the material. In Fig. 4, the shift of the main diffraction peak ((224) reflection) at increasing temperature is shown. Starting at 298 K, the supra described pattern was found. The peak at 28.7° 2θ shifted to lower angle upon heating to 673 K. At higher temperatures, the relative intensities of the left and right peak change, up to 1373 K. At 1373 K, the rise of a peak at 28.3° 2θ was observed, which resulted in a single, more intense peak at 1473 K. After cooling, it was found that the structure changed irreversibly, as only a single intense peak at 28.7° 2θ was visible. This means that there are at least two phase transitions in the studied temperature window; however, the diffraction data quality does not allow for full elucidation of the crystal pattern, because many low-intensity peaks are not observed with the current signal-to-noise ratio. The group-theoretical considerations explain the possible phase transition pathway, however. As explained, the diffraction pattern obtained at room temperature after heating till 1270 K can be indexed in the space groups I4/m and I4/mmm. For the double perovskite Sr₂CuWO₆, the structure was found to evolve as:⁴¹

$$I4/m {\longrightarrow}^{873\,{{\rm{K}}}}_{{{{\mathrm{continuous}}}}} I4/mmm {\longrightarrow}^{1173\,{{\rm{K}}}}_{{{\rm{first}}}\,{{\rm{order}}}} \, Fm{\bar{3}}m$$

(1)

Fig. 4: Shift of the main diffraction peak of Ba_2.875PuO_5.875.

The material is from synthesis 1 after 1200 K and is measured at various increasing temperatures; the measurement after the heating rate (298 K final) is shown as well. The different line-styles are a guide to the eye to the phase transitions proposed in the main text.

The first transition means a change from a space group that allows for both deformations and rotations of the octahedra (I4/m) to a space group that allows for only deformations of the octahedra (I4/mmm) and it should be a continuous, reversible, second order transition. Symmetry breaking can lower the energy of the electronic state, usually with an odd number of electrons in degenerate states as in the cited example of Sr₂CuWO₆ with Cu²⁺ in a d⁹-system. The Pu⁶⁺ electron configuration of [Rn]5f² is interpreted as a non-degenerate singlet ground state based on magnetic susceptibility measurements (vide infra), so the mechanism is not driven electronically in the current case. The second transition seems a transition to the ideal cubic perovskite structure, although the present data does not allow for full assignment.

Although we propose a slightly different stoichiometry, it can be hypothesised with caution that the cubic crystal structure by Keller may correspond to our material obtained after heat treatment at 1423 K or higher, so the material has passed an irreversible phase transition temperature, as opposed to Gens et al.²² and the initial material obtained in the current work, which were both obtained at lower temperatures. In addition to this, Keller makes the general statement that after the end of reaction, the samples were quenched¹⁴. Thus, high-temperature X-ray diffraction hints at the assignment of space group I4/m to the room-temperature crystal structure of Ba_2.875PuO_5.875 and allows to determine the cell parameters of a rather big cell. Smaller cell parameters seem not to be possible because the peaks in between 20 and 30° 2θ have odd Miller indices.

The following model for the room temperature crystal structure of Ba_2.875PuO_5.875 is developed: The crystal structure can be thought of as an array of Pu and Ba1, Ba2 and Ba3 atoms occupying the centres of 15/16th of the corner-connected oxygen octahedra that build a ReO₃-like structure, while Ba4 and Ba5 occupy the so-formed 12-oxygen polyhedra, thus building a perovskite-related structure with structural formula (Pu_1/2Ba_7/16Va_1/16)BaO_47/16. The tetragonal symmetry is subject to the presence of four-fold axes, several of which have Pu and Ba atoms. Following Howard and Carpenter⁴⁰, the only tetragonal subgroup of the I4/mmm archetype form compatible with the preservation of these axes is I4/m (Table 2), in which the . m. and . . m mirrors in particular would disappear, thus allowing the PuO₆ octahedra to tilt around the [001] direction. This distortion could be evidenced by localising the oxygen equatorial corners, but the low atomic mass of these atoms compared to plutonium and barium does not allow to observe them from the present XRD data; in other words, no tilt can be evidenced. On the opposite, heavy plutonium (Z = 94) and barium (Z = 56) can be located far more precisely, but most of them occupy fixed positions in both space groups, which makes them insensitive to the possible distortion (Table 2). The only relevant markers appeared to be Ba4, Ba5 and Pu3, which could shift from their ideal . m. or . . m mirror position in the I4/m symmetry. The crystal structure was therefore refined in the latter space group, except for the oxygen atoms, which were fixed on the ideal positions defined by Treiber et al.¹⁸. The diffraction patterns of the materials obtained in synthesis 1 at 1273 K and in synthesis 2 at 1323 K were used and the refinement of the latter is shown in Fig. 5, while the former is shown in the Supplementary Note 1. Cell parameters are given in Table 1. The cell volumes between the syntheses differ less than 1%. The quality of the fit is moderate because of the signal-to-noise ratio that did not allow to observe significant reflections beyond 2θ ≈ 90^o. Solving the structure, in particular, the determination of the space group, was made difficult by several factors linked to the nature of the sample. On the one hand, the very small amount of material, the unusual geometry and the resin-embedded sample resulted in somewhat imprecise XRD data, with regard to the usual data collection standards. On the other hand, the overwhelming presence of heavy barium and very heavy plutonium atoms resulted in an exceedingly high contrast with lighter oxygen atoms, that hampered the determination of their position. This proved particularly critical when it came to deciding whether the oxygen atoms were located or not on the special positions corresponding to the vertical mirrors of the I4/mmm space group. For these reasons, the oxygen atoms were assigned to these fixed ‘ideal’ positions. According to the estimated standard uncertainties on atomic positions, the Ba and Pu atoms were rather correctly located this way, but secondary parameters like their atomic displacement parameters obviously suffered of this non-ideal procedure. The refined atomic positions for the Ba and Pu ions are given in Table 2; all the standard uncertainties given by FullProf were multiplied by Bérar and Lelann’s statistic factor for the sake of realism⁴². The difference between I4/mmm and I4/m for the Ba3, Ba4 and Pu3 atoms is small but measurable. Pu3 is almost on its ideal position (y ≈ x), while the difference for Ba4 and Ba5 (y − x − 0.25) is more significant. Typical metal-metal bond distances are given in Table 3, where they are compared with the EXAFS refinement. Although these results tend to support the I4/m symmetry for the room-temperature form, this hypothesis cannot be considered a certainty due to the relatively high standard deviations in regard to the measured atoms shifts. Visualisations of the crystal structure are shown in Fig. 6.

Fig. 5: XRD pattern of Ba_2.875PuO_5.875 with profile refinement.

Experimental (Y_obs, in red) and calculated (Y_calc, in black) powder XRD patterns of Ba_2.875PuO_5.875 at ambient temperature. The sample is taken from the material obtained from synthesis 2 after 1323 K. Measurement at λ = Cu K_α1. The angular positions of Bragg reflections are shown in green. The difference between calculated and experimental intensities Y_obs−Y_calc is shown in blue for the Rietveld refinement in space group I4/m. The uncertainties on optimised cell parameters and atomic positions are given in Tables 1 and 2.

Table 1 Cell parameters obtained at ambient temperature for synthesis 1 and synthesis 2

Table 2 Refined atomic positions, Wyckoff symbol and local symmetry of the heavy atoms in the I4/mmm and I4/m space groups

Table 3 Bond lengths and Debye-Waller Factors obtained from the fit to the EXAFS data

Fig. 6: Crystal structure of Ba_2.875PuO_5.875 obtained after refinement in space group I4/m.

Left, from top to bottom: views along the a, b, and c axes. Right, from top to bottom: visualisation of the 100, 010 and 001 faces. Ba4 and Ba5 are the atoms shifted with respect to space group with extra symmetry elements I4/mmm. The visualisations are made using VESTA⁶⁷.

This model gives a rather good fit to the experimentally measured diffraction pattern, but the Ba:Pu ratio does not correspond to the weighed amounts of material and proper composition and molar mass are important for the (thermo)physical properties. Therefore, it was attempted to refine the model in such a way that the B-site of the perovskite contains vacancies, but the Ba:Pu ratio remains 3:1 overall, i.e. change the occupancy factors to ${{{\rm{Ba}}}}_{2}({{{\rm{Ba}}}}_{\frac{29}{32}}\,{{{\rm{Pu}}}}_{\frac{31}{32}}\,{{{\rm{Va}}}}_{\frac{4}{32}}){{{\rm{O}}}}_{{5}{\frac{26}{32}}}$ instead of ${{{\rm{Ba}}}}_{2}({{{\rm{Ba}}}}_{\frac{28}{32}}\,{{{\rm{Pu}}}}_{\frac{32}{32}}\,{{{\rm{Va}}}}_{\frac{4}{32}}){{{\rm{O}}}}_{{5}{\frac{28}{32}}}$ as refined by Treiber et al. for the U-analogue. Since the Ba and Pu atoms are both heavy but still differ a lot in atomic number, this effect may be measurable by refining the occupancy factors of the respective lattice positions. Technically, this means refining the 3 Pu sites with a Pu_1−xBa_x mix. This attempt did not result in an improvement of the fit. Moreover, the empty Ba-site was tested for excess electron density but it turned out to be completely empty.

BaO-deficiency is thus justifiable by the XRD pattern, and a number of possible explanations for the concomitant BaO-loss during the synthesis have been suggested. First of all, Keller wrote that Ba₃PuO₆ is stable under Ar until 1673 K, above which temperature oxygen loss takes place with formation of BaPuO₃. In our case, the material does not even reach this temperature. The vaporisation behaviour of the related compound BaPuO₃ was studied by Nakajima et al.⁴³, who observed Ba(g) and BaO(g) vapour species. At 1673 K, the total vapour pressure is still lower than 1 Pa. Interaction with the alumina crucible is highly unlikely, even if the phase diagram gives possible Al₂O₃-BaO phases⁴⁴, because the crucibles are high-fired ceramic materials. Thirdly, the formation of an amorphous phase was considered but judged unlikely. Next to this, the Ba:Pu ratio was analysed by Gens et al. during their synthesis and they found a 3:1 ratio²². Recently, in the synthesis of BaPuO₃ and SrPuO₃, stoichiometric excesses of 7.5 and 10% of the respective earth alkali oxalates were added to obtain a stoichiometric compound⁴. Similarly, an excess BaCO₃ was added during the synthesis of BaThO₃¹³. Gens et al. write about slow heating to avoid Ba-losses, which they seem to confirm with their elemental analysis²². A close look at the crystal structure proposed in this work for Ba_2.875PuO_5.875 reveals that the large Ba-atoms move towards the empty Ba-sites. Therefore, we conjecture that the empty Ba-sites are necessary to allow for a stable structure and the material obtained in this work for both syntheses should be treated as a stoichiometric compound with a Ba:Pu ratio of 2.875:1. From electrostatic considerations, disappearance of 1 Ba is accompanied by 1 oxygen, for which statistical distribution should be assumed with the current data.

As Pu-O distances are inherently difficult to study using XRD, the EXAFS signal at the Pu L₃-edge was analysed to obtain insights into the local Pu environment. The EXAFS and Fourier-transformed spectra at the Pu L₃-edge are shown in Fig. 7, together with the fit to the data. Bond lengths are reported in Table 3 and compared to refined interatomic distances from XRD if possible. The scattering paths for Pu1, Pu2 and Pu3 contribute 25%, 25% and 50%, respectively, to the total EXAFS signal. Only an average Pu-O distance was refined in each case for the first coordination shell, given the complexity of the structure, the lack of information from XRD on the oxygen positions, and the expected similar distances. The Pu sites are in all cases six-fold coordinated. A common Debye-Waller factor was imposed for all oxygen atoms. This resulted in a fit with indistinguishable distances for Pu1-O and Pu3-O at 2.01(1) A, and a Pu2-O distance of 2.4(3) Å. Using Shannon’s ionic radii, the Pu-O distance is expected to be about 2.11 Å⁴⁵, which means that the Pu-O distances obtained for Ba_2.875PuO_5.875 are in a physically realistic range. In addition, Pu-Ba distances in the second coordination shell could also be captured with the fit. Here again, some simplifications were made to account for indistinguishable distances. Pu1 is surrounded by 14 Ba atoms: 2 Ba2 + 4 Ba3 at a distance of 4.51(9) Å, 4 Ba4 at 3.9(5) Å and 4 Ba5 at 3.43(9) Å. Similarly, for Pu2 the Ba4 and Ba5 distances were merged, yielding 3.8320(8) Å, while the Pu1-Ba3 distance equals 4.28(15) Å. The distances Pu3-Ba3, Pu3-Ba4 and Pu3-Ba5 equal 3.9(5), 3.531(12) and 3.67(5) Å, respectively. Comparison between distances obtained via XRD data refinement and EXAFS data refinement yields the same distances within error in most cases. Combining the determination of the average Pu oxidation state with the Ba/Pu ratio locates the obtained material thus on a unique position in Fig. 1 and allows to further study its physical properties. In the remainder of the article, the stoichiometry and molar mass of net Ba_2.875PuO_5.875 is used for all analyses.

Fig. 7: EXAFS spectrum of Ba_2.875PuO_5.875.

The black dots show the extracted signals, the red line the fitted spectrum. For details of the fitiing see the section Methods.

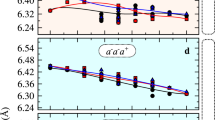
The high-temperature XRD was further analysed in order to obtain the thermal expansion coefficient of the material. Because of the large unit cell and the two phase transitions that seem to occur, it was not trivial to establish the thermal expansion coefficients. The data from room temperature up to 673 K was refined using space group I4/m, while the data up to 1273 K was refined using I4/mmm. The pattern at 1373 K was multiphase. The pattern at 1473 K was indexable using DICVOL as cubic with cell parameter 4.4327 Å, with 1 peak unaccounted for (2θ = 27.8°)⁴⁶. The pattern obtained after cooling was not indexable as cubic, but as tetragonal with cell parameters a = 4.3865 Å and c = 17.6094 Å. The obtained volume as function of temperature and relative expansion of the a- and c-axes are shown in Fig. 8. Towards the first phase transition, the volume increases non-linear, mainly caused by the c-axis expansion, while after the phase transition, the axes expand linearly. A single volumetric thermal expansion coefficient of α_V = 7 × 10⁻⁵ K⁻¹ fits the data rather well. This is about twice as high as BaThO₃, BaUO₃, BaZrO₃ and BaCeO₃, with linear thermal expansion values of 11.9 × 10⁻⁶ K⁻¹, 11.01 × 10⁻⁶ K⁻¹, 7.13 × 10⁻⁶ K⁻¹ and 11.2 × 10⁻⁶ K⁻¹, respectively^47,48,49. These values are close to the thermal expansion coefficients of the actinide dioxides⁵⁰, and rather high when compared to uranium-containing double perovskites^51,52. The most interesting comparison is with high-temperature X-ray diffraction on Sr₃UO₆, measured under both oxygen-rich and reducing atmospheres⁵³. This compound has a volumetric thermal expansion of 33 × 10⁻⁶ K⁻¹, but seems also able to lose oxygen under inert or reducing conditions. The high thermal expansion of Ba_2.875PuO_5.875 compared to BaMO₃ can be explained by the unusual high amount of Ba for a perovskite: half of the medium-size, high-charge M cations are replaced by big, low-charge Ba-ions that make weaker bonds to oxygen and are more prone to thermal expansion. The anisotropic expansion hints at antiferrodistorsive behaviour. A tentative Landau model with the c-axis distortion as order parameter with T_c = 758 K is proposed (Supplementary Note 3 and Fig. S.5). This mechanism supposed the Ba4 and Ba5 atoms to align from their position in I4/m to the I4/mmm form. The twisted c-directed chains straighten, therefore expanding faster than the other axes. Beyond the transition, the chains should be straight along the 3 axes, so the expansion becomes similar.

Fig. 8: The thermal expansion of Ba_2.875PuO_5.875 as measured in this work.

See for explanation of the fits in the main text. Inset: Relative expansion of the a- and c-axes with temperature. The vertical line in both figures indicates the tentative first transition I4/m → I4/mmm. Trend 1 and Trend 2 are a guide for the eye. If not visible, the standard deviations are smaller than the data points.

The low-temperature heat capacity of Ba_2.875PuO_5.875 obtained using PPMS is shown in Fig. 9. No anomalies were observed in the measured temperature window, and the C_p(T) increases with temperature, yielding a value slightly above the classical Dulong-Petit value for C_v at ambient temperature. There is a small artefact between 47 and 61 K that is ascribed to the machine; these data points are excluded in all fits and calculations. The commonly used strategy to compare the heat capacity of complex oxides to the sum of simple oxides (Neumann-Kopp) cannot be used directly, since PuO₃ does not exist. The heat capacity was fit to a polynomial from the lowest measured temperature up to 14 K and to a combination of one Debye and three Einstein fits in the temperature range 14–270 K. The difference between the fit and the experimental data is shown in the inset in Fig. 9. Based on these fits, the heat capacity at 298.15 K C_p = (251 ± 8) J⋅K⁻¹⋅mol⁻¹, and the standard entropy ${S}_{m}^{0}=(318\pm 8)\,{{\rm{J}}}\cdot {{{\rm{K}}}}^{-1}{{{\rm{mol}}}}^{-1}$ (see Fig. 10) are derived. Heat capacity data at high temperature for Ba_2.875PuO_5.875 have not been reported. Data for similar alkaline-earth actinide oxide compounds are limited to Ba₃UO₆ and Ba_2.875UO_5.875. Dash and Singh reported the low-temperature heat capacity of these two compounds from 127 to 303 K measured by DSC and joined this to high-temperature heat capacity⁵⁴. As is shown in Figure S.6 in Supplementary Note 4, the heat capacities of Ba₃UO₆ and Ba_2.875PuO_5.875 are almost equal at 125 K, but the reported heat capacity of Ba₃UO₆ flattens faster and reaches a point close to the Neumann-Kopp value for Ba₃UO₆ of 222.85 J⋅K⁻¹⋅mol⁻¹ based on BaO and γ-UO₃^55,56.

Fig. 9: Heat capacity of Ba_2.875PuO_5.875.

The heat capacity as measured in this work is shown and fitted to a polynomial fit (fit 1) and a combined Debye-Einstein fit (fit 2) with comparison to the classical Dulong-Petit limit. See for explanation of the fits the main text. The error bar represents a 3% error on the heat capacity as explained in the main text. Inset: Relative difference between the experimental heat capacity data and the polynomial and combined Debye–Einstein fit.

Fig. 10: Heat capacity of Ba_2.875PuO_5.875 as plotted in C_p/T vs. T.

The shaded areas represent the contributions to the standard entropy as calculated using the two fits in their respective domains. See main text for explanation of the fits.

In Fig. 11 the heat capacity close to 0 K is shown as C_p/T versus T². In case of a perfectly insulating crystalline material, the signal should intersect the origin, i.e. γ = 0. For this freshly annealed Ba_2.875PuO_5.875, a very minor excess towards lower temperature is found and a linear fit gives 4.2 mJ⋅K⁻¹⋅mol⁻¹, which may be attributed to disorder, the origin of which are structural vacancies of the oxygen sublattice or Frenkel pairs created by radioactive decay of the actinides (²³⁹Pu, ²⁴¹Am)^57,58. As can be seen in the Figure, however, with an applied field of 14 T the heat capacity shows a very pronounced upturn. The fact that the addendum curve was only collected at 0 T cannot account for such a pronounced effect, indicating some physical explanation should be given for this upturn towards 5 K. This upturn cannot be explained by disorder due to radiation damage, as there is no significant difference between a measurement after a few days after annealing and a week after annealing with no applied field, ruling out this as the main source. The low-temperature upturn may be attributed to a maximum below 5 K at 0 T, shifted to slightly higher temperatures at 14 T. This is reminiscent of behaviour of the Schottky-anomaly in CePO₄ under magnetic field⁵⁹ and atypical for a magnetic transition⁶⁰. If a Schottky anomaly is assumed in Ba_2.875PuO_5.875, an herein small, unquantified entropy term corresponding to a Schottky anomaly should be added to the supra calculated standard entropy at 298.15 K. This small entropy term depends on the degeneracy of the energy split, most probably of the ³H₄ ground state of the [Rn]5f² ion.

Fig. 11: Heat capacity of Ba_2.875PuO_5.875 as plotted in C_p/T vs. T² in the low-temperature limit.

The error bar is determined based on the 3% error on the heat capacity as explained in the main text.

The temperature dependence of the magnetic susceptibility χ_measured − χ_diagmagnetic of Ba_2.875PuO_5.875 is shown in Fig. 12, while a plot of 1/χ versus temperature is shown in Fig. 13. The magnetisation curve is shown in the inset in Fig. 12. The magnetisation curve was obtained by increasing the field up to 70 kOe, decreasing to −70 kOe and increasing to 0 kOe. The curves overlap. The observed magnetic behaviour classifies the studied material best as paramagnetic. The formal oxidation state of Pu(VI) translates to an electron configuration of [Rn]5f², and with a even number of electrons and singlet ground state, there are no unpaired electrons and therefore there is no reason to assume local magnetic moments and apply the Curie–Weiss law. Nevertheless, as the shape of the susceptibility after subtraction of the diamagnetic contribution is similar in shape to Curie-Weiss behaviour, the data obtained at 70 kOe was fitted to:

$${\chi }_{M}=\frac{C}{T}+{\chi }_{0}$$

(2)

Fig. 12: Magnetic susceptibility of Ba_2.875PuO_5.875.

The magnetic susceptibility is acquired at various applied magnetic field strengths. Inset: Magnetisation curve of Ba_2.875PuO_5.875 collected at 2 K and at 5 K.

Fig. 13: Inverse magnetic susceptibility of Ba_2.875PuO_5.875.

The magnetic susceptibility is acquired at various applied magnetic field strengths. The data obtained at 70 kOe was fitted; see for explanation the main text. Fit for Ba₃NpO₆ from Hinatsu and Edelstein⁶⁴.

The fitting parameters are C = 0.0090 emu mol⁻¹ K⁻¹ and a temperature-independent contribution χ₀ = 121 × 10⁻⁶ emu mol⁻¹. The uncertainty on χ₀ should include the estimation of the estimated χ_dia as described supra. As far as the current authors are aware, no full temperature-dependent magnetic susceptibility curve of a Pu-based 5f² system has been reported, making good comparison difficult^61,62. However, 5f²-systems based on U have been reported⁶³. Moreover, Hinatsu and Edelstein discuss the magnetic susceptibility of (impurity) Np⁵⁺ in their study into Ba₃NpO₆⁶⁴. They write that if a 5f² ion is octahedrally coordinated by six oxygens, its susceptibility shows a large temperature independent paramagnetism over a wide temperature range. To give rise to magnetic ordering in oxide actinide system, the distance An-An should be less than 450 pm, as is summarised for [Rn]5f¹ and [Rn]5f³ configurations by Keller⁵. Therefore, Ba₃NpO₆ also has no magnetic ordering because of the too long Np-Np distance. Theoretically, the Pu-Pu distance in the Ba_2.875PuO_5.875 host could be minimised by a non-standard ordering of Pu in octahedral sites, forming chains instead of being in a rock-salt fashion with Ba. Since the distance for fully oxidised Pu(VI) would already result in too long Pu-Pu distances, the magnetic behaviour cannot be explained by diluted Pu(V) contributions ([Rn]5f³) in the crystal structure.

Conclusions

Proper study of Ba-An-O perovskite related phases needs to account for the average formal An oxidation state and the Ba/An ratio. In the attempt to synthesise Ba₃PuO₆, a perovskite-related phase with the actual composition Ba_2.875PuO_5.875 was found. This alkaline-earth plutonium containing perovskite-related phase Ba_2.875PuO_5.875 has been synthesised for the first time using solid state synthesis starting from BaCO₃ and PuO₂. X-ray Absorption Spectroscopy at the Pu M₅ and L₃ edges showed Pu to be present as Pu(VI). The Ba_2.875PuO_5.875 spectra were like ‘-ate’ species and agree well with FDMNES calculations. The Ba/Pu ratio was indirectly deduced from the analysis of the XRD pattern which was best modelled by introducing BaO deficiency. The positions of the heavy metal atoms Ba and Pu in the crystal structure were refined in space group I4/m instead of I4/mmm proposed for the U-analogue, yielding an overall satisfactory model with ordered empty Ba-sites. The change of the space group with temperature was proposed based on high-temperature X-Ray Diffraction measurements. The EXAFS data are in line with the FDMNES calculations and the local Pu-environments derived from crystallography were found to yield a good model to the EXAFS data. The low-temperature heat capacity was measured, yielding the heat capacity and standard entropy at 298.15 K. Moreover, the magnetic susceptibility was measured, which is the first reported full temperature-dependent curve for a [Rn]5f² Pu-based compound.

Methods

Synthesis

218.7 mg BaCO₃ (Merck, 99.98% trace metal basis) and 100 mg PuO₂ (see Supplementary Methods in SI) were weighed and thoroughly mixed to obtain Ba_3.0Pu_1.0O₆. The mixture was subsequently heated in simulated air in a furnace at 900, 1000, 1100 and 1200 K for 48 h at each step. After each thermal treatment, XRD analysis was performed. After the thermal treatment at 1200 K, part of the product was separated for an additional thermal treatment at 1273 K for another 48 h. This synthesis will be referred to as synthesis 1. All spectroscopic and physical analyses have been performed on this batch.

38.2 mg of the reaction mixture of 3.0 BaCO₃ and 1.0 PuO₂ in an open alumina crucible was heated in simulated air from room temperature to 1773 K using a Netzsch STA 449C thermogravimetric analysis apparatus to study the thermal behaviour using heating and cooling rates of 10 K/min. Pt-PtRh (10%) was used as thermocouple for temperature control. The experimental error is less than 1% on temperature and mass reading. See Supplementary Note 2 and Figs. S.3 and S.4 for analysis.

A second mixture was made using 39.6 mg BaCO₃ and 18.6 mg PuO₂, which corresponds to Ba_2.9Pu_1.0O₆. This mixture was thermally treated in simulated air at 1273 K for 48 h and at 1323 K for 24 h. After each step, XRD analysis was performed. This second synthesis will be referred to as synthesis 2; material from this synthesis was only used for room-temperature X-ray diffraction.

X-ray diffraction

Powder XRD at ambient temperature was measured using a Bruker D8 X-ray diffractometer mounted in the Bragg-Brentano configuration with the Cu K_α1 radiation (40 kV, 40 mA, Ge(111) monochromator). About 10 mg of the specimen was immobilised in bi-component epoxy resin on a sample holder to prevent spreading of radioactive powder. Data were collected from 10 to 120° 2θ with a step size of 0.013° 2θ using a LynxEye detector for up to 24 h per measurement. A second Bruker D8 X-ray diffractometer was used to collect data at elevated temperatures. The sample was dispersed on the surface of a Pt heating strip using a few drops of alcohol in a N₂-filled glove box and measured every 100 K under vacuum (10⁻³ bar). Analysis of the diffraction data was performed using the FullProf package⁶⁵ using the profile refinement method developed by Loopstra, Van Laar and Rietveld^27,66. Visualisations of the crystal structures were made using VESTA⁶⁷.

X-ray absorption spectroscopy

About 1 mg sample was mounted with bicomponent glue on a sample holder and doubly encapsulated with 12 μm Kapton. X-ray Absorption Near-Edge Structure (XANES) and Extended X-ray Absorption Fine Structure (EXAFS) spectroscopy at the Pu L₃-edge were measured at the INE-Beamline⁶⁸ and High-energy Resolution X-ray Absorption Near-Edge Structure (HR-XANES, equivalent to HERFD-XANES) Spectroscopy at the Pu M₅-edge was performed at the ACT station of the CAT-ACT beamline of the KIT Light Source in Karlsruhe, Germany^69,70. The storage ring operates at 2.5 GeV and has a maximum stored current of 170 mA.

The Pu L₃ edge (18,057 eV) was measured in both transmission and fluorescence mode. For calibration, the K-edge of a metallic Zr foil (17,998 eV) was measured between the second and third ionisation chamber. Ge(422) crystals are used in the double-crystal monochromator (DCM). The X-ray beam is collimated and focussed to a spot size of 500 μm × 500 μm by means of two Rh-coated mirrors, respectively located before (cylindrically bent) and after (toroidal) the DCM. EXAFS spectra were collected at room temperature in fluorescence mode, using a combination of two silicon drift detectors, viz. a Vortex- ME4 (4 elements) and a Vortex-60EX (1 element, Hitachi/SIINT). The transmission data was exploited for XANES and the fluorescence signal was used for EXAFS.

The XANES-region of the spectrum was analysed using the ATHENA software and the inflection point of the edge was taken as the threshold position E₀⁷¹. The white line position is the maximum of the spectrum. The EXAFS data were collected up to 16 Å⁻¹ and Fourier-transformed using the Hanning window over the k-range 3.5–14.5 Å⁻¹ (dk = 2). The ARTEMIS software suite was used to fit the data in k²-space⁷¹. The ab initio code FEFF8.40 was used to calculate the phases and amplitudes for the interatomic scattering paths. The shift in the threshold energy (ΔE₀) was varied as a global parameter. The bond distances were optimised, but the coordination numbers were kept constant. The amplitude for all paths ${S}_{0}^{2}$ was fixed to 0.9. A single value of ΔE₀ for all scattering paths was allowed to vary, while the Debye-Waller parameters σ² were allowed to vary as well. The distance resolution ΔR, i.e. the ability to differentiate neighbouring atom shells in the EXAFS spectrum, is given by ΔR = π/(2 ⋅ Δk) where Δk is the k-range of the spectra, resulting in ΔR = 0.14 Å for the present k-range. This means that distances with differences shorter than 0.14 Å cannot be fitted independently. The distances found in the XRD model as listed in Table 3 for synthesis 2, which was preferred from XRD perspective over synthesis 1, were used as starting parameters and further optimised. Independent Pu1-O, Pu2-O and Pu3-O scattering pathways were used in the EXAFS fitting procedure, to reflect the fact that three different crystal positions and environments exist in the compound under study.

Pu L₃-edge XANES spectra have been calculated with the FDMNES code using the herein proposed crystal structure and earlier published BaPuO₃^72,73,74. The simulations were performed with a cluster radius of 6 Å using Greens function, relativistic effect and spin-orbit coupling. The simulated spectra were normalised and shifted by the Pu L₃ edge (18,057 eV) for comparison with the experimental spectrum.

HR-XANES at the Pu M₅ edge (3775 eV) was collected at the ACT-station of the CAT-ACT beamline, using the Pu M_α1 emission (3351 eV) with a Si(220) analyser crystal of 0.5m bending radius. Si collimating and focussing mirrors and Si(111) DCM crystals were used and the size of the beamspot was decreased to 500 μm × 500 μm using slits to increase the energy resolution of the collected spectra. The analyser crystal was positioned at 142° scattering angle relative to the incident beam. The spectrophotometer was placed in a He-flushed glovebox to minimise tender X-ray absorption in the beam path^69,70.

Low-temperature heat capacity

The material obtained after heat treatment at 1200 K in synthesis 1 was pressed in a pellet and given another heat treatment at 1270 K to have a freshly annealed specimen. A piece of 13.67(10) mg was encapsulated in 4.99(10) mg Stycast⁷⁵. The low temperature heat capacity was measured using the Physical Property Measurement System (PPMS) from Quantum Design from 270 K down to 5 K with no applied magnetic field. 1 week after the annealing, an additional measurement below 50 K was done at 0 T and 14 T. The addendum and Stycast 2850 FT contribution were subtracted from the total heat capacity, yielding the sample heat capacity. The uncertainty on the heat capacity was estimated to be 3%, and the uncertainty on the standard entropy follows from the 3 % uncertainty on the determined heat capacity^76,77,78.

Magnetic susceptibility

A 22.77(10) mg piece freshly annealed at 1270 K was enclosed in a blank tube. The magnetic susceptibility was measured on a Quantum Design MPMS-3 instrument by the SQUID technique. DC magnetisation M(T) was achieved from 2 to 320 K under constant magnetic field H of 10, 30, 50 and 70 kOe. Moreover, the magnetisation M was measured as function of applied field H from -70 to 70 kOe. The magnetic contribution of the blank was fitted to a curve. The magnetic susceptibility was obtained by subtracting the susceptibility of the blank from the total measured susceptibility. To correct for the diamagnetic contribution, values for Ba²⁺, U⁶⁺ and O²⁻ ions were taken from Bain and Berry, yielding −170.5 × 10⁻⁶ emu mol⁻¹⁷⁹. The value for the U⁶⁺ ion was taken as substitute for the Pu⁶⁺ ion, as we are not aware of any tabulated value for the Pascal constant of Pu⁶⁺.