Introduction

Many industries are actively pursuing or have already implemented automation systems where machines replace humans in labor-intensive tasks for product manufacturing. Just as Henry Ford revolutionized industrial production in the 20th century with the introduction of the assembly line, commonly referred to as Fordism, the concept of fully automated workflows may similarly drive innovation in today’s industrial systems. Organic synthesis, which involves the creation of molecular-scale products, also stands to benefit from automation1,2. Machines can now perform various synthetic operations such as reagent addition3,4, reaction monitoring5, and product purification6,7, thereby reducing or eliminating the need for human intervention. Since organic synthesis is often labor-intensive and requires delicate manipulation, the introduction of machines into the process can significantly enhance both efficiency and reproducibility.

In addition to large-scale chemical manufacturing, automation also holds significant promise for synthetic chemists working in research and development (R&D)8. R&D frequently demands the synthesis of novel compounds with specific functions or biological activities, which requires performing a large number of reactions and optimizing reaction conditions. Automation can greatly accelerate these demanding workflows. In this context, flow reactors9,10 are especially well-suited for automated synthesis because of their inherent compatibility with high-throughput experimentation11. Furthermore, flow systems offer precise control over time-12,13,14, temperature-15,16, and concentration17,18 to perform precisely controlled reactions19,20,21,22,23. In contrast, conventional batch reactors often suffer from variability and limited control, which can reduce reproducibility.

Although automated flow systems can significantly accelerate the execution of reactions, R&D in organic synthetic chemistry remains a time-consuming process. Synthesis represents only one aspect of the workflow. The most time-consuming tasks, such as analyzing reaction products and designing new reaction conditions, still largely depend on human expertise. Automation of analysis and condition design can, in principle, be achieved using autosamplers to perform automatic measurements. For instance, Jamison and Jensen demonstrated a strategy in which inline sampling was coupled with HPLC analysis to optimize reaction conditions by maximizing the peak area of the desired product24. However, chromatographic methods lack immediacy and are therefore not ideally suited for fully exploiting the advantages of flow chemistry. In contrast, spectroscopic techniques such as infrared (IR) spectroscopy allow real-time, inline analysis. This makes them highly attractive for rapid optimization and process monitoring. Jamison and Jensen also performed automatic optimization by minimizing the carbonyl peak intensity using inline IR analysis24. Knight extended the applicability of inline IR analysis to reaction systems lacking distinctive spectral features—an area where traditional peak-based approaches are not easily applicable25. However, their method provided only qualitative insights and could not support accurate yield prediction. Notably, these limitations are not resolved even by incorporating internal standards or calibration curves, as accurate quantification still requires clearly assignable spectral features. In systems such as ours—where peaks are weak, overlapping, or entirely absent—traditional quantification methods are inherently limited. Therefore, an alternative approach is needed to achieve quantitative analysis under these conditions.

In cases where characteristic peaks are absent—or when spectral differences are too subtle for human interpretation—machine learning becomes especially powerful. It offers the potential to extract meaningful patterns from nuanced spectral variations and enable quantitative predictions that would otherwise be inaccessible through conventional analysis. However, machine learning typically requires large, high-quality datasets derived from a wide range of experimentally measured reaction mixtures. This demand poses a substantial experimental burden, especially when the spectral data lack distinct, easily identifiable features. Additionally, existing methods for automated reaction analysis based on repeated inline measurements still require a vast number of experiments to achieve precise yield prediction.

To address this, we propose a streamlined approach in which IR spectra are generated by linearly combining the spectra of the reactants and products to produce “mimicked spectra” that approximate those of actual reaction mixtures. These mimicked spectra serve as effective substitutes for experimentally measured data, enabling the rapid and efficient construction of training datasets without exhaustive experimentation. Using this method, we demonstrate a fully automated system for organic synthesis that integrates real-time inline analysis with a neural network-based predictive model. This system enables closed-loop reaction optimization with minimal experimental burden (Fig. 1).

Fig. 1: Schematic for fully-automated reaction optimization with our strategy for model construction.
figure 1

A schematic illustration of the proposed strategy integrating machine-controlled flow synthesis, machine learning-based analysis, and reaction design.

Full size image

Results and discussion

We began this study using an existing flow system equipped with an inline monitoring unit26 capable of real-time, high-accuracy analysis. Real-time inline analysis, where the reaction solution is continuously analyzed without manual sampling, is widely used to monitor reaction progress27,28. Among the available analytical techniques29, Fourier-transform infrared spectroscopy (FTIR) is one of the most commonly employed because of its speed, sensitivity, and resolution30. Historically, FTIR analysis has been extensively used for the characterization of organic molecules, as it provides valuable information linking specific vibrational frequencies to molecular substructures (e.g., carbonyl groups typically exhibit a strong peak near 1715 cm−1). As a result, changes in reagent consumption or product formation be tracked by monitoring specific peaks in the spectrum. However, this peak-based approach is limited to reactions that involve significant changes in functional groups31,32. Although the fingerprint region of the spectrum, typically from 1500 to 650 cm−1, is unique to each molecule, its complexity often makes it difficult for humans to interpret all of the peaks. Machine learning, when combined with multivariate data analysis, can help address this issue by interpreting complex spectral features. However, building an accurate model still requires a large and diverse training dataset33.

To address this challenge, we focused on the fundamental principles of FTIR spectroscopy. The intensity of each peak in an FTIR spectrum reflects the abundance of the corresponding molecular species. When molecules are mixed, the resulting spectrum can be approximated as a linear combination of the spectra of the individual components. We hypothesized that it would be possible to simulate the spectrum of a reaction mixture by linearly combining the spectra of the materials involved, including the products. This approach would allow for rapid generation of a large training dataset using only a small number of measured spectra34.

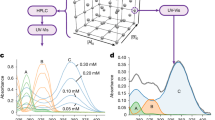
As a model reaction, we selected the Suzuki–Miyaura cross-coupling (SMC) reaction due to its wide applicability in organic synthesis. SMC forms a carbon–carbon bond between the organic groups from a boronic ester and a (pseudo)halide, typically without significant changes in the FTIR spectrum. This is characteristic of many cross-coupling reactions, especially those in diluted conditions35. Indeed, the FTIR spectra of representative reactants, boronic ester 1 (0.049 M) and iodoarene 2 (0.033 M), and product 3 (0.033 M) in THF/MeOH (50/50 volume ratio) showed minimal differences to the naked eye (Fig. 2a). o prepare the training dataset, we first performed FTIR measurements on compounds 1, 2, and 3. Each compound was measured five times, and one measurement was randomly selected for use in linear combination, in order to prevent the model from learning noise patterns. Based on our previous study on flow coupling reactions36, we assumed that using 1.5 equivalents of compound 1 would be optimal for the reaction. Because the reaction system is well-characterized and known to involve few significant side products—particularly as 2 exhibits nearly ideal mass balance—we considered that the reaction mixture could be reasonably represented by a combination of the spectra of 1, 2, and 3. The training dataset was constructed as shown in Fig. 2b. In this dataset, y denotes the virtual percent yield of 3 (cyield), and X represents a one-dimensional data vector corresponding to a simulated spectrum as a linear combination of the FTIR spectra of compounds, reflecting a reaction that would produce 3 at cyield% yield. To account the decomposition of compound 1, a random number “r” was introduced to represent the decomposition rate. By varying cyield and r from 0 to 100 in integer steps, we generated 10,000 (X, y) datasets.

Fig. 2: Preparation of the inline Fourier-transform infrared spectroscopy (FTIR) prediction model.
figure 2

a FTIR spectra of the compounds and solvent. b Preparation of training data. c Model evaluation, where the x-axis represents the experimentally determined percent yield (cyield) of the prepared solution, and the y-axis indicates the predicted percent yield from its FTIR. d Inline FTIR and yield prediction of actual reactions. Gas chromatography (GC) yields were determined using an internal standard.

Full size image

To evaluate the model, test solutions were prepared by dissolving compounds 1, 2, and 3 in arbitrary proportions, similar to the combinations used in Fig. 2b (see Supplementary Information section 2.2 and Table S1 for detail). FTIR measurements were then conducted to determine whether the model could predict the concentration of compound 3 (cyield) based on the spectral data. However, the initial attempt resulted in complete failure (Fig. 2c, left); the model predicted a cyield of approximately 100 for all spectra. We found that applying spectral differentiation significantly improved the prediction accuracy (Fig. 2c, middle). Furthermore, when we limited the spectral analysis to the fingerprint region (699–1692 cm−1) and applied differentiation, the model was able to predict cyield with high accuracy (Fig. 2c, right). These results indicate that restricting the spectral range can enhance the performance of the prediction model, and that using a larger number of data points is not necessarily beneficial. We note that while more complex spectral combination methods could be considered (e.g., weighted or nonlinear combinations), we deliberately selected simple linear combinations to prioritize methodological simplicity and ease of implementation, while still achieving high predictive accuracy. We applied the model to predict the yields of the SMC reaction under various conditions. According to our previous study34, the reaction was carried out in a column reactor packed with silica-supported palladium(0). A solution of 2 (0.033 M), containing 1 (1.5 equivalents) KOH (2 equivalents), was flowed through the column at 70 °C. By varying the flow rate, we generated multiple reaction conditions to evaluate the model’s prediction accuracy (Fig. 2d). This demonstrates that our linear combination approach allows the construction of a model using only the spectra of substrates and products, yet provides accurate yield prediction—a task challenging to achieve through manual interpretation. Importantly, the rapid yield prediction enabled by our model allows seamless integration into real-time, closed-loop optimization frameworks. Because the model requires only inline FTIR measurements and can be trained with synthetic spectra derived from pure compounds, it eliminates the need for extensive experimental screening. This makes it especially well-suited for Bayesian optimization, where each new experimental condition is selected based on predicted performance. The immediacy and accuracy of our predictive framework offer a practical advantage over conventional methods, enabling fast, data-efficient reaction optimization. This efficient analytical framework can accelerate the analysis stage of R&D.

Having established the inline analysis model, we turned our attention to the development of a fully automated reaction optimization system. A schematic overview of the setup is shown in Fig. 3a. A programmable logic controller (PLC) was connected to the pump and the water bath heater to control the flow rate and temperature, respectively. To monitor system stability, the PLC was also connected to a flowmeter, pressure gauge (labeled “gauge” in Fig. 3a), and thermometer. Finally, the PLC was connected to a laptop computer, which controlled and monitored the entire system, including the FTIR unit. A process flowchart is shown in Fig. 3b. Initially, the reaction was carried out under randomly selected conditions from a total of 30 possibilities (five flow rates and six temperatures), defined as the “Initial” state in the flow chart. This initial state was repeated a predefined number of times, typically once or twice. After collecting the initial dataset, Bayesian optimization (BO)37,38,39,40,41 was applied to suggest the next candidate condition. The reaction was carried out automatically under the suggested conditions, and the resulting yield was analyzed. This iterative process continued until BO suggested a previously tested condition42.

Fig. 3: Automated optimization.
figure 3

a Schematic of setup. b Process flowchart. “Initial” means to collect initial data set. c Results of optimization trials. d Assessment of the accuracy of the prediction model.

Full size image

In the first optimization trial, the initial conditions (6.0 mL/min and 50 °C, and 4.0 mL/min and 80 °C) were selected randomly. After six reaction runs, BO suggested conditions that had already been tested (2.0 mL/min, 80 °C). The system thus concluded that 2.0 mL/min and 80 °C were the optimal reaction conditions, yielding the highest predicted yield (Fig. 3c, 1st trial). Notably, this entire process required only 70 min to reach optimization. In the second trial, using a different set of initial conditions, the system again identified the same optimal parameters (Fig. 3c, 2nd trial). Although three more reactions were needed in the second trial, the total experimental time remained short at approximately 2 h. In our previous study36, we found that increasing the concentration fourfold under high-yielding conditions did not result in decreased yield. Therefore, it is likely that the optimal conditions identified here could be applied at higher, more productive concentrations, thereby improving throughput without compromising efficiency. These results highlight the rapidity and reproducibility of the developed automated optimization system.

We assessed the accuracy of the prediction model by comparing the predicted yields with those determined by gas chromatography (GC) using an internal standard for the reaction solutions obtained during the optimization process. To further validate the model, we conducted 63 additional reactions under varied conditions and similarly compared the predicted yields with experimentally measured values. As shown in Fig. 3d, the results demonstrated excellent agreement, with a high coefficient of determination (R² = 0.96). These findings confirm the robustness and general applicability of the model across a broader range of conditions.

Finally, we applied the prediction model for real-time analysis, demonstrating its utility as an example of process analytical technology (PAT)43, as described above and shown in Fig. 3a. Our optimization system allows for continuous monitoring of reaction parameters, with thermometer, flowmeter, and pressure gauge connected to the PLC. These instruments monitor the temperature, flow rate, and pressure in real time, while reaction yields are recorded every minute using inline FTIR analysis. Figure 4 shows a log of these measurements. The red line indicates the predicted yield based on FTIR data, demonstrating that the model can function effectively as a PAT system without further refinement. At some points, we collected the reaction solution, and confirmed the predicted yield is in good agreement with the yield determined by GC with the internal standard. Notably, the monitoring system was able to detect subtle differences in stabilized reaction conditions that were not evident from physical parameters alone, such as slight variations in temperature.

Fig. 4: Real-time reaction monitoring.
figure 4

Red bald line: yields predicted by the model, black dash line: pressure measured by the pressure gage (Pres), blue dotted line: temperature measured by the thermometer (Temp), gray line: flow rate measured by the flowmeter (Rate).

Full size image

Conclusion

In conclusion, we have developed a concise method for preparing FTIR data for machine learning, where individual FTIR spectra of the reactants and products are linearly combined to simulate the spectrum of a reaction mixture. With appropriate data preprocessing, we successfully constructed an accurate model for yield prediction. This was achieved with limited experimental input, as the model was trained on mimicked spectra generated from only the FTIR data of pure reactants and products, reducing the need for extensive reaction sampling. This framework enables real-time prediction of reaction yield within an integrated system, allowing us to achieve fully automated optimization of the Suzuki–Miyaura cross-coupling reaction. While this study employed a grid of reaction conditions, future implementations could incorporate dynamic flow techniques to further enhance experimental efficiency44. Furthermore, we demonstrated that the prediction model can function as a practical example of process analytical technology (PAT), capable of detecting subtle differences in reaction conditions that are not evident from physical parameters alone. We believe that the proposed system represents a meaningful step toward industrial automation. As often envisioned in science fiction45,46, it is becoming increasingly plausible that future industries may be operated entirely by robotic systems, without the need for human intervention.

Methods

Development of prediction model

Phenylboronic acid pinacol ester (1, 230 mg, 1.13 mmol) was dissolved in THF/MeOH (23 mL, 1:1 volume ratio) to be a 0.0049 M solution. The solution of 4-iodobenzonitrile (2, 0.033 M) and 4-cyanobiphenyl (3, 0.033 M) were similarly prepared. Each solution was pumped with a syringe pump at a flow rate of 1.0 mL/min and then in-line measurement was carried out. Five spectra were recorded in each solution considering noise patterns. Raw spectra were differentiated using the numpy.gradient function provided by the NumPy library. Only a spectral range from 1506 to 699 cm−1 (434 datapoints) was used for neural network (NN) training and prediction.

Training data was created with spectra of each compound (1, 2, and 3) according to the following equation;

$${{Spec}}_{{LC}}=\left(\frac{150-{c}_{{yield}}}{150}\right)\times \frac{r}{100}\times {{Spec}}_{{{\bf{1}}}}+\left(\frac{100-{c}_{{yield}}}{100}\right)\times {{Spec}}_{{{\bf{2}}}}+\frac{{c}_{{yield}}}{100}\times {{Spec}}_{{{\bf{3}}}}$$

where cyield and r are the yield and decomposed rate (integers from 0 to 100), SpecLC means the spectrum of the generated, Spec1, Spec2, Spec3 mean the spectra of 1, 2, and 3 respectively. In order to avoid learning noise pattern, one spectrum was randomly chosen for each linear combination. In this study, the number of training data was set to 10,000 throughout.

Automated optimization and reaction monitoring

Overall system control including file management and data logging, among other things, was written in C#.NET. Machine learning tasks (Bayesian optimization and prediction by NN model) were conducted using Python and the script was executed in C#.NET. The software for ReactIR (iC IR) was controlled through a mouse simulation. The pumps, sensors, heater and chiller were connected to PLC (Mitsubishi Electronic, MELSEC iQ-F series), and PLC was controlled via SoftGOT 2000 (Mitsubishi Electronic). The pump motor’s rotation speed was controlled through a voltage control (0–10 V). Values of pressure gauges and flowmeters were red through current measurements (4–20 mA). Thermocouples were connected to a dedicated unit of PLC, and the temperature was recorded. these values were logged every second. Power supply to a heater and a chiller pump were switched on and off by relays. According to our previous work39, the script was written in Python with GPyOpt library.

Process flow is as follows. At first, the search space in Bayesian optimization was determined, and a process was begun. In this work, a search space contained temperature (30, 40, 50, 60, 70, 80 °C, discrete) and flow rate (2, 3, 4, 5, 6 mL/min, discrete). The initial reaction condition was selected randomly, and the temperature and the flow rate were adjusted to the selected condition. After those values achieved the target ones, the system started stabilizing phase. The stabilizing phase lasted 480/F seconds (F means the flow rate). After stabilization, the system measured IR, and if necessary, sample solution was collected for GC analysis. After measurement, the flow rate was changed to 1.0 mL/min (stand-by mode) in order to reduce the waste of the reagents. During the stand-by mode, yield was predicted from the spectrum by using NN model, and the next candidate condition was selected randomly (as continuing Initial), or was suggested by the Bayesian optimization algorithm. If the suggested condition had not already selected in previous iterations, the next iteration began. If the suggested condition had already selected, the process completed

As a stock solution, 1 (9.356 g, 45.8 mmol), 2 (6.998 g, 30.6 mmol), potassium hydroxide (3.421 g, 61 mmol), n-tridecane (2.363 g, an internal standard) were dissolved in THF/MeOH (926 mL, 1:1 volume ratio). The stock solution was pumped into the tube reactor containing the polymer-supported palladiums in the water bath with heater and cooling jacket. In order to cool reaction mixture, another water bath was placed between tube reactor and spectrometer. In optimization process, first two iterations were carried out to obtain initial data and Bayesian optimization was executed from the third iteration onwards.

For the real-time yield monitoring, IR spectrum was measured every minute (128 scans). Moreover, additional waiting times of 240 and 120 seconds were taken before the spectrum measurement and after the sampling step, respectively.