Contact spacing controls the on-current for all-carbon field effect transistors

Abstract

All-carbon field-effect transistors, which combine carbon nanotubes and graphene hold great promise for many applications such as digital logic devices and single-photon emitters. However, the understanding of the physical properties of carbon nanotube (CNT)/graphene hybrid systems in such devices remained limited. In this combined experimental and theoretical study, we use a quantum transport model for field-effect transistors based on graphene electrodes and CNT channels to explain the experimentally observed low on currents. We find that large graphene/CNT spacing and short contact lengths limit the device performance. We have also elucidated in this work the experimentally observed ambipolar transport behavior caused by the flat conduction- and valence-bands and describe non-ideal gate-control of the contacts and channel region by the quantum capacitance of graphene and the carbon nanotube. We hope that our insights will accelerate the design of efficient all-carbon field-effect transistors.

Introduction

With technological progress, semiconductor devices are rapidly shrinking in size and conventional silicon systems reach their physical limits^1,2. As an alternative, the low-dimensional carbon structures graphene and carbon nanotubes (CNT) have enormous potential for future electronics. Graphene exhibits excellent material properties such as high charge mobility, mechanical strength, transparency, and flexibility^3,4,5,6. Semiconducting CNTs combine most of the exceptional characteristics of graphene with a direct, structure-dependent bandgap^7,8,9,10. Both types of nanostructures can be scalably fabricated and integrated as building blocks for electronic devices serving as electrical contacts and channels in carbon nanotube field-effect transistors (CNTFETs)^11,12,13. Other promising applications include nanocomposite materials¹⁴, biosensors¹⁵, scaffolds for tissue engineering¹⁶, light emitters^17,18, and in particular single-photon sources¹⁹ or photodetectors^20,21, respectively. All-carbon ultra-flat, flexible, and transparent graphene/CNT -transistors offer outstanding possibilities for fundamental and applied research^22,23. The electrical properties of CNTFETs with metallic contacts were extensively studied in previous works^24,25,26. Despite the variety of possible device geometries, the performance of the considered devices was limited due to the inevitable Schottky barriers in the case of chemisorbed metals (e.g. Ti, Ni) and the enhancement of contact resistance upon contact length downscaling in the case of physisorbed metals (e.g. Pt or Sc)^25,27. The work-function difference between CNTs and graphene is negligible²⁸ thus all-carbon CNTFETs exhibit ambipolar electrical properties which make them particularly interesting for light-emitting devices²⁹. Furthermore, graphene is chemically stable, easy to fabricate in large areas using chemical vapor deposition (CVD), and its two-dimensional structure causes weak screening of the gate electric field³⁰. However, it has been shown that the electronic properties of the atomistic CNT/graphene system depend critically on the distance between the tube and graphene electrode³¹. Presently, rational design of high-quality all-carbon transistors is constrained by challenges in the fabrication of the devices, requiring site-selective integration of individual CNTs between graphene electrodes which is barely possible using conventional lithography techniques, but is feasible with the help of dielectrophoresis³². Nevertheless, Xiao et al.¹² have demonstrated field-effect transistors with graphene/CNT junctions and Scandium drain-electrodes with steep subthreshold-switching properties and high on-state currents. The efforts to understand the CNT-graphene system theoretically encounter obstacles as well. In the past, theoretical studies on transport in CNT-based devices have been conducted using nonequilibrium Green function formalism (NEGF) combined with density functional theory (DFT)^{33,34,35,36,37,38}. Recent studies used the DFT + NEGF method to treat single molecular junctions with carbon-based electrodes^39,40. However, simulations of all-carbon transistors with realistic contact and channel sizes remained unfeasible due to the necessity to simulate quantum-mechanical systems comprising thousands of atoms. In the work of Fediai et al.⁴¹, a rigorous method to treat quantum transport through 2D-3D extended contacts, utilizing DFT and NEGF was developed, enabling full quantum transport simulations from first principles. We have adapted this method to a CNT transistor with graphene electrodes, which exhibits 1D/2D junctions. The aim of our work is to understand the fundamental properties of the graphene-CNT junction. We approach this problem through well-defined experiments and atomistic simulations where we developed a dedicated combination of DFT and NEGF specifically for graphene-CNT contacts, based on earlier work⁴¹. This method pushes the limits of the conventional combined DFT+NEGF methods^{33,34,35,36,37} toward the channel and contact lengths of ≈ 100 nm so that quantum mechanical treatment of the whole all-carbon transistor becomes feasible. On the experimental side, we fabricated and electrically characterized all-carbon transistors with a structure similar to the simulated atomistic structures in terms of bandgap and channel length. A dielectrophoretic deposition allows precise placement of single CNTs with defined chirality between the electrodes. Using our method, we have analyzed the spectral function of the CNT on top of the graphene to understand the effect of the CNT/graphene spacing on the charge injection and computed the local density of states and band bending in the device at different drain- and gate-source voltages. Hence, the effect of the quantum capacitance of the CNT and graphene was considered to realistically include the electrostatics inside the atomistic channel and contact region. We observe that large CNT/graphene spacing and short channel lengths reduce the current flow through the transistor by approximately three orders of magnitude. The model was validated by comparing it with the measured current-voltage characteristics. The gained insights can assist a rationalization of the design of various devices based on CNTs and graphene electrodes.

Results and discussion

Experimental set-up and simulated system

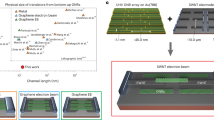
The experimental devices and their virtual counterparts were designed to be as similar as technical facilities and computer resources allowed. We fabricated devices that consist of graphene electrodes and preliminary sorted semiconducting CNTs. To this end, CVD-graphene was patterned on top of a SiO₂/Si layer using electron lithography to form the electrodes with a channel length of 100 nm. Individual nanotubes that bridged the contacts were suspended from a toluene-based suspension, in which the majority of carbon nanotubes have (9,8) chirality (Fig. 1a). The deposition was performed using ac-dielectrophoresis adapted for the graphene electrodes. Figure 1b shows a scanning electron micrograph of an exemplary device. Afterward, we placed the sample in a continuous-flow cryostat and characterized it under vacuum conditions at 10 − 6 mbar. After vacuum annealing at 350 K to remove the remaining water layer, the sample was cooled down and the electrical characterization of the all-carbon transistors was performed at temperatures down to 4 K. Figure 1c shows the simulated atomistic structure of the virtual counterpart of the fabricated devices and denote the contact and channel length, L_contact and L_channel, respectively. To enable the computational feasibility of the developed model, instead of chiral (9,8)-CNTs, we chose (13,0)-zigzag nanotubes, which have a much smaller period but similar bandgap⁴². Since the current-voltage characteristics are mainly governed by the bandgap of the channel material, the use of (13,0)-CNTs is justified (see method section for more details). Figure 1d shows the virtual device we use for the simulations, illustrating the electrodes (source ϕ_S, drain ϕ_D, gate ϕ_G) and the gr/CNT d_gr/CNT spacing. The channel of the model system is 17 nm long, while the contact length is a variable parameter with an arbitrary upper limit. Conventional NEGF+DFT software^35,38,43,44 cannot simulate quantum transport in systems with extended contacts, with an electrode-channel overlap of more than a few Angstrom. Therefore, we have theoretically developed and programmatically implemented a dedicated NEGF+DFT method for simulating quantum transport in a transistor with arbitrary graphene/CNT overlap(see methods section).

Fig. 1: Fabricated all-carbon transistor devices and their virtual counterparts.

a The predominant chirality of the carbon nanotubes (CNT) is (9,8) as seen from the absorption spectrum of the CNT suspension, where the 1400 nm peak corresponds to the (9,8)-CNTs. b Scanning electron micrograph of a graphene-CNT-graphene device. An approximately 100 nm long CNT bridges the graphene source- and drain-electrodes. Scale bar: 100 nm. c In the virtual all-carbon transistor, the CNT channel and graphene electrodes are treated quantum-mechanically at the atomistic level. The channel- and contact length is given by L_channel and L_contact, respectively. d Schematic view of the all-carbon field effect transistor. The CNT/graphene spacing is denoted with d_gr/CNT and the graphene layers serve as the source- (ϕ_S) and drain- (ϕ_D) electrodes, respectively. The gate-electrode is denoted with ϕ_G. The SiO₂ oxide layer is 300 nm thick (orange) and isolates the carbon system from the highly doped Si gate electrode on top of the Si substrate (blue).

Interaction strength between the CNT and graphene electrodes

The peculiarity of the all-carbon CNTFET is the use of graphene for the source and drain electrodes. A profound understanding of the electrical properties of extended CNT/graphene contacts is necessary to identify potential bottlenecks and, if possible, to circumvent those by designing devices appropriately. We analyze the spectral function A(E, k_z), to provide information about the energy-momentum relation of the electrons in the all-carbon system. Experimental methods for determining the spectral function, such as angle-resolved photoemission spectroscopy (ARPES), apply only to planar systems^45,46. Our developed model does not have this limitation, and thus we have computed the spectral function in the part of the tube sitting on the graphene electrode with equation (11) for CNTs with different CNT/graphene spacings, as discussed in detail in the methods section. The geometry files for the CNT/graphene system with different CNT/graphene spacings are provided in Supplementary Data 1. We used the spacing between the graphene and the CNT to mimic the effect of residual polymers helically wrapped around the CNT that remain after the selective dispersion processes to obtain monochiral, semiconducting CNTs out of a polychiral suspension^47,48. With this, we assume that the residual polymer does not affect the electrical properties of either CNT or graphene. Figure 2 shows the simulated spectral functions for the (13,0)-CNT on top of the graphene layer plotted in a heat map plot. For a large spacing d_gt/CNT of 5.0 Å (Fig. 2a), sharp and distinct peaks are observed in the spectral function. A reduced spacing (Fig. 2b-d) results in a broadening of the peaks. Even at a distance of 3.0 Å which is smaller than the sum of two carbon van der Waals radii (Fig. 2d), the typical band structure of the carbon nanotube is visible. Hence, we do not expect that the graphene electrode will distort the band structure of the carbon nanotube, even after the removal of the residual polymer. Due to weak graphene/CNT interaction, we expect the current to flow over the entire contact region of the CNT and graphene²⁷. The preservation of the band structure is similar to conventional metallic Pd or Pt contacts. This is in stark contrast to Ni or Ti contacts which destroy the band structure of the CNT upon the contact by “metalizing" it (that is, introducing states in the vicinity of the Fermi level). As a consequence, the Fermi level in the CNT on top of Ti or Ni is pinned near the center of the bandgap leading to the formation of ambipolar Schottky contacts²⁷. We point out that our method is sensitive to the chirality of the carbon nanotube in the gr/CNT junction. For example, (12,0) CNT, remains gapless in contact with graphene (supplementary figure 6).

Fig. 2: The spectral function of the carbon nanotube at varying carbon nanotube/graphene spacing.

The interaction strength between the graphene electrode and the carbon nanotube (CNT) on top is related to the broadening of the peaks in the spectral function A(E, k_z): strong interactions cause smearing of A(E, k_z). The spectral function is plotted in a 2D-heatmap plot over the Energy E (with respect to the Fermi level E_F) and the wavevector k_z. a At a spacing of d_gr/CNT = 5.0 Å, the peaks are sharp and distinct. Smaller spacings lead to a smearing of the peaks, although the key features (bands and bandgap) are still visible (b and c). d At a spacing of 3.0 Å, some bands overlap while the semiconducting property of the CNT remains. This indicates that graphene electrodes do not destroy the semiconducting property of the CNT by metalizing it, as reported for Ni or Ti contacts²⁷. The scale bar shows the logarithmic spectral function ${{{{{{\mathrm{log}}}}}}}\,A(E,{k}_{{{\mbox{z}}}})$ normalized to the range of values between 0 and 1.

The efficiency of the bottom gate

Another distinctive feature of the graphene electrodes is that they do not perfectly screen the CNT in the contact region from the electrostatic field of the gate electrode. Consequently, the parts of the CNT sitting above the graphene electrodes can be electrostatically doped by the gate-source voltage V_GS. Our considered device is fundamentally different from conventional CNTFETs with metallic electrodes, where the gate electrode controls only the bands in the channel region. To describe the gating efficiency in the center of the channel region and the contacts, we define the gate-induced band shifts ξ_contact and ξ_center, respectively. Treating the electrostatics by self-consistently solving the Poisson equation would be numerically too expensive for a model of this complexity. However, to describe the electrostatics realistically, the quantum capacitance C_Q⁴⁹ (Eq. (28)) of the graphene-CNT system in the contacts and the channel center was computed and taken into account. The band shift can now be determined by numerically solving the differential equation (27). The quantum capacitance in line with the position of the gate electrode determines a gate-induced band shift in the contact and the channel region depending on the gate-source voltage V_GS. One can understand the influence of quantum capacitance as an increased screening of the electrostatic field due to electrostatic doping of the particular region of the device. We solved equation (27) for the contact and channel region separately, where the dimensionless fitting parameters α_contact = 0.05 and α_channel = 0.18 were used, respectively (see method section). Figure 3 shows the band shift as a function of the applied gate-source voltage V_GS in the center of the channel (solid blue line) and the contact region (dashed yellow line). Despite an applied voltage of ± 20 V, the band shift in the contact region is only about ∓ 0.5 eV, which can be explained by the fact that graphene is a semi-metal whose density of states is zero only at the Dirac point. Upon applying a gate voltage, the energy levels are shifted w.r.t. the Fermi level, and the screening mechanism by the quantum capacitance comes into effect immediately. The behavior of the band shift in the center of the channel, on the other hand, shows a nearly linear V_GS dependence at V_GS ≈ 0 because the Fermi level is within the bandgap of the CNT where the quantum capacitance is zero. If V_GS is increased (decreased), a cusp occurs after crossing the first van Hove singularity, and we observe a strongly nonlinear response. The cusps, which originate from the van-Hove singularities, are annotated by the red markers in Fig. 3. In the contact region, we do not see any linear behavior. This is because graphene is a semi-metal and the partial screening of the CNT occurs even at small voltages.

Fig. 3: Gate efficiency in the center of the channel and the contact region.

The gate induced shift of the energy bands ξ in the channel center (solid blue line) and the contact region (dashed yellow line) as a function of the gate-source voltage V_GS. Compared to metallic electrodes, the graphene electrodes cannot entirely screen the carbon nanotube (CNT) from the gate field, whereby the CNT can also be electrostatically doped in the contact region. We explain the almost linear behavior of the band shift in the channel center by the fact that the Fermi level lies within the bandgap of the CNT, where the quantum capacitance is zero. For slightly increased (decreased) gate-source voltages, the linear behavior is damped rapidly because the Fermi level reaches the first van Hove singularity (VHS).

Band diagram from the first principles

We obtain insights into the quantum transport in CNTFETs with graphene electrodes by extracting the band diagram along the CNT axis, i.e., the z-dependence of the valence and conduction band edges, E_V and E_C Eq. (37), respectively. These were plotted together with another z-dependent quantity, the local density of states D(E, z) Eq. (24), shown as a logarithmic color map (Fig. 4). The simulated atomistic system has a channel length of L_contact = 17 nm and semi-infinite contacts (L_channel = ∞). The geometry file for the CNT/graphene system used in this simulation can be found in Supplementary Data 2. Figure 4a shows E_V, E_C, and D(E, z) at zero bias (V_DS = 0, V_GS = 0). The simulated bandgap of the carbon nanotube is 0.816 eV, which is close to the experimental value for (9,8) carbon nanotubes (0.879 eV)⁴². The Fermi level in the channel region is 0.155 eV below the center of the bandgap and slightly higher at the contact region, indicating a weak p-doping of the CNT. This weak p-doping is a consequence of the similar work functions of the graphene and the carbon nanotube. We observe an almost flat band diagram along the z-axis because the hole inflow from the graphene to the tube is small. Ambipolar Schottky barriers for electrons and holes (defined as E_C − E_F and E_F − E_V, respectively) can be observed at the contact/channel interfaces (white vertical lines). Analogous to Fig. 4a, in Fig. 4b, we show the unbiased band diagram for CNTFETs with Pd contacts. In contrast to the flat bands in gr/CNT contacts, CNTs in contact with Pd show strong doping which results from the large work function difference. The Fermi level in the contact regions falls several hundred eV below the valence band edge, resulting in a strong band bending and Ohmic contacts for holes (see Fig. 4b)²⁴. Fig. 4c, d show the band bending of the devices with graphene contacts at a constant drain-source voltage (V_DS = −0.5 V) and a gate-source voltage of V_GS = 20 V and V_GS = −20 V, respectively. As discussed in the previous paragraph, the graphene electrodes do not thoroughly screen the CNT in the contact region from the electrostatic field of the gate-electrode. This causes gate-induced electrostatic doping of the CNT in the contact regions and eliminates the Schottky barriers for holes and electrons.

Fig. 4: Band diagram and local density of states along carbon nanotube axis of the all-carbon transistor.

a Local density of states D(E, z) plotted as a 2D-colormap over the Energy E (with respect to the Fermi level E_F) and the position along the tube z. The conduction- (E_C) and valence- (E_V) band-edges of the all-carbon transistor at zero drain-source (V_DS = 0) and zero gate-source (V_GS = 0) voltage are plotted as white solid lines. The channel length is L_channel = 17.0 nm, and the carbon nanotube-graphene overlap is semi-infinite (L_contact = ∞). The vertical white lines indicate the interfaces between the channel and contact regions. The similar work function of graphene and the carbon nanotube (CNT) causes a weak p-doping of the CNT in the contact regions. b Conventional CNT field effect transistors with metallic (Pd) contacts: The CNT is strongly p-doped in the contact regions, causing Ohmic contacts for holes and a strong band bending. c Band bending and local DOS inside the device with applied drain-source (V_DS = −0.5 V) and gate-source voltage (V_GS = −20 V). The Fermi-level in the contact region is not pinned between the bandgap of the CNT. Instead, the CNT undergoes electrostatic p-doping in the contact region, caused by the negative gate-source voltage. We explain the low gate efficiency, which causes the doping-induced screening of the electrostatic field. d The transistor is in the on-state with opposite polarity V_GS = 20 V (n-polarity). Here the CNT in the contact regions is n-doped (caused by a positive V_GS). The scale bar shows the logarithmic spectral function ${{{{{{\mathrm{log}}}}}}}\,D(E,z)$ normalized to the range of values between 0 and 1.

Conductivity scaling with the contact length and CNT/graphene spacing

To understand the effect of the contact length L_contact and graphene/CNT spacing d_gr/CNT on the performance of the all-carbon FET and to derive design rules for high-efficient devices, we extracted the on-state conductivity for systems with gr/CNT spacings d_gr/CNT ranging from 3.0 Å to 5.0 Å and contacts lengths of L_contact = [50 nm, 200 nm, ∞]. The on-state conductivity is defined as G ≡ I_on/∣V_DS∣, where we obtain the on-state current I_on ≡ I_DS(−20 V, −0.5 V) with the Landauer equation (38). The transmission functions T(E) at different gr/CNT spacings are shown in supplementary figures 3, 4, and 5. Figure 5 shows the scaling of the on-state conductivity G with the gr/CNT spacing d_gr/CNT. For devices with contact lengths of 50 nm and 200 nm, we observe a significant decrease in the on-state conductivity with increasing contact spacing d_gr/CNT. For a contact spacing of 3.0 Å, the conductivity is 0.1G₀ for L_contact = 50 nm and 0.5G₀ for 200 nm contact length. The conductivity at infinite contact length is 0.6G₀, regardless of the contact spacing. In summary, we observe that the charge transport between the graphene electrodes and the CNT strongly depends on the contact spacing d_gr/CNT (see Fig. 2). Therefore, contact spacing is the limiting factor in the simulated devices with finite contact length. For devices with infinite contact lengths, the contact spacing is irrelevant for the conductivity since the charge inflow in the contact region is saturated in any case. Our results imply that high on-state currents in all-carbon FETs can be achieved by either reducing the contact spacing (by removing the polymer residues around the CNT) or employing longer CNTs to increase the contact length.

Fig. 5: Scaling of the on-state conductivity with respect to CNT/graphene spacing.

The on-state conductivity is plotted against the carbon nanotube/graphene (CNT/graphene) spacing d_gr/CNT on a logarithmic scale. The applied bias is V_DS = −0.5 V and V_GS = −20 V. We observe a strong dependence on d_gr/CNT for devices with finite contact lengths (L_contact = 50 nm blue and L_contact = 200 nm yellow). The on-state conductivity of devices with infinite contact length (green) does not depend on the CNT/graphene spacing. We explain this by a saturation of the charge inflow from the electrodes. To improve the on-state conductivity, either the contact spacing must be reduced by purifying the CNT from residual polymers, or the contact length has to be increased by depositing longer CNTs. With infinite contact length, the conductivity reaches a theoretical limit of 0.6G₀.

Experimental verification

As already discussed, the experimental devices and their virtual twins display similarities regarding their architecture, especially in the case of the single CNT channel. Hence, we compare the measured IV characteristics with the simulations to verify the model. The electrical characterization of the experimental devices was performed at different temperatures and with gate-source voltages ranging from −20 V to 20 V. We estimate a channel length of 100 nm for the experimental devices by measuring the distance between source- and drain electrodes in the scanning electron micrograph (Fig. 1b). Since the contrast between the graphene electrodes and the CNT is too weak for the SEM method, we could not measure the contact length. In the theoretical part of this work, we simulated quantum transport through the atomistic structure (Fig. 1d) with a 50 nm contact length and a channel length of 18.4 nm. The channel length was taken to be smaller than in the experiment to reduce computational costs. We regard the CNT channel as a potential barrier with finite height and length, where the length primarily plays a role in so-called interband tunneling processes. The longer the channel, the more the tunneling processes are suppressed. For 100 nm long channels, we assume that no tunneling currents occur, whereas they do so in devices with short channel lengths. By suppressing the transmission coefficient within the energy regimes, corresponding to interband tunneling, we justify the simulation of 18.4 nm channel devices and compare the results with experimental devices with 100 nm channel lengths (see the Method section for more details). Due to the surface roughness of the SiO₂ substrate, the uneven graphene electrodes, and the remaining polymer wrapped around the CNT and it is not feasible experimentally to control or measure the CNT/graphene spacing. Therefore, we investigated the temperature and V_DS dependence of the fabricated devices and the simulation model to broaden the parameter space for experimental verification. We calculate the current using the Landauer formula (38) and compare the experimental with the simulated currents for the following aspects: On-state currents and the off-state interval.

Figure 6 a shows the experimental currents of devices D1 and D2 at different temperatures T = [4 K, 25 K, 100 K, 150 K] and fixed drain-source voltage V_DS = −0.9 V. For T < 150 K, the off-state regime for D1 is between −5 V and 10 V, whereas the off-state regime of D2 ranges between 0 V and 10 V. The difference in off-state regimes between D1 and D2 can be due to a variety of reasons, including trap states in the channel region. The p-branch on-state current (V_GS = −20 V) of D1 agrees well with the current of D2. However, the n-branch currents (V_GS = 20 V) differ significantly between D1 and D2. For the simulated currents at different temperatures (see Fig. 6b), the off-state regime ranges from approximately −2.0 V to 10 V to 15 V, depending on the temperature. Particularly noteworthy is the fact that simulated p-state currents agree well with the measured ones. The simulated n-branch currents differ from all experiments, whereas the experiments differ from each other as well. To find the reason for the strong n-branch discrepancy, further experimental studies are needed. We suspect that trap-states in the oxide layer cause immobilization of the electrons which leads to strong differences in the n-branch. The variability of the IV characteristics is discussed in e.g. Franklin et al.⁵⁰. Overall, the temperature-induced variations of the simulated currents are less pronounced than the variations in the experiments. The V_DS dependence at constant temperature (T = 4 K) of D1 and D2 are shown in Fig. 6c. We observe similar off-state regimes and p-branch on currents as presented in Fig. 6a. But the variations in the currents of the n-branch increased greatly. The simulation results at constant temperature (T = 4 K) and varying drain-source voltage V_DS are shown in Fig. 6d. Again, p-polar on-state currents and off-regime seem to be consistent but as mentioned above further investigations into the n-branch currents need to be done. In general, we consider our model to be capable of predicting p-currents and the off-state regimes for all-carbon FETs.

Fig. 6: Comparing experimental and simulated drain-source current I_DS.

a, b Experimental and simulated temperature dependence at fixed drain-source voltage V_DS = −0.9 V plotted against the gate-source voltage V_GS. Two devices are shown here: device 1 (D1) and device 2 (D2). The p-polar currents in the on-state (V_GS = −20 V) agree well, while the n-polar (V_GS = 20 V) currents show large differences between experiment and simulation (about three orders of magnitude). c, d At constant temperature (T = 4 K) and different drain-source voltages the p-polar on-state currents and the off-state regimes of experiment and theory agree again. However, our model cannot correctly reproduce the n-polar on-state currents. The results imply that the experimental devices in this work, had a contact length of about 50 nm and a carbon nanotube/graphene spacing of ≈ 4.0 Å in both devices.

Conclusion

Previous works^{51,52,53,54,55} have investigated CNT/graphene hybrid structures and advocated them for future electronic devices. However, there is still a lack of knowledge about the parameters which critically affect the efficiency of such structures and how they can be systematically improved. Here, we have developed an ab-initio based model of quantum transport in all-carbon transistors, capable of simulating all-carbon atomistic structures with arbitrary contact lengths and graphene-CNT spacing. By using both experimental and simulation data we have discovered the following properties of this device: (a) at zero bias, the all-carbon transistor is an ambipolar electronic device with Schottky barriers for electrons and holes at the contact/channel interfaces; (b) in stark contrast to CNTFETs with metallic contacts, the electric field from the bottom gate is only partially screened by the graphene electrodes, so – in addition to the channel region – the CNT in the contact region can also be electrostatically doped to turn the Schottky contacts to Ohmic contacts for electrons (V_GS > 0) or holes (V_GS < 0); (c) the conductivity of the all-carbon transistor can be increased up to almost G₀ by either purifying the CNTs to reduce the contact spacing or by increasing the contact length; (d) we attributed the low p-branch on currents in the experimental devices to residual polymers wrapped around carbon nanotubes. Our developed and verified method allows us to simulate quantum transport for systems with realistic geometries at the quantum-mechanical level and thus paves the way for a rational design of all-carbon electronic devices. The immediate practical implication of our work is this: To increase the on-state current in all-carbon transistors, either increasing the contact length, or removing the residual polymer is necessary.

Methods

CNT Synthesis

SWCNTs enriched with (9,8) nanotubes were synthesized using CoSO4/SiO2 catalysts by chemical vapour deposition. SEM images of the catalysts before and after SWCNT synthesis are shown in supplementary figure 1. Following the previously published methods^56,57,58, CoSO4/SiO2 catalysts with 1 wt% Co were prepared by incipient wetness impregnation using Co (II) sulfate heptahydrate (CoSO47H2O, Sigma-Aldrich) and fumed silica (SiO2, Cab-O-Sil M-5, Sigma-Aldrich). During SWCNT growth, catalysts loaded in a quartz tube reactor were first reduced in pure H2 (1 bar, 99.99%) from room temperature to 540 ∘C. Then the temperature was increased to 780 ∘C under Ar (99.99 %). At 780 ∘C, catalysts were exposed to pressured CO (6 bar, 99.99%) with a flow rate of 200 ssc for 1 h. CO was purified by a purifier (Nanochem, Matheson Gas Products) before entering the reactor to remove carbonyl residues. As-synthesized SWCNTs deposited on catalysts were refluxed in a 1.5 M NaOH aqueous solution for 2 hours to dissolve SiO2. Afterwards, carbon materials filtered on a nylon membrane were used for further purification and enrichment. The Raman spectrum of as-synthesized SWCNTs deposited on catalysts and UV-vis-NIR spectrum of the SWCNT suspension are shown in supplementary figure 2.

Device fabrication and characterization

P-doped silicon wafer with 300 nm thermal oxide (Active Business Company, resistance Ω < 0.005 cm) was used as substrate and diced into 10 × 10 mm² samples. In three lithography steps tungsten markers, nanocrystalline graphene (NCG) electrodes, and tungsten electrical contacts were fabricated as described elsewhere⁵⁹. At first, samples were cleaned with isopropanol, acetone, and oxygen plasma and spin-coated with 950 k PMMA. Using electron-beam lithography (Leo 1530) markers were defined, followed by development in methyl isobutyl ketone (MIBK), sputtering of 40 nm tungsten, and subsequent lift-off in acetone and isopropanol. In the second step, photoresist Microposit S1805 (Rohm&Haas), diluted with propylene glycol monomethyl ether acetate (PGMEA) 1: 12, was used for the synthesis of nanocrystalline graphene. Samples were spin-coated with the photoresist and loaded into Gero Sr-A 70-500/11 high-temperature oven, where polymer graphitized at 800 ∘C for 10 h, covering the entire sample. Afterwards samples were spin-coated with PMMA and NCG electrodes were lithographically defined. After development 15 nm Aluminum layer was evaporated over NCG electrodes. Unprotected NCG was etched in oxygen plasma using Oxford Plasmalab 80 Plus reactive ion etching system (RIE)). The aluminum resists layer was etched in 3% metal ion-free tetramethylammonium hydroxide (MIF 726), releasing NCG electrodes. Finally, in the third lithography step, electrical contacts to NCG were fabricated by sputtering 40 nm tungsten under conditions identical to the first lithography step. The preparation of the suspension⁶⁰ dominated by (9,8)-CNTs is described in detail elsewhere¹⁸. Integration of CNTs between graphene electrodes was performed using ac-dielectrophoresis⁶¹. The suspension was diluted in toluene (1:10) and a 10 μl droplet was placed over the sample. Using an Agilent 33250 function generator, an alternating voltage (0.5 V, 100 kHz) was applied between common and gate electrodes for 5 min, leading to bridging graphene electrodes by individual CNTs. Afterwards the sample was rinsed with toluene and annealed for 1.5 h at 160 ∘C. For the electrical measurements samples were mounted in helium-flow, sample-in-vacuum cryostat system (MicrostatHiResII, Oxford) and characterized in the temperature range between 4 K and 300 K at 10 mbar − 6 by using an Agilent 4155B Semiconductor Parameter Analyzer¹⁸.

Modular DFT+NEGF approach for graphene-CNT contacts

Quantum transport in the CNTFET with graphene electrodes is simulated using a combined density functional theory and nonequilibrium Green functions (DFT+NEGF) method, whose general theoretical background is discussed in the books of Ryndyk⁶² and Di Ventra⁶³. In its present-day software implementations^33,34,35, this approach can be used to treat only so-called local contacts, where the overlap between the electrodes and molecule (in this case, carbon nanotube) is restricted by several hundreds of orbitals. These implementations become numerically prohibitively expensive as the overlap between the electrodes and the quantum system exceeds a few nanometers, which corresponds to thousands of overlapping orbitals. Such contacts are called extended^36,37. Being unable to use the present-day implementations of the NEGF+DFT method, we have developed a dedicated approach for 1D-2D contacts, based on the principles of the so-called “modular approach" proposed in the works of Fediai et al.^26,27,41,64 for 1D-3D contacts, specifically, metal-CNT contacts. Following the general ideas of this approach, DFT simulations of two representative modules (module 1 shown in Fig. 7a and module 2 in Fig. 7e) of the atomistic graphene-CNT-graphene system were performed. These modules contain all Hamiltonian and Overlap matrix elements necessary to create the Hamiltonian of the full transistor-like structure as shown in Fig. 1 and thus to perform quantum transport calculations for the entire system in principle, but not in practice because of the size of the overlap matrix between CNT and graphene orbitals. We overcome this obstacle by extracting the on-site and “hopping" elements between adjacent cells of the self-energy of the graphene electrodes to “decorate" the corresponding CNT elements inside the contact regions, which allows describing the original 1D-2D system as an effective block tight-binding chain represented by equations (13) and (14). Physical quantities such as the local density of states D(E, z) and the transmission coefficient T(E) through the channel of the transistor are then determined using the standard NEGF formalism for one-dimensional systems, considering the charge transfer between the 2D graphene-electrodes and the CNT by means of the graphene self-energy. All DFT simulations were performed using the quantum chemistry code cp2k⁶⁵. The SZV-MOLOPT-SR-GTH basis-set⁶⁶ and GTH-PBE-q4 pseudopotential⁶⁷ were used for the carbon atoms.

Fig. 7: Schematic overview of the procedure to calculate the graphene self-energy and the following decoration of the carbon nanotube (CNT) contact elements.

a Module 1 represents the carbon system of the all-carbon field effect transistor deep within the contact region and is visualized as a 3D block tight-binding system with the red and blue spheres representing the CNT and graphene unit cells, respectively. The reference unit cells for the k_z-space transformations are denoted with R₀ (CNT) and r₀ (graphene). b After k_z-transformation, one obtains a planar block tight-binding system where the k_z-dependent CNT element is depicted in purple, while the graphene on-site cells are green. c Decimation of the semi-infinite chain results in a finite planar system with an additional energy dependence from which the graphene self-energy in k_z − space can be computed. d Inverse Fourier transformation is used to obtain the on-site σ₀(E) and hopping σ_t(E) elements of the self-energy. e Visualization of module 2 as an effective one-dimensional tight-binding chain. All matrix elements relevant for quantum transport calculations of CNTFETs with arbitrary contact lengths are extracted from the finite matrices H⁽²⁾ and S⁽²⁾. In accordance with the usual non-equilibrium Greens function scheme, the left H_L, central H_C, and right H_R subsystems are specified. On- and off-site hopping matrices in the contact regions are decorated with the self-energies, which have been obtained from module 1.

Computational method for the graphene electrodes self-energy

Module 1 consists of three periods of a (13,0)-CNT on a graphene sheet with 27 unit cells (3 longitudinal and 9 perpendiculars to the CNT axis). The perpendicular edges of the graphene sheet are zigzag-shaped, and the total number of carbon atoms is 264 (156 in the CNT and 108 in the graphene sheet). The dotted line in Fig. 7a illustrates the alignment of the CNT with respect to the graphene sheet and h denotes the mutual distance.

As mentioned above, CNTs used as a channel material in the manufactured devices had (9,8) chirality. We justify the use of (13,0) CNTs, since their bandgap is comparable to one of the (9,8) tubes and the current-voltage characteristics are mostly governed by the bandgap. The advantage of zigzag-CNTs is the easier handling of unit cells during the k_z-space transformation, which will be discussed later, due to coinciding unit cell sizes of the graphene and CNT unit cells. The size of the DFT simulation box is L_z = 3 ⋅ dz = 12.78 Å in the longitudinal direction, L_x = 25.00 Å and L_y = 23.00 Å in the perpendicular directions. Here d_z = 4.26 Å is the size of the graphene and CNT supercell in the z-direction. Periodic boundary conditions in all three dimensions were used to imitate a system with translation-symmetry along the tube-axis. L_x and L_y were chosen large enough to suppress fictitious transverse interactions. The extracted overlap matrix and Hamiltonian are S⁽¹⁾ and H⁽¹⁾ respectively. Exemplary input and geometry (xyz-format) files can be found in supplementary data 1. The overlap matrix S⁽¹⁾ and the Hamiltonian H⁽¹⁾ can be visualized by the block tight-binding scheme shown in Fig. 7. The red and blue beads represent the on-site block matrices of graphene and the CNT, respectively. The inter-block interactions are not explicitly displayed. Using the translation symmetry, we perform a Fourier transformation from z − to k_z-space^64,68 and obtain N_kz planar block tight-binding systems shown in Fig. 7b, where ${N}_{{k}_{{{\mbox{z}}}}}$ is the number of k_z − sampling points and ${k}_{{{\mbox{z}}}}\in \left[-\pi /{d}_{{{\mbox{z}}}};\,\pi /{d}_{{{\mbox{z}}}}\right]$. The k_z-dependent on- and off-site matrices are obtained by:

$${H}_{{{\mbox{cnt}}}}({k}_{{{\mbox{z}}}})=\mathop{\sum}\limits_{{n}_{{{\mbox{z}}}}\in \{-1,0,1\}}{H}^{(1)}[{{{{{{{{\bf{R}}}}}}}}}_{0};\,{{{{{{{{\bf{R}}}}}}}}}_{0}+{n}_{{{\mbox{z}}}}\cdot {d}_{{{\mbox{z}}}}{{{{{{{{\bf{e}}}}}}}}}_{{{\mbox{z}}}}]{{{\mbox{e}}}}^{i{k}_{{{\mbox{z}}}}\cdot {n}_{{{\mbox{z}}}}\cdot {d}_{{{\mbox{z}}}}}\qquad\qquad\qquad\qquad$$

(1)

$${t}_{{n}_{{{\mbox{x}}}}}({k}_{{{\mbox{z}}}})=\mathop{\sum}\limits_{{n}_{{{\mbox{z}}}}\in \{-1,0,1\}}{H}^{(1)}[{{{{{{{{\bf{R}}}}}}}}}_{0};\,{{{{{{{{\bf{r}}}}}}}}}_{0}+{n}_{{{\mbox{x}}}}\cdot {d}_{{{\mbox{x}}}}{{{{{{{{\bf{e}}}}}}}}}_{{{\mbox{x}}}}+{n}_{{{\mbox{z}}}}\cdot {d}_{{{\mbox{z}}}}{{{{{{{{\bf{e}}}}}}}}}_{{{\mbox{z}}}}]{{{\mbox{e}}}}^{i{k}_{{{\mbox{z}}}}\cdot {n}_{{{\mbox{z}}}}\cdot {d}_{{{\mbox{z}}}}}\qquad\qquad$$

(2)

$${\alpha }_{{n}_{{{\mbox{x}}}}}({k}_{{{\mbox{z}}}})=\mathop{\sum}\limits_{{n}_{{{\mbox{z}}}}\in \{-1,0,1\}}{H}^{(1)}[{{{{{{{{\bf{r}}}}}}}}}_{0}+{n}_{{{\mbox{x}}}}\cdot {d}_{{{\mbox{x}}}}{{{{{{{{\bf{e}}}}}}}}}_{{{\mbox{x}}}};\,{{{{{{{{\bf{r}}}}}}}}}_{0}+{n}_{{{\mbox{x}}}}\cdot {d}_{{{\mbox{x}}}}{{{{{{{{\bf{e}}}}}}}}}_{{{\mbox{x}}}}+{n}_{{{\mbox{z}}}}\cdot {d}_{{{\mbox{z}}}}{{{{{{{{\bf{e}}}}}}}}}_{{{\mbox{z}}}}]{{{\mbox{e}}}}^{i{k}_{{{\mbox{z}}}}\cdot {n}_{{{\mbox{z}}}}\cdot {d}_{{{\mbox{z}}}}}$$

(3)

$${\beta }_{{n}_{{{\mbox{x}}}}}({k}_{{{\mbox{z}}}})= \, \mathop{\sum}\limits_{{n}_{{{\mbox{z}}}}\in \{-1,0,1\}}{H}^{(1)}[{{{{{{{{\bf{r}}}}}}}}}_{0}+{{{{{{{\rm{sign}}}}}}}}({n}_{{{\mbox{x}}}})(| {n}_{{{\mbox{x}}}}| -1)\cdot {d}_{{{\mbox{x}}}}{{{{{{{{\bf{e}}}}}}}}}_{{{\mbox{x}}}};\,{{{{{{{{\bf{r}}}}}}}}}_{0}+{n}_{{{\mbox{x}}}}\cdot {d}_{{{\mbox{x}}}}{{{{{{{{\bf{e}}}}}}}}}_{{{\mbox{x}}}}\\ \, +{n}_{{{\mbox{z}}}}\cdot {d}_{{{\mbox{z}}}}{{{{{{{{\bf{e}}}}}}}}}_{{{\mbox{z}}}}]{{{\mbox{e}}}}^{i{k}_{{{\mbox{z}}}}\cdot {n}_{{{\mbox{z}}}}\cdot {d}_{{{\mbox{z}}}}}\,,$$

(4)

where R₀ denotes the center of mass position of the CNT unit cell in the center of module 1 and r₀ the graphene unit cell beneath. H⁽¹⁾[v; u] indicates the interaction between the unit cells at position v and u (on-site element for v = u) and n_x stands for the x-coordinate. The CNT block H_cnt(k_z) is represented in the basis of atomic orbitals by an N × N matrix for each sampling point in momentum-space. The graphene on- and off-site elements (${\alpha }_{{n}_{{{\mbox{x}}}}}({k}_{{{\mbox{z}}}})$ and ${\beta }_{{n}_{{{\mbox{x}}}}}({k}_{{{\mbox{z}}}})$) form M × M matrices, so the coupling matrices between the CNT and graphene subsystems (t_−1,0,+1(k_z)) are N × M matrices. The overlap matrices in k_z-space are obtained by replacing H⁽¹⁾ with S⁽¹⁾ in equations (1)-(4).

The graphene on- and off-site matrices with ∣n_x∣ > 2 are replaced by α_±2(k_z) and β_±2(k_z) respectively, since the influence of the CNT on these and any further elements can be neglected. The resulting tight-binding system is composed of two semi-infinite block tight-binding chains on the left ${H}_{\infty }^{(-)}$ and right ${H}_{\infty }^{(+)}$ and a finite two-dimensional system in between (see Fig. 7b). The Hamiltonian of the semi-infinite systems is given as:

$${H}_{\infty }^{(\pm )}({k}_{{{\mbox{z}}}})=\mathop{\sum }\limits_{i=1}^{\infty }{\alpha }_{\pm 2}({k}_{{{\mbox{z}}}})\left|i\right\rangle {\left\langle i\right|}_{M\times M}+\mathop{\sum }\limits_{i=1}^{\infty }\left[{\beta }_{\pm 2}({k}_{{{\mbox{z}}}})\left|i\right\rangle {\left\langle i+1\right|}_{M\times M}+{\beta }_{\pm 2}^{{{{\dagger}}} }({k}_{{{\mbox{z}}}})\left|i+1\right\rangle {\left\langle i\right|}_{M\times M}\right]\,,$$

(5)

where $\left|i\right\rangle {\left\langle j\right|}_{M\times M}$ denotes the (i, j), M × M matrix.

To account for the influence of the semi-infinite block tight-binding chains, we use a highly convergent method^69,70 to compute the retarded surface Green’s functions of the left and right parts. The remaining on-site matrices at n_x = ± 1 are decorated using ${g}_{\,{{\mbox{0}}}}^{(\pm )}(E,{k}_{{{\mbox{z}}}})$ as follows:

$${\tilde{\alpha }}_{\pm 1}(E,{k}_{{{\mbox{z}}}})={\alpha }_{\pm 1}({k}_{{{\mbox{z}}}})+\left[E{S}_{{\beta }_{\pm 2}}({k}_{{{\mbox{z}}}})-{\beta }_{\pm 2}({k}_{{{\mbox{z}}}})\right]{g}_{0}^{(\pm )}(E,{k}_{{{\mbox{z}}}}){\left[E{S}_{{\beta }_{\pm 2}}({k}_{{{\mbox{z}}}})-{\beta }_{\pm 2}({k}_{{{\mbox{z}}}})\right]}^{{{{\dagger}}} }\,,$$

(6)

which yields an additional energy dependence. The number of energy-sampling points is denoted with N_E.

The originally three-dimensional periodic system is represented by ${N}_{{k}_{{{\mbox{z}}}}}\cdot {N}_{E}$ two-dimensional, finite block- tight-binding systems (Fig. 7c), whose Hamilton and overlap matrix read:

$$H(E,{k}_{{{\mbox{z}}}})=\left(\begin{array}{cc}{H}_{{{\mbox{cnt}}}}({k}_{{{\mbox{z}}}})&{{{{{{{\mathscr{T}}}}}}}}({k}_{{{\mbox{z}}}})\\ {{{{{{{{\mathscr{T}}}}}}}}}^{{{{\dagger}}} }({k}_{{{\mbox{z}}}})&{H}_{{{\mbox{gr}}}}(E,{k}_{{{\mbox{z}}}})\end{array}\right)\qquad S({k}_{{{\mbox{z}}}})=\left(\begin{array}{cc}{S}_{{{\mbox{cnt}}}}({k}_{{{\mbox{z}}}})&{S}_{{{{{{{{\mathscr{T}}}}}}}}}({k}_{{{\mbox{z}}}})\\ {S}_{{{{{{{{\mathscr{T}}}}}}}}}^{{{{\dagger}}} }({k}_{{{\mbox{z}}}})&{S}_{{{\mbox{gr}}}}({k}_{{{\mbox{z}}}})\end{array}\right)$$

(7)

with:

$${H}_{{{\mbox{gr}}}}(E,{k}_{{{\mbox{z}}}}) \equiv \, \left(\begin{array}{ccc}{\alpha }_{0}({k}_{{{\mbox{z}}}})&{\beta }_{-1}({k}_{{{\mbox{z}}}})&{\beta }_{+1}({k}_{{{\mbox{z}}}})\\ {\beta }_{-1}^{{{{\dagger}}} }({k}_{{{\mbox{z}}}})&{\tilde{\alpha }}_{-1}(E,{k}_{{{\mbox{z}}}})&{0}_{M\times M}\\ {\beta }_{+1}^{{{{\dagger}}} }({k}_{{{\mbox{z}}}})&{0}_{M\times M}&{\tilde{\alpha }}_{+1}(E,{k}_{{{\mbox{z}}}})\end{array}\right)\\ {S}_{{{\mbox{gr}}}}({k}_{{{\mbox{z}}}}) \equiv \, \left(\begin{array}{ccc}{S}_{{\alpha }_{0}}({k}_{{{\mbox{z}}}})&{S}_{{\beta }_{-1}}({k}_{{{\mbox{z}}}})&{S}_{{\beta }_{+1}}({k}_{{{\mbox{z}}}})\\ {S}_{{\beta }_{-1}}^{{{{\dagger}}} }({k}_{{{\mbox{z}}}})&{S}_{{\alpha }_{-1}}({k}_{{{\mbox{z}}}})&{0}_{M\times M}\\ {S}_{{\beta }_{+1}}^{{{{\dagger}}} }({k}_{{{\mbox{z}}}})&{0}_{M\times M}&{S}_{{\alpha }_{+1}}({k}_{{{\mbox{z}}}})\end{array}\right)$$

(8)

and

$${{{{{{{\mathscr{T}}}}}}}}({k}_{{{\mbox{z}}}})\equiv \left({t}_{0}({k}_{{{\mbox{z}}}})\quad {t}_{-1}({k}_{{{\mbox{z}}}})\quad {t}_{+1}({k}_{{{\mbox{z}}}})\right)\qquad {S}_{{{{{{{{\mathscr{T}}}}}}}}}({k}_{{{\mbox{z}}}})\equiv \left({S}_{{t}_{0}}({k}_{{{\mbox{z}}}})\quad {S}_{{t}_{-1}}({k}_{{{\mbox{z}}}})\quad {S}_{{t}_{+1}}({k}_{{{\mbox{z}}}})\right)\,.$$

(9)

Now the self-energy of the graphene electrode can be computed in k_z-space:

$$\tilde{\sigma }(E,{k}_{{{\mbox{z}}}})=\left[E{S}_{{{{{{{{\mathscr{T}}}}}}}}}({k}_{{{\mbox{z}}}})-{{{{{{{\mathscr{T}}}}}}}}({k}_{{{\mbox{z}}}})\right]{\left[E{S}_{{{\mbox{gr}}}}({k}_{{{\mbox{z}}}})-{H}_{{{\mbox{gr}}}}(E,{k}_{{{\mbox{z}}}})\right]}^{-1}{\left[E{S}_{{{{{{{{\mathscr{T}}}}}}}}}({k}_{{{\mbox{z}}}})-{{{{{{{\mathscr{T}}}}}}}}({k}_{{{\mbox{z}}}})\right]}^{{{{\dagger}}} }\,.$$

(10)

The spectral function is calculated according to:

$$A(E,{k}_{{{\mbox{z}}}})=-\frac{2}{\pi }{{\mbox{Im}}}\,\left[{[E{S}_{{{\mbox{cnt}}}}({k}_{{{\mbox{z}}}})-{H}_{{{\mbox{cnt}}}}({k}_{{{\mbox{z}}}})-\tilde{\sigma }(E,{k}_{{{\mbox{z}}}})]}^{-1}{S}_{{{\mbox{cnt}}}}({k}_{{{\mbox{z}}}})\right]\,.$$

(11)

Applying inverse Fourier transformation on the k_z-space self-energy, we obtain the self-energies in real-space representation:

$${\sigma }_{i,j}(E)=\frac{1}{{N}_{{k}_{{{\mbox{z}}}}}}\mathop{\sum}\limits_{{k}_{{{\mbox{z}}}}\in {{\mbox{1.BZ}}}\,}\tilde{\sigma }(E,{k}_{{{\mbox{z}}}}){{{\mbox{e}}}}^{-i{k}_{{{\mbox{z}}}}{d}_{{{\mbox{z}}}}(j-i)}\,,$$

(12)

where σ_i,i(E) ≡ σ₀(E) and σ_i,i+1(E) ≡ σ_t(E) stand for the on- and off-site self-energies (see Fig. 7d). All farther elements starting from σ_i,i+2 are rapidly decaying (see Appendix A in Fediai et al.⁴¹) and computationally costly and therefore ignored. The elements σ₀(E) and σ_t(E) are used below to decorate the CNT matrices in the contact regions.

Decoration of the CNT

Module 2 is composed of two modules 1, bridged by 20 unit cells of the CNT (see Fig. 7e). The free-standing portion of the CNT is referred to as the channel region. The total number of carbon atoms is 1568, and the simulation box is L_z = 26 ⋅ d_z = 110.76 Å in the z-direction. Exemplary input and geometry files are provided in supplementary data 2. The Hamiltonian and the overlap matrix for module 2 are denoted with H⁽²⁾ and S⁽²⁾.

As shown in Fig. 7, the matrix elements for the contact and channel regions are extracted from H⁽²⁾ and S⁽²⁾ and divided into three parts: the left H_L(E) and right H_R(E) parts consist of decorated on- and off-site elements:

$$\begin{array}{r}{H}_{{{\mbox{L}}}}(E)\equiv \left(\begin{array}{ccc}{\tilde{H}}_{3}&{\tilde{T}}_{3}&{0}_{N\times N}\\ {\tilde{T}}_{3}^{{{{\dagger}}} }&{\tilde{H}}_{2}&{\tilde{T}}_{2}\\ {0}_{N\times N}&{\tilde{T}}_{2}^{{{{\dagger}}} }&{\tilde{H}}_{1}\end{array}\right)\qquad {H}_{{{\mbox{R}}}}(E)\equiv \left(\begin{array}{ccc}{\tilde{H}}_{1}&{\tilde{T}}_{2}&{0}_{N\times N}\\ {\tilde{T}}_{2}^{{{{\dagger}}} }&{\tilde{H}}_{2}&{\tilde{T}}_{3}\\ {0}_{N\times N}&{\tilde{T}}_{3}^{{{{\dagger}}} }&{\tilde{H}}_{3}\end{array}\right)\,,\end{array}$$

(13)

with the decorated CNT Hamiltonian for each unit cell in the contact region $\tilde{{H}_{i}}={H}_{i}^{\,{{\mbox{con}}}\,}+{\sigma }_{0}(E)$ and ${\tilde{T}}_{i}={T}_{i}^{\,{{\mbox{con}}}}+{\sigma }_{{{\mbox{t}}}}(E)$ the decorated off-site matrices. The parts of H⁽²⁾, which correspond to the on- and off-site matrices in the contact regions are denoted with ${H}_{i}^{\,{{\mbox{con}}}\,}$ or ${T}_{i}^{\,{{\mbox{con}}}\,}$. The overlap matrices S_L(R) are similarly arranged.

The Hamiltonian and the overlap matrix corresponding to the channel are given by:

$${H}_{{{\mbox{C}}}}=\mathop{\sum }\limits_{i=1}^{n}{H}_{i}\left|i\right\rangle {\left\langle i\right|}_{N\times N}+\mathop{\sum }\limits_{i=1}^{n-1}{T}_{i}\left|i\right\rangle {\left\langle i+1\right|}_{N\times N}+\mathop{\sum }\limits_{i=1}^{n-1}{T}_{i}^{{{{\dagger}}} }\left|i+1\right\rangle {\left\langle i\right|}_{N\times N}$$

(14)

$${S}_{{{\mbox{C}}}}=\mathop{\sum }\limits_{i=1}^{n}{S}_{i}\left|i\right\rangle {\left\langle i\right|}_{N\times N}+\mathop{\sum }\limits_{i=1}^{n-1}{T}_{{S}_{i}}\left|i\right\rangle {\left\langle i+1\right|}_{N\times N}+\mathop{\sum }\limits_{i=1}^{n-1}{S}_{i}^{{{{\dagger}}} }\left|i+1\right\rangle {\left\langle i\right|}_{N\times N}\,.$$

(15)

With the introduced elements of H_L and H_R, it is possible to simulate CNTFETs with arbitrary contact lengths. Therefore it is assumed that the matrices further within the contact regions do not differ from ${\tilde{H}}_{3}$ and $\tilde{{T}_{3}}$. The contact length needs to be chosen in units of the unit cell size L_contact = d_z ⋅ N_contact, with N_contact = 1, 2, ….

The decorated contacts are iteratively decimated using the Green’s function:

$${G}_{\,{{\mbox{L(R)}}}\,}^{(1)}={\left[E{S}_{3}^{{{\mbox{con}}}}-{\tilde{H}}_{3}(E)\right]}^{-1}$$

(16)

$${G}_{\,{{\mbox{L}}}\,}^{(i)}=\left\{\begin{array}{ll}{\left[E{S}_{3}^{{{\mbox{con}}}}-{\tilde{H}}_{3}-{[E{S}_{{T}_{3}}^{{{\mbox{con}}}}-{\tilde{T}}_{3}]}^{{{{\dagger}}} }{G}_{{{\mbox{L}}}}^{(i-1)}[E{S}_{{T}_{3}}^{{{\mbox{con}}}}-{\tilde{T}}_{3}]\right]}^{-1}\quad &\,{{\mbox{for}}}\;1 \, < \, i\, < \, {N}_{{{\mbox{contact}}}}-1\\ {\left[E{S}_{2}^{{{\mbox{con}}}}-{\tilde{H}}_{2}-{[E{S}_{{T}_{3}}^{{{\mbox{con}}}}-{\tilde{T}}_{3}]}^{{{{\dagger}}} }{G}_{{{\mbox{L}}}}^{(i-1)}[E{S}_{{T}_{3}}^{{{\mbox{con}}}}-{\tilde{T}}_{3}]\right]}^{-1}\quad &\,{{\mbox{for}}}\; i={N}_{{{\mbox{contact}}}}-1\hfill\\ {\left[E{S}_{1}^{{{\mbox{con}}}}-{\tilde{H}}_{1}-{[E{S}_{{T}_{2}}^{{{\mbox{con}}}}-{\tilde{T}}_{2}]}^{{{{\dagger}}} }{G}_{{{\mbox{L}}}}^{(i-1)}[E{S}_{{T}_{2}}^{{{\mbox{con}}}}-{\tilde{T}}_{2}]\right]}^{-1}\quad &\,{{\mbox{for}}}\; i={N}_{{{\mbox{contact}}}}\hfill\end{array}\right.$$

(17)

$${G}_{\,{{\mbox{R}}}\,}^{(i)}=\left\{\begin{array}{ll}{\left[E{S}_{3}^{{{\mbox{con}}}}-{\tilde{H}}_{3}-[E{S}_{{T}_{3}}^{{{\mbox{con}}}}-{\tilde{T}}_{3}]{G}_{{{\mbox{R}}}}^{(i-1)}{[E{S}_{{T}_{3}}^{{{\mbox{con}}}}-{\tilde{T}}_{3}]}^{{{{\dagger}}} }\right]}^{-1}\quad &\,{{\mbox{for}}}\; 1\, < \, i\, < \, {N}_{{{\mbox{contact}}}}-1\\ {\left[E{S}_{2}^{{{\mbox{con}}}}-{\tilde{H}}_{2}-[E{S}_{{T}_{3}}^{{{\mbox{con}}}}-{\tilde{T}}_{3}]{G}_{{{\mbox{R}}}}^{(i-1)}{[E{S}_{{T}_{3}}^{{{\mbox{con}}}}-{\tilde{T}}_{3}]}^{{{{\dagger}}} }\right]}^{-1}\quad &\,{{\mbox{for}}}\; i={N}_{{{\mbox{contact}}}}-1\hfill\\ {\left[E{S}_{1}^{{{\mbox{con}}}}-{\tilde{H}}_{1}-[E{S}_{{T}_{2}}^{{{\mbox{con}}}}-{\tilde{T}}_{2}]{G}_{{{\mbox{R}}}}^{(i-1)}{[E{S}_{{T}_{2}}^{{{\mbox{con}}}}-{\tilde{T}}_{2}]}^{{{{\dagger}}} }\right]}^{-1}\quad &\,{{\mbox{for}}}\; i={N}_{{{\mbox{contact}}}}\hfill.\end{array}\right.$$

(18)

The iterative procedure is conducted until all contact elements have been decimated to compute the final self-energies with the obtained surface Green’s functions ${G}_{\,{{\mbox{L}}}}^{({N}_{{{\mbox{contact}}}})}$ and ${G}_{\,{{\mbox{R}}}}^{({N}_{{{\mbox{contact}}}})}$:

$${{{\Sigma }}}_{{{\mbox{L}}}}(E)={\left[E{S}_{{V}_{{{\mbox{LS}}}}}-{V}_{{{\mbox{LS}}}}\right]}^{{{{\dagger}}} }{G}_{{{\mbox{L}}}}^{({N}_{{{\mbox{contact}}}})}(E)\left[E{S}_{{V}_{{{\mbox{LS}}}}}-{V}_{{{\mbox{LS}}}}\right]$$

(19)

$${{{\Sigma }}}_{{{\mbox{R}}}}(E)=\left[E{S}_{{V}_{{{\mbox{SR}}}}}-{V}_{{{\mbox{SR}}}}\right]{G}_{{{\mbox{R}}}}^{({N}_{{{\mbox{contact}}}})}(E){\left[E{S}_{{V}_{{{\mbox{SR}}}}}-{V}_{{{\mbox{SR}}}}\right]}^{{{{\dagger}}} }\,.$$

(20)

For infinitely long contacts, the highly convergent method^69,70 used earlier is used to obtain the surface Greens functions.

The last step is to decorate the matrices that belong to the left and right end of the channel region with the self-energies:

$${H}_{\,{{\mbox{C}}}\,}^{\prime}(E)= \, [{H}_{1}+{{{\Sigma }}}_{{{\mbox{L}}}}(E)]\left|1\right\rangle {\left\langle 1\right|}_{N\times N}+[{H}_{n}+{{{\Sigma }}}_{{{\mbox{R}}}}(E)]\left|n\right\rangle {\left\langle n\right|}_{N\times N}\\ \, +\ \mathop{\sum }\limits_{i=2}^{n-1}{H}_{i}\left|i\right\rangle {\left\langle i\right|}_{N\times N}+\mathop{\sum }\limits_{i=1}^{n-1}{T}_{i}\left|i\right\rangle {\left\langle i+1\right|}_{N\times N}+\mathop{\sum }\limits_{i=1}^{n-1}{T}_{i}^{{{{\dagger}}} }\left|i+1\right\rangle {\left\langle i\right|}_{N\times N}.$$

(21)

The original system consisting of 1D (CNT) and 2D (graphene) components was reduced to an effective quasi-1D system with energy dependence using the modular approach. The method was developed based on the CNT/graphene contact as an exemplary system but can effortlessly be applied to various 1D/2D extended contacts.

To calculate the local density D(E, i) of states and transmission coefficient T(E), the retarded Green’s function of the decorated channel system is required:

$${G}_{{{\mbox{C}}}}(E)={[E{S}_{{{\mbox{C}}}}-{H}_{{{\mbox{C}}}}^{\prime}(E)]}^{-1}\,.$$

(22)

Depending on the channel length, it is be numerically costly to determine G_C with equation (22), hence the recursive algorithm suggested by Klimeck⁷¹ is used to obtain the relevant elements of the Green’s function, namely, G_C,ii, G_C,i1, G_C,in, G_C,ii+1 and G_C,ii−1, where G_C,ab is an N × N matrix and the [a, b]-element of the block-matrix G_C.

Afterward, the transmission coefficient and density of states can be found:

$$T(E)=\,{{\mbox{Trace}}}\,\left[{{{\Gamma }}}_{{{\mbox{L}}}}{G}_{{{\mbox{C}}},1n}{{{\Gamma }}}_{{{\mbox{R}}}}{G}_{{{\mbox{C}}}\,,1n}^{{{{\dagger}}} }\right]$$

(23)

$$D(E,i)=-\frac{2}{\pi }\,{{\mbox{Im}}}\,\left\{\begin{array}{ll}\,{{\mbox{Tr}}}\,\left[{G}_{{{\mbox{C}}},ii}{S}_{i}+{G}_{{{\mbox{C}}},ii+1}{S}_{{T}_{i}}^{{{{\dagger}}} }\right]\quad \hfill&\,{{\mbox{for}}}\,i=1\hfill\\ \,{{\mbox{Tr}}}\,\left[{G}_{{{\mbox{C}}},ii-1}{S}_{{T}_{i}}+{G}_{{{\mbox{C}}},ii}{S}_{i}+{G}_{{{\mbox{C}}},ii+1}{S}_{{T}_{i}}^{{{{\dagger}}} }\right]\quad &\,{{\mbox{for}}}\,1 \, < \, i\, < \, n\\ \,{{\mbox{Tr}}}\,\left[{G}_{{{\mbox{C}}},ii-1}{S}_{{T}_{i}}+{G}_{{{\mbox{C}}},ii}{S}_{i}\right]\hfill\quad &\,{{\mbox{for}}}\,i=n\hfill\end{array}\right.\,,$$

(24)

where ${{{\Gamma }}}_{{{\mbox{L(R)}}}}=i({{{\Sigma }}}_{{{\mbox{L(R)}}}}-{{{\Sigma }}}_{\,{{\mbox{L(R)}}}\,}^{{{{\dagger}}} })$ is related to the rates of elastic electron scattering from the electrodes to the channel region and the other way round.

Electrode model

For the drain and gate-source electrodes, an idealized model was used (Fig. 1c). Highly doped silicon served as the gate electrode, followed by 300 nm SiO2 as an insulator layer. The graphene sheets were used as source and drain electrodes. In the model, the source electrode is grounded and the voltages are defined as:

$${V}_{{{\mbox{GS}}}}\equiv {\phi }_{{{\mbox{G}}}}-{\phi }_{{{\mbox{S}}}}$$

(25)

$${V}_{{{\mbox{DS}}}}\equiv {\phi }_{{{\mbox{D}}}}-{\phi }_{{{\mbox{S}}}}\,,$$

(26)

where ϕ_G(D) is the electrostatic potential at the gate- (drain-) electrode. Unlike metallic electrodes, it is assumed that gate-voltage-induced doping of the CNT occurs not only in the channel but also in the contact regions since graphene is semi-metallic. The electrically driven shift ξ of the CNT band structure is described by⁷²:

$$\frac{\partial \xi }{\partial (-e{V}_{{{\mbox{GS}}}})}=\frac{1}{1+\alpha \frac{{C}_{{{\mbox{Q}}}}({V}_{{{\mbox{GS}}}})}{{C}_{i}}}\,,$$

(27)

where C_i = ϵ₀ϵ_i/L denotes the classical capacitance of the insulating layer (ϵ_r = 3.9) with thickness L, α is a dimensionless parameter and C_Q(V_GS) stands for the quantum capacitance, defined as:

$${C}_{{{\mbox{Q}}}}({V}_{{{\mbox{GS}}}})={e}^{2}\int D(E)\left(-\frac{\partial {f}_{0}(E-e{V}_{{{\mbox{GS}}}})}{\partial E}\right)\,{{{{{{{\rm{d}}}}}}}}E\,.$$

(28)

Eq. (27) is solved separately for the contact region and the channel where α_contact = 0.05 for the contact and α_channel = 0.18 for the channel yielded results that most closely matched the experiment. The “CNT on graphene" is deemed two quantum capacitances in a parallel circuit, yielding a total quantum capacitance in the contacts:

$${C}_{\,{{\mbox{Q}}}}^{\prime}={C}_{{{\mbox{Q,cnt}}}}+{C}_{{{\mbox{Q,gr}}}}\,,$$

(29)

in which, the quantum capacitance of the CNT is calculated with equation (28). For the graphene-part, an analytic expression⁷³:

$${C}_{{{\mbox{Q,gr}}}}({V}_{{{\mbox{GS}}}})=\frac{2}{\pi }{\left(\frac{e}{\hslash {v}_{{{\mbox{F}}}}}\right)}^{2}{k}_{{{\mbox{B}}}}T{{{{{{\mathrm{ln}}}}}}}\,\left(2+2\cosh \left(\frac{e{V}_{{{\mbox{GS}}}}}{{k}_{{{\mbox{B}}}}T}\right)\right)\,,$$

(30)

was used, where v_F ≈ 10⁸ cm/s is the typical Fermi-velocity in graphene.

The band shift along the channel is determined by the empiric formula^26,27:

$$\, {\xi }_{{{\mbox{channel}}}}(z,{V}_{{{\mbox{GS}}}},{V}_{{{\mbox{DS}}}})=({\xi }_{{{\mbox{contact}}}}-{\xi }_{{{\mbox{center}}}}){{{\mbox{e}}}}^{-\frac{(z-{z}_{0})}{\lambda }}\\ \,+{\xi }_{{{\mbox{center}}}}-({\xi }_{{{\mbox{center}}}}+e{V}_{{{\mbox{DS}}}}-{\xi }_{{{\mbox{contact}}}}){{{\mbox{e}}}}^{\frac{({z}_{n}-z)}{\lambda }}\,.$$

(31)

with the right (left) end position of the channel z₀(z_n), the decay length, and the CNT diameter d_cnt. Again, equation (27) is used to find the band shift in the center of the channel ξ_center.

Combined electrode model and modular approach

To rigorously incorporate the electrostatics into the quantum transport calculation, the Kohn-Sham equations need to be solved self-consistently for each (V_GS, V_DS)-configuration. With the electrode model at hand, one is capable of calculating a realistic response of the carbon system to externally applied fields, which is then combined with the modular DFT+NEGF approach to compute a voltage-dependent transmission coefficient. Therefore, the matrices in equation (13) need to be adapted according to:

$${H}_{\,{{\mbox{L}}}}^{\prime}(E,{V}_{{{\mbox{GS}}}})={H}_{{{\mbox{L}}}}(E)+{\xi }_{{{\mbox{contact}}}}({V}_{{{\mbox{GS}}}}){S}_{{{\mbox{L}}}}$$

(32)

$${H}_{\,{{\mbox{R}}}}^{\prime}(E,{V}_{{{\mbox{GS}}}},{V}_{{{\mbox{DS}}}})={H}_{{{\mbox{R}}}}(E)+[{\xi }_{{{\mbox{contact}}}}({V}_{{{\mbox{GS}}}})-e{V}_{{{\mbox{DS}}}}]{S}_{{{\mbox{R}}}}\,,$$

(33)

which results in voltage dependence of the self-energies Σ_L(E, V_GS) and Σ_R(E, V_GS, V_DS).

Following the same logic, each element in the decorated channel Hamiltonian (14) is modified individually:

$${H}_{\,{{\mbox{C}}}}^{\prime}(E,{V}_{{{\mbox{GS}}}},{V}_{{{\mbox{DS}}}})= \, [{H}_{1}+{{{\Sigma }}}_{{{\mbox{L}}}}+{\xi }_{{{\mbox{channel}}}}({z}_{1}){S}_{1}]\left|1\right\rangle {\left\langle 1\right|}_{N\times N}\\ \, +\ \mathop{\sum }\limits_{i=2}^{n-1}[{H}_{i}+{\xi }_{{{\mbox{channel}}}}({z}_{i}){S}_{i}]\left|i\right\rangle {\left\langle i\right|}_{N\times N}\\ \, +\ [{H}_{n}+{{{\Sigma }}}_{{{\mbox{R}}}}+{\xi }_{{{\mbox{channel}}}}({z}_{n}){S}_{n}]\left|n\right\rangle {\left\langle n\right|}_{N\times N}\\ \, +\ \mathop{\sum }\limits_{i=1}^{n-1}[{T}_{i}+{\xi }_{{{\mbox{channel}}}}({z}_{i}){S}_{{T}_{i}}]\left|i\right\rangle {\left\langle i+1\right|}_{N\times N}.$$

(34)

Again, the corresponding block elements of Green’s function will be extracted using recursive method⁷¹ and the transmission coefficient T(E, V_GS, V_DS) is obtained using equation (23).

Supression of the interband tunneling

The choice of the channel length n is a trade-off between a realistic representation of the manufactured CNTFETs (L_channel ≈ 100 nm) and the computing time required to simulate quantum transport through systems with long channel lengths. In the used model, the impact of channel length is primarily relevant to interband tunneling processes which are promoted by short channels. Therefore, quantum transport was simulated for short channel systems by suppressing interband tunneling. For this purpose, the band-bending along the symmetry axis of the CNT needs to be determined and the energy range between the maximum of the conduction band edge and the minimum of the valence band edge is extracted. The conduction and valence band at point z_i = i ⋅ d_z is computed by the following steps: First, the corresponding, biased on- and off-site Hamiltonian and overlap matrices are extracted for the site i and the on-site matrices in momentum space at k_z = 0 are computed:

$${{{{{{{{\mathscr{H}}}}}}}}}_{i}({k}_{{{\mbox{z}}}}=0)={H}_{{{\mbox{X}}},ii}^{\prime}+{H}_{{{\mbox{X}}},ii+1}^{\prime}+{H}_{{{\mbox{X}}}\,,i+1i}^{\prime}$$

(35)

$${{{{{{{{\mathscr{S}}}}}}}}}_{i}({k}_{{{\mbox{z}}}}=0)={S}_{{{\mbox{X}}},ii}^{\prime}+{S}_{{{\mbox{X}}},ii+1}^{\prime}+{S}_{{{\mbox{X}}}\,,i+1i}^{\prime}\,,$$

(36)

where X = {L,S,R} stands for the above-defined regions of the entire Hamiltonian. For the sake of simplicity, the selfenergies Σ_R,L, σ_0, and σ_t were neglected in the following steps.

Secondly, the general eigenvalue problem

$${{{{{{{{\mathscr{H}}}}}}}}}_{i}{\psi }_{i}^{(\mu )}={E}_{i}^{(\mu )}{{{{{{{{\mathscr{S}}}}}}}}}_{i}{\psi }_{i}^{(\mu )}\,,$$

(37)

where μ denotes the band-index, is solved using the eigh method implemented in the scipy library. The N obtained eigenvalues correspond to the electronic bands of the CNT unit cell at position z_i. The valence and conduction band edges are given by ${E}_{{{\mbox{V}}},i}={E}_{i}^{(\lfloor N/2\rfloor -1)}$ and ${E}_{{{\mbox{C}}},i}={E}_{i}^{(\lfloor N/2)\rfloor }$.

Finally, the energy range associated with the interband tunneling is inhibited: T(min{E_V,i} < E < max{E_C,i}, V_GS, V_DS) = 10⁻¹⁰.

Landauer-B"uttiker formula

The simulated transmission curves exhibit numerical oscillations depending on the number of evaluation points. To obtain reasonably smooth current-voltage curves, the transmission coefficients are additionally smoothed with a one-dimensional Gaussian filter implemented in the scipy ndimage library⁷⁴. For N_E = 10001 sampling points on the energy axis, we chose a σ of 40 sampling points.

Finally, the current at a given gate- and drain-source voltage is computed with the Landauer formula⁶²:

$${I}_{{{\mbox{DS}}}}({V}_{{{\mbox{GS}}}},{V}_{{{\mbox{DS}}}})=\frac{e}{h}\int T(E,{V}_{{{\mbox{GS}}}},{V}_{{{\mbox{DS}}}})({f}_{0}(E)-{f}_{0}(E-e{V}_{{{\mbox{DS}}}}))\,{{{{{{{\rm{d}}}}}}}}E\,.$$

(38)