Introduction

Point defects have been widely used to control the optical and electronic properties of semiconductors. Recently, the magnetic properties of these materials have also been tailored by paramagnetic defects giving rise to various microscopic and mesoscopic magnetic phenomena. At low defect counteractions, controllable few-spin systems can be realized that has led to the development of point defect quantum bits1,2 (qubits) and quantum nodes3,4,5. In contrast to other qubit implementations, point defect qubits in wide-bandgap semiconductors are highly coherent and robust even at elevated temperatures2,6. Such optically addressable spin qubits, realized for example by the NV center in diamond7, the silicon vacancy8,9 in silicon carbide (SiC), and divacancy-related defects in SiC10,11, can possess as long coherence time as 1 ms at room temperature8,12,13. Research activities in this area have gained considerable momentum over the last decades and point defect-based quantum devices have become leading contenders in several areas of quantum technologies, such as quantum sensing and quantum internet14.

The coherence of spin qubits in light element semiconductors is often limited by spin-spin interactions with paramagnetic defects and nuclei. In high-purity samples, the magnetic environment of a spin qubit is defined by the surrounding nuclear spin bath15,16. Point defect spins interact with nuclear spins through the hyperfine coupling that depends on the spatial distribution of the defect’s spin density and the position of the nuclear spins. The hyperfine spin Hamiltonian term is parameterized by the hyperfine tensor, whose elements can be measured by various magnetic resonance techniques and calculated by using first-principles electronic structure methods. Conventionally, electron spin resonance (ESR) has been used to determine the hyperfine tensor for the closest nuclear spins giving rise to ~ 10–300 MHz hyperfine splitting of the nuclear spin sublevels. The high controllability and the long coherence time of point defect qubits have enabled more sophisticated nuclear spin detection techniques to be developed. Optically detected magnetic resonance (ODMR) measurement of individual point defect qubits allowed the detection of nuclear spins 2.5–7 Å distances from the NV center with hyperfine splitting ranging from 430 kHz to 14 MHz17,18. Dynamic decoupling techniques can be used to boost further the sensitivity of the measurements19,20,21,22,23. Using such techniques, nuclear spins as distant as 30 Å could be detected with hyperfine splitting of ~1 kHz22,23. These developments have opened new directions in magnetic resonance and magnetic resonance imaging in nanometer scales19,20,21,22,23. In addition, the characterized nearby nuclear spins can be utilized as additional highly coherent quantum resources for quantum computation and quantum internet4,5.

Hyperfine coupling tensors can be calculated using different first-principles methods, such as density functional theory (DFT) and wave functions-based methods. The accuracy of the computed hyperfine tensors for close nuclear spins is remarkable. For example, considering paramagnetic point defects in semiconductors a mean absolute relative error of 4.7% has been reported24. Since the hyperfine structure of the point defect’s spin sublevels is unique like a bar code, one can compare the measured and computed hyperfine tensors to identify paramagnetic defects in semiconductors unambiguously, see for instance refs. 9,25,26.

As demonstrated recently by a supercell-size-scaling test in ref. 27, the accuracy of the computed hyperfine parameters is only limited to the closest nuclear spin in 1-5 Å distances from the defect. The relative error sharply increases for nuclear spins located at large distances. As discussed in ref. 27, this is presumably due to the periodic boundary condition and related finite-size effects. Using finite cluster models, such as the C291H172 cluster and the C510H252 cluster used in refs. 28,29 to calculate the hyperfine coupling tensors at 1.5–8 Å distances from the defect, errors related to the periodic boundary condition can be eliminated. Another limitation of first-principles calculations is the model size that maximizes the number of lattice sites that can be considered.

In this work, we first demonstrate the inaccuracy of the numerical hyperfine parameters obtained with the industry standard VASP code30,31. To resolve the underlying methodological issues we introduce a real-space integration method and the use of a large support lattice for considering nuclear spins outside the boundaries of the supercell. To benchmark our method, we carry out large-scale calculations for the NV center in diamond using different exchange-correlation functionals and compare the numerical results with available experimental hyperfine data sets. From the comparison, we conclude that the HSE0632,33 functional with 0.2 mixing parameter performs best for the NV center in diamond resulting in a mean absolute percentage error of 1.7% for nuclear spins 6-30 Å distances from the NV center. This is a significant improvement compared to previous theoretical predictions obtained by using VASP. We show that the residual errors are likely related to the inaccurate calculation of the Fermi contact term. High-accuracy hyperfine tensors of ≈ 104 lattice sites as well as volumetric hyperfine data with < 0.1 Å spatial resolution are published together with this article (theoretical hyperfine tensors for all lattice sites within 30 Å distance from the NV center are available at https://ivadygroup.elte.hu/hyperfine) and ready to be used for modeling NV center quantum nodes and positioning nuclear spins around the NV center in diamond in nano-NMR measurements.

Results and discussion

The hyperfine interaction describes the weak coupling between the electron and the nuclear spins. Integrating out the spatial degrees of freedom, the corresponding hyperfine spin Hamiltonian term can be written as

$${H}_{{{{{{{{\rm{HF}}}}}}}}}={{{{{{{\bf{S}}}}}}}}{{{{{{{\bf{{{{{{{{\mathcal{A}}}}}}}}}}}}}}}}{{{{{{{\bf{I}}}}}}}},$$
(1)

where \({{{{{{{\bf{{{{{{{{\mathcal{A}}}}}}}}}}}}}}}}\) is the hyperfine tensor and S and I are the electron spin and the nuclear spin operator vectors with S = 1 and I = 1/2 quantum numbers for the NV center and adjacent 13C nuclear spins of the diamond lattice, respectively. The two dominant contributions to the hyperfine tensor are the Fermi contact interaction, \({{{{{{{{\mathcal{A}}}}}}}}}_{{{{{{{{\rm{FC}}}}}}}}}\), and the magnetic dipole–dipole coupling of the electron and nuclear spins, \({{{{{{{{\mathcal{A}}}}}}}}}_{{{{{{{{\rm{SS}}}}}}}}}\).

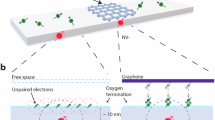
Elements of the hyperfine tensor can be calculated given the spin density of the electron spin σ(r), see Fig. 1 for the NV center, and the position RJ of nuclear spin J as24

$${{{{{{{{\mathcal{A}}}}}}}}}_{ij}^{J}=\frac{1}{2S}{\gamma }_{J}{\gamma }_{e}{\hslash }^{2}\left[\frac{8\pi }{3}\int\,\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{R}}}}}}}}}_{J})\sigma ({{{{{{{\bf{r}}}}}}}})d{{{{{{{\bf{r}}}}}}}}+{{{{{{{{\mathcal{W}}}}}}}}}_{ij}({{{{{{{{\bf{R}}}}}}}}}_{J})\right],$$
(2)

where γJ and γe are the gyromagnetic ratios of nucleus J and the electron, respectively. The first term on the r.h.s. of Eq. (2) accounts for the Fermi contact interactions, where the Dirac-delta function δ(r − RJ) takes the value of the spin density at the position of the nucleus whose spatial distribution is neglected. The largest contribution to the Fermi contact term originates from electronic states of s orbit character exhibiting non-zero probability at the nucleus site. The second term on the r.h.s. of Eq. (2) accounts for the dipole–dipole interaction, where the integral \({{{{{{{{\mathcal{W}}}}}}}}}_{ij}\) can be expressed as

$${{{{{{{{\mathcal{W}}}}}}}}}_{ij}({{{{{{{\bf{R}}}}}}}})=\int\,\left(\frac{3{({{{{{{{\bf{r}}}}}}}}-{{{{{{{\bf{R}}}}}}}})}_{i}{({{{{{{{\bf{r}}}}}}}}{{{{{{{\bf{R}}}}}}}})}_{j}}{| {{{{{{{\bf{r}}}}}}}}-{{{{{{{\bf{R}}}}}}}}{| }^{5}}-\frac{{\delta }_{ij}}{| {{{{{{{\bf{r}}}}}}}}-{{{{{{{\bf{R}}}}}}}}{| }^{3}}\right)\sigma ({{{{{{{\bf{r}}}}}}}})d{{{{{{{\bf{r}}}}}}}}.$$
(3)
Fig. 1: Spin density of the NV center in diamond.
figure 1

a and b depict top and side views, respectively. Red (blue) lobs indicate positive (negative) spin density isosurfaces and gray dots and bars show the lattice of the diamond. The isosurface value is set to ± 0.003. The blue lobs indicate weak antiferromagnetic couplings with neighboring atoms, e.g., the nitrogen of the NV center.

Full size image

First-principles electronic structure codes for solid state physics often use periodic boundary conditions, plane-wave basis sets, and pseudo-potentials to describe valance states of periodic lattices. For example, the industry standard VASP software package30,31 calculates the hyperfine tensor using the method of P. E. Blöchl34 while taking core polarization contributions into account24 in periodic boundary conditions. Employing the projector augmented wave (PAW) method35, the total spin density of the system is composed of three parts24,34

$$\sigma =\tilde{\sigma }+{\sigma }^{1}-{\tilde{\sigma }}^{1}{{{{{{{\rm{,}}}}}}}}$$
(4)

where σ1 and \({\tilde{\sigma }}^{1}\) are the atomic core-centered true and pseudo-spin densities, respectively, and \(\tilde{\sigma }\) is the total spin density of the valance electrons calculated using pseudo-potentials. With this differentiation, the Fermi contact interaction can be written as

$$\frac{8\pi }{3}\int\,\delta ({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{R}}}}}}}}}_{{{{{{{{\bf{J}}}}}}}}})\sigma ({{{{{{{\bf{r}}}}}}}})d{{{{{{{\bf{r}}}}}}}}=\frac{8\pi }{3}\left[{\sum}_{{{{{{{{\bf{G}}}}}}}}}\tilde{\sigma }({{{{{{{\bf{G}}}}}}}}){e}^{i{{{{{{{\bf{G}}}}}}}}{{{{{{{\bf{R}}}}}}}}}+\right.$$
(5)
$$\left.+\int\,{\delta }_{T}(r){\sigma }_{s{{{{{{{\bf{R}}}}}}}}}^{1}(r)dr-\int{\delta }_{T}(r){\tilde{\sigma }}_{s{{{{{{{\bf{R}}}}}}}}}^{1}(r)dr\right]{{{{{{{\rm{,}}}}}}}}$$
(6)

where \({\sigma }_{s{{{{{{{\bf{R}}}}}}}}}^{1}\) and \({\tilde{\sigma }}_{s{{{{{{{\bf{R}}}}}}}}}^{1}\) are the s-like contributions to the true and pseudo-core-centered spin densities respectively, and δT (r) is an extended Dirac-delta function, that takes into account the relativistic effects24. Spin polarization of the core electrons can be calculated within the frozen valence approximation24,36. The computed core polarization is added to σ1 and the corresponding hyperfine contribution \({{{{{{{{\mathcal{A}}}}}}}}}_{{{{{{{{\rm{1c}}}}}}}}}\) is determined. With a similar line of thought, the dipole–dipole interaction can also be expressed as

$${{{{{{{{\mathcal{W}}}}}}}}}_{ij}({{{{{{{\bf{R}}}}}}}})={\tilde{{{{{{{{\mathcal{W}}}}}}}}}}_{ij}({{{{{{{\bf{R}}}}}}}})+{{{{{{{{\mathcal{W}}}}}}}}}_{ij}^{1}({{{{{{{\bf{R}}}}}}}})-{\tilde{{{{{{{{\mathcal{W}}}}}}}}}}_{ij}^{1}({{{{{{{\bf{R}}}}}}}}){{{{{{{\rm{,}}}}}}}}$$
(7)

where the valance electrons’ contribution \({\tilde{{{{{{{{\mathcal{W}}}}}}}}}}_{ij}\) is obtained from the pseudo-spin density \(\tilde{\sigma }\) as

$${\tilde{{{{{{{{\mathcal{W}}}}}}}}}}_{ij}({{{{{{{\bf{R}}}}}}}})=-4\pi {\sum}_{{{{{{{{\bf{G}}}}}}}}}\left(\frac{{G}_{i}{G}_{j}}{{G}^{2}}-\frac{{\delta }_{ij}}{3}\right)\tilde{\sigma }({{{{{{{\bf{G}}}}}}}}){e}^{i{{{{{{{\bf{G}}}}}}}}{{{{{{{\bf{R}}}}}}}}}{{{{{{{\rm{,}}}}}}}}$$
(8)

and the one-center contributions to the dipole–dipole term can be obtained from d-like contribution to the one-center spin density24,34.

First, we use this method as implemented in VASP to calculate hyperfine tensors of all sites in a 512-atom and a 1728-atom supercell of diamond including a single NV center in the middle of the supercell, see Fig. 1. For the calculations, we use HSE06 exchange-correlation functional, 500 eV cutoff energy of the plane-wave basis set, Γ-point sampling of the Brillouin zone, and high convergence criteria. The structure of the defect is optimized as far as the largest force is smaller than 10−3 eV/Å. To compare our results with the experimental values, see Fig. 2a, we either compute the hyperfine splitting as \({A}_{z}=\scriptstyle\sqrt{{A}_{xz}^{2}+{A}_{yz}^{2}+{A}_{zz}^{2}}\)18, where Aij are the elements of the hyperfine tensor, which is compared with experimental values in the data set I taken from ref. 18, or compare the Azz hyperfine tensor element with experimental Azz values obtained from high-precision measurements in ref. 19 (data set II) and ref. 23 (data set III). Note that the latter data set is a refined and extended version of the data published in ref. 22. From the reported 50 nuclear spins, we consider only those for which both the position and the hyperfine parameter are reported with high accuracy, see Fig. 2a. When comparing the computed Azz values with data sets II–III, we found a consistent sign difference between theory and experiment. The sign of our hyperfine values agrees with other theoretical calculations, i.e., VASP’s values as well as the values reported in refs. 28,29. Therefore, we anticipate that the discrepancy originates from the convention used in the experiments. Hereinafter, we omit this sign difference.

Fig. 2: Comparison of experimental and theoretical hyperfine parameters.
figure 2

a Experimental data sets of hyperfine parameters reported in ref. 18 (data set I), in ref. 19 (data set II.), and in ref. 23 (data set III). Gray columns depict the measured hyperfine parameters, Az for data set I and Azz for data sets II and III. The red bars depict the absolute error of the measurements. b Absolute relative error (ARE) of the calculated hyperfine values showing increasing error due to finite-size effects. Blue columns with squares and red columns with circles depict the ARE of calculations with supercells containing respectively 512-, and 1728 atomic positions. When no bars are depicted for certain elements of the data sets, the corresponding nuclei site is outside the supercell used for the calculations. Value 1 on the y-scale corresponds to a 100% absolute percentage error.

Full size image

In Fig. 2b, we depict the absolute relative error of the computed hyperfine splitting values for data sets I–III. As can be seen, the absolute relative error of the theoretical values rapidly increases with decreasing value of the experimental hyperfine parameter, and below ~ 1 MHz wildly fluctuates. It is also clear that the use of a large supercell does not improve the comparison with the experiments. Finally, we note that for making the comparison between theory and experiment we needed to position the nuclear spins measured in data sets I and II. For this, we used our improved hyperfine tensor computation discussed next.

Finite-size correction of hyperfine tensors computed in periodic supercell models has not been thoroughly investigated before. There are several possible sources of finite-size effects that can lead to non-physical interaction of nuclear spins and period defect structures. For instance, the spin density of a defect and its periodic replicas may overlap in small supercell models giving rise to overestimated Fermi contact interaction terms and perturbed dipole–dipole interaction terms for certain nuclei sites. This error is, however, assumed to decay exponentially with the size of the supercell since localized defect states decay exponentially. More difficult-to-handle finite-size effects arise from the long-range dipole–dipole interaction that decays with the third power of the distance of the spins. In periodic supercell models, nuclear spins interact with a lattice of defects. In contrast to the Coulomb interaction, the dipole–dipole interaction does not diverge, although the interaction strength and the hyperfine tensor’s principal axis may be considerably perturbed. A nuclear spin halfway between the defect and one of its periodic replicas interacts with two spin densities with approximately the same coupling strength that can give rise to \({{{{{{{\mathcal{O}}}}}}}}(100 \% )\) error explaining our observations depicted in Fig. 2b. In the following, we remedy these finite-size effects.

The errors are derived from the long-ranged interaction term, i.e., the pseudo-dipole–dipole integral \({\tilde{{{{{{{{\mathcal{W}}}}}}}}}}_{ij}\) defined in Eq. (8). The periodicity of the spin density and thus the finite-size effects are encoded into the pseudo-spin density \(\tilde{\sigma }({{{{{{{\bf{G}}}}}}}})\). The point defect and its replicas cannot be separated in Fourier space; however, in real space, this can be easily achieved by simply limiting the range of integration. To overcome the finite-size dependence of the dipolar hyperfine interaction term, we utilize this strategy and combine it with the PAW method. To this end, we calculate \({\tilde{{{{{{{{\mathcal{W}}}}}}}}}}_{ij}\) as

$${\tilde{{{{{{{{\mathcal{W}}}}}}}}}}_{ij}({{{{{{{\bf{{R}}}}}}}^{+}}})=\int\limits ^{{\overline{\Omega }}_{{{{{{{{\rm{SC}}}}}}}}}}\left(\frac{3{({{{{{{{\bf{r}}}}}}}}-{{{{{{{\bf{{R}}}}}}}^{+}}})}_{i}{({{{{{{{\bf{r}}}}}}}}-{{{{{{{\bf{{R}}}}}}}^{+}}})}_{j}}{| {{{{{{{\bf{r}}}}}}}}-{{{{{{{\bf{{R}}}}}}}^{+}}}{| }^{5}}-\frac{{\delta }_{ij}}{| {{{{{{{\bf{r}}}}}}}}-{{{{{{{\bf{{R}}}}}}}^{+}}}{| }^{3}}\right)\sigma ({{{{{{{\bf{r}}}}}}}})d{{{{{{{\bf{r}}}}}}}}{{{{{{{\rm{,}}}}}}}}$$
(9)

where the extended position coordinates R+ include the lattice sites within the supercell (R) and outside the supercell provided by a support lattice within a sphere of 30 Å radius centered on the NV center. The support lattice is aligned with the supercell, although it does not contain the atomic sites of the supercell. This way the hyperfine interaction calculation is not limited by the size of the supercell. Note that for the integration we use the full spin density σ(r) expressed on a fine grid and not the pseudo-spin density in contrast to Eq. (8). For nuclear spins contained within the supercell, the real-space integration is carried out over the supercell except a sphere of rPAW radius centered at the nuclear spin position R, i.e., \({\overline{\Omega }}_{{{{{{{{\rm{SC}}}}}}}}}={\Omega }_{{{{{{{{\rm{SC}}}}}}}}}-{\Omega }_{{{{{{{{\rm{PAW}}}}}}}}}({{{{{{{\bf{R}}}}}}}})\). The total dipole–dipole interaction term is defined as \({{{{{{{{\mathcal{W}}}}}}}}}_{ij}({{{{{{{\bf{R}}}}}}}})={\tilde{{{{{{{{\mathcal{W}}}}}}}}}}_{ij}({{{{{{{\bf{R}}}}}}}})+{{{{{{{{\mathcal{W}}}}}}}}}_{ij}^{1}({{{{{{{\bf{R}}}}}}}})\) in contrast to Eq. (7). The Fermi contact interaction with a core polarization contribution is obtained using the VASP’s implementation24. For lattice sites outside the supercell’s boundaries, the spin density is considered to be zero at the nuclear spin site, i.e., both the \({{{{{{{{\mathcal{W}}}}}}}}}_{ij}^{1}({{{{{{{\bf{{R}}}}}}}^{+}}})\) and the Fermi contact terms are approximated to be zero. The sole non-zero term for these sites is given by Eq. (9), where the integration is carried over the full supercell volume. With these modifications, the computed tensors account for the case when the nuclear spins interact with an isolated defect and not with a lattice of defects. We anticipate that the leading finite-size effects will be removed within our approach.

To compute the hyperfine tensors for a large number of lattice sites, ~ 20000 sites within a sphere \({R}_{{{{{{{{\rm{cut}}}}}}}}}^{+}=30\) Å around the NV center, we implement the real-space integration method in an in-house code that post-processes the VASP output files. The ground state calculations of the NV center are carried out in 512-atom and 1728-atom supercells using the experimental lattice parameter of 3.567 Å. We use both the semi-local PBE37 and various forms of the HSE06 hybrid functional, which are labeled as HSE(α), where α is the mixing parameters, e.g., HSE(0.25) = HSE06. The ground state spin density used in the calculation of Eq. (9) is defined on a real-space grid of 0.036 Å spacing. The positions of the nuclear spins for data set III are taken from ref. 23. For data sets I and II we use the following strategy for positioning the nuclear spins: Considering an experimental hyperfine value, we look for the closest theoretical value in our data set. Depending on the error bar of the measurement and the calculations, we can position nuclear spin up to symmetrically equivalent sites with this method.

The hyperfine splitting values computed with our method are significantly improved compared to the currently available implementation24. The relative error of the theoretical values reduces from \({{{{{{{\mathcal{O}}}}}}}}(100 \% )\) to \({{{{{{{\mathcal{O}}}}}}}}(1 \% )\), see Figs. 2b and  3. For different data sets, we obtain different mean absolute percentage errors (MAPE). For data set I we obtain a MAPE of 3.8%, while the experimental data exhibit an averaged relative error margin of 1.2%18. The obtained MAPE of the improved theoretical values for data set II is 1.5%, which is better than the relative error margin of the experimental data of 3.3%19. This suggests that the theoretical values are “overfitted" for data set II, i.e., multiple matching hyperfine values were found within the error margin of the experimental data. By selecting the closest ones, we could obtain a MAPE smaller than the experimental error bar. The most accurate hyperfine values, with a relative error margin of 6 × 10−3%, together with nuclear spin positions are provided for data set III23. These high-precision measurements allow us to make a reliable assessment of the error bar of the theoretical values. Considering the 29 most accurately measured and positioned nuclear spins, we obtain a MAPE of 1.79%. In Fig. 3, we also depicted the ARE of hyperfine values obtained with the PBE functional. As can be seen, the HSE06 functional consistently improves on the PBE values, especially for nuclear spins found close to the NV center. We also note that the use of accurate DFT spin density has high relevance. Considering point spin density approximation, i.e., σ(r) = δ(r − r0) where r0 is the center of the NV center, we obtain a mean absolute relative error (MARE) of 76% for data set III (see Supplementary Fig. S1).

Fig. 3: Absolute relative error of the hyperfine splitting values calculated with our improved integration method.
figure 3

Gray columns depict the absolute relative error (ARE) of the experimental data, red thin columns with circles depict the ARE of the computed hyperfine values obtained with HSE06 functional, and light blue lines with squares depict the ARE of the theoretical values obtained with PBE functional, see “Methods” for details of the calculations. The values provided on the upper horizontal axis are the PBE absolute relative errors being out of the range of the vertical axis.

Full size image

Finally, we investigate the source of residual errors and possible further measures to improve the computed hyperfine tensors. For this study, we use data set III. First of all, it is notable that the mean signed relative error (MSRE) of −0.12% is significantly smaller than the MARE of 1.79%, suggesting that there are no large systematic errors and the discrepancies may be related to numeral uncertainties. Next, we plot the MARE as a function of the Fermi contact term, see Fig. 4, and as a function of the distance, see Supplementary Fig. S2. There seems to be a correlation between the largest errors and the value of the Fermi contact term. Due to the distance dependence of the Fermi contact term, the MARE seems to decay with the distance of the nuclear spins, see Supplementary Fig. S2. It should be noted; however, that large errors are also obtained for a few nuclear spins that are beyond the boundaries of the supercell, where we explicitly neglect the Fermi contact terms. Here, the neglect of the Fermi contact term may be the source of the error. To attempt to reduce the errors, we tune the mixing parameter α of the HSE functional and study the variation of the MARE obtained for data set III, see Supplementary Fig. S3. By reducing the mixing parameter from 0.25 to 0.2, we obtain a slightly decreased MARE of 1.69%, although an enlarged MSRE of −0.32%. These results indicate that tuning the functional’s inner parameters may lead to an improved description of the spin density, which in turn can reduce the relative error between theory and experiments. Overall, the hyperfine values may be further improved by enhancing numerical accuracy for the core/Fermi contact contribution and by fine-tuning the function.

Fig. 4: Absolute relative error of the theoretical values as a function of the Fermi contact contribution to the computed hyperfine parameter.
figure 4

The theoretical values are obtained by using HSE06 functional and 1728 atom supercell. Green, blue, and red columns depict the absolute relative error (ARE) values corresponding to data sets I, II, and III, respectively.

Full size image

In summary, we demonstrated in this article that high-accuracy, finite-size effect-free hyperfine tensors can be calculated using an improved integration method. Compared to the industry standard VASP code, we could achieve a ~ 100-fold reduction of the MARE of the theoretical values. Having more experimental data of high precision and further improved numerical accuracy in larger supercells may help to obtain superior theoretical hyperfine data compared to what has been presented here. The obtained and potentially improved future data is available online [34]. The provided data can be used for high-precision simulation of the NV center-nuclear spin few-body quantum systems as well as positioning nuclear spin around the NV center.

Methods

For VASP calculations, we use a 512-atom and a 1728-atom supercell of diamond including a single NV center in the middle of the supercell. For the calculations, we use the Perdew–Burke–Ernzerhof (PBE)37 and the Heyd-Scuseria-Ernzerhof (HSE06)32,33 exchange-correlation functional, 500 eV cutoff energy of the plane-wave basis set, Γ-point sampling of the Brillouin zone, and high convergence criteria (PREC = Accurate). The energy threshold for the self-consistent field calculations is set to 10−6 eV. The structure of the defect is optimized as far as the largest force is smaller than 10−3 eV/Å. For the real-space hyperfine tensor calculations, we use the convergent spin density of the 1728-atom supercell model defined on a fine real-space grid of 0.036 Å (a0/600) spacing obtained by VASP.