Synthetic ${{\mathbb{Z}}}_{2}$ gauge theories based on parametric excitations of trapped ions

Abstract

Resource efficient schemes for the quantum simulation of lattice gauge theories can benefit from hybrid encodings of gauge and matter fields that use the native degrees of freedom, such as internal qubits and motional phonons in trapped-ion devices. We propose to use a parametric scheme to induce a tunneling of the phonons conditioned to the internal qubit state which, when implemented with a single trapped ion, corresponds to a minimal ${{\mathbb{Z}}}_{2}$ gauge theory. To evaluate the feasibility of this scheme, we perform numerical simulations of the state-dependent tunneling using realistic parameters, and identify the leading sources of error in future experiments. We discuss how to generalize this minimal case to more complex settings by increasing the number of ions, moving from a single link to a ${{\mathbb{Z}}}_{2}$ plaquette, and to an entire ${{\mathbb{Z}}}_{2}$ chain. We present analytical expressions for the gauge-invariant dynamics and the corresponding confinement, which are benchmarked using matrix product state simulations.

Introduction

Understanding the role of symmetry and its breakdown in the emergence of various forms of order has played a key historical role in many-body physics¹. In this context, the spontaneous breakdown of a global symmetry can unveil a local order parameter², which is crucial to understand phase transitions between different phases of matter, as well as scaling and universality in the vicinity of certain types of critical points separating these phases³. Ultimately, it is this scaling and universality that underly our understanding of renormalization-group fixed points and the very definition of a quantum field theory (QFT)^4,5. It is within the realm of a particular type of QFTs, relativistic ones, where symmetry has also played a pivotal historic role⁶. In addition to symmetry breaking, and the consequences it brings when the global symmetry being broken is continuous^7,8, the gauging of some of these global symmetries has also been paramount of importance⁹. By the introduction of additional gauge fields, these symmetries are converted into local ones, and determine the way in which particles interact with each other.

In particular, gauging of SU(2)_L × U(1) and SU(3) symmetries underlies our understanding of nature at its most fundamental level, leading to our models of the electroweak^{10,11,12,13,14} and strong^{15,16,17,18,19} interactions, as well as their interplay with the breakdown of continuous symmetries^20,21. Altogether, the interplay of global and local symmetries, and how gauge fields get intertwined with matter fields, culminates in the standard model of particle physics²², our most fundamental theory of nature that has been tested with unprecedented precision. In spite of all the progress and detailed understanding of many facets of the standard model of physics, there still remain open questions that do not require looking for other theories beyond. These open problems arise in non-perturbative phenomena that are somehow linked to the (de)confinement of particles²³, and the dynamical and static phenomena that occur at high densities²⁴, or in non-equilibrium heavy ion collisions²⁵. These questions must be addressed non-perturbatively, e.g., on a lattice²⁶, where great progress has taken place over the years leading, for instance, to the precise ab-initio determination of the hadron masses in agreement with the quark-model predictions²⁷. Yet, the so-called sign problem^28,29 has partially hindered further progress for finite-density and real-time problems using numerical Monte Carlo path-integral techniques.

To make further progress, important insights can be gained by looking at lower dimensions and simpler gauge groups. For example, the study of gauge theories in one spatial dimension has improved our understanding of confinement in high-energy physics^{30,31,32,33,34}. Focusing also on discrete groups, such as the ${{\mathbb{Z}}}_{2}$ gauge theory in two spatial dimensions³⁵, one can unveil the role of non-local order parameters in a confinement-deconfinement phase transition^26,35. The deconfined phase of this model displays an exotic collective ordering, so-called topological order^36,37, with a ground state with two characteristic features. First, it has a degeneracy that depends on topological invariants related to the homology of the low-energy excitations. Secondly, it displays long-range entanglement in spite of a non-zero energy gap.

It is worth mentioning that discrete-group gauge theories also appear as effective descriptions in condensed matter³, e.g., high-temperature superconductivity and magnetism^38,39,40. Here, one typically deals with Hamiltonian gauge theories⁴¹ in which Gauss’ law restricts the system to a specific super-selection sector characterized by a background charge density. Whereas the vacuum is the privileged super-selection sector in high-energy physics, any other sector is in principle equally valid in condensed matter⁴². Moreover, Gauss’ law need not be a strict constraint, but can instead arise as soft constraint due to an energetic penalty in the Hamiltonian⁴³. For a ${{\mathbb{Z}}}_{2}$ gauge theory, this approach allows to unveil another characteristic property of topological order, namely the mutual anyonic statistics of the excitations, which becomes relevant for fault-tolerant quantum computation^44,45. Due to all of these cross-disciplinary connections between high-energy physics, condensed matter, and quantum computation, the study of ${{\mathbb{Z}}}_{2}$ lattice gauge theories^{46,47,48,49,50,51,52,53,54}, and also the larger ${{\mathbb{Z}}}_{d}$ groups⁵⁵, has shown a remarkable progress in recent years^{56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73}. This interest has been further encouraged by key advances in the field of quantum simulators (QSs)^{74,75,76,77,78}: experimental systems that can be controlled to realize a target Hamiltonian gauge theory in the laboratory. This approach exploits the discrete nature of the gauge groups to find efficient experimental encodings of the gauge fields. Starting with the pioneering cold-atom proposals for the digital^79,80,81,82 and analog^{83,84,85,86,87,88,89} QSs for lattice gauge theories, a considerable effort has been devoted to push these QSs along various novel research directions (see reviews^{90,91,92,93,94,95,96,97,98,99}). In this regard, an alternative to discrete gauge groups is the so-called “quantum-link” approach^100,101,102, both for Abelian and non-Abelian gauge groups^{103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120}. These advances have stimulated the experimental efforts to build the first prototype QSs for lattice gauge theories^{121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142}. Gauge-theory QSs do not suffer from the sign problem of Monte Carlo methods with fermionic matter at finite densities and real-time dynamics^28,29. Therefore, they have the potential of addressing questions that have remained elusive for decades. Since solving the sign problem lies in the class of NP (nondeterministic polynomial time)-hard problems²⁸, such that no polynomial-time classical algorithm is likely to be found, large-scale QSs of gauge theories are good candidates to demonstrate practical quantum advantage. In fact, QSs of the real-time dynamics of even simpler field theories have been proven to be BQP (bounded-error quantum polynomial time)-hard problems^143,144,145 and, thus, among the hardest problems that can be solved with a quantum computer. Unless a collapse of the complexity classes occurs, large-scale QSs of gauge theories should lead to stronger instances of quantum advantage that go beyond the superiority with respect to the sign problem of a certain type of classical algorithms, and are instead ultimately supported by the complexity of problems that can be solved by quantum computers. In light of this promising future, an outstanding question for gauge-theory QSs is to find viable schemes that allow one to move from the initial prototypes towards the large-scale regime, both in terms of lattice sizes (i.e., qubit numbers) and simulation times (i.e., circuit depths). Experiments based on schemes that use specific concatenation of gates have already allowed for small-scale QSs of certain gauge theories^{121,123,125,127,131,132,133,134,135,136,138,139,140,142}. However, the existing levels of noise and errors, which accumulate along the circuits, will most likely require the use of future quantum-errror-corrected devices in order to reach very large scales. Although less flexible, the experiments on analog QSs for gauge fields^{122,124,126,128,129,130,137,141} are, in principle, more amenable for scaling, even in the presence of noise¹⁴⁶. In this work, we thus focus on analog QSs, and choose the ${{\mathbb{Z}}}_{2}$ lattice gauge theory with dynamical matter as our target. In spite of its apparent simplicity, analog QSs of this gauge theory have only been recently realized for two matter sites coupled by an intermediate gauge link in recent cold-atom experiments¹²⁴. Other experiments targeting this model in superconducting-qubit arrays¹³⁷ are limited by the appearance of terms that explicitly break the gauge symmetry. Therefore, it would be desirable to find alternatives that allow one to reach the desired large-scale QSs. In this manuscript, we present a detailed toolbox for the QS of ${{\mathbb{Z}}}_{2}$ lattice gauge theories coupled to dynamical matter using trapped-ion systems that can overcome these limitations.

Our toolbox exploits the versatility of trapped-ion platforms, which not only contain qubits/spins that can be used to encode directly the ${{\mathbb{Z}}}_{2}$ fields, which can be understood as a binary truncation of an electric-field line, but also have quantized vibrational degrees of freedom, i.e., phonons, that can play the role of matter fields. As discussed in detail below, this hybrid spin-motional toolbox includes simple building blocks that can be realized already with state-of-the-art technologies, benefiting from the current techniques used by ion trappers for quantum computation in the context of high-precision phonon-mediated gates. The key novel aspect is that these phonons are no longer used as auxiliary buses to mediate the entangling gates between the qubit degrees of freedom, but instead become dynamical degrees of freedom themselves mimicking discretised matter fields in the QS. In order to make the connection to ${{\mathbb{Z}}}_{2}$ gauge theories, we show how a particular state-dependent parametric excitation can lead to a frequency conversion between a pair of excitations of different phonon modes mediated by the ion qubit, which can be interpreted as a gauge-invariant tunneling along a single link. Building on this result, we present more scalable schemes, going from a single plaquette to a full chain, which could be implemented upon realistic technological developments. We believe that the results presented open an interesting direction to extend the QSs of ${{\mathbb{Z}}}_{2}$ lattice gauge theories to more challenging scenarios, and set the stage for future trapped-ion studies that explore gauge-theory QSs in higher spatial dimensions.

Results and discussion

Dynamical gauge fields: the ${{\mathbb{Z}}}_{2}$ theory on a link

State-dependent parametric tunneling

The use of periodic resonant modulations allows to design quantum simulators on a lattice that has a connectivity different from the original one. This leads to the concept of synthetic dimensions^147,148, as recently reviewed in ref. ¹⁴⁹, which have been realized in various experimental platforms^{150,151,152,153,154,155,156,157,158,159,160,161}. A particular form of these resonant modulations can be achieved by a parametric excitation/driving, which will be the main tool exploited in this work. In its original context, a parametric excitation induces couplings between different modes of the electromagnetic field, leading to a well-known technique for frequency conversion and linear amplification of photons^{162,163,164,165,166}. For instance, as originally discussed in ref. ¹⁶², a small periodic modulation of the dielectric constant of a cavity can lead to different couplings between the cavity modes that can be controlled by tuning the modulation frequency to certain resonances. In the particular case of frequency conversion, this scheme can be understood in terms of a parametric tunneling term between two synthetic lattice sites labeled by the frequencies of the two modes, which is the essence of the schemes for synthetic dimensions discussed in refs. ^147,148. As emphasised in ref. ¹⁶⁷, this simple parametric tunneling already inherits the phase of the drive¹⁶², such that one could design and implement¹⁶⁸ non-trivial schemes where this phase mimics the Aharonov-Bohm effect of charged particles moving under a static background magnetic field¹⁶⁹. These ideas can also be exploited when the modes belong to distant resonators coupled via intermediate components, such as mixers¹⁷⁰ or tunable inductors¹⁷¹. This leads to parametric tunneling terms where the phase can be tuned locally, leading to quantum simulators of quantum Hall-type physics¹⁷². Furthermore, periodic modulations of the mode frequencies with a relative phase difference can also lead to these synthetic background gauge fields^173,174, as demonstrated in experiments that exploit Floquet engineering in optical lattices^{175,176,177,178}, symmetrically-coupled resonators¹⁷⁹, and trapped-ion crystals¹⁸⁰. We should mention that there are other schemes for static background gauge fields that do not exploit periodic modulations, but instead mediate the tunneling by an intermediate quantum system^{181,182,183,184,185,186,187}.

In the Supplementary Note 1, we present a detailed description of the use of parametric excitations in this context, and the possible implementation of quantum Hall-type physics in crystals of trapped ions. We emphasize that the parametric schemes discussed in the Supplementary Note 1 lead to a background static gauge field, the dynamics of which does not follow from a gauge theory. In this section, we start by discussing how to generalize the scheme towards the quantum simulation of the simplest discrete gauge theory: a ${{\mathbb{Z}}}_{2}$ gauge link. We consider two modes $d\in {{{{{{{\mathcal{D}}}}}}}}=\{1,2\}$ of energies ω_d (ℏ = 1 henceforth) and an additional spin-1/2 system/qubit¹⁸⁸, which is initially decoupled from the modes. The bare Hamiltonian is

$${\tilde{H}}_{0}={\omega }_{1}{a}_{1}^{{{{\dagger}}} }{a}_{1}+{\omega }_{2}{a}_{2}^{{{{\dagger}}} }{a}_{2}+\frac{{\omega }_{0}}{2}{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z},$$

(1)

where we have introduced the qubit transition frequency ω₀, the Pauli matrix ${\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}=\vert {\uparrow }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \langle {\uparrow }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\vert -\vert {\downarrow }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \langle {\downarrow }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\vert$, and the creation annihilation operators ${a}_{d}^{{{{\dagger}}} },{a}_{d}$ for each mode of frequency ω_d. The choice of the convoluted notation for the index of the qubit will be justified below once we interpret the effective model in the light of a synthetic lattice gauge theory.

The idea now is to consider a generalization of a frequency-conversion parametric driving that includes two tones $\tilde{V}(t)={\tilde{V}}_{1}+{\tilde{V}}_{2}$. One of them yields a parametric drive

$${\tilde{V}}_{1}={\Omega }_{{{{{{{{\rm{d}}}}}}}}}{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}{a}_{2}^{{{{\dagger}}} }{a}_{1}\cos ({\phi }_{{{{{{{{\rm{d}}}}}}}}}-{\omega }_{{{{{{{{\rm{d}}}}}}}}}t)+{{{{{{{\rm{H.c.}}}}}}}},$$

(2)

which has an amplitude that depends on the state of the qubit. Additionally, the other tone drives transitions on the qubit

$${\tilde{V}}_{2}={\tilde{\Omega }}_{{{{{{{{\rm{d}}}}}}}}}{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}\cos ({\tilde{\phi }}_{{{{{{{{\rm{d}}}}}}}}}-{\tilde{\omega }}_{{{{{{{{\rm{d}}}}}}}}}t)+{{{{{{{\rm{H.c.}}}}}}}},$$

(3)

where we have introduced an additional Pauli matrix ${\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}=\vert {\uparrow }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \langle {\downarrow }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\vert +\vert {\downarrow }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \langle {\uparrow }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\vert$. Considering that the frequency and strength of this additional driving are constrained by

$${\tilde{\omega }}_{{{{{{{{\rm{d}}}}}}}}}={\omega }_{0},| {\tilde{\Omega }}_{{{{{{{{\rm{d}}}}}}}}}| \,\ll \,4{\omega }_{0},$$

(4)

we can follow the exact same steps as those discussed in the Supplementary Note 1 to show that, after setting ${\phi }_{{{{{{{{\rm{d}}}}}}}}}={\tilde{\phi }}_{{{{{{{{\rm{d}}}}}}}}}=0$, the two-tone drive leads to a time-independent effective Hamiltonian ${\tilde{V}}_{I}(t)\,\approx \,{\tilde{H}}_{{{{{{{{\rm{eff}}}}}}}}}$ that supersedes the discussion in the supplementary material, and reads

$${H}_{{{{{{{{\rm{eff}}}}}}}}}=\left({t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}{a}_{2}^{{{{\dagger}}} }{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}{a}_{1}+{{{{{{{\rm{H.c.}}}}}}}}\right)+h{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}$$

(5)

where we have introduced the effective couplings

$${t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}=\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{2},\,{{{{{{{\rm{and}}}}}}}}\,h=\frac{{\tilde{\Omega }}_{{{{{{{{\rm{d}}}}}}}}}}{2}.$$

(6)

There are two important aspects to highlight. First, we have again managed to engineer a synthetic link connecting the two modes via the tunneling of particles. However, in contrast to the discussion in the supplementary material, the qubit enters in this process and mediates the tunneling. In the spirit of synthetic dimensions, we can say that the qubit effectively sits on the synthetic link (see Fig. 1a). It is for this reason that the label used for the qubit (1, e₁) refers to the link that connects the synthetic site 1 to its nearest neighbor 2 via the direction specified by the vector e₁. This notation has a clear generalization to larger lattices and different geometries, and is common in the context of lattice gauge theories¹⁸⁹. The second important aspect to remark is that the dynamics dictated by the Hamiltonian of Eq. (5), considering also the term proportional to h, has a local/gauge ${{\mathbb{Z}}}_{2}$ symmetry. This gauge symmetry is related to the previous U(1) phase rotation of the modes discussed in the supplementary material when restricting to a π phase. More importantly, this π phase can be chosen locally. We can transform either ${a}_{1},{a}_{1}^{{{{\dagger}}} } \,\, \mapsto -{a}_{1},-{a}_{1}^{{{{\dagger}}} }$, or ${a}_{2},{a}_{2}^{{{{\dagger}}} } \,\, \mapsto -{a}_{2},-{a}_{2}^{{{{\dagger}}} }$ by a local π phase, and retain gauge invariance in the Hamiltonian by simultaneously inverting the link qubit ${\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}\mapsto -{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z},{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}\mapsto {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}$. Accordingly, the qubit can be interpreted as a ${{\mathbb{Z}}}_{2}$ gauge field introduced to gauge the global ${{\mathbb{Z}}}_{2}$ inversion symmetry of the Hamiltonian paralleling the situation with other groups where gauge fields are introduced in the links of the lattice and mediate the tunneling of matter particles¹⁸⁹. Accordingly, we see that the analogy with gauge theories is not a mere notational choice due to our qubit labeling, but rests on the effective gauging of the symmetry: the engineered tunneling leads to a discretised version of the covariant derivative that is required to upgrade a global symmetry into a local one.

Fig. 1: Synthetic ${{\mathbb{Z}}}_{2}$ gauge links and Gauss’ law.

a Schematic representation of the effective Hamiltonian in Eq. (5). The two modes labeled by 1,2, which play the role of matter fields, are coupled by a synthetic tunneling of strength ${t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$(6) that is mediated by a qubit that plays the role of the gauge field, and effectively sits on the synthetic link. In addition to the tunneling, the electric-field term of strength h(6) drives transitions in the qubit (inset). b For a single particle, Gauss' law (8) for a distribution of background charges q₁ = 0, q₂ = 1, is fulfilled by the two states $\vert {1}_{1},{-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}},{0}_{2}\rangle ,\vert {0}_{1},{+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}},{1}_{2}\rangle$, characterized by the absence or presence of an electric field attached to the matter particle sitting on the leftmost or rightmost site. These electric-field states are represented by arrows parallel (anti-parallel) to the external field h, and the presence (absence) of the corresponding electric-field line is represented by a thicker (shaded) golden link.

In Hamiltonian approaches to lattice gauge theories⁴¹, one can work in Weyl’s temporal gauge, such that there is a residual redundancy that is dealt with by imposing Gauss’ law. As usually in the literature^{46,47,48,49,50,51,52,53,54,56,57,58,59,60,61,62,63,64,66,68,69,70,71,72}, one refers to the external field h as the electric field term, and talks about the Hadamard states $\vert {\pm }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle =(\vert {\uparrow }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \pm \vert {\downarrow }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle )/\sqrt{2}$ as the electric-field basis, such that the $\vert {+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle$ state describes an electric field line connecting two neighboring sites. The generators of the aforementioned local symmetries [H_eff, G₁] = [H_eff, G₂] = [G₁, G₂] = 0 are thus

$${G}_{1}={{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {a}_{1}^{{{{\dagger}}} }{a}_{1}}{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x},{G}_{2}={\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {a}_{2}^{{{{\dagger}}} }{a}_{2}},$$

(7)

and Gauss’ law is imposed by fixing a specific super-selection sector that fulfills

$${G}_{1}\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}\rangle ={{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {q}_{1}}\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}\rangle ,{G}_{2}\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}\rangle ={{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {q}_{2}}\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}\rangle .$$

(8)

Here, q_i ∈ {0, 1} are the so-called background charges, and $\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}\rangle$ is a generic state of the physical system that is a common eigenstate of the local-symmetry generators. These generators, which fulfill ${G}_{i}^{2}={\mathbb{I}}$, and thus only have the two discrete eigenvalues ± 1, can be used to define orthogonal projectors ${P}_{\{{q}_{i}\}}=\prod\limits_{j}\frac{1}{2}({\mathbb{I}}+{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {q}_{j}}{G}_{j})$. Due to the gauge symmetry, the Hamiltonian is block-diagonal in subspaces with a fixed arrangement of background charges ${H}_{{{{{{{{\rm{eff}}}}}}}}}={\sum}_{\{{q}_{i}\}}{P}_{\{{q}_{i}\}}{H}_{{{{{{{{\rm{eff}}}}}}}}}{P}_{\{{q}_{i}\}}$, and the different super-selection sectors cannot be connected by the gauge-invariant dynamics.

In Fig. 1b, we depict the possible states for this physical subspace in the case of a single particle, where one can see how the link qubit must lie in a specific electric-field state such that Gauss’ law is fulfilled for the choice q₁ = 0, q₂ = 1. In particular, when a single particle sits in the rightmost site 2, an electric field line is created by flipping the qubit in the link that connects it to the leftmost site 1. This is a clear analogy to Maxwell electrodynamics, where the regions with a net charge act as sinks/sources of the electric field. In fact, for (1 + 1)-dimensional quantum electrodynamics, i.e., the Schwinger model^30,31,32, a U(1) positive charge acts as a source of an electric field that remains constant in space until a negative charge is found, which acts a sink. This leads to an electric field string connecting the electron-positron pair³². As we will discuss in more detail below, a similar effect occurs when the ${{\mathbb{Z}}}_{2}$ gauge theory (5) is extended to larger chains. Here, the particle moves by stretching or compressing the electric field string, which resembles the Dirac string construction that attaches an infinitely-thin solenoid carrying magnetic flux to a magnetic charge, i.e., a magnetic monopole¹⁹⁰. The electric analog is, nonetheless, a 1D effect and, furthermore, it is gauge-invariant and observable as emphasised below.

Before going to these generalizations, let us discuss simple dynamical manifestations of this electric field string that will be a guide for the trapped-ion implementation discussed in the following section. Although the quantum simulation scheme leading to Eq. (5) works for both fermionic and bosonic matter, we will thus focus on the later that will be mapped onto trapped-ion phonons. For two bosonic modes and a single gauge qubit, the Hilbert space is infinite dimensional ${{{{{{{\mathcal{H}}}}}}}}={{{{{{{\mathcal{F}}}}}}}}\otimes {{\mathbb{C}}}^{2}$, where ${{{{{{{\mathcal{F}}}}}}}}={\oplus }_{n = 0}^{\infty }{{{{{{{{\mathcal{F}}}}}}}}}_{n}$, and each subspace ${{{{{{{{\mathcal{F}}}}}}}}}_{n}={{{{{{{\rm{span}}}}}}}}\{\vert {n}_{1}\rangle \otimes \vert {n}_{2}\rangle :{n}_{1}+{n}_{2}=n\}$ contains n bosonic particles in total. These subspaces can be spanned by the corresponding Fock states $\vert {n}_{i}\rangle ={({a}_{i}^{{{{\dagger}}} })}^{{n}_{i}}\vert {0}_{i}\rangle /\sqrt{{n}_{i}!}$, where $\vert {0}_{i}\rangle$ is the vacuum of the i-th mode. As a consequence of the global U(1) symmetry and Gauss’ law (8), we can reduce the size of the subspace where the dynamics takes place, and find some neat manifestations of the correlations between the charge and electric field degrees of freedom. In particular, we will show how the dynamics of the ${{\mathbb{Z}}}_{2}$ link can be understood in terms of typical phenomena in quantum optics, such as Rabi oscillations, dark states, and mode entanglement.

One-boson sector: Rabi oscillations and matter-gauge-field correlated dynamics

When the initial state contains a single particle, we can restrict the Hilbert space to ${{{{{{{{\mathcal{F}}}}}}}}}_{1}\otimes {{\mathbb{C}}}^{2}$ using the global U(1) symmetry. Moreover, Gauss’ law (8) for q₁ = 0, q₂ = 1 allows us to restrict the physical states further to a two-dimensional subspace ${{{{{{{{\mathcal{V}}}}}}}}}_{{{{{{{{\rm{phys}}}}}}}}}\subset {{{{{{{\mathcal{H}}}}}}}}$, such that the states have the form $\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}(t)\rangle ={c}_{r}(t)\vert {{{{{{{\rm{R}}}}}}}}\rangle +{c}_{l}(t)\vert {{{{{{{\rm{L}}}}}}}}\rangle$, where we have introduced

$$\vert {{{{{{{\rm{L}}}}}}}}\rangle =\vert {1}_{1}\rangle \otimes \vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {0}_{2}\rangle ,\vert {{{{{{{\rm{R}}}}}}}}\rangle =\vert {0}_{1}\rangle \otimes \vert {+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {1}_{2}\rangle .$$

(9)

According to the effective Hamiltonian of Eq. (5), these levels are split in energy by 2h, and transitions between them are induced by the gauge-invariant tunneling of strength ${t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$(6). The problem thus reduces to that of Rabi oscillations¹⁹¹ of a driven two-level atom¹⁹² (see Fig. 2), and has an exact solution ${{{{{{{\boldsymbol{c}}}}}}}}(t)={{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{\Omega }_{0}t{{{{{{{\boldsymbol{n}}}}}}}}\cdot {{{{{{{\boldsymbol{\sigma }}}}}}}}}{{{{{{{\boldsymbol{c}}}}}}}}(0)$, where ${{{{{{{\boldsymbol{c}}}}}}}}(t)={({c}_{r}(t),{c}_{l}(t))}^{{{{{{{{\rm{t}}}}}}}}}$, and we have introduced the vector of Pauli matrices σ = (σ^x, σ^y, σ^z), and the following quantities

$${\Omega }_{0}=\sqrt{{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{2}+{h}^{2}},{{{{{{{\boldsymbol{n}}}}}}}}=\frac{1}{{\Omega }_{0}}({t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}},0,h).$$

(10)

Assuming that the particle occupies initially the leftmost site $\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}(0)\rangle =\vert {{{{{{{\rm{L}}}}}}}}\rangle$, we see that the tunneling to the right is accompanied by the build-up of an electric field line across the gauge link, which is thus attached to the dynamical ${{\mathbb{Z}}}_{2}$ charge carried by the particle. This correlated dynamics can be observed by measuring the periodic oscillations of the following gauge-invariant observables

$${\overline{n}}_{2}(t):= \langle {a}_{2}^{{{{\dagger}}} }{a}_{2}(t)\rangle =\frac{{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{2}}{{\Omega }_{0}^{2}}{\sin }^{2}({\Omega }_{0}t),\\ {\overline{n}}_{1}(t):= \langle {a}_{1}^{{{{\dagger}}} }{a}_{1}(t)\rangle =1-\frac{{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{2}}{{\Omega }_{0}^{2}}{\sin }^{2}({\Omega }_{0}t),\\ {\overline{s}}_{x}(t):= \langle {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle =\frac{2{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{2}}{{\Omega }_{0}^{2}}{\sin }^{2}({\Omega }_{0}t)-1.\\ $$

(11)

Fig. 2: Effective two-level system for ${{\mathbb{Z}}}_{2}$-link tunneling.

In the super-selection sector (8) with background charges q₁ = 0, q₂ = 1, the physical subspace for a single particle is composed of two states (9) depicted in Fig. 1b. The gauge-invariant Hamiltonian (5) can then be mapped onto the problem of detuned Rabi oscillations of a two-level atom in the rotating frame, where the tunneling plays the role of the Rabi frequency, and the electric-field term is proportional to the detuning of the Rabi drive.

In Fig. 3a, we compare these analytical predictions (11) for h = 0 to the numerical simulation for an initial state $\vert \Psi (0)\rangle =\vert {1}_{1}\rangle \vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \vert {0}_{2}\rangle$. Note that, for the numerical simulation, we do not restrict the Hilbert space to the single-particle subspace, nor to the gauge-invariant basis of Eq. (9). We truncate the maximal number of Fock states in each site to ${n}_{i}\le {n}_{\max }$, and compute the exact dynamics of the ${{\mathbb{Z}}}_{2}$-link Hamiltonian (5) after this truncation, checking that no appreciable changes appear when increasing ${n}_{\max }$. The lines depicted in this figure represent the numerical results for matter and gauge observables ${\overline{n}}_{1}(t)=\langle {a}_{1}^{{{{\dagger}}} }{a}_{1}(t)\rangle$, ${\overline{n}}_{2}(t)=\langle {a}_{2}^{{{{\dagger}}} }{a}_{2}(t)\rangle$ and ${\overline{s}}_{x}(t)=\langle {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle$. Fig. 3a also shows the expectation value of the sum of Gauss’ generators (7) which, according to the specific distribution of external background charges q₁ = 0, q₂ = 1, should vanish exactly at all times, i.e., $\langle {G}_{1}(t)+{G}_{2}(t)\rangle /2=({{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {q}_{1}}+{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {q}_{2}})/2=0$. The symbols represent the respective analytical expressions in Eq. (11). The picture shows a clear agreement of the numerical and exact solutions, confirming the validity of the picture of the correlated Rabi flopping in the matter and gauge sectors. As the boson tunnels to the right $\vert {1}_{1},{0}_{2}\rangle \to \vert {0}_{1},{1}_{2}\rangle$, the electric field line stretches to comply with Gauss’ law until, right at the exchange duration, the qubit gets flipped $\vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \to \vert {+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle$. This behavior is repeated periodically as the boson tunnels back and forth, and is a direct manifestation of gauge invariance.

Fig. 3: ${{\mathbb{Z}}}_{2}$-invariant tunneling and correlated Rabi flopping.

a Dynamics of an initial state $\left\vert \Psi (0)\right\rangle =\left\vert {{{{{{{\rm{L}}}}}}}}\right\rangle$ characterized by the gauge invariant observables ${\overline{n}}_{1}(t)=\langle {a}_{1}^{{{{\dagger}}} }{a}_{1}(t)\rangle$, ${\overline{n}}_{2}(t)=\langle {a}_{2}^{{{{\dagger}}} }{a}_{2}^{{{{\dagger}}} }(t)\rangle$ and ${\overline{s}}_{x}(t)=\langle {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle$, as well as the averaged expectation value of the local-symmetry generators 〈G₁(t) + G₂(t)〉/2. The symbols correspond to the numerical evaluation in the full Hilbert space, whereas the lines display the analytical predictions for h = 0 (11). The dhased line at Δt_ex represents the time to exchange a phonon between the two synthetic sites (b) Dynamics for the ${{\mathbb{Z}}}_{2}$ gauge link when the electric field h is increased. The symbols correspond to the numerical simulations, and the lines to the corresponding analytical expressions (11).

From the two-level scheme in the right panel of Fig. 2, we see that a non-zero electric field h > 0 plays the role of a detuning in the Rabi problem¹⁹². Accordingly, as the electric field gets stronger, i.e., $h\,\gg \,| {t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}|$, it costs more energy to create an electric field line, and the particle ceases to tunnel, i.e., the contrast of the Rabi oscillations between the L/R levels diminishes (see Fig. 3b). It is worth comparing to the case of Peierls’ phases and static/background gauge fields discussed in the supplementary material. There, four modes were required to define a plaquette and get an effective flux that can lead to Aharonov-Bohm destructive interference, which inhibits the tunneling of a single boson between the corners of the synthetic plaquette. In the case of the ${{\mathbb{Z}}}_{2}$ gauge model on a link, only two modes and a gauge qubit are required. The tunneling of the boson is inhibited by increasing the energy cost of stretching/compressing the accompanying electric field line. As discussed in more detail below, for larger lattices, this electric-field energy penalty is responsible for the confinement of matter particles in this ${{\mathbb{Z}}}_{2}$ gauge theory, a characteristic feature of this type of discrete gauge theories^{46,47,48,49,50,51,52,53,54,56,57,58,59,60,61,62,63,64,66,68,69,70,71,72}.

Two-boson sector: Dark states and entanglement between modes of the matter fields

Let us now move to the two-particle case, and describe how the connection to well-known effects in quantum optics can be pushed further depending on the exchange statistics. A pair of fermions can only occupy the state $\vert {1}_{1}\rangle \otimes \vert {+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {1}_{2}\rangle$, and do not display any dynamics due to the Pauli exclusion principle. On the other hand, if the particles are bosonic, the dynamics can be non-trivial and lead to interesting effects such as mode entanglement. Due to the U(1) symmetry and Gauss’ law (8) for q₁ = q₂ = 0, the physical subspace can now be spanned by three different states

$$\begin{array}{l}\vert {{{{{{{\rm{L}}}}}}}}\rangle =\vert {2}_{1}\rangle \otimes \vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {0}_{2}\rangle ,\\ \vert {{{{{{{\rm{C}}}}}}}}\rangle =\vert {1}_{1}\rangle \otimes \vert {+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {1}_{2}\rangle ,\\ \vert {{{{{{{\rm{R}}}}}}}}\rangle =\vert {0}_{1}\rangle \otimes \vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {2}_{2}\rangle .\end{array}$$

(12)

A pair of charges sitting on the same site have a vanishing net ${{\mathbb{Z}}}_{2}$ charge $1\oplus 1=(1+1){{{{{{{\rm{mod}}}}}}}}\,2=0$, and cannot act as a source/sink of electric field. Therefore, the L and R states in Eq. (12) do not sustain any electric field. On the other hand, when the pair of ${{\mathbb{Z}}}_{2}$ charges occupy the two different sites, Gauss’ law imposes that an electric field line must be established at the link. Since creating this electric field costs energy, these three levels are then separated in energy by 2h, and the gauge-invariant tunneling of the Hamiltonian in Eq. (5) leads to a Λ-scheme in quantum optics (see Fig. 4).

Fig. 4: Λ-scheme for 2-boson ${{\mathbb{Z}}}_{2}$-invariant tunneling.

In the left panel, we depict the three possible states in Eq. (12) for the distributions of the ${{\mathbb{Z}}}_{2}$ charges and electric field, using thick and thin yellow lines to represent the presence and absence of an electric field, respectively. In the right panel, we depict the quantum-optical level scheme, in which the gauge-invariant tunneling couples the $\left\vert {{{{{{{\rm{L}}}}}}}}\right\rangle$ and $\left\vert {{{{{{{\rm{R}}}}}}}}\right\rangle$ states to the state $\left\vert {{{{{{{\rm{C}}}}}}}}\right\rangle$ with one boson at each site, and a electric-field string in the link. The electric field h acts as a detuning of these transitions, leading to a Λ-scheme.

As it is known to occur for three-level atoms^193,194, one can find the so-called bright $\vert {{{{{{{\rm{B}}}}}}}}\rangle =(\vert {{{{{{{\rm{L}}}}}}}}\rangle +\vert {{{{{{{\rm{R}}}}}}}}\rangle )/\sqrt{2}$ and dark $\vert {{{{{{{\rm{D}}}}}}}}\rangle =(\vert {{{{{{{\rm{L}}}}}}}}\rangle -\vert {{{{{{{\rm{R}}}}}}}}\rangle )/\sqrt{2}$ states, which here correspond to the symmetric and anti-symmetric super-positions of the doubly-occupied sites at the left and right sites. In general, the state of the system can be expressed as a superposition of $\vert {{{{{{{\rm{B}}}}}}}}\rangle$, $\vert {{{{{{{\rm{D}}}}}}}}\rangle$ and $\vert {{{{{{{\rm{C}}}}}}}}\rangle$, namely $\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}(t)\rangle =d(t)\vert {{{{{{{\rm{D}}}}}}}}\rangle +{c}_{b}(t)\vert {{{{{{{\rm{B}}}}}}}}\rangle +{c}_{c}(t)\vert {{{{{{{\rm{C}}}}}}}}\rangle$. However, as the dark state decouples completely from the dynamics, its amplitude evolves by acquiring a simple phase d(t) = e^ihtd(0). Conversely, the amplitudes of the remaining states mix and display periodic Rabi oscillations ${{{{{{{\boldsymbol{c}}}}}}}}(t)={{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{\tilde{\Omega }}_{0}t\tilde{{{{{{{{\boldsymbol{n}}}}}}}}}\cdot {{{{{{{\boldsymbol{\sigma }}}}}}}}}{{{{{{{\boldsymbol{c}}}}}}}}(0)$ where, in this case ${{{{{{{\boldsymbol{c}}}}}}}}(t)={({c}_{b}(t),{c}_{c}(t))}^{{{{{{{{\rm{t}}}}}}}}}$, and

$${\tilde{\Omega }}_{0}=\sqrt{4{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{2}+{h}^{2}},\tilde{{{{{{{{\boldsymbol{n}}}}}}}}}=\frac{1}{{\tilde{\Omega }}_{0}}(2{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}},0,h).$$

(13)

We can now discuss a different manifestation of the gauge-invariant dynamics with respect to the single-particle case (11). Let us consider the initial state to be $\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}(0)\rangle =\vert {{{{{{{\rm{C}}}}}}}}\rangle$ with one boson at each site, and an electric-field line at the link in between. If we look at the local number of bosons, we do not observe any apparent dynamics ${\overline{n}}_{1}(t):= \langle {a}_{1}^{{{{\dagger}}} }{a}_{1}(t)\rangle =1=\langle {a}_{2}^{{{{\dagger}}} }{a}_{2}(t)\rangle =:{\overline{n}}_{2}(t)$. However, looking into the electric field at the link, we find periodic Rabi flopping again, i.e.,

$${\overline{s}}_{x}(t):=\langle {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle =1-\frac{8{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{2}}{{\tilde{\Omega }}_{0}^{2}}{\sin }^{2}({\tilde{\Omega }}_{0}t).$$

(14)

Since the gauge field cannot have independent oscillations with respect to the matter particles, there must be a non-trivial dynamics within the matter sector which, nonetheless, cannot be inferred by looking at the local number of particles. In this context, it is the interplay of the superposition principle of quantum mechanics and gauge symmetry, which underlies a neat dynamical effect. This effect becomes manifest by inspecting the state after a single exchange period $\Delta {t}_{{{{{{{{\rm{ex}}}}}}}}}=\pi /2{\tilde{\Omega }}_{0}$ for h = 0. After this time, a boson can either tunnel to the left or to the right. In both cases, the electric field string compresses, since a doubly-occupied site amounts to a vanishing net ${{\mathbb{Z}}}_{2}$ charge, and there is thus no sink/source of electric field. Accordingly, when the bosons tunnel along either path respecting gauge invariance, the state ends up with the same link configuration, namely ${\vert -\rangle }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$. Then, according to the superposition principle, both paths must be added, and the state of the system at time t_e is given by

$$\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}(\Delta {t}_{{{{{{{{\rm{ex}}}}}}}}})\rangle =\frac{1}{\sqrt{2}}\left(\vert {2}_{1},{0}_{2}\rangle +\vert {0}_{1},{2}_{2}\rangle \right)\otimes \vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle .$$

(15)

We see that, as a consequence of the dynamics, mode entanglement¹⁹⁵ has been generated in the matter sector since the state cannot be written as a separable state $\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}(\Delta {t}_{{{{{{{{\rm{ex}}}}}}}}})\rangle \, \ne \, P({a}_{1}^{{{{\dagger}}} })Q({a}_{2}^{{{{\dagger}}} })\vert {0}_{1},{0}_{2}\rangle \otimes \vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle$ for any polynomials P, Q. The specific state (Eq. 15) in the matter sector is a particular type of NOON states, which have been studied in the context of metrology^{196,197,198,199,200}. Note that this state cannot be distinguished from the initial state if one only looks at ${\overline{n}}_{1}(t)={\overline{n}}_{2}(t)=1$. The non-trivial dynamics becomes manifest via the link and the quantum mode-mode correlations.

In Fig. 5, we present a comparison of the analytical predictions with the corresponding numerical results where, once more, we do not restrict to the basis in Eq. (12), nor to the 2-boson subspace. We initialize the system in $\vert \Psi (0)\rangle =\vert {1}_{1}\rangle \vert {+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \vert {1}_{2}\rangle$, and numerically truncate the Hilbert space such, that ${n}_{i}\le {n}_{\max }$, computing numerically the Schrödinger dynamics for the ${{\mathbb{Z}}}_{2}$-link Hamiltonian (5). In Fig. 5a, we represent these numerical results with lines for the observables ${\overline{n}}_{1}(t),{\overline{n}}_{2}(t),{\overline{s}}_{x}(t)$, as well as the average of the local-symmetry generators 〈G₁(t) + G₂(t)〉/2. Once again, these numerical results agree perfectly with the corresponding analytical expressions (14), which are represented by the symbols. In Fig. 5b, we show the fidelity of the system state with respect the NOON state of Eq. (15), namely ${{{{{{{{\mathcal{F}}}}}}}}}_{{{{{{{{\rm{NOON}}}}}}}}}(t)=| \langle {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}({t}_{e})\vert {{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}t{H}_{{{{{{{{\rm{eff}}}}}}}}}}\vert \Psi (0)\rangle {| }^{2}$ at different evolution times. We see that this fidelity tends to unity at the periodic exchange periods $t=m{t}_{e},\,\,m\in {{\mathbb{Z}}}^{+}$. Note that the timescale in the horizontal axis is the same as the one for the one-particle case in Fig. 3, but the periodic oscillations are twice as fast. This two-fold speed-up is caused by the bosonic enhancement due to the presence of two particles in the initial state, providing a $\sqrt{2}$ factor, and the enhancement due to the bright state, which brings the additional $\sqrt{2}$ factor. This total speed-up is the only difference if one compares the dynamics of the bosonic sector with that of a standard beam splitter leading to the Hong-Ou-Mandel interference²⁰¹. In fact, in the trapped-ion literature, the bare tunneling terms between a pair of vibrational modes are commonly referred to as a beam splitter due to the formal analogy with the optical device that splits an incoming light mode into the transmitted and reflected modes²⁰².

Fig. 5: Two-boson ${{\mathbb{Z}}}_{2}$-invariant tunneling and entanglement.

a Dynamics of an initial state $\left\vert \Psi (0)\right\rangle =\left\vert {{{{{{{\rm{L}}}}}}}}\right\rangle$ characterized by the gauge invariant observables ${\overline{n}}_{1}(t)=\langle {a}_{1}^{{{{\dagger}}} }{a}_{1}(t)\rangle$, ${\overline{n}}_{2}(t)=\langle {a}_{2}^{{{{\dagger}}} }{a}_{2}(t)\rangle$ and ${\overline{s}}_{x}(t)=\langle {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle$, as well as the averaged expectation value of the local-symmetry generators 〈G₁(t) + G₂(t)〉/2. The symbols correspond to the numerical evaluation in the full Hilbert space, whereas the lines display the analytical predictions for h = 0(6). b State fidelity with respect to a mode-entangled 2-boson NOON state (15), which tends to unity at the integer exchange periods Δt_ex, and 2Δt_ex.

After the results presented in this section, we can more to the discussion of two possible schemes for implementing the state-dependent parametric excitation (2) in trapped-ion experiments. The first scheme (I) is based on trapped-ion analog quantum simulators. The second scheme (II) exploits recent ideas developed for continuous-variable quantum computing²⁰³.

Trapped-ion toolbox: phonons and qubits

Before delving into the details of the trapped-ion schemes, let us first review the progress of trapped-ion-based QSs for lattice gauge theories. As discussed in^121,204,205, certain gauge theories can be mapped exactly onto spin models that represent the fermionic matter with effective long-range interactions mediated by the gauge fields. Following these ideas, the U(1) Schwinger model of quantum electrodynamics in 1+1 dimensions^121,133 and variational quantum eigensolvers¹²⁵ have been simulated digitally in recent trapped-ion experiments. As discussed in^205,206, there are theoretical proposals to generalize this approach to gauge theories in 2 + 1 dimensions. Although not considered in the specific context of trapped ions, digital quantum simulators, and variational eigensolvers have also been recently considered for ${{\mathbb{Z}}}_{2}$ gauge theories^{207,208,209,210}. Rather than eliminating the gauge fields as in the cases above^121,204,205 one could consider the opposite, and obtain effective models for the gauge fields after eliminating the matter content^211,212.

In order to move beyond those specific models, it would be desirable to simulate matter and gauge fields on the same footing. Trapped-ion schemes for the quantum-link approach to the Schwinger model have been proposed in^213,214. In particular, for the specific spin-1/2 representation of the link operators, the gauge-invariant tunneling becomes a three-spin interaction. This could be implemented using only the native two-spin interactions in trapped-ion experiments and by imposing an additional energetic Gauss penalty²¹³. Alternatively, one may also generate three-spin couplings²¹⁴ directly by exploiting second-order sidebands that use the phonons as carriers of these interactions^215,216,217. We note that there have also been other proposals^218,219 to use the motional modes to encode the U(1) gauge field, whereas the fermionic matter is represented by spin-1/2 operators. In this case, the gauge-invariant tunneling can be achieved via other second-sideband motional couplings²¹⁸, or by combining digital and analog ingredients in a “hybrid” approach²¹⁹. A different possibility is to use the collective motional modes to simulate bosonic matter and reserve the spins to represent the quantum link operators for the gauge fields²¹⁸. In this way, one can simulate a quantum link model provided that all the collective vibrational modes can be individually addressed in frequency space²¹⁸, which can be complicated by frequency crowding as the number of ions increases. We note that engineering the collective-motional-mode couplings has also been recently considered in the context of continuous-variable quantum computing, boson sampling, and quantum simulation of condensed-matter models^{203,220,221,222}. In the following, we present a trapped-ion scheme for the quantum simulation of ${{\mathbb{Z}}}_{2}$ gauge theories based on our previous idea of a state-dependent parametric tunneling (2), and using motional states along two different transverse directions, and a pair of electronic states to encode the particles and the gauge field.

Analog scheme for the ${{\mathbb{Z}}}_{2}$ gauge link

Light-shift-type parametric tunneling

In the Supplementary Note 2, we discuss how a parametric excitation between the two local transverse vibrations in an ion chain could be synthesized by exploiting an optical potential created by a far-detuned two-beam laser field. In order to achieve this, we considered that all of the ions were initialized in the same ground-state level. However, depending on the nuclear spin of the ions, the ground-state manifold can contain a variety of levels $\{\vert s\rangle \}$ that can be used to obtain the state-dependent parametric tunneling of Eq. (2). In general, when the field is far-detuned from any atomic transition, the light-shift potential becomes state-dependent²²³, namely

$${V}_{1}(t)=\sum\limits_{n,{n}^{{\prime} }=1,2}\sum\limits_{i,s}{\Omega }_{n,{n}^{{\prime} }}^{(s)}\vert {s}_{i}\rangle \left\langle {s}_{i}\right\vert {{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}({{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{L}}}}}}}},n}-{{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{L}}}}}}}},{n}^{{\prime} }})\cdot {{{{{{{{\boldsymbol{r}}}}}}}}}_{i}-({\omega }_{{{{{{{{\rm{L}}}}}}}},n}-{\omega }_{{{{{{{{\rm{L}}}}}}}},{n}^{{\prime} }})t}+{{{{{{{\rm{H.c.}}}}}}}}.$$

(16)

Here, ${\Omega }_{n,{n}^{{\prime} }}^{(s)}$ is the amplitude of the light-shift terms discussed in the supplementary material, in which the corresponding Rabi frequencies now refer to the particular ground-state level $\vert {s}_{i}\rangle$ of the i-th ion involved in the two virtual transitions. These light shifts then depend on the specific state and the intensity and polarization of the laser fields. As discussed in the context of state-dependent dipole forces^223,224,225, one can focus on a particular pair of states s₁, s₂ and tune the polarization, detuning, and intensity of the light, such that the corresponding amplitudes for the crossed beat note terms attain a differential value^224,225. To obtain the local gauge symmetry, it is important that this amplitude is equal in absolute value but opposite in sign for each of the two electronic states

$${\Omega }_{1,2}^{(0)}=-{\Omega }_{1,2}^{(1)}.$$

(17)

If this condition is not satisfied, one can still obtain a state-dependent tunneling, but this would not have the desired local gauge invariance under the above ${{\mathbb{Z}}}_{2}$ group (8). Nonetheless, such state-dependent tunneling can be interesting for other purposes in the context of hybrid discrete-continuous variable quantum information processing, as realized in ref. ²²⁶.

One can now follow the same steps as before, introducing the local transverse phonons via the position operators, and performing a Lamb-Dicke expansion discussed in the Supplementary Note 2. Using the same set of constraints as for the standard parametric drive discussed in the supplementary material, we find that

$${V}_{1}(t)\, \approx \,\sum\limits_{i}\Delta {E}_{{{{{{{{\rm{ac}}}}}}}}}{\sigma }_{i}^{z}+\sum\limits_{i}{\Omega }_{{{{{{{{\rm{d}}}}}}}}}{\sigma }_{i}^{z}\cos ({\phi }_{i}-{\omega }_{{{{{{{{\rm{d}}}}}}}}}t){a}_{i,y}^{{{{\dagger}}} }{a}_{i,x}+{{{{{{{\rm{H.c.}}}}}}}},$$

(18)

where we have introduced ω_d = ω_L,1 − ω_L,2, together with

$${\Omega }_{{{{{{{{\rm{d}}}}}}}}}=| {\Omega }_{1,2}| {\eta }_{x}{\eta }_{y},{\phi }_{i}={{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{d}}}}}}}}}\cdot {{{{{{{{\boldsymbol{r}}}}}}}}}_{i}^{0}+\arg (-{\Omega }_{1,2}).$$

(19)

where we have introduced

$${{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{d}}}}}}}}}={{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{L}}}}}}}},1}-{{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{L}}}}}}}},2},{\eta }_{\alpha }={{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{d}}}}}}}}}\cdot {{{{{{{{\bf{e}}}}}}}}}_{\alpha }/\sqrt{2m{\omega }_{\alpha }}.$$

(20)

We are already close to the idealized situation in which the effective model would lead to a gauge-invariant tunneling to a full ion chain. However, a simple counting argument shows that the effective model cannot achieve ${{\mathbb{Z}}}_{2}$ gauge invariance. For a string of N ions, we have 2N local motional modes along the transverse directions, which lead to the synthetic two-leg ladder with 3N − 2 links, each of which would requires a gauge qubit to achieve a local ${{\mathbb{Z}}}_{2}$ symmetry. Since we only have N trapped-ion qubits at our disposal, i.e., one qubit per ion, it is not possible to build a gauge-invariant model for the synthetic ladder in a straightforward manner. We present a solution to this problem by introducing a mechanism that we call synthetic dimensional reduction.

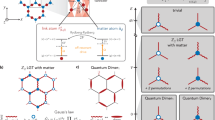
Prior to that, we can discuss the minimal case in which gauge invariance can be directly satisfied in the trapped-ion experiment: a single ${{\mathbb{Z}}}_{2}$ link. This link requires a single ion: one gauge qubit for the link, and two motional modes for the matter particles, which can be the vibrations along any of the axes. In Fig. 6, we consider the two transverse modes, and thus restrict Eq. (18) to a single ion. Following the same steps as in the derivation of Eq. (5), we move to an interaction picture and neglect rapidly rotating terms. We obtain a time-independent term that corresponds to a ${{\mathbb{Z}}}_{2}$ gauge-invariant tunneling

$${V}_{1}(t)\, \approx \,\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{2}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{\phi }_{{{{{{{{\rm{1}}}}}}}}}}{a}_{1,y}^{{{{\dagger}}} }{\sigma }_{1}^{z}{a}_{1,x}+{{{{{{{\rm{H.c.}}}}}}}},$$

(21)

At this point, the driving phase ϕ_d = ϕ₁ is irrelevant and can be set to zero without loss of generality. Identifying the trapped-ion operators with those of the lattice gauge theory

$$\begin{array}{l}{a}_{1,x},{a}_{1,x}^{{{{\dagger}}} }\,\mapsto \,{a}_{1},{a}_{1}^{{{{\dagger}}} },\\ {a}_{1,y},{a}_{1,y}^{{{{\dagger}}} }\,\mapsto \,{a}_{2},{a}_{2}^{{{{\dagger}}} },\\ {\sigma }_{1}^{x},{\sigma }_{1}^{z}\,\mapsto \,{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x},{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z},\end{array}$$

(22)

we obtain a realization of the ${{\mathbb{Z}}}_{2}$ gauge-invariant tunneling on a link (5) using a single trapped ion, such that

$${t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}=\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{2}=\frac{| {\Omega }_{1,2}| }{2}{\eta }_{x}{\eta }_{y}.$$

(23)

Fig. 6: Trapped-ion synthetic ${{\mathbb{Z}}}_{2}$ gauge theory on a link.

Schematic representation of the single-ion system that can realize the ${{\mathbb{Z}}}_{2}$ gauge theory on a synthetic link (5). On the left, we depict an ion vibrating in the transverse x direction, and the inset represents the state of the corresponding qubit in $\left\vert {-}_{1}\right\rangle =({\left\vert \!\! \uparrow \right\rangle }_{1}-\left\vert {\downarrow }_{1}\right\rangle )/\sqrt{2}$. On the right, we can see how, as a consequence of the trapped-ion effective Hamiltonian (21), the vibrational excitation along x is transferred into a vibrational excitation along y, while simultaneously flipping the qubit into $\left\vert {+}_{1}\right\rangle =({\left\vert \!\! \downarrow \right\rangle }_{1}+\left\vert {\uparrow }_{1}\right\rangle )/\sqrt{2}$. This dynamics, which is fully consistent with the local gauge symmetry, can be engineered by shining a far-detuned two-beam laser field with wave-vectors associated to each frequency represented by green and blue arrows, leading to a beat note along the gray arrow that yields the desired term (21).

As explained above, this exploits the qubit as the gauge field, and two vibrational modes to host the ${{\mathbb{Z}}}_{2}$-charged matter. In the next subsection, we present alternative schemes that do not depend on this condition for the differential light shift.

Let us now test the validity of this scheme for realistic trapped-ion parameters, considering a ⁸⁸Sr⁺ ion confined in the setup of refs. ^227,228, and a ground state-qubit encoding with experimentally-realistic parameters described in the Supplementary Note 2. Note that for a single ${{\mathbb{Z}}}_{2}$ link, any two of the three motional modes can be used. In the following simulations, with the trapped-ion parameters of the considered setup, we encode the matter particles in an axial (z) and a transverse (x) mode, such that we can benefit from the larger Lamb-Dicke parameter of the axial mode, as well as the higher frequency separation of the two motional modes. We model numerically the possible deviations of a realistic trapped-ion implementation from the above-idealized expressions used in Fig. 3. For the simulations presented below, we perform exact numerical integration of the Schrödinger equation under the time-dependent trapped-ion Hamiltonians using the QuantumOptics.jl package in Julia²²⁹. In particular, we consider the full Hamiltonian (16), using experimentally feasible parameters, and do not assume the Lamb-Dicke expansion, and thus include possible off-resonant carrier excitations as well as other non-linear terms neglected in Eq. (18). We use a single ion and two of its motional modes, truncating their individual Hilbert spaces at phonon number ${n}_{\max }=7$.

The results are shown in Fig. 7, where the colored lines represent the analytical predictions for the various observables in Eq. (11) using the effective tunneling strength (23). The colored symbols stand for the full numerical simulations including non-linear terms in the trapped-ion case, leading thus to a trapped-ion counterpart of Fig. 3a following Scheme I. We note that, in order to find a better agreement with the idealized evolution (11), we have incorporated an adiabatic pulse shaping of the light-matter coupling that restricts the minimal duration of the real-time dynamics as discussed in the caption of Fig. 7. For the specific choice of parameters detailed in the Supplementary Note 2, we see that the exchange duration of the phonon tunneling and the stretching of the electric-field line is about several tens of μs, which is sufficiently fast compared to other possible sources of noise such as heating and dephasing, as discussed in more detail below. In the Supplementary Note 2, we make a more detailed error analysis, distinguishing those that arise from non-linearities or from non-resonant corrections. As discussed there, the analog scheme can also be accomplished with optical qubits.

Fig. 7: ${{\mathbb{Z}}}_{2}$ gauge dynamics with analog trapped-ion scheme.

We simulate the ${{\mathbb{Z}}}_{2}$ dynamics using the Raman-based light-shift parametric tunneling and try to replicate Fig. 3a. The markers are full numerical simulations including non-linear terms (16) beyond the desired Lamb-Dicke expansion, while the continuous lines are analytical predictions in Eq. (11) using the effective tunneling strength (23) and h = 0. The adiabatic pulse shaping sets the minimum pulse duration to the rising and falling edge (10 μs each).

Mølmer-Sørensen-type parametric tunneling

In this section, we present an alternative scheme for synthesizing the gauge-invariant tunneling that doe not require a fine tuning of the differential ac-Stark shifts (17) to achieve the desired gauge invariance and, moreover, leads to a technically simpler method to induce the electric-field term. In this case, the parametric tunneling arises from a “bichromatic” field that is no longer far-detuned from the qubit transition but, instead, has two components symmetrically detuned from the qubit frequency, which connects to the Mølmer-Sørensen(MS) scheme used for high-fidelity trapped-ion gates^230,231,232. The main difference of our scheme is that the bichromatic field is not tuned to first sidebands, but to the frequency conversion between the two motional modes.

As discussed in more detail in theSupplementary Note 2, either for ground state or optical qubits, the MS-type scheme leads to the following term instead of Eq. (16),

$${\tilde{V}}_{1}(t)=\Omega \cos (\delta t)\sum\limits_{i}\vert {\uparrow }_{i}\rangle \left\langle {\downarrow }_{i}\right\vert {{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{d}}}}}}}}}\cdot {{{{{{{{\boldsymbol{r}}}}}}}}}_{i}}+{{{{{{{\rm{H.c.}}}}}}}}.$$

(24)

As in our previous derivation, we expand in the Lamb-Dicke parameters. By focusing again on a single trapped ion, and choosing the detuning to be resonant with δ = ω_x − ω_z, we reach the frequency conversion. We refer to this scheme as a Mølmer-Sørensen(MS) parametric tunneling

$${\tilde{V}}_{1}(t)\,\approx \,\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{2}{a}_{1,z}^{{{{\dagger}}} }{\sigma }_{1}^{x}{a}_{1,x}+{{{{{{{\rm{H.c.}}}}}}}},{\Omega }_{{{{{{{{\rm{d}}}}}}}}}=\Omega {\eta }_{x}{\eta }_{z}.$$

(25)

The gauge-invariant tunneling rate (5) then reads

$${t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}=\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{2}=\frac{| \Omega | }{2}{\eta }_{x}{\eta }_{z}.$$

(26)

which is analogous to the light-shift case of Eq. (23). We thus obtain a rotated version of the gauge-invariant tunneling in Eq. (21), the only difference being that the operators need to be transformed as ${\sigma }_{1}^{z}\,\mapsto \,{\sigma }_{1}^{x}$, and ${a}_{1,y},{a}_{1,y}^{{{{\dagger}}} }\,\mapsto \,{a}_{1,z},{a}_{1,z}^{{{{\dagger}}} }$, which must also be considered in the mapping to the operators of the lattice gauge theory in Eq. (22). Accordingly, the generators of the local symmetries now read

$${G}_{1}={{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {a}_{1}^{{{{\dagger}}} }{a}_{1}}{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z},{G}_{2}={\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {a}_{2}^{{{{\dagger}}} }{a}_{2}}.$$

(27)

In the Supplementary Note 2, we provide a more detailed error analysis of the validity of this scheme using realistic experimental parameters for ⁸⁸Sr⁺ ions^227,228, and include figures that support the validity of the MS scheme at the same level as the previous dipole light-shift one. The advantage will become apparent in the following section.

Electric field and experimental considerations

So far, we have restructured to the gauge-invariant tunneling in Eq. (5), but we also need a term that drives the qubit transition (3) with Rabi frequency ${\tilde{\Omega }}_{{{{{{{{\rm{d}}}}}}}}}$, which corresponds to the electric field $h={\tilde{\Omega }}_{{{{{{{{\rm{d}}}}}}}}}/2$ in Eq. (6). The technique to induce this term depends on the specific scheme. For the scheme based on the light-shift potential, one needs to add a field driving the qubit transition resonantly. For an optical qubit, this term would arise from a resonant laser driving the quadrupole-allowed transition. On the other hand, if the qubit is encoded in the ground state, this term can be induced by either a resonant microwave field or a pair of Raman laser beams. In both cases, trapped-ion experiments routinely work in the regime of Eq. (4), where the value of ${\tilde{\Omega }}_{{{{{{{{\rm{d}}}}}}}}}$ can be controlled very precisely by tuning the amplitude of the laser or microwave field²³³. Note that the resonance condition (4) must account for the ac-Stark shifts shown in Eq. (18), namely

$${\tilde{\omega }}_{{{{{{{{\rm{d}}}}}}}}}={\omega }_{0}+2\Delta {E}_{{{{{{{{\rm{ac}}}}}}}}},| {\tilde{\Omega }}_{{{{{{{{\rm{d}}}}}}}}}| \,\ll\, 4({\omega }_{0}+2{E}_{{{{{{{{\rm{ac}}}}}}}}}).$$

(28)

This leads to the desired Hamiltonian

$${V}_{1}(t)\,\approx \,\left(\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{2}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{\phi }_{{{{{{{{\rm{d}}}}}}}}}}{a}_{1,z}^{{{{\dagger}}} }{\sigma }_{1}^{z}{a}_{1,x}+{{{{{{{\rm{H.c.}}}}}}}}\right)+\frac{{\tilde{\Omega }}_{{{{{{{{\rm{d}}}}}}}}}}{2}{\sigma }_{1}^{x},$$

(29)

which maps directly onto the ${{\mathbb{Z}}}_{2}$ gauge link in Eqs. (5)–(6) with the new term playing the role of the electric field

$$h=\frac{{\tilde{\Omega }}_{{{{{{{{\rm{d}}}}}}}}}}{2}.$$

(30)

For the Mølmer-Sørensen-type scheme, the spin conditioning of the tunneling occurs in the Hadamard basis $\vert {\pm }_{\!1}\rangle$, such that the effective electric field must also be rotated with respect to Eq. (5). We can introduce this term by simply shifting the center frequency of the bichromatic laser field (24) relative to the qubit resonance by a detuning δ_s. In a rotating frame, this modifies Eq. (24) by introducing an additional term, namely

$${\tilde{V}}_{1}(t)\,\approx \,\left(\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{2}{a}_{1,z}^{{{{\dagger}}} }{\sigma }_{1}^{x}{a}_{1,x}+{{{{{{{\rm{H.c.}}}}}}}}\right)+\frac{{\delta }_{{{{{{{{\rm{s}}}}}}}}}}{2}{\sigma }_{1}^{z},$$

(31)

which leads to the effective electric-field term

$$h=\frac{{\delta }_{{{{{{{{\rm{s}}}}}}}}}}{2}.$$

(32)

This is a considerable advantage with respect to the light-shift scheme, as no additional tones are required to implement the electric field term. A detailed analysis of the errors for current trapped-ion parameters is presented in the Supplementary Note 2.

Pulsed scheme for the ${{\mathbb{Z}}}_{2}$ gauge link

Orthogonal-force parametric tunneling

We now discuss an alternative strategy to realize the ${{\mathbb{Z}}}_{2}$ gauge link based on digital quantum simulation and the concatenation of gates. First, we focus on a new way of engineering the gauge-invariant tunneling term using two orthogonal state-dependent forces and, then, explain how it can be used to experimentally implement the ${{\mathbb{Z}}}_{2}$ gauge model in Eq. (5). As before, we consider the case of a single ${{\mathbb{Z}}}_{2}$ link, i.e., one single ion and two vibrational modes. Following the scheme proposed in ref. ²⁰³ for hybrid discrete-continuous variable approaches in trapped-ion quantum information processing, we consider two orthogonal state-dependent forces acting on the two vibrational modes with Lamb-Dicke parameters η_z and η_x, respectively. We thus start from two terms like Eq. (24), each of which will be tuned to yield a different state-dependent force, i.e., k_d,1∣∣e_x, and k_d,2∣∣e_z,

$${\tilde{V}}_{1}(t)=\Omega \cos (\delta t)\sum\limits_{i}\sum\limits_{n=1,2}\vert {\uparrow }_{i}\rangle \left\langle {\downarrow }_{i}\right\vert {{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{d}}}}}}}},n}\cdot {{{{{{{{\boldsymbol{r}}}}}}}}}_{i}+{\phi }_{{{{{{{{\rm{d}}}}}}}},n}}+{{{{{{{\rm{H.c.}}}}}}}}.$$

(33)

In the interaction picture with respect to the qubit frequency, ω₀, motional frequencies, ω_z and ω_x, the interaction reads

$${V}_{1}(t)\,\approx \,{\eta }_{x}\Omega {\sigma }_{1}^{x}{a}_{1,x}{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}\delta t}+{\eta }_{z}\Omega {\sigma }_{1}^{y}{a}_{1,z}{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}\delta t}+\,{{\mbox{H.c.}}}\,,$$

(34)

where η_αΩ is the coupling strength to the respective vibrational mode, and δ is the detuning away from the sidebands ω₀ ± ω_x/z. These two terms can be derived using similar steps as before, which only differ on the specific selection of the leading contribution by the appropriate choice of the laser frequencies. The interference of these two forces can lead, in the second order, to an effective state-dependent tunneling. After using a Magnus expansion for the time-ordered evolution operator $U(t)={{{{{{{\mathcal{T}}}}}}}}\{\exp \{-{{{{{{{\rm{i}}}}}}}}\int_{0}^{t}{{{{{{{\rm{d}}}}}}}}s{V}_{1}(s)\}\}$²³⁴, the second-order term $U(t)\,\approx \exp \{-{{{{{{{\rm{i}}}}}}}}{H}_{{{{{{{{\rm{eff}}}}}}}}}t\}$ yields the following interaction

$${H}_{{{{{{{{\rm{eff}}}}}}}}}=\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{2}{a}_{1,z}^{{{{\dagger}}} }{\sigma }_{1}^{z}{a}_{1,x}+{{{{{{{\rm{H.c.}}}}}}}},{\Omega }_{{{{{{{{\rm{d}}}}}}}}}={{{{{{{\rm{i}}}}}}}}\frac{{\Omega }^{2}}{\delta }{\eta }_{x}{\eta }_{z},$$

(35)

which maps directly onto the desired gauge-invariant tunneling of Eq. (5) with a tunneling strength of

$${t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}=\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{2}={{{{{{{\rm{i}}}}}}}}\frac{{\Omega }^{2}}{2\delta }{\eta }_{x}{\eta }_{z}.$$

(36)

In this derivation, we have neglected higher-order contributions in the Magnus expansion that would lead to errors ϵ = O([ηΩ/δ]³) that must be kept small (we assumed that η_x and η_z are the same order of magnitude η). If a fixed error ϵ in these higher-order terms is considered, δ is then linear in η. Consequently, the tunneling coupling rate is also linear in η. This linear dependence is in contrast to the analog scheme, where the coupling is quadratic in η. Additionally, the first-order term in the Magnus expansion must be accounted for, which leads to additional state-dependent displacements in the joint phase space of both vibrational modes. As in the case of trapped-ion entangling gates, these displacements vanish for specific evolution times corresponding to integer multiples of 2π/δ. Hence, the tunneling term (5) can be achieved by applying the interaction for a duration that is multiple of 2π/δ.

In the Supplementary Note 2, we present the specific experimental parameters for this pulsed scheme, which are then used to numerically validate the above derivations. A characteristic numerical simulation is shown in Fig. 8, which shows that one can also recover the desired gauge-invariant dynamics using this pulsed scheme, provided on considers the pulse switching discussed in the Supplementary Note 2. There, we also provide a more detailed discussion about the errors.

Fig. 8: ${{\mathbb{Z}}}_{2}$ gauge dynamics with pulsed trapped-ion scheme.

We simulate the ${{\mathbb{Z}}}_{2}$ dynamics using two orthogonal spin-dependent forces and try to replicate Fig. 3a. The markers are the numerical simulation data considering the evolution under the two state-dependent forces in Eq. (34), but also including the additional off-resonant carriers that stem from the Lamb-Dicke expansion of Eq. (33). The colored lines are the analytical predictions in Eq. (11), considering the effective tunneling strength in Eq. (36) and h = 0.

Electric field and experimental considerations

For this scheme, the electric field term $h{\sigma }_{1}^{x}$ in Eq. (5) can be introduced through Trotterization. For this, we split the interaction time into segments with durations that are integer multiples of 2π/δ, and we alternate between applying the tunneling term and the external field term $h{\sigma }_{1}^{x}$, which can be achieved by a carrier driving (see discussion in the supplementary material). In this way, the electric field term can be easily introduced by interleaving short carrier pulses with periods of small evolution under the combination of the two orthogonal state-dependent forces.

Comparison of ${{\mathbb{Z}}}_{2}$ gauge link schemes

Let us start by discussing how an experiment would proceed. One of the advantages of trapped ions is that they offer a variety of high-precision techniques for state preparation and readout²³³. For a single trapped ion, it is customary to perform optical pumping to the desired qubit state, say $\vert \uparrow \rangle$. One can then use laser cooling in the resolved-sideband limit for both vibrational modes, and prepare them very close to the vibrational ground state. Using a blue sideband directed along a particular axis, say the x-axis, one can flip the state of the qubit and, simultaneously, create a Fock state with a single vibrational excitation in the mode. We note that the initial state of the ${{\mathbb{Z}}}_{2}$ gauge theory would correspond to $\vert {{{{{{{\rm{L}}}}}}}}\rangle =\vert {1}_{1}\rangle \otimes \vert {\downarrow }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {0}_{2}\rangle$, which is the rotated version of the one discussed previously and is thus directly valid for the Mølmer-Sørensen-type scheme. For the light-shift scheme, one must apply a Hadamard gate to initialise the system in $\vert {{{{{{{\rm{L}}}}}}}}\rangle =\vert {1}_{1}\rangle \otimes \vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {0}_{2}\rangle$, which can be accomplished by driving a specific single-qubit rotation.

One can then let the system evolve for a fixed amount of time under the effective Hamiltonian in either Eq. (29) for the light-shift scheme, or Eq. (31) for the Mølmer-Sørensen-type scheme. We have shown that the effective Hamiltonians approximate the ideal Hamiltonian accurately. After this real-time evolution, the laser fields are switched off. Then, the measurement stage starts, where one tries to infer the matter-gauge field correlated dynamics in Eq. (11). In order to do that, one would take advantage of the readout techniques developed in trapped ions²³³, which typically map the information of the desired observable onto the qubit. After this mapping, the qubit can be projectively measured in the z-basis via state-dependent resonance fluorescence. In order to measure the electric field operator of the Mølmer-Sørensen-type scheme ${\overline{s}}_{z}(t)=\langle {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}(t)\rangle$, one can collect the state-dependent fluorescence. For the light-shift scheme, one needs to measure ${\overline{s}}_{x}(t)=\langle {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle$, which requires an additional single-qubit rotation prior to the fluorescence measurement. On the other hand, in order to infer the phonon population $\langle {a}_{2}^{{{{\dagger}}} }{a}_{2}(t)\rangle$ = $\langle {a}_{1,z}^{{{{\dagger}}} }{a}_{1,z}(t)\rangle$, and observe the gauge-invariant tunneling, one would need to map the vibrational information onto the qubit first prior to the fluorescence measurement²³⁵. These techniques are well developed, e.g.,²³⁶.

At this point, it is worth commenting on the relative strengths of the different schemes. The analog and pulsed schemes presented above outline different viable strategies to implement the gauge-invariant model (5) using current trapped-ion hardware. There are, however, several experimental challenges worth highlighting. It is crucial that the tunneling rates are large compared to any noise process present in the physical system. The dominating sources are the qubit and motional decoherence. In the considered experimental setup^227,228, the decoherence time of the qubit is the most stringent one with T₂ ≈ 2.4 ms for the ground state qubit and T₂ ≈ 5 ms for the optical qubit. These numbers could be improved by several orders of magnitude by using a clock-qubit encoding. However, in this encoding, the differential dipole light-shift that leads to Eq. (21) would vanish and, hence, the method proposed would not work. Light shifts can be created using quadrupole-Raman transitions²³⁷ but extra care needs to be taken to symmetrize the shift induced on each qubit state. An alternative way of increasing the qubit coherence would be to use magnetic shielding or active magnetic-field stabilization.

In terms of motional coherence, the heating rate is limiting the coherence time for the longitudinal motional mode to be ca. 14 ms. The coherence time for the transverse modes has not been properly characterized in the current system and it might be further limited by noise in the trap rf drive. However, actively stabilizing the amplitude of the rf drive has shown improvement in the coherence time²³⁸. We note that a similar, yet non-gauge-invariant tunneling, has been implemented in a trapped-ion experiment²²⁶ in the context of continuous-variable quantum computing. This experiment successfully used the transverse modes and measured coherence times of 5.0(7) and 7(1) ms for ¹⁷¹Yb⁺ ions.

Therefore, we can conclude that the exchange timescales of the ${{\mathbb{Z}}}_{2}$ tunneling implementations investigated in this paper using the analog scheme (≈40 μs and ≈100 μs, using Raman beams), as well as the pulsed scheme (≈200 μs, using quadrupole beams) are an order of magnitude faster than the qubit or motional decoherence, and hence experimentally feasible. We note that the analog schemes are operationally simpler and do not suffer from Trotterization and loop closure errors. However, the pulsed scheme can obtain substantially higher tunneling rates for fixed intensity and Lamb Dicke factors as the tunneling rate scales linearly in η instead of quadratically. For the considered parameters of the quadrupole transition, the exchange duration in the pulsed scheme is four times faster than the analog one. Hence, this method would be amenable to the quadrupole transition or if the laser intensities are limited.

Before closing this section, it is also worth commenting on the realization of the ${{\mathbb{Z}}}_{2}$ gauge link in other experimental platforms. In fact, there has been a pioneering experiment with cold atoms^124,239, which relies on a different scheme designed for double-well optical lattices that exploit Floquet engineering to activate a density-dependent tunneling in the presence of strong Hubbard interactions^240,241,242. By playing with the ratio of the modulation and interaction strengths, the tunneling of the atoms in one electronic state (i.e., matter field) can depend on the density distribution of atoms in a different internal state (i.e., gauge field). On the contrary, the atoms playing the role of the gauge field can tunnel freely between the minima of the double well. As realized in refs. ^124,239, using a single atom of the gauge species per double well, one can codify the ${{\mathbb{Z}}}_{2}$ gauge qubit, those being the qubit states where the atom resides in either the left or the right well. Then, its bare tunneling realizes directly the electric-field term, whereas the density-dependent tunneling of the matter atoms can be designed to simulate the gauge-invariant tunneling of the ${{\mathbb{Z}}}_{2}$ gauge theory (5). The dynamics of the matter atom observed experimentally is consistent with Eq. (11), displaying periodic Rabi oscillations that get damped due to several noise sources¹²⁴. Although the cold-atom experiments can also infer $\langle {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}(t)\rangle$ via the measure of the atomic density of the gauge species, measuring $\langle {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle$ amounts to a bond density that would require measuring the equal-time Green’s function. This would require inferring correlation functions between both sites, which is more challenging and was not measured in the experiment¹²⁴. Although the reported measurements show $\langle {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}(t)\rangle \,\approx \,0$, which is consistent with the link field being always in the electric-field basis; it would be desirable to measure the correlated Rabi flopping of the gauge link (11), which directly accounts for how the electric-field line stretches/compresses synchronous with the tunneling of the matter particle according to Gauss’ law. Since in the trapped-ion case $\langle {\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle$ can be inferred by applying a single-qubit gate and collecting the resonance fluorescence, the present scheme proposed in this work could thus go beyond these limitations, and directly observe the consequences of gauge invariance in the correlated oscillations (11). Moreover, as discussed in the following section, there are also promising pathways in the trapped-ion case that could allow extending the quantum simulation beyond the single link case.

Minimal plaquettes and synthetic dimensional reduction for a ${{\mathbb{Z}}}_{2}$ gauge chain

There are various directions to increase the complexity of the trapped-ion quantum simulator of ${{\mathbb{Z}}}_{2}$ gauge fields. The first non-trivial extension is to consider two matter sites joined by two gauge links, which form the smallest-possible plaquette that is consistent with ${{\mathbb{Z}}}_{2}$ gauge symmetry. We discuss, in this section, how to achieve this ${{\mathbb{Z}}}_{2}$ plaquette simulator by using a pair of ions and exploiting their collective vibrational modes^243,244,245. We then present a scheme that effectively reduces the dimension of the synthetic ladder, and allows us to scale the gauge-invariant model of Eq. (5) to a full lattice, in this case, a one-dimensional chain. We note that these extensions require additional experimental tools, and longer timescales, making the quantum simulation more challenging. Nonetheless, the proposed schemes set a clear road map that emphasises the potential of trapped ions for the simulation of real-time dynamics in lattice gauge theories.

${{\mathbb{Z}}}_{2}$ plaquette: Wegner-Wilson and ’t Hooft loops for gauge-field entanglement

We consider a couple of ions leading to a pair of qubits and four vibrational modes, two per transverse direction. In principle, we could apply the previous scheme based on a global state-dependent parametric drive of Eq. (18). However, this would lead to a synthetic plaquette where two of the links have a tunneling that does not depend on any gauge qubit (see Fig. 9a), failing in this way to meet the requirements for local gauge invariance. In fact, this goes back to the simple counting of synthetic lattice sites and effective gauge fields we mentioned below Eq. (18). To remedy this problem, the idea is to modify the constraints on the strength of the light-shift optical potential, such that it becomes possible to address certain common vibrational modes instead of the local ones. Although we will focus on the light-shift scheme for now on, we note that similar ideas would apply to the Mølmer-Sørensen-type and orthogonal-force schemes. We will show in this section that, by addressing the collective modes, we can effectively deform the plaquette (see Fig. 9b) such that the model is consistent with the local ${{\mathbb{Z}}}_{2}$ symmetry.

Fig. 9: Scheme for synthetic ${{\mathbb{Z}}}_{2}$ plaquette.

a The application of Eq. (18) to N = 2 ions would result in a synthetic rectangular plaquette, where the four sites correspond to the local transverse modes of the two ions. The vertical links are induced by the state-dependent parametric tunneling of Eq. (21), and thus incorporate a gauge qubit (note that in the Mølmer-Sørensen-type scheme, the Pauli matrices in the links need to be rotated). The horizontal links describe the bare tunneling caused by dipole-dipole interactions, such that no gauge qubit mediates the tunneling, and gauge invariance is explicitly broken. b By modifying the set of constraints on the optical potential according to Eq. (38), one can resolve collective vibrational modes such as the center of mass (c.o.m), and reduce the quadrangular synthetic plaquette of (a) with 4 sites and 4 links, into a rhomboidal one composed of two sites and two links, both of which contain now a gauge qubit such that the effective tunneling respects a local ${{\mathbb{Z}}}_{2}$ symmetry.

The transverse collective modes of the two-ion crystal are the symmetric and anti-symmetric superpositions of the local vibrations, and are referred to as the center-or-mass (c) and zigzag (z) modes within the trapped-ion community. The creation operators for these modes are then defined by

$$\begin{array}{l}{a}_{{{{{{{{\rm{c}}}}}}}},\alpha }=\frac{1}{\sqrt{2}}({a}_{1,\alpha }+{a}_{2,\alpha }),{\omega }_{{{{{{{{\rm{c}}}}}}}},\alpha }={\omega }_{\alpha },\\ {a}_{{{{{{{{\rm{z}}}}}}}},\alpha }=\frac{1}{\sqrt{2}}({a}_{1,\alpha }-{a}_{2,\alpha }),{\omega }_{{{{{{{{\rm{z}}}}}}}},\alpha } \, < \, {\omega }_{\alpha }.\\ \end{array}$$

(37)

We now substitute these equations in the expressions for the light-shift optical potential of Eq. (16), and proceed by performing the subsequent Lamb-Dicke expansion that leads to a sum of terms containing all possible powers of the creation-annihilation operators. We can now select the desired tunneling term between a single mode, say the center of mass, along the two transverse directions (see Fig. 9b). Since we can also get terms that couple the center of mass and the zigzag modes, we need to consider the constraints

$${\omega }_{{{{{{{{\rm{d}}}}}}}}}={\omega }_{{{{{{{{\rm{c}}}}}}}},y}-{\omega }_{{{{{{{{\rm{c}}}}}}}},x},| {\Omega }_{{{{{{{{\rm{d}}}}}}}}}| \,\ll \,| {\omega }_{{{{{{{{\rm{c}}}}}}}},y}-{\omega }_{{{{{{{{\rm{c}}}}}}}},x}| ,\frac{| {\omega }_{{{{{{{{\rm{c}}}}}}}},\alpha }-{\omega }_{{{{{{{{\rm{z,\beta }}}}}}}}}| }{{\eta }_{\alpha }{\eta }_{\beta }},$$

(38)

such that those terms become off-resonant and can be neglected. Note that these new constraints will make the gauge-invariant tunneling weaker, and the targeted dynamics slower, making the experimental realizations more challenging.

In the following, we will present the expressions for the light-shift schemes, although any of the other possibilities should be analogous. By moving to the interaction picture with respect to the full vibrational Hamiltonian, and neglecting the off-resonant terms by a rotating-wave approximation that rests upon Eq. (38), the leading term stemming from the aforementioned light-shift optical potential is

$${V}_{I}(t)\,\approx \,\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{4}{a}_{{{{{{{{\rm{c}}}}}}}},y}^{{{{\dagger}}} }{\sigma }_{1}^{z}{a}_{{{{{{{{\rm{c}}}}}}}},x}+\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{4}{a}_{{{{{{{{\rm{c}}}}}}}},y}^{{{{\dagger}}} }{\sigma }_{2}^{z}{a}_{{{{{{{{\rm{c}}}}}}}},x}+{{{{{{{\rm{H.c.}}}}}}}}.$$

(39)

Here, we recall that the drive strength is Ω_d = η_xη_yΩ_1,2, and we have neglected the irrelevant phase that can be gauged away in this simple two-mode setting. As depicted in Fig. 10, there are now two different gauge-invariant processes in which a center-of-mass phonon along the x-axis can tunnel into a center-of-mass phonon along the y-axis. Each of these processes flips the Hadamard state of one, and only one, of the trapped-ion qubits (see Fig. 10).

Fig. 10: Trapped-ion ${{\mathbb{Z}}}_{2}$ tunneling in a rhomboidal plaquette.

Schematic representation of the gauge-invariant tunneling of a vibrational excitation, which is initially in the center of mass (c.o.m) mode along the x axis, and “tunnels” into the c.o.m mode along the y axis. The blue and green arrow represent the wavevectors of the lasers that induce the parametric excitation. In the upper insets, this tunneling is mediated by a spin flip in the Hadamard basis of the first ion qubit ${\left\vert -\right\rangle }_{1}\,\mapsto \,{\left\vert +\right\rangle }_{1}$, whereas in the lower inset it involves the second ion qubit ${\left\vert -\right\rangle }_{2}\,\mapsto \,{\left\vert +\right\rangle }_{2}$. These two paths can be interpreted as the two effective links of the synthetic rhomboidal plaquette displayed in Fig. 9.

We can now modify the interpretation in terms of synthetic matter sites and ${{\mathbb{Z}}}_{2}$ gauge qubits (22), which must now include a pair of ${{\mathbb{Z}}}_{2}$ links, as we have two qubits dressing the tunneling

$${a}_{{{{{{{{\rm{c}}}}}}}},x},{a}_{{{{{{{{\rm{c}}}}}}}},x}^{{{{\dagger}}} }\,\mapsto \,{a}_{1},{a}_{1}^{{{{\dagger}}} },{a}_{{{{{{{{\rm{c}}}}}}}},y},{a}_{{{{{{{{\rm{c}}}}}}}},y}^{{{{\dagger}}} }\,\mapsto \,{a}_{2},{a}_{2}^{{{{\dagger}}} }{\sigma }_{i}^{x},{\sigma }_{i}^{z}\,\mapsto \,{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{i}}^{x},{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{i}}^{z}.$$

(40)

As depicted in Fig. 9b, we need to introduce two links that connect the synthetic site 1 to 2, requiring two synthetic directions specified by the vectors e₁, e₂, and allowing us to interpret the model in terms of a rhomboidal plaquette. In addition to the gauge-invariant tunneling, we also apply the additional tone of Eq. (3), which drives the carrier transition on both qubits, and leads to the electric-field term. Altogether, the ${{\mathbb{Z}}}_{2}$ gauge theory on this plaquette is

$${H}_{{{{{{{{\rm{eff}}}}}}}}}=\sum\limits_{n=1,2}\left({t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{n}}{a}_{2}^{{{{\dagger}}} }{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{n}}^{z}{a}_{1}+{{{{{{{\rm{H.c.}}}}}}}}\right)+\sum\limits_{n=1,2}h{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{n}}^{x},$$

(41)

where the microscopic parameters for the tunneling strength and the electric field are the same as in Eq. (5), except for the tunneling strengths. These get halved with respect to the previous ones by working with the center-of-mass mode instead of the local vibrations, namely

$${t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}={t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{2}}=\frac{{\Omega }_{1,2}}{4}{\eta }_{x}{\eta }_{y},h=\frac{{\tilde{\Omega }}_{{{{{{{{\rm{d}}}}}}}}}}{2}.$$

(42)

Let us also note that, since we now have an increased connectivity, the generators of the ${{\mathbb{Z}}}_{2}$ gauge symmetry which, in the single-link case were defined in Eq. (7), now read

$${G}_{1}={{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {a}_{1}^{{{{\dagger}}} }{a}_{1}}{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{2}}^{x},{G}_{2}={\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}{\sigma }_{1,{{{{{{{{\bf{e}}}}}}}}}_{2}}^{x}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {a}_{2}^{{{{\dagger}}} }{a}_{2}}.$$

(43)

As we have a pair of synthetic ${{\mathbb{Z}}}_{2}$ links emanating from each of the two matter sites, the generators include products of the corresponding Pauli matrices. Note that these generators fulfill the same algebra as before, and define projectors onto super-selection sectors, such that the effective Hamiltonian gauge theory (41) can be block decomposed into the different sectors (8) characterized by two static charges q₁, q₂ ∈ {0, 1}. In addition to the previous effective Hamiltonian, one could also include other gauge-invariant terms, such as

$${\tilde{H}}_{{{{{{{{\rm{eff}}}}}}}}}={H}_{{{{{{{{\rm{eff}}}}}}}}}+{\Delta }_{1}{a}_{1}^{{{{\dagger}}} }{a}_{1}+{\Delta }_{2}{a}_{2}^{{{{\dagger}}} }{a}_{2},$$

(44)

where Δ_i can be controlled by a small detuning of the state-dependent parametric drive.

Once the scheme for the quantum simulation of the single ${{\mathbb{Z}}}_{2}$ plaquette has been discussed, let us describe some interesting dynamical effects that arise when considering, as in the single-link case, the one-particle sector. Following our previous approach, one can exploit the global U(1) symmetry and Gauss’ law to reduce the dimensionality of the subspace where the dynamics takes place. If we consider a single bosonic particle, this subspace is spanned by four states

$$\begin{array}{l}\vert {{{{{{{\rm{{L}}}}}}}_{1}}}\rangle =\vert {1}_{1}\rangle \otimes \vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{2}}\rangle \otimes \vert {0}_{2}\rangle ,\\ \vert {{{{{{{\rm{{L}}}}}}}_{2}}}\rangle =\vert {1}_{1}\rangle \otimes \vert {+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{2}}\rangle \otimes \vert {0}_{2}\rangle ,\\ \vert {{{{{{{\rm{{R}}}}}}}_{1}}}\rangle =\vert {0}_{1}\rangle \otimes \vert {+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{2}}\rangle \otimes \vert {1}_{2}\rangle ,\\ \vert {{{{{{{\rm{{R}}}}}}}_{2}}}\rangle =\vert {0}_{1}\rangle \otimes \vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \otimes \vert {+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{2}}\rangle \otimes \vert {1}_{2}\rangle ,\end{array}$$

(45)

where the corresponding background charges are q₁ = 1, q₂ = 0. In comparison to the single-link case, the plaquette gives us further possibilities for the stretching and compressing of the electric-field line when the matter boson tunnels back and forth (see Fig. 3). On the one hand, an electric-field loop around the plaquette, a so-called ’t Hooft loop, does not require further sinks/sources since the electric field line enters and exists all sites in the plaquette. In addition, the stretched electric field can now wind along the two possible paths of the loop. This leads to the doubling of the gauge arrangements for a fixed layout of the matter boson in Eq. (45) and Fig. 11.

Fig. 11: ♢-scheme for ${{\mathbb{Z}}}_{2}$ tunneling in a plaquette.

On the left, we represent schematically the four possible gauge-invariant states in the sector with background charges q₁ = 1, q₂ = 0, which correspond to Eq. (45). We use thick and thin yellow lines to represent the presence and absence of an electric field, respectively. Likewise, dark and bright red circles represent the presence and absence of a matter particle, respectively. We see that, when the matter particle resides on the left or right site, a 't Hooft electric field line that winds around the plaquette can be present or absent, doubling the number of possible states. On the right, we depict an effective ♢-scheme in quantum optics, in which the gauge-invariant tunneling induces two copies of the Λ-scheme of Fig. 4, which appeared for a single link and two bosons that lead to bright and dark states, and mode entanglement.

We are interested in exploring new dynamical effects, in particular the possibility of creating entanglement between the ${{\mathbb{Z}}}_{2}$ gauge fields by the tunneling of the bosonic ${{\mathbb{Z}}}_{2}$ charge. The dynamics due to this effective Hamiltonian can now be depicted as a four-level system in a ♢-scheme. Setting Δ₁ = Δ₂ = 0 in Eq. (44), the states with the particle on the right site have zero energy, whereas those with the particle on the left have energies ± 2h. Moreover, they are coupled by the gauge-invariant tunneling with strengths ${t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}},{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{2}}$ according to the ♢ scheme on the right panel of Fig. 11. As apparent from this figure, we can define bright $\vert {{{{{{{\rm{B}}}}}}}}\rangle =(\vert {{{{{{{\rm{{R}}}}}}}_{1}}}\rangle +\vert {{{{{{{\rm{{R}}}}}}}_{2}}}\rangle )/\sqrt{2}$ and dark $\vert {{{{{{{\rm{D}}}}}}}}\rangle =(\vert {{{{{{{\rm{{R}}}}}}}_{1}}}\rangle -\vert {{{{{{{\rm{{R}}}}}}}_{2}}}\rangle )/\sqrt{2}$ states once more, such that the effective dynamics corresponds to that of a 3-level atom. This case also has an exact solution in terms of an effective spin-1 particle that precesses under an effective magnetic field. Defining $\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}(t)\rangle =d(t)\vert {{{{{{{\rm{D}}}}}}}}\rangle +{c}_{l,1}(t)\vert {{{{{{{\rm{{L}}}}}}}_{1}}}\rangle +{c}_{b}(t)\vert {{{{{{{\rm{B}}}}}}}}\rangle +{c}_{l,2}(t)\vert {{{{{{{\rm{{L}}}}}}}_{2}}}\rangle$, the amplitude of the dark state remains constant d(t) = d(0), whereas the amplitudes of the remaining states evolve as ${{{{{{{\boldsymbol{c}}}}}}}}(t)={{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}t{{{{{{{{\boldsymbol{B}}}}}}}}}_{0}\cdot {{{{{{{\boldsymbol{S}}}}}}}}}{{{{{{{\boldsymbol{c}}}}}}}}(0)$. Here, ${{{{{{{\boldsymbol{c}}}}}}}}(t)={({c}_{l,1}(t),{c}_{b}(t),{c}_{l,2}(t))}^{{{{{{{{\rm{t}}}}}}}}}$,

$${{{{{{{{\boldsymbol{B}}}}}}}}}_{0}=(2{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}},0,2h),$$

(46)

and the spin-1 operators are defined as

$${S}_{z}=\vert {{{{{{{\rm{{L}}}}}}}_{2}}}\rangle \left\langle {{{{{{{\rm{{L}}}}}}}_{2}}}\right\vert -\vert {{{{{{{\rm{{L}}}}}}}_{1}}}\rangle \left\langle {{{{{{{\rm{{L}}}}}}}_{1}}}\right\vert ,{S}_{x}=\frac{1}{\sqrt{2}}(\vert {{{{{{{\rm{{L}}}}}}}_{2}}}\rangle \left\langle {{{{{{{\rm{B}}}}}}}}\right\vert +\vert {{{{{{{\rm{B}}}}}}}}\rangle \left\langle {{{{{{{\rm{{L}}}}}}}_{1}}}\right\vert )+{{{{{{{\rm{H.c.}}}}}}}}.$$

(47)

If one now switches on the detuning Δ₂ > 0 = h = Δ₁, the intermediate bright state gets shifted in energies such that, for $| {t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{n}}| \, \ll \, {\Delta }_{2}$, the bright state will only be virtually populated when one starts from the configuration $\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}(0)\rangle =\vert {{{{{{{\rm{{L}}}}}}}_{1}}}\rangle$. In this initial state, the matter particle is in the left site, and no electric-field line winds around the plaquette (see Fig. 12). The dynamics can then be understood from a second-order process in which the particle tunnels to the right, while the electric field line stretches, followed by a second tunneling event to the left. Due to the high energy offset ${\Delta }_{2}\,\gg \,{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$, the right site is only virtually populated in the intermediate states of Fig. 12. Note that, during the subsequent tunneling from these virtual states, the particle can either follow the same link/path of the first tunneling event, flipping the corresponding link qubit back to the original one $\vert {{{{{{{\rm{{L}}}}}}}_{1}}}\rangle$ or, alternatively, it can choose to follow the other link/path, going around the plaquette and ending in state $\vert {{{{{{{\rm{{L}}}}}}}_{2}}}\rangle$. Since one must superpose the possible histories in quantum mechanics, the state after half the exchange time $\Delta {t}_{{{{{{{{\rm{ex}}}}}}}}}/2=\pi {\Delta }_{2}/4{t}_{1,{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}}^{2}$ becomes

$$\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}({t}_{e})\rangle =\frac{1}{\sqrt{2}}(\vert {{{{{{{\rm{{L}}}}}}}_{1}}}\rangle -{{{{{{{\rm{i}}}}}}}}\vert {{{{{{{\rm{{L}}}}}}}_{2}}}\rangle )=\vert {1}_{1}\rangle \otimes \vert {\Psi }_{{{{{{{{\rm{Bell}}}}}}}}}^{-}\rangle \otimes \vert {0}_{2}\rangle .$$

(48)

Here, the boson has returned to the initial lattice site, but the gauge fields have evolved into an entangled state that is equivalent to a Bell pair in the Hadamard basis

$$\vert {\Psi }_{{{{{{{{\rm{Bell}}}}}}}}}^{-}\rangle =\frac{1}{\sqrt{2}}\left(\vert {-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}},{-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{2}}\rangle -{{{{{{{\rm{i}}}}}}}}\vert {+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}},{+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{2}}\rangle \right).$$

(49)

It is interesting to remark that this entangled state is the result of summing over the two tunneling histories of the charged particle, leading to a linear superposition between two different electric-field strings. In the first one, there is no electric field within the loop, as the boson tunnels forth and back along the same link. Conversely, in the second case, a t’ Hooft electric-field loop winding around the plaquette has been created since the boson has enclosed a loop around the plaquette during the virtual process. In Fig. 13, we represent the dynamics of such internal state as a function of time by representing the state fidelities of the time-evolved state with the $\vert {{{{{{{{\rm{L}}}}}}}}}_{1}\rangle ,\vert {{{{{{{{\rm{L}}}}}}}}}_{2}\rangle$ and the target Bell state $\vert {\Psi }_{-}\rangle$(49). On sees how the Bell-state fidelity approaches unity after half the exchange duration Δt_ex/2. Since the dynamics is i second order, we see that the timescale is larger than that of Figs. 3 and 5.

Fig. 12: ’t Hooft loop entanglement in the gauge qubits.

We represent a scheme for the second-order virtual tunneling of a boson, which initially occupies the left site (upper state) and aims to tunnel to right, which is penalized energetically by the on-site energy ${\Delta }_{2}\,\gg \,{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{n}}$. After the virtual tunneling and the accompanying stretching of the electric-field line (intermediate states), the second tunneling process back to the left site can either compress the string, or stretch it further until it winds around the plaquette. The superposition of these possible transitions (lower state) leads to an entangled state. We use thick and thin yellow lines to represent the presence and absence of an electric field, respectively.

Fig. 13: Gauge entanglement in a minimal plaquette.

We represent the state fidelities ${{{{{{{{\mathcal{F}}}}}}}}}_{i}=| \langle {\Psi }_{i}| \Psi (t)\rangle {| }^{2}$ for the target state $\left\vert {\Psi }_{i}\right\rangle$ that can either be $\left\vert {{{{{{{{\rm{L}}}}}}}}}_{1}\right\rangle ,\left\vert {{{{{{{{\rm{L}}}}}}}}}_{2}\right\rangle$ in Eq. (45), or the Bell state $\left\vert {\Psi }_{{{{{{{{\rm{Bell}}}}}}}}}^{-}\right\rangle$ in Eq. (48). The time evolved state $\left\vert \Psi (t)\right\rangle$ is obtained by solving numerically the dynamics for ${\Delta }_{2}=10{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$, and h = Δ₁ = 0. The dashed line at Δt_ex/2 represents half the exchange time, at which the fidelity with the Bell state (blue line) becomes maximized.

${{\mathbb{Z}}}_{2}$ chain: synthetic dimensional reduction

In the previous subsection, we have seen that introducing more ions and playing with collective vibrational modes allows us to extend the ${{\mathbb{Z}}}_{2}$ gauge-field toolbox towards interesting and more complex real-time phenomena. We discussed how, by working with only two ions, the spectral crowding of collective modes can still be handled, and one can selectively address the gauge-invariant tunneling between a pair of collective modes along the two different transverse directions. In this subsection, we present a scheme that exploits these collective modes with reduced crowding, together with the idea of synthetic dimensional reduction, to scale the quantum simulator of ${{\mathbb{Z}}}_{2}$ gauge theories to chains of arbitrary size. We start the discussion by considering the generalization of Eq. (21) to a chain of N trapped ions, namely

$${V}_{1}(t) \, \approx \sum\limits_{i}\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{2}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{\phi }_{i}}{a}_{i,y}^{{{{\dagger}}} }{\sigma }_{i}^{z}{a}_{i,x}+{{{{{{{\rm{H.c.}}}}}}}},$$

(50)

where we recall that the microscopic parameters were

$${\Omega }_{{{{{{{{\rm{d}}}}}}}}}=| {\Omega }_{1,2}| {\eta }_{x}{\eta }_{y},{\phi }_{i}={{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{d}}}}}}}}}\cdot {{{{{{{{\boldsymbol{r}}}}}}}}}_{i}^{0}+\arg (-{\Omega }_{1,2}).$$

(51)

If we align the laser wave-vectors such that ${{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{d}}}}}}}}}\cdot {{{{{{{{\boldsymbol{r}}}}}}}}}_{i}^{0}=0$, the driving phase becomes homogeneous, and can be gauged away without loss of generality. The Hamiltonian can still be described in terms of the tight-binding model discussed in the supplementary material, but one must introduce a state-dependent tunneling matrix

$${\hat{t}}_{(i,\alpha )(j,\beta )}={t}_{(i,\alpha )(j,\beta )}{{\mathbb{I}}}_{2}+\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{2}{\sigma }_{i}^{z}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{\epsilon }_{\alpha ,\beta }{\phi }_{j}}{\delta }_{i,j}(1-{\delta }_{\alpha ,\beta }).$$

(52)

Using the same mapping to a synthetic ladder, we would obtain an effective model, where only the vertical synthetic links in yellow contain a ${{\mathbb{Z}}}_{2}$ gauge field that mediates the tunneling. On the other hand, the horizontal tunnelings are still c-numbers, and the complete model is thus not consistent with the local gauge symmetry. This caveat generalizes the situation in the plaquette of Fig. 9a to the full rectangular ladder: we would need 3N − 2 gauge qubits to make the model gauge invariant, but only have N at our disposal.

Accordingly, the horizontal links cannot be gauged with the available ${{\mathbb{Z}}}_{2}$ fields, which are already in use to gauge the vertical ones. In order to obtain a gauge-invariant model, the idea is to make a synthetic dimensional reduction by exploiting the collective normal modes as follows. We first introduce a site-dependent shift of the effective on-site energies

$$\begin{array}{l}{\omega }_{2i-1,y}-{\omega }_{2i,y}=0,{\omega }_{2i+1,y}-{\omega }_{2i,y}=\tilde{\Delta },\\ {\omega }_{2i-1,x}-{\omega }_{2i,x}=\tilde{\Delta },{\omega }_{2i+1,x}-{\omega }_{2i,x}=0,\end{array}$$

(53)

where we have introduced a parameter for these shifts $\tilde{\Delta }$ that fulfills $| {t}_{(i,\alpha )(j,\alpha )}| \,\ll \,| \tilde{\Delta }|$. In this regime, the tunneling of phonons vibrating along the x-axis (y-axis) can only take place within dimers, i.e., pairs of neighboring sites, composed of even-odd (odd-even) sites (see Fig. 14a). In analogy with ultracold atoms, this dimerization could be obtained from the light shift of a tilted optical super-potential, or by working with micro-fabricated traps that allow one to design the local trap frequencies individually^{246,247,248,249,250,251,252,253,254,255,256,257,258}. As depicted in Fig. 14), the normal vibrational modes of the chain then break into a collection of center-of-mass and zigzag modes (37) that only have support on the alternating dimers

$$\begin{array}{l}{a}_{{{{{{{{\rm{c}}}}}}}},2i-1,y}=\frac{1}{\sqrt{2}}({a}_{2i-1,y}+{a}_{2i,y}),{a}_{{{{{{{{\rm{z}}}}}}}},2i-1,y}=\frac{1}{\sqrt{2}}({a}_{2i-1,y}-{a}_{2i,y}),\\ {a}_{{{{{{{{\rm{c}}}}}}}},2i,x}=\frac{1}{\sqrt{2}}({a}_{2i,x}+{a}_{2i+1,x}),{a}_{{{{{{{{\rm{z}}}}}}}},2i,x}=\frac{1}{\sqrt{2}}({a}_{2i,x}-{a}_{2i+1,x}),\end{array}$$

(54)

where the index i ∈ {1, ⋯ N/2} labels the different dimers.

Fig. 14: Synthetic dimensional reduction for a ${{\mathbb{Z}}}_{2}$ chain.

a We represent the transverse vibrational degrees of freedom of a trapped-ion chain in a frequency scheme, where the corresponding trap frequencies ω_x < ω_y can be resolved by external parametric drives. The introduction of the site-dependent shift of the frequencies in Eq. (53) leads to a two-site gradient here depicted by $\tilde{\Delta }$. For $| {t}_{ij}| \,\ll \,\tilde{\Delta }$, the exchange of vibrational quanta leads to alternating dimers, here depicted by green solid lines. b As a consequence of this exchange, the vibrational states inside the dimers split into center of mass (com) and zigzag (zz) modes, which can also be resolved in energies. As shown in the inset, we apply a pair of state-dependent parametric drives addressed to even-odd or odd-even dimers for the com modes, respectively, in order to induce the desired light-shift potential underlying the state-dependent tunneling of Eq. (55).

The additional ingredient of the proposed scheme is a pair of light-shift optical potentials, each of which is only addressed to the ions that sit on the even or odd sites of the chain, and can be described by Eq. (18) with the corresponding restrictions in the addressed ions. As depicted in the inset of Fig. 14b, the even (odd) optical potentials are tuned to required energy offsets ω_d = ω_y − ω_x (${\omega }_{{{{{{{{\rm{d}}}}}}}}}={\omega }_{y}-{\omega }_{x}+\tilde{\Delta }$). In this expression, we further assume that the even terms lie in the resolved-sideband limit of Eq. (38) and, analogously, the odd ones lie in the resolved-sideband limit taking into account the additional energy shift by $\tilde{\Delta }$. As a result of these conditions, using the lessons learned from the previous simpler setups, one can check that the corresponding state-dependent parametric couplings will dress the tunneling between the center-of-mass modes of neighboring x and y dimers while minimizing the tunneling between the zigzag modes. In this way, we are halving the number of degrees of freedom, a precursor of the aforementioned synthetic dimensional reduction, and the available trapped-ion qubits serve to simulate the ${{\mathbb{Z}}}_{2}$ gauge field defined on the links of a dimension-reduced chain.

As depicted in Fig. 14b, this allows us to derive an effective dressed tunneling

$${V}_{1}(t)\,\approx \,\sum \limits_{i=1}^{N/2}\frac{{\Omega }_{{{{{{{{\rm{d}}}}}}}}}}{4}\left({{{{{{{{\rm{e}}}}}}}}}^{+{{{{{{{\rm{i}}}}}}}}{\phi }_{2i}}{a}_{{{{{{{{\rm{c}}}}}}}},2i-1,y}^{{{{\dagger}}} }{\sigma }_{2i}^{z}{a}_{{{{{{{{\rm{c}}}}}}}},2i,x}\right.\\ \left. +{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{\phi }_{2i+1}}{a}_{{{{{{{{\rm{c}}}}}}}},2i,x}^{{{{\dagger}}} }{\sigma }_{2i+1}^{z}{a}_{{{{{{{{\rm{c}}}}}}}},2i+1,y}\right)+{{{{{{{\rm{H.c.}}}}}}}},$$

(55)

where the microscopic parameters are again those of Eq. (51). Note that the alternation in the sign of the tunneling phases ${{{{{{{{\rm{e}}}}}}}}}^{+{{{{{{{\rm{i}}}}}}}}{\phi }_{2i}}$ and ${{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{\phi }_{2i+1}},$ is caused by the fact that the light-shift potential provides (absorbs) the missing (excess) energy to activate the tunneling against the corresponding energy offset $\tilde{\Delta }$, making the dressed tunneling resonant. In this case, in order to make this complex phase irrelevant, we should align the laser wave-vector in a direction orthogonal to the chain ${{{{{{{{\boldsymbol{k}}}}}}}}}_{{{{{{{{\rm{d}}}}}}}}}\cdot {{{{{{{{\boldsymbol{r}}}}}}}}}_{i}^{0}=0$.

In addition to these ingredients, we would again need a second tone that drives the qubit transition (3), corresponding to a carrier term with a resonance condition that includes the ac-Stark shifts (28). We can then perform the aforementioned dimensional reduction by considering the formal mapping

$${a}_{{{{{{{{\rm{c}}}}}}}},2i,x},{a}_{{{{{{{{\rm{c}}}}}}}},2i,x}^{{{{\dagger}}} }\,\mapsto \,{a}_{2i},{a}_{2i}^{{{{\dagger}}} },{a}_{{{{{{{{\rm{c}}}}}}}},2i-1,y},{a}_{{{{{{{{\rm{c}}}}}}}},2i-1,y}^{{{{\dagger}}} }\,\mapsto \,{a}_{2i-1},{a}_{2i-1}^{{{{\dagger}}} },$$

(56)

for i ∈ {1, ⋯  , N/2}, such that the odd (even) matter sites correspond to the y-axis (x-axis) center-of-mass modes. Besides, the gauge qubits are identified via the standard mapping

$${\sigma }_{i}^{x},{\sigma }_{i}^{z}\,\mapsto \,{\sigma }_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x},{\sigma }_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z},$$

(57)

where the index now covers all links i ∈ {1, ⋯  , N − 1}.

In this way, we have reduced the synthetic two-leg ladder onto a chain (see Fig. 15a), halving the number of matter sites and reducing the required links. Accordingly, the available number of physical qubits suffice to gauge all synthetic tunnelings, obtaining an effective gauge-invariant model that generalizes the single-link case (5) to the full chain

$${H}_{{{{{{{{\rm{eff}}}}}}}}}=\sum\limits_{i=1}^{N-1}\left(\left({t}_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}{a}_{i+1}^{{{{\dagger}}} }{\sigma }_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}{a}_{i}+{{{{{{{\rm{H.c.}}}}}}}}\right)+h{\sigma }_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}\right).$$

(58)

Here, the gauge-invariant tunneling (see Fig. 15b) has a strength that is homogeneous along the chain, and gets halved with respect to the single-link case (5), while the electric field remains to be the same

$${t}_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}=\frac{{\Omega }_{1,2}}{4}{\eta }_{x}{\eta }_{y},h=\frac{{\tilde{\Omega }}_{{{{{{{{\rm{d}}}}}}}}}}{2}.$$

(59)

Paralleling our discussion of the single-link case, the invariance under local ${{\mathbb{Z}}}_{2}$ transformations of this gauge theory is generated by the following operators

$${G}_{i}={{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {a}_{i}^{{{{\dagger}}} }{a}_{i}}\prod\limits_{\ell \in {{{{{{{\mathcal{L}}}}}}}}\{i\}}{\sigma }_{i,\ell {{{{{{{{\bf{e}}}}}}}}}_{1}}^{x},$$

(60)

where $j\in {{{{{{{\mathcal{L}}}}}}}}\{i\}$ is the set of links that surround a given matter site labeled by i, namely ± e₁ in the bulk (Fig. 15a), and + e₁ ( − e₁) at the leftmost (rightmost) boundary sites i = 1 (i = N).

Fig. 15: Gauss’ law and gauge-invariant tunneling in a bosonic ${{\mathbb{Z}}}_{2}$ chain.

a Schematic representation of a ${{\mathbb{Z}}}_{2}$ gauge theory of bosonic matter on a one-dimensional chain. The bosons sit on the lattice sites (red circles), whereas the gauge fields reside on the links and correspond to qubits. The shaded area represents the Gauss' law in the bulk. b At each matter site, we can have any integer number of bosons, whereas the gauge fields in the links have two possible states in a given basis, here the electric-field Hadamard basis. On the right panel, we represent schematically the gauge-invariant tunneling of a boson towards a neighboring site, which is already occupied by two bosons. As depicted with the yellow arrow, this requires the gauge qubit to be flipped $\vert {-}_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle \to \vert {+}_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}\rangle$, such that the electric string grows.

Once this method has been presented, let us discuss neat dynamical effects that go beyond the previous periodic oscillations in the link/plaquette limits. Let us recall that, as depicted in Fig. 3b, the gauge-invariant tunneling gets inhibited as one increases the electric field h, which we referred to as a precursor of confinement in larger lattice gauge theories. In the following subsections, we discuss how the trapped-ion quantum simulator (58) would allow for a clear manifestation of this confinement, focusing particularly in the one- and two-particle sectors. We will then move to half-filling, where minor modifications of the quantum simulator will allow to explore if the phenomenon of string breaking in real-time dynamics^{61,106,259,260,261} also occurs in this gauge theory.

We consider a chain of N bosonic matter sites, and (N − 1) gauge fields (see Fig. 15a), such that the full Hilbert space is ${{{{{{{\mathcal{H}}}}}}}}={{{{{{{\mathcal{F}}}}}}}}\otimes {{\mathbb{C}}}^{2(N-1)}$, with ${{{{{{{\mathcal{F}}}}}}}}={\oplus }_{n = 0}^{\infty }{{{{{{{{\mathcal{F}}}}}}}}}_{n}$. Here, each subspace is ${{{{{{{{\mathcal{F}}}}}}}}}_{n}={{{{{{{\rm{span}}}}}}}}\{\vert {n}_{1}\rangle \otimes \vert {n}_{2}\rangle \otimes \cdots \otimes \vert {n}_{N}\rangle :{n}_{1}+{n}_{2}+\cdots {n}_{N}=n\}$. Due to the global U(1) symmetry in the matter sector, the dynamics will take place within one of these subspaces depending on the number of bosons of the initial state. In addition, due to the gauge symmetry, the physical states are further restricted via Gauss’ law, which now imposes N constraints

$${G}_{i}\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}\rangle ={{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\pi {q}_{i}}\vert {\Psi }_{{{{{{{{\rm{phys}}}}}}}}}\rangle ,\,\,\forall i\in \{1,\cdots \,,N\}.$$

(61)

We recall that q_i ∈ {0, 1} are the background ${{\mathbb{Z}}}_{2}$ charges that specify the super-selection sector where the dynamics occurs. This Gauss’ law at the bulk has also been depicted in Fig. 15a. In Fig. 15b, we represent the Hilbert spaces of the bosonic matter sites and qubit links, as well as the transitions involved in a gauge-invariant tunneling.

One-boson sector: Wannier-Stark localization

In this case, the physical subspace ${{{{{{{{\mathcal{V}}}}}}}}}_{{{{{{{{\rm{phys}}}}}}}}}={{{{{{{\rm{span}}}}}}}}\{\vert \sim \!\! \sim {\bullet }_{i}\rangle :i\in \{1,\cdots \,,N\}\}\subset {{{{{{{{\mathcal{F}}}}}}}}}_{1}\otimes {{\mathbb{C}}}^{2(N-1)}$ can be be spanned by

$$\vert \sim \!\! \sim {\bullet }_{i}\rangle =\left(\prod\limits_{\ell < i}{\sigma }_{\ell ,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}\right){a}_{i}^{{{{\dagger}}} }\vert {{{{{{{\rm{vac}}}}}}}}\rangle .$$

(62)

Here, as the lattice starts and finishes with a matter site, the vacuum $\vert {{{{{{{\rm{vac}}}}}}}}\rangle =\vert {0}_{1},{-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}},\cdots \,,{0}_{N-1},{-}_{N-1,{{{{{{{{\bf{e}}}}}}}}}_{1}},{0}_{N}\rangle$ belongs to the super-selection sector with a single background charge at the leftmost boundary q₁ = 1, and zero elsewhere q_j = 0,   ∀ j ≠ 1. As a result of the composite operator in Eq. (62), the basis states represent a boson at site i, together with a domain-wall configuration of the gauge qubits in the Hadamard basis $\vert \sim \!\! \sim {\bullet }_{i}\rangle =\vert {0}_{1},{+}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}},\cdots \,,{+}_{i-1,{{{{{{{{\bf{e}}}}}}}}}_{1}},{1}_{i},{-}_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}},\cdots \,,{-}_{N-1,{{{{{{{{\bf{e}}}}}}}}}_{1}},{0}_{N}\rangle$. This has been depicted in Fig. 16a, where the boson at site i is connected to an electric field line that extends towards the left boundary, connecting the static charge and the dynamical one. We thus see that the dynamics, which in principle is defined in an exponentially-large Hilbert space, gets restricted to a much smaller subspace whose size only grows linearly with the length of the chain. Up to an irrelevant shift of the zero of energies, the Hamiltonian (58) can be rewritten as

$${H}_{{{{{{{{\rm{eff}}}}}}}}}= \sum\limits_{i=1}^{N-1}\left({t}_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}\vert \sim \!\! \sim {\bullet }_{i+1}\rangle \left\langle \sim \!\! \sim {\bullet }_{i}\right\vert +{{{{{{{\rm{H.c.}}}}}}}}\right)\\ +2h\sum\limits_{i=1}^{N}i\vert \sim \!\! \sim {\bullet }_{i}\rangle \left\langle \sim \!\! \sim {\bullet }_{i}\right\vert ,$$

(63)

which corresponds to a tight-binding problem where a single composite particle built from the dynamical ${{\mathbb{Z}}}_{2}$ charge with the attached electric string, tunnels in the background of a linear potential. This problem maps exactly to the tight-binding Wannier-Stark ladder^{262,263,264,265,266}. In contrast to the analogous problem in classical physics, where the particle would simply fall down the linear slope until reaching the bottom, the quantum particle can only oscillate around the initial position, leading to the so-called Wannier-Stark localization. In the present context of the ${{\mathbb{Z}}}_{2}$ gauge theory (58), these oscillations will be accompanied by the periodic stretching and compressing of the attached electric-field line, as we now discuss in detail.

Fig. 16: Wannier-Stark localization of a single ${{\mathbb{Z}}}_{2}$ charge in the chain.

a Single bosonic particle (filled red circle), with an attached electric-field string that connects it to the background charge q₁ = 1 at the left boundary. b Contour plots for the dynamics of the boson distribution ${\overline{n}}_{i}(t)=\langle {a}_{i}^{{{{\dagger}}} }{a}_{i}(t)\rangle$, the electric field on the links ${\overline{s}}_{i}^{x}(t)=\langle {\sigma }_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle$, as well as the block entanglement entropy $S({\rho }_{A})=-{{{{{{{\rm{Tr}}}}}}}}\{{\rho }_{A}\log {\rho }_{A}\}$. We consider a chain of N = 16 sites, and set the transverse electric field to $h=0.6{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$ (upper row), and $h=0.4{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$ (lower row). The initial state is $\left\vert \Psi (0)\right\rangle =\left\vert \sim \!\! \sim {\bullet }_{7}\right\rangle$ in the notation of Eq. (62), which corresponds to a product state for the boson being localized at the center of the chain, and a domain wall of the gauge qubits with respect to the Hadamard x-basis magnetization.

In the Supplementary Note 3, we present a detailed discussion of an exact solution of the real-time dynamics in the boson sector. These analytical expressions serve as a benchmark for a numerical method that can be easily adapted to other matter contents in which an exact solution no longer exists: matrix product states (MPSs)^267,268. The MPSs are major tools for the classical numerical simulation of 1D strongly correlated models. These methods capture the interplay of locality and entanglement by expressing an entangled many-body wave function in terms of local tensors. For static calculations, the MPS-based density matrix renormalization group (DMRG)²⁶⁹ has become a common choice for obtaining the ground and a few low-lying excited states of many-body Hamiltonians, as it can reach remarkable accuracy and reliability. In the case of real-time evolution, the breakthrough came with the development of the time-evolving- block-decimation (TEBD) algorithm²⁷⁰, but it can also be treated using a variety of methods²⁷¹. Among these, the time-dependent variational principle (TDVP)²⁷², which uses a Lie-Trotter decomposition to integrate a train of tensors sequentially, is less error prone and more accurate than other available methods. We thus select it as our method of choice for the current work.

In TDVP, the MPS ansatz $\vert \psi (t)\rangle$ can be understood as a variational manifold of reduced dimensionality within the full many-body Hilbert space. The time evolution of the MPS is obtained by computing the action of the Hamiltonian H along the tangent direction to this variational manifold, which we recall is described by the MPS bond dimension χ. This approach leads to an effective Schrödinger equation for states constrained to the MPS manifold that reads as follows

$${{{{{{{\rm{i}}}}}}}}\frac{d}{dt}\vert \psi (t)\rangle ={P}_{{T}_{\vert \psi \rangle }}H\vert \psi (t)\rangle$$

(64)

where ${P}_{{T}_{\vert \psi \rangle }}$ is an orthogonal projector onto the tangent space of $\vert \psi (t)\rangle$. In our work, we follow the prescription described in Ref. ²⁷³ to implement a one-site version of TDVP. Moreover, we use the time-step $\delta t=0.05/{t}_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}$ and χ = 100 for the TDVP calculations. In the Supplementary Note 3, we present a detailed benchmark of the MPS numerics using this specific expectation value. We can now move beyond it, and look into other observables that give further insight in the localization phenomenon. As depicted in the first two panels of Fig. 16b, the boson density and the attached electric-field line remain localized around the initial position. On the left of this figure, we present two contour plots for the expectation value of the boson number operator ${\overline{n}}_{i}(t)=\langle {a}_{i}^{{{{\dagger}}} }{a}_{i}(t)\rangle$ as a function of time and the site index of the lattice. The two plots correspond to different values of the electric field $h=0.6{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$ and $h=0.4{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$, and one can see how the spread of the breathing-type oscillations of the boson decreases as the value of the electric field h grows. The next column shows the corresponding contour plots of the electric field sustained by the gauge qubits ${\overline{s}}_{i}^{x}(t)=\langle {\sigma }_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle$. In these two plots, one can see how the electric-field string oscillates periodically instead of spreading ballistically, which distorts the initial domain-wall correlations. In the third column of Fig. 16b, we also represent the block entanglement entropy $S({\rho }_{A})=-{{{{{{{\rm{Tr}}}}}}}}\{{\rho }_{A}\log {\rho }_{A}\}$, showing that the region where the stretching and compressing of the electric-field line takes place coincides with the region where entanglement is built up in the real-time dynamics.

Note that, after multiples of the exchange period Δt_ex = 2π/h, the boson and the domain wall on the qubits fully refocus to the initial position. The resulting state becomes a product state, as can be inferred from the vanishing entanglement entropy at those instants of time. This is different from the trend in the limit of a single link (11), where the time it takes to the boson to return to the initial site depends on the ratio of the tunneling and the electric field (see Fig. 3b). As we increase the value of the electric field h, the oscillations become faster and the breathing-type dispersion is more localized. This so-called Wannier-Stark localization is particularly transparent in the regime 2γ ≪ 1, where the asymptotic of Bessel functions allows us to show that the boson remains exponentially localized around the center ${\overline{n}}_{N/2+r}(t)\le {J}_{r}^{2}(2\gamma )\,\approx \,\exp \{-r/{\xi }_{{{{{{{{\rm{loc}}}}}}}}}\}$ with ${\xi }_{{{{{{{{\rm{loc}}}}}}}}}=-1/2\log \gamma$. By using the maximum of the first-order Bessel function, one can also predict the short-time dynamics of the boson ${\overline{n}}_{N/2\pm 1}(t)\,\approx \,{J}_{1}^{2}(2\gamma ht)$ to be ballistic, displaying an initial linear light-cone-like spreading. However, as time elapses, the effects of the stretching/compressing electric-field string start becoming manifest, and the dynamics is no longer ballistic but, instead, displays a breathing-type periodic behavior. This also contrast with the dynamics of disordered one-dimensional systems²⁷⁴, where an initially-localized particle tends to a stationary exponentially-localized solution characteristic of Anderson localization, which can also be observed with trapped ions²⁷⁵. In such Anderson localized system, there is no breathing-like behavior as displayed in this case. Let us now move to a two-particle sector, where one can see how the Wannier-Stark localization develops into a specific confinement phenomenon.

Two-boson sector:Wannier-Stark confinement

In the two-boson sector, the physical subspace ${{{{{{{{\mathcal{V}}}}}}}}}_{{{{{{{{\rm{phys}}}}}}}}} = {{{{{{{\rm{span}}}}}}}}\left\{ {\vert}_{i}\bullet \sim \!\! \sim {\bullet }_{j}\rangle :i,j\in \{1,\cdots \,,N\},\,\,{{{{{{{\rm{and}}}}}}}}\,\,j\ge i \right\}\subset {{{{{{{{\mathcal{F}}}}}}}}}_{2}\otimes {{\mathbb{C}}}^{2(N-1)}$ can be be spanned by the following states

$$\begin{array}{l}{\vert}_{i}\bullet \sim \!\! \sim {\bullet }_{j}\rangle ={a}_{i}^{{{{\dagger}}} }\left({\prod}_{i\le \ell < j}{\sigma }_{\ell ,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}\right){a}_{j}^{{{{\dagger}}} }\vert {{{{{{{\rm{vac}}}}}}}}\rangle .\end{array}$$

(65)

These states contain a pair of bosons connected by an electric-field line (see Fig. 17a). In analogy to the single-boson sector ??, one can expand these two-particle solutions as

$${|{\epsilon}_{m,p}\rangle} = \sum\limits_{i=1}^{N}\, \sum\limits_{j{\ge}i} c_{i,j} {{|}_{i}\bullet\sim\sim{\bullet}_{j}\rangle} = \sum\limits_{i,j}{\prime}c_{i,j}\,\alpha^{{{\dagger}}}_{i}\left(\prod\limits_{-{\le}{\ell} < {j}}\sigma_{\ell,e1}^{z} \right)\,{\alpha}^{{{\dagger}}}_{j}{|{{{{{\rm{vac}}}}}}\rangle},$$

(66)

where the matrix of coefficients is symmetric c_i,j = c_j,i, and is further constrained by normalization 〈ϵ_m,P∣ϵ_m,P = 1〉. This type of states have been used as Bethe-type ansatz for the two-body problem of a Bose-Hubbard model²⁷⁶, where they allow one to determine the scattering and bound states^277,278,279. In our case, the recurrence relation obtained after applying the ${{\mathbb{Z}}}_{2}$ gauge-theory Hamiltonian reads

$$\begin{array}{rcl}{t}_{i-1,{{{{{{{{\bf{e}}}}}}}}}_{1}}{c}_{i-1,j}+{t}_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{* }{c}_{i+1,j}&+&{t}_{j-1,{{{{{{{{\bf{e}}}}}}}}}_{1}}{c}_{i,j-1}+{t}_{j,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{* }{c}_{i,j+1}\\ &+&2h(j-i)\,{c}_{i,j}={\epsilon }_{m,P}{c}_{i,j}.\end{array}$$

(67)

In addition to the tunneling, which resembles a 2D tight-binding problem, we see that the potential only depends on the relative distance of the two bosons. Hence, the problem is different from the Wannier-Stark case of a pair of tight-binding charges subjected to a constant background electric field. In the Supplementary Note 3, we present a detailed discussion of the exact solution in this two-boson sector, and use the analytical expressions for the density to benchmark the MPS numerics.

Fig. 17: Wannier-Stark confinement of a pair of ${{\mathbb{Z}}}_{2}$ charges in the chain.

a Two bosonic particles (filled red circles), with an attached electric-field string connecting them. b Contour plots for the dynamics of the boson distribution ${\overline{n}}_{i}(t)=\langle {a}_{i}^{{{{\dagger}}} }{a}_{i}(t)\rangle$, the electric field on the links ${\overline{s}}_{i}^{x}(t)=\langle {\sigma }_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle$, as well as the block entanglement entropy $S({\rho }_{A})=-{{{{{{{\rm{Tr}}}}}}}}\{{\rho }_{A}\log {\rho }_{A}\}$. We consider a chain of 32 sites, and set the electric field to $h=1.2{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$ (upper row), and $h=0.3{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$ (lower row). The initial state is ${\vert}_{i}\bullet \sim \!\! \sim {\bullet }_{j}\rangle$ in the notation of Eq. (65), which corresponds to a product state for the bosons being localized at sites i. j, and a domain wall of the gauge qubits for the links in between.

In order to highlight other aspects of the two-charge confinement, we present in Fig. 17b the MPS numerical results for other observables. As shown in the first column, where we present a contour plot for the boson distribution ${\overline{n}}_{i}(t)=\langle {a}_{i}^{{{{\dagger}}} }{a}_{i}(t)\rangle$ for $h=1.2{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$ (upper row) and $h=0.3{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$ (lower row), the center of mass of the two bosons remains at the center of the chain as time evolves. In this dynamics, the two particles disperse developing a pair of breathing-type oscillations similar to the single-boson case discussed in Fig. 16b. For sufficiently-large electric field (upper row), the pair of bosons only perform small oscillations about the initial position, but do not interfere. For weaker electric fields (lower row), the width of the breathers is big enough such that their oscillations overlap, and we find interference effects through which the probability to find a boson at the center of the chain adds constructively for given instants of time. As a result, new breathing-type oscillations are superposed. In the center and rightmost columns of Fig. 16b, we represent the corresponding electric field ${\overline{s}}_{i}^{x}(t)=\langle {\sigma }_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle$, as well as the block entanglement entropy S(ρ_A). One can clearly see that the interference also appears in the gauge degrees of freedom via the structure of the initial domain wall, i.e., electric-field line. Regarding the evolution of the block entanglement, we see that quantum correlations build up at the edges of the initial electric-field line, and then grow defining a light-cone like dispersion. After this expansion, inside the mutual effective light cone, entanglement can grow further and show a characteristic interference pattern that coincides with the region where the electric field string stretches and compresses.

After the same periodic exchange durations found in the single-particle case, namely multiples of Δt_ex = 2π/h, the dispersion and interference of the bosons refocuses completely, and we come back to the original situation in which the boson pair and the intermediate electric-field line have a distance of 2r₀. We thus see that, for sufficiently-large systems in any non-zero electric field h, the pair or bosons do not spread ballistically but, instead, disperse up to a maximal distance and then refocus periodically. This unveils an additional aspect of the confinement discussed previously in terms of the bound-state solutions. The Bessel-function envelope of these solutions, which decays rapidly with the inter-boson distance, underlies the lack of excitations with a non-zero ${{\mathbb{Z}}}_{2}$ charge from the energy spectrum of the model, which is the ultimate smoking gun for confinement. Given the connection to the Wannier-Stark physics, we refer to this neat manifestation of confinement as Wannier-Stark confinement.

At this point, it should be pointed out that similar real-time signatures of confinement have also been explored numerically for fermionic^{61,106,259,280,281} and bosonic²⁶¹ versions of the one-dimensional Schwinger model, including more recent results on jet production²⁸² and particle collisions^283,284. The dynamics in these cases is richer, as there can also be spontaneous production of particle-antiparticle pairs due to the presence of the electric field associated to the electric-field string, i.e., Schwinger pair production mechanism²⁸⁵. In the fermionic case^{61,106,259,280,281}, after this pair production and subsequent recombination, there is a string-breaking mechanism, whereby the intermediate electric field relaxes and there is a screening effect for the outer charges, which form new particle-antiparticle pairs of zero net charge that can move freely as a bound meson. Then, the process is reversed by creating an inverted electric-field line (anti-string) in the bulk that connects an antiparticle-particle pair (anti-pair), which can then be screened again creating new mesons that travel freely and so on. In order to explore if a string breaking mechanism can occur in our model, we explore the half-filled sector for our simpler ${{\mathbb{Z}}}_{2}$ gauge theory in the following section, and introduce the local term in Eq. (58), to account for the energy cost of the pair production.

Half-filled sector: Partial string breaking

Let us now consider a charge-density-wave distribution of the bosons. In the case of half filling, one can distribute N/2 bosons to populate the odd sites of the chain, whereas the link spins all point in the opposite direction of the transverse term, such that there is no electric field in the initial state. This state can be considered as a metastable ground state

$$\vert \overline{{{{{{{{\rm{vac}}}}}}}}}\rangle =\vert {1}_{1},{-}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}},{0}_{2},{-}_{2,{{{{{{{{\bf{e}}}}}}}}}_{1}},{1}_{3},{-}_{3,{{{{{{{{\bf{e}}}}}}}}}_{1}},\cdots \,,{1}_{N-1},{-}_{N-1,{{{{{{{{\bf{e}}}}}}}}}_{1}},{0}_{N}\rangle$$

(68)

of a new gauge-invariant Hamiltonian that contains an additional staggered mass term with respect to Eq. (58), namely

$${H}_{{{{{{{{\rm{eff}}}}}}}}}=\sum\limits_{i=1}^{N-1}\left(\left({t}_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}{a}_{i+1}^{{{{\dagger}}} }{\sigma }_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}{a}_{i}+{{{{{{{\rm{H.c.}}}}}}}}\right)+h{\sigma }_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}\right)+\mu \sum\limits_{i=1}^{N}{(-1)}^{i}{a}_{i}^{{{{\dagger}}} }{a}_{i}.$$

(69)

Let us note that this additional term is a specific case of the generic detunings in the state-dependent parametric tunneling, which were already discussed around Eq. (44). In the limit of a very large “mass” $\mu \,\gg \,{t}_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}$, and for hard-core bosons, this state (68) is the gauge-invariant ground state of the Hamiltonian (69) in a super-selection sector in which Gauss’ law (61) has a staggered distribution of static ${{\mathbb{Z}}}_{2}$ charges

$${q}_{i}=\frac{1}{2}(1-{(-1)}^{i}),\forall i\in \{1,\cdots \,,N\}.$$

(70)

In the case of standard bosons, the odd sites are not restricted to single occupancy by the hardcore constraint, and the ground state becomes a highly degenerate manifold. In any case, since we are interested in real-time dynamics, we can always consider this configuration as a reference to build a specific initial state, and then study its real-time dynamics.

We can now start from this state, and consider a meson-like excitation by adding a particle-hole excitation in which a single even (odd) site is populated (emptied) by moving a single boson between two nearest-neighbor sites. To comply with Gauss’ law, an electric field must be established at the link in between, leading to

$${\vert}_{2i}\bullet \sim \!\! \sim {\circ }_{2i+1}\rangle ={a}_{2i}^{{{{\dagger}}} }\left({\sigma }_{2i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}\right){a}_{2i+1}\vert \overline{{{{{{{{\rm{vac}}}}}}}}}\rangle .$$

(71)

In the large-mass limit, this state corresponds to an excitation with an energy of ${\epsilon }_{{{{{{{{\rm{ex}}}}}}}}}^{{{{{{{{\rm{1m}}}}}}}}}\,\approx \,2\mu +2h$ with respect to the vacuum state (68). The half-filling and the staggered mass change the physics considerably, as the tunneling dynamics can now generate more of these meson states by pair production, even when the total number of bosons is conserved and fixed to N/2. There can be thus production of particle-antiparticle pairs within this interpretation, making the lattice model (69) closer to a discretisation of a quantum field theory of gauge and matter fields. This connection can be pushed further in the staggered-fermion approach⁴¹ to lattice gauge theories. In the following, we stick to the simpler bosonic version, and study the analog of the aforementioned string breaking.

By analogy to the two-boson state (65), one could indeed separate the particle and the hole to a couple of distant sites by creating an electric-field string in between, namely

$${\vert}_{2i}\bullet \sim \!\! \sim {\circ}_{2j+1}\rangle ={a}_{2i}^{{{{\dagger}}} }\left(\prod\limits_{2i\le \ell < 2j+1}{\sigma }_{\ell ,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{z}\right){a}_{2j+1}\vert \overline{{{{{{{{\rm{vac}}}}}}}}}\rangle .$$

(72)

This string state has an excitation energy of ${\epsilon }_{{{{{{{{\rm{ex}}}}}}}}}^{{{{{{{{\rm{1s}}}}}}}}}\,\approx \,2\mu +2hr$ in the large-mass limit, where r is the distance between the particle and the hole. The difference with respect to the previous two-boson case is that, due to the dynamics of the gauge-invariant Hamiltonian (69), these string states do not span the complete physical subspace where the dynamics takes place, as occurred previously with Eq. (65). In fact, if one abandons the large-mass condition, the gauge invariant tunneling can lead to further meson-type excitations by itself, and the problem is no longer exactly solvable by mapping it to a Wannier-Stark ladder. Moreover, since there are N_m≤ N/2 mesons that can be formed by a redistribution of the original bosonic particles in the half-filled vacuum (71), and these mesons can move and be created-annihilated, the problem is no longer numerically tractable by a brute force approach that aims at finding the full spectrum.

Nonetheless, we can use the same MPS algorithm as before, and explore how the real-time dynamics differs from the previous Wannier-Stark confinement. The possible novelty is that, in analogy to lattice gauge theories with fermionic matter^{61,106,259,280,281}, mesons can be created, distorting the initial electric-field string, which can lead to the screening of charges and the emission of pairs of mesons that propagate freely. This leads to the aforementioned string breaking. We need to set the parameters in such a way that it could be energetically favorable for the above string can decay into a pair of meson-like states (71), which may then travel freely towards the edges. Since a 2-meson state has the excitation energy ${\epsilon }_{{{{{{{{\rm{ex}}}}}}}}}^{{{{{{{{\rm{2m}}}}}}}}} \, \approx \, 4\mu +4h$ in the large-mass limit, we see that r > μ/h + 2 for the meson configuration to be energetically favorable with respect to the string state.

In Fig. 18, we consider the initial string state $\vert \Psi (0)\rangle ={\vert}_{2{i}_{0}}\bullet \sim \!\! \sim {\circ }_{2{j}_{0}+1}\rangle$ for i₀ = 32, j₀ = 48 and a chain for N = 80 lattice sites, such that r = 16. We solve numerically for the time evolution using our MPS algorithm with $\mu /{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}=0.2$, and $h/{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}=0.2$, such that the 2-meson state can be favorable. As can be seen in Fig. 18a, for hardcore bosons, the dynamics is reminiscent of previous studies on the fermionic Schwinger model. We find that the initial pair production distorts the intermediate electric-field string, and there is some partial screening leading to 2 meson-like excitations that initially spread from the edges of the string towards the boundaries of the chain. However, as can be seen in the second panel of Fig. 18a, there is no perfect screening and no string inversion, such that these meson-like states bend and finally refocus in a breathing-type dynamics. This partial string breaking has been previously found in a bosonic Schwinger model²⁶¹. In the present case, we believe that the lack of perfect screening is likely caused by the different nature of the electric field term in the ${{\mathbb{Z}}}_{2}$ gauge theory with respect to the Schwinger model. In our model, the two possible electric field eigenstates, i.e., the ± Hadamard basis, have a very different electric-field energy. On the contrary, in the Schwinger model, the electric energy is quadratic in the electric field, and would thus be the same for these two states, such that the string inversion seems energetically more plausible. This type of electric-field energy is however not possible in light of the underlying Pauli-matrix representation of our ${{\mathbb{Z}}}_{2}$ gauge theory. It is likely this difference which is responsible for the lack of screening and string inversion in our model, and thus leads to the final refocusing.

Fig. 18: Partial String breaking in the bosonic ${{\mathbb{Z}}}_{2}$ gauge chain.

Contour plots for the dynamics of the boson distribution ${\overline{n}}_{i}(t)=\langle {a}_{i}^{{{{\dagger}}} }{a}_{i}(t)\rangle$, the electric field on the links ${\overline{s}}_{i}^{x}(t)=\langle {\sigma }_{i,{{{{{{{{\bf{e}}}}}}}}}_{1}}^{x}(t)\rangle$. We consider a chain of N = 80 sites, and set the transverse electric field to $h=0.2{t}_{1,{{{{{{{{\bf{e}}}}}}}}}_{1}}$ and a mass μ = h. The initial state is ${\vert}_{2i}\bullet \sim \!\! \sim {\circ }_{2j+1}\rangle$ in the notation of Eq. (72), which corresponds to a product state for the bosons being localized at even sites i, and a domain wall of the gauge qubits for the links in between the sites i₀ = 32 and j₀ = 48. In (a) we show the results for the hard core bosons case instead in (b) we present the results for the soft core bosons where we fixed the local dimension ${n}_{\max }=4$.

Moving away from the artificial hardcore constraint, which is the relevant case for the trapped-ion system, we find that the evolution is now described by Fig. 18b. In the left panel, we see that the dynamics in the charge sector is very similar to the hardcore case. The main differences, however, appear when looking into the gauge-field sector. As shown in the right panel, Here, t the possibility of populating the sites with more than one boson changes appreciably the dynamics, as the mirror symmetry of the dynamics is broken by a boson-enhanced tunneling. The electric string can get distorted by particle-hole pair creation, but this distortion is asymmetric and no longer resembles the hardcore case of Fig. 18b.

Conclusions and outlook

In this article, we have presented a rich toolbox for the quantum simulation of ${{\mathbb{Z}}}_{2}$ gauge theories using trapped ions that spans several levels of complexity. In this toolbox, the matter particles are simulated by the vibrational excitations of the ions, and the gauge field corresponds to a qubit encoded in two electronic states. In general, we have shown how to exploit a state-dependent parametric tunneling, which arises from a specific laser-ion interaction, to induce the desired gauge-invariant tunneling of a ${{\mathbb{Z}}}_{2}$ gauge theory in the ion dynamics. Furthermore, we have shown that it is possible to explore the competition of this term with a confining electric-field term, which can be readily implemented by a direct resonant driving of the qubit transition.

At the simplest-possible level, that of a ${{\mathbb{Z}}}_{2}$ gauge theory on a single link, we have presented two quantum simulation schemes that take into account realistic numbers, and are at reach for various experiments working with a single ion. Here, by exploiting the idea of synthetic dimensions, two vibrational modes of the ion encode the matter bosons, whereas the ${{\mathbb{Z}}}_{2}$ gauge field is represented by the ion qubit, which sits in a synthetic link and effective mediates frequency conversion between such modes. We have discussed several manifestations of gauge invariance, which have neat quantum-optical counterparts, and are at reach of current trapped-ion experiments: observing the correlated dynamics of a single matter boson, and the attached electric-field string, which would go beyond the available measurement capabilities of¹²⁴. Moreover, we have also explored the two-boson dynamics, unveiling interesting connections to dark states in Λ-systems and entanglement between the matter bosonic modes that could also be explored in the trapped-ion experiment.

Increasing in complexity, we have discussed a scheme with a two-ion crystal that can be used to simulate a ${{\mathbb{Z}}}_{2}$ gauge theory on the simplest plaquette. Provided that the parametric tunnelings can resolve the structure of the collective vibrational modes along two directions of the crystal, we have shown that the qubits of the two ions can be arranged in the links of a circular plaquette that can be pierced by a gauge-invariant ${{\mathbb{Z}}}_{2}$ flux known as a Wegner-Wilson loop. The related ${{\mathbb{Z}}}_{2}$-plaquette dynamics would be slower, requiring further improvements to minimize noise sources below this timescale. For a single boson in the matter sector, we have shown that the gauge-invariant tunneling can lead to a ’t Hooft loop of the electric-field variables and that this can give rise to entanglement between the gauge qubits. Once again, the gauge-invariant dynamics of the plaquette have a quantum-optical analog in terms of a double-Λ system.

Finally, we have shown how one can exploit the parametric excitations in the resolved-mode regime for a larger N-ion crystal. We have introduced a generic idea of synthetic dimensional reduction, by means of which, it is possible to obtain a trapped-ion quantum simulator of a ${{\mathbb{Z}}}_{2}$ gauge theory on a full chain. This will require further developments in which the mode frequencies used to encode the matter particles can be tailored in an inhomogeneous fashion. We have shown that a single phonon in the trapped-ion chain will evolve under this ${{\mathbb{Z}}}_{2}$ gauge theory in complete analogy to the problem of Wannier-Stark ladders, showing in this way localisation and breathing dynamics due to a periodically stretching electric-field string. By going to the two-phonon sector, we have presented quantitative expressions for the confinement of the simulated ${{\mathbb{Z}}}_{2}$ charges, which have been benchmarked with exhaustive numerical simulations based on matrix product states (MPS). Finally, we have also explored the half-filled sector, and shown that our analog quantum simulator can host a string-breaking mechanism, contributing in this way to the initial progress in the digital approach¹²¹.

Future work will include the generalization of the presented toolbox towards the two-dimensional case. As a starting point, it would be interesting to develop schemes that allow for the quantum simulation of one-dimensional arrays of the simple ${{\mathbb{Z}}}_{2}$ plaquettes studied in this work. This would allow to explore the interplay of the electric confining term and the magnetic flux term that would here reduce to a two-spin interaction that is also at reach of trapped-ion quantum simulators. This playground is simple enough such that analytical results and numerical simulations based on MPS could be developed. Going beyond this limiting case, it would also be interesting to explore full two-dimensional models coupled to matter, even if the Wegner-Wilson higher-weight plaquette terms cannot not be realized in the experiment. There are known examples where the intertwining of the matter particles with the gauge fields can actually lead to deconfined phases⁶⁹.