Introduction

When the Coulomb interaction (U) between charge carriers overcomes their kinetic energy (U), correlations emerge in condensed matter systems. To reduce the total energy, correlated charge carriers tend to break certain symmetries, resulting in a variety of ordered ground states1,2,3,4,5,6,7,8,9,10,11,12,13,14. In light of this, flat bands with almost quenching kinetic energy have long been sought to explore the various exotic quantum phases. Motivated by the flat bands generated by band folding and reconstruction, together with the effective external modulations, moiré superlattices of two-dimensional (2D) materials have attracted intense interest in the past few years.

To realize exotic quantum phases, the valley and spin degeneracies of the flat bands are manipulated to be lifted to form symmetry-broken gapped states with isospin-flavor polarization. Among graphene moiré superlattices, twisted monolayer-bilayer graphene (tMBG) (Fig. 1a), holds fewer crystal symmetries, and hence hosts more possibilities. Correlated insulator, ferromagnetism, and quantum anomalous Hall states have been observed at partial fillings of the flat conduction band in tMBG15,16,17,18,19,20,21. Especially, due to the broken mirror reflection symmetry, the electronic band structure totally differs under opposite electric fields15,18,19. The most obvious and typical examples are the ground states at half filling of the flat conduction band, which show different temperature and magnetic-field dependence under opposite electric fields. Nevertheless, the symmetry breakings of these ground states are still not fully understood. These symmetry breakings not only have different magnetic-field dependence, it is also closely related to the symmetry-broken Chern insulator (SBCI) states emanating near the half filling. The Chern number of these SBCI states might reveal the isospin-flavor polarization of the half-filling ground states.

Fig. 1: Twisted monolayer-bilayer graphene with 1° angle.
figure 1

a The schematic of our tMBG device and the structure of moiré pattern formed by monolayer graphene and Bernal stacked bilayer graphene. The positive electric displacement field (\(D\)) is defined as pointing from monolayer to bilayer graphene. The black arrows manifest the moiré wavelength. b, c Longitudinal resistance \({R}_{{xx}}\) measured at T = 28 mK and \(B\,=\,0\,{{\mbox{T}}}\) (b) and antisymmetrized transverse resistance \({R}_{{yx}}\) measured at T = 100 mK and \({{\mbox{|}}}{B}_{\perp }{{\mbox{|}}}\,=\,0.5\,{{\mbox{T}}}\) (c). The top and bottom axis shows the filling factor (\(\nu\)) of a moiré unit cell and carrier density (n) clearly. d Typical calculated band dispersion of tMBG with 1° twist angle at D = 0.4 V/nm and D = −0.4 V/nm. Flat bands are highlighted and their Chern numbers are labeled.

Full size image

In this work, we report abundant electric-field tunable symmetry-broken states including a SBCI state under magnetic field in tMBG with a 1° twist angle. With a relatively small twist angle, the tMBG belongs to an intermediately correlated regime with U/W∼1 (see Figure S10 in Supplementary Information) that no valley and spin degeneracies are fully lifted8, which shows more apparent magnetic field dependence. At the half filling of the flat conduction band, gaps open under external magnetic fields. However, the gaps under positive and negative electric fields show totally opposite magnetic-field dependence, indicating that these ground states have distinct dominant symmetry breakings. They are spin-polarization dominant (SPD) and valley-polarization dominant (VPD) under positive and negative electric fields, respectively, confirmed by our theoretical calculations. In addition, a SBCI with C = 3 emanating from 1.5 electrons per moiré unit cell under negative electric field emerges at high magnetic field, which breaks the superlattice symmetry with enlarged unit cells containing two moiré units. The Chern number 3 suggests the filling of one and a half valley-polarized Chern 2 bands22, consistent with the valley-polarization dominant nature of the half filling under negative electric field. We should emphasize that the above conclusion of the half-filling ground states is true not only in 1° twist angle but in a range from to 1° ~ 1.3° (see Supplementary Note 3). Besides the abundant electric-field tunable symmetry-broken states in tMBG, our work also sheds light on the study of the rich phase diagram in the intermediately correlated twisted graphene systems.

Results and discussion

Device characterization

Figures 1b, c present the longitudinal (at 0 T) and Hall resistance (at 0.5 T), respectively, of a 1° ± 0.02° tMBG sample as a function of the carrier density n and electric field D. The definition of D is shown in Fig. 1a that D > 0 when it is pointing from the monolayer to the bilayer. It is obvious that the longitudinal resistance shows peaks at v = 0 and v = ± 4, accompanied by sign changes of the corresponding Hall resistance. Here, \(\nu\) is the filling factor, i.e., the number of electrons per moiré unit cell. Similar to the previous reports15,16,17,18,19, v = 0 insulating state appears when \(D\) exceeds some critical values, ~0.4 V/nm for D > 0 and ~−0.25 V/nm for D < 0 in our sample (Fig. 1b). Moreover, the gaps of v = ±4 insulating states gradually close with increasing D, consistent with our calculations of the band structure and the basic properties of tMBG (Fig. 1d and Supplementary Note 1). Clearly, the resistance mapping shows asymmetry of ±D, which comes from the symmetry breaking of the two-fold rotation C2 and the mirror reflection My in tMBG15. In addition, the absence of v = 1, 2, 3 correlated gap states in Fig. 1b reveals the failure of the strong-correlated limit (\(U/W\gg 1\)) but advent of the intermediately correlated regime in 1° tMBG8.

Different ground states at \({{{{{\boldsymbol{\nu}}}}}} \, = \, 2\)

Due to the intermedia correlation, no correlated gapped states appear at B = 0 T, similar to the devices with 0.9° and 0.97° twisted angles (see Fig. S14)18. However, there emerge multiple intriguing states under external magnetic field. Figures 2a and 2b show the longitudinal resistance measured at perpendicular magnetic fields of 6 T and 10 T, respectively. The charge neutrality point (CNP) resistance peaks gradually disappear as the increasing magnetic field due to the spin/valley Zeeman effect15,16. On the other hand, when a magnetic field is applied, the bands become flatter. As a result, correlated insulating states will emerge which show D dependence. Meanwhile, a series of Landau levels develop, forming the resistance peaks at different v15,16.

Fig. 2: Different ground states at ν = 2 for opposite D.
figure 2

a–c Longitudinal resistance \({R}_{{xx}}\) as a function of carrier density n and electric displacement field D measured at \(T=100\,{{\mbox{mK}}}\) and \(B_{\perp}=6\,{{\mbox{T}}}\) (a), \(B_{\perp}=10\,{{\mbox{T}}}\) (b), B|| = 12 T (c). Peaks at filling factor ν = 2 are visible. d \({R}_{{xx}}\) measured as a function of n at various parallel magnetic field from 2 T to 12 T at D = 0.5 V/nm. The inset plots Rxx(B||) (blue points) extracted at ν = 2 and the left axis is log scale. The red arrow shows the critical magnetic field of gapped state (highlighted in green region).

Full size image

We will focus on the emerging states at v = 2. As is shown in Fig. 1c and Fig. S2a, Rxx shows a weak peak accompanied by a sign change of Ryx at v = 2 under a perpendicular magnetic field B⊥ = 0.5 T near D = 0.4 V/nm, indicating a weak correlated state induced by B⊥ although it is rapidly destroyed under higher B⊥ (Fig. 2a, b and Fig. S2b). However, when a parallel magnetic field is applied, a strong peak appears at v = 2 under D > 0, and the resistance increases monotonously with B|| (Fig. 2c, d and Fig. S4). By plotting the Rxx against B|| at v = 2 in a semilog manner (inset in Fig. 2d), it is clear that ln (Rxx) linearly depends on B|| when B|| > 6.5 T, suggesting a gap opening with the size \(\triangle\) proportional to B||. All these findings indicate a hidden correlated state at \(\nu =2\) under D > 0. On the contrary, the v = 2 state under D < 0 shows totally different field dependence. From Fig. 2a, b, we can see that the v = 2 correlated insulator under D < 0 emerges at certain B⊥ (see Fig. S8 for the evolution of the state with various B⊥). By detecting B⊥ dependence of \({R}_{{xx}}\) at various \(T\) (see Fig. S3), we get a critical magnetic field \({B}_{\perp }^{{{{{\rm{c}}}}}}{\sim}3.55\,{{{{\rm{T}}}}}\) for \(\nu =2\) at D = −0.35 V/nm. Nevertheless, when a parallel magnetic field is applied, no sign of correlated gap state exists at v = 2 for D < 0 (Fig. 2c and Fig. S4) even when B|| reaches 12 T, opposite to the situation under D > 0. Similar field dependence has been observed in devices with slightly larger twisted angles, except that the correlated insulating state at v = 2 under D > 0 has already existed at zero field due to the stronger correlations15,16,18. These distinct field dependence illustrates two different ground states at v = 2 under D > 0 and D < 0. It is also worth pointing out that the CNP resistance peak remains almost intact even at B|| = 12 T (Fig. 2d). Similar behaviors have been observed in devices with other twist angles ranging from 1° to 1.3° (see Figs. S11–S14).

We then extract the thermal activation gaps of two different insulating state at D > 0 and D < 0 as a function of B|| and B⊥, respectively, from the Arrhenius fit and estimate the \(g\) factors (see Supplementary Note 2). As expected, the g factor of D > 0 insulating state ~2 (Fig. 3a), similar to the \(g\) factor of free electrons. On the contrary, for D < 0 insulating state \(g \sim 8\) (Fig. 3b) manifests a dominant role played by valley instead of spin, which breaks orbital time-reversal symmetry and leads to giant orbital magnetism.

Fig. 3: Spin and valley polarization dominant states.
figure 3

a, b Thermal activation gap at filling factor ν = 2 versus B|| at electric displacement field D = 0.45 V/nm, 0.50 V/nm (a) and B⊥ at D = −0.3 V/nm, −0.5 V/nm (b), respectively. The Lande g factors are extracted from the linear fittings. Error bar represents the standard deviation. c, d Schematics of band dispersion evolution in B|| and B⊥ for the two different ground states at ν = 2, spin polarization dominant state (c) and valley polarization dominant state (d), respectively. The solid (dashed) line refers to K (K′) valley. Blue (red) line and arrows refer to spin up (down). The green dashed line is Fermi level at ν = 2. w(\({w}^{\prime }\)) is the width of the overlap of different spin (valley) polarized bands.

Full size image

Since the intrinsic spin-orbit coupling is negligible in graphene systems, the SU(4) symmetry should be maintained. However, spontaneous SU(4) symmetry breaking has been verified in graphene moirés frequently, because strong correlation can renormalize the flat bands with different flavors and thus lift the degeneracy of spin and valley degree of freedom1,2,3,4,5,6,7,8,9,10,12,13. In a 1° tMBG, \(U/W\) is roughly 1 that the correlation is not strong enough to fully lift the degeneracies. The ground state at v = 2 could be SPD or VPD states. To get an insight of the magnetic field dependence of these states, we consider a Bloch state in a magnetic field BT (including B⊥ and B||), sequentially the energy of the band with a single spin and valley can be expressed as4:

$${{E}}_{{\sigma},{\tau}}={{E}}_{0}+{{E}}_{{{{{\rm{spin}}}}}}+{{E}}_{{{{{\rm{valley}}}}}}={{E}}_{0}+\frac{1}{2}{\sigma}{{g}}_{{{{{\rm{s}}}}}}{{\mu}}_{{{{{\rm{B}}}}}}{{B}}_{{{{{\rm{T}}}}}}+{m}\left({\tau}\right){{B}}_{\perp }$$
(1)

Here, the second (third) term is spin (orbital/valley) Zeeman splitting, \(\sigma =\pm 1\) the spin index, \(\tau =\pm 1\) the valley index, gs the g factor of spin, \({\mu }_{{{{{\rm{B}}}}}}\) the Bohr magneton, and \(m(\tau )\) the orbital magnetization with \(m(-\tau )=-m(\tau )\) protected by the time-reversal symmetry. In the third term, orbital magnetization is not sensitive to parallel magnetic field, owning to the atomic scale confinement of electronic wavefunctions to the plane of 2D materials.

Figures 3c, d display the evolution of the band structure with magnetic field for the two possible different ground states, respectively. For SPD state, gap opening can occur after applying B|| under the condition of \({\varDelta }_{{{{{\rm{spin}}}}}}\, > \, w\), where w refers to the width of the overlap of different spin-polarized bands, as shown in Fig. 3c. On the other hand, under B⊥, gap opening depends on the competition of \({E}_{{{{{\rm{spin}}}}}}\) and \({E}_{{{{{\rm{valley}}}}}}\), and can occur only if \({E}_{{{{{\rm{spin}}}}}}\) dominates (\({E}_{{{{{\rm{spin}}}}}}\, > \, {E}_{{{{{\rm{valley}}}}}}\)). However, orbital \(g\) factor is much larger than the spin \(g\) factor4 (Fig. 3a, b) that \({E}_{{{{{\rm{valley}}}}}}\) dominates over \({E}_{{{{{\rm{spin}}}}}}\) and no gap opening will happen. On the opposite, when the ground state is a VPD state, only spin responds to B|| that gap opening will never occur under B|| (Fig. 3d). But when B⊥ is applied, the condition for a gap opening is \(2{E}_{{{{{\rm{valley}}}}}}\, > \,{\varDelta }_{{{{{\rm{spin}}}}}}+\acute{w}\), where \(\acute{w}\) is the width of the overlap of different valley-polarized bands. Taking the fact that \({E}_{{{{{\rm{valley}}}}}}\) dominates over \({E}_{{{{{\rm{spin}}}}}}\) in our tMBG sample, the gap opening for a VPD state under B⊥ is possible. Therefore, the responses of the SPD and VPD states to B|| and B⊥ agree well with the experiment results of \(\nu =2\) states at \(D\, > \,0\) and \(D\, < \, 0\), respectively. We should mention that the response to tilted \(B\) of these two states are also consistent with our proposal (see Fig. S5 in Supplementary Information).

We then perform the Hartree-Fock mean-field calculations to find the interacting ground states at the zero magnetic field. The calculations show that the interacting ground state behaves mainly spin-polarized under positive electric field, but valley-polarized under negative electric field, in agreement with the experimental results (see Figure S9 in Supplementary Information). Because the bandwidths of flat band in the near 1° tMBG are larger than those near 1.25° tMBG, the Coulomb interaction is not strong enough to open a global gap. Thus, these states at \(\nu =2\) behaves correlated metal with partial flavor polarization and large band dispersion. When a magnetic field is applied to the tMBG, the bandwidth W decreases drastically, and U/W is enhanced into strong-correlated regime. Consequently, a global gap exists due to renormalized band dispersion and Zeeman splitting induced by magnetic field.

Symmetry-broken Chern insulator under high magnetic field

For electrons under high perpendicular magnetic field and periodic potential, flat bands in graphene moirés will further modulate the spin and valley relationship and evolve into a series of Hofstadter minibands, hosting non-zero Chern numbers23,24. In order to explore more symmetry-breaking and Hofstadter characters in 1° tMBG, we perform Landau fan measurements under \(D < 0\). Figure 4a shows Landau fan diagram at D = −0.35 V/nm, manifesting many well-developed gapped states that consist with the Hofstadter butterfly scheme. We also display Landau fan diagram at another D = −0.24 V/nm and it shows similar results (see Fig. S6 in Supplementary Information).

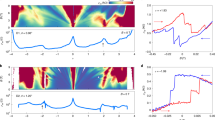
Fig. 4: Landau fan in twisted monolayer-bilayer graphene at D = −0.35 V/nm.
figure 4

a Landau fan diagram up to 14 T at electric displacement field D = −0.35 V/nm. The purple dashed line locates at B⊥ = 11 T, corresponding to (c). b The schematic of Landau fan at D = −0.35 V/nm. Different colors correspond to gapped states of different numbers of electrons in a moiré unit cell s. c Symmetrized longitudinal resistance \({R}_{{xx}}\) and antisymmetrized Hall conductance \({\sigma }_{{yx}}\) as a function of filling factor ν at B⊥ = 11 T, D = −0.35 V/nm. The shaded regions labels the position of Chern insulators. d, e Zoom-in Landau fan diagram for symmetrized longitudinal resistance \({R}_{{xx}}\) (d) and antisymmetrized Hall resistance \({R}_{{yx}}\) (e). f \({R}_{{yx}}\) extracted along the line cuts of (3, 1.5) and (2, 2) states from (e). g The schematic of Chern number C = 3 symmetry breaking Chern insulator at D < 0. Bands below ν = 2 are in the same valley K′. Red (blue) arrows refer to spin up (down). Under high magnetic field, the Berry curvature will redistribute uniformly in the moiré Brillouin zone. Thus, one C = 2 Chern band will split into two C = 1 Chern number in the double moiré superlattice.

Full size image

In Fig. 4b, we schematically plot out all the emergent trajectories of gapped states. All the gapped states follow the linear trajectories expressed as the Diophantine equation25:

$${\nu}={t}{{n}}_{{\varphi}}+{s}$$
(2)

where \({n}_{{\varphi}}=\varPhi /{\varPhi }_{0}\) (\({\varPhi }_{0}\) is quantum magnetic flux) is the normalized magnetic flux. We then use the notation (\(t\), \(s\)) to describe the gapped states, where t represents the Chern number of these gapped states and s stands for the number of electrons in a graphene moiré unit cell. Normally, based on the value of (t, s), gapped states can be sorted into several categories, including integer quantum Hall states (\(s=0,{t}\in {{{{\rm{Z}}}}}\)) and Chern insulator (CI) (\(\left|s\right|\, > \,0,\left|t\right|\, > \, 0\)). Especially, if \(s \, \notin \, {{{{\rm{Z}}}}}\) and \(t\in {{{{\rm{Z}}}}}\), this CI state is called a symmetry-breaking Chern insulator (SBCI)26. To make the schematic plot clearer, we use different colors for trajectories with different \(s\), and the CIs emanating from \(\nu ={{{{\mathrm{1,2,3}}}}}\) are obvious. Figure 4c plot \({R}_{{xx}}\) and \({\sigma }_{{yx}}\) curves under \(B_{\perp}=11{{{{\rm{T}}}}}\) at D = −0.35 V/nm. All the emergent quantized Hall plateaus accompanied with suppressed \({R}_{{xx}}\) are marked, further confirming the existence of CI at \(\nu ={{{{\mathrm{1,2,3}}}}}\).

Apart from a variety of CIs in our sample, which have been widely found in many graphene moirés, we have also identified a robust linear trajectory with non-integer \(s\), thus the SBCI. In Fig. 4a a trajectory with (\(t\), \(s\)) = (3, 1.5) appears between 10.5 and 11.5 T, seen more clearly in the zoom-in Landau fan diagram (Fig. 4d). In Fig. 4c\({\sigma }_{{yx}}\) also shows a quantized plateau with C = 3 accompanied by a suppressed \({R}_{{xx}}\) at D = −0.35 V/nm under \(B=11{{{{\rm{T}}}}}\) (marked by purple labels). In addition, by changing the perpendicular magnetic field, we verify that the SBCI can be repeated and the quantized Hall signal also follows Diophantine equation in a wide range of B (Fig. 4e, f). All these results can be repeated in another D = −0.24 V/nm, which shows a larger range of 10–11.5 T (Fig. S6). In addition, in Fig. S7, SBCI disappears gradually with the increase of \({{{{\rm{|}}}}}D{{{{\rm{|}}}}}\), which might be caused by the modulated band dispersion of the flat band and its overlapping with remote bands. All these observations evident a \(D\)-controllable SBCI with C = 3 under high \(B\) for D < 0.

The emergence of SBCI has been studied in some moiré systems and it is widely considered that SBCI originates from enlarging the moiré unit cell17,26,27,28,29,30,31,32. Specially, SBCI state emanating from \(\nu \, {{{{\rm{=}}}}}\, 1.5\) has been reported in ~1.25° tMBG at D > 017, but has not been observed at D < 0. It is worth mentioning that although the conduction band of 1° tMBG under D < 0 hosts the same Chern number (C = 2, Fig. 1d) as the one of ~1.25° tMBG under D > 0 in theoretical calculations22,33,34, the Chern number of the SBCI is totally different. This can be understood from the different ground states of half filling in the two systems. In ~1.25° tMBG under D > 0, the total Chern number 1 of the SBCI indicates that one and a half bands with different valley index are filled at 1.5 electrons per moiré unit, consistent with its spin-polarized half-filling ground state. However, in 1° tMBG under D < 0, the half-filling ground state is VPD. Therefore, the C = 3 SBCI emanating from \(\nu =\,1.5\) suggests that one and a half bands with the same valley index are filled (Fig. 4g). In other words, the emergence of C = 3 large-Chern-number SBCI closely relates to the \(\nu =\,2\) VPD ground state at D < 0.

Conclusions

We have observed different response to magnetic field at opposite electric displacement field of tMBG system and studied intriguing ground states with distinct flavors at v = 2. Symmetry breaking leads to spin polarization dominant state at D > 0 but valley polarization dominant state at D < 0. Furthermore, a SBCI with 3 Chern number emerges in high perpendicular magnetic field, which can be understood from the formation of density-wave state hold by enlarged unit cells containing double moiré cells. This unusual Chern number originates from one and a half filling of C = 2 flavor-polarized bands with the same valley index, resulting a C = 3 total Chern number, consistent with our conclusions of v = 2 ground state at D < 0. Except the aforementioned states, more symmetry-broken gapped states emerge in our tMBG sample under high perpendicular magnetic field. From Fig. 2b, an insulating state at v = 3 for D < 0 emerges. This v = 3 insulating state emerges around 7 T but disappears around 12 T (see Fig. S8 in Supplementary Information). Also, it stays at v = 3 but shifts toward more negative \(D\) with increasing B⊥. In addition, under B||, this insulating state does not appear up to 12 T. Similarly, from Fig. 2a, b, another emergent insulating state at v = −3 is observed for \(D\) slightly below 0 under high B⊥. Our results enrich the phase diagram of intermedia correlated regime, enhance the understanding of symmetry breaking in tMBG, and inspire the exploration of small twisted-angle devices.

Methods

Sample preparations

The twist monolayer bilayer graphene (tBMG) heterostructures are stacked layer by layer using dry transfer technique in which the twist structure is prepared by ‘cut and stack’ technique. All the flakes (hBN, graphene with monolayer and bilayer domains, few-layer WSe2 and few-layer graphite as gate) were first exfoliated from corresponding crystals to Si substrate covered by 285 nm SiO2. Aiming to avoid strain in sample assembly, graphene was cut by tungsten needle in advance, which has been widely used in scanning tunneling microscope experiments, and divided into monolayer and bilayer parts. Then polypropylene carbonate (PC)/PDMS stamp was used to pick up hBN (about 20–50 nm confirmed by atomic force microscope (AFM)) at 90 °C (or hBN/graphite/hBN for geometry with graphite top gate) followed by lifting few-layer WSe2 (only in D1) and bilayer graphene part at about 50 °C. Before assembled by bottom hBN and graphite, the remaining monolayer part of graphene on substrate was rotated by θ angle and picked up. Finally, the van der Waals heterostructure was released to SiO2/Si substrate with Au marks at 170 °C.

PC residual was removed by soaking in chloroform for 10 min followed by cleaning in acetone and IPA. For geometry without graphite top gate, Cr(5 nm)/Au(25 nm) top gate was then deposited onto the bubble-free region of sample checked by AFM. Aiming to weaken the effect of graphene contact and get better data in our measurements, we shape top gate like Hall bar and ensure the similar size of both top and bottom gates, eliminating the region tuned by only single gate in graphene contacts (Fig. S1b). Finally, Devices were fabricated using e-beam lithography, reactive-ion etching and deposition of Cr/Pd/Au(5 nm/5 nm/80 nm).

Absence of spin-orbital coupling effect induced by WSe2 in D1

Spin-orbital coupling (SOC) effect induced by a proximate WSe2 has been shown in twisted graphene system7,27,35,36,37. However, to maximize the SOC effect of WSe2, some details of the device fabrications were emphasized, including the layer number of the WSe2 (monolayer WSe2 is the best) and angle between the WSe2 and the graphene (~16° to maximize the SOC strength)7. In device D1 in our work, a few-layer WSe2 was used and the angle between WSe2 and graphene deviated from ~16° (Fig. S1). As a result, the SOC effect is very weak that no obvious SOC effect has been detected in experiments, which can be seen from the similarities between D1 and D4 (Fig. S14). Also, previous studies have already shown that no SOC effect is observed in devices with a proximate WSe238,39,40.

Device characterization

Measurements were performed by standard lock-in techniques with 1–10 nA a.c. current excitation at 17.777 HZ. All the transport data were collected in a four-terminal geometry at either the base-temperature of our dilution refrigerator (28 mK) without magnetic field or 100 mK with a magnetic field, unless mentioned specifically.

Although we have measured the hBN thickness by AFM before, the accurate thickness of hBN was further determined by quantum Hall effect in high magnetic field, which we choose to be 6 T. With the accurate thickness of hBN, the carrier density \(n\) and electric field \(D\) are calculated by \(n=\frac{{\varepsilon }_{0}{\varepsilon }_{{{{{\rm{r}}}}}}}{e{d}_{{{{{\rm{t}}}}}}}{V}_{{{{{\rm{tg}}}}}}+\frac{{\varepsilon }_{0}{\varepsilon }_{{{{{\rm{r}}}}}}}{e{d}_{{{{{\rm{b}}}}}}}{V}_{{{{{\rm{bg}}}}}}\) and \(D=\frac{\frac{{\varepsilon }_{{{{{\rm{r}}}}}}}{{d}_{{{{{\rm{b}}}}}}}{V}_{{{{{\rm{bg}}}}}}-\frac{{\varepsilon }_{{{{{\rm{r}}}}}}}{{d}_{{{{{\rm{t}}}}}}}{V}_{{{{{\rm{tg}}}}}}}{2}\), where ε0 is the vacuum permittivity, dt (db) the thickness of the top (bottom) hBN, εr the relative dielectric constant of the hBN, and \(e\) the electron unit charge. The carrier density of v = 4 band insulator was extracted and used to calculate the twist angle of our sample by \({n}_{{{{{\rm{s}}}}}}=\frac{8{\theta }^{2}}{{a}^{2}\sqrt{3}}\), where \({n}_{{{{{\rm{s}}}}}}\) represent the carrier density of v = 4 band insulator, \(\theta\) is the twist angle and \(a\,=\,0.246\,{{{{\rm{nm}}}}}\) is the lattice constant of graphene. Also, the twist angle of sample was further confirmed by Landau Fan diagram. Finally, the four devices investigated in paper, D1–D4, hold 1°(±0.02°), 1.3°(±0.03°), 1.2°(±0.02°), and 0.97°(±0.03) twist angles, respectively.