Dynamical suppression of many-body non-Hermitian skin effect in anyonic systems

Abstract

The non-Hermitian skin effect (NHSE) is a fascinating phenomenon in nonequilibrium systems where eigenstates massively localize at the systems’ boundaries, pumping (quasi-)particles loaded in these systems unidirectionally to the boundaries. Its interplay with many-body effects has been widely explored recently, and inter-particle repulsion or Fermi degeneracy pressure have been shown to limit the boundary accumulation induced by the NHSE both in their eigensolutions and dynamics. However, in this work we find that anyonic statistics can even more profoundly affect the NHSE dynamics, suppressing or even reversing the state dynamics against the localizing direction of the NHSE. This phenomenon is found to be more pronounced when more particles are involved. The spreading of quantum information in this system shows even more exotic phenomena, where NHSE affects only the information dynamics for a thermal ensemble, but not that for a single initial state. Our results open up a new avenue on exploring novel non-Hermitian phenomena arisen from the interplay between NHSE and anyonic statistics, and can potentially be demonstrated in ultracold atomic quantum simulators and quantum computers.

Introduction

Anyons represent a general class of particles^1,2,3, whose unusual statistics induce many fascinating phenomena^{4,5,6,7,8,9,10,11,12,13,14,15} and hold the promise to eventual fault-tolerant topological quantum computation and information processing^{16,17,18,19,20,21,22,23}. Such unusual properties originate from their peculiar behavior upon application of exchange, as they inherit an arbitrary phase factor. Originally considered as two-dimensional quasiparticles, 1D anyonic statistics have also been predicted to emerge in cold bosonic atoms^9,10 and photonic systems^9,10,24,25, and have been emulated in circuit lattices by mapping their eigenmodes to two-anyon eigenstates^26,27. Assisted by Floquet engineering, arbitrary statistical phase of 1D anyons has been recently realized by Greiner’s group¹⁵ in cold atom systems.

In the recent years, great attention has also been drawn towards another physical mechanism behind asymmetric dynamics, the non-Hermitian skin effect (NHSE)^28,29, which manifests as colossal accumulation of static eigen-wavefunctions and states evolving over time^{30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49}. Entering the realm of many-body physics, novel extensions of NHSE have been uncovered during the past few years^{50,51,52,53,54,55,56,57,58,59,60,61,62,63}. In particular, it has been found that NHSE can induce real-space Fermi surfaces for fermions and boundary condensation for bosons^53,54,55, while the latter will be suppressed by a strong repulsive interaction^52,56. In a recent study, an occupation-dependent NHSE is uncovered for hardcore bosons and fermions, whose different exchange symmetries lead to distinguishable behaviors despite residing in the same Fock space⁶³. On the other hand, the interplay between anyonic statistics and NHSE still remains largely unexplored.

In this paper, we report the discovery of a dynamical suppression of NHSE in a 1D non-Hermitian anyon-Hubbard model, revealing the intricate consequences of anyonic statistics acting on non-Hermitian physics. Explicitly, we find that the dynamical evolution is not always in accordance with the static localization direction of eigenstates, which suffer from qualitatively the same NHSE at different statistical angles of the anyons. In particular, the state evolution may even experience a reversed density pumping process, during which the density evolves against the non-Hermitian pumping direction induced by NHSE. Such a reversed pumping is found to be more pronounced when increasing the number of particles loaded in the system. More drastically, by examining the out-of-time-ordered correlator (OTOC), we find that the information spreading is dominated by NHSE for a thermal ensemble, but immune to NHSE for a single initial state at zero temperature.

Results

NHSE in a 1D anyonic lattice

We consider a one-dimensional non-Hermitian anyon-Hubbard model (NHAHM) described by the Hamiltonian

$${\hat{H}}_{A}=-{\sum}_{j=1}^{L-1}\left({J}_{L}{\hat{a}}_{j}^{{{\dagger}} }{\hat{a}}_{j+1}+{J}_{R}{\hat{a}}_{j+1}^{{{\dagger}} }{\hat{a}}_{j}\right)+\frac{U}{2}{\sum}_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1),$$

(1)

where J_L = e^−α and J_R = e^α with α > 0 describe the non-Hermitian nearest-neighbor hopping amplitudes that induce NHSE, U is the onsite Hubbard interaction, and ${\hat{n}}_{j}={\hat{a}}_{j}^{{{\dagger}} }{\hat{a}}_{j}$. The commutation relations are obeyed by the anyonic creation (${\hat{a}}_{j}^{{{\dagger}} }$) and annihilation (${\hat{a}}_{j}$) operators,

$$\begin{array}{l}{[{\hat{a}}_{j},{\hat{a}}_{k}]}_{\theta }\equiv {\hat{a}}_{j}{\hat{a}}_{k}-{e}^{-i\theta {{{\rm{sgn}}}}(j-k)}{\hat{a}}_{k}{\hat{a}}_{j}=0,\\ {[{\hat{a}}_{j},{\hat{a}}_{k}^{{{\dagger}} }]}_{-\theta }\equiv {\hat{a}}_{j}{\hat{a}}_{k}^{{{\dagger}} }-{e}^{i\theta {{{\rm{sgn}}}}(j-k)}{\hat{a}}_{k}^{{{\dagger}} }{\hat{a}}_{j}={\delta }_{jk},\end{array}$$

(2)

where ${{{\rm{sgn}}}}(x)$ is the sign function and θ is the statistical angle. θ = 0 and θ = π represent normal bosons and “pseudofermions” that obey bosonic statistic only when occupying the same lattice site, respectively⁹. Via a generalized Jordan-Wigner transformation $\hat{{a}_{j}}=\hat{{b}_{j}}{e}^{-i\theta {\sum }_{k = 1}^{j-1}{\hat{n}}_{k}}$, the anyonic model can be mapped to an extended Bose-Hubbard model with a density-dependent phase factor acquired by particles hopping between sites, which facilitates further analysis. Under this mapping, the anyonic Hamiltonian ${\hat{H}}_{A}$ is mapped to

$${\hat{H}}_{B}= -{\sum}_{j=1}^{L-1}\left({J}_{L}{\hat{b}}_{j}^{{{\dagger}} }{e}^{-i\theta {\hat{n}}_{j}}{\hat{b}}_{j+1}+{J}_{R}{\hat{b}}_{j+1}^{{{\dagger}} }{e}^{i\theta {\hat{n}}_{j}}{\hat{b}}_{j}\right)\\ +\frac{U}{2}{\sum}_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1),$$

(3)

where ${\hat{b}}_{j}^{{{\dagger}} }$ (${\hat{b}}_{j}$) is bosonic creation (annihilation) operators and ${\hat{n}}_{j}={\hat{a}}_{j}^{{{\dagger}} }{\hat{a}}_{j}={\hat{b}}_{j}^{{{\dagger}} }{\hat{b}}_{j}$. Using Floquet engineering, similar density-dependent terms giving rise to anyonic statistics have recently been realized in ultracold ⁸⁷Rb atoms¹⁵, and the asymmetric hopping amplitudes J_L and J_R may be implemented with site-dependent atomic loss induced by near-resonant light with position-dependent intensity^51,64, making it possible to realize our model in cold atom systems.

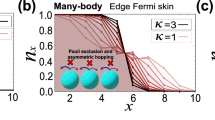
Diagonalizing the Hamiltonian ${\hat{H}}_{B}$, we confirm that complex eigenenergies and NHSE arise in this model due to the asymmetric hopping, as shown in the top row of Fig. 1. The divergence between PBC and OBC spectra indicates the emergence of NHSE under OBCs, as evidenced by the massive accumulation of eigenstates in Fig. 1(a2–d2). The NHSE can be further characterized by a spectral winding number in terms of a U(1) gauge field^34,35,36,65, as demonstrated in the Supplementary Note 3. A key observation is that the spatial distribution for all eigenstates and their average are seen to be roughly the same under different statistical angle θ and the interaction strength U [Fig. 1(e)], implying that the anyonic statistics have little effect on the NHSE at the static level. Physically, this is because the statistic angle does not affect the left and right hopping magnitudes, whose difference gives raise to the NHSE, as further elaborate in the Methods section. In particular, to have a better demonstration between the interplay between NHSE and anyonic properties, θ = −π/2 is chosen as it corresponds to the strongest asymmetric anyonic dynamics to the left¹⁴ (also see later “Discussion”), opposite to the non-Hermitian pumping for the parameters we consider.

Fig. 1: Static properties and density evolutions for N = 2 particles with different statistical angles θ and interaction strength U.

a Bosons (θ = 0) with zero interaction, with (a1) eigenenergies of the model under periodic boundary conditions (PBCs) (red) and open boundary conditions (OBCs) (blue); (a2) particle distribution ρ(x) of all many-body eigenstates (pink); and (a3) density evolution for two particles evenly distributed at the center of the 1D chain. (b1–b3), (c1–c3), (d1–d3) displayed the same quantities for systems with different statistical angles and interaction strengths, as labeled on top of each panel. e The almost identical average density ${\bar{\rho }}_{x}$ for all states in (a2–d2), represented by cyan star, red square, black line, and blue triangular, respectively. It is seen that anyonic statistics have little effect on the distribution of eigenstates, even though they cause distinguished dynamics. Other parameters are J_L = e^−α, J_R = e^α, α = 0.1 and L = 30. In each of (b1), (d1), some eigenenergies form a loop separated from the others, corresponding to two-particle bound states induced by the Hubbard interaction (see Supplementary Note 1).

Dynamical suppression of NHSE

It is commonly assumed that the localizing direction of NHSE indicates the tendency of the state dynamics governed by the non-Hermitian Hamiltonian⁶³. However, despite the nearly identical behavior of NHSE in our model, we find that the dynamics depends strongly on the interaction strength and statistic angle, and may even violate the prediction of NHSE to a certain extent. We consider the density evolution for anyons uniformly distributed at the center of a chain with one particle per site, with the initial state given by $\left\vert {\Psi }_{0}^{A}\right\rangle ={\prod }_{i}\hat{{a}}_{i}^{{{\dagger}} }\left\vert 0\right\rangle$. With the generalized Jordan-Wigner transformation, the time-dependent density distribution of anyons can be expressed as

$${n}_{j}^{A}(t) =\left\langle {\Psi }_{0}^{A}\right\vert {e}^{i{{\hat{H}}_{A}}^{{{\dagger}} }t}{\hat{n}}_{j}{e}^{-i{\hat{H}}_{A}t}\left\vert {\Psi }_{0}^{A}\right\rangle \\ =\left\langle {\Psi }_{0}^{B}\right\vert {e}^{i{{\hat{H}}_{B}}^{{{\dagger}} }t}{\hat{n}}_{j}{e}^{-i{\hat{H}}_{B}t}\left\vert {\Psi }_{0}^{B}\right\rangle ={n}_{j}^{B}(t),$$

(4)

thus the anyon dynamics can be directly measured from the mapped bosonic density ${n}_{j}^{B}(t)$. We note that in our model, the time-dependent density satisfies ${\langle \hat{{n}}_{j}^{B}(t)}\rangle _{+U,\theta }={\langle \hat{{n}}_{j}^{B}(t)}\rangle _{-U,-\theta }$, protected by a combined symmetry ${{{\mathcal{K}}}}\hat{{H}_{B}}{{{{\mathcal{K}}}}}^{{{\dagger}} }={\hat{H}}_{B}^{{{\dagger}} }$ of the Hamiltonian with ${{{\mathcal{K}}}}={{{{\mathcal{R}}}}}_{z}{{{\mathcal{I}}}}{{{\mathcal{T}}}}$, where ${{{\mathcal{I}}}},{{{\mathcal{T}}}}$, and ${{{{\mathcal{R}}}}}_{z}={e}^{-i\theta {\hat{n}}_{j}({\hat{n}}_{j}-1)/2}$ represent the operators for inversion symmetry, time-reversal symmetry, and a number-dependent gauge transformation, respectively (see Methods). That is, cases with repulsive and attractive interactions can be mapped to each other by reversing the sign of θ. Thus we shall focus only on the case with U ⩾ 0 and θ ranging from  −π to π without loss of generality.

Following, we focus on how a state evolves under a non-Hermitian Hamiltonian. Specifically, for an initial state $\left\vert {\psi }_{0}^{A}\right\rangle$, we normalize the final state at time t as

$$\left\vert \psi (t)\right\rangle =\frac{{e}^{-i\hat{H}t/\hslash }\left\vert {\psi }_{0}^{A}\right\rangle }{\sqrt{\left\langle {\psi }_{0}^{A}\left\vert {e}^{i{\hat{H}}^{{{\dagger}} }t/\hslash }{e}^{-i\hat{H}t/\hslash }\right\vert {\psi }_{0}^{A}\right\rangle }}.$$

(5)

The density evolutions for N = 2 anyons with different interaction strengths and statistical angles are shown in bottom panels of Fig. 1. Unbalanced pumping induced by NHSE can be most clearly seen in Fig. 1(a3) with θ = 0 and U = 0, where the particle density shows a unidirectional ballistic evolution toward the right. A finite interaction is known to suppress the expansion of bosons and lead to a diffusive dynamics⁶⁶, thus weakening the unidirectional evolution, as can be seen in Fig. 1(b3).

Away from the bosonic limit at θ = 0, the anyonic statistics induce an asymmetric particle transport^14,15,67 (also see Methods). It can further suppress the NHSE-induced right-moving tendency, and the dynamics show signatures more of a diffusive evolution instead of a ballistic one, as can be seen in Fig. 1(c3) and (d3) for θ = − π/2. Note that the seemingly ballistic evolution with a smaller velocity in Fig. 1(c3) is an exception only for N = 2 particles, and becomes diffusive when the particle number increases, as shown in Supplementary Note 2D. The most peculiar thing is that upon turning on the interaction, the asymmetric transport of anyons may even overwhelm the NHSE at the beginning of the evolution, resulting in an evolution opposite to the direction of skin localization for a short period of time, as shown in Fig. 1(d3).

Reversed density pumping

To characterize the competition between NHSE and statistics-induced asymmetric dynamics, we study the time-dependent density imbalance $\Delta N={\sum }_{i = 1}^{L/2}({n}_{i+L/2}-{n}_{i})$ between the two halves of the 1D chain. As shown in Fig. 2(a) for N = 2, at θ = −π/2 and U = 4, the anyonic density evolution shows a reversed pumping against the NHSE, with ΔN decreases with time t when 0.5 ≲ t ≲ 1. Such a reversed pumping is seen to be robust even under relatively strong non-Hermitian pumping strengths, e.g., α = 0.3 in the figure, where the density imbalance always favors the direction of NHSE (ΔN > 0) and saturated to ΔN = 2 rapidly. It should be noted that for a much weaker non-Hermiticity, the pumping of NHSE will be fully suppressed (with ΔN < 0) during a longer period of time, as shown in the Supplement Note 2C. For comparison, we also plot ΔN versus time for α = 0.1 and U = 4 at different statistical angles in Fig. 2(b). For the several chosen values of θ, the reversed-pumping process with decreasing ΔN can be clearly identified only when θ = −π/2. Furthermore, ΔN is seen to increase faster for θ ≠ −π/2, showing a domination of NHSE on the state dynamics. To characterize the magnitude of reversed pumping, we further consider its duration Δt as an indicator, defined as the time interval where $\frac{d\Delta N}{dt} < \,0$. As shown in Fig. 2(c), Δt reaches it maximum at θ ≈ −π/2 and U ≈ 3. We note that such a reversed density pumping relies crucially on the anyonic statistics, and may disappear if the particles initially occupy the same lattice site (acting as bosons with θ = 0), or are separated from each other by at least one site (acting as single particles), as shown in Supplementary Note 2B. In addition, Δt also takes small but nonzero values for θ ∈ [0, π]. This is because the diffusive anyonic dynamics causes interference between different portions of the evolving state, resulting in certain fluctuation of ΔN that shows weak reversed pumping, as can be seen from the data for θ = π/2 in Fig. 2(b).

Fig. 2: Reversed pumping and density-density correlation for N = 2 particles.

a The density imbalance ΔN for θ = −π/2 with U = 4, for different non-Hermitian amplitudes with α = 0.05, 0.1, 0.2, and 0.3, respectively. b The same density imbalance ΔN for various θ with α = 0.1, U = 4. c A phase diagram demonstrating the reversed-pumping time Δt, defined as the interval with $\frac{d\Delta N}{dt} < 0$. Nonzero Δt is also seen around θ ∈ (0, π) with relatively large U, which is resulted from the fluctuation of ΔN at larger t induced by the interference dynamics in Fig. 1 (see Supplementary Note 2A). d–f Density-density correlation of the evolved state at different time t, with θ = −π/2, α = 0.1 and L = 20, and U = 0, 4, and 8 from (d–f) respectively. As U increases, the diagonal spreading of the correlation shows a bidirectional pumping toward both q = r = L and q = r = 1, indicating the NHSE and the reversed density pumping induced by anyonic statistics, respectively.

To provide a full picture of the different diffusive and unidirectional dynamics in the system, we calculate the density-density correlation defined as

$${\Gamma }_{qr}=\langle \psi (t)| {\hat{n}}_{q}{\hat{n}}_{r}| \psi (t)\rangle ,$$

(6)

and display the results for two particles with θ = −π/2 and different values of U in Fig. 2(d–f). When U = 0, the dynamics mainly reflects the unidirectional pumping of NHSE, as nonzero Γ_qr mostly distributes along diagonal (q = r), and its peak moves toward q = r = L during the evolution [Fig. 2(d)]. Turning on the interaction, we can see in Fig. 2(e) and (f) that nonzero off-diagonal correlations appear with the distance between the two position (∣q − r∣) increases with time, indicating the diffusion enhanced by interaction. On the other hand, a second peak of diagonal correlation appears and move toward q = r = 1, signals the reversed density pumping caused by anyonic statistics. The above discussion is focused on N = 2 and we stress that it also holds for larger N, as shown in Supplementary Note 4.

Reversed pumping with larger particle numbers N

As our model contains only nearest-neighbor hopping, the anyonic statistics can function normally only for adjacent particles. Therefore, the reversed pumping it induces is expected to become more prominent with more particles in the system, distributing next to each other initially. In Fig. 3(a), we demonstrate the reversed-pumping time Δt for N = 2, 3, 4, and 6 of θ = −π/2 with various interaction U. For N = 2, Δt is increasing fast around 0.5 and reaches its maximum approximately at U = 3, then it shows a slightly decreasing behavior. While for N = 3, 4 and 6, Δt is increasing with the increase of U (also see Supplementary Note 6). Interestingly, for U ≳ 3, the reversed-pumping effect shows an interaction enhanced tendency, as can be clearly seen from the Fig. 3(b) for U = 5. Note that the slope of N = 2 is seen to be smaller than the others for t ≳ 2. This is because with fewer particles, it takes shorter time for their wave-function to be mostly pumped to the right half of the lattice by NHSE, after which (t ≈ 2 for N = 2) dΔN/dt becomes smaller as the remaining density on the left becomes negligible. For N > 2, the slope of ΔN also decreases similarly at larger t, as shown in Supplementary Note 2E. In addition, weak damped fluctuation of ΔN is seen even when the dynamics are dominated by NHSE at larger t, resultant from the interplay between anyonic interference and density diffusion. Namely, while the interference of anyons induces the fluctuation, the diffusion reduces local density, weakening the density being pumped across the center and resulting in an overall damping effect.

Fig. 3: Reversed pumping for various particle numbers with statistical angle θ = −π/2.

a Reversed-pumping time Δt for N = 2, 3, 4, and 6, represented by red triangles, blue pluses, gold squares, and black stars, respectively. b Density imbalance at U = 5 with N = 2, 3, 4, and 6, represented by red dotted line, blue dashed line, gold dot line, and black solid line, respectively. α = 0.1 is chosen for both panels. The system’s size is chosen to be L = 30 for N = 2, 4, and 6, and L = 31 for N = 3. In the latter case, the density at the center of the system (j = 16) is excluded when calculating ΔN.

Out-of-time correlator and information spreading

Having unveiled the sophisticated evolution of particle density in non-Hermitian anyonic systems. it is natural to ask how the anyonic statistics and NHSE simultaneously affect the dynamics of other physical quantities, such as the spreading of quantum information that can be characterized by the OTOC in non-Hermitian systems⁶⁸. To describe the information spreading, we first consider the OTOC of anyons for an ensemble defined as (see Supplementary Note 5A for more details).

$${C}_{jk}(t)={\left\langle {\left\vert {\left[{\hat{a}}_{j}(t),{\hat{a}}_{k}(0)\right]}_{\theta }\right\vert }^{2}\right\rangle }_{\beta },$$

(7)

where β is the inverse temperature and ${\left\langle \hat{O}\right\rangle }_{\beta }$ means the thermal ensemble average ${{{\rm{Tr}}}}({e}^{-\beta {\hat{H}}_{A}}\hat{O})/{{{\rm{Tr}}}}({e}^{-\beta {\hat{H}}_{A}})$ of an operator $\hat{O}$. C_jk(t) describes the information propagated from site k to site j at time t, and C_jk(0) = 0 is ensured by the generalized commutation relations of Eqs. (2). The out-of-time-ordered part of the commutator is then given by^69,70

$${\bar{F}}_{jk}(t)={\left\langle {\hat{a}}_{j}^{{{\dagger}} }(t){\hat{a}}_{k}^{{{\dagger}} }(0){\hat{a}}_{j}(t){\hat{a}}_{k}(0)\right\rangle }_{\beta }{e}^{i\theta {{{\rm{sgn}}}}(j-k)}.$$

(8)

The numerical results with θ = −π/2 and U = 4, i.e., under the parameters where the reversed density pumping strength nearly reaches its maximum, in Fig. 4(a–c). It is seen that the direction of OTOC reverses from left to right when increasing the non-Hermiticity, reflecting the competition between NHSE and the statistic-induced asymmetric OTOC spreading. This is in contrast to bosonic systems without the anyonic asymmetric OTOC spreading, where the NHSE-induced asymmetric OTOC spreading can be observed even with a very weak non-Hermiticity, as shown in Supplementary Note 5B. Physically, this is because the ensemble average represents a linear combination of eigenstates with different powers, which are all skin-localized toward the right when J_R > J_L in our model.

Fig. 4: Information spreading with statistical angle θ = −π/2 and interaction strength U = 4.

Out-of-time-ordered correlator (OTOC) for a thermal ensemble at finite temperature with (a) J_R = 1.0, (b) J_R = 1.02, and (c) J_R = 1.25. The system has L = 7 lattice sites and N = 4 particles, with the inverse temperature β = 1/6. The information spreading tends to move towards the right side with the increasing of J_R. d–f OTOC for a single state with L = 11, N = 5. For a single state, the information spreading hardly changes with the increase of J_R. d ∣F_j6∣ for L = 11, U = 4, and J_R = 1.5. The initial state is chosen as $\psi (0)\left.\right\rangle =\left\vert {\hat{a}}_{4}{\hat{a}}_{5}{\hat{a}}_{6}{\hat{a}}_{7}{\hat{a}}_{8}\right\rangle$. e ∣F_1,6∣ and ∣F_11,6∣ for J_R = 1, 1.25, 1.5, respectively. f ∣F_4,6∣ and ∣F_8,6∣ for J_R = 1, 1.25, 1.5, respectively. J_L = 1 is set in all panels. Results are normalized by setting ${\max }_{j,t}| {\bar{F}}_{j,4}| =1$ in (a–c), ${\max }_{t}| {F}_{j,6}| =1$ in (d), and ${\max }_{t}| {F}_{j,6}| =1$ in (e) and (f).

In contrast, we find qualitatively different behaviors of the OTOC for a single initial state, whose definition is similar to Eqs. (7) and (8) but with β = 0 and the ensemble average replaced by the average on the state. In Fig. 4(d), we find that the information spreading for a single initial state [F_jk(t)] with a uniform distribution at the center of the 1D chain shows a clear asymmetric distribution with large value of OTOC at the left side and nearly unchanged even with a strong non-Hermiticy, reflecting the statistic-induced asymmetric OTOC spreading and immunity to NHSE.

In Fig. 4(e, f), we illustrate the information propagated from the center (k = 6) to a few different positions j, with different non-Hermitian parameters. As the initial state does not occupy the two ends of the system (with 11 lattice sites), we can see that F_j6 vanishes for j = 1 or 11 at small t, and increases monotonically with time. On the other hand, we have F_j6 = 1 at the beginning and decreases with time for j = 4 and 8, which are the lattice sites occupied by the initial state. Nonetheless, these trends of OTOC are found to remain the same for both Hermitian (J_R = 1) and non-Hermitian cases (J_R ≠ 1), further verifying the dissimilar behaviors of OTOC for an ensemble at finite temperature (dominated by NHSE) and for a single initial state (immune to NHSE).

Conclusions

We have revealed a dynamical suppression of NHSE by anyonic statistics, where the density evolutions show different diffusive or reversed-pumping dynamics at different statistic angles. In recent literature, it has been shown that NHSE can be suppressed through various means, e.g., by introducing magnetic^71,72 or electric fields⁷³ with both the static solutions and dynamical evolutions changed drastically from ones of the NHSE in the suppression phase.

However, our results show that the anyonic statistics will affect only the density dynamics, whereas static solutions still manifest the same properties of NHSE under different statistical angles. The reversed-pumping process is shown to have a longer duration with larger numbers of particles, indicating that it may be easier for observation in the thermodynamic limit. The coexistence between different diffusive dynamics, non-Hermitian pumping of NHSE, and reversed pumping are further demonstrated by the density-density correlation of the evolved state. Finally, we also calculate the OTOC to characterize the quantum information spreading, which is found to be governed by NHSE only for a thermal ensemble. On the other hand, OTOC calculated for a single initial state curiously follows that that of Hermitian limit dynamics, regardless of the strength of non-reciprocal pumping induced by non-Hermiticity. These observations challenge the correspondence between static NHSE and unidirectional state dynamics, which is commonly assumed to be true in most theoretical^{63,74,75,76,77,78,79} and experimental investigation^{80,81,82,83,84,85,86,87} in the NHSE, particularly in quantum simulators^83,87. Following this path, we may expect even more sophisticated non-Hermitian phenomena to arise from the interplay between anyonic statistics and other novel single-particle dynamics induced by NHSE, such as the non-Hermitian edge burst^88,89 and self-healing of skin modes⁹⁰. Another potential direction is to investigate non-Hermitian anyonic dynamics in the hardcore limit, which has been found to induce an occupation-dependent particle separation for bosons and fermions⁶³. Nonetheless, long-range couplings are required for our model to manifest anyonic features in the hardcore limit (see Supplementary Note 7 for results or our model in the hardcore limit). Finally, we note that in this paper we only address Abelian anyons in a 1D lattice. Beyond this simple picture, non-Abelian anyons may also emerge as quasiparticles in other higher-dimensional systems, such as fractional quantum Hall systems and quantum spin liquids, where anyonic porperties may affect NHSE in different manners. For example, it has been demonstrated that non-Abelian fusion of Fibonacci anyons induces exotic Bloch oscillations⁹¹, whose interplay with non-Hermitian pumping may lead to distinct dynamical behaviors that await further investigation.

Methods

Static NHSE and its independence from anyonic statistics

The origin of NHSE can be understood from a similarity transformation of the Hamiltonian matrix. For the OBC Hamiltonian

$${\hat{H}}_{B}= -{\sum }_{j=1}^{L-1}\left({J}_{L}{\hat{b}}_{j}^{{{\dagger}} }{e}^{-i\theta {\hat{n}}_{j}}{\hat{b}}_{j+1}+{J}_{R}{\hat{b}}_{j+1}^{{{\dagger}} }{e}^{i\theta {\hat{n}}_{j}}{\hat{b}}_{j}\right)\\ +\frac{U}{2}\mathop{\sum}_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1),$$

(9)

we introduce a set of operators defined as

$${\hat{g}}_{l}^{{{\dagger}} }={e}^{-l\alpha }{\hat{b}}_{l}^{{{\dagger}} },{\hat{g}}_{l}={e}^{l\alpha }{\hat{b}}_{l}.$$

(10)

Then the above Hamiltonian can be rewritten as

$${\hat{H}}_{B}= -{\sum}_{j=1}^{L-1}\left({\hat{g}}_{j}^{{{\dagger}} }{e}^{-i\theta {\hat{n}}_{j}}{\hat{g}}_{j+1}+{\hat{g}}_{j+1}^{{{\dagger}} }{e}^{i\theta {\hat{n}}_{j}}{\hat{g}}_{j}\right)\\ +\frac{U}{2}{\sum}_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1),{\hat{n}}_{j}={\hat{g}}_{j}^{{{\dagger}} }{\hat{g}}_{j}.$$

(11)

This transformation results in a Hermitian Hamiltonian matrix ${H}_{B}^{{\prime} }$ given by ${H}_{B}^{{\prime} }=S{H}_{B}{S}^{-1}$, with H_B the matrix form of ${\hat{H}}_{B}$ in the Fock basis of ${\sum }_{l}{\hat{b}}_{l}^{{{\dagger}} }\left\vert 0\right\rangle$, ${H}_{B}^{{\prime} }={({H}_{B}^{{\prime} })}^{{{\dagger}} }$ the matrix form of ${\hat{H}}_{B}$ in the new Fock basis of ${\sum }_{l}{\hat{g}}_{l}^{{{\dagger}} }\left\vert 0\right\rangle$, and S the transformation matrix describing the relation between operators ${\hat{b}}_{l}$ and ${\hat{g}}_{l}$.

Note that by definition, S is a similarity transformation that keeps only the eigenvalues unchanged. On the other hand, the eigenvectors in the original basis can be obtained as $\psi ={S}^{-1}{\psi }^{{\prime} }$, with ${\psi }^{{\prime} }$ an eigenvector of ${H}_{B}^{{\prime} }$. As ${H}_{B}^{{\prime} }$ is a Hermitian matrix describing a system with translational symmetry within the bulk, ${\psi }^{{\prime} }$ generally describes extended states with uniform distributions of particles in the bulk. However, the mapping between operators in Eq. (10) indicates that the similarity transformation of S is not uniform, where a particle created at site l has a position-dependent magnitude e^−lα. Thus, for a positive α, an extended state of ${\psi }^{{\prime} }$ with uniform distribution of particles becomes a boundary-localized state with amplified magnitude toward larger l. Finally, as the mapping of Eq. (10) is irrelevant to the statistic angle θ, we can conclude that the anyonic statistic do not affect the localizing direction of static NHSE.

Pseudo-Hermitian symmetry of the static Hamiltonian

The Hamiltonian of the non-Hermitian anyon-Hubbard model is given by

$${\hat{H}}_{A}=-{\sum}_{j=1}^{L-1}\left({J}_{L}{\hat{a}}_{j}^{{{\dagger}} }{\hat{a}}_{j+1}+{J}_{R}{\hat{a}}_{j+1}^{{{\dagger}} }{\hat{a}}_{j}\right)+\frac{U}{2}{\sum}_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1).$$

(12)

With a generalized Jordan-Wigner transformation $\hat{{a}_{j}}=\hat{{b}_{j}}{e}^{-i\theta {\sum }_{k = 1}^{j-1}{\hat{n}}_{k}}$, the model is mapped to a boson-Hubbard model with a density-dependent phase factor,

$${\hat{H}}_{B}= -{\sum}_{j=1}^{L-1}\left({J}_{L}{\hat{b}}_{j}^{{{\dagger}} }{e}^{-i\theta {\hat{n}}_{j}}{\hat{b}}_{j+1}+{J}_{R}{\hat{b}}_{j+1}^{{{\dagger}} }{e}^{i\theta {\hat{n}}_{j}}{\hat{b}}_{j}\right)\\ +\frac{U}{2}{\sum}_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1).$$

(13)

We find that this Hamiltonian satisfies a pseudo-Hermitian symmetry⁹²

$${{{\mathcal{K}}}}\hat{{H}_{B}}{{{{\mathcal{K}}}}}^{{{\dagger}} }={\hat{H}}_{B}^{{{\dagger}} },$$

(14)

with ${{{\mathcal{K}}}}={{{{\mathcal{R}}}}}_{z}{{{\mathcal{I}}}}{{{\mathcal{T}}}}$ an anti-unitary operator, which guarantee that the eigenenergies must be real (as under OBCs) or come in complex-conjugate pair (as under PBCs). Explicitly, ${{{\mathcal{I}}}}$ represents the inversion symmetry that transforms j to L + 1 − j, so that

$${H}_{B}^{{\prime} } = {{{\mathcal{I}}}}{H}_{B}{{{{\mathcal{I}}}}}^{{{\dagger}} }\\ = -{\sum}_{j=1}^{L-1}\left({J}_{L}{\hat{b}}_{j+1}^{{{\dagger}} }{e}^{-i\theta {\hat{n}}_{j+1}}{\hat{b}}_{j}+{J}_{R}{\hat{b}}_{j}^{{{\dagger}} }{e}^{i\theta {\hat{n}}_{j+1}}{\hat{b}}_{j+1}\right)\\ +\frac{U}{2}{\sum}_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1).$$

(15)

Next, ${{{\mathcal{T}}}}$ represents the time-reversal symmetry for spinless particles (i.e., a complex conjugation), which leads to

$${H}_{B}^{{\prime\prime} } = {{{\mathcal{T}}}}{H}_{B}^{{\prime} }{{{{\mathcal{T}}}}}^{{{\dagger}} }\\ = -{\sum}_{j=1}^{L-1}\left({J}_{L}{\hat{b}}_{j+1}^{{{\dagger}} }{e}^{i\theta {\hat{n}}_{j+1}}{\hat{b}}_{j}+{J}_{R}{\hat{b}}_{j}^{{{\dagger}} }{e}^{-i\theta {\hat{n}}_{j+1}}{\hat{b}}_{j+1}\right)\\ +\frac{U}{2}{\sum}_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1).$$

(16)

Finally, ${{{{\mathcal{R}}}}}_{z}={e}^{-i\theta {\hat{n}}_{j}({\hat{n}}_{j}-1)/2}$ is a rotation operator that transforms the annihilation and creation operators as

$$\begin{array}{l}{b}_{j}^{{{\dagger}} }\to {e}^{-i\theta {\hat{n}}_{j}({\hat{n}}_{j}-1)/2}{b}_{j}^{{{\dagger}} }{e}^{i\theta {\hat{n}}_{j}({\hat{n}}_{j}-1)/2}={b}_{j}^{{{\dagger}} }{e}^{-i\theta {\hat{n}}_{j}},\\ {b}_{j}\to {e}^{-i\theta {\hat{n}}_{j}({\hat{n}}_{j}-1)/2}{b}_{j}{e}^{i\theta {\hat{n}}_{j}({\hat{n}}_{j}-1)/2}={e}^{i\theta {\hat{n}}_{j}}{b}_{j}.\end{array}$$

(17)

Applying this rotation operation to the Hamiltonian, we have

$${H}_{B}^{{\prime\prime} {\prime} } ={{{\mathcal{R}}}}_{z}{H}_{B}^{{\prime\prime} }{{{\mathcal{R}}}}_{z}^{{\dagger} }\\ =-{\sum }_{j=1}^{L-1}\left({J}_{L}{{{\mathcal{R}}}}_{z}{\hat{b}}_{j+1}^{{\dagger} }{{{\mathcal{R}}}}_{z}^{{\dagger} }{{{\mathcal{R}}}}_{z}{e}^{i\theta {\hat{n}}_{j+1}}{\hat{b}}_{j}{{{\mathcal{R}}}}_{z}^{{\dagger} }+{J}_{R}{{{\mathcal{R}}}}_{z}{\hat{b}}_{j}^{{\dagger} }{{{\mathcal{R}}}}_{z}^{{\dagger} }{{{\mathcal{R}}}}_{z}{e}^{-i\theta {\hat{n}}_{j+1}}{\hat{b}}_{j+1}{{{\mathcal{R}}}}_{z}^{{\dagger} }\right)+\frac{U}{2}{\sum }_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1)\\ =-{\sum }_{j=1}^{L-1}\left({J}_{L}{b}_{j+1}^{{\dagger} }{e}^{-i\theta {\hat{n}}_{j+1}}{e}^{i\theta {\hat{n}}_{j+1}}{e}^{i\theta {\hat{n}}_{j}}{b}_{j}+{J}_{R}{b}_{j}^{{\dagger} }{e}^{-i\theta {\hat{n}}_{j}}{e}^{-i\theta {\hat{n}}_{j+1}}{e}^{i\theta {\hat{n}}_{j+1}}{b}_{j+1}\right)+\frac{U}{2}{\sum }_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1)\\ =-{\sum }_{j=1}^{L-1}\left({J}_{L}{b}_{j+1}^{{\dagger} }{e}^{i\theta {\hat{n}}_{j}}{b}_{j}+{J}_{R}{b}_{j}^{{\dagger} }{e}^{-i\theta {\hat{n}}_{j}}{b}_{j+1}\right)+\frac{U}{2}{\sum }_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1)\\ ={H}_{B}^{{\dagger} }.$$

(18)

Note that the pseudo-Hermitian symmetry also ensures that the eigeneneriges must either be real or come in complex-conjugate pairs⁹². To see this, let us assume $\left\vert \psi \right\rangle$ is an eigenstate of ${\hat{H}}_{B}$ with an eigenenergy E,

$${\hat{H}}_{B}\left\vert \psi \right\rangle =E\left\vert \psi \right\rangle .$$

(19)

The pseudo-Hermitian symmetry leads to

$${\hat{H}}_{B}^{{{\dagger}} }{{{\mathcal{K}}}}\left\vert \psi \right\rangle ={{{\mathcal{K}}}}{\hat{H}}_{B}\left\vert \psi \right\rangle =E{{{\mathcal{K}}}}\left\vert \psi \right\rangle ,$$

(20)

Namely, $\left\vert \phi \right\rangle ={{{\mathcal{K}}}}\left\vert \psi \right\rangle$ is an eigenstate of ${\hat{H}}_{B}^{{{\dagger}} }$, or in other words, a left eigenstate of ${\hat{H}}_{B}$ with

$$\left\langle \phi \right\vert {\hat{H}}_{B}={E}^{* }\left\langle \phi \right\vert .$$

(21)

Therefore, there must be a right eigenstate $\left\vert {\phi }^{{\prime} }\right\rangle$ of ${\hat{H}}_{B}$ satisfying

$${\hat{H}}_{B}\left\vert {\phi }^{{\prime} }\right\rangle ={E}^{* }\left\vert {\phi }^{{\prime} }\right\rangle .$$

(22)

As a conclusion, the pseudo-Hermitian symmetry ensures either a real eigenenergy E if $\left\vert \psi \right\rangle =\left\vert {\phi }^{{\prime} }\right\rangle$ (so that E = E^*), or a complex-conjugate pair of E and E^* if $\left\vert \psi \right\rangle \ne \left\vert {\phi }^{{\prime} }\right\rangle$.

Dynamical symmetry

In the Hermitian limit of our model (J_L = J_R), it has been shown that¹⁴

$${\left\langle {\hat{n}}_{j}\left(t\right)\right\rangle }_{+U}={\left\langle {\hat{n}}_{{j}^{{\prime} }}\left(t\right)\right\rangle }_{-U},{\left\langle {\hat{n}}_{j}\left(t\right)\right\rangle }_{+\theta }={\left\langle {\hat{n}}_{{j}^{{\prime} }}\left(t\right)\right\rangle }_{-\theta },$$

(23)

with ${j}^{{\prime} }=L+1-j$, and ⟨⟩ denoting the average of a Heisenberg operator on the initial state $\left\vert {\Psi }_{0}\right\rangle ={\prod }_{i}\hat{{b}_{i}^{{{\dagger}} }\left\vert 0\right\rangle }$. Yet these relations no longer hold when J_L ≠ J_R and the symmetry between different values of U and θ need to be reexamined for the non-Hermitian Hamiltonian

$$\hat{{H}_{B}}= -{\sum}_{j=1}^{L-1}\left({J}_{L}{\hat{b}}_{j}^{{{\dagger}} }{e}^{i\theta {\hat{n}}_{j}}{\hat{b}}_{j+1}+{J}_{R}{\hat{b}}_{j+1}^{{{\dagger}} }{e}^{-i\theta {\hat{n}}_{j}}{\hat{b}}_{j}\right)\\ +\frac{U}{2}{\sum}_{j=1}^{L}{\hat{n}}_{j}({\hat{n}}_{j}-1).$$

(24)

The pseudo-Hermitian symmetry operation leads to the following relations:

$${{{\mathcal{K}}}}{e}^{-i{\hat{H}}_{B}t}{{{{\mathcal{K}}}}}^{{{\dagger}} }={e}^{i{\hat{H}}_{B}^{{{\dagger}} }t},{{{\mathcal{K}}}}{n}_{j}{{{{\mathcal{K}}}}}^{{{\dagger}} }={{{\mathcal{I}}}}{n}_{j}{{{{\mathcal{I}}}}}^{{{\dagger}} }=\hat{{n}_{{j}^{{\prime} }}}.$$

(25)

Thus we obtain

$$\begin{array}{l}{\left\langle {\hat{n}}_{j}\left(t\right)\right\rangle }_{+\theta ,+U}\equiv \left\langle {\Psi }_{0}\right\vert {e}^{i{\hat{H}}_{B,+\theta ,+U}^{{{\dagger}} }t}{\hat{n}}_{j}{e}^{-i{\hat{H}}_{B,+\theta ,+U}t}\left\vert {\Psi }_{0}\right\rangle \\ =\left\langle {\Psi }_{0}\right\vert {{{{\mathcal{K}}}}}^{{{\dagger}} }{e}^{-i{\hat{H}}_{B,+\theta ,+U}t}{{{\mathcal{K}}}}{\hat{n}}_{j}{{{{\mathcal{K}}}}}^{{{\dagger}} }{e}^{i{\hat{H}}_{B,+\theta ,+U}^{{{\dagger}} }t}{{{\mathcal{K}}}}\left\vert {\Psi }_{0}\right\rangle \\ =\left\langle {\Psi }_{0}\right\vert {e}^{-i{\hat{H}}_{B,+\theta ,+U}t}{\hat{n}}_{{j}^{{\prime} }}{e}^{i{\hat{H}}_{B,+\theta ,+U}^{{{\dagger}} }t}\left\vert {\Psi }_{0}\right\rangle .\end{array}$$

(26)

We then consider the time-reversal operation

$$\begin{array}{l}{{{\mathcal{T}}}}{\hat{H}}_{B,+\theta ,+U}{{{{\mathcal{T}}}}}^{-1}={\hat{H}}_{B,-\theta ,+U}\\ \Rightarrow {{{\mathcal{T}}}}{e}^{-i{\hat{H}}_{B,+\theta ,+U}t}{{{{\mathcal{T}}}}}^{-1}={e}^{i{\hat{H}}_{B,-\theta ,+U}t}.\end{array}$$

(27)

with ${{{\mathcal{T}}}}$ the complex conjugation operator for spinless particles, and an operation

$${{{\mathcal{P}}}}{\hat{H}}_{B,+\theta ,+U}{{{{\mathcal{P}}}}}^{{{\dagger}} }=-{\hat{H}}_{B,+\theta ,-U}\Rightarrow {{{\mathcal{P}}}}{e}^{-i{\hat{H}}_{B,+U}t}{{{{\mathcal{P}}}}}^{{{\dagger}} }={e}^{i{\hat{H}}_{B,-U}t}.$$

(28)

with ${{{\mathcal{P}}}}={e}^{i\pi {\sum }_{r}{\hat{n}}_{2r+1}}$ the number parity operator measuring the parity of total particle number on the odd sites. Then, we have

$${\left\langle {\hat{n}}_{j}\left(t\right)\right\rangle }_{+\theta ,+U} =\left\langle {\Psi }_{0}\right\vert {e}^{i{\hat{H}}_{B,+\theta ,+U}^{{{\dagger}} }t}{\hat{n}}_{j}{e}^{-i{\hat{H}}_{B,+\theta ,+U}t}\left\vert {\Psi }_{0}\right\rangle \\ =\left\langle {\Psi }_{0}\right\vert {{{{\mathcal{T}}}}}^{-1}{e}^{-i{{\hat{H}}^{{{\dagger}} }}_{B,-\theta ,+U}t}{{{\mathcal{T}}}}{\hat{n}}_{j}{{{{\mathcal{T}}}}}^{-1}{e}^{i{\hat{H}}_{B,-\theta ,+U}t}{{{\mathcal{T}}}}\left\vert {\Psi }_{0}\right\rangle \\ =\left\langle {\Psi }_{0}\right\vert {e}^{-i{{\hat{H}}^{{{\dagger}} }}_{B,-\theta ,+U}t}{\hat{n}}_{j}{e}^{i{\hat{H}}_{B,-\theta ,+U}t}\left\vert {\Psi }_{0}\right\rangle \\ =\left\langle {\Psi }_{0}\right\vert {{{{\mathcal{P}}}}}^{{{\dagger}} }{e}^{i{{\hat{H}}^{{{\dagger}} }}_{B,-\theta ,-U}t}{{{\mathcal{P}}}}{\hat{n}}_{j}{{{{\mathcal{P}}}}}^{{{\dagger}} }{e}^{-i{\hat{H}}_{B,-\theta ,-U}t}{{{\mathcal{P}}}}\left\vert {\Psi }_{0}\right\rangle \\ =\left\langle {\Psi }_{0}\right\vert {e}^{i{{\hat{H}}^{{{\dagger}} }}_{B,-\theta ,-U}t}{\hat{n}}_{j}{e}^{-i{\hat{H}}_{B,-\theta ,-U}t}\left\vert {\Psi }_{0}\right\rangle \\ ={\left\langle {\hat{n}}_{j}\left(t\right)\right\rangle }_{-\theta ,-U}.$$

(29)

Thus, we have a dynamic symmetry combined the changing the sign of θ and U at the same time,

$${\left\langle {\hat{n}}_{j}\left(t\right)\right\rangle }_{+\theta ,+U}={\left\langle {\hat{n}}_{j}\left(t\right)\right\rangle }_{-\theta ,-U}.$$

(30)

Perturbation explanation for asymmetric spreading

In order to explain the asymmetric density spreading, we reproduce the derivation in ref. ¹⁴ that expands the evolution operator and evaluates the interferences effect between different order. The time evolution operator can be expanded as

$$\hat{{{{\mathcal{U}}}}}={e}^{-i{\hat{H}}_{B}t}={\sum}_{n=0}^{\infty }\frac{{\left(-i{\hat{H}}_{B}t\right)}^{n}}{n!}=1-i\hat{{H}_{B}}t+\frac{{\left(i{\hat{H}}_{B}t\right)}^{2}}{2!}-...$$

The initial state $\left\vert {\psi }_{0}\right\rangle$ is symmetric around the lattice center with $\left\vert {\psi }_{0}\right\rangle ={{{\mathcal{I}}}}\left\vert {\psi }_{0}\right\rangle$ and the final state can be superimposed with product states in Fock space. To show that the interference between the different order leads to asymmetric density evolution, we consider a state $\left\vert {\psi }_{1}\right\rangle$ with an imbalanced distribution between the left and right halves of the system, and its spatial inversion $\left\vert {\psi }_{2}\right\rangle ={{{\mathcal{I}}}}\left\vert {\psi }_{1}\right\rangle$. Asymmetric dynamics occurs when $\left\langle {\psi }_{1}\right\vert \hat{{{{\mathcal{U}}}}}\left\vert {\psi }_{0}\right\rangle \ne \left\langle {\psi }_{2}\right\vert \hat{{{{\mathcal{U}}}}}\left\vert {\psi }_{0}\right\rangle$. The kth-order expansion of these inner products can be written as

$${M}_{k}^{\left(1\right)}=\left\langle {\psi }_{1}\right\vert \frac{{\left(-i{\hat{H}}_{B}t\right)}^{k}}{k!}\left\vert {\psi }_{0}\right\rangle =\frac{{\left(-it\right)}^{k}}{k!}{A}_{k},$$

with ${A}_{k}=\left\langle {\psi }_{1}\right\vert {\left({\hat{H}}_{B}\right)}^{k}\left\vert {\psi }_{0}\right\rangle$, and

$${M}_{k}^{\left(2\right)}=\left\langle {\psi }_{2}\right\vert \frac{{\left(-i{\hat{H}}_{B}t\right)}^{k}}{k!}\left\vert {\psi }_{0}\right\rangle =\frac{{\left(-it\right)}^{k}}{k!}{B}_{k},$$

with ${B}_{k}=\left\langle {\psi }_{2}\right\vert {\left({\hat{H}}_{B}\right)}^{k}\left\vert {\psi }_{0}\right\rangle$. Taking the symmetry properties into consideration, we obtain

$${B}_{k} =\left\langle {\psi }_{2}\right\vert {\hat{H}}_{B}^{k}\left\vert {\psi }_{0}\right\rangle \\ =\left\langle {\psi }_{1}\right\vert {{{{\mathcal{I}}}}}^{{{\dagger}} }{\hat{H}}_{B}^{k}{{{\mathcal{I}}}}\left\vert {\psi }_{0}\right\rangle \\ ={e}^{i({\phi }_{2}-{\phi }_{0})}\left\langle {\psi }_{1}\right\vert {{{{\mathcal{I}}}}}^{{{\dagger}} }{{{{\mathcal{R}}}}}^{{{\dagger}} }{\hat{H}}_{B}^{k}{{{\mathcal{R}}}}{{{\mathcal{I}}}}\left\vert {\psi }_{0}\right\rangle \\ ={e}^{i({\phi }_{2}-{\phi }_{0})}\left\langle {\psi }_{1}\right\vert {{{\mathcal{T}}}}{{{{\mathcal{K}}}}}^{{{\dagger}} }{\hat{H}}_{B}^{k}{{{\mathcal{K}}}}{{{{\mathcal{T}}}}}^{-1}\left\vert {\psi }_{0}\right\rangle \\ ={e}^{i({\phi }_{2}-{\phi }_{0})}{\left(\left\langle {\psi }_{1}\right\vert {{{{\mathcal{K}}}}}^{{{\dagger}} }{\hat{H}}_{B}^{k}{{{\mathcal{K}}}}\left\vert {\psi }_{0}\right\rangle \right)}^{* }.$$

(31)

In the above derivation, we have used following equations:

$$\begin{array}{l}{{{\mathcal{K}}}}={{{\mathcal{R}}}}{{{\mathcal{I}}}}{{{\mathcal{T}}}}\Rightarrow {{{\mathcal{K}}}}{{{{\mathcal{T}}}}}^{-1}={{{\mathcal{R}}}}{{{\mathcal{I}}}}\Rightarrow {{{\mathcal{T}}}}{{{{\mathcal{K}}}}}^{{{\dagger}} }={{{{\mathcal{I}}}}}^{{{\dagger}} }{{{{\mathcal{R}}}}}^{{{\dagger}} },\\ {{{\mathcal{K}}}}{\hat{H}}_{B}^{k}{{{{\mathcal{K}}}}}^{{{\dagger}} }={\hat{H}}_{B}^{k{{\dagger}} }\Rightarrow {\hat{H}}_{B}^{k}={{{{\mathcal{K}}}}}^{{{\dagger}} }{\hat{H}}_{B}^{k{{\dagger}} }{{{\mathcal{K}}}}.\end{array}$$

In Eq. (31) we have used ${{{\mathcal{R}}}}\left\vert {\psi }_{0,2}\right\rangle ={e}^{i{\phi }_{0,2}}\left\vert {\psi }_{0,2}\right\rangle .$There is difference between the Hermitian case and non-Hermitian case. The non-zero contribution of the interference between kth and (k + 1)th orders

$${S}_{1} =\left\vert {M}_{k}^{(1)}+{M}_{k+1}^{(1)}\right\vert =\frac{{t}^{k}}{k!}\left\vert {A}_{k}+\frac{-it}{k+1}{A}_{k+1}\right\vert ;\\ {S}_{2} =\left\vert {M}_{k}^{(2)}+{M}_{k+1}^{(2)}\right\vert =\frac{{t}^{k}}{k!}\left\vert {B}_{k}+\frac{-it}{k+1}{B}_{k+1}\right\vert ,\\ \Rightarrow {S}_{2}=\frac{{t}^{k}}{k!}\left\vert {B}_{k}^{* }-\frac{-it}{k+1}{B}_{k+1}^{* }\right\vert .$$

(32)

Thus, we obtain

$${S}_{1} =\frac{{t}^{k}}{k!}\left\vert \left\langle {\psi }_{1}\right\vert {\left({\hat{H}}_{B}\right)}^{k}\left\vert {\psi }_{0}\right\rangle +\frac{-it}{k+1}\left\langle {\psi }_{1}\right\vert {\left({\hat{H}}_{B}\right)}^{k+1}\left\vert {\psi }_{0}\right\rangle \right\vert ,\\ {S}_{2} =\frac{{t}^{k}}{k!}\left\vert \left\langle {\psi }_{1}\right\vert {{{{\mathcal{K}}}}}^{{{\dagger}} }{\left({\hat{H}}_{B}\right)}^{k}{{{\mathcal{K}}}}\left\vert {\psi }_{0}\right\rangle -\frac{-it}{k+1}\left\langle {\psi }_{1}\right\vert {{{{\mathcal{K}}}}}^{{{\dagger}} }{\left({\hat{H}}_{B}\right)}^{k+1}{{{\mathcal{K}}}}\left\vert {\psi }_{0}\right\rangle \right\vert .$$

(33)

Thus, $\left\langle {\psi }_{1}\right\vert \hat{{{{\mathcal{U}}}}}\left\vert {\psi }_{0}\right\rangle \ne \left\langle {\psi }_{2}\right\vert \hat{{{{\mathcal{U}}}}}\left\vert {\psi }_{0}\right\rangle$ is satisfied since S₁ ≠ S₂ in general cases, meaning that the final state is asymmetric. Without further restriction of the model, the only exceptions are the Hermitian cases (J_L = J_R) with θ = 0 or π, namely for bosons or “pseudofermions”, where S₁ = S₂ has been proven in ref. ¹⁴.