Dynamic transfer of chiral edge states in topological type-II hyperbolic lattices

Abstract

The discovery of hyperbolic lattice, a discretized regularization of non-Euclidean space with constant negative curvature, has provided an unprecedented platform to extend topological phases of matter from Euclidean to non-Euclidean spaces. To date, however, all previous hyperbolic topological states are limited to conventional type-I hyperbolic lattice with a single edge, leaving the dynamic transfer of hyperbolic topological states between different edges completely unresolved. Here, by extending the hyperbolic topological physics from the conventional type-I hyperbolic lattices to the newfangled type-II hyperbolic lattices, we report the type-II hyperbolic Chern insulator featuring outer and inner chiral edge states and demonstrate their dynamic transfer across the bulk to the opposite edge via two distinct mechanisms: anti-parity-time phase transition and Landau-Zener single-band pumping. Our work lays the foundation for further exploring the dynamic evolution of hyperbolic topological effects, with the final goal of inspiring applications leveraging dynamic manipulations of the hyperbolic topological states.

Introduction

Exploring and discovering novel topological phases of matter has emerged as the most pivotal and fascinating research area in condensed-matter physics^1,2, photonics^3,4, acoustics^5,6,7, mechanics^7,8, electric circuits^9,10,11, and even thermal diffusions^12,13. To date, most of the nontrivial topological states have been established in the Euclidean spaces with zero curvature. Recently, the discovery of hyperbolic lattices, which are the regular tessellations in non-Euclidean spaces with constant negative curvature, in circuit quantum electrodynamics¹⁴ and electric circuits¹⁵ has opened up new avenues to extend topological physics from the Euclidean to non-Euclidean spaces and simulated numerous research advances in hyperbolic topological physics with novel topological states, including the hyperbolic quantum spin Hall effect¹⁶, hyperbolic Haldane^17,18,19 and Kane Mele models¹⁸, hyperbolic Hofstadter butterfly²⁰, hyperbolic band topology with second Chern number²¹, hyperbolic graphene²², hyperbolic photonic topological insulators²³, anomalous and Chern edge states in hyperbolic networks²⁴, hyperbolic non-abelian semimetal²⁵, higher-order topological hyperbolic lattices^17,26,27 and so on.

However, so far, all previous studies on hyperbolic topological physics have been limited to conventional type-I hyperbolic lattices and only focus on the hyperbolic topological states associated with a single edge^{16,17,18,19,20,21,22,23,24,25,26,27}. In this context, a significant class of topological processes, namely the dynamic transfer of topological states between different edges, such as Thouless pumping^28,29, Laughlin pumping^30,31,32,33, and Landau-Zener (LZ) transition^34,35,36,37, cannot be achieved in the existing framework of type-I hyperbolic lattices. These dynamic topological effects are crucial for advancing hyperbolic topological physics in that they not only provide a powerful approach to manipulate hyperbolic topological states but also offer a crucial method for characterizing hyperbolic topological invariants and exploring higher-dimensional hyperbolic topological physics^38,39. Fortunately, the recently discovered type-II hyperbolic lattices^40,41 feature inner and outer edges, thereby offering a natural platform to fill this long-standing gap in hyperbolic topological physics.

In this work, by mapping the celebrated Qi-Wu-Zhang (QWZ) model onto a type-II hyperbolic lattice, we report a type-II hyperbolic Chern insulator (HCI) whose inner and outer edges support counterpropagating chiral edge states (CESs). More significantly, we demonstrate that these CESs can be dynamically transferred between the outer and inner edges of a type-II HCI by leveraging the power-flow conversion at an anti-parity-time symmetric (APT-S) exceptional point (EP)⁴² or adiabatic evolution along a single band in LZ model^36,37, which cannot be achieved in type-I HCIs with only a single edge. Our findings not only lay the foundation for future studies on the dynamic transfer of hyperbolic topological states but also inspire potential applications that harness non-Hermitian phase transitions and adiabatic evolution as new degrees of freedom to manipulate hyperbolic topological states, thereby expanding the research scope of hyperbolic topological physics.

Results

Type-I and type-II hyperbolic lattices

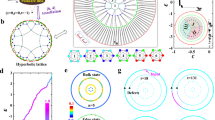
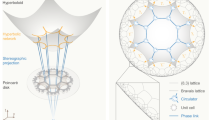
We start with classifying hyperbolic planes with constant negative curvatures in three-dimensional (3D) Minkowski spacetime and their projection onto planar hyperbolic models. In general, hyperbolic planes can be fundamentally categorized as two-sheet (Fig. 1a) and one-sheet (Fig. 1d) hyperboloids (see Methods). Under stereographic projection, these two types of hyperboloids can be further mapped as planar “Poincaré disk” (Fig. 1b) and “Poincaré ring” (Fig. 1e) models, respectively (see Methods), while preserving their local constant negative curvatures and global topologies. More intriguingly, by applying regular polygon tessellation that discretizes a flat plane into a crystal lattice, these two types of Poincaré model can be further discretized as type-I (Fig. 1c) and type-II hyperbolic lattices (Fig. 1f), respectively.

Fig. 1: Type-I and type-II hyperbolic lattices.

a One brunch of a two-sheet hyperboloid (${t}^{2}-{x}^{2}-{y}^{2}=1$) in (2 + 1)-dimensional (x,y,t) Minkowski spacetime is mapped onto a Poincaré disk (z = 0) by stereographic projection through the point (0, 0, −1) (green dot). b Poincaré disk with unit radius. c A type-I hyperbolic lattice with {8, 3}-tessellation constructed by discretizing the Poincaré disk with octagons. d One-sheet hyperboloid (${u}^{2}+{v}^{2}-{z}^{2}=1$) in (1 + 2)-dimensional (u,v,z) Minkowski spacetime is mapped onto a set of overlapped line segments at z axis by stereographic projection through the point (0,1,0) (green dot). Inset displays a Poincaré band configuration formed by extending the line segments along angular position φ. e Poincaré ring with unit outer radius, inner radius ${r}_{{in}}$, and characteristic radius ${r}_{h}$ generated by wrapping and gluing the Poincaré band in d. f A type-II hyperbolic lattice with {${r}_{h}$, 8, 3}-tessellation constructed by discretizing the Poincaré ring with octagons.

In contrast to the type-I hyperbolic lattice whose geometric degrees of freedom can be fully characterized by a Schläfli symbol {p, q}, an extended Schläfli symbol {${r}_{h}$, p, q} has to be adopted to label the unique geometric topology of the type-II hyperbolic lattice, where p and q represent q copies of p-sided polygons meeting at each vertex, ${r}_{h}={{{\rm{e}}}}^{-2\pi /{kP}}$ represents the characteristic radius (radius of the yellow circle in Fig. 1e, f), P is a geometry constant (see Methods) and k is a positive integer representing the rotation symmetry of the type-II hyperbolic lattice (in this work we fix k as even numbers unless otherwise specified). The inner radius ${r}_{{in}}$ can be determined by the characteristic radius ${r}_{h}$ via the relation ${r}_{{in}}={r}_{h}^{2}$. Here, we adopt a finite type-II hyperbolic {0.365, 8, 3} lattice ($k=4,P=1.559$) with a total of 1240 sites.

Type-II hyperbolic Chern insulators

To construct a type-II HCI, as illustrated in Fig. 2a, we map the QWZ model onto the type-II hyperbolic lattice which can be described by a tight-binding model (TBM) Hamiltonian:

$${H}_{{{\rm{CI}}}}={\sum}_{\left\langle i,j\right\rangle }{c}_{i}^{{\dagger} }{J}_{{ij}}{c}_{j}+{\sum}_{i}\left(M+2{t}_{2}\right){c}_{i}^{{\dagger} }{\sigma }_{z}{c}_{i}$$

(1)

where ${c}_{i}^{{\dagger} }$ and ${c}_{i}$ are the creation and annihilation operators of electrons at the site i, ${\sigma }_{x,y,z}$ are the Pauli matrices. Matrix ${J}_{{ij}}=-[i{t}_{1}\left({\sigma }_{x}\cos {\theta }_{{ij}}+{\sigma }_{y}\sin {\theta }_{{ij}}\right)+{t}_{2}{\sigma }_{z}]/2$ depicts the hopping between two neighboring connected sites, where ${\theta }_{{ij}}$ represents the polar angle of the vector from site i to site j (see label in Fig. 2a), serving as a hopping phase to break the time-reversal symmetry of the system. Note that although the mirror symmetry of the sublattices outside and inside ${r}_{h}$ is broken by the current hopping phase setting, the amplitudes of all couplings are identical, ensuring the nature of negative constant curvature. We henceforth set system parameters ${t}_{1}={t}_{2}=1$, $M=-1$. We directly diagonalize the Hamiltonian ${H}_{{{\rm{CI}}}}$ to obtain the energy spectrum, as shown in Fig. 2c. The bulk energy gap (orange region), indicated by the vanished bulk density of states (DOS) (see Methods) shown in Fig. 2b, is occupied by paired inner (red dots) and outer (blue dots) CESs, whose intensity distributions are displayed in Fig. 2e.

Fig. 2: Type-II hyperbolic Chern insulator (HCI).

a Schematic illustration of Qi-Wu-Zhang model on a type-II hyperbolic {0.365, 8, 3} lattice. b Bulk density of state (DOS) of the Type-II HCI in a, the energy region with vanished DOS indicates the bulk energy gap (orange region). c Energy spectrum of the Type-II HCI in a, inner (red dots) and outer (blue dots) chiral edge states (CESs) fill the energy gap. The inset displays the zoomed-in view of the CESs near zero energy. d Real-space Bott index ${C}_{B}$ as a function of energy. e Intensity distributions of the outer and inner CESs marked in the inset of c. f Instantaneous intensity distributions of wave-packet excited by two edge sources (green stars) at time 60, 172, 292, and 424, respectively.

To further verify the nontrivial topological properties of these CESs, we first calculate their corresponding real-space Bott index ${C}_{B}$, as shown in Fig. 2d. In the gap region, ${C}_{B}=-1$ indicates the nontrivial band topology of the type-II HCI phase (see Methods). Next, to characterize the nonreciprocal and robust transport of these CESs, we inject wave packets ${\psi }_{0}(t)=\exp \left(-\frac{{t}^{2}}{2{\sigma }^{2}}\right)\sin (2\pi {\varepsilon }_{0}t)$ with ${\varepsilon }_{0}=0.0064$ and σ = 50 (green stars in Fig. 2f) into the outer and inner edges to investigate their dynamic time evolution and introduce several on-site potential defects (white circles in Fig. 2f) to test their topological protection. Figure 2f presents the instantaneous intensity distributions of $\left|{\psi }_{0}(t)\right|$ at different times t = 60, 172, 292, 424, respectively. It can be seen that the wave packet is well-confined to the outer (inner) edge of the type-II HCI and propagates nonreciprocally along the counterclockwise (CCW) [clockwise (CW)] direction, smoothly passes through the defects without any backscattering. These results prove that both the inner and outer edges of type-II HCIs can support robust and nonreciprocal CESs.

Dynamic transfer of CESs in modulated type-II HCIs

The key to achieving the dynamic transfer between the outer and inner CESs lies in introducing interaction and controlling the evolution path of the coupled states in real space or parameter space. In real space, a straightforward paradigm is to completely couple a CCW-propagating CES at the outer edge, through the bulk, to a CW-propagating CES at the inner edge, and vice versa. This implies that these two CESs coalesce as one state with zero power flow, which is the characteristic signature of an APT EP^42,43,44. We start by considering a two-level model and selecting the two modes in Fig. 2d as its orthonormal basis $\left\{|{\psi }_{o} \left\rangle, | {\psi }_{i}\right\rangle \right\}$, representing the CESs localized at the outer and inner edges, respectively. The CCW and CW power flows of the bases are defined as ${\beta }_{o}={\left|\left\langle {\psi }_{o} | {\psi }_{o}\right\rangle \right|}^{2}-{\left|\left\langle {\psi }_{i} | {\psi }_{o}\right\rangle \right|}^{2}=1=\Delta$ and ${\beta }_{i}={\left|\left\langle {\psi }_{o} | {\psi }_{i}\right\rangle \right|}^{2}-{\left|\left\langle {\psi }_{i} | {\psi }_{i}\right\rangle \right|}^{2}=-1=-\Delta$, respectively. To manipulate the interactions between these two counterpropagating CESs, we introduce a radial coupling channel (pink region) consisting of seven modulated couplings (pink short lines) ${T}_{{ij}}(\rho )=\rho {\cdot J}_{{ij}}$, as illustrated in Fig. 3a. Figure 3b shows the eigenenergy of the system as a function of the modulation strength ρ. As ρ increases, the approximately degenerate states $|{\psi }_{\rho ,k}\rangle \left(k={\mathrm{1,2}}\right)$ gradually split, and their power flows, given by ${\beta }_{k}={ | \langle {\psi }_{o} | {\psi }_{\rho ,k} \rangle |}^{2}-{ | \langle {\psi }_{i} | {\psi }_{\rho ,k} \rangle |}^{2}$, change from 1 (blue color) or −1 (red color) to 0 (green color) simultaneously. This phenomenon of power flow evolution can be described by a two-level effective Hamiltonian ${H}_{{eff}}=\left(\begin{array}{cc}{\beta }_{o} & {\kappa }_{{oi}}\\ {\kappa }_{{io}} & {\beta }_{i}\end{array}\right)$, where the coupling factors are derived as purely imaginary numbers ${\kappa }_{{oi}}={\kappa }_{{io}}=i\kappa$ due to the power-flow-difference conservation in the contra-directional coupling process^42,43,44 (see Supplementary Note 1). Hence, we arrive at the Hamiltonian written as:

$${H}_{{APT}}=\left(\begin{array}{cc}\Delta & i\kappa \\ i\kappa & -\Delta \end{array}\right)$$

(2)

which is APT-S, i.e., $\left\{{H}_{{APT}},\hat{P}\hat{T}\right\}=0$ and gives eigenvalues:

$$\beta =\pm \sqrt{{\Delta }^{2}-{\kappa }^{2}}$$

(3)

Fig. 3: Dynamic transfer of chiral edge states via anti-parity-time (APT) phase transition.

a Schematic illustration of a modulated type-II hyperbolic Chern insulator for implementing an effective two-level anti-parity-time symmetric (APT-S) model. b Eigenenergy of the system in a as a function of the modulation strength ρ, where the color indicates the power flow β of each eigenstate. c β as a function of κ. The solid lines (dots) are analytic (numerical) results calculated from the APT Hamiltonian ${H}_{{APT}}$ (tight-binding model calculations). Pink and blue regions denote the anti-parity-time-symmetry-broken (APT-B) and APT-S phase, respectively. The yellow star represents an APT exceptional point (EP). d Intensity distributions of quasi-EP eigenstates marked by yellow stars in b and c. e Wave packet transmissions of outer-outer (${S}_{21}$) and outer-inner (${S}_{31}$) edge transports as a function of ρ. Inset illustrates that a wave packet excited by an outer edge source (green star), is splitted into two wave packets by the channel, which are detected by outer (blue dot) and inner (red dot) edge probes. f Instantaneous intensity distributions of wave-packet at time 40, 84, 104, and 292, respectively, for ρ = 100 marked by yellow dashed line in e.

As shown by solid lines in Fig. 3c, in the weakly coupled regime |κ| < |∆| (pink region), β appear as two real numbers, corresponding to an anti-parity-time-symmetry-broken (APT-B) phase which hosts two propagating eigenstates with CCW (blue line) or CW (red line) power flows. Especially, when the coupling reaches a critical point |κ| = |∆| (yellow dashed line), β coalesces to zero, corresponding to an EP (yellow star) and non-propagating eigenstates with vanishing power flow. Additionally, β in Fig. 3b can also be retrieved as a function of effective κ, as demonstrated by circles in Fig. 3b, which exhibits a quantitative agreement with the analytic results from Eq. (4). Figure 3d shows the EP eigenstates corresponding to the yellow stars in Fig. 3b, c, which exhibit nearly identical intensity distributions that conform to the coalescence of eigenvectors at the EP, and the equal intensity distribution between the outer and inner edges coincide with the vanishing power flow at the EP.

We then examine the dependence of outer edge to inner edge transmissions on the modulation strength ρ. As illustrated in the inset of Fig. 3e, we inject the formerly used wave-packet ${\psi }_{0}\left(t\right)$ from an outer edge source (green star marked 1), and then evaluate the transmission ${S}_{21}$ (${S}_{31}$) from an outer (inner) edge probe [blue dot marked 2 (red dot marked 3)] for different ρ. Figure 3e reveals that, for sufficiently weak ρ (<8), ${S}_{21}$ (${S}_{31}$) remains stable at 1 (0), indicating the wave-packet only propagates along the outer edge. As ρ increases, the system gradually approaches the EP, ${S}_{21}$ (${S}_{31}$) exponentially decays (increases) to 0 (1), signifying the dynamic transfer from the outer CESs to the inner CESs. Figure 3f presents the instantaneous intensity distributions of $\left|{\psi }_{0}(t)\right|$ at different times t = 40, 84, 104, 292 with ρ = 101, respectively. It can be seen that the wave packet initially propagates CCW along the outer edge, and then gradually crosses the coupling channel and continues to propagate CW along the inner edge, thereby achieving the dynamic transfer of CESs in type-II HCIs via the APT phase transition which has never been reported before.

Next, to overcome the challenge of the CESs failing to dynamically transfer under sufficiently small ρ (i.e., far from EP), we harness a robust mechanism regardless of modulation strength, namely the dynamic state pumping along an adiabatically evolved path in parameter space, such as LZ single-band pumping. As illustrated in Fig. 4a, we introduce additional non-reciprocal phases Φ into the couplings ${T}_{{ij}}\left(\rho \right)$ as a new degree of freedom. For ρ=6, which is an extremely weak modulation strength that cannot induce CES transfer using the APT phase transition. Figure 4b shows the eigenenergy of the coupled outer and inner CESs near zero energy as a function of the non-reciprocal phases Φ, where the blue and red colors represent the weighting of the corresponding eigenstates on the bases $|{\psi }_{o}\rangle$ and $|{\psi }_{i}\rangle$ with a CES gap (green region) of a size of ∆E = 0.000446 at Φ = π. These two gapped bands can be modeled as a two-level LZ Hamiltonian^36,37:

$${H}_{{LZ}}\left(\delta \Phi \right)=\left(\begin{array}{cc}-\alpha \delta \Phi & \Gamma \\ \Gamma & \alpha \delta \Phi \end{array}\right)$$

(4)

where $\Gamma =\Delta E/2$ is determined by the gap size and α=0.002 is a fitting parameter. If the initial state is $|{\psi }_{i}\rangle$ at Φ = π-1 (red stars in Fig. 4b, c), there are two possible routes of state evolution, as illustrated by the dashed red and blue arrows in Fig. 4b. When it follows the red arrow path, the $|{\psi }_{i}\rangle$ component always dominates during this process, and the final state (red rhombus in Fig. 4b, c) remains localized at the inner edge. In contrast, when it is pumped along the blue arrow path, the final state (blue rhombus in Fig. 4b, c) will be dominated by $|{\psi }_{o}\rangle$, leading to the transition from the inner edge to the outer edge and the final states will be localized at the outer edge.

Fig. 4: Dynamic transfer of chiral edge states via Landau-Zener (LZ) single-band pumping.

a Schematic illustration of a modulated type-II hyperbolic Chern insulator for implementing an effective two-level LZ model. b Eigenenergy of the system in a as a function of modulation phase Φ, where the color indicates the weightings of each eigenstate on the bases $|{\psi }_{i}\rangle$ (red color) and $|{\psi }_{o}\rangle$ (blue color). The solid lines (dots) are analytic (numerical) results calculated from the LZ Hamiltonian ${H}_{{LZ}}$ (tight-binding model calculations). The green region represents the energy gap. c The intensity distributions of the initial state (red star) and the two possible final states (red and blue rhombuses) along different state evolution paths. d The weightings of final state $|{\psi }_{f}\rangle$ on the bases $|{\psi }_{i}\rangle$ and $|{\psi }_{o}\rangle$ as a function of the number of evolution step T. e and f The changes in intensity distribution of state during a nonadiabatic (e) and an adiabatic (f) evolution, corresponding to the red and blue dashed lines in d, respectively.

The final state $|{\psi }_{f}\rangle$ is a superposition of bases $|{\psi }_{o}\rangle$ and $|{\psi }_{i}\rangle$ given by $|{\psi }_{f}\rangle =O\left(t\right)|{\psi }_{o}\rangle +I(t)|{\psi }_{i}\rangle$, where the composition $O\left(t\right)$ and $I\left(t\right)$ satisfy:

$$-i\frac{d}{{dt}}\left(\begin{array}{c}O\left(t\right)\\ I\left(t\right)\end{array}\right)=\left(\begin{array}{cc}\eta t & \Gamma \\ \Gamma & -\eta t\end{array}\right)\left(\begin{array}{c}O\left(t\right)\\ I\left(t\right)\end{array}\right)$$

(5)

where $\eta =\alpha (\Delta \Phi /T)$ characterizes the adiabaticity that depends on the evolution rate $\Delta \Phi /T$, i.e., the ratio of phase range ΔΦ=2 and the number of evolution steps T. The state evolution starts with the initial state dominated by $|{\psi }_{i}\rangle$, i.e., the initial condition is ${({\mathrm{0,1}})}^{T}$. Using Eq. (6), the weightings of the final state on the bases $|{\psi }_{i}\rangle$ and $|{\psi }_{o}\rangle$ can be derived as a function of T: ${P}_{|{\psi }_{i}\rangle }=I{\left(T\right)}^{2}={e}^{-\pi {\Gamma }^{2}/\eta }$ and ${P}_{|{\psi }_{o}\rangle }=O{\left(T\right)}^{2}=1-{e}^{-\pi {\Gamma }^{2}/\eta }$^36,37. We plot the weightings as solid lines in Fig. 4d, it can be seen that ${P}_{|{\psi }_{i}\rangle }$ and ${P}_{|{\psi }_{o}\rangle }$ intersects at ${T}_{t}=\frac{\alpha \Delta \Phi {\mathrm{ln}}2}{\pi {\Gamma }^{2}}=17747$ (black dashed line), which is the LZ transition point. When $T \, \gg \, {T}_{t}$ (blue dashed line in Fig. 4d), the state evolves sufficiently slowly to remain adiabatic and stays on the same band with the final state dominated by $|{\psi }_{o}\rangle$, corresponding to the LZ single-band pumping (blue arrow in Fig. 4b). However, when the same process occurs with $T \, \ll \, {T}_{t}$ (red dashed line in Fig. 4d), the state evolution will be fast enough to be nonadiabatic and tunnel across the energy gap, populating the upper band with the final state dominated by $|{\psi }_{i}\rangle$ and corresponding to the LZ tunneling (red arrow in Fig. 4b).

For the initial state (red star) shown in Fig. 4b, c, we calculate the evolved final state at different evolution rates and determine its weightings on the bases $|{\psi }_{i}\rangle$ and $|{\psi }_{o}\rangle$ as functions of T, as plotted by colored dots in Fig. 4d, which coincide with the results of the LZ model. Figure 4e, f display the intensity distributions of the state during the nonadiabatic ($T={T}_{1}=1001$) and adiabatic $(T={T}_{2}=125001)$ evolution, respectively. As predicted in our theoretical analysis, for the LZ tunneling with nonadiabatic evolution (Fig. 4e), the initial inner CESs remain localized at the inner edge, while for the LZ single-band pumping with adiabatic evolution (Fig. 4f), the initial inner CESs pump across the bulk to the outer edge, achieving the dynamic transfer of the CESs in type-II HCIs. Given that the characteristic radius ${r}_{h}$ plays a pivotal role in type-II hyperbolic lattices, we have discussed the influence of ${r}_{h}$ on the dynamic transfer of CESs via two mechanisms. We find that the transfer efficiency of CESs in the process of APT phase transition is not significantly affected by ${r}_{h}$, whereas in the process of LZ single-band pumping, a larger ${r}_{h}$ leads to a lower transfer efficiency (see Supplementary Note 2).

Conclusion

In conclusion, we have theoretically demonstrated the nontrivial CESs and their dynamic transfer in topological type-II hyperbolic lattices. By extending the QWZ model to the type-II hyperbolic space, we achieve a type-II HCI featuring inner and outer CESs with opposite chirality, in contrast to its type-I counterpart which only has outer CESs with a single chirality. More interestingly, we demonstrate that the counterpropagating CESs at the outer and inner edges of type-II HCIs can be dynamically transferred via two distinct mechanisms: the completely reversed power-flow conversion at an APT-S EP and the adiabatic evolution along a single-band in LZ model. Our work thus significantly expands the research scope of hyperbolic topological physics and establishes a paradigm for exploring novel topological effects in more complex non-Euclidean spaces. We envision the dynamic transfer of hyperbolic surface states or hyperbolic hinge states that can be achieved in three-dimensional stacked type-II HCIs. Given current experimental techniques, the dynamic transfer of the CESs in topological type-II hyperbolic lattices can be readily realized in circuit quantum electrodynamics¹⁴, electric circuits^15,17,21,22, integrated nanophotonic chips²³, and nonreciprocal networks²⁴. Our work may inspire potential applications in robust and compact hyperbolic topological devices by leveraging dynamic manipulations of the hyperbolic topological states, such as hyperbolic topological laser^45,46 and optical frequency combs^47,48,49.

Methods

Embedding infinite hyperbolic planes into 3D Minkowski spacetimes

(1) ${{\mathbb{R}}}^{{{\boldsymbol{2}}}}$ topology In the (2 + 1)-dimensional (x,y,t) Minkowski spacetime with metric:

$$d{s}_{1}^{2}=-d{t}^{2}+d{x}^{2}+d{y}^{2},$$

(6)

the two-sheet hyperboloid described by ${t}^{2}-{x}^{2}-{y}^{2}=1$ can be parameterized by:

$$t=\cosh \alpha ,x=\sinh \alpha \cos \beta ,y=\sinh \alpha \sin \beta .$$

(7)

The induced metric on the hyperboloid sheet is:

$$d{s}_{I}^{2}=d{\alpha }^{2}+{\sinh }^{2}\alpha d{\beta }^{2},$$

(8)

the Gaussian curvature Κ of this metric can be calculated as:

$${\rm K}=-\frac{1}{2\sqrt{{g}_{\alpha \alpha }{g}_{\beta \beta }}}\left({\partial }_{\alpha }\frac{{\partial }_{\alpha }{g}_{\beta \beta }}{\sqrt{{g}_{\alpha \alpha }{g}_{\beta \beta }}}+{\partial }_{\beta }\frac{{\partial }_{\beta }{g}_{\alpha \alpha }}{\sqrt{{g}_{\alpha \alpha }{g}_{\beta \beta }}}\right)=-1$$

(9)

where ${g}_{\mu \nu }={\mbox{diag}}[1,{\sinh }^{2}\alpha ]$, μ and ν are space indices, running from α to β. This reveals that two-sheet hyperboloid in (x,y, t) Minkowski spacetime indeed has constant negative curvature and therefore effectively realizes the hyperbolic plane with ${{\mathbb{R}}}^{2}$ topology.

(2) ${{\mathbb{R}}} \times {{\mathbb{S}}}$ topology In the (1 + 2)-dimensional (z, u,v) Minkowski spacetime with metric:

$$d{s}_{2}^{2}=-d{u}^{2}-d{v}^{2}+d{z}^{2},$$

(10)

the one-sheet hyperboloid described by ${u}^{2}+{v}^{2}-{z}^{2}=1$ can be parameterized by:

$$u=\cosh \alpha \cos \beta ,v=\cosh \alpha \sin \beta ,z=\sinh \alpha .$$

(11)

The induced metric on the hyperboloid sheet is:

$$d{s}_{{II}}^{2}=d{\alpha }^{2}-{\cosh }^{2}\alpha d{\beta }^{2},$$

(12)

the Gaussian curvature Κ of this metric can be calculated as:

$${\rm K}=-\frac{1}{2\sqrt{{\eta }_{\alpha \alpha }{\eta }_{\beta \beta }}}\left({\partial }_{\alpha }\frac{{\partial }_{\alpha }{\eta }_{\beta \beta }}{\sqrt{{\eta }_{\alpha \alpha }{\eta }_{\beta \beta }}}+{\partial }_{\beta }\frac{{\partial }_{\beta }{\eta }_{\alpha \alpha }}{\sqrt{{\eta }_{\alpha \alpha }{\eta }_{\beta \beta }}}\right)=-1$$

(13)

where ${\eta }_{\mu \nu }={\mbox{diag}}[1,-{\cosh }^{2}\alpha ]$, μ and ν are space indices, running from α to β. This reveals that one-sheet hyperboloid in (z,u,v) Minkowski spacetime indeed has constant negative curvature and therefore effectively realizes the hyperbolic plane with ${{\mathbb{R}}} \times {{\mathbb{S}}}$ topology.

Stereographically projecting infinite hyperboloids in 3D Minkowski spacetimes as planar Poincaré models

(1) Two-sheet hyperboloid The stereographical projection, as illustrated by black rays in Fig. 1a, that maps the two-sheet hyperboloid into a planar hyperbolic model can be completely and mathematically described by the coordinate transformation:

$${\rho }_{I}=\tanh \left(\frac{\alpha }{2}\right),$$

(14)

The Eq. (9) thus reduces to a conformally flat form:

$$d{s}_{{{\rm{disk}}}}^{2}=\frac{4}{{\left(1-{\rho }_{I}^{2}\right)}^{2}}\left(d{{\rho }_{I}}^{2}+{{\rho }_{I}}^{2}d{\beta }^{2}\right).$$

(15)

Applying the complex coordinate $z={\rho }_{I}{e}^{i\beta }$ the Eq. (16) can be rewritten as:

$$d{s}_{{{\rm{disk}}}}^{2}=\frac{4}{{\left(1-{z}^{2}\right)}^{2}}{dzd}{z}^{* }.$$

(16)

which indicates a disk configuration dubbed as Poincaré disk.

(2) One-sheet hyperboloid The stereographical projection, as illustrated by black rays in Fig. 1d, that maps the one-sheet hyperboloid into a planar hyperbolic model is mathematically equivalent to a conformal mapping:

$$f\left(z\right)=\frac{2}{\pi }\log \left(\frac{1+z}{1-z}\right),$$

(17)

on the Poincaré disk, as shown in Fig. 5a. The Eq. (17) thus reduces as:

$$d{s}_{{{\rm{band}}}}^{2}=\frac{{\pi }^{2}}{4{\cos }^{2}\left(\frac{\pi }{2}{{\rm{Im}}}\left(f\right)\right)}{dfd}{f}^{* }.$$

(18)

which indicates a band configuration dubbed as Poincaré band, as shown in Fig. 5b.

Fig. 5: Conformal rules for mapping a Poincaré disk to a Poincaré ring.

a Poincaré disk. b Poincaré band transformed from Poincaré disk with conformal rule $f(z)$. c Poincaré ring transformed from Poincaré band with conformal rule w(f).

The transformation that warps and glues this band model as ring model can be mathematically described by the conformal mapping:

$$w\left(f\right)={{{\rm{e}}}}^{i\frac{\pi }{2{r}_{h}}(f+i)},$$

(19)

The Eq. (19) thus reduces as:

$$d{s}_{{{\rm{ring}}}}^{2}=\frac{{{r}_{h}}^{2}}{{\left(\left|w\right|\sin \left({r}_{h}\log \left(\left|w\right|\right)\right)\right)}^{2}}{dwd}{w}^{* }.$$

(20)

which indicates a ring configuration dubbed as Poincaré ring, as shown in Fig. 5c.

Construction of type-II hyperbolic lattice Fig. 6a shows an infinite type-I hyperbolic lattice with {8, 3} tessellation. After the conformal mapping in Eq. (18), the type-I hyperbolic lattice is stretched as an infinite band with a discrete translation symmetry along the horizontal direction, as illustrated in Fig. 6b. The period is the width of a unite cell (blue region) as P=1.559. Subsequently, after the conformal mapping in Eq. (20) with ${r}_{h}={e}^{-\frac{2\pi }{{kP}}}$ (here we set k=8), the band lattice is wrapped and glued as an infinite type-II hyperbolic lattice, as shown in Fig. 6c.

Fig. 6: Octagon tessellations in Poincaré models.

Infinite {8, 3} tessellation in a Poincaré disk, b Poincaré band, and c Poincaré ring.

Calculation of bulk density of states Given a tight-banding Hamiltonian H on a finite type-II hyperbolic lattice, we perform exact diagonalization to obtain its eigensystem ${\left\{\left({E}_{i},|{\psi }_{i}\rangle \right)\right\}}_{i=1}^{N}$, where $|{\psi }_{i}\rangle$ is an eigenvector with eigenvalue ${E}_{i}$, and N is the number of sites. For each state $|{\psi }_{i}\rangle$ we define a bulk weight factor as follows:

$${w}_{i}={\sum}_{a=1}{\left|{\psi }_{i,a}\right|}^{2},$$

(21)

where the subscript a represents the innermost bulk site indices. We then convert the information about the eigenvalues and eigenvectors into a continuous DOS function via

$${\rho }_{{{\rm{bulk}}}}\left(E\right)={\sum}_{i=1}{w}_{i}\frac{1}{\eta \sqrt{2\pi }}\exp \left[-\frac{{\left(E-{E}_{i}\right)}^{2}}{2{\eta }^{2}}\right].$$

(22)

We use η = 0.05 throughout the manuscript.

Calculation of real-space Bott index In conventional flat lattices, topological edge states are characterized by Chern number in momentum space. Since there is no well-defined translation symmetry in the type-II hyperbolic lattice, we utilize the real-space Bott index to characterize the topological nontrivial phase of the chiral edge states in type-II hyperbolic chern insulators. The real-space Bott index ${C}_{B}$ is defined as:

$${C}_{B}=\frac{1}{2\pi }{{\rm{Im\; tr}}}[\log \left({VU}{V}^{{\dagger} }{U}^{{\dagger} }\right)],$$

(23)

with $U=P{e}^{i2\pi X}P$ and $V=P{e}^{i2\pi Y}P$, where X (Y) is a diagonal matrix whose diagonal element ${x}_{i}$ (${y}_{i}$) is the new coordinate of the ith site after rescaling the coordinate interval ${x}_{j}({y}_{j})\in$ (-1, 1) to ${x}_{j}({y}_{j})\in$ (0, 1), $P={\sum }_{n}^{{N}_{{occ}}}\left|{\psi }_{n}\right\rangle \left\langle \left.{\psi }_{n}\right|\right.$ is the projector operator of the occupied states $|{\psi }_{n}\rangle$.