Dynamical blockade of a reservoir for optimal performances of a quantum battery

Abstract

The development of fast and efficient quantum batteries is crucial for the prospects of quantum technologies. In the present paper we demonstrate that both requirements are accomplished in the paradigmatic model of a harmonic oscillator strongly coupled to a highly non-Markovian thermal reservoir. We show that at short times, a dynamical blockade of the reservoir prevents the leakage of energy towards its degrees of freedom, promoting a significant accumulation of energy in the battery with high efficiency. The possibility of implementing these conditions in LC quantum circuits opens up new avenues for solid-state quantum batteries.

Introduction

The progressive broadening of the horizons of thermodynamics towards individual quantum mechanical systems out-of-equilibrium opened the way to the field of quantum thermodynamics^1,2,3,4. In this context, the possibility to properly characterize the energetics of miniaturized thermal machines represented a major boost for the development of quantum technologies devoted to energy storage and manipulation. Among them, quantum batteries (QBs) are currently assuming a pivotal role^5,6.

After the first appearance of the concept more than ten years ago⁷, these devices have been characterized by a frantic theoretical investigation⁸ followed recently by the first experimental realizations⁹. The majority of the proposals discussed so far identify the QB as a collection of two-level systems charged by means of quantum^{7,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23} or classical^24,25,26,27 external sources. However, in recent years, the possibility to address multilevel QBs in view of achieving high storage capacity has been discussed^28,29.

Indubitably, among multilevel systems the quantum harmonic oscillator plays a prominent role due to its versatility. Indeed, a plethora of different physical systems can be ultimately described in terms of this simple and universal model. It is therefore not a surprise that also in the QB domain proposals for implementable multilevel devices based on quantum harmonic oscillators have appeared^{13,30,31,32,33,34,35,36,37}. Among the others, interesting schemes have considered the possibility to charge a harmonic oscillator QB by switching on the coupling with a reservoir for a suitable period of time^30,38. However, in previous investigations the efficiency of these protocols, defined as the ratio between the maximum extractable energy through unitary operations (known as ergotropy³⁹) and the energy required to switch on and off the coupling with the charger, remained very poor.

In this paper, we show that this limitation can be overcome and that both high efficiency and fast charging can be achieved, provided that: (i) the reservoir is engineered in a strongly non-Markovian regime characterized by a cut-off frequency ω_D ≳ ω₀, with ω₀ frequency of the oscillator and, counter-intuitively, (ii) the dissipation is very strong, with intensity γ₀ ≫ ω₀. In such a regime, at short enough times, the switch-on coupling energy between QB and reservoir is almost completely transferred directly to the QB itself with only marginal dissipation onto the reservoir degrees of freedom, due to a dynamical blockade of the reservoir⁴⁰. Consequently, the unit efficiency limit predicted for a QB and a reservoir initially in a thermal state⁴¹ can be saturated. We explain this dynamical blockade in terms of the hybridization between the QB and the reservoir modes with frequency close to a new emergent frequency $\Omega =\sqrt{{\gamma }_{0}{\omega }_{{{\rm{D}}}}} \, \gg \, {\omega }_{0}$. We point out that, in this underdamped regime, almost all the energy accumulated in the QB can be extracted. In addition, for sufficiently short times the energy oscillates back and forth in an almost periodic and coherent way between the coupling energy and the QB, and the robustness of this effect over various periods of these energy oscillations can be exploited to mitigate the need for precise fine-tuning of the charging time. Furthermore, our results are robust up to the thermal energies comparable with ℏΩ. Due to the robustness of our protocol and the possibility to experimentally implement it by means of a quantum LC circuit, playing the role of the QB, embedded in a dissipative environment, with suitably engineered cut-off frequency and dissipation strength^42,43,44, we strongly believe that the present study can open fascinating perspectives towards the realization of fast and highly efficient energy manipulation in solid-state devices.

Results

Model of the quantum battery, charger and environment

The QB is a quantum harmonic oscillator, strongly coupled to a many–modes reservoir described as a large collection of quantum harmonic oscillators in the framework of the Caldeira-Leggett model^45,46,47,48. The Hamiltonian of the system consists of three terms

$${\hat{H}}^{(t)}={\hat{H}}_{{{\rm{B}}}}+{\hat{H}}_{{{\rm{R}}}}+\theta (t){\hat{H}}_{{{\rm{C}}}},$$

(1)

where θ(t) = 0 for times t ≤ 0 while θ(t) = 1 for t > 0. The QB is described by

$${\hat{H}}_{{{\rm{B}}}}=\frac{{\hat{p}}^{2}}{2m}+\frac{m{\omega }_{0}^{2}}{2}{\hat{x}}^{2},$$

(2)

with $\hat{x}$ and $\hat{p}$ position and momentum operators, and m and ω₀ respectively its mass and characteristic frequency. The reservoir Hamiltonian reads

$${\hat{H}}_{{{\rm{R}}}}=\mathop{\sum}\limits_{k}{\hat{H}}_{{{\rm{R}}}}^{(k)}=\mathop{\sum}\limits_{k}\left(\frac{{\hat{p}}_{k}^{2}}{2{m}_{k}}+\frac{{m}_{k}{\omega }_{k}^{2}}{2}{\hat{x}}_{k}^{2}\right),$$

(3)

where ${\hat{x}}_{k}$ and ${\hat{p}}_{k}$ are the position and momentum of the k–th mode, with mass m_k and characteristic frequencies ω_k. The QB and the reservoir are coupled through the term

$${\hat{H}}_{{{\rm{C}}}}=\mathop{\sum}\limits_{k}{\hat{H}}_{{{\rm{C}}}}^{(k)}=-\left(\mathop{\sum}\limits_{k}{c}_{k}{\hat{x}}_{k}\right)\hat{x}+\frac{1}{2}m{\Omega }^{2}{\hat{x}}^{2}$$

(4)

which, as will be shown, plays the role of a quantum charger. Eq. (4) is composed of two terms: a bilinear coupling between $\hat{x}$ and ${\hat{x}}_{k}$ – with c_k coupling constants which will be specified later on – and a counter–term $\propto {\hat{x}}^{2}$, where

$${\Omega }^{2}=\mathop{\sum}\limits_{k}\frac{{c}_{k}^{2}}{m{m}_{k}{\omega }_{k}^{2}}.$$

(5)

Since Ω vanishes for c_k → 0, the counter–term is itself a part of the coupling Hamiltonian even though it only depends on the QB coordinate. It is needed to prevent the renormalization of the static potential of the QB pinning its frequency to the bare value ω₀^45,46. Its presence depends on the specific considered model, in particular it naturally emerges e.g. in the description of solid-state platforms based on superconducting circuits⁴² as will be discussed in more details in the final Section of this paper, devoted to the experimental feasibility. Moreover, it plays a relevant role in the context of energy storage and extraction, as will be clear in the following.

The equations of motion for the QB and reservoir position operators in the Heisenberg picture read (from now on, ℏ = k_B = 1):

$$\hat{\ddot{x}}(t)+({\omega }_{0}^{2}+{\Omega }^{2})\hat{x}(t)=\mathop{\sum}\limits_{k}\frac{{c}_{k}}{m}{\hat{x}}_{k}(t),$$

(6)

$${\hat{\ddot{x}}}_{k}(t)+{\omega }_{k}^{2}{\hat{x}}_{k}(t)=\frac{{c}_{k}}{{m}_{k}}\hat{x}(t).$$

(7)

Eq. (7) can be formally solved considering $\hat{x}(t)$ a given external field, yielding

$${\hat{x}}_{k}(t)= \, {\hat{x}}_{k}(0)\cos \left({\omega }_{k}t\right)+\frac{{\hat{p}}_{k}(0)}{{m}_{k}{\omega }_{k}}\sin \left({\omega }_{k}t\right)\\ +\frac{{c}_{k}}{{m}_{k}{\omega }_{k}}\int_{0}^{t}d{t}^{{\prime} }\sin \left[{\omega }_{k}(t-{t}^{{\prime} })\right]\hat{x}({t}^{{\prime} }).$$

(8)

Replacing this solution into Eq. (6) one obtains the full operatorial quantum Langevin equation for the QB^46,49,50,51

$$\hat{\ddot{x}}(t)+{\omega }_{0}^{2}\hat{x}(t)+\int_{0}^{t}d{t}^{{\prime} }\gamma (t-{t}^{{\prime} })\hat{\dot{x}}({t}^{{\prime} })+\gamma (t)\hat{x}(0)=\frac{\hat{\xi }(t)}{m},$$

(9)

where the damping kernel

$$\gamma (t)=\frac{1}{m}\theta (t)\mathop{\sum}\limits_{k}\frac{{c}_{k}^{2}}{{m}_{k}{\omega }_{k}^{2}}\cos \left({\omega }_{k}t\right)$$

(10)

and the reservoir fluctuating noise operator

$$\hat{\xi }(t)=\mathop{\sum}\limits_{k}{c}_{k}\left[{\hat{x}}_{k}(0)\cos \left({\omega }_{k}t\right)+\frac{{\hat{p}}_{k}(0)}{{m}_{k}{\omega }_{k}}\sin \left({\omega }_{k}t\right)\right]$$

(11)

have been introduced. Notice that the momentum operator is directly $\hat{p}(t)=m\hat{\dot{x}}(t)$.

The solution of Eq. (9) can always be decomposed into a transient homogeneous (h) and a non-homogeneous or thermal part (th):

$$\hat{x}(t)={\hat{x}}_{{{\rm{h}}}}(t)+{\hat{x}}_{{{\rm{th}}}}(t).$$

(12)

The first term is independent of the fluctuating field $\hat{\xi }(t)$ and is expressed via the response function χ(t) in terms of the initial conditions at time t = 0 as

$${\hat{x}}_{{{\rm{h}}}}(t)=\hat{\dot{x}}(0)\chi (t)+\hat{x}(0)\dot{\chi }(t).$$

(13)

All the properties of χ(t), which satisfies initial conditions χ(0) = 0, $\dot{\chi }(0)=1$ and $\ddot{\chi }(0)=0$, are encoded into its Laplace transform (defined as $\hat{\tilde{x}}(\lambda )=\int_{0}^{+\infty }dt{e}^{-\lambda t}\hat{x}(t)$)

$$\tilde{\chi }(\lambda )=\frac{1}{{\lambda }^{2}+{\omega }_{0}^{2}+\lambda \tilde{\gamma }(\lambda )},$$

(14)

where $\tilde{\gamma }(\lambda )$ is the Laplace transform of Eq. (10).

The term ${\hat{x}}_{{{\rm{th}}}}(t)$ in Eq. (12) depends instead on the fluctuating field $\hat{\xi }(t)$ and is given by

$${\hat{x}}_{{{\rm{th}}}}(t)=\int_{0}^{t}\frac{d{t}^{{\prime} }}{m}\chi (t-{t}^{{\prime} })\hat{\xi }({t}^{{\prime} }).$$

(15)

The charging/discharging protocol: energy balance and figures of merit

The charging/discharging protocol is comprised of four steps:

• (I) At t = 0, switching on ${\hat{H}}_{{{\rm{C}}}}$ the QB and the reservoir are connected;

• (II) Energy flows for a short amount of time t;

• (III) Switching off ${\hat{H}}_{{{\rm{C}}}}$, the QB and the reservoir are disconnected;

• (IV) The maximum amount of energy is extracted from the QB, to be employed elsewhere. In steps (I) and (III) the switching on and off times are assumed as the shortest time scales involved in the problem.

A suitably engineered reservoir, especially within the protocol described above, will prove to be a valuable resource allowing fast and optimal charging of the QB. In the following we will introduce the energy exchanges involved in the protocol and suitable figures of merit to quantify its performances.

Energy accumulated into the QB and ergotropy

To begin with, let us introduce the energy accumulated into the QB over the charging time t as¹²

$$\Delta {E}_{{{\rm{B}}}}(t)=\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle -\left\langle {\hat{H}}_{{{\rm{B}}}}(0)\right\rangle$$

(16)

where $\left\langle ...\right\rangle \equiv {{\rm{Tr}}}\left[...\hat{\rho }(0)\right]$ with $\hat{\rho }(0)$ the total initial density matrix of the system, which will be specified in the following, and where $\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle$ is the energy stored in the QB at time t. Here and in what follows, all operators evolve in the Heisenberg picture.

Clearly, not all the accumulated energy can actually be extracted from it. The ergotropy is defined as the maximum energy that can be extracted from the QB acting only with unitary operations^7,39. For a general setup the evaluation of the ergotropy is only possible via numerical approaches. However, for Gaussian states a closed expression is present^35,38. To this effect we notice that the time evolution of the model under consideration maps Gaussian states at t = 0 into Gaussian states at any later time t. Therefore, anticipating our choice of a Gaussian initial condition, the ergotropy of the QB at time t is given by

$${{\mathcal{E}}}(t)=\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle -{\omega }_{0}\sqrt{\det {\sigma }_{{{\rm{B}}}}(t)},$$

(17)

where σ_B(t) is the covariance matrix⁵² at time t.

Work performed by the quantum charger

Switching on and off of the quantum charger over a time t requires a finite amount of work

$$W(t)={W}_{{{\!\!\rm{on}}}}+{W}_{{{\!\!\rm{off}}}}(t),$$

(18)

where

$${W}_{{{\rm{on}}}}=\left\langle {\hat{H}}_{{{\rm{C}}}}(0)\right\rangle \quad ;\quad {W}_{{{\rm{off}}}}(t)=-\left\langle {\hat{H}}_{{{\rm{C}}}}(t)\right\rangle ,$$

(19)

with $\left\langle {\hat{H}}_{{{\rm{C}}}}(t)\right\rangle$ the coupling term in Eq. (4). The above expressions depend on the assumption of very short switching on and off times of the coupling between the QB and the reservoir. In the case of a much smoother switching modelled by means of a more general function f(t) the quantities W_on and W_off would be given by the integral of $\dot{f}(t)$ times the expectation value of ${\hat{H}}_{{{\rm{C}}}}(t)$ in analogy with what discussed in Crescente et al.¹⁶. In general terms, in this case one could expect an increase of W(t) leading to a worsening of the battery performance whose precise entity crucially depends of the precise form of f(t). Using the Langevin equation (6), $\left\langle {\hat{H}}_{{{\rm{C}}}}(t)\right\rangle$ can be expressed in terms of the QB variables only as

$$\frac{\left\langle {\hat{H}}_{{{\rm{C}}}}(t)\right\rangle }{m}= \langle {\hat{\dot{x}}}^{2}(t) \rangle -\frac{1}{2}\frac{{d}^{2}}{d{t}^{2}} \left\langle {\hat{x}}^{2}(t)\right\rangle -\left({\omega }_{0}^{2}+\frac{{\Omega }^{2}}{2}\right)\left\langle {\hat{x}}^{2}(t)\right\rangle .$$

(20)

It is worth noting that this contribution explicitly depends on the counter-term in Eq. (4).

In full analogy with what defined in Eq. (16), the total work can be alternatively written as

$$W(t)=-\left[\left\langle {\hat{H}}_{{{\rm{C}}}}(t)\right\rangle -\left\langle {\hat{H}}_{{{\rm{C}}}}(0)\right\rangle \right]=-\Delta {E}_{{{\rm{C}}}}(t).$$

(21)

Energy balance and spectral decomposition

Since the total system is closed, after the switching on, we can easily write the total energy balance

$$\Delta {E}_{{{\rm{B}}}}(t)+\Delta {E}_{{{\rm{R}}}}(t)=W(t)$$

(22)

with a clear meaning: the total work W(t) is distributed among the accumulated energy of the battery ΔE_B(t) and the energy exchanged with the reservoir during the time t:

$$\Delta {E}_{{{\rm{R}}}}(t)=\left\langle {\hat{H}}_{{{\rm{R}}}}(t)\right\rangle -\left\langle {\hat{H}}_{{{\rm{R}}}}(0)\right\rangle .$$

(23)

Eq. (22) further underlines the role of ${\hat{H}}_{{{\rm{C}}}}$ as a quantum charger.

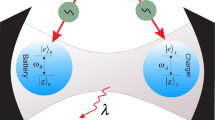
In this respect, an efficient charging protocol predominantly exchanges energy between the charger and the QB, see Fig. 1a, while an inefficient protocol wastes most of its energy in the reservoir with little power delivered to the QB, as shown Fig. 1b. Even though achieving an efficient charging seems almost hopeless in this context, given that the reservoir has a very large number of degrees of freedom which can collect energy with respect to the single one of the QB, we will show that this is indeed possible via a careful engineering of the reservoir spectral density at strong coupling.

Fig. 1: Scheme of operation of ${\hat{H}}_{{{\rm{C}}}}$ as a quantum charger.

Green boxes, reservoir with Hamiltonian ${\hat{H}}_{{{\rm{R}}}}$ defined in Eq. (3). Red boxes, charger with Hamiltonian ${\hat{H}}_{{{\rm{C}}}}$ defined in Eq. (4). Blue boxes, QB with Hamiltonian ${\hat{H}}_{{{\rm{B}}}}$ defined in Eq. (2). a shows an efficient charging protocol where the energy is predominantly exchanged between the charger and the QB and (b) shows an inefficient charging protocol where the energy is predominantly exchanged between the charger and the reservoir. In both panels, the solid thick lines connect the two parts of the system where the dominant energy exchange occurs, while the dashed lines connect the parts where this energy exchange is small.

For later convenience we also introduce the contributions to the charger and to the reservoir energy due to the k–th mode of the latter, defined as (ν = C, R)

$$\Delta {E}_{\nu }(t,{\omega }_{k})=\left\langle {\hat{H}}_{\nu }^{(k)}(t)\right\rangle -\left\langle {\hat{H}}_{\nu }^{(k)}(0)\right\rangle$$

(24)

which satisfy the sum rules

$$\Delta {E}_{\nu }(t)=\mathop{\sum}\limits_{k}\Delta {E}_{\nu }(t,{\omega }_{k}).$$

(25)

Performances of the charging/discharging protocol

In order to assess the performances of the charging procedure, two different efficiencies are usually considered. The first is

$${\eta }_{{{\rm{B}}}}(t)=\frac{{{\mathcal{E}}}(t)}{\left\langle {H}_{{{\rm{B}}}}(t)\right\rangle }=1-\frac{{\omega }_{0}\sqrt{\det {\sigma }_{{{\rm{B}}}}(t)}}{\left\langle {H}_{{{\rm{B}}}}(t)\right\rangle },$$

(26)

the ratio between the ergotropy and the energy stored in the QB. The second figure of merit, which is the most relevant when energy to connect and disconnect the charger is paid off (W(t) > 0, see below and Hovhannisyan et al.³⁰ for a discussion on this condition), is

$${\eta }_{{{\rm{W}}}}(t)=\frac{{{\mathcal{E}}}(t)}{W(t)}$$

(27)

representing the ratio between the maximum work that can be extracted from the QB and the work paid to switch on and off the charger. In accordance to what discussed above, η_W(t) can be expected to achieve its best values for very rapid switching of the coupling, while slower protocols may lead to a worse performance. Note also that the above definition is consistent with what usually done in the quantum battery literature, where the energy associated to engineering the bath is typically neglected³⁰. This is justified by the fact that the bath can be model, within the Caldeira-Legget picture employed here, as a collection of passive elements such as capacitances and inductances⁴² kept at a fixed temperature and thermalized before starting the charging protocol.

Engineered reservoir and operating regimes

The response function

To proceed further we need to specify the couplings c_k in the charging Hamiltonian ${\hat{H}}_{{{\rm{C}}}}$. Among the possible choices, we consider the paradigmatic case of Ohmic coupling which is the most common dissipation, especially when the reservoir is represented by quantum circuits⁵³. We have^46,54,55,56

$${c}_{k}={\omega }_{k}\sqrt{\frac{2{\gamma }_{0}m{m}_{k}\Delta }{\pi }\frac{{\omega }_{{{\rm{D}}}}^{2}}{{\omega }_{{{\rm{D}}}}^{2}+{\omega }_{k}^{2}}}.$$

(28)

Here, γ₀ is the coupling strength, ω_D the Drude cut-off, and ω_k = kΔ (k positive integer) with Δ the constant level spacing of the modes of the reservoir. The behaviour of the couplings defines the spectral density

$$J(\omega )=\frac{\pi }{2}\mathop{\sum}\limits_{k}\frac{{c}_{k}^{2}}{{m}_{k}{\omega }_{k}}\delta (\omega -{\omega }_{k}),$$

(29)

and the damping kernel – see Eq.(10). Letting the number of modes to infinity, with Δ → 0, one eventually gets the continuum limit

$$J(\omega )=m{\gamma }_{0}\omega \frac{{\omega }_{{{\rm{D}}}}^{2}}{{\omega }^{2}+{\omega }_{{{\rm{D}}}}^{2}}$$

(30)

$$\gamma (t)={\gamma }_{0}{\omega }_{{{\rm{D}}}}{e}^{-{\omega }_{{{\rm{D}}}}t}\theta (t)\,;\,\tilde{\gamma }(\lambda )=\frac{{\gamma }_{0}{\omega }_{{{\rm{D}}}}}{\lambda +{\omega }_{{{\rm{D}}}}}.$$

(31)

We can also identify the frequency scale Ω in Eq. (5) as

$$\Omega =\sqrt{{\gamma }_{0}{\omega }_{{{\rm{D}}}}},$$

(32)

which, as we will see, will play a crucial role on the charging dynamics of the QB.

As clear from the shape of γ(t), the reservoir is highly non–Markovian when ω_D, the inverse of a memory time scale, is small ω_D ≈ ω₀, a regime of particular interest for this work. Such a regime has in the past drawn theoretical attention^30,57,58,59, and has recently been shown to be a resource in quantum thermodynamics⁶⁰. It is also important to stress that such a strong non–Markovian environment can nowadays be experimentally engineered in the context of quantum circuits^{44,61,62,63,64,65}.

We can now explicitly write the Laplace transform of the response function in Eq. (14)⁴⁶

$$\tilde{\chi }(\lambda )=\frac{\lambda +{\omega }_{{{\rm{D}}}}}{\left({\lambda }^{2}+{\omega }_{0}^{2}\right)\left(\lambda +{\omega }_{{{\rm{D}}}}\right)+\lambda {\gamma }_{0}{\omega }_{{{\rm{D}}}}}$$

(33)

which, in the time domain, can be written as

$$\chi (t)=\mathop{\sum}\limits_{j=1}^{3}{\chi }_{j}{e}^{-{\lambda }_{j}t}.$$

(34)

Here, λ_j satisfies

$${\lambda }^{3}-{\lambda }^{2}{\omega }_{{{\rm{D}}}}+\lambda \left({\omega }_{0}^{2}+{\gamma }_{0}{\omega }_{{{\rm{D}}}}\right)-{\omega }_{{{\rm{D}}}}{\omega }_{0}^{2}=0,$$

(35)

and

$${\chi }_{j}=\left({\omega }_{{{\rm{D}}}}-{\lambda }_{j}\right){\prod}_{{j}^{{\prime} }\ne j}\frac{1}{{\lambda }_{{j}^{{\prime} }}-{\lambda }_{j}}.$$

(36)

Operating regimes

As clear from Eq. (34), the nature of the roots λ_j – governed by the system parameters – determines the characteristics of χ(t). From now on, we will elect ω₀ as a typical energy scale and thus consider γ₀ and ω_D as free parameters. As shown in Fig. 2, due to the third-degree polynomial with real coefficients, only two regimes can occur:

• a underdamped (UD) regime (blue part), characterized by one purely real and two complex conjugate roots.

• a overdamped (OD) regime (red part), where three real solutions occur.

Fig. 2: Operating regimes.

As inferred by the nature of the zeroes of Eq. (35), as a function of γ₀ and ω_D (units ω₀), the red area denotes the overdamped (OD) regime, while the blue one corresponds to the underdamped (UD) one and, in particular, the strongly underdamped (SUD) in the right part. The bottom corner of the OD regime, marked as a yellow dot, has coordinates ${\gamma }_{0}=\frac{8}{3\sqrt{3}}{\omega }_{0}$ and ${\omega }_{{{\rm{D}}}}=3\sqrt{3}{\omega }_{0}$. The dash--dotted and dashed lines denote the boundaries between UD and OD for ω_D ≫ ω₀.

To enter more into the details let us begin discussing the underdamped regime, by identifying the two representative regions. The first is the weakly underdamped one, with γ₀ ≪ ω₀, ω_D, to the left of the OD part. Here, to leading order in ω_D, χ(t) exhibits oscillations at the bare frequency ω₀, damped by the coupling with the reservoir^46,56

$$\chi (t)\approx \frac{1}{{\omega }_{0}}{e}^{-\frac{{\gamma }_{0}}{2}t}\sin \left({\omega }_{0}t\right).$$

(37)

This regime has already been discussed at large in the literature also about QBs, typically employing a Lindblad master equation approach^34,35,38,66. Due to the small coupling, the charging performances are here very poor. Therefore we are not going to investigate it in the rest of the paper.

The second region is to the right of OD at large coupling γ₀ ≫ ω_D, ω₀: it corresponds to a strongly underdamped (SUD) case. This region, has seldomly been discussed⁶⁷, however it presents a peculiar behaviour which, as we will see, will play a fundamental role in the QB dynamics. Here we have (see first part of the Methods for details)

$$\chi (t)\approx \frac{1}{\Omega }{e}^{-\frac{{\omega }_{{{\rm{D}}}}}{2}t}\sin \left(\Omega t\right).$$

(38)

As is clear, in this regime $\Omega =\sqrt{{\gamma }_{0}{\omega }_{{{\rm{D}}}}}$ takes the role of the new natural frequency of the QB. Notice that since the strong coupling γ₀ ≫ ω_D, ω₀ implies Ω ≫ ω_D, ω₀, this frequency is strongly renormalized with respect to the bare one. In addition, its value is outside the bandwidth of the reservoir (Ω ≫ ω_D). As we will see, this point is crucial to achieve the best charging protocol, discussed in Fig. 1 since the reservoir is dynamically blockaded around the frequency Ω of the QB preventing the energy absorption. For this reason in the rest of the paper, we will mainly focus on this regime showing that it indeed produces the best short–time charging performances.

We close commenting on the overdamped regime (red region), where χ(t) displays no oscillations. As a typical example we remind the leading order behaviour in ω_D, with γ₀ > 2ω₀ (dashed-dotted line in the figure)^46,56

$$\chi (t)\approx \frac{{e}^{-\frac{{\gamma }_{0}}{2}t}}{\sqrt{{({\gamma }_{0}/2)}^{2}-{\omega }_{0}^{2}}}\sinh \left[t\sqrt{{({\gamma }_{0}/2)}^{2}-{\omega }_{0}^{2}}\right].$$

(39)

Here, the dynamics of the QB is damped and, as shown in Supplementary Note 1, it is not very useful for our purposes since the reservoir absorbs the main part of the incoming energy with an inefficient charging protocol similar to Fig. 1b.

Main achievements

Relevant quantities

To study in details the charging dynamics we start by specifying the initial conditions. We assume that, prior to the charge phase, the QB and the reservoir are disconnected. In addition, we consider an initial Gaussian state with the QB in its ground state $\left\vert g\right\rangle$ (i.e. a completely depleted battery) and the reservoir in its thermal equilibrium at temperature T. This corresponds to a factorized initial density matrix $\hat{\rho }(0)={\hat{\rho }}_{{{\rm{B}}}}(0)\otimes {\hat{\rho }}_{{{\rm{R}}}}(0)$ with (β = 1/T):

$${\hat{\rho }}_{{{\rm{B}}}}(0)=\left| g\right\rangle \left\langle g\right| \,;\,{\hat{\rho }}_{{{\rm{R}}}}(0)=\frac{{e}^{-\beta {\hat{H}}_{{{\rm{R}}}}(0)}}{{{\rm{Tr}}}\left\{{e}^{-\beta {\hat{H}}_{{{\rm{R}}}}(0)}\right\}}.$$

(40)

With this choice, the averages of position and momentum of both the QB and the reservoir variables are zero at t = 0, while the second moments are $\langle {\hat{x}}^{2}(0) \rangle =\frac{1}{2m{\omega }_{0}}$, $\langle {\hat{p}}^{2}(0)\rangle =\frac{m{\omega }_{0}}{2}$, $\left\langle \{\hat{x}(0),\hat{p}(0)\}\right\rangle =0$, for the QB and $\langle {x}_{k}(0){x}_{{k}^{{\prime} }}(0)\rangle =\frac{1}{2m{\omega }_{k}}\coth (\beta {\omega }_{k}/2){\delta }_{k,{k}^{{\prime} }}$, $\langle {p}_{k}(0){p}_{{k}^{{\prime} }}(0) \rangle =\frac{1}{2}m{\omega }_{k} \coth (\beta {\omega }_{k}/2 ){\delta }_{k,{k}^{{\prime} }}$, and $\left\langle \{{x}_{k}(0),{p}_{{k}^{{\prime} }}(0)\}\right\rangle =0$ for the reservoir. Due to these conditions the fluctuating noise ξ(t) in Eq.(11) has zero average $\langle \hat{\xi }(t)\rangle =0$ and time–translational invariant autocorrelation function⁴⁶

$$\left\langle \hat{\xi }(t)\hat{\xi }(0)\right\rangle =\int_{0}^{\infty }\frac{d\omega }{\pi }J(\omega )\mathop{\sum}\limits_{n=\pm 1}\frac{{e}^{in\omega t}}{2}\left[\coth \left(\frac{\beta \omega }{2}\right)-n\right].$$

(41)

Since the initial density is Gaussian, all previous considerations about the ergotropy hold true. All relevant quantities can be then evaluated from the covariance matrix σ_B(t), given here by

$${\sigma }_{{{\rm{B}}}}(t)=m\left(\begin{array}{cc}{\omega }_{0}\left\langle {\hat{x}}^{2}(t)\right\rangle &\frac{1}{2}\frac{d}{dt}\left\langle {\hat{x}}^{2}(t)\right\rangle \\ \frac{1}{2}\frac{d}{dt}\left\langle {\hat{x}}^{2}(t)\right\rangle &\frac{1}{{\omega }_{0}} \big\langle {\hat{\dot{x}}}^{2}(t)\big\rangle \end{array}\right).$$

(42)

Much like the decomposition of $\hat{x}(t)$ into a homogeneous and thermal part, given in Eq. (12), the same holds for the covariance matrix: σ_B(t) = σ_B,h(t) + σ_B,th(t) where the h (th) term only contains the homogeneous (thermal) contributions to $\left\langle {\hat{x}}^{2}(t)\right\rangle$ and $\langle {\hat{\dot{x}}}^{2}(t) \rangle$.

The homogeneous terms are easily written in terms of the response function

$$\left(\begin{array}{c}\left\langle {\hat{x}}_{{{\rm{h}}}}^{2}(t)\right\rangle \\ \left\langle {\hat{\dot{x}}}_{{{\rm{h}}}}^{2}(t)\right\rangle \end{array}\right)=\frac{{\omega }_{0}}{2m}\left(\begin{array}{c}{\chi }^{2}(t)\\ {\dot{\chi }}^{2}(t)\end{array}\right)+\frac{1}{2m{\omega }_{0}}\left(\begin{array}{c}{\dot{\chi }}^{2}(t)\\ {\ddot{\chi }}^{2}(t)\end{array}\right).$$

(43)

More cumbersome are the thermal contributions, which can be written in the compact form

$$\left(\begin{array}{c}\left\langle {\hat{x}}_{{{\rm{th}}}}^{2}(t)\right\rangle \\ \big\langle {\hat{\dot{x}}}_{{{\rm{th}}}}^{2}(t)\big\rangle \end{array}\right) = {\sum} _{j,{j}^{{\prime} }}\left(\begin{array}{c}1\\ {\lambda }_{j}{\lambda }_{{j}^{{\prime} }}\end{array}\right)\int_{-\infty }^{\infty }\frac{d\omega }{2\pi {m}^{2}}\left\{\frac{J(\omega )\coth \left(\frac{\beta \omega }{2}\right)}{({\lambda }_{j}-i\omega )({\lambda }_{{j}^{{\prime} }}+i\omega )}\right. \\ \left.\cdot {\chi }_{j}{\chi }_{{j}^{{\prime} }}\left[1-{e}^{-({\lambda }_{j}-i\omega )t}-{e}^{-({\lambda }_{{j}^{{\prime} }}+i\omega )t}+{e}^{-({\lambda }_{j}+{\lambda }_{{j}^{{\prime} }})t}\right]\right\}.$$

(44)

Details are presented in the second part of the Methods and in Supplementary Note 2.

Concerning the efficiencies in Eqs. (26) and (27) we can deduce their constraints. For η_B it follows directly that η_B(t) ≤ 1. Moreover, in the considered case, one also has η_W(t) ≤ 1 as can be seen reasoning as follows. Starting from Eqs. (17) and (22) one can write

$$W(t)-{{\mathcal{E}}}(t)= \left[{\omega }_{0}\sqrt{\det {\sigma }_{{{\rm{B}}}}(t)}+\left\langle {\hat{H}}_{{{\rm{R}}}}(t)\right\rangle \right]\\ -\left[\left\langle {\hat{H}}_{{{\rm{B}}}}(0)\right\rangle +\left\langle {\hat{H}}_{{{\rm{R}}}}(0)\right\rangle \right],$$

(45)

where the first line on the right-hand side represents the total energy of QB+reservoir after the disconnection and the ergotropy extraction, while the second one is the initial internal energy. Assuming, consistently with what done in Eq. (40), a passive initial state for the system and taking into account the fact that all the considered operations (time evolution of the system and ergotropy extraction) are unitary the internal energy can only increase or at most remain constant⁴¹. Since ${{\mathcal{E}}}(t)\ge 0$, one has $W(t)\ge {{\mathcal{E}}}(t)\ge 0$ finally proving the bound on η_W(t).

Finally, the (initial) work required to switch on the interaction (see Eq. (19)) is

$${W}_{{{\rm{on}}}}=\frac{{\gamma }_{0}{\omega }_{{{\rm{D}}}}}{4{\omega }_{0}}=\frac{{\Omega }^{2}}{4{\omega }_{0}}.$$

(46)

The underdamped strong coupling regime

We can now study the charging/discharging protocol, at short times in the underdamped strong coupling regime, which – as will be shown – provides the best performances. All results are obtained numerically. However, we will also provide analytical expressions to support our results. In addition, we will focus on custom tailored reservoirs with quite small ω_D ≳ ω₀, i.e. with a narrow band and thus strongly non–Markovian, as this choice is one of the keys to obtain the best short–time performances among all the operating regimes.

To begin our discussion, Fig. 3a shows the energy accumulated in the QB ΔE_B(t) (blue line), the energy delivered by the charger ΔE_C(t) = −W(t) (red line) and the energy dissipated into the reservoir ΔE_R(t) (green line) as a function of time, in the quantum regime T = 0.1ω₀ for parameters within the SUD regime.

Fig. 3: Energetics and efficiency in the strongly underdamped (SUD) regime.

a plot of ΔE_ν(t) (units ω₀) with ν = B (blue curve), ν = C (red curve) and ν = R (green curve) as a function of Ωt/π; (b) plot of η_μ(t) with μ = B (blue curve), and μ = W (red curve) as a function of Ωt/π. Parameters are ω_D = 2ω₀, γ₀ = 300ω₀ (corresponding to Ω ≈ 24.5ω₀) and T = 0.1ω₀.

As is clear ΔE_B(t) shows oscillations with a period π/Ω, damped over a time scale ${\omega }_{{{\rm{D}}}}^{-1}$, and is locally maximum at times ${t}_{n}\approx \frac{\pi }{2\Omega }+n\frac{\pi }{\Omega }$, with n ≥ 0 an integer. Notice that this energy is large: in particular, the maximum amount accumulated in the QB, occurring at the shortest time t = t₀ ≈ π/2Ω, is almost equal to W_on = Ω²/4ω₀. These are already hints of a fast and extremely effective charging protocol. Notice that the oscillations of ΔE_B(t) are strikingly synchronized in phase opposition with respect to ΔE_C(t), suggesting that at short times the charger and the QB almost perfectly exchange energy in lockstep. As a consequence, and as confirmed by the behaviour of ΔE_R(t), during the first oscillations only a small fraction of energy is dissipated in the reservoir, whose dynamics seems to show an effective blockade at short times. We will turn back to this interpretation shortly. Concerning the state of the QB, as discussed in the last part of the Methods, in correspondence of the first maxima we find it to be well described by a squeezed state strongly compressed along $\hat{x}$ and very elongated in the $\hat{p}$ direction. This observation could be in principle used as a starting point to elaborate efficient protocols for energy extraction, a task that is however beyond the aim of the present work.

The extreme effectiveness of the protocol is definitively confirmed by the behaviour of the efficiencies η_B(t) and η_W(t), shown in panel (b). Except around the minima of ΔE_B(t) we find η_B(t) ~ 1 which implies the best ergotropy ${{\mathcal{E}}}(t)$: almost equal to the energy stored in the QB. This in turns implies that almost all the energy accumulated in the QB can be effectively retrieved to produce useful work. Most importantly, however, η_W(t) – the ratio between the ergotropy and the switch on/off work – is excellent: around the first maximum it is very close to the best attainable performance exceeding 0.85 (recall that in our case η_W(t) ≤ 1), and it is still very good around the fourth maximum where it reaches values above 0.5.

These results are indeed striking, especially in comparison with other similar charging-discharging protocols³⁰ that achieve significantly smaller values of η_W(t). In this respect, one common critique of a fast charging/discharging protocol – such as the one shown here – is the difficulty to fine–tune parameters in order to achieve the best performances³⁰. However, in our scenario the almost perfect periodicity of all the quantities constitutes a key advantage: one is not forced to disconnect the QB from the charger at one peculiar time. Instead, the sequence of optimal times t_n is highly predictable with charging energies and, as we have seen and as will be shown later on, performances remain remarkable (and thus, stable) over several oscillation periods.

To close this part, we turn back to interpret this optimal charging protocol in terms of a dynamical blockade of the reservoir. We remind that the reservoir is heavily structured with a small band–width (ω_D ≪ Ω): this means that only the modes with ω_k ≲ ω_D ≪ Ω have a significant weight in the spectral density J(ω) – see Eqs. (29) and (28). However, these modes are completely off resonance with the QB and then we expect that they can hardly absorb energy, thus allowing a back-and-forth energy transfer between QB and charger.

To demonstrate this scenario we inspect the spectral contributions of the reservoir ΔE_R(t, ω_k) defined in Eq. (24)– see Supplementary Note 3 for details. Figure 4a shows a density plot of ΔE_R(t, ω_k), the dashed line represents the time window of Fig. 3. During the initial times the reservoir absorbs very little energy at all, due to the small value of the cut–off ω_D ≪ Ω. This allows the important process of energy exchange between the QB and the charger with anti-phase synchronization. This oscillating dynamics is clearly visible in the spectral contribution ΔE_C(t, ω_k) of the charger – shown in panel (b) – that oscillates between positive and negative values around ω_k = Ω. In particular the positive values signal that energy back–flows from the QB to the charger, since the energy in the reservoir slowly increases monotonically. On the other hand, away from the resonance ΔE_C(t, ω_k) < 0.

Fig. 4: Spectral decomposition of the reservoir and coupling energies in the strongly underdamped (SUD) regime.

Density plots of (a) ΔE_R(t, ω_k) and (b) ΔE_C(t, ω_k), both in units Δ, as a function of Ωt/π and ω_k (units Ω). The dashed line represents the time window considered in Fig. 3. Here ω_D = 2ω₀, γ₀ = 300ω₀ (Ω ≈ 24.5ω₀) and T = 0.1ω₀.

As time goes by, however, a sizeable amount of energy eventually accumulates into the reservoir: indeed the the latter starts to respond revealing a clear resonance precisely around the modes with ω_k ≈ Ω. As already pointed out, modes at such frequencies have a very small weight in J(ω) but still succeed to open a narrow “energy pathway" into the reservoir – albeit a slow one. In this time window, the reservoir absorbs energy mainly at these frequencies, with all the other modes, including those at ω_k ≲ ω_D, contributing sensibly less. Ultimately, the fact that energy flows considerably into the reservoir only for times $t \, > \, \frac{\pi }{\Omega }$, and essentially only via this narrow channel, strongly slows down damping which in turns boosts the charging performances, promoting the back–and–forth exchange of energy between the charger and the QB at short times.

We will now study the stability of the above results with respect to variations of Ω and T, showing that very good performances are achieved even if we choose less extreme parameters.

We begin by varying Ω, which we achieve by tuning γ₀ at fixed ω_D. Figure 5 shows the results for ω_D = 2ω₀ and low-temperature T = 0.1ω₀. As can be seen, the qualitative behaviour is essentially unchanged within this wide range of Ω, and the best charging performances always occur at the shortest times. As shown in panels (a) and (c), the energy accumulated in the QB and η_B(t) increase for increasing Ω. This implies that at strong(er) coupling more useful energy (η_B → 1) is stored in the QB. The almost out-of-phase behaviour of ΔE_B(t) and ΔE_C(t) is also confirmed – see Panel (b). Also, the efficiency η_W(t), shown in Panel (d), increases around the maxima for increasing coupling. It is even more important to observe, though, that even for the smallest value Ω ~ 7ω₀ considered here, very good performances around the first maximum are achieved with a very good maximum for η_W(t) of about 0.6.

Fig. 5: Effects of Ω.

Plot of (a) ΔE_B(t) (units ω₀), (b) ΔE_C(t) (units ω₀), (c) η_B(t), and (d) η_W(t) as a function of Ωt/π for ω_D = 2ω₀ and different values of γ₀: from black to colour γ₀ = 25ω₀ (Ω ≈ 7.1ω₀), 50ω₀ (Ω = 10ω₀), 100ω₀ (Ω ≈ 14.1ω₀), 300ω₀ (Ω ≈ 24.5ω₀), 600ω₀ (Ω ≈ 34.6ω₀) and 900ω₀ (Ω ≈ 42.4ω₀). The dashed arrow marks the increasing direction of Ω. In all panels T = 0.1ω₀.

Concerning the effects of temperature, we show in Fig. 6 the results for the same parameters of Fig. 3 (SUD regime), for temperatures ranging from very low to high ones. As can be seen, the behaviour of all the quantities of interest is essentially independent of the temperature and only when T > Ω deviations are found. In particular, notice that even though at the largest temperatures considered here η_B(t) slightly decreases, its value around the maxima still is ≳ 0.8, which means that a high ergotropy can be retrieved from the QB even in this regime. Also, when T > Ω the oscillations of η_W(t) tend to become slightly less pronounced as T increases, although we stress that the first maximum exhibits an exceptional resilience.

Fig. 6: Effects of T.

Plots of (a) ΔE_B(t) (units ω₀), (b) ΔE_C(t) (units ω₀), (c) η_B(t), and (d) η_W(t) as a function of Ωt/π for different values of T: from black to colour T = 0.1ω₀ (T ≈ 4 ⋅ 10⁻³Ω), ω₀ (T ≈ 4 ⋅ 10⁻²Ω), 10ω₀ (T ≈ 4 ⋅ 10⁻¹Ω), 10²ω₀ (T ≈ 4Ω), and 10³ω₀ (T ≈ 40Ω). The dashed arrow marks the increasing direction of T. In all panels ω_D = 2ω₀ and γ₀ = 300ω₀.

These results show strong stability with respect to Ω and T. This leads to the important conclusion that our fast charge protocol is within reach of state-of-the-art experimental platforms, without requiring exceedingly fast control or exceedingly low temperatures, see discussion about experimental feasibility below.

In the SUD regime, when Ω ≫ ω_D, ω₀ and in the short times limit t ≲ nπ/Ω (with n > 1 an integer of order unity), analytic expressions for $\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle$, the ergotropy and for the total work W(t) can be obtained, that support our findings. Deferring all derivations to Supplementary Note 2, here we just quote the main results valid near the local maxima of ΔE_B(t).

At low temperature, all quantities are dominated by homogeneous terms and one finds, to leading order in Ω, that

$$\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle \approx {\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle }_{{{\rm{h}}}}\,;\,{{\mathcal{E}}}(t)\approx {\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle }_{{{\rm{h}}}}\,;\,W(t)\approx {W}_{{{\rm{h}}}}(t),$$

with

$${\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle }_{{{\rm{h}}}}=\frac{{\Omega }^{2}}{4{\omega }_{0}}{e}^{-{\omega }_{{{\rm{D}}}}t}{\sin }^{2}(\Omega t).$$

(47)

Notice that in this regime the ergotropy is optimal, since it essentially matches the energy stored in the QB. One also has

$${W}_{{{\rm{h}}}}(t)=\frac{{\Omega }^{2}}{4{\omega }_{0}}\left[1-{e}^{-{\omega }_{{{\rm{D}}}}t}{\cos }^{2}(\Omega t)\right],$$

(48)

which allows to obtain a closed expression for the efficiency

$${\eta }_{{{\rm{W}}}}(t)=\frac{{e}^{-{\omega }_{{{\rm{D}}}}t}{\sin }^{2}(\Omega t)}{1-{e}^{-{\omega }_{{{\rm{D}}}}t}{\cos }^{2}(\Omega t)}.$$

(49)

These equations provide results in excellent agreement with the numerical ones (see Supplementary Note 2).

Conversely at high temperature (T ≫ ω_D) the energy of the QB, the ergotropy and the work acquire thermal contributions in addition to the homogeneous ones in Eqs. (47) and (48). We find $\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle ={\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle }_{{{\rm{h}}}}+{\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle }_{{{\rm{th}}}}$, with

$${\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle }_{{{\rm{th}}}}=\frac{T}{2}\left[{e}^{-{\omega }_{{{\rm{D}}}}t}{\sin }^{2}(\Omega t)+(1-{e}^{-{\omega }_{{{\rm{D}}}}t})\right],$$

(50)

Concerning the total work W(t) = W_h(t) + W_th(t) we have

$${W}_{{{\rm{th}}}}(t)=\frac{T}{2}\left[{e}^{-{\omega }_{{{\rm{D}}}}t}{\sin }^{2}(\Omega t)+\frac{{\Omega }^{2}}{{\omega }_{0}^{2}}\left(1-{e}^{-\frac{2{\omega }_{0}^{2}{\omega }_{{{\rm{D}}}}t}{{\Omega }^{2}}}\right)\right].$$

(51)

Comparing the additional thermal parts with respect to the homogeneous ones we see how the former become effectively dominant only for T > Ω. The situation is slightly more complicated for the ergotropy ${{\mathcal{E}}}(t)$, since at high temperatures its expression deviates from that of ${\left\langle {\hat{H}}_{{{\rm{B}}}}(t)\right\rangle }_{{{\rm{h}}}}$ – see Fig. 6c – signalling that the contribution of the covariance matrix becomes non negligible – see Eq. (17). One can still obtain an analytical expression for this quantity by evaluating the corrections due to the latter term starting from the approximated form of the variances reported in Eqs. (S1) and (S16) of the Supplementary Note 2. The final form is however too cumbersome to be reported.

All the above expressions are in excellent agreement with our numerical results (see Supplementary Note 2).

To close this Section, it is interesting to answer the question: what would happen, in the SUD regime, if one would defer the disconnection of the charger to very long times t → + ∞? Notice that in this regime the reduced density matrix of the QB is given by the trace over the reservoir⁴⁶ ${\hat{\rho }}_{{{\rm{B}}}}(+\infty )={{{\rm{Tr}}}}_{{{\rm{R}}}} \{\frac{{e}^{-\beta \hat{H}}}{Z} \}$, where $\hat{H}={\hat{H}}_{{{\rm{B}}}}+{\hat{H}}_{{{\rm{R}}}}+{\hat{H}}_{{{\rm{C}}}}$ the total Hamiltonian (see Eq. (1)) and with $Z={{\rm{Tr}}} \{{e}^{-\beta \hat{H}} \}$. Leaving all analytical details to Supplementary Note 2, here we quote the main results for both low and the high temperatures.

At low temperatures one finds $\left\langle {\hat{H}}_{{{\rm{B}}}}(+\infty )\right\rangle \approx {{\mathcal{E}}}\approx \frac{\Omega }{4}$ and $W(+\infty )\approx \frac{{\Omega }^{2}}{4{\omega }_{0}}$. Charging is still possible, and the ergotropy remains comparable with the energy stored in the QB. Observe however that in this case, the latter quantity is ∝ Ω, while in the quick charge protocol outlined above the QB energy and ergotropy are of the order of Ω², see Eq. (47). Thus, in this case much less energy can be effectively stored and retrieved. Even more importantly, in this regime charging requires a very large work so that one has η_W(+ ∞) ≈ ω₀/Ω ≪ 1 and thus a much poorer efficiency with respect to the short–time performances.

In the high temperature regime (T ≫ Ω), dominated by energy equipartition, the situation is even worse. Indeed one finds $\left\langle {\hat{H}}_{{{\rm{B}}}}(+\infty )\right\rangle \approx T$ but, crucially, ${{\mathcal{E}}}\propto {T}^{-1}$ – implying η_W( + ∞) → 0. This means that no useful work can be extracted from the QB: the charging is useless.

Even more, also for other parameters the long–time performances never come even close to those obtained at short times in the SUD regime.

Considerations about experimental feasibility

We conclude this part by commenting on the fact that the ideal platform to test the functioning of the discussed device is represented by a quantum LC circuit, playing the role of the QB, embedded in a dissipative environment.

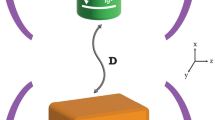
The essence of the Caldeira-Leggett model is to replace a linear dissipative element characterized by a frequency-dependent admittance Y(ω) by an infinite set of LC oscillators⁴², all wired in parallel, with a properly designed distribution of parameters {L_k, C_k} (see the scheme in Fig. 7). The particular choice of L_k and C_k allows to fine-tune the shape of the admittance Y(ω). This infinite set of oscillators leads the admittance to acquire both an imaginary and a real contribution, ultimately responsible for dissipation. The validity of this approach in the framework of quantum thermodynamic studies based on quantum circuits has been recently discussed in refs. ^64,65, where indeed the authors have mimicked the behaviour of a heat bath in terms of a huge number of LC oscillators, eventually terminated with a resistive element and with properly distributed parameters, coupled with the quantum system under investigation (a qubit in their case).

Fig. 7: Schematic representation of a possible implementation of the discussed device.

The quantum LC circuit, playing the role of the QB, is coupled to a dissipative environment (black box). Within the Caldeira-Leggett model the latter, characterized by an admittance Y(ω), is described in terms of an infinite set of LC oscillators in parallel, with properly distributed parameters L_k and C_k. Here, V and V_k denote the (generally time dependent) voltages associated to the corresponding nodes.

According to the circuit depicted in Fig. 7, the charge trapped into the capacitor C is given by Q(t) = CV(t) where V(t) is the voltage drop across the capacitor, while the current flowing into the inductor L is given by I(t) = L⁻¹ϕ(t), with

$$\phi (t)=\int_{0}^{t}V({t}^{{\prime} })d{t}^{{\prime} }.$$

(52)

According to this, the energy stored into the LC circuit realizing the QB (dashed box in Fig. 7) can be written as

$${U}_{{{\rm{LC}}}}(t)=\frac{C}{2}{V}^{2}(t)+\frac{L}{2}{I}^{2}(t)=\frac{{Q}^{2}(t)}{2C}+\frac{{\phi }^{2}(t)}{2L}.$$

(53)

In order to quantize the following circuit one can identify the two conjugate variables⁴³

$$Q\leftrightarrow \hat{p},\qquad \phi \leftrightarrow \hat{x}$$

(54)

where, from here on, for notational simplicity, we omit the time arguments in all operators and consequently

$$C\leftrightarrow m,\qquad L\leftrightarrow \frac{1}{m{\omega }_{0}^{2}},$$

(55)

with ${\omega }_{0}=1/\sqrt{LC}$. This leads to the QB Hamiltonian reported in Eq. (2).

Considering the dissipative part of the circuit, the charge stored in each capacitor is Q_k(t) = C_kV_k(t), while the current going through the inductors is ${I}_{k}(t)={L}_{k}^{-1}[\phi (t)-{\phi }_{k}(t)]$, with

$${\phi }_{k}(t)=\int_{0}^{t}{V}_{k}({t}^{{\prime} })d{t}^{{\prime} }.$$

(56)

Proceeding in full analogy with what was done above, one has that the total energy stored in this part of the circuit can be written as^42,53

$${U}_{{{\rm{diss}}}}(t)=\mathop{\sum}\limits_{k}\left\{\frac{{Q}_{k}^{2}(t)}{2{C}_{k}}+\frac{{\left[{\phi }_{k}(t)-\phi (t)\right]}^{2}}{2{L}_{k}}\right\}.$$

(57)

As can be seen, now ϕ(t) plays the role of a overall offset for the inductive part.

Through the identifications

$${Q}_{k}\leftrightarrow \frac{{c}_{k}}{{m}_{k}{\omega }_{k}^{2}}{\hat{p}}_{k},\qquad {\phi }_{k}\leftrightarrow \frac{{m}_{k}{\omega }_{k}^{2}}{{c}_{k}}{\hat{x}}_{k},$$

(58)

and

$${C}_{k}\leftrightarrow \frac{{c}_{k}^{2}}{{m}_{k}{\omega }_{k}^{4}},\qquad {L}_{k}\leftrightarrow \frac{{m}_{k}{\omega }_{k}^{2}}{{c}_{k}^{2}},$$

(59)

satisfying ${\omega }_{k}=1/\sqrt{{L}_{k}{C}_{k}}$, one finally obtains⁶⁸

$$ \frac{1}{2}\mathop{\sum}\limits_{k}\left[\frac{{\hat{p}}_{k}^{2}}{{m}_{k}}+\frac{{c}_{k}^{2}}{{m}_{k}{\omega }_{k}^{2}}{\left(\frac{{m}_{k}{\omega }_{k}^{2}}{{c}_{k}}{\hat{x}}_{k}-\hat{x}\right)}^{2}\right]\\ = \mathop{\sum}\limits_{k}\left(\frac{{\hat{p}}_{k}^{2}}{2{m}_{k}}+\frac{{m}_{k}{\omega }_{k}^{2}}{2}{\hat{x}}_{k}^{2}-{c}_{k}{\hat{x}}_{k}\hat{x}+\frac{1}{2}\frac{{c}_{k}^{2}}{{m}_{k}{\omega }_{k}^{2}}{\hat{x}}^{2}\right)\\ = {\hat{H}}_{{{\rm{R}}}}+{\hat{H}}_{{{\rm{C}}}},$$

(60)

as can be seen by comparison with Eqs. (3)–(5).

On the other hand, for such an environment it is known that, in the time domain, the admittance can be written as⁵³

$$Y(t)=\mathop{\sum}\limits_{k}\frac{1}{{L}_{k}}\cos \left({\omega }_{k}t\right).$$

(61)

According to the previous identifications of Eqs. (55) and (59) this allows, for the times t ≥ 0 relevant to our dynamics, to identify

$$\frac{Y(t)}{C}\leftrightarrow \gamma (t),$$

(62)

where the damping kernel γ(t) has been defined in Eq. (10). In the frequency domain, we also note that the real part of the admittance is related to the spectral density J(ω) given in Eq. (29) by

$${{\rm{Re}}}\left\{Y(\omega )\right\}=\frac{J(\omega )}{\omega }.$$

(63)

Owing to the already mentioned identifications, this allows to conclude that in our model

$${{\rm{Re}}}\left\{Y(\omega )\right\}=C{\gamma }_{0}\frac{{\omega }_{{{\rm{D}}}}^{2}}{{\omega }^{2}+{\omega }_{{{\rm{D}}}}^{2}}.$$

(64)

Let us now estimate typical parameters for the QB and for the environment.

Concerning the QB, one can assume for example values of L ≈ 50 μH for the inductance and C ≈ 5 pF for the capacity in such a way that the QB can be described as a quantum harmonic oscillator with characteristic frequency ω₀/2π ≈ 10  MHz (with ${\omega }_{0}=1/\sqrt{LC}$)^42,43. Note that these values are comparable to those used in real state-of-the-art experiments with superconducting LC circuits⁶⁹. Focusing on this frequency regime, which is typically smaller with respect to what usually considered in circuit QED experiments⁷⁰, has the practical advantage to allow a control of the device on a time scale in the nanosecond range which is compatible with the discussed features of the figures of merits (the first maximum of η_W occurring at t₀ ≈ 1 ns assuming for example γ₀ = 300ω₀ and ω_D = 2ω₀ as in Fig. 3). The possibility to observe the discussed phenomenology is also assured by its great stability with respect to thermal effect as long as k_BT ≲ ℏΩ (see Fig. 6). Within the discussed range of parameters this leads to the threshold temperature T ≈ 12 mK compatible with the cryogenic temperatures typically reached in quantum transport and quantum computing experiments carried out in solid-state devices.

As for the environment, Eq. (64) can be identified as the real part of the admittance of a series RL circuit with resistance R_E and impedence L_E given respectively by

$${R}_{{{\rm{E}}}}=\frac{1}{C{\gamma }_{0}}\quad ;\quad {L}_{{{\rm{E}}}}=\frac{{R}_{{{\rm{E}}}}}{{\omega }_{{{\rm{D}}}}}.$$

(65)

For ω ≪ ω_D the environment behaves ohmically, while for higher frequencies ω ≳ ω_D the inductive component induces a frequency roll–off.

From the estimates given above one can obtain typical values R_E ≈ 10 Ω and L_E ≈ 500nH. To conclude, we note that quantum couplers can be used to realize a fast control of the coupling between the QB and the charger^71,72,73.

Conclusions

In this paper, we have proposed a scheme for a quantum battery based on a quantum harmonic oscillator, strongly coupled to a non–Markovian reservoir via a quantum charger. The considered procedure relies on the transient dynamics which occurs right after the battery is connected to the quantum charger, thus ensuring a quick charging protocol. We have shown that the evolution of the energy stored in the battery is almost periodic, which allows to avoid a too precise fine-tuning of the time at which the battery need to be disconnected from the charge. Moreover, we have shown that this protocol is very efficient, allowing in principle to extract through unitary operations practically all the energy stored in the quantum battery, with a ratio between the energy that can be extracted and the work done by the charger which approaches the ideal unit limit. These features are due to two key ingredients, namely the non-Markovianity due to a reservoir with a spectral density with a cut-off of the order of the oscillator frequency, and a peculiar – and as yet almost unexplored – working regime in the underdamped regime at strong coupling. Crucially, these result in a dynamical blockade of the reservoir dynamics, which allows an almost coherent exchange of energy between the charger and the quantum battery at short enough times.

Such a protocol may be envisioned with a quantum LC circuit playing the role of the battery and with the required environment being suitably engineered via state–of–the–art quantum circuits, and thus may genuinely contribute to a significant advancement in the field of quantum energy storage in solid state devices.

This work will contribute to future advancements in the field of quantum energy routing and management, opening for instance the possibility to study the charging of, and energy transfer between, two or more quantum batteries strongly coupled to a highly non–Markovian reservoir acting as a energy bus or energy router.

Methods

The response function χ(t) in the strong underdamped regime

In this part we give some details on the behaviour of the response function χ(t).

The cubic equation in Eq. (35)

$${\lambda }^{3}-{\lambda }^{2}{\omega }_{{{\rm{D}}}}+\lambda \left({\omega }_{0}^{2}+{\gamma }_{0}{\omega }_{{{\rm{D}}}}\right)-{\omega }_{{{\rm{D}}}}{\omega }_{0}^{2}=0$$

(66)

yields the general Vieta’s relations

$${\lambda }_{1}+{\lambda }_{2}+{\lambda }_{3}={\omega }_{{{\rm{D}}}},$$

(67)

$${\lambda }_{1}{\lambda }_{2}+{\lambda }_{1}{\lambda }_{3}+{\lambda }_{2}{\lambda }_{3}={\omega }_{0}^{2}+{\gamma }_{0}{\omega }_{{{\rm{D}}}},$$

(68)

$${\lambda }_{1}{\lambda }_{2}{\lambda }_{3}={\omega }_{{{\rm{D}}}}{\omega }_{0}^{2}.$$

(69)

We remind that, for finite damping, all roots have positive real parts. In addition, in the underdamped regime two roots are complex and one is real, so they can be written as

$${\lambda }_{1,2}=\Gamma \pm i\nu ,\quad {\lambda }_{3}\in {\mathbb{R}},$$

(70)

where $\Gamma ,\nu \in {\mathbb{R}}$. Using Eqs. (67) and (69) we have

$$\Gamma =\frac{{\omega }_{{{\rm{D}}}}-{\lambda }_{3}}{2},\quad {\Gamma }^{2}+{\nu }^{2}=\frac{{\omega }_{{{\rm{D}}}}{\omega }_{0}^{2}}{{\lambda }_{3}}.$$

(71)

According to this, the χ_j defined in Eq. (36) are

$${\chi }_{1}=\frac{i}{2\nu }\left[\frac{2\nu +i\left({\lambda }_{3}+{\omega }_{{{\rm{D}}}}\right)}{2\nu +i\left(3{\lambda }_{3}-{\omega }_{{{\rm{D}}}}\right)}\right],\quad {\chi }_{2}={\chi }_{1}^{* }$$

(72)

$${\chi }_{3}=4\frac{{\omega }_{{{\rm{D}}}}-{\lambda }_{3}}{{\left({\omega }_{{{\rm{D}}}}-3{\lambda }_{3}\right)}^{2}+4{\nu }^{2}}.$$

(73)

We now derive analytic expressions at strong coupling with γ₀ ≫ ω_D, ω₀, that is $\Omega =\sqrt{{\gamma }_{0}{\omega }_{{{\rm{D}}}}}\,\, \gg \,\, {\omega }_{0},{\omega }_{{{\rm{D}}}}$. Here, to leading order in Ω, the real the solution of Eq. (66) is

$${\lambda }_{3}\approx \frac{{\omega }_{0}^{2}{\omega }_{{{\rm{D}}}}}{{\Omega }^{2}}.$$

(74)

Inserting this results in Eqs. (71) one has

$$\Gamma \approx \frac{{\omega }_{{{\rm{D}}}}}{2},\quad \nu \approx \Omega \,.$$

(75)

Concerning χ_j we find

$${\chi }_{1}\approx \frac{i}{2\Omega }\left[1+i\frac{{\omega }_{{{\rm{D}}}}}{\Omega }\right],\,\,{\chi }_{2}={\chi }_{1}^{* },\,\,{\chi }_{3}\approx \frac{{\omega }_{{{\rm{D}}}}}{{\Omega }^{2}}.$$

(76)

This leads to the following expression for the response function $\chi (t)={\sum }_{j}{\chi }_{j}{e}^{-{\lambda }_{j}t}$

$$\chi (t)\approx \frac{{e}^{-\frac{{\omega }_{{{\rm{D}}}}}{2}t}}{\Omega }\left[\sin \left(\Omega t\right)-\frac{{\omega }_{{{\rm{D}}}}}{\Omega }\cos \left(\Omega t\right)\right]+\frac{{\omega }_{{{\rm{D}}}}}{{\Omega }^{2}}{e}^{-\frac{{\omega }_{0}^{2}{\omega }_{{{\rm{D}}}}}{{\Omega }^{2}}t},$$

(77)

whose leading order expansion is

$$\chi (t)\approx \frac{{e}^{-\frac{{\omega }_{{{\rm{D}}}}}{2}t}}{\Omega }\sin \left(\Omega t\right)$$

(78)

as quoted in Eq. (38).

Explicit expression for QB variances

In this part we give details on how to get the general expressions of the variances $\left\langle {x}^{2}(t)\right\rangle$ and $\left\langle {\dot{x}}^{2}(t)\right\rangle$ quoted in the main text – see Eqs. (43) and (44).

We start by recalling that the solution of the Langevin equation (9) can be decomposed as $\hat{x}(t)={\hat{x}}_{{{\rm{h}}}}(t)+{\hat{x}}_{{{\rm{th}}}}(t)$: this will be the building block for evaluating the above quantities. The homogeneous part is given by

$${\hat{x}}_{{{\rm{h}}}}(t)=\hat{\dot{x}}(0)\chi (t)+\hat{x}(0)\dot{\chi }(t),$$

(79)

while the thermal one is

$${\hat{x}}_{{{\rm{th}}}}(t)=\int_{0}^{t}\frac{d{t}^{{\prime} }}{m}\chi (t-{t}^{{\prime} })\hat{\xi }({t}^{{\prime} }),$$

(80)

which, due to the initial condition χ(0) = 0 implies also

$${\hat{\dot{x}}}_{{{\rm{th}}}}(t)=\int_{0}^{t}\frac{d{t}^{{\prime} }}{m}\dot{\chi }(t-{t}^{{\prime} })\hat{\xi }({t}^{{\prime} }).$$

(81)

Here, the dot represents the derivative with respect to the first argument.

On a very general ground, given initial decoupled conditions and $\langle \hat{\xi }(t)\rangle = \langle \hat{x}(t) \rangle =0$, $\langle \hat{\dot{x}}(t)\rangle =0$, the homogeneous and thermal terms factorize as

$$ \langle {\hat{x}}^{2}(t) \rangle =\langle {\hat{x}}_{{{\rm{h}}}}^{2}(t) \rangle + \langle {\hat{x}}_{{{\rm{th}}}}^{2}(t) \rangle ,\\ \langle {\hat{\dot{x}}}^{2}(t) \rangle = \langle {\hat{\dot{x}}}_{{{\rm{h}}}}^{2}(t) \rangle + \langle {\hat{\dot{x}}}_{{{\rm{th}}}}^{2}(t) \rangle .$$

(82)

These matrix elements completely define the contributions to the covariance matrix σ_B(t) = σ_B,h(t) + σ_B,th(t) given by

$${\sigma }_{{{\rm{B,h/th}}}}(t)=m\left(\begin{array}{cc}{\omega }_{0} \langle {\hat{x}}_{{{\rm{h/th}}}}^{2}(t) \rangle &\frac{1}{2}\frac{d}{dt} \langle {\hat{x}}_{{{\rm{h/th}}}}^{2}(t) \rangle \\ \frac{1}{2}\frac{d}{dt} \langle {\hat{x}}_{{{\rm{h/th}}}}^{2}(t) \rangle &\frac{1}{{\omega }_{0}} \langle {\hat{\dot{x}}}_{{{\rm{h/th}}}}^{2}(t) \rangle \end{array}\right).$$

(83)

We now observe that the homogeneous part is independent of the temperature and can be easily written in term of the response function χ(t). Taking into account the initial conditions and using Eq. (79) one straightforwardly arrives to the expressions

$$\left(\begin{array}{c}\left\langle {\hat{x}}_{{{\rm{h}}}}^{2}(t)\right\rangle \\ \langle {\hat{\dot{x}}}_{{{\rm{h}}}}^{2}(t) \rangle \end{array}\right)=\frac{{\omega }_{0}}{2m}\left(\begin{array}{c}{\chi }^{2}(t)\\ {\dot{\chi }}^{2}(t)\end{array}\right)+\frac{1}{2m{\omega }_{0}}\left(\begin{array}{c}{\dot{\chi }}^{2}(t)\\ {\ddot{\chi }}^{2}(t)\end{array}\right).$$

(84)

As expected, σ_B,h(t → ∞) = 0.

Concerning the thermal contributions we need a more careful manipulation of Eqs. (80) and (81). In the following we describe how to explicitly write $\left\langle {\hat{x}}_{{{\rm{th}}}}^{2}(t)\right\rangle$.

Using Eq. (80) we have

$$\left\langle {\hat{x}}_{{{\rm{th}}}}^{2}(t)\right\rangle =\frac{1}{{m}^{2}}\int_{0}^{t}d{t}_{1}\int_{0}^{t}d{t}_{2}\chi (t-{t}_{1})\chi (t-{t}_{2})\left\langle \hat{\xi }({t}_{1})\hat{\xi }({t}_{2})\right\rangle$$

(85)

Since the integrand is symmetric under exchange of t₂ with t₁, only the symmetric part of the correlation function $\langle \hat{\xi }({t}_{1})\hat{\xi }({t}_{2}) \rangle$ contributes. We call it^74,75

$${{{\mathcal{L}}}}_{s}({t}_{1}-{t}_{2})=\int_{0}^{\infty }\frac{d\omega }{\pi }J(\omega )\coth \left(\frac{\beta \omega }{2}\right)\cos \left[\omega ({t}_{1}-{t}_{2})\right],$$

(86)

see Eq. (41), with Fourier transform

$${{{\mathcal{L}}}}_{s}(\omega )=J(\omega )\coth \left(\frac{\beta \omega }{2}\right).$$

(87)

Inserting now the general expression of χ(t), given in Eq. (34), and integrating over time one finally obtains

$$\begin{array}{rcl}&&\left\langle {\hat{x}}_{{{\rm{th}}}}^{2}(t)\right\rangle =\mathop{\sum }\limits_{j,{j}^{{\prime} }=1}^{3}{\chi }_{j}{\chi }_{{j}^{{\prime} }}\int_{-\infty }^{+\infty }\frac{d\omega }{2\pi {m}^{2}}\frac{{{{\mathcal{L}}}}_{s}(\omega )}{({\lambda }_{j}-i\omega )({\lambda }_{{j}^{{\prime} }}+i\omega )}\\ &&\left[1-{e}^{-\left({\lambda }_{j}-i\omega \right)t}-{e}^{-\left({\lambda }_{{j}^{{\prime} }}+i\omega \right)t}+{e}^{-\left({\lambda }_{j}+{\lambda }_{{j}^{{\prime} }}\right)t}\right].\end{array}$$

(88)

The last term to be evaluated is $\langle {\hat{\dot{x}}}_{{{\rm{th}}}}^{2}(t)\rangle$. This follows straightforwardly by inserting the expression in Eq. (81) which gives

$$\left\langle {\hat{\dot{x}}}_{{{\rm{th}}}}^{2}(t)\right\rangle =\frac{1}{{m}^{2}}\int_{0}^{t}d{t}_{1}\int_{0}^{t}d{t}_{2}\dot{\chi }(t-{t}_{1})\dot{\chi }(t-{t}_{2})\left\langle \hat{\xi }({t}_{1})\hat{\xi }({t}_{2})\right\rangle .$$

(89)

Following similar steps as done for $\left\langle {\hat{x}}_{{{\rm{th}}}}^{2}(t)\right\rangle$ a form similar to Eq. (88) is found, except for the substitutions ${\chi }_{j}\cdot {\chi }_{{j}^{{\prime} }}\to {\lambda }_{j}{\chi }_{j}\cdot {\lambda }_{{j}^{{\prime} }}{\chi }_{{j}^{{\prime} }}$ – see also Eq. (44)

$$\begin{array}{rcl}&&\left\langle {\hat{\dot{x}}}_{{{\rm{th}}}}^{2}(t)\right\rangle =\mathop{\sum }\limits_{j,{j}^{{\prime} }=1}^{3}{\lambda }_{j}{\chi }_{j}{\lambda }_{{j}^{{\prime} }}{\chi }_{{j}^{{\prime} }}\int_{-\infty }^{+\infty }\frac{d\omega }{2\pi {m}^{2}}\frac{{{{\mathcal{L}}}}_{s}(\omega )}{({\lambda }_{j}-i\omega )({\lambda }_{{j}^{{\prime} }}+i\omega )}\\ &&\left[1-{e}^{-\left({\lambda }_{j}-i\omega \right)t}-{e}^{-\left({\lambda }_{{j}^{{\prime} }}+i\omega \right)t}+{e}^{-\left({\lambda }_{j}+{\lambda }_{{j}^{{\prime} }}\right)t}\right].\end{array}$$

(90)

We close this part by commenting on the long time limit. For t → + ∞ only the first term in the squared brackets of $\langle {\hat{x}}_{{{\rm{th}}}}^{2}(t)\rangle$ and $\langle {\hat{\dot{x}}}_{{{\rm{th}}}}^{2}(t)\rangle$ survives (see Eqs. (88) and (90)) since ${{\rm{Re}}}\{{\lambda }_{j}\} \, > \, 0$. Then, after some manipulations, we arrive to the form

$$\left\langle {\hat{x}}_{{{\rm{th}}}}^{2}(+\infty )\right\rangle =\int_{-\infty }^{+\infty }\frac{d\omega }{2\pi m}\coth \left(\frac{\beta \omega }{2}\right){{\rm{Im}}}\left[\tilde{\chi }\left(\lambda =-i\omega \right)\right],\\ \left\langle {\hat{\dot{x}}}_{{{\rm{th}}}}^{2}(+\infty )\right\rangle =\int_{-\infty }^{+\infty }\frac{d\omega }{2\pi m}{\omega }^{2}\coth \left(\frac{\beta \omega }{2}\right){{\rm{Im}}}\left[\tilde{\chi }\left(\lambda =-i\omega \right)\right].$$

(91)

In addition, we can easily see from Eq. (88) that

$${\lim }_{t\to \infty }\frac{d}{dt}{\hat{x}}_{{{\rm{th}}}}^{2}(t)=0.$$

(92)

This confirms the expected fluctuation-dissipation theorem⁴⁶.

State of the QB at maximum efficiency and possible work extraction

In this Section, we characterize in more detail the state of the QB by means of its Wigner function^76,77

$${{\mathcal{W}}}(x,p,t)=\frac{1}{2\pi \sqrt{{{\rm{Det}}}[{\sigma }_{{{\rm{B}}}}(t)]}}{e}^{-\frac{1}{2}{{{\bf{r}}}}^{{{\rm{t}}}}{\sigma }_{{{\rm{B}}}}^{-1}(t){{\bf{r}}}},$$

(93)

where r^t = (x, p) is the (transposed) vector of the variables x and p in the QB quantum phase space.

Right before the QB is coupled to the charger it sits in its ground state, shown in Fig. 8a. In correspondence of the first maxima of the efficiencies (η_B and η_W), the state of the QB is instead very close to an extremely squeezed state along the momentum direction, as clearly shown in panel (b) of the above figure – please notice the change in scales between the two panels.

Fig. 8: Wigner functions of the QB state.

Plot of ${{\mathcal{W}}}(x,p,t)$ (units ℏ⁻¹ = 1) as a function of x (units ${x}_{0}=\sqrt{\frac{\hslash }{2m{\omega }_{0}}}$) and p (units ${p}_{0}=\sqrt{\frac{\hslash m{\omega }_{0}}{2}}$). Here, darker (lighter) colours denote smaller (larger) values. (a) shows the Wigner function of the QB in its ground state right before coupling to the charger (t = 0). b represents it in correspondence of the first maxima of the efficiencies η_B and η_W. It is worth to note that the axis scales of the two figures differ by a factor of about 10. The considered parameters are ω_D = 2ω₀ (corresponding to Ω ≈ 24.5ω₀) and γ₀ = 300ω₀, T = 0.1ω₀.

From this observation, one can infer that an unitary operation able to almost completely extract the energy from the QB is an “anti-squeezing” operator, namely the hermitian conjugate of the conventional squeezing operator $\hat{S}(\xi )={e}^{\frac{1}{2}\left[{\xi }^{* }{\left(\hat{a}\right)}^{2}-\xi {\left({\hat{a}}^{{\dagger} }\right)}^{2}\right]}$, where $\hat{a}$ and ${\hat{a}}^{{\dagger} }$ are the ladder operators associated to $\hat{x}$ and $\hat{p}$ and where ξ is a squeezing parameter which, in the present case, depends on the action of the reservoir during the charging phase. This operation is able to bring the QB very close to the initial ground state. This kind of operation has been discussed in other platforms, such as quantum optics, under the name of deamplification⁷⁸ and could be implemented also in solid-state devices exploiting for example exotic two-photon interaction⁷⁹.