Introduction

The band degeneracies have been extensively recognized as topological defects in parameter space1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20. A very typical example of such defects in the three-dimensional (3D) Hermitian setting is the Weyl point1,2,3,4,5,6,7. Its topological invariant, generally obtained by integrating Berry curvature on a closed surface enclosing the Weyl point, is a crucial measure for predicting Fermi-arc surface states at system boundaries1,2,3,4,5,6. Recently, non-Hermitian physics has attracted growing interest as it addresses the ubiquitous open systems that exchange energy with the surrounding environment. The energy exchange is represented by the imaginary parts of the complex eigenvalues, which significantly expands the classes of topological phases of matter10,11,12,13,14,15,16,17,18,19,20,21,22,23. The exceptional point (EP) is a unique feature of non-Hermiticity, featuring the coalescence of both eigenvalues and eigenstates. In two-dimensional (2D) systems, a pair of EPs of order two (EP2) can be obtained by splitting a topologically nontrivial Dirac point by introducing non-Hermitian perturbations. Due to the eigenvalue braiding around each EP, the EPs generally carry half-quantized topological invariants, known as energy vorticity, resulting in a stable bulk-Fermi-arc (BFA) linking the pair of EP2s11,12,13. This is fundamentally distinct from the commonly observed Fermi-arc surface states that arise from the 2D projection of Weyl points in 3D Hermitian systems1,3,4,5,6, while the BFA resides in the bulk dispersion of a 2D system supporting the EP pairs11,12,13. So far, the BFA is widely recognized as a stable link of EP2s. However, other forms of BFAs that link higher-order EPs, remain unexplored.

In this study, we unveil an unconventional BFA linking paired exceptional points of order three (EP3), which can widely exist in 2D non-Hermitian systems with parity-time (PT) symmetry and an additional pseudo-Hermitian symmetry. High-order exceptional points, unlike second-order ones, are multifold degeneracies where three or more eigenvalues and their eigenstates coalesce21,22,23,24. These points, common in non-Hermitian systems, enable unique applications such as enhanced sensitivity and the realization of exotic topological structures, making them useful for advancing sensing technologies and exploring novel physical phenomena18,25. In 2D systems with multiple eigenstates, the EP3s can exist in the form of cusps that are located entirely on exceptional lines (EL) under the protection of PT symmetry20,21,22,23. Here we reveal that by imposing an additional pseudo-Hermitian symmetry, EP3s can emerge in pairs. Unexpectedly, these paired EP3s are stably connected by an unconventional form of BFA, on which the three eigenvalues possess identical real parts but disparate imaginary parts, significantly distinguished from the conventional form. By defining winding numbers using a resultant vector22, we find that the paired EP3s possess opposite winding numbers, indicating inverse exchanging processes of Riemannian sheets around the two EP3s, which stabilizes the unconventional BFA. The two EP3s linked by the BFA originate from the splitting of an accidental three-fold degeneracy that holds two linearly independent eigenstates (dubbed a defective triple point, DTP), which is also distinguished from the conventional case. It is known that paired EP2s stably linked by a BFA carry nontrivial eigenvector topology11,12. However, prior topological characterization for high-order EPs that utilize the resultants, which primarily focus on the eigenvalues21,22, cannot reveal the topological nontriviality of eigenvectors of the EP3 pair. To address this limitation, we incorporate the eigenvectors and employ the notion of eigenframe deformation and rotation, which aligns with the intersection homotopy26,27, to characterize the topology of such singularities that are located entirely on ELs. The paired EP3s, which possess opposite winding numbers of resultant vectors and are connected by the BFA, are shown to have a nontrivial topology identical to that of the DTP. Therefore, the splitting of the EP3s from the DTP is topologically protected. Finally, by realizing such systems with nonreciprocal circuits, the new form of BFA is experimentally demonstrated.

Results and discussion

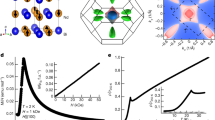
We start with a direct comparison between the two forms of BFAs. As shown in Fig. 1a, a 2D Hermitian system with PT symmetry generally displays Dirac point degeneracies as linear crossings of two bands. By introducing non-Hermitian perturbations with specific symmetries, the Dirac point is split into a pair of EP2s (see Fig. 1b), which are stably connected by the conventional BFA with two eigenvalues sharing identical real parts but different imaginary parts11,12,13. The unconventional BFA we study is inherently different. We consider the following 2D non-Hermitian Hamiltonian with three eigenstates,

$$H=\left[\begin{array}{ccc}-g({f}_{x},{f}_{y})-{f}_{x}+1 & -g({f}_{x},{f}_{y}) & -{f}_{x}\\ g({f}_{x},{f}_{y}) & g({f}_{x},{f}_{y})+{f}_{y} & -{f}_{y}\\ {f}_{x} & -{f}_{y} & {f}_{x}+{f}_{y}\end{array}\right]$$
(1)

where fx and fy are real and constitute the 2D parameter space. This non-Hermitian Hamiltonian is chosen to manifest both PT symmetry and an additional η-pseudo-Hermitian symmetry28,29 (ηHη-1 = H†, η takes the form of Minkowski metric η = diag(−1,1,1)30). The specific function g(fx, fy) = 0.343-fx + b is chosen because it exhibits an accidental three-fold degeneracy at b = 0, as shown in Fig. 1c. This degeneracy is defective and has two linearly independent eigenstates, which we therefore refer to as a defective triple point (DTP). By introducing perturbations while preserving the symmetries (simply by tuning b), this DTP can split into a pair of EP3s lying on the cusps of ELs. The EP3s are stably connected by a special type of BFA, which resides in the broken phase region, as displayed in Fig. 1d. We note that the three eigenvalues on the BFA have identical real parts, while their imaginary parts are different. The DTP should be distinguished from the EP3, despite that they are both defective three-fold degeneracies, due to the fact that the EP3 only has one eigenstate.

Fig. 1: Comparison between the conventional BFA and the unconventional BFA.
figure 1

a Dispersion diagram near the 2D Dirac point (DP), obtained with the PT symmetric Hermitian Hamiltonian \(H={f}_{x}{\sigma }_{1}+{f}_{y}{\sigma }_{3}\). Re(ω) denotes the real part of eigenvalues as a function of fx and fy for the two eigenvalues in orange and blue, respectively. b Paired second-order exceptional points (EP2, red dots) obtained from splitting the DP by introducing gain and loss term \(qi{\sigma }_{3}\) to the Dirac Hamiltonian (\({\sigma }_{1 \sim 3}\) denote Pauli matrices), where q is the perturbation term. The paired EP2s are stably connected by the conventional bulk-Fermi-arc (BFA). The eigenvalues on the conventional BFA are conjugate to each other (real parts coalescence). c Dispersion diagram near the defective triple point (DTP) on the 2D parameter space. The red lines denote ELs, and the DTP is embedded in the ELs. The three real eigenvalues are marked in orange, blue, and green, respectively. d Paired EP3s obtained from splitting the DTP by introducing perturbations with symmetries preserved. EP3s are both cusps of ELs, which are stably connected by the unconventional BFA residing in the broken phase domain. The three eigenvalues on the unconventional BFA share identical real parts and have different imaginary parts. Two of the three eigenvalues on the unconventional BFA are conjugate to each other, while the other eigenvalue is real.

Full size image

To experimentally observe the unconventional BFA, we employ a nonreciprocal electric circuit that incorporates three nodes (labeled A, B, and C in Fig. 2a) to emulate the hoppings in a three-state non-Hermitian model. The tight-binding hopping parameters are utilized to construct a synthetic 2D parameter space. The electric circuit platform31,32,33,34,35 offers significant advantages over others in implementing and precisely controlling complex nonreciprocal hoppings, thanks to the diverse range of readily available active circuit elements. Nonreciprocity in electric circuits refers to the direction-dependent transfer of signals or energy between two nodes, enabling functionalities such as directional amplification and robust unidirectional transport. This is often achieved using a negative impedance converter with current inversion (INIC), an active circuit element that breaks reciprocity by introducing asymmetric hopping parameters32,35. The PT symmetry inherent to the non-Hermitian system ensures that these asymmetric hopping parameters are real and can be implemented using conductance or inductance combined with the INIC33. The structure of the circuit elements and their corresponding hopping parameters are shown in the left panel of Fig. 2a. Specifically, an INIC in series with a capacitor, denoted as ±Ci (see right panel of Fig. 2a), is employed to achieve the nonreciprocal hoppings depicted. In this setup, the circuit’s admittance matrix J and its eigenvalues, labeled j, are analogous to the Hamiltonian matrix and energy spectra, respectively31,32,34. In the experiment, we applied current inputs to each of the three nodes and measured the resulting voltage responses. From these measurements, we constructed the matrix-form Green’s function, whose inverse yields the circuit Laplacian, enabling the analysis of its eigenvalue and eigenstate spectra. Further details on the experimental implementation and measurements can be found in Methods.

Fig. 2: Experimental observation of the unconventional BFA with topological circuit.
figure 2

a Implementation of the Hamiltonian. Left panel: The system includes three nodes A, B, and C. The hoppings between A and B, and between A and C are nonreciprocal hoppings, implemented using an impedance converter with a current inversion (INIC) circuit in series with capacitors (C1, Cx). The hopping between B and C is reciprocal, realized with a pure capacitor (Cy). The hoppings between A and C and between B and C implement synthetic dimensions fx and fy, and the hopping between A and B is a linear function of fx and fy, g(fx,fy) = 0.343-fx + b. Here, b in the linear function denotes the perturbation term. Rag, Rbg, and Rcg are all grounded resistors; Cag, Cbg, and Ccg are all grounded capacitors. Right panel: INIC structure, with two equal resistors Ra in both the positive and negative feedback paths, and capacitor Ci in series. b–d Experimental measurements of admittance eigenvalues for the cut planes with perturbation terms b = 0 (b), b = 0.0299 (c), and b = 0.0569 (d), respectively. Left panels: Degeneracies in the synthetic 2D parameter space on these cut planes. The ELs, DTP, and BFAs are denoted by the orange lines, red star, and blue line, respectively. The experimentally identified degeneracies are marked with solid dots. Dashed lines in different colors correspond to the measured lines (fy = t) on the right panels. Right panels: Real parts of the dispersion of eigenvalues as a function of fx for different fy lines (fy = t) on the corresponding cut planes. The eigenvalues are ordered in exact phases from small to large. The experimentally measured admittance eigenvalues are marked in circles, and all the degeneracies (EL, DTP, EP3, and BFA) are indicated by arrows. The experimental error bars are provided in Supplementary Note 1. The unconventional BFA can be found to stably connect the paired EP3s. Increasing the perturbation simply enlarges the interspace between the two EP3s, but cannot eliminate the BFA, demonstrating the stability of the BFA. Experimental raw data for plotting (b–d) is provided in the Supplementary Data.

Full size image

We first observe the unperturbed case (b = 0) where the DTP is present on the 2D plane of the dispersion diagram. From the left panel of Fig. 2b, we see that four ELs (orange lines) emerge from the DTP (red star), three with fy > 0.121 and one with fy < 0.121, and we measured the admittance bands marked by the three dashed lines (fy = 0.3, 0.121 and 0.01), which are shown in the right panel of Fig. 2b. It can be identified that three of the ELs are formed by the degeneracies of the 2nd and the 3rd bands (fy = 0.3 and 0.01, right panel), while the other is formed by the 1st and the 2nd bands (fy = 0.3, right panel). The DTP, therefore, serves as the aggregation node of all the ELs. By introducing the perturbations (b = 0.0299), the DTP is split into two EP3s lying on the cusps of ELs (see the left panel of Fig. 2c). We see that each of the EP3s is connected by two ELs, and one EL is formed by the degeneracy of the 1st and the 2nd bands, while the other is formed by the degeneracy of the 2nd and the 3rd bands (see the right panel of Fig. 2c). The unconventional BFA (blue line in Fig. 2c), on which the real parts of all three eigenvalues coalesce, can be clearly indicated by the experimental results in the right panel of Fig. 2c. By further increasing the perturbations (b = 0.0569), the separation between the paired EP3s in parameter space becomes larger. However, the BFA is stable against this perturbation, which still stably links the two EP3s, as shown in the left panel of Fig. 2d. Additionally, from the right panel of Fig. 2d, we observe that the dispersive nature of the BFA that the real parts of all three eigenvalues coalesce remains intact regardless of increasing the perturbation in the Hamiltonian. This experimental result demonstrates the stability of the BFA, which comes from the topological nontriviality of the paired EP3s.

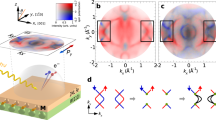
Now we delve into the topological aspects of the stability of the unconventional BFA. As we have claimed, the assembling of the paired EP3s is topologically nontrivial. This point of view compliments the conventional understanding where the winding number of cusps of ELs are defined with the resultant vector21,22,

$$W=\frac{1}{2\pi }{\sum}_{\alpha =x,y}{\oint _{{l}_{\lambda }}}\frac{({R}_{1}\partial {R}_{2}/\partial {f}_{\alpha }-{R}_{2}\partial {R}_{1}/\partial {f}_{\alpha })d{f}_{\alpha }}{|{R}_{2}^{2}+{R}_{1}^{2}|}$$
(2)

and the integration results for the two EP3s are W = ± 1. Here lλ denotes a closed loop enclosing a single EP3, e.g., L1 or L2, as displayed in the lower panel of Fig. 3a. R1 and R2 denote the components of the resultant vector field. Details on obtaining the resultant vector and deriving Eq. (2) are shown in Supplementary Note 2. The opposite windings arise from the fact that the eigenvalues undergo converse exchanges of Riemannian sheets around the two EP3s. As can be observed in Fig. 3b, c (theoretical: solid lines, experimental: symbols), along loops L1 and L2, the eigenvalues j2 and j3 are initially coincident because the starting point (SP) of loop L1 is selected to be on the EL formed by j2 and j3 (see stars in the lower panel of Fig. 3a). As the tracking point on L1 departs from the EL, the degeneracy point of j2 and j3 bifurcates. j2 will then coalesce with j1 as the tracking point approaches the other EL along L1. From this point, j1 and j2 form a common Riemannian sheet in their real part dispersions because they become conjugated. Finally, when the eigenvalues continue to evolve with the moving of the tracking point along L1, the three eigenvalues exchange their order j1j2 ↔ j3 (indicated by the vertical dashed lines), which indicates the exchange of two Riemannian sheets—one shared by Re(j1) and Re(j2), and the other by j3. The eigenvalues on loop L2 simply experience the reverted order exchange process. As shown in Fig. 3c, j1 and j2, initially coalesce at SP, bifurcate as the tracking point departs from the EL. Next, j2 coalesces, bifurcates, and finally coalesces again with j3, through which they swap with j1 (j1 ↔ j2j3, indicated by the dashed lines). The BFA is stable because it arises from the intersection of the two Riemannian sheets, an inevitable consequence when these sheets exchange orders (indicated by the nonzero winding W) as they evolve around the EP3s.

Fig. 3: Topological understanding of the unconventional BFA and the paired EP3s.
figure 3

a Two closed loops encircling each of the paired EP3s (purple loop L1, and blue loop L2), and another loop encircling both (green loop L3). The eigenvalues on the loops are shown in the upper panel, and the structures of the loops in the 2D parameter space are shown in the lower panel. b, c The eigenvalue evolution processes along L1 (b) and L2 (c), respectively. The eigenvalues j1, j2, and j3 are colored in yellow, blue, and green, respectively. The order exchange processes are inverse along L1 and L2. For L1, j1 and j2 coalesce and swap with j3 (j1,2 ↔ j3), while for L2, j2 and j3 coalesce and swap with j1 (j1 ↔ j2,3). d The eigenvalue evolution processes along L3. The eigenvalues do not experience order exchange along L3. The solid lines and rhombus symbols in panels (b, c, and d) correspond to theoretical and experimental results, respectively. e, f Demonstration of the nontrivial topology of the paired EP3s with the evolution process of eigenframe along L3, corresponding to the real and imaginary parts of eigenstates, respectively. The eigenstates φ1, φ2, and φ3 are also colored in yellow, blue, and green, respectively. The lower panels show the corresponding accumulated angles to the initial states. We see that the imaginary parts of eigenstates serve as an intermediate process. Eigenstates φ1 and φ3 accumulate nontrivial quantized angle π, and thus their final states are on the antipodal points to the initial states. The accumulated angle for φ2 is zero. The experimental raw data for plotting the symbols in (b–d) is provided in the Supplementary Data.

Full size image

We expect that the assembling of paired EPs linked by the BFA should carry nontrivial topology11,12. However, applying Eq. (2) on a closed loop encircling both EP3s (on loop L3) yields a trivial result (W = 0) because the order exchange of eigenvalues cancels out on L3. This is clearly indicated by the vertical dashed lines in Fig. 3d, showing the evolution of eigenvalues along the loop. Therefore, considering only the eigenvalues is insufficient to demonstrate the topological nontriviality of the paired EP3s. In topological band theories, additional topological characteristics are encoded in the evolution of eigenstates, such as the Berry phase36 and the homotopical invariants8. However, such approaches may not be applicable here due to the presence of ELs on the loops. We, therefore, employ an intuitively meaningful approach that utilizes the notion of intersection homotopy20,21,26,27 to characterize the topology of such non-isolated singularities. The symmetry of system (PT and pseudo-Hermitian) reveals that the eigenstates obey the Minkowski-type orthogonal relation

$${\varphi }_{i}^{T}\eta {\varphi }_{j}\left\{\begin{array}{c}=0\,i\ne j\\ \ne 0\,i=j\end{array}\right.$$
(3)

which further determines that the eigenframe evolves in the form of deformation and rotation when the Hamiltonian changes in parameter space. Here we employ the eigenframe approach to implement topological characterization because the eigenframe deformation allows the eigenstates to be parallel within the evolution process, and thus intersecting ELs by the loop (i.e. L3 in Fig. 3a) is allowed. Additionally, the topological characterization result with eigenframe does not depend on how the conjugate eigenstates are ordered in broken phase sectors (see details in Supplementary Note 3.3). This approach therefore effectively addresses the gap closing on the ELs where the loops intersect20. The evolution process along L3 is provided in Fig. 3e, f, corresponding to the real and imaginary parts of eigenstates, respectively. The eigenframe deformation process is obvious because the right eigenstates are not always orthogonal to each other, and sometimes they become parallel or antiparallel when the tracking point approaches ELs, resulting from the Minkowski-type orthogonal relationship (see Supplementary Fig. S6). After a cycle of evolution along L3, the eigenstates \({\varphi }_{1}\) and \({\varphi }_{3}\) evolve to their antipodal points (indicated by the red and black dashed lines) but \({\varphi }_{2}\) evolves to the initial state without changing the sign (\({\varphi }_{1}\to -{\varphi }_{1}\),\({\varphi }_{2}\to {\varphi }_{2}\) and \({\varphi }_{3}\to -{\varphi }_{3}\)), which is protected by the PT symmetry. This indicates that both \({\varphi }_{1}\) and \({\varphi }_{3}\) experience quantized accumulated angle π (see the lower panel of Fig. 3e) to their initial states \(\theta =\arccos ({\varphi }^{T}\cdot {\varphi }_{i})\) (here \({\varphi }_{i}\) denotes the initial state). The imaginary parts of eigenstates serve as an intermediate process because the initial and final states (and the accumulated angle) are real (see Fig. 3f). Notably, the accumulated angles of the eigenstates are not quantized along L1 and L2, because eigenstates exchange orders within the evolution process (see Fig. 3b, c). By tuning the system parameters, the two EP3s can merge into a DTP, with the eigenframe evolution on a closed loop encircling the DTP being identical to that in Fig. 3e, f (results provided in Supplementary Fig. S7 to avoid redundancy). This demonstrates that the EP3 pair is topological equivalent to the DTP from an eigenframe rotation/deformation perspective. Therefore, the merging of the paired EP3s into a single DTP is a consequence of topological conservation. Additionally, due to this topological nontriviality, the DTP cannot be totally eliminated, but will be split into an intersection of ELs and an isolated Dirac point by varying b from 0 to negative.

Conclusion

In summary, we unveil an unconventional BFA that stably connects paired EP3s located at the cusps of ELs in non-Hermitian systems with PT symmetry and an additional pseudo-Hermitian symmetry. The winding numbers of the EP3s can be defined with the resultant vectors, and the assembling of EP3s carrying opposite windings of resultant vectors is topologically nontrivial and can coalesce into a DTP under symmetry-preserving parameter changes. This perspective complements the conventional topological understandings of cusps ELs based on resultant vectors21,22. The topological nontriviality of the EP3 pair (or the DPT) is characterized through the eigenframe deformation and rotation process. Our topological characterization transcends the traditional theories that only consider the evolution of eigenvalues, offering a more holistic theoretical understanding for a generic non-Hermitian singularities. Moreover, by implementing the system in a nonreciprocal circuit, we experimentally demonstrate the BFA. The study extends the notion of BFA from EP2s to higher-order EP3s. It is thus a direct motivation for exploring other forms of BFA linking even higher-order EP pairs (e.g., EP4s) that are protected by symmetries in parameter space. Future work may focus on realizing the BFA in periodic systems, offering platforms to explore the finite-size effects associated with it. Our discovery also opens new avenues for wave manipulation and precise control in non-Hermitian systems. The topological robustness of these bulk-Fermi-arcs serves as a basis for designing advanced devices tailored for energy transport, high-sensitivity sensing, and sophisticated signal processing. These results lay a solid foundation for innovative applications in wave engineering and next-generation photonic technologies.

Methods

In our circuit design, a Negative Impedance Converter through Current Inversion (INIC) is implemented, using two equal resistors Ra in both the positive and negative feedback paths (Fig. 2b), enabling precise emulation of nonreciprocal hoppings. The output current Iout is opposite to the input current Iin, making the capacitance behave as Ci when observed from the output node, while as −Ci when observed from the input node. The designed circuit sample includes three nodes (labeled A, B, and C in Fig. 2a) that simulate the nonreciprocal hoppings in the three-state non-Hermitian model [Eq. (1)]. The circuit obeys Kirchhoff’s law, expressed as I = JV, where I is the input current vector, V represents the node voltages, and J is the admittance matrix. In the grounded configuration, the system is described by:

$$J=D+W-C,$$
(4)

where D is the conductance matrix, W is the ground matrix, and C is the adjacency matrix. For our circuit sample in Fig. 2a, the three matrixes can be respectively expressed as:

$$D={{\rm{diag}}}(-i\omega {C}_{1}-i\omega {C}_{x},\,i\omega {C}_{1}+i\omega {C}_{y},\,i\omega {C}_{x}+i\omega {C}_{y}),$$
(5)
$$W\,={{\rm{diag}}}(i\omega {C}_{ga}+1/{R}_{ga},\,i\omega {C}_{gb}+1/{R}_{gb},\,\,i\omega {C}_{gc}+1/{R}_{gc}),$$
(6)
$$C=i\omega \left[\begin{array}{ccc}0 & {C}_{1} & {C}_{x}\\ -{C}_{1} & 0 & {C}_{y}\\ -{C}_{x} & {C}_{y} & 0\end{array}\right]$$
(7)

In our design, we set the grounded capacitance and resistance, respectively, as

$${C}_{gb}={C}_{gc}={C}_{0},\,{C}_{ga}={C}_{0}+c,\,{R}_{ga}={R}_{gb}={R}_{gc}={R}_{0}$$
(8)

and the hopping capacitance as:

$${C}_{1}=g({f}_{x},{f}_{y})c,\,{C}_{x}={f}_{x}c\,,\,{C}_{y}={f}_{y}c$$
(9)

where C0 = 1 nF, R0 = 1 MΩ and c = 10 nF. By inserting Eqs. (5–9) into Eq. (4), The admittance matrix yields:

$$J=(i\omega \, {C}_{0}+1/{R}_{0} \, )+i\omega c\,\underbrace{\, \left[\begin{array}{ccc}-g({f}_{x},{f}_{y})-{f}_{x}+1 & -g({f}_{x},{f}_{y}) & -{f}_{x}\\ g({f}_{x},{f}_{y}) & g({f}_{x},{f}_{y})+{f}_{y} & -{f}_{y}\\ {f}_{x} & -{f}_{y} & {f}_{x}+{f}_{y}\end{array}\right]}_{H}$$
(10)

Here, we can confirm that the second term realizes the three-state non-Hermitian matrix H in Eq.(1). Since the driving frequency is an external parameter (1 kHz in experiments), ω = 2πf is also constant. The first term is also unchanged, causing only a complex shift in the eigenvalues without affecting the eigenstates. As a result, the parameters can be precisely adjusted by modifying the corresponding capacitances in Eq. (9) as needed.

The experimental setup, including the circuit samples, is shown in Supplementary Fig. S1. we use surface-mounted device (SMD) capacitors, resistors, and operational amplifiers (OpAmps, model ADA4625-1ARDZ-R7) on a printed circuit board (PCB). Capacitors are connected in parallel between adjacent nodes, with toggle switches allowing flexible selection of capacitance values.

In experimental operation, the OpAmps are powered by two DC power supplies (RS PRO Bench Power Supply, 0 → 30 V, 0 → 5 A) with dual voltages of +5 V and −5 V. A waveform generator (Keysight: M3201A) drives sinusoidal voltage (1V–2 V at 1 kHz) applied to each node, with the voltage response measured via an oscilloscope (RS PRO IDS1074B). Input current is determined by a shunt resistor (4.21 kΩ) connected from the input node to the voltage source. Analyzing the voltage response to the input current yields the admittance matrix J, which contributes to the admittance eigenvalues and eigenstates, facilitating observation of the bulk-Fermi-arc.