Introduction

One of the most important tasks that remain unresolved in modern physics is the detection of dark matter particles (DM, hereafter referring to dark matter rather than dispersion measure), and numerous candidates of DM have been proposed. Axion-like particles (ALPs), a type of ultralight bosons, have emerged as the most prevailing candidates in the search for DM1,2,3,4,5,6. Thanks to the special properties of ultralight scalar particles (ma ~10−22 eV), they can provide a natural solution to the challenges encountered in small-scale structures of the Universe7,8,9. A lot of strategies for finding axion-like DM have been explored, including photons from axion conversion10,11,12,13, nuclear magnetic resonance14,15, periodic oscillations of linearly polarized light16,17,18,19,20, and other terrestrial or astronomical experiments21,22.

Among the various axion-like DM detection methods, detecting periodic oscillations of polarized light has been regarded as a promising approach in astrophysics16,17,18,19,20,23,24,25,26,27. When light propagates through the ALP field, photons would interact with ALPs, and the interaction term is \({{{{\mathcal{L}}}}}_{a\gamma }=\frac{1}{4}{g}_{a\gamma }a{F}_{\mu \nu }{\tilde{F}}^{\mu \nu }\), where gaγ represents the coupling strength between the axion field (a) and the electromagnetic field (Fμν). The interaction leads to modifications in the dispersion relations28,29. The left- and right-handed circular polarization modes of light experience opposite corrections due to their different dispersion relations. This effect is known as cosmic birefringence, resulting in changes in the polarization angles (PAs) of the light. Therefore, in the presence of an ALP field, if the light is linearly polarized, its PAs will oscillate with the ALP field, with an amplitude proportional to gaγ.

Fast radio bursts (FRBs) are brief and intense radio transients that originate from cosmological distances30,31,32,33,34,35,36. FRBs have been powerful astrophysical laboratories for studying cosmology37,38,39,40,41,42,43,44,45,46,47,48 and also have the potential to play an important role in the detection of DM25,49,50,51,52,53,54,55,56. To date, no studies have utilized real polarization observations of FRBs to constrain axion-like DM directly. The necessary conditions for FRBs to serve as axion-like DM probes include: (i) active repeating bursts, (ii) nonmagneto-ionic local environments with stable PAs, (iii) highly linear polarization, and (iv) precise localizations within host galaxies. The repetition pattern of FRBs enables us to monitor their polarization properties long-term to detect axion-like DM on extragalactic distance scales, complementary to other galactic DM probes. The schematic illustration is shown in Fig. 1. One intriguing sample for such a study is FRB 20220912A, an active repeating source with highly linear polarization57,58, and its local environment is nonmagneto-ionic59. Its long-term polarization observations from the Five-hundred-meter Aperture Spherical radio Telescope (FAST)58 provide a remarkable opportunity to detect extragalactic axion-like DM through searching for a periodic oscillation in the PAs.

Fig. 1: Illustration of detecting extragalactic axion-like dark matter (DM) with polarization measurements of FRBs.
figure 1

The interaction between photons and ALPs leads to modifications in the dispersion relations, resulting in a difference in phase velocity between the two modes. This phenomenon, known as cosmic birefringence, causes changes in the polarization angles (PAs) of the light. If axion-like DM is distributed around the FRB 20220912A's host galaxy, ALP-induced PA oscillations (ϕ(t)) can emerge. The repeating FRBs enable us to monitor their polarization properties long-term to detect axion-like DM on extragalactic distance scales.

Full size image

In this work, we constrain the ALP-photon coupling constant gaγ using polarization data of FRBs. We analyze the polarization angle variations of linearly polarized emission from FRB 20220912A observed by FAST. All currently available observations from October 28th, 2022 to December 5th, 2022 are adopted for our study. The observational time coverage of  ~38 days with a cadence of  ~1 day is sensitive to ALPs with mass ranging from 1.4 × 10−21 eV to 5.2 × 10−20 eV. By estimating the periodic variations in linear PAs, we can place upper limits on gaγ directly. Finally, we also predict further constraints from continued polarization observations of FRB 20220912A in the future.

Results

The Polarization angles detected by FAST

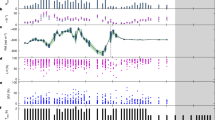
After the initial discovery of FRB 20220912A, subsequent observations from multiple telescopes have consistently detected a large number of bursts from this specific source58,59,60,61,62,63,64,65,66,67,68,69. It is noteworthy that FRB 20220912A was monitored by FAST for a period of several dozen days, during which a total of 1076 bursts were recorded58. Most of these bursts exhibit nearly 100% linear polarization. The rotation measure (RM) of FRB 20220912A is very close to 0 and did not show any variation during the FAST observation period, indicating that FRB 20220912A is located in a likely nonmagneto-ionic local environment58,59. The non-variable RM also means that the PAs of FRB 20220912A are relatively stable.

In our analysis, the PAs of FRB 20220912A are processed from the raw data of FAST. The detailed data processing can be found in the subsection The PA Data Analysis of Methods. Figure 2 displays PA measurements of FRB 20220912A as a function of time (MJD 59880 to MJD 59918), and the median value of the PAs is calculated for each day. As illustrated in this plot, the PAs exhibit considerable variation within a day, but they are relatively stable on the monthly timescale during the observational period. Because of the timing of the observations, there is a concentration of data for a single day within narrow time intervals, which results in poor data continuity from one day to the next. Therefore, our analysis focuses on PA variations with a minimum oscillation period of one day. In this case, the minimum time interval is 1 day, while the total observational time is 38 days. According to the theory presented in the subsection ALP-photon Coupling of Methods, the ALP mass ma can be determined through \({m}_{a}=2\pi (1+z)/{T}^{{\prime} }\). It is clear from this formula that the lower and upper limits of the mass ma depend on the total observational time (\({T}^{{\prime} }=38\) days) and the minimum time interval (\({T}^{{\prime} }=1\) day), respectively. That is, the sensitive ALP mass ma falls within the range of 1.4 × 10−21 eV to 5.2 × 10−20 eV.

Fig. 2: Linear polarization measurements of the bursts from FRB 20220912A detected by FAST.
figure 2

The observed polarization angle (PA, ϕobs) of each burst is depicted by a yellow point, the purple points represent the daily medians, and the light purple shaded area encompasses the 1σ confidence range. The dashed line represents the mean background 〈ϕbkg〉 = − 24.98°.

Full size image

Search for ALP-induced oscillations

As described in the subsection ALP-photon Coupling of Methods, when a linearly polarized light propagates in an external ALP field, the corresponding PAs would have a time-dependent change due to the ALP-photon coupling effect. By analyzing the periodic variations of PAs, we thus can constrain the ALP-photon coupling strength, thereby facilitating the potential detection of axion-like DM.

The Lomb-Scargle (LS) Periodogram is a general tool for searching periodic signals, and has also been applied to axion detection16,26. The significance of the peak values in the LS Periodogram can be assessed by the False Alarm Probability (FAP). The LS periodogram and FAP can be calculated using the python package Astropy, and the results from the time series of polarization measurements for FRB 20220912A with ionospheric corrections are shown in Fig. 3. More details can be found in the subsection The Lomb-Scargle Periodogram of Methods. We can find that all values are much lower than the 32% FAP line. Consequently, there is insufficient evidence to support ALP-induced periodic oscillations present in the PAs of FRB 20220912A based on current observations. Therefore, we can only determine an upper limit of the ALP-photon coupling constant gaγ using an alternative method.

Fig. 3: The LS periodogram for the time series of polarization measurements for FRB 20220912A.
figure 3

The purple line represents the power spectrum (PLS(ν)) of the LS periodogram. The red dashed line marks the False Alarm Probability (FAP) threshold at 32%. The signals with PLS(ν) values below this line are not considered to oscillate periodically at the 1σ confidence level.

Full size image

The resulting constraints and comparisons

We employ two analysis methods to constrain the ALP-photon coupling constant: the standard deviation (SD) method and the LS Periodogram-Monte Carlo method70,71,72. The former is cruder but more convenient for estimation. Further details of the two methods can be found in the subsections The Standard Deviation of PAs and LS Periodogram-Monte Carlo Method of Methods, respectively.

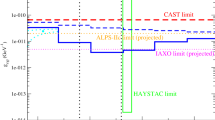
For the estimation from the SD method, we obtain upper limits of gaγ < (2.7 × 10−11−1.0 × 10−9) GeV−1 for the ALP masses ma ~ (1.4 × 10−21−5.2 × 10−20) eV. For the LS Periodogram-Monte Carlo method, the obtained upper limits are gaγ < (3.4 × 10−11−1.9 × 10−9) GeV−1 for the same ALP mass range, which is consistent with the results of the first method. The resulting constraints on gaγ from the LS Periodogram-Monte Carlo method are shown in Fig. 4, along with other 95% CL upper limits from different astrophysical sources. Finally, we also forecast a future constraint. If the polarization observations of FRB 20220912A last up to one year, the limit obtained from the LS Periodogram-Monte Carlo method would extend to lower ALP masses, yielding gaγ < 3.3 × 10−12 GeV−1 for an ALP mass ma ~1.4 × 10−22 eV.

Fig. 4: The resulting constraints on the ALP-photon coupling constant gaγ for different ALP mass ma, obtained from the polarization measurements of FRB 20220912A.
figure 4

The yellow shaded area corresponds to the upper limits of gaγ derived from the LS Periodogram-Monte Carlo method. The yellow dot-dashed line represents future constraints from continued polarization observations of FRB 20220912A for up to one year. Other 95% CL upper limits from different astrophysical sources are also displayed for comparison, including the VLBA polarization observations of jets from active galaxies (blue solid line)16, the Chandra observation of the quasar H1821+643 (blue dot-dashed line)98, the Extended CAST experiment (purple shaded area)73, the polarized light of pulsar from the Parkes Pulsar Timing Array (PPTA) project (gray shaded area)26, the Fermi-LAT observation of supernovae (red dot-dashed line)22, the observations of the cosmic microwave background (CMB) from BICEP/Keck (gray dotted line)74 and SPT-3G (gray solid line)75, and the mass constraint from the Lyman-α forest data (vertical dotted line)76. For a more complete summary, please refer to this link99.

Full size image

Recently, Gao et al.56 proposed gravitationally lensed FRBs as probes for hunting Galactic axion DM, predicting that the ALP-photon coupling could be constrained to be gaγ < 7.3 × 10−11 GeV−1 for an axion mass ma ~10−21 eV. This forecast limit is similar to our result of gaγ < 2.1 × 10−11 GeV−1 for the same axion mass from real FRB polarization observations. Furthermore, as shown in Fig. 4, our result is slightly better than the constraint from the extended CERN Axion Solar Telescope (CAST) (gaγ < 5.8 × 10−11 GeV−1)73 and comparable with the constraint from the supernovae observed by the Fermi Large Area Telescope (LAT) (gaγ < 2.6 × 10−11 GeV−1)22. In contrast to the galactic probes, such as pulsars18,25,26, black hole19,20, and protoplanetary disk24, our method can detect ALPs on kiloparsec scales, which highlights the potential of FRBs for detecting extragalactic axion-like DM.

Discussion

In this work, we attempted to detect extragalactic ALPs in the host galaxies of the hyperactive repeating FRBs. Thanks to the nonmagneto-ionic local environment, highly linear polarization, and relatively stable PAs within the observation period, FRB 20220912A is hitherto the most suitable repeating source for carrying out such a study. Note that the distance of FRBs does not provide an advantage in detecting axion-like DM. This is because the PA shift depends on the axion field at the initial and final positions, independent of the propagation distance (see Equation (3) in Methods). With the state-of-the-art PAs observations of the bursts from the repeating source FRB 20220912A taken by FAST, we obtained upper limits on the ALP-photon coupling constant of gaγ < (3.4 × 10−11−1.9 × 10−9) GeV−1 for the ALP masses ma ~ (1.4 × 10−21 −5.2 × 10−20) eV. If the polarization observations of FRB 20220912A are expected to last for one year, the gaγ limit would be gaγ < 3.3 × 10−12 GeV−1 for an ALP mass ma ~1.4 × 10−22 eV.

Although the constraints on gaγ from FRBs are not as competitive as those from other sources, such as the active galaxies16, the quasar H1821+643 and the cosmic microwave background74,75, and the mass range of ma < 2 × 10−21 eV have been excluded by the Lyman-α Forest Data76, our attempt can serve as an alternative and complementary method. FRBs have the advantage of being abundant in extragalactic systems. Numerous extragalactic FRBs offer an alternative way to detect axion-like DM in various DM-rich extragalactic systems, thereby obtaining tighter constraints on gaγ that complement other galactic DM probes, such as pulsars.

In the era of Square Kilometre Array (SKA), a large sample of localized FRBs will significantly enhance their applications. When numerous FRBs are combined, the constrained precision on the ALP-photon coupling constant will statistically increase by a factor of \(\sqrt{N}\). According to Zhang et al.48, \({{{\mathcal{O}}}}(1{0}^{5})\)-\({{{\mathcal{O}}}}(1{0}^{6})\) FRBs can be detected by the mid-frequency array of the first phase of SKA (SKA1-MID) in a 10-year observation period. To date, more than 800 FRBs have been detected77, and among them, only one, FRB 20220912A, has been identified as a repeating FRB with a nonmagneto-ionic environment. Assuming there are N ~ 100 (0.1% of the total) FRBs like FRB 20220912A in SKA1-MID, the upper limit of the coupling constant would improve by approximately an order of magnitude.

It should be underlined here that the implicit assumption on our results is that the ALP mass exceeds the Hubble parameter in the appropriate epoch of the Universe. In this condition, the ALP-induced PA oscillations can begin and lead to an evolution of energy density in the form of DM5,9. If the ALP mass is so low that it approaches the Hubble constant, ma ~ 10−33 eV, it will be frozen and manifest as a form of dark energy rather than DM.

Methods

ALP-photon coupling

ALPs can be described as a pseudo-scalar field a(x, t) with mass ma, where x is the spatial coordinates and t is the time. The ALP field can interact with the electromagnetic field, and its dynamics can be captured by the Lagrangian terms78:

$${{{\mathcal{L}}}}=-\frac{1}{4}{F}_{\mu \nu }{F}^{\mu \nu }+\frac{1}{2}{\partial }^{\mu }a{\partial }_{\mu }a-\frac{1}{2}{m}_{a}^{2}{a}^{2}+\frac{1}{4}{g}_{a\gamma }a{F}_{\mu \nu }{\tilde{F}}^{\mu \nu },$$
(1)

where Fμν denotes the electromagnetic field tensor, \({\tilde{F}}^{\mu \nu }=\frac{1}{2}{\epsilon }^{\mu \nu \lambda \sigma }{F}_{\lambda \sigma }\) is the dual of Fμν, and gaγ represents the ALP-photon coupling constant which characterizes the strength of interaction. This coupling leads to a modification in the dispersion relation16:

$${\omega }_{\pm }\simeq k\pm \frac{1}{2}{g}_{a\gamma }{n}^{\mu }{\partial }_{\mu }a,$$
(2)

where nμ is null tangent vector of light, k is the wave vector, and the frequency ω± corresponds to two circular polarization states. The natural unit system ℏ=c=1 is employed here. When two vertically polarized electromagnetic waves of these two states propagate, a phase shift occurs between them due to the disparity in their phase velocities. This phase shift leads to the rotation of the polarization plane, known as cosmic birefringence. Specifically, the frequency difference between the two polarization components is Δω = ω+ − ω− = gaγnμ∂μa. If waves emitted from the source at position x1 at time t1 are received by an observer at position x2 and time t2, the ALP-induced PA shift is then expressed as

$$\phi = \frac{1}{2}{\int}_{\!\!\!\!\!C}\Delta \omega {{{\rm{d}}}}s=\frac{1}{2}{g}_{a\gamma }\int_{\!\!\!\!{x}_{1}}^{{x}_{2}}{\partial }_{\mu }a{{{\rm{d}}}}x\\ = \frac{1}{2}{g}_{a\gamma }\left[a({x}_{2},{t}_{2})-a({x}_{1},{t}_{1})\right],$$
(3)

where C is the propagation path of waves. From Equation (3), it is evident that the PA shift ϕ is determined by the time-dependent axion field a(x, t) at the initial and final positions, since it arises from the path integral of the axion field gradient (∂μa). The equation of motion for the ALP field is given by the Klein-Gordon equation. When we neglect the friction term, the solution simplifies and exhibits an oscillating form:

$$a(x,t)={a}_{0}(x)\sin \left({m}_{a}t+\delta \right),$$
(4)

where δ is the position-dependent phase. a0(x) is the amplitude that relates to the energy density of the ALP field ρ (or equivalently the energy density of DM, if the dominant DM is assumed to be made up of ALPs), i.e., \(\rho =\frac{1}{2}{m}_{a}^{2}{\alpha }^{-2}{a}_{0}^{2}\), where α is a random nonnegative variable following the Rayleigh distribution \(f(\alpha )=\alpha \exp (-{\alpha }^{2}/2)\)79. When the observed time scale is much smaller than the coherence time scale, it becomes essential to consider this stochastic nature of the connection between the amplitude a0 and the energy density ρ79,80. The oscillation period of the ALP field is given by T = 2π/ma, which depends on the ALP mass. If the energy density of the ALP field at the observer is much lower than the one at the source (i.e., a(x2, t2) ≪ a(x1, t1)), Equation (3) can be converted to an oscillatory expression,

$$\phi (t)=-\frac{\sqrt{2}}{2}{g}_{a\gamma }\,{m}_{a}^{-1}{\rho }^{\frac{1}{2}}\alpha \sin \left(2\pi \frac{t}{{T}^{{\prime} }}+\delta \right),$$
(5)

where \({T}^{{\prime} }=T(1+z)\) is the observed period on Earth, taking into account cosmic expansion. Equation (5) describes that the PAs have the periodic oscillation characteristic when linearly polarized waves are coupled with ALPs.

DM density profile of the host galaxy

Outside the solitonic cores of galaxies, the DM density distribution ρ(r) can be approximately described by the generalized Navarro-Frenk-White (NFW) profile81:

$$\rho (r)=\frac{{\rho }_{0}}{{\left(r/{r}_{{{{\rm{s}}}}}\right)}^{\beta }{\left(1+r/{r}_{{{{\rm{s}}}}}\right)}^{3-\beta }},$$
(6)

where r is the distance from the galaxy center, ρ0 is the characteristic density, rs is the scale radius, and β is the power-law index. Also, ρ(r) ∝ r−β when r ≪ rs and ρ(r) ∝ rβ−3 when r ≫ rs. For the case of β = 1, Equation (6) is reduced to the original NFW profile82. In principle, these coefficients (ρ0, rs, and β) can be determined by fitting the rotation curves of galaxies. The physical origins of FRBs are still unknown, but some of them have been localized in extragalactic host galaxies. Once we have enough observational information about the FRB host galaxy, we can estimate the DM density ρ in the vicinity of the FRB source.

The Deep Synoptic Array localized the repeater FRB 20220912A to a host galaxy, PSO J347.2702 + 48.7066, at redshift z = 0.077157. The host galaxy has a stellar mass of approximately 1010 M⊙, a star-formation rate of ≳ 0.1 M⊙ yr−1, and an effective radius of 2.2 kpc. Gordon et al.83 compared the optical host luminosities of repeating and nonrepeating FRBs across redshift, and defined a demarcation at luminosity 109 L⊙ below which a host can be classified as a dwarf galaxy. FRB 20220912A sits just above the borderline at  ≈ 1.1 × 109 L⊙, suggesting that its host may be a dwarf galaxy83.

Since they have higher fractions of DM compared to more massive systems, dwarf galaxies are deemed as ideal systems to probe the DM density profile84. However, we currently lack rotation curve observations of the host of FRB 20220912A to investigate its DM density distribution. Here we use the DM density profile of a dwarf galaxy, NGC 4451 (with a similar stellar mass of  ~ 1010 M⊙ and a similar radius of  ~ 2.2 kpc84), as a reference. Note that the differences in DM density profiles between NGC 4451 and FRB 20220912A’s host have negligible effects within the precision range of our study. Based on the stellar rotation curve, Cooke et al.84 determined the coefficients of the generalized NFW profile (Equation (6)) for NGC 4451, i.e., ρ0 = 0.41 M⊙ pc−3, rs = 2.2 kpc, and β = 0. Furthermore, a recent milliarcsecond localization of FRB 20220912A shows that its transverse offset from the host galaxy center is r ≈ 0.8 kpc85. With this information, an estimate of the DM density at the location of FRB 20220912A from Equation (6) is ρ ~0.16 M⊙ pc−3. This value is much larger than the DM density near our Earth, which is  ~ 0.01 M⊙ pc−3 estimated by the Galactic NFW profile86.

The PA Data Analysis

The PAs of FRB 20220912A were derived from the raw data of FAST. The central frequency, bandwidth, number of frequency channels, and sampling time for the raw data were 1.25 GHz, 0.5 GHz, 4096, and 49.152 μs, respectively. We used the GPU-accelerated transient search software HEIMDALL and processed the data on FAST’s high-performance computer facilities. A dispersion measure range of 200 to 250 pc cm−3 was searched, with a signal-to-noise ratio threshold of 6.5 and a maximum boxcar of 512. After determining the dispersion measures, the de-dispersed polarization data were calibrated using the psrchive software package with correction for differential gain and phase between the receivers achieved through the injection of a noise diode signal before each observation. The rotation of the telescope and the variation of the receiver across the days were calibrated through pac. The RM was searched from  −2000 to 2000 rad m−2 in steps of 1 rad m−2 using the rmfit program87. Ionospheric RMs in the direction of FRB 20220912A at each burst’s arrival time were computed using FRion package88. The ionosphere model is sourced from the International GNSS Service (IGS), which provides ionosphere vertical total electron content (TEC) maps daily. FRion downloads these TEC maps from NASA CDDIS archive. After correcting the data with the best-fitted RMs, we derive the PAs of the linearly polarized component. During a total of 9.2 hours of observations between October 28th, 2022 and December 5th, 2022 (corresponding to MJD 59880 and MJD 59918), we obtain 674 bursts with RM measurements. The PA data of these bursts are available in Supplementary Data 1.

The standard deviation of PAs

Variations in PAs of FRBs are complex and puzzling89,90,91. The prevailing understanding is that these variations are mainly attributed to the significant fluctuations in the magnetic fields surrounding FRB sources. However, if the axion-like DM exits in the host galaxy and envelops the FRB sources, the observed PA (ϕobs) is expected to be composed of two components: one from the PA contribution of the astrophysical background (e.g., the magnetic field), ϕbkg, and the other one is the ALP-induced PA shift, ϕ(t), i.e.,

$${\phi }_{{{{\rm{obs}}}}}={\phi }_{{{{\rm{bkg}}}}}+\phi (t)\simeq \langle {\phi }_{{{{\rm{bkg}}}}}\rangle +\Delta {\phi }_{{{{\rm{bkg}}}}}+\phi (t),$$
(7)

where 〈ϕbkg〉 represents the mean value of the PA caused by the background magnetic field and Δϕbkg corresponds to the PA fluctuation arising from the magnetic field changes. Since Δϕbkg is unpredictable, we simply assume that the magnetic field is time-invariant, which means that the observed PA fluctuations are attributed to the ALP-photon coupling effect, i.e., ϕobs = 〈ϕbkg〉 + ϕ(t). Actually, the fluctuations caused by time-varying magnetic fields are quite real, which means that ignoring the contribution from Δϕbkg will conduct conservative upper limits on the ALP-photon coupling constant gaγ for different ALP masses, except in a case of coincidences where ϕ(t) and Δϕbkg cancel out in opposite phases.

Given the randomness of the value of the phase δ (see Equation (5)), we use the SD of ALP-induced PA shift ϕ(t) to characterize its oscillation amplitude18. This yields

$$\Delta \phi \equiv \, \sqrt{\left\langle {\phi }^{2}(t)\right\rangle } \simeq 1.9{6}^{\circ }\,{\left(\frac{\rho }{0.16\, {M}_{\odot }{{{{\rm{pc}}}}}^{-3}}\right)}^{\frac{1}{2}}\\ \times {\left(\frac{{m}_{a}}{1{0}^{-21}\,{{{\rm{eV}}}}}\right)}^{-1}\left(\frac{{g}_{a\gamma }}{1{0}^{-11}\,{{{{\rm{GeV}}}}}^{-1}}\right).$$
(8)

The mean value of the observed daily median PAs is 〈ϕMed〉 = − 24.98 ± 3.83°. Here the mean  − 24.98° is regarded as the mean background 〈ϕbkg〉, and the 1σ SD 3.83° is regarded as Δϕ. From Equation (8), we can see that Δϕ is proportional to gaγ for a given ALP mass ma. With the ALP mass ranging from 1.4 × 0−21 eV to 5.2 × 10−20 eV, the corresponding upper limits on gaγ can be obtained as gaγ < (2.7 × 10−11 −1.0 × 10−9) GeV−1.

Lomb-Scargle periodogram

The LS periodogram is a commonly used technique to identify the periodic signals in time series70,71. It is widely applied in astronomy72,92, and has also been employed in axion search16,26. The LS Periodogram involves the computation of the power spectrum PLS(ν), which is associated with the probability of a periodic signal at frequencies ν. A higher PLS(ν) value indicates a greater probability of periodicity. We consider a time series (yi,  ti) with SD σi of length N (i = 1, . . . , N), and then the required symbols are defined as follows:92

$$\begin{array}{rcl}{Y}_{Y}&=&{\sum}_{i=1}^{N}{w}_{i}{y}_{i}^{2}-Y\cdot Y,\qquad \qquad {Y}_{C}={\sum}_{i=1}^{N}{w}_{i}{y}_{i}{c}_{i}-Y\cdot C,\\ {Y}_{S}&=&{\sum}_{i=1}^{N}{w}_{i}{y}_{i}{s}_{i}-Y\cdot S,\qquad \quad {C}_{C}={\sum}_{i=1}^{N}{w}_{i}{c}_{i}^{2}-C\cdot C, \hfill \\ {S}_{S}&=&1-{\sum}_{i=1}^{N}{w}_{i}{c}_{i}^{2}-S\cdot S,\qquad {C}_{S}={\sum}_{i=1}^{N}{w}_{i}{c}_{i}{s}_{i}-C\cdot S, \hfill \end{array}$$
(9)

where \({w}_{i}=\left(1/{\sigma}_{i}^2 \right)/\left({\sum }_{i = 1}^{N}1/{\sigma }_{i}^{2}\right)\) is the normalized weight, \({s}_{i}= \sin (2\pi \nu {t}_{i})\), \({c}_{i}=\cos (2\pi \nu {t}_{i})\), \(Y=\mathop{\sum }_{i = 1}^{N}{w}_{i}{y}_{i}\), \(C={\sum }_{i=1}^{N}{w}_{i}\cos (2\pi \nu {t}_{i})\), and \(S=\mathop{\sum }_{i = 1}^{N}{w}_{i}\sin (2\pi \nu {t}_{i})\). The power spectrum PLS(ν) is defined as

$${P}_{{{{\rm{LS}}}}}(\nu )=\frac{1}{{Y}_{Y}\cdot D}\left[{S}_{S}\cdot {Y}_{C}^{2}+{C}_{C}\cdot {Y}_{S}^{2}-2{C}_{S}\cdot {Y}_{C}\cdot {Y}_{S}\right],$$
(10)

where \(D={C}_{C}{S}_{S}-{C}_{S}^{2}\). Additionally, the significance of the peak values in PLS(ν) can be assessed by the False Alarm Probability (FAP). The FAP quantifies the probability of periodic signals arising from random fluctuations72, thereby enabling to exclude false periodic signals. We implement this analysis using the Python package Astropy, but no periodic signals have been verified in the PA shift ϕ(t) of FRB 20220912A. The results from the time series of polarization measurements for FRB 20220912A with ionospheric corrections are shown in Fig. 3, where the frequency resolution is 0.002 day−1.

LS periodogram-Monte Carlo Method

To obtain a robust constraint on the ALP-photon coupling constant gaγ, we reference and adjust the method in refs. 16,26. We perform Monte-Carlo simulations to generate the artificial time series that keep the temporal coordinates and exhibit periodic oscillations based on the real distributions of 674 PA data with ionospheric corrections. This enables us to simulate the power spectrum PLS(ν) in the presence of the ALP-induced PA oscillations, and to estimate 95% CL upper limits on gaγ by comparing it with PLS(ν) from real data. To illustrate our approach, for a quantity X, we use distinguishable symbols: X for real data and \(\hat{X}\) for simulated data. For a given frequency νa and the corresponding PLS(νa), the constraint process is summarized as follows:

  1. 1.

    First, we generate 2500 sets of simulated PA data \((\hat{\phi },\hat{\sigma },t)\) by randomly sampling from the histogram distributions of the full PA dataset, and insert a periodic signal \(\Delta \hat{\phi }=\hat{\alpha }\hat{\varphi }\sin (2\pi {\nu }_{a}t+\hat{\delta })\), where the stochastic fluctuation \(\hat{\alpha }\) is sampled from a Rayleigh distribution \(f(\hat{\alpha })=\hat{\alpha }\exp \left(-{\hat{\alpha }}^{2}/2\right)\), the amplitude \(\hat{\varphi }\) is uniformly sampled in the range [0,  15] degrees, and the phase \(\hat{\delta }\) is uniformly sampled in the range [0,  2π].

  2. 2.

    Next, we calculate \({\hat{P}}_{{{{\rm{LS}}}}}({\nu }_{a})\) for each of the 2500 sets of simulated PA data and pair it with the amplitude \(\hat{\varphi }\) to form an array \((\hat{\varphi },{\hat{P}}_{{{{\rm{LS}}}}}({\nu }_{a}))\).

  3. 3.

    Then, we extract all amplitudes \(\hat{\varphi }\) that yield the same power spectrum as the real data at frequency νa. Specifically, we search for \(\hat{\varphi }\) in the array \((\hat{\varphi },{\hat{P}}_{{{{\rm{LS}}}}}({\nu }_{a}))\) that satisfies the condition that the simulated spectrum value \({\hat{P}}_{{{{\rm{LS}}}}}({\nu }_{a})\) falls within a narrow interval [PLS(νa) − ϵ,  PLS(νa) + ϵ] of the real spectrum value. In other words, all \(\hat{\varphi }\) must satisfy \({\hat{P}}_{{{{\rm{LS}}}}}({\nu }_{a})\in [{P}_{{{{\rm{LS}}}}}({\nu }_{a})-\epsilon ,\,{P}_{{{{\rm{LS}}}}}({\nu }_{a})+\epsilon ]\) (here we set ϵ = 0.005).

  4. 4.

    In the set \(\hat{\varphi }\) extracted in step 3, we determine a value φ95 such that 95% of \(\hat{\varphi }\) satisfy \(\hat{\varphi } < {\varphi }_{95}\), representing a 95% CL upper limit of ALP-induced amplitude at frequency νa. Finally, an upper limit on gaγ for an ALP mass ma can be inferred with a 95% CL by providing a SD of \({\varphi }_{95}/\sqrt{2}\) and a frequency νa according to Equation (8).

The above process is performed for each \({\nu }_{a}\in \left\{\nu | 1/38\le \nu \le 1\right\}\) (in units of day−1) to obtain 95% CL upper limits of gaγ for all sensitive ALP mass ranges. The constraint results (purple shaded area) are presented in Fig. 5, where the results obtained from the case of fixing α = 1 (i.e., without considering the stochastic nature of the amplitude of the axion field; denoted by red line) and the SD method (denoted by orange line) is also plotted for comparison. Similar results indicate that the estimation from the SD method of the daily PA medians is reasonable.

Fig. 5: The resulting constraints on the ALP-photon coupling constant gaγ for different ALP mass ma.
figure 5

The orange line represents the estimation from the standard deviation (SD) method. The purple solid line and red line correspond to the derived upper limits of gaγ for the cases of random α and fixed α = 1, respectively (see Equation (5)). The purple dot-dashed line represents future constraints from continued polarization observations of FRB 20220912A up to one year.

Full size image

The significant variations in PA within a single day are not relevant to the long-period signal we focus on (1-38 days). This is because long-period signals change very little over short timescales, effectively adding a constant to the daily PAs. Additionally, we can infer that the effects of the stochastic nature of DM are negligible in our analysis, which can be attributed to the expectation of the Rayleigh distribution being \(\sqrt{\pi /2}\), which is close to the fixed value of 1. We obtain upper limits on the ALP-photon coupling constant of gaγ < (3.4 × 10−11 − 1.9 × 10−9) GeV−1 for the ALP masses ma ~ (1.4 × 10−21−5.2 × 10−20) eV. Based on the current distribution and accuracy of PA data, we simulate the PA variation over the course of a year and apply the same methods to find φ95. With future polarization observations of FRB 20220912A for one year, the gaγ limit would extend to lower ALP masses, i.e., gaγ < 3.3 × 10−12 GeV−1 for an ALP mass ma ~1.4 × 10−22 eV.

The influence of the Faraday rotation

Stable PAs are essential requirements for our study. For most FRBs, the dominant mechanism of PA variation is the Faraday rotation effect when propagating through magnetized plasma. The RM is a crucial parameter for quantifying this effect. The PAs induced by Faraday rotation can be expressed as ϕ = RM(c/ν)2, where c is the light speed and ν is the frequency. In our FRB 20220912A dataset, the mean value of the daily median RM is 〈RMMed〉 = − 0.91 ± 1.12 rad m−2. Such a small RM may imply that the RM contribution from its host galaxy is comparable to that of the Milky Way58, which is  ~−16 rad m−293. Nevertheless, the RM from the galactic medium is stable and thus has negligible influence. Additionally, the long-term variation of RM is also stable58, with a slope of 0.017 rad m−2 day−1 (0.06° day−1). The SD of ALP-induced PA shift is  ~ 2° at a mass of 10−21 eV, which can be estimated using Equation (8). If the Faraday rotation contributes a comparable PA shift, the RM needs to reach  ~ 0.6 rad m−2. The SD of 〈RMMed〉 for FRB 20220912A is comparable with this value. This indicates that although it is reasonable to disregard the PA caused by the magnetic field in our analysis, the influence of the Faraday rotation prevents us from further improving accuracy.

The influence of the circular polarization degree

Despite the highly linear polarization observed in FRB 20220912A, observations have shown that this source also exhibits a fraction of circular polarization. The possible explanations include intrinsic radiation mechanisms94,95 or propagation effects within a magnetar’s magnetosphere96,97. To investigate the influence of the circular polarization degree, we calculate the cumulative probability distribution of the linear polarization degree of 674 bursts and employ the SD method to quantify constraint results. Figure 6 presents the cumulative probability distribution of linear polarization, which shows that over 80% of bursts have a linear polarization fraction exceeding 90%. After removing those PA data below a given linear polarization threshold, we can calculate the coupling constant gaγ for the remaining PA data. This gaγ value is then divided by that obtained from the total PA dataset for normalization. Taking the linear polarization threshold from 60% to 100%, the relative variations of gaγ are also depicted in Fig. 6. The absence of a significant reduction in gaγ after removing the low polarization degree data suggests that non-linearly polarized data have little impact on our results.

Fig. 6: The cumulative probability distribution of the linear polarization degrees of 674 bursts from FRB 20220912A and the relative variation of the coupling constant gaγ.
figure 6

The left y axis: the cumulative probability distribution of the linear polarization degrees (purple line). The right y axis: the relative variation of the coupling constant gaγ obtained by the standard deviation (SD) method after removing those data below a given linear polarization threshold and then dividing by the gaγ constraint obtained from the total dataset (orange line).

Full size image

The influence of the Dark matter density

The assumption of DM density employed in this paper is approximate, but it can be shown that its impact on our results is negligible. The precision of the VLBI localization corresponds to a physical length of less than 10 pc85, allowing us to disregard the location error. The errors associated with the generalized NFW profile, characterized by three parameters and their errors, are as follows: \({\rho }_{0}=0.4{1}_{-0.24}^{+0.47}\,{M}_{\odot }\,{{{{\rm{pc}}}}}^{-3}\), \({r}_{s}=2.{2}_{-0.7}^{+0.8}\,{{{\rm{kpc}}}}\), and \(\beta =0.{0}_{-0.6}^{+0.5}\)84. We estimate the errors in DM density by randomly sampling parameters from their error distributions. The best-fit generalized NFW profile of NGC 4451 and its 95% CL are shown in Fig. 7. We find that the 95% CL lower limit of DM density at a radius of 0.8 kpc is similar to that near the Earth. Therefore, in the worst-case scenario, the DM density is set to a value near the Earth (ρ ~ 0.01 M⊙ pc−3), resulting in a coupling constant limit gaγ that is four times larger. In general, since gaγ is proportional to the square root of DM density, any estimation deviation in DM density must be significant to meaningfully affect our results.

Fig. 7: The best-fitting generalized Navarro-Frenk-White (gNFW) profile of NGC 4451 (purple solid line) with a 95% confidence region (gray shade).
figure 7

The relation between the dark matter (DM) density ρ(r) and the distance r from the galaxy center is displayed (see Equation (6)). The location of FRB 20220912A (red dashed line) and the estimated DM density near our Earth based on the Galactic NFW profile (orange dashed line) are indicated.

Full size image