Introduction

As one of the most important semiconductor devices, diodes are widely used in the modern electronics industry, yet several limitations, such as heat generation, power consumption, and limited operating frequency put obstacles in their further developments. The recently emerged superconducting diode can address these problems to some extent, owing to their evident advantages of low energy consumption and ultrahigh frequency1,2. The so-called superconducting diode effect (SDE) describes an intriguing nonreciprocity of critical supercurrents: the device acts as a superconductor for currents along one direction, but as a resistive metal for the opposite direction of current flow3. Up to date, SDE has been observed in various superconducting systems, such as artificial superlattices4,5,6, thin flakes of two-dimensional materials7, and Josephson junctions (JJs)8,9,10,11,12,13,14,15. Unfortunately, the SDE can only be manifested in superconducting systems with spontaneous breaking of the inversion symmetry (IS) and the time-reversal symmetry (TRS)3,16,17,18,19,20; whereas the IS breaking is inherently achieved in noncentrosymmetric superconductors or artificially stacked JJs, the TRS breaking (TRSB) mostly requires the introduction of external magnetic fields (H), which seriously hinders the application of superconducting diodes for a device perspective.

A JJ is typically composed of two superconductors connected by an insulating barrier or a conducting/superconducting weak link21. In common cases, the critical currents in JJs are reciprocal (i.e., identical for opposite current directions) and are described by the Josephson relations22. SDE in JJ, known as the Josephson diode effect (JDE), requires explicit symmetry breakings as well. A JJ with broken IS still exhibits reciprocal critical current at H = 0 (∣Ic+(0)∣ = ∣Ic−(0)∣) as long as the TRS is inherently preserved; in such case, nonreciprocity is expected at H ≠ 0, i.e., ∣Ic+(H)∣ ≠ ∣Ic−(H)∣(H ≠ 0)3,11,16,17. Therefore, the JDE occurs at zero magnetic field only if both IS and TRS are simultaneously broken3. In the absence of H, JDE can be invoked by insertion of magnetic barrier layer between the two superconductors, which causes TRSB by providing a spin-splitting stray field9. An alternative approach to applicable zero-field JDE is to establish intrinsic TRSB in the superconducting state via manipulating the phases of order parameters between two superconductors; theoretically, this usually relies on the involvement of unconventional pairing symmetries23,24 or multi-band superconductivity25,26.

Layered dichalcogenide 2H-NbSe2 is a van der Waals (vdW) crystal exhibiting robust superconductivity, thus naturally serves as a promising candidate for building highly transparent JJs by a simple stacking of thin flakes27,28. Field-induced SDE and field-free JDE have been reported in NbSe2 few-layer flakes7 and the NbSe2/Nb3Br8/NbSe2 heterostructures11, respectively. In particular, the latter represents a rare example of realizing zero-field JDE without introducing any magnetic components, despite that the exact origin of TRSB is still elusive. In this work, we report a field-free JDE in the basic vdW JJs composed of two NbSe2 thin flakes (thickness ≈ 10 nm), which can exhibit abundant properties that are distinct from the bulk crystal or thick flakes, such as the orbital Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) state and Ising pairing29,30. A sharp superconducting transition appears at 6.4–6.6 K proves the high quality of our devices. Surprisingly, an asymmetric current-voltage characteristic can be observed in the superconducting regime. The field-free JDE occurs in both underdamped and overdamped JJs, featured by stable and rapid superconducting half-wave rectification. Under external magnetic field, the nonreciprocal component of critical currents, ΔIc (∣Ic+∣ − ∣Ic−∣), shows a sign reversal and displays symmetric field dependence. Our observations highlight an emergent TRSB effect in vdW JJs even without peculiar tunnel barriers, which calls for further theoretical understandings. Meanwhile, they provide opportunities for constructing practical superconducting electronic devices.

Results

Basic characteristics of NbSe2 JJs

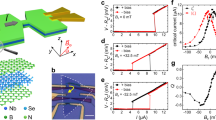
The 2H-NbSe2 JJ devices were fabricated using a dry-transfer method in a top-down process31, which can avoid interface contact with polymers. Fig. 1a depicts a schematic illustration of our JJ device structure with two sets of four-terminal Ti/Au bottom electrodes contact on each NbSe2 flake, enabling simultaneous measurements of electrical transport on individual flakes as well as across the junction. Fig. 1b presents a typical optical micrograph of a 2H-NbSe2 JJ device. To examine the device quality, we carried out cross-sectional high-angle annular dark-field (HAADF)-scanning transmission electron microscopy (STEM) measurement. Figure 1c shows HAADF-STEM image of device 1 with the top and bottom NbSe2 layers having the same thickness of approximately 11 nm. Obviously, the interface is atomically smooth and flat without defects or impurities. As shown in the atomically resolved image, Fig. 1d, both NbSe2 flakes exhibit the same lattice structures with bulk NbSe2 crystal with a 0.63 nm period and there is no evidence of oxidation at the interface. The distance between the two Nb atomic layers at the interface is 0.97 nm. This vdW gap leads to the decouple of the top and bottom NbSe2 flakes, thereby forming a JJ27,32.

Fig. 1: The van der Waals Josephson junction of NbSe2.
figure 1

a The schematic of a typical NbSe2 Josephson junction device, showing the h-BN protective layer, NbSe2 thin flakes, Ti/Au electrodes, and SiO2/Si substrate. Inset, the vertical architecture of junction, consisting of two NbSe2 thin flakes. b Optical micrograph of device 1. Top and bottom NbSe2 flakes are highlighted by red and yellow lines. c Cross-sectional high-angle annular dark-field (HAADF)-scanning transmission electron microscopy (STEM) image of device 1. The top and bottom NbSe2 flakes have the same thickness of around 11 nm. d Atomically resolved HAADF-STEM image of device 1, showing the vicinity of the interface. The distances between Nb layers in NbSe2 crystals and at the interface are 0.63 and 0.97 nm, respectively. e Temperature dependence of resistance measured in device 1 (blue) and device 2 (red). Both devices show a sharp superconducting transition, occurring at 6.5 and 6.6 K, respectively. Inset: an expanded view of the superconducting transition.

Full size image

Figure 1e shows the T-dependent resistance of device 1 (Fig. 1b–d) and device 2 (composed of a 9 nm top NbSe2 layer and a 7 nm bottom NbSe2 layer, see Supplementary Fig. S7b). Both devices exhibit a sharp superconducting transition. The transition temperature Tc, defined as the temperature corresponding to 50% drop in resistance, is 6.5 K (6.6 K) for device 1 (2).

Field-free JDE

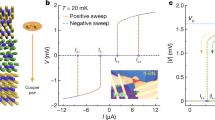
We measured the voltage versus current characteristic (I–V curve) to examine the JDE. A sweeping DC current was applied in both forward and backward directions at 2 K in the absence of H. Results for devices 1 and 2 are displayed in Fig. 2a–d. The I–V curve measurement consists of two steps: the DC current first sweeps from negative to positive (n-0-p, as indicated by blue solid lines in Fig. 2a, b), then sweeps back from positive to negative (p-0-n, as indicated by blue dashed lines in Fig. 2a, b). Ic is defined as the critical current at which the the junction enters the normal state and Ir is the retrapping current returning to the superconducting state22. As shown in Fig. 2a, device 1 shows non-hysteretic behavior in I–V curves, i.e., Ir = Ic, indicating that the JJ device is in the strongly overdamped regime. Only a single superconducting transition occurs during the current sweeps. By contrast, for device 2, all the I–V curves exhibit hysteresis between forward and backward sweeps with Ic > Ir, as shown in Fig. 2b. Furthermore, the Stewart–McCumber parameter21\({\beta }_{{{{\rm{c}}}}}\approx {(\frac{4{I}_{{{{\rm{c}}}}}}{\pi {I}_{{{{\rm{r}}}}}})}^{2}\) of device 2 is calculated to be 4.15; βc >  1 suggests that the JJ is in the underdamped region. Additionally, there is another transition at 1.84 mA above the Ic of JJ, which is attributed to the current-driven superconducting-to-normal transition of the NbSe2 flakes. This transition has been reported in several previous reports11,27,33. We point out that our devices are free of the influence of inhomogeneous current density distribution that is usually expected in a wide JJ, wherein the junction width W is larger than the Josephson penetration depth λJ22,28,33. λJ can be calculated as \({\lambda }_{{{{\rm{J}}}}}=\sqrt{\frac{\hslash }{2{\mu }_{0}e\Lambda {J}_{{{{\rm{c}}}}}}}\) (ℏ is the reduced Planck’s constant, μ0 is the vacuum permeability, e is the electron charge, Λ is the effective junction length and equals to 2λ + d, λ is the London penetration depth of NbSe2, d is the thickness of barrier, and Jc is the supercurrent density). We summarized the values of Jc, W, and λJ of all the fabricated NbSe2/NbSe2 junctions in Fig. 2e. λJ is determined to be larger than the JJ’s size in devices, demonstrating that our devices are still in the narrow junction regime.

Fig. 2: The zero-field nonreciprocal electronic transport properties.
figure 2

The voltage versus current characteristic (I–V curve) of device 1 (a) and device 2 (b) at 2 K and zero field. The I–V curve measurement contains two steps, i.e., forward and backward as shown by the blue solid and dashed lines, respectively. Device 1 is in the strongly overdamped regime implied by the non-hysteretic behavior in I–V curves, whereas device 2 is an underdamped Josephson junction showing a hysteretic I-V behavior. c,d The four branches of I–V curves: n-0, 0-p, p-0, and 0-n, denoted by orange, green, blue, and red lines, respectively. The critical supercurrents Ic+ and ∣Ic−∣ are different in both devices 1 and 2. e The supercurrent density Jc (blue dots), the junction width W (red dots), and the Josephson penetration depth λJ (red circles) in all fabricated NbSe2 vdW devices. The error bars represent the standard deviation of the critical supercurrent density values obtained from averaging multiple measurements. f The magnitude of zero-field Josephson diode effect (JDE) plotted against the thickness of NbSe2 flakes for all devices. Blue shaded region highlights the emergence of finite zero-field JDE only in devices composed of flakes thinner than  ~12 nm. The error bars are estimated from the standard deviation of the critical current values from multiple measurements.

Full size image

We divide the I–V curve into four branches: (i) negative to zero (n → 0), (ii) zero to positive (0 → p), (iii) positive to zero (p → 0), and (iv) zero to negative (0 → n). Subsequently, the absolute values of branches (i) and (iv) were plotted in the first quadrant together with (ii) and (iii) for a comparison, as shown in Fig. 2c,d. Ic+ and Ir+ are defined as the critical currents in the positive current regime (ii and iii), while Ic− and Ir- are the critical currents in the negative regime (iv and i). Due to its non-hysteretic behavior, device 1 has equal Ic and Ir in the same sweep direction (Ic+ = Ir+, Ic− = Ir-). However, these currents are asymmetric with regard to the zero point. As shown in Fig. 2c, Ic+ and ∣Ic−∣ are evidently different. The ΔIc of device 1 is ~−22 μA at zero field. For device 2, Ic+ does not equal to ∣Ic−∣ either, with a ΔIc of −130 μA. There is a very small difference between Ir+ and ∣Ir-∣ with a ΔIr of only 10 μA, considering their absolute values. These characteristics confirm the presence of a field-free JDE in both devices 1 and 2.

The discovery of JDE in NbSe2/NbSe2 vdW JJs without the application of H or introduction of special tunneling barriers is highly unusual. Such effect has been overlooked in all the previous works11,27,34,35. In these works, the thickness of the studied NbSe2 flakes is typically above 20 nm, i.e., the flakes are thicker than those in devices 1 and 2 mentioned above. We confirmed that the zero-field JDE is always absent in our devices fabricated using the same technique but comprising thicker flakes (30–45 nm, Supplementary Fig. S8); on the other hand, the thick-flake-based JJs exhibit diode effect under H (Supplementary Fig. S9). These behaviors are in agreement with the existing results7,11. In Fig. 2f, the magnitude of zero-field JDE, defined to be the ratio \(\frac{\Delta {I}_{{{{\rm{c}}}}}}{ < {I}_{{{{\rm{c}}}}} > }\), where \( < {I}_{{{{\rm{c}}}}} > =\frac{{I}_{{{{\rm{c}}}}+}+| {I}_{{{{\rm{c}}}}-}| }{2}\) is the average of positive and negative critical currents, are plotted against the NbSe2 flake thickness in all devices. It can be immediately figured out that zero-field JDE unambiguously emerges only in devices composed of NbSe2 flakes thinner than 12 nm; this suggests the existence of a threshold thickness of approximately 12 nm for the realization of zero-field JDE (with the only exception of device 6 represented by the red symbol in Fig. 2f, which consists of two 6 nm flakes but is characterized by the absence of zero-field JDE). The fact that the occurrence of zero-field JDE is associated with reduced flake thickness demonstrates the intrinsic nature of such phenomenon in the thin-flake-based devices, i.e., it cannot be a spurious effect introduced by defective experimental setups. We further verified this point by measuring the JDE using different designs of electric circuit configurations; the outcomes are fully consistent (see Fig. S3 of Supplementary Note 2), precluding the possibility that the zero-field JDE is due to artifacts in circuits. Moreover, we also determined that the observation is not caused by trapped vortices or residual flux which smear the real zero point of H. The details and results are available in Supplementary Notes 2 and 3.

The difference between Ic+ and ∣Ic−∣ and the sharp superconducting transition in I–V curve mean that if a current between Ic+ and ∣Ic−∣ is applied to the device, the JJ will be a superconductor with zero resistance for current along one direction but a normal metal with a finite resistance for the opposite direction. Therefore, we can demonstrate a rapid and clear half-wave rectification effect for a square-wave excitation. For device 1, Ic+ = 116 μA, ∣Ic−∣ = 138 μA, a square-wave excitation with an amplitude of 132 μA (between Ic+ and ∣Ic−∣) and a frequency of 0.1 Hz was applied. As illustrated in Fig. 3a, when the current is positive, a voltage of 1.75 mV can be measured, indicative of the JJ device in normal state with finite resistance. Upon the current switching to negative, the junction voltage dropped below 10−5 V, indicating the superconducting state of the JJ device. Furthermore, we applied the square-wave excitation current more than 50,000 s consisting of 5000 continuous cycles at 2 K without H. As shown in Fig. 3b, the junction voltage maintained consistent periodicity and can switch between high (1.75 mV) and low (near to 0) states sharply and stably throughout all cycles. Figure 3c presents the histograms of the measured junction voltages over 5000 cycles. The data are concentrated closely around the high and low voltage values, which suggests a high degree of durability and robustness in the half-wave rectification of the JJ device. The realization of stable rectification effect in absence of an external magnetic field or specific tunneling barrier can provide a promising avenue for application. It is noteworthy that this device represents the rare field-free overdamped JDE with robust superconducting rectification and high rectification ratio. The overdamped JJ has more advantages for the application of quantum devices, attributable to its single-valued I–V curve and the ultrahigh operation frequency up to THz36,37.

Fig. 3: The half-wave rectification of device 1 at 2 K and zero field.
figure 3

a Half-wave rectification of Josephson diode effect (JDE). The green line in the top panel shows a square-wave current with an amplitude of 132 μA and a frequency of 0.1 Hz which is applied to device 1, and the blue line in the bottom panel is the voltage measured across the junction. The red dashed lines indicate the zero value. The voltage is approximately zero within the experimental resolution under the application of negative currents, yet develops a finite value when the current is switched to positive. b The durability test of JDE. The same square-wave current with a is applied more than 50,000 s consisting of 5000 continuous cycles, plotted with green line and the blue line is the junction voltage, showing no degradation of JDE. c Histograms of the measured voltage data in the 5000 continuous cycles of b.

Full size image

Temperature dependence of JDE

The zero-field JDE was further studied by measuring I–V curves between 2 and 6 K at zero field. The DC current with a small AC excitation was swept in two steps, the same as the process mentioned above and we were able to measure the differential resistance (dV/dI) of the JJ simultaneously. As shown in Fig. 4a, there is no hysteretic behavior in the I–V curves of device 1 at all temperature, indicating that the JJ is in the overdamped regime.

Fig. 4: Temperature dependence of the Josephson diode effect (JDE).
figure 4

a The voltage versus current characteristic (I–V curve) measured on device 1 for temperature from 2 to 6 K at zero field. All the curves show non-hysteretic and asymmetric behaviors. b Temperature dependence of critical currents on the opposite directions. The critical supercurrents Ic+ and ∣Ic−∣ are represented by blue and green dots, respectively. Both critical currents increase monotonically with temperature decreasing. Inset, the non-monotonic temperature dependence of nonreciprocal component of critical currents ∣ΔIc∣. c The differential resistance dV/dI as a function of current I at different temperatures. Only a single pair of peaks can be seen and the positions of peaks shift toward zero upon warming. d The ∣Ic−∣ as a function of temperature for device 1. The black dashed line denotes the numerical fit using AB theory (Equation 1 in the subsection “Temperature dependence of JDE” of results). Inset is the same fit for Ic+. e The temperature dependence of superconducting gap obtained from the differential conductance curves; data show good agreement with the fitting curve based on BCS theory (dashed line, Equation 2 in the subsection “Temperature dependence of JDE” of results).

Full size image

We plot the temperature dependence of critical currents in two directions in Fig. 4b, and the critical currents determined from the I–V curve are identical with whose from dV/dI, as shown in Fig. 4c. The single peak in dV/dI curve confirms that there is only one superconducting transition. Both Ic+ and ∣Ic−∣ exhibit a monotonic increase as the temperature decreasing. The nonreciprocity of critical currents appears simultaneously with the superconducting transition. The inset in Fig. 4b shows the non-monotonic behavior of the ∣ΔIc∣, as a function of temperature. Initially, the ∣ΔIc∣ increases as temperature decreasing until 4.6 K, and then ∣ΔIc∣ decreases. Below 3.2 K, ∣ΔIc∣ increases again and reaches its maximum value at 2 K.

To further determine the temperature dependence of the superconducting state of the JJ, we calculated the critical currents using Ambegaokar–Baratoff (AB) theory38:

$$\frac{{I}_{{{{\rm{c}}}}}\left(T\right)}{{I}_{{{{\rm{c}}}}}\left(0\right)}=\frac{\Delta \left(T\right)}{\Delta \left(0\right)}\tanh \left[\frac{\Delta \left(T\right)}{2{k}_{{{{\rm{B}}}}}T}\right],$$
(1)

where Δ is the superconducting gap and kB is the Boltzmann constant. The numerical fit curve is plotted as the black dashed line alongside the ∣Ic−∣ data (blue circles). As shown in Fig. 4d, the ∣Ic−∣ data fits well with AB theory and the superconducting gap at 0 K was determined as a fitting parameter, Δ(0) = 0.868 meV. The differential conductance, dI/dV, as a function of bias voltage, can be obtained from the I–V curve data. As shown in Supplementary Fig. S10, the peaks of differential conductance emerge at the value twice of superconducting gap, attributable to the tunneling of Cooper pairs27. The gap from differential conductance can be fitted with Bardeen–Cooper–Schrieffer (BCS) theory:

$$\Delta \left(T\right)=\Delta \left(0\right)\tanh \left(2.2\sqrt{\frac{{T}_{{{{\rm{c}}}}}-T}{T}}\right),$$
(2)

where Δ(0) is the superconducting gap at 0 K and Tc is the critical temperature of the superconductivity. As shown in Fig. 4e, the experimental data is well described by the BCS theory and Δ(0) is obtained as 0.958 meV, which shows good agreement with the value from the fitting of ∣Ic−∣ and is very close to the superconducting gap of NbSe2 flakes (≈1 meV)39, indicating no degradation of superconductivity in the JJ.

Magnetic field dependence of JDE

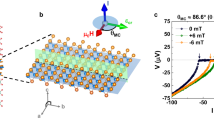
In our studies of H-dependent critical currents, an in-plane H was applied perpendicular to the tunneling current on the JJ device (as illustrated in the inset of Fig. 5b). Figure 5a displays the color map of differential resistance as a function of the in-plane H; the critical current defined by the differential resistance (bright curve) exhibits an unusual oscillatory behavior, manifesting a deformed Fraunhofer pattern. Considering the high interface quality of our device evidenced by HAADF-STEM results (Fig. 1c,d), the non-ideal Fraunhofer pattern is likely to be associated with extrinsic effects. It is known that the Fraunhofer oscillation pattern can be influenced by many factors, including the self-field effect of supercurrent33, the orientation of in-plane H34 and magnetic vortices in the superconducting electrodes11,40. In particular, the widely observed irregular Fraunhofer pattern in vdW junctions can be attributed to the inhomogeneous widths of the device along the direction of H, which naturally explains our data34. Despite these, an oscillation period of 42.1 mT was observed; considering the fundamental form of Fraunhofer pattern22:

$$\frac{{I}_{{{{\rm{c}}}}}\left(H\right)}{{I}_{{{{\rm{c}}}}}\left(0\right)}=\left\vert \frac{\sin \left(\pi \Phi /{\Phi }_{0}\right)}{\pi \Phi /{\Phi }_{0}}\right\vert ,$$
(3)

where Φ = (2λ + d)WH, λ is the London penetration depth of NbSe2, d is the thickness of barrier, W is the width of JJ, and Φ0 is the magnetic flux quantum. For device 1, d is 0.34 nm as determined by HAADF-STEM result in Fig. 1d and W is 3.75 μm, we can figure out that λ is 6.5 nm, which is in agreement with previously reported values for NbSe2 in JJs11,27. Simultaneously, we measured the temperature dependence of the upper critical field for in-plane H of the NbSe2 flake in device 1. It significantly exceeded the Pauli limit and an anomalous upturn was observed, as shown in Supplementary Fig. S11, suggesting the existence of an orbital FFLO state above a threshold in-plane H29; the FFLO state may have an influence on the field-induced SDE/JDE10 in the NbSe2 flakes7, but is unlikely to contribute to the zero-field JDE reported herein.

Fig. 5: Magnetic field dependence of the Josephson diode effect (JDE).
figure 5

a Color map of differential resistance (dV/dI) as a function of in-plane magnetic field and current at 2 K, showing a non-ideal Fraunhofer pattern with an oscillation period of 42.1 mT. Additional features are observed around zero field. b The nonreciprocal component of critical currents ΔIc versus the in-plane field, showing a roughly symmetric field dependence with a sign reversal occurring for both negative and positive fields. Inset is a schematic of the experimental setup. c,d The absolute value of the voltage versus current characteristic (I–V curve) at μ0H = 40 mT and −40 mT, respectively. For both fields, the non-reciprocal behavior is observed but with critical supercurrents Ic+ larger than ∣Ic−∣, which is contrary to the curve at zero field.

Full size image

Figure 5b displays ΔIc of device 1 plotted as a function of H. In this device, ΔIc is negative (i.e., Ic+ < ∣Ic−∣) at low fields (see Fig. 2c). As the in-plane field is ramped up, ΔIc approaches zero, and a sign reversal of ΔIc occurs at around 32 mT. At higher fields ΔIc remains positive with Ic+ > ∣Ic−∣, as shown in Fig. 5c. Such field dependence is independent of the field sweep direction. Figure 5d displays the I–V curve measured at −40 mT, where the Ic+ also exceeds ∣Ic−∣, similar to the I–V curve taken at +40 mT (Fig. 5c). For device 2 that also exhibits zero-field JDE (Fig. 2d) and half-wave rectification (Supplementary Fig. S12), ΔIc is consistently symmetric in H (yet without the sign reversal, Supplementary Fig. S12b). In contrast, JJs composed of thicker NbSe2 flakes (devices 3, 4, and 5) in which the zero-field nonreciprocal transport is absent are characterized by a centrosymmetric ΔIc (H) profile (Supplementary Figs. S8 and S9). This field-induced diode effect, which is antisymmetric in H, has been widely reported in many superconducting devices4,7,10. The distinct field evolutions strongly imply different physical origins of field-free and field-induced JDE in these JJs. According to existing understandings, the field-induced JDE has several possible origins (such as magnetochiral anisotropy, finite momentum Cooper pairing, or spin–orbit interaction); since the TRSB results from H, the sign of JDE thus depends on the polarity of H. Conversly, the field-free JDE in our devices do not rely on the field-induced TRSB and is thus irrelevant of the polarity of H. The symmetric field suppression of this effect again points toward its intrinsic nature, speaking against the trivial origins, such as residual flux or trapped vortex (Supplementary Note 3).

Discussion

According to the most recent understandings for equilibrium systems, the diode effect in retrapping current, ∣Ir+∣ ≠ ∣Ir-∣, can be achieved in devices in which only the IS is broken (i.e., under a TR-invariant condition); in contrast, the prerequisite of observing JDE with ∣Ic+∣ ≠ ∣Ic−∣ is the simultaneous breaking of IS and TRS3,16,17,18,19,20. Our data of JDE (Fig. 2) clearly point to the latter case, thus the breaking of both TRS and IS is an rigorous requirement for our vdW JJ devices 1 and 2. The IS breaking is a common phenomenon in JJ devices because of their stacked structure: there are misalignment and misorientation at the vdW interface27; moreover, at the interface, the topmost NbSe2 layers on each flakes naturally experience a top-bottom asymmetry due to the fact that the vdW gap is much larger than the interlayer spacing in the NbSe2 crystals (Fig. 1d). The strain effect arising during the transfer and stacking process is an important factor affecting the electronic structures of thin flakes and can also lead to the IS breaking due to the distinct strains on the top and bottom flakes of junctions41. In addition, the 2H-NbSe2 monolayer at the interface itself has a noncentrosymmetric crystal structure. Consequently, it is not surprising that our vdW JJs inherently break the IS.

The mechanism of the TRSB in our devices is more intricate. The zero-field JDE unambiguously corroborates spontaneous TRSB in the superconducting state, yet such an unusual symmetry-breaking effect is totally unexpected for the well-known conventional s-wave superconductor 2H-NbSe2. We examined the 2H-NbSe2 crystals used in experiments. They all have very high crystal quality and the magnetic impurity is negligible, as shown in Supplementary Fig. S13, excluding extrinsic magnetism as the origin of TRSB. (We also measured the I–V curve of NbSe2 flake in device 1 and observed symmetric critical current at H = 0, as shown in Fig. S13d.) Nonetheless, the skewed and centrosymmetric features appearing in the Fraunhofer pattern (Fig. 5a) and a local minimum of Ic at a small finite field (Supplementary Fig. S14), both of which resemble the typical behaviors of magnetic JJs14,28, point toward the realization of a nontrivial JJ with non-zero phase at zero field. Such phenomenon again provides evidence supporting the spontaneous TRSB in our 2H-NbSe2 vdW JJs. Several theoretical proposals have suggested that spontaneous TRSB can occur in JJs between a multi-band superconductor and a conventional (single-gap) superconductor due to the frustration between order parameters25,26. Although 2H-NbSe2 is an exemplary two-band superconductor42,43, our devices are homostructures composed of two identical NbSe2 flakes without apparent factors provoking the order parameter frustration between them. The applicability of these multi-band TRSB models is thus questionable. The NbSe2 flakes used to fabricate our devices were exfoliated from the same crystals and the flakes in device 1 even have the same thicknesses. Therefore, the nonreciprocity in our devices is unlikely to come from the nonlinear capacitance17. Recent studies have reported that the nonreciprocity at H = 0 may alternatively stem from the TRSB effect introduced by dissipation in the presence of strong electron correlations; in such case, the diode effects are characteristics of a nonequilibrium system41,44. Nonetheless, this is unlikely to serve as the explanation of our observations because the electron correlation in NbSe2 is believed to be rather weak.

It should be mentioned that not all our 2H-NbSe2 JJs composed of thin NbSe2 flakes exhibit the zero-field JDE; an exception (device 6) in which the nonreciprocal critical current is absent is shown in Supplementary Figs. S15 and S16. The distinct behaviors between devices may be indicative of TRSB mechanisms relying on the junction geometry, such as the twist angle between the top and bottom layers. Theoretical works on twisted JJs between nodal superconductors23,24,45 point out that spontaneous TRSB can happen around specific twist angles (so-called “magic angles”) and a field-free JDE can thus be established; these proposals have been recently verified in a twisted JJ composed of Bi2Sr2CaCu2O8+x crystals15. Numerous studies have confirmed that 2H-NbSe2 is an anisotropic s-wave superconductor with strongly k-dependent superconducting gap27,39,46. Therefore, it is worthy to test whether the twisted JJ models for nodal superconductors are valid in our devices. We examined the twist angles between two NbSe2 layers using electron back-scattered diffraction (EBSD) (see Supplementary Fig. S7). The twist angles of devices 1 and 2 (both show zero-field JDE) were determined to be 21∘ and 25∘, respectively, whilst device 6 featuring the absence of zero-field JDE has a twist angle of 26∘, i.e., very close to that in device 2. Whereas orbital magnetism driven by twist angle can give rise to spontaneous TRSB and consequently field-free SDE in graphene-based devices12,47,48, this mechanism is most likely irrelevant in our devices as suggested by the lack of characteristic hysteretic features under field sweeps (Supplementary Note 4 and Supplementary Fig. S6). Therefore all the existing evidence seems to contradict the scenario that TRSB corresponds to specific twist angles in our NbSe2 JJs. The origins of TRSB as well as difference between devices are yet to be determined at this stage.

Our results nevertheless demonstrate that it is unnecessary to introduce external fields, stray fields, or exotic superconductivity to realize JDE: a zero-field JDE can even develop in a vdW JJ between two s-wave superconductors, without the incorporation of special tunneling barriers or ferromagnetic layers. Benefiting from their simple design, broad range for potential material choice and high device performance (as justified by the stable and robust superconducting half-wave rectification effect over 5000 continuous cycles, Fig. 3), these vdW JJs may serve as promising candidates for practical device application. On the other hand, mechanism of the spontaneous TRSB effect herein is not fully understood within the framework of any existing theories. Further theoretical explorations are urgently awaited to interpret the observed zero-field JDE in vdW JJs composed of only conventional superconductors.

Methods

Crystal growth

High-quality 2H-NbSe2 single crystals used in this work were synthesized through chemical vapor transport method. Stoichiometric ratio of Nb (powder) and Se (pellet) were evacuated and sealed in a 250 mm long and 20 mm diameter quartz tube with 0.2% excess of Se and 150 mg iodine. We added a very slight excess of Se to ensure stoichiometry in crystals. Then, the tube was placed in a double zone furnace horizontally with a temperature gradient from 690 ∘C to 750 ∘C for three weeks. After that, sheet crystals of 2H-NbSe2 can be found at the low-temperature end.

Device fabrication

The JJ devices were fabricated through a dry-transfer method in a top-down process which can avoid the residue of polymers. To minimize surface oxidation and decay of NbSe2 layers, the entire fabrication process was carried out in an Ar-filled glovebox (H2O, O2 < 0.1 ppm). NbSe2 and h-BN crystals were exfoliated on SiO2 (285 nm)/Si substrates using Scotch tapes. Ti (3 nm)/Au (20 nm) bottom electrodes were deposited onto SiO2/Si substrate using photolithography and electron beam evaporation. The h-BN thin flake, the top NbSe2, and bottom NbSe2 were sequentially picked up at 40 ∘C by a thick polydimethylsiloxane film coated with a thin layer of polypropylene carbonate (PPC), which was prepared on a glass slide31. The stack was then transferred onto the pre-patterned metal electrode at 90 ∘C and the PPC was removed in chloroform. Devices 1, 2, and 6 were fabricated with thin NbSe2 flakes of around 10 nm and devices 3, 4, and 5 were fabricated with thicker flakes (more than 30 nm).

Transport measurements

Transport measurements were carried out in physical property measurement systems (Quantum Design) down to 2 K. For the measurement of T-dependent resistance, an AC current of 10 μA with a frequency of 19.711 Hz was applied and the voltage signal across the junction was measured using a SR830 lock-in amplifier. The DC and square-wave measurements were performed by a Keithley 6221 current source and a Keithley 2182A nanovoltmeter. For I–V and dV/dI (including the Fraunhofer pattern) measurements, a Keithley 6221 was used to inject DC current and a small AC excitation (10 nA and 277 Hz) was supplied by the SR830 lock-in amplifier combined with a 1 MΩ high precision resistor. The DC voltage was measured by Keithley 2182A nanovoltmeter and the AC voltage signal was amplified by the SR560 preamplifier and measured by SR830. To obtain a better signal-to-noise ratio, two sets of filters were used in the dV/dI measurement : (i) four homemade low-pass filters with cut-off frequency around 470 kHz, (ii) the built-in filter of the preamplifier SR560. More details of the measurement setups are available in Supplementary Note 1.

Structural analysis of devices

Scanning electron microscope (SEM)-EBSD experiments were performed using an Oxford Symmetry S2. For cross-sectional STEM measurement, the samples were prepared using a focused ion beam with Ga ions. Then, STEM experiments were conducted on a 300 kV Themis Z microscope. The atomic resolved HAADF-STEM images were collected with a 25 mrad convergent angle and a collection angle of 41–200 mrad.