Introduction

Plasma-based wakefield acceleration with an ultrahigh accelerating field above 100 GV/m is now becoming an aspiring technology in the acceleration community1,2,3. The trapped charged particles can obtain an ultrahigh energy gain within a short acceleration length, characterized by inherent synchronization with the driving source. Recently, the generation of bright and stable multi-GeV electron bunches4,5,6,7,8 has been reported by exploiting the laser-driven wakefield accelerator (LWFA), as well as the efficient high-energy electron or positron acceleration in the particle-driven wakefield accelerator (PWFA)9,10,11. The bright bunch from a plasma-based accelerator (PBA), possessing its unique advantages, has been applied in developing compact X-ray free-electron lasers (FELs)12,13,14, bright high-energy radiation sources and even future colliders15,16. However, the minimum energy spread reported so far is just below one percent, which is still far from enough for realizing a high-gain FEL. Breaking through the barrier of one-thousandth energy spread to a one-ten-thousandth level is thus badly desired but remains one of the key challenges for developing extremely bright particle sources.

The energy spread in a PBA is primarily introduced and accumulated during both the injection and acceleration processes. Nowadays, with the optimized injection schemes, such as density transition injection17,18,19, optical ionization20,21, or colliding injection22,23, the intrinsic energy spread of the injected beam could be reduced to a few MeV or even to hundreds of keV level. Therefore, the deterioration of the energy spread mainly comes from the longitudinal energy chirp accumulation due to the acceleration phase variance of a PBA. In order to overcome this issue, quite a few schemes have been explored to reduce the energy spread in a PBA, such as by introducing beam loading effect24,25,26,27,28,29, inserting a plasma compressor30, a plasma dechirper31,32, a magnetic chicane33, longitudinal phase-space manipulation34 or using a periodical density-modulated plasma to generate a flat accelerating field35. Using a tailored plasma to control laser-beam evolution to minimize the energy spread to a few per-mille level has also been demonstrated8,29,36. But it is still very hard and unforeseeable to break through the barrier of the per-mille energy spread in a LWFA.

Generally, the LWFA is operated in the nonlinear blowout regime in order to trap electrons and obtain a high accelerating electric field where the accelerating field profile is highly nonlinear in sawtooth-shape and unstable, providing little room for manipulation of the electron dynamics with more freedom since it has a much wider area with positive-slope accelerating field Ez but a very narrow area with negative-slope accelerating field. Owing to the positive-slope acceleration field, an initially negatively chirped electron bunch undergoes self-compensate energy de-chirping first and then continuous chirping growth in acceleration8,27,30,37. A negative-slope acceleration field should be introduced to de-chirp the energy spectrum to implement energy spread reduction. By contrast, a quasi-linear laser-wakefield accelerator (QLWFA) driven by a moderately intense laser pulse will have a longitudinal sinusoidal-like wakefield with a symmetrical distribution for both the negative- and positive-slope acceleration field. It can provide a good solution to de-chirp the electron bunch by introducing it into the negative-slope acceleration zone. On the other hand, in a QLWFA, the plasma wave provides a λp/4 region that is both focusing and accelerating for either electrons or positrons, without requiring a hollow plasma channel38,39,40, donut-shaped electron beam41 or Laguerre-Gaussian driving laser42 to provide the extra transverse focusing force and emittance preservation particularly for positron acceleration. Besides, a stable propagation without significant fluctuation of laser intensity and the wakefield in the quasi-linear regime would be beneficial for the de-chirping manipulation as well as stable acceleration, because the unfavorable nonlinear instabilities in the blowout regime can be minimized.

Here, we thus propose a promising scheme to break through the barrier of one-thousandth energy spread by designing a quasi-linear laser-driven wakefield accelerator with density-modulated plasmas to periodically chirp and de-chirp the seeded electron or positron bunch in the plasma wave while implementing GeV-energy acceleration. By using a uniquely designed density-modulated plasma, a quasi-linear plasma wave, with a sinusoidal-like wakefield structure and stable propagation of more than 30-fold Rayleigh lengths, can be generated to stably accelerate both the electron and positron bunches up to GeV scale in quasi-three-dimensional particle-in-cell (quasi-3D PIC) simulations. The accumulated energy chirp of the particle bunch is almost eliminated in each period during the periodical quasi-phase-stable acceleration to possess an ultimate root-mean-squared (rms) energy spread less than 0.05% while maintaining its small beam emittance, indicating this scheme is highly feasible and desirable for achieving an ultralow-energy-spread plasma-based accelerator.

Results

Periodical de-chirpings with a density-modulated plasma

For this purpose, we design a QLWFA with a density-modulated plasma (DMP) to periodically chirp and de-chirp the seeded electron bunch in the plasma wave for implementing acceleration and energy spread reduction, and the scenario is generally presented in Fig. 1. In the QLWFA scheme, a quasi-linear plasma wave is formed behind the laser with the propagating group velocity \({\nu }_{g}\simeq c{(1-{\omega }_{p}^{2}/{\omega }_{0}^{2})}^{1/2}\) and its longitudinal and transverse fields can be given by

$${E}_{z}(r,\xi )={E}_{z,0}{e}^{-\frac{{r}^{2}}{2{\sigma }_{r}^{2}}}\! \cos ({k}_{p}\xi )$$
(1)
$${E}_{r}(r,\xi )-c{B}_{\theta }(r,\xi )=-{E}_{z,0}\frac{r}{{k}_{p}{\sigma }_{r}^{2}}{e}^{-\frac{{r}^{2}}{2{\sigma }_{r}^{2}}}\!\sin ({k}_{p}\xi )$$
(2)
Fig. 1: Bunch energy chirping and de-chirping in plasma wake.
figure 1

a A schematic diagram of a QLWFA with a density-modulated plasma to achieve high-energy acceleration with the energy spread reduction to the one-ten-thousandth level via periodical de-chirpings. The insets show the repeated energy chirping and de-chirping process for each period. b, c Electron bunch located at positive-slope (\({{{\rm{d}}}}{E}_{z}(\xi )/{{{\rm{d}}}}\xi \, > \, 0\)) and negative-slope (\(d{E}_{z}(\xi )/d\xi \, < \, 0\)) acceleration zones in one period, respectively.

Full size image

with Ez,0 the amplitude of the longitudinal field component2. For a plasma electron density of np = 1018 cm−3, the plasma wavelength is λp ≈ 33.4 μm and the maximum accelerating gradient is around \({E}_{z,0} \sim 0.15{E}_{wb}\), corresponding to 15 GV/m, where \({E}_{wb}(V/m)\approx 96\sqrt{{n}_{p}(c{m}^{-3})}\) is the wave-breaking electric field. The gradient of the longitudinal acceleration field \({{{\rm{d}}}}{E}_{z}(\xi )/{{{\rm{d}}}}\xi\) is proportional to \({k}_{p}{E}_{z,0}sin({k}_{p}\xi )\), the chirping strength varying from −1.8 to 1.8 MV/mm/μm and possessing two symmetrical zones with negative and positive slope respectively, which can imprint an energy chirp change \({\alpha }_{i}(\xi )\approx -e{\sigma }_{z}\cdot d{E}_{z}(\xi )/d\xi\) on the bunch with a length of σz. By designing a periodical DMP (see Fig. 1a), the seeded electrons in the wave can be switched from a positive-slope zone to a negative-slope one periodically when the driving laser propagates through the DMP, as the wave cavity size is inversely proportional to the plasma density in Fig. 1b, c. Assuming an appropriately designed periodic DMP, the electron bunch can undergo periodical chirping and de-chirping processes many times and the relative energy spread can be reduced without limitation theoretically.

Since the accelerated bunch has a slightly higher velocity than the laser group velocity, it will experience a dephasing process, slipping forward to make the de-chirping and acceleration terminated rapidly. Therefore, the phase matching among the electron bunch, periodical DMP and the driving laser should be satisfied for realizing this chirp mitigation strategy, with the bunch repeated switching around the field crest Ecrest at ξ = 0 to get an efficient acceleration without the beam degradation. For this purpose, a quasi-phase-stable acceleration is required and the plasma is designed to have a periodical density distribution but with a slow stepwise rise of density in each following period, as shown in Fig. 1a and Fig. 2d. The modulated plasma density profile along the laser propagation can be generally given by

$$\begin{array}{c}n(z)={n}_{1}\cdot H(z,0,{z}_{0})\frac{z}{{z}_{0}}+{\sum }_{i=1}^{N}{n}_{i}\cdot H(z,{z}_{1,i},{z}_{1,i+1})+\left[2-cos\left(\frac{2\pi }{{L}_{2,i}}(z-{z}_{2,i})\right)\right]\cdot \\ \frac{\Delta {n}_{i}}{{L}_{2,i}}(z-{z}_{2,i})\cdot H(z,{z}_{2,i},{z}_{1,i+1}),\\ H(z,{z}_{1},{z}_{2})=\Theta (z-{z}_{1})-\Theta (z-{z}_{2}),\\ {z}_{1,i}={z}_{2,i-1}+{L}_{2,i-1} \quad (i \, > \, 1),\\ {z}_{2,i}={z}_{1,i}+{L}_{1,i}\end{array}$$
(3)

where H(z, z1, z2) is equal to one between z1 and z2 as composited by the Heaviside function \(\Theta (x)\), z11 = z0 and Δni, L2,i = L0 and L1,i(i = 1,2,3…N) are the corresponding density difference, modulation pedriod and flat plasma length for the ith-stage, respectively.

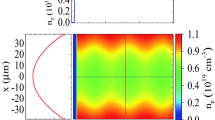
Fig. 2: Generation of DMP from a structured gas cell and laser propagation inside it.
figure 2

a A structured gas cell to produce a periodical density-modulated gas flow. b Snapshot of the corresponding stable gas density profile at t = 15 ms after injecting the helium gas into the inlets in the 3D fluid simulations. c Evolution of laser intensity (blue line) during the channel-guided propagation in the DMP. d Typical on-axis plasma density profiles along the laser propagation for the cascaded DMP are plotted from the corresponding 2D (red dashed line) and 3D (blue line) fluid dynamics simulations, in good consistence with the one in the PIC simulations (green line). e Evolution of the gas flow from the gas injecting at t = 0.5 ms to the stabilized state at t = 10 ms as designed.

Full size image

For convenience, each DMP can be made of one flat plasma with a suitable length \({L}_{1,i}\) and a cosine-profile-like modulated plasma with the same modulation period L0 by connecting the two adjacent stages, as shown in Fig. 2a and d. In order to maximize the energy gain, a preformed plasma channel is used to guide the laser for a long-distance propagation, having a transverse density distribution as \(n\left(r\right)={n}_{0}+\Delta n{r}^{2}/{r}_{0}^{2}\), where n0 is the on-axis density and ∆n the channel depth. These required plasmas, analogous to the corrugated-like plasma channel43,44,45, can be created via the plasma machining in the structured gas cell, as shown in Fig. 2a, which has been utilized in analogous experiments46. In order to make clear the generation of the cascaded DMP in practice, as shown in Fig. 2b, the relevant 2D and 3D fluid dynamics simulations of the gas flow in the channel are also carried out with ANSYS Fluent code47 to justify the density profile (see Methods). It’s seen that the required DMP, as shown in Fig. 2d, can be produced by carefully cascading the gas stages and independently controlling the input gas pressure for each stage, matching well with the density profile in the PIC simulations. The simulated gas flow has already become stabilized around t = 10 ms after the gas injecting into the inlets and the fluctuation of the on-axis plasma density profile can be smaller than 2%, which is in favor of manipulating the periodical de-chirpings and beam rephasing in a robust and flexible way.

Electron acceleration and chirp modulation in a QLWFA

In order to get insight into the periodical de-chirping and acceleration process in detail, we have performed quasi-3D PIC simulations with the code FBPIC48,49 to concurrently investigate the dynamic evolutions of the seeded bunch and driving laser in a DMP (see Methods). This kind of a QLWFA just needs an on-target peak power of 20 TW, which is much lower than the previous hundreds of TW or PW laser system, and an average plasma density of ~7 × 1017 cm−3 is used here for a DMP to eliminate the unfavorable intense nonlinear effects and make the high-repetition operation feasible as well. A matched quasi-linear propagation of the laser beam in a plasma50 is realized as shown in Fig. 2c. Besides, periodical de-chirpings and quasi-phase-stable acceleration of the seeded electron bunch (see Methods) are achieved by optimizing the DMP and its injection location.

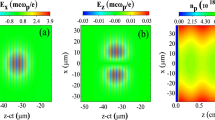
Figure 3a–e shows the dynamic evolution of the electron bunch’s energy chirp in one period of the DMP. In the beginning, the tested Gaussian-profile electron bunch (see Methods) with a negative energy chirp, having a beam charge of 1 pC, short duration of 4 fs and transverse size of 2 μm, is firstly located on the right side of the field crest (ξ > 0) and will be accelerated while undergoing energy de-chirping and chirp reversal during the following flat low-density stage from z = 32 mm to z = 44 mm, as shown in Fig. 3a, b. Then this positively chirped electron bunch is shifted backward to the negative-slope acceleration zone (ξ < 0) by increasing the plasma density from z = 45 mm. Similarly, the electron bunch is then accelerated while undergoing energy de-chirping and chirp reversal once again, which is shown in Fig. 3c–e. This cycle of energy chirping and de-chirping can be repeated many times if an appropriate DMP is designed. The final energy chirp from the wake accumulated as \(\delta E\approx {\int }_{0}^{z}-e{\sigma }_{z} \, {{{\rm{\cdot }}}} \, ({{{\rm{d}}}}{E}_{z}/{{{\rm{d}}}}\xi ){{{{\rm{d}}}}z}\) can thus be optimized to keep a small absolute energy spread (AES), and the RES will be significantly reduced accordingly owing to the continuous energy gain during the quasi-phase-stable acceleration51,52 and beam rephasing among the stages53,54 in Fig. 3f. However, it’s worth noting that for the small beam charge, the unfavorable beam loading effect has been avoided or weakened as much as possible to avoid the undesired chirp modulation on the longitudinal accelerating field itself or the spoiling of rephasing process. Nevertheless, by properly matching the parameters of the seeded bunch with the DMP and laser pulse, it’s possible to implement the effective periodical de-chirpings and bunch rephasing for reducing the RES down to a one-thousandth level in such a QLWFA even with a beam charge up to 5 pC.

Fig. 3: Chirp modulation of the seeded electron bunch with and without the DMP.
figure 3

a–e Evolution of the correlated energy chirp and the plasma wave while undergoing the chirp modulation due to the DMP in one period. f, g The localized chirp characteristic dEz/dξ experienced by the electron bunch (dash black) for the cases with and without the DMP, respectively. The laser (red dashed) slips backward with respect to the bunch during the acceleration.

Full size image

In each period of this DMP, the electron bunch is confined well around the longitudinal axis of the wake to obtain good transverse focusing to preserve emittance, and the field crest (ξ = 0) is shifted forward accordingly by increasing the plasma density in a stepwise way to catch up with the accelerating bunch for implementing a quasi-phase-stable acceleration, as shown in Fig. 4a–i. During the periodical de-chirpings, the AES of the seeded bunch evolves repeatedly between 0.21 MeV and 0.79 MeV in the acceleration and the corresponding RES is then decreased to be smaller than 0.06% at z = 45.8 mm. This ultralow energy spread is kept well until the electron bunch with its initially small size is accelerated to the peak energy of 0.72 GeV at z = 67.4 mm in Fig. 4j.

Fig. 4: GeV-energy electron acceleration and emittance maintenance within a DMP.
figure 4

Snapshots of electron density distribution in (a–c), transverse focusing field in (d–f), on-axis longitudinal field in (g–i) of the wake at different z. The insets in (g–i) represent the corresponding electron energy phase space distribution. j Evolution of the energy (black solid line) and RES (red solid line) for the electron bunch with the same beam charge of 1 pC, short duration of 4 fs and transverse size of 2 μm, while performing the DMP, in comparison with the flat-profile plasma (the dash lines). k Evolution of the beam emittance along its propagation for the DMP case.

Full size image

However, when the plasma density of the DMP is gradually increased to exceed 9 × 1017 cm−3 from z = 68 mm, the laser beam starts self-focusing and an undesired nonlinear wake is excited to hinder the subsequent de-chirping, making a rapid increase of the RES larger than 1 × 10−3 and significant emittance growth hereafter. Nevertheless, after matching the seeded beam with stable laser evolution and tailored plasma from the very begining55, the matched transport before z = 68 mm is still obtained in the whole DMP and the beam degradation is suppressed to sustain the initial small beam emittance in Fig. 4k but only with an overall growth of ~ 0.12 mm mrad. This relatively minor emittance growth is mainly induced owing to the weak transverse defocusing field during the de-chirpings in the negative-slope acceleration zone and the accumulated mismatching as for the following unavoidable nonlinear focusing forces and transverse chromatic phase spreading in plasma. These results make clear that both the accumulated energy spread and emittance growth can be minimized effectively by implementing periodical de-chirpings with a uniquely designed DMP. It’s also worth noting that some weak nonlinear energy chirp will appear on both ends of the electron bunch after several-period de-chirping, which are mainly caused by the local weakly distorted accelerating field Ez affected by the Gaussian-profile electron bunch as shown in the insets of Fig. 4g–i. Nevertheless, it doesn’t have a significant effect on the energy spread minimization.

For the case of no DMP, a uniform plasma with a density of 7 × 1017 cm−3 but with the same laser and bunch parameters is performed to make a comparison. As observed, the transversely matched electron bunch always slips forward and only experiences one-way energy chirping in the positive-slope accelerating field, as shown in Fig. 3g, which is universal for a PBA. Consequently, the AES after its initial self-compensation increases rapidly up to 14.4 MeV with an obvious RES deterioration up to 3.1% after z = 60 mm in Fig. 4j. Moreover, due to the absence of quasi-phase-stable acceleration, the maximum energy gain is only 423.3 MeV, which is almost halved as compared with the DMP case.

Positron acceleration and energy-spread reduction

In addition to the electron acceleration, the GeV-energy acceleration and energy-spread reduction of a positron bunch are also realized with this DMP scheme. Similarly, the positron bunch is injected with a proper phase into a QLWFA with a DMP to undergo the periodical de-chirpings and quasi-phase-stable acceleration, which are shown in Fig. 5a–d. As a result, the injected positron bunch can obtain a higher energy gain of 1.28 GeV after a longer acceleration and dephasing length of 95 mm. The positrons are all focused transversely in close vicinity to the axis and located in the front λp/4 region of the second wave where the positrons witness both the transverse focusing field Ex and the longitudinal accelerating field Ez in Fig. 5e–h, which can minimize emittance growth during the acceleration. Actually, the phase space matching for emittance preservation56 has also been taken into consideration for positron bunch propagation between stages to reduce the undesired chromatic emittance growth in the density ramp57 as far as possible. When optimized by a suitable DMP, the AES can be kept smaller than 1 MeV until z = 89.6 mm with the peak energy being increased up to 1.13 GeV in Fig. 5i. The minimum RES of 0.045% is obtained at z = 61.2 mm, corresponding to the peak energy of 574 MeV with an AES of 0.26 MeV there.

Fig. 5: Positron acceleration with a DMP in simulations.
figure 5

Snapshots of the electron density distribution in (a–d), longitudinal accelerating and transverse focusing fields in (e–h) of the wake experienced by the positron bunch while using a DMP. i Evolution of the peak energy (black) and AES (blue) of the positron bunch. j The resulted energy spread and energy gain as a function of the beam charge for the GeV-energy positron acceleration.

Full size image

Benefiting from the utilizing of the DMP, the emittance growth of the positron bunch is suppressed well to be less than 20% even after a 60-mm-long propagation from the beginning, as shown in Fig. 6. However, once the quasi-linear wake starts turning into the nonlinear one with the increasing plasma density, the emittance of the accelerating positron bunch begins degrading faster from z = 82.4 mm (see light blue area in Fig. 6) and the decoherence or phase mixing of the energy slices appear therewith, on account of the imperfect transverse fields and undesirable chirp modulation. Meanwhile, out of operation in QLWFA, the energy spread also grows quickly from z = 90 mm, together with the larger emittance growth. Extra mitigation strategies for the existed chromatic phase spreading or nonlinear energy chirp58,59 can further improve the brightness of the particle bunch in the future.

Fig. 6: Evolution of positron energy spectra and emittance.
figure 6

Typical energy spectra and the emittance (brown and cyan) of the positron bunch evolved along its acceleration in a DMP. The inset represents the energy spectrum (green) and beam current (blue) at z = 60 mm, which has an ultralow energy spread of 0.048%.

Full size image

While increasing the beam charge with the matched bunch length, this QLWFA is still capable of accelerating a kA-current positron bunch with the energy gain above 1 GeV and energy spread reduction below one thousandth, as shown in Fig. 5j. But for a larger beam charge up to 8 pC, the beam loading effect comes into play by locally flattening the desired slope of accelerating fields and deteriorating the beam emittance and projected energy spread. Nonetheless, the desired periodical de-chirpings and efficient acceleration of a higher charge bunch can be correspondingly realized by increasing the plasma density, the laser spot size or using a transversely shaped driver profile60 with this scheme. For this specific parameter setup, the typical energy spectra and emittance evolution of the positron bunch are plotted in Fig. 6, where these rms energy spreads are all < 0.1% and the emittance growth is suppressed to be less than 0.1 mm mrad over a 72-mm-length propagation. To the best of our knowledge, this kind of high-quality GeV-energy positron acceleration with a rms energy spread reaching 0.05%, together with emittance preservation, has not been achieved or reported in a PBA yet.

Conclusion

We have demonstrated an effective and promising scheme to break through the barrier of one-thousandth energy spread by designing a QLWFA with a unique DMP to periodically chirp and de-chirp the injected particle bunch. Combined with the quasi-phase-stable acceleration, the high-energy high-quality particle acceleration is accomplished for both the electron and the positron bunch with the rms energy spread being reduced to the order of 0.05% for 1 pC charge beams while preserving a low emittance over the long-distance beam acceleration. By performing this kind of DMP with a lower average density and a higher-power driving laser, this QLWFA scheme has the potential to reduce the energy spread further to a one-hundred-thousandth (1 × 10−5) level when the electron bunch is accelerated to multi-GeV. It can also be scaled up to higher energy by employing a cascade acceleration scheme in a straightforward way. Such an advanced QLWFA with minimized nonlinear instabilities can act as an ideal high-performance plasma accelerator, which has elaborately integrated the techniques of periodical de-chirpings and quasi-phase-stable acceleration to manipulate the energy spread flexibly, making it highly feasible and desirable to generate ultralow-energy-spread high-energy particle bunches and therefore facilitate broader applications such as the development of the future compact free-electron laser and beyond.

Methods

Fluid dynamics simulations for DMP generation

The two-dimensional (2D) and three-dimensional (3D) fluid dynamics simulations are carried out with the CFD software ANSYS Fluent47 solving the Navier-Stokes equations. The k-ω shear stress transport (k-ω SST) turbulence model61,62 is used in a robust and efficient way, which adopts the k-ω formulation near the boundary layers and then switches to the k-ϵ formulation in the free-stream. Simulations are performed using helium gas and each gas entrance of the structured gas cell is provided with different back pressure as required to get the matched gas density profile as used in the PIC simulations. The mesh of the gas cell is refined to have a resolution of 5 μm around regions of interest at each DMP and the convergence has been guaranteed to ensure the accuracy. Full-multigrid initialization (FMG) has also been used to obtain an initial guess of the solution thus allowing faster convergence.

Particle-in-cell simulations

Quasi-three-dimensional (Quasi-3D) particle-in-cell (PIC) simulations are performed with the code FBPIC48,49. The grid cell size has a resolution of Δz = 0.04 μm in longitudinal and Δr = 0.125 μm in the radial directions, with 16 macroparticles per cell and an azimuthal mode number of Nm = 2, for a moving simulation window of z × r = 120 × 100 μm2. A linearly polarized laser pulse with the wavelength of λ0 = 0.8 μm, a normalized amplitude of a0 = 0.8, a pulse duration of τ = 30 fs, and a focal spot size of w0 = 30 μm, having a Rayleigh length of ZR = πw02/λ0 ≈ 3.5 mm, is then incident on the DMP with density rising periodically from 3 × 1017 to 2 × 1018 cm−3 to drive a QLWFA.

The on-target peak power of 20 TW is much lower than the previous hundreds of TW or PW laser systems and satisfies \(P \, < \, {P}_{c}\approx 17.4{\omega }_{0}^{2}/{\omega }_{p}^{2}[{GW}]\), where the critical power Pc ≈ 44 TW is estimated for an average plasma density of ~7 × 1017 cm−3 here. It is beneficial for eliminating the unfavorable intense nonlinear effects and making the high-repetition operation feasible as well.

Seeded particle bunch in simulations

An external Gaussian-profile electron or positron bunch of 50 MeV, with an initial relative energy spread (RES) of σγ/γ = 1%, bunch length of σz = 4 fs, transverse size of σr = 2 μm, beam charge of 1 pC and normalized emittance of εn = 0.3 mm mrad, is injected into the plasma-based wakefield at a matched position from the entrance. The electron bunch with a negative or positive energy chirp is firstly released on the right (ξ > 0) or left (ξ < 0) side of the field crest in the sinusoidal-like wake and will be accelerated while undergoing energy de-chirping and chirp reversal from the beginning. A similar strategy is used for the positron bunch to re-install its initial location and should ensure the phase matching in demand with the driving laser pulse. The bunch charge and other specific profile can also be tailored based on the demand of the actual energy gain and target energy spread in this scheme.