Uncooled thermal infrared detection near the fundamental limit using a silicon nitride nanomechanical resonator with a broadband absorber

Abstract

Thermal infrared detection plays a critical role in applications like environmental monitoring and biomedical sensing. While many infrared detectors operate at room temperature with broadband spectral detection, their sensitivity is limited by noise from sources such as electronic readout and photothermal back-action. This paper introduces a thermal infrared detector using a nano-optomechanical silicon nitride resonator with a free-space impedance-matched platinum thin-film absorber, achieving an average broadband absorptance of 47%. To reduce photothermal back-action, the absorber incorporates a circular clearance for the laser. The thermal time constant is τ_th = 14 ms for the smallest 1 mm resonators, which also exhibit the best sensitivity with a noise equivalent power of 27 pWHz^−1/2 and a specific detectivity of $3.8\times 1{0}^{9}\,{{{\rm{cm}}}}\sqrt{{{{\rm{Hz}}}}}{{{{\rm{W}}}}}^{-1}$. Experimental results are compared to analytical models and finite element method simulations. These results place our resonators among the most sensitive room-temperature infrared detectors reported to date.

Introduction

Infrared (IR) detectors are crucial tools in a wide range of applications, including spectroscopy, imaging, environmental monitoring, and thermal sensing. They can be broadly categorized into two types: photon detectors and thermal detectors¹. Photon detectors, such as quantum well and HgCdTe (MCT) detectors, are highly sensitive but typically require cryogenic cooling to achieve optimal performance. In contrast, thermal IR detectors, such as thermopiles, bolometers, and pyroelectric detectors, operate effectively at room temperature, making them more practical and cost-effective for many applications. These thermal detectors measure IR radiation by converting it into a temperature change, which then induces a measurable response. This room-temperature operation, coupled with the ability to detect a broad spectral range, gives thermal IR detectors a distinct advantage in applications where cooling is impractical or where spectral broadband detection is required.

Despite advancements in uncooled thermal detectors, their sensitivity has remained significantly below the fundamental detection threshold at room temperature given by the specific detectivity ${D}^{* }=1.4\times 1{0}^{10}\,{{{\rm{cm}}}}\sqrt{{{{\rm{Hz}}}}}{{{{\rm{W}}}}}^{-1}$ for front and backside coupled detectors, which is dictated by temperature fluctuations of both the detector and its surrounding environment^1,2,3,4. Conventional thermal detectors that rely on thermoelectric detection schemes are typically limited by electronic noise, e.g., Johnson noise or 1/f noise, which restrict their sensitivity, particularly when operating at room temperature. This noise originates from the electronic readout circuits that convert thermal signals into electrical signals, making it challenging to achieve a sensitivity close to the fundamental limit.

To overcome the existing limitations of thermoelectric detectors, alternative thermal detection mechanisms have been explored. One approach is thermal IR detection with a temperature-sensitive mechanical resonator. The idea of a mechanical resonator used as thermal IR detectors dates back to 1969⁵. Microelectromechanical system-based (MEMS) IR detectors have been introduced in 1996⁶. Advancement in nanofabrication techniques allowed the development of the first nanoelectromechanical system (NEMS) for frequency-shift-based infrared thermal sensing⁷. This work was shortly followed by others^8,9 and nowadays, NEMS resonators are used in applications ranging from IR spectroscopy¹⁰ to the detection of visible¹¹, IR¹², and terahertz (THz) radiation^13,14.

To maximize the amount of absorbed IR light, a widely used strategy is to exploit the optical properties of metamaterials, such as plasmonic antennas, which reach almost 100% absorptance^{13,15,16,17,18,19,20}. However, the exceptional absorption properties of such devices are limited to a narrow spectral range^{13,17,18,19,20} and their fabrication is complex¹⁵. Free space impedance-matched (FSIM) absorbers are an alternative to high-efficiency narrow-band absorbers. FSIM absorbers offer a nominal absorptance of 50% over a wide spectral range spanning the entire infrared regime. A constant absorptance is essential, e.g., for use in IR spectroscopy. FSIM absorbers can be made of a few nanometer-thin metal films, such as Au²¹ or Pt¹². The small thermal mass of such thin metal films is important to the detector’s performance.

While NEMS-based IR detectors featuring an FSIM absorber have achieved sensitivities as low as 7 pWHz^−1/212, the sensitivity remained significantly below the fundamental limit. It has been shown that the readout noise of high-Q nanomechanical resonators can negatively affect the resonator’s frequency stability, due to the so-called Leeson effect in oscillator circuits^22,23,24. Here, we present a nanomechanical IR detector with an optical interferometric readout instead of an electric readout. Such a square nanomechanical silicon nitride (SiN) membrane resonator, featuring an FSIM absorber, is shown in Fig. 1. To mitigate frequency noise from the photothermal back action of the readout laser, which can be significant²⁴, the membrane features a clearance in the FSIM absorber located at anti-nodal points of the (2,2) or (3,3) mode. Furthermore, the detector is placed within an artificial thermal bath during measurements to stabilize the radiative heat transfer of the resonator with the environment.

Fig. 1: Schematic representation of the infrared measurement setup.

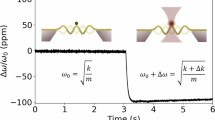
The resonator is housed inside a copper block, which is placed within a vacuum chamber. A laser vibrometer probes the membrane’s vibration through the upper optical aperture. The signal is fed into a lock-in amplifier with a phase-locked loop (PLL) that continuously corrects the phase error between the membrane’s oscillation and the internal oscillator, ensuring accurate tracking of the resonance frequency and controlling the actuation frequency of the piezoelectric element. For thermal characterization, an infrared source is coupled into an optical fiber and focused onto the resonator using two gold-coated parabolic mirrors through the bottom optical aperture. The infrared beam is modulated by an optical chopper positioned between the mirrors. The lock-in amplifier output is recorded for later analysis. Inset: optical microscope picture of a 1 mm membrane featuring a free-space impedance-matched absorber, showing a circular clearance for the readout laser. Scale bar is 200 μm.

The performance of IR detectors is characterized by the following figures of merit: the thermal time constant τ_th, the noise equivalent power NEP, and the specific detectivity D^*1. The NEP represents the sensitivity in units [WHz^−1/2]. As nanomechanical resonators detect incident IR radiation via detuning of the resonance frequency, the NEP is given by²³

$$\,{{\mbox{NEP}}}\,(\omega )=\frac{\sqrt{{S}_{{{{\rm{y}}}}}(\omega )}}{{R}_{{{{{\rm{P}}}}}_{{{{\rm{0}}}}}}(\omega )\alpha },$$

(1)

where S_y(ω) is the frequency stability of the resonator (fractional frequency noise power spectral density) with units [Hz⁻¹], ${R}_{{{{{\rm{P}}}}}_{{{{\rm{0}}}}}}$ is the relative power responsivity with units [W⁻¹], and α is the absorptance of the NEMS detector, the ratio between the absorbed power P and the impinging source power P₀.

The responsivity of a nanomechanical resonator characterizes the detuning of its eigenfrequency ω₀ per absorbed radiation power P and is defined by²³

$${R}_{{{{\rm{P}}}}}(\omega )=\frac{\partial {\omega }_{0}}{\partial P}\frac{1}{{\omega }_{0}}{H}_{{{{\rm{th}}}}}(\omega )$$

(2)

with the low-pass filter transfer function

$${H}_{{{{\rm{th}}}}}(\omega )=\sqrt{\frac{1}{1+{(\omega {\tau }_{{{{\rm{th}}}}})}^{2}}}.$$

(3)

For quantum detectors or thermal detectors operating at the quantum limit, the sensitivity scales with the square root of the detector area A²⁵. Normalizing the sensitivity with A results in the specific detectivity D^* in units [${{{\rm{cm}}}}\sqrt{{{{\rm{Hz}}}}}{{{{\rm{W}}}}}^{-1}$]^2,26

$${D}^{* }=\frac{\sqrt{A}}{\,{\mbox{NEP}}\,}.$$

(4)

Subsequently, we evaluate the performance of the nanomechanical IR detector based on these figures of merit.

Methods

Resonator fabrication

The resonators consist of 50 nm thick LPCVD deposited silicon nitride membranes of 1000 μm, 2000 μm and 3000 μm side lengths. The initial nominal stress of the SiN was 50 MPa. A Pt thin film, with a target thickness of 5 nm, was deposited by e-beam physical vapour deposition. The circular clearance was created by a lift-off process. Finally, the membranes were released from the backside by a KOH wet etch through the wafer. To protect the metal film during the wet etching process we use a wafer holder which exposes only the backside of the wafer.

Measurement setup

For the measurements, a membrane is placed inside a custom-made, high-vacuum (~ 10⁻⁵ mbar) chamber. This has the double benefit of increasing the Q factor (getting rid of medium losses²³) and reducing thermal losses (convection heat transfer can be neglected for pressures  < 10⁻³ mbar). The chamber has two optical accesses, one for the measurement laser (top) and one for the IR light (bottom). The enclosures feature a silica glass window on the top and a diamond window (Diamond Materials GmbH) on the bottom, the latter specifically designed to ensure optimal transmission of mid-infrared (MIR) light. Furthermore, the membrane is placed inside an artificial thermal bath made from a copper block. Both the lid and the bottom provide a hole aligned with the respective optical access of the chamber. The primary role of the copper block is to provide stable boundary conditions for the resonator, reducing fluctuations in the ambient temperature T₀. This stabilization enhances the reliability of the measured responsivity, bringing it closer to the theoretical prediction²⁷. A schematic representation of the measuring setup is displayed in Fig. 1.

The IR source (Arclight-MIR from Arcoptix) is focused on the area of interest using an optical fiber (FIB-PIR-900-100 from Arcoptix) and two gold-coated, parabolic mirrors (from Thorlabs) with a focal length of 101.6 mm and 50.8 mm. An optical chopper can be placed between the mirrors to study the transient response of the resonator to characterize the thermal time constant of each membrane.

The membranes are mechanically excited using a piezoelectric crystal placed below the resonators, controlled by a lock-in amplifier (MFLI from Zurich Instruments). The vibration of the resonator is detected using a laser Doppler vibrometer (LDV MSA-500 from Polytech). The equipment uses a 633 nm laser which is focused on the clearance in the absorber on the membrane. The backscattered light is frequency-shifted due to the Doppler effect. When this light mixes with the reference beam, a frequency modulation is produced, which is proportional to the velocity of the vibration²⁸. A light sensor inside the LDV converts the changes in light intensity into an electric signal that is fed into the lock-in amplifier. After pinpointing the frequency of the harmonic mode of interest, a closed loop is established with a phase-locked loop (PLL).

Results & discussion

Thermal time constant

Figure 2 a shows the frequency response to intensity-modulated IR radiation for a 1000 μm membrane, designed to be measured at its (2,2) mode. The time constant was calculated using the 90-10 method. The results of the measurements of the 18 membranes tested in this work are displayed in Fig. 2b, together with the analytical model, given by^12,23,29,30:

$${\tau }_{{{{\rm{th}}}}}=\frac{C}{G}$$

(5)

with the heat capacity

$$C={L}^{2}{\sum}_{{{{\rm{i}}}}}{h}_{{{{\rm{i}}}}}{\rho }_{{{{\rm{i}}}}}{c}_{{{{{\rm{p}}}}}_{{{{\rm{i}}}}}}$$

(6)

and thermal conductance

$$G=8\pi {\sum}_{i}{h}_{{{{\rm{i}}}}}{\kappa }_{{{{\rm{i}}}}}+8L^{2}\epsilon {\sigma }_{{{{\rm{SB}}}}}{T}^{3},$$

(7)

where, for every i-th stacked material that composes the detector, h is the thickness, ρ the mass density, c_p the specific heat capacity, and κ is the thermal conductivity; L is the side dimension of the membrane, ϵ, σ_SB, and T are the emissivity, the Stefan-Boltzmann constant, and the temperature, respectively.

Fig. 2: Thermal and optical behaviour of 50 nm thick membranes covered with a thin Pt layer.

a Frequency signal of a 1 mm membrane recorded when using the optical chopper. IR power is 7.5 μW. Δf_90% and Δf_10% delimit the portion of the transient used for calculation of τ_th. The shaded grey and red areas represent the portions of the signal corresponding to when the optical path of the infrared beam is blocked and unblocked, respectively. b τ_th for 18 membranes of different dimensions and vibrational modes (purple and yellow crosses) and comparison with the theoretical model (black solid line). The blue area around the black curve represents the uncertainty band coming from different material parameters listed in Table 1. c FTIR absorptance spectra of five 1 mm membrane covered with a Pt thin-film-based FSIM absorber. Grey areas of the plots are the ranges not transmitted by the IR optical fiber.

The agreement with the theory (black lines) is good. The largest uncertainty in the model comes from the thermal conductivity (κ) of the ultrathin Pt film. In literature, different values can be found or calculated, ranging from 29.5 Wm⁻¹ K⁻¹³¹ to 14.5 Wm⁻¹ K⁻¹³². All material parameter-based uncertainty is represented in the plot through the colored blue band. The other material parameters for SiN and Pt used for the model are reported in Table 1.

Table 1 Material parameters for silicon nitride and platinum used in the analytical model

Building on the findings of Luhmann et al.²¹, based on the impedance-matched theory³³, we decided to deposit 5 nm of Pt. This specific thickness has a 50% nominal absorbtance over the entire mid-IR wavelength range (See Supplementary Fig. 1b) which is the maximum achievable for a supported metal layer³³. In this work the Pt-based FSIM absorber, which typically provides a constant absorptance¹², has a slight spectral dependency shown in Fig. 2c. This is due to the Pt film thickness that is below the target thickness of 5 nm, as discussed in the Supplementary Note I. Calculations of the effective emissivity yield a value of ϵ ≈0.48.

Responsivity

The calculation of NEP (1) requires the knowledge of the responsivity. The responsivity (2) of a square membrane resonator for an even heating of the membrane can be derived analytically and yields^23,29

$${R}_{{{{\rm{P}}}}}(\omega )=\frac{\partial {\omega }_{0}}{\partial T}\frac{1}{{\omega }_{0}}\frac{\partial T}{\partial P}{H}_{{{{\rm{th}}}}}(\omega )=\frac{{R}_{{{{\rm{T}}}}}}{G}{H}_{{{{\rm{th}}}}}(\omega )$$

(8)

with the temperature responsivity

$${R}_{{{{\rm{T}}}}}=-\frac{{\alpha }_{{{{\rm{th}}}}}}{2(1-\nu )}\frac{E}{\sigma }.$$

(9)

In Fig. 3a absorptance-normalized responsivities computed with FEM for the given IR beam diameter of 600 μm are compared to the analytical model (8) for an evenly distributed heating and for point-like heating. The latter model predicts values that are a factor of 2 larger^23,29. The absorptance of the Pt FSIM absorber over the spectral window of the IR light source effectively transmitted by the optical fiber is α = 0.47 (see Fig. 2c). The comparison shows that the model for even heating is the correct model approximation for the smallest membranes, while the point-like model is the correct approximation for the larger membranes.

Fig. 3: Steady-state power responsivity R_P/α for square membranes resonators.

a Comparison between the analytical models for a distributed source (solid line) and a point-like source (dashed line), alongside FEM simulations (COMSOL Multiphysics) for an IR beam with a 600 μm diameter (black, purple and yellow rhombuses). b Experimental measurements (black, purple and yellow crosses) compared to the distributed source model (black solid line). The blue band indicates the model’s uncertainty due to variations in material parameters (Table 1).

The comparison of the analytical model to FEM simulations further reveals that the model accurately predicts the (1,1) and (3,3) modes, while it shows a significant deviation for the (2,2) mode. This discrepancy for the (2,2) mode can be explained by the strong mismatch between the temperature field and the displacement field. The former has a maximum while the latter has a minimum in the membrane center. The overlap between the two fields is better for uneven modes than it is for even modes. A more detailed investigation of the relationship between mode shape responsivity is presented in the Supplementary Note II.

Figure 3 b compares the measured responsivities to (8). Since the absolute frequency shift depends on the initial resonance frequency ω₀, normalizing by ω₀ provides a dimensionless measure that allows for a more general comparison across different resonators. This normalization ensures that the responsivity is independent of the specific resonance frequency of the device, making it a more intrinsic figure of merit. The IR light power impinging on the membranes is P = 7.5 μW. The measured values for the smallest membranes match the model within the given uncertainties. The discrepancy between the model and measured responsivities for larger membranes is attributed to increased radiative losses. At the power levels used in this study, the resulting temperature increase leads to a significant radiative heat flux $(\propto ({T}^{4}-{T}_{0}^{4}))$, causing a nonlinear decrease in both temperature and power responsivity²⁹. This effect is more pronounced in larger membranes due to their greater surface area, which enhances radiative coupling with the environment. The measured values for the smallest membranes match the model within the given uncertainties. In addition to radiative losses, a further reduction in responsivity is observed for higher-order vibrational modes, particularly the (2,2) mode. This is consistent with FEM simulations (Fig. 3a) and can be attributed to the mismatch between the temperature distribution and the stress field in this mode.

Frequency stability

In addition to the responsivity, NEP (1) is defined by the frequency stability. The main sources of frequency noise in our nanomechanical photothermal system come from²⁹: additive phase noise ${S}_{{{{{\rm{y}}}}}_{\theta }}(\omega )$, temperature fluctuation noise ${S}_{{{{{\rm{y}}}}}_{{{{\rm{th}}}}}}(\omega )$, and photothermal back-action noise S_y,δP(ω).

S_y,δP(ω) is the frequency noise induced by power fluctuations of the readout laser (photothermal back-action). It readily can be modeled as²⁹:

$${S}_{{{{\rm{y}}}},\delta {{{\rm{P}}}}}(\omega )={\alpha }^{2}{R}_{{{{\rm{P}}}}}^{2}{S}_{{{{\rm{I}}}}}(\omega ),$$

(10)

where S_I(ω), with units [W²/Hz], is the source’s relative intensity fluctuation power spectral density. For a typical laser, this is the sum of three components³⁴: i) laser shot noise, ii) flicker noise, and iii) random walk noise.

Frequency stability is best analyzed through a frequency signal’s Allan variance, which can be calculated by

$${\sigma }_{{{{\rm{y}}}}}^{2}(\tau )=\frac{1}{2\pi }\frac{8}{{\tau }^{2}}\int_{0}^{\infty }\frac{{\left[\sin (\omega \tau /2)\right]}^{4}}{{\omega }^{2}}{S}_{{{{\rm{y}}}}}(\omega )\,{\mbox{d}}\,\omega .$$

(11)

Photothermal back-action noise has been shown to limit the frequency stability in silicon nitride string resonators²⁴. For a given laser intensity noise, (10) can be minimized by reducing the absorptance α. The solution we implemented in this work is to spare an area in the Pt absorber thin film (see Fig. 1) so that the readout laser can be reflected off the silicon nitride instead of the Pt absorber. The effectiveness of this solution is demonstrated in Fig. 4a, which compares the frequency stability (in terms of the Allan deviation) for the two scenarios. On the one hand, the frequency stability strongly deteriorates when the readout laser is pointed directly at the Pt absorber. On the other hand, when pointed at the clearance, the frequency stability is unaffected by photothermal back-action. The measured Allan deviation obtained on the Pt matches the calculated Allan deviation (10) based on the measured laser’s intensity fluctuation spectral density S_I(ω). This data shows the effectiveness of pointing the readout laser onto the clearance in the Pt absorber, by which photothermal back-action can be circumvented.

Fig. 4: Frequency stability study by means of Allan deviations.

a Study of the photothermal back-action frequency noise (black line) induced by the readout laser for a 1 mm membrane (yellow and purple line). The laser power was 15.4 μW. b Frequency stability of the (2,2) mode of a well-performing 2 mm resonator (solid yellow line) compared to theoretical thermal fluctuation noise (dotted black curve) and total phase noise (solid black curve). The experimental detection to thermomechanical noise ratio was ${{{\mathcal{K}}}}=0.006$, the laser power was 6.78 μW and the thermomechanical peak amplitude was ${S}_{{{{{\rm{y}}}}}_{{{{\rm{th}}}}}}({\omega }_{0})=9.8\times 1{0}^{-23}\,{{{{\rm{m}}}}}^{2}{{{{\rm{Hz}}}}}^{-1}$. The blue band highlights the uncertainty due to different possible material parameter values (Table 1).

Additive phase noise ${S}_{{{{{\rm{y}}}}}_{\theta }}$ is the result of the conversion of thermomechanical noise ${S}_{{{{{\rm{z}}}}}_{{{{\rm{thm}}}}}}(\omega )$ and detection noise ${S}_{{{{{\rm{z}}}}}_{{{{\rm{d}}}}}}(\omega )$ into phase noise, ultimately resulting into frequency noise^22,35:

$${S}_{{{{{\rm{y}}}}}_{\theta }}(\omega )=\frac{1}{2{Q}^{2}}\frac{{S}_{{{{{\rm{z}}}}}_{{{{\rm{thm}}}}}}({\omega }_{0})}{{z}_{0}^{2}}\left[| {H}_{{\theta }_{{{{\rm{thm}}}}}}({{{\rm{i}}}}\omega ){| }^{2}+{{{{\mathscr{K}}}}}^{2}| {H}_{{\theta }_{{{{\rm{d}}}}}}({{{\rm{i}}}}\omega ){| }^{2}\right],$$

(12)

with the resonator’s quality factor Q, eigenfrequency ω₀, displacement amplitude z₀, and thermomechanical amplitude noise at resonance

$${S}_{{{{{\rm{z}}}}}_{{{{\rm{thm}}}}}}({\omega }_{0})=\frac{4{k}_{{{{\rm{B}}}}}TQ}{{m}_{{{{\rm{eff}}}}}{\omega }_{0}^{3}},$$

(13)

with the Boltzmann constant k_B, temperature T, and effective resonator mass m_eff. Detection noise is defined relative to the resonator’s thermomechanical noise peak as follows ${S}_{{{{{\rm{z}}}}}_{{{{\rm{d}}}}}}(\omega )={{{{\mathscr{K}}}}}^{2}{S}_{{{{{\rm{z}}}}}_{{{{\rm{thm}}}}}}({\omega }_{0})$. Finally, the two transfer functions in (12) for a phase-locked loop are given by²²

$$\begin{array}{rcl}{H}_{{\theta }_{{{{\rm{thm}}}}}}({{{\rm{i}}}}\omega )&=&\frac{{H}_{{{{\rm{L}}}}}(\omega )}{{H}_{{{{\rm{L}}}}}(\omega )+{{{\rm{i}}}}\omega {\tau }_{{{{\rm{PLL}}}}}}\\ {H}_{{\theta }_{{{{\rm{d}}}}}}({{{\rm{i}}}}\omega )&=&\frac{1}{{H}_{{{{\rm{R}}}}}(\omega )}{H}_{{\theta }_{{{{\rm{thm}}}}}}(\omega )\end{array}$$

(14)

with the low-pass transfer functions H_R(ω) and H_L(ω) of the resonator, with a time constant τ_R = 2Q/ω₀, and the oscillator circuit, respectively. For the resonators used in this work, all the Q factors are in the order of 10⁵.

Temperature fluctuation noise ${S}_{{{{{\rm{y}}}}}_{{{{\rm{th}}}}}}(\omega )$ defines the ultimate sensitivity limit of a thermal detector²³. It originates from the heat exchange of a thermal detector with the environment, both via conduction and radiation. Because of the statistical nature of this process, temperature fluctuation noise can be assumed to be white. These random fluctuations provoke a shift in the resonance frequency that depends on the resonator’s thermal conductance G and temperature responsivity R_T. This fractional frequency-noise PSD for an optomechanical sensor can be modelled with^23,29,30:

$${S}_{{{{{\rm{y}}}}}_{{{{\rm{th}}}}}}(\omega )=\frac{4{\kappa }_{{{{\rm{B}}}}}{T}^{2}}{{G}_{{{{\rm{eff}}}}}}{R}_{{{{\rm{T}}}}}^{2}{H}_{{{{\rm{th}}}}}^{2}(\omega ).$$

(15)

with the effective thermal conductance

$${G}_{{{{\rm{eff}}}}}=4\pi {\sum}_{{{{\rm{i}}}}}{h}_{{{{\rm{i}}}}}{\kappa }_{{{{\rm{i}}}}}+8{L}^{2}\varepsilon {\sigma }_{{{{\rm{SB}}}}}{T}^{3}$$

(16)

Figure 4b shows a comparison of an experimental to the theoretical frequency stability of the best-performing membrane resonator. The measured Allan deviations closely follow the modelled values dominated by additive phase noise, that is, thermomechanical and detection noise. For longer integration times, the frequency stability would approach the ultimate limit given by temperature fluctuation frequency noise. For this specific membrane the thermal time constant is τ_th = 22.3 ms.

NEP and D^*

When calculating the NEP (Eq. (1)) the frequency stability is evaluated using the Allan deviation, as described in the “Frequency Stability” subsection in the Results and Discussion. For each membrane, we extract the Allan deviation value at τ = τ_th. This approach ensures that the noise is assessed over a timescale that accounts for the thermal response of the resonator, thereby preventing any limitation in responsivity (Eq. (8)). Figure 5 presents the measured NEP and D^* values compared to theory. The performance varies strongly between different resonators, with the best values of NEP = 27 pWHz^−1/2 and ${D}^{* }=3.8\times 1{0}^{9}\,{{{\rm{cm}}}}\sqrt{{{{\rm{Hz}}}}}{{{{\rm{W}}}}}^{-1}$ for a 1 mm resonator in the (2,2) mode, approaching the theoretically predicted limit due to temperature fluctuations, which can be obtained by assuming a perfectly isolated detector from the frame (only right term in (16)) with (15) and (4), which yields²³

$${{{{\bf{D}}}}}^{* }=\sqrt{\frac{\varepsilon }{32{\sigma }_{{{{\rm{SB}}}}}{k}_{{{{\rm{B}}}}}{T}^{5}}}.$$

(17)

Fig. 5: The noise equivalent power (NEP) and specific detectivity (D^*) of membranes optimized for the second and third harmonic modes.

a NEP values (purple and yellow crosses) were calculated using the power spectral density (PSD) at the thermal time constant frequency. b The D^* was also calculated (purple and yellow crosses). The results indicate minimal differences in performance between the different modes and dimensions of the membranes, with values approaching the fundamental limit at room temperature calculated for 50% absorptance (dashed black line). Here too the blue band stands for the uncertainty due to different material parameters (Table 1).

The ultimate specific detectivity for a nominal emissivity ε = 0.5 then becomes ${D}^{* }\approx 1.0\times 1{0}^{10}\,{{{\rm{cm}}}}\sqrt{{{{\rm{Hz}}}}}{{{{\rm{W}}}}}^{-1}$ at room temperature. The measured value is only a factor of 3 below this fundamental limit indicated by the horizontal dashed black line in Fig. 5b. For an IR detector with a perfect absorber (ε = 1), the specific detectivity limit would increase only slightly to ${D}^{* }\approx 1.4\times 1{0}^{10}\,{{{\rm{cm}}}}\sqrt{{{{\rm{Hz}}}}}{{{{\rm{W}}}}}^{-1}$. The plot further reveals that the theoretical performance of a membrane resonator remains slightly below the fundamental limit.

In Fig. 6 we compare D^* across the thermal time constant τ_th for different uncooled IR detectors^{13,15,36,37,38,39,40,41}. This analysis includes a range of pyroelectric detectors, resistive bolometers, thermoelectric detectors, and thermomechanical detectors of which we selected the best performing ones, alongside results from our current and previous work¹². Our latest result stands out in terms of specific detectivity, ranking on par as the most sensitive room-temperature IR detector among state-of-the-art devices while maintaining an operating speed comparable to other detectors. Compared to¹⁵, our structure is significantly easier and faster to fabricate, requiring only a straightforward two-step photolithography process. In contrast, the Ti-SiN-Ni resonator involves four steps of electron beam lithography, making our technology not only more accessible but also more cost-effective.

Fig. 6: Specific detectivity and thermal time constant of uncooled IR detectors.

Comparison of specific detectivity (D*) as a function of the thermal time constant (τ_th) for uncooled IR detectors, including data from¹² and this work. Our device ranks as the most sensitive room-temperature IR detector, sharing the top position, with a similar operating speed to most detectors and a simple, cost-effective fabrication process.

Conclusions

The results for NEP and D^* demonstrate that our sensors are among the most sensitive room-temperature IR detectors. The minimum noise equivalent power achieved is 27 pWHz^−1/2, and the maximum specific detectivity reaches $3.8\times 1{0}^{9}\,{{{\rm{cm}}}}\sqrt{{{{\rm{Hz}}}}}{{{{\rm{W}}}}}^{-1}$. The latter value is less than a factor of 3 below the fundamental limit at room temperature for an IR detector with 50% absorptance. The obtained sensitivity is on par with state-of-the-art uncooled optomechanical infrared detectors featuring subwavelength-structured meta-absorbers^13,15. In contrast to previous approaches, the FSIM absorber extends the spectral range from the near-infrared to the terahertz regime. Simultaneously, its nominal 50% absorptance results in only a 1.4-fold reduction in ultimate sensitivity. As a result, the achieved sensitivity is less than a factor of 4 below the fundamental limit for an ideal IR detector with 100% absorptance.

The performance of the presented nanomechanical IR detector is on par with state-of-the-art commercial pyroelectric detectors with a NEP and specific detectivity of 40 pWHz^−1/2 and $4\times 1{0}^{9}\,{{{\rm{cm}}}}\sqrt{{{{\rm{Hz}}}}}{{{{\rm{W}}}}}^{-1}$, respectively, at 10 Hz³⁶. As demonstrated in this work, the nanomechanical membrane detectors achieve the expected theoretical performance, albeit below the fundamental limit. To further approach the thermal fluctuation noise limit, we aim to explore trampoline resonators as a promising alternative, leveraging their superior thermomechanical properties²⁹. Combined with the FSIM absorber strategy employed here, trampoline resonators hold the potential to advance room-temperature IR detectors to the fundamental sensitivity threshold.