Tensor networks for lattice gauge theories beyond one dimension

Abstract

Tensor network methods are numerical tools and algorithms to study many-body quantum systems in and out of equilibrium, based on tailored variational wave functions. They have found significant applications in simulating lattice gauge theories that approach relevant problems in high-energy physics. Compared to Monte Carlo methods, they do not suffer from the sign problem, allowing them to explore challenging regimes such as finite chemical potentials and real-time dynamics. Further development is required to tackle fundamental challenges, such as accessing continuum limits or computations of large-scale quantum chromodynamics. This work reviews the state-of-the-art tensor network methods and discusses a possible roadmap for algorithmic development and strategies to enhance their capabilities and extend their applicability to open high-energy problems. We provide tailored estimates of the theoretical and computational resource scaling for attacking large-scale lattice gauge theories.

Introduction

Gauge theories play a role of paramount importance in our understanding and description of the fundamental constituents of matter, their spectrum, and their interactions. At low energies, gauge theories characterize a large variety of collective phases of matter and phenomena, such as ferromagnetic superconductivity, spin liquids, topological order, and the fractional quantum Hall effect^1,2,3. At high energies, as elegantly summarized in the standard model of particle physics, they are at the heart of the microscopical description of the building blocks of our universe, i.e., quarks, leptons, and their interactions mediated by gauge bosons^4,5.

A powerful approach to studying and simulating gauge theories in nonperturbative regimes lies in lattice gauge theories (LGTs), where matter and gauge degrees of freedom are discretized and regularized on a finite lattice. LGTs were originally introduced by Wilson to encode quantum chromodynamics (QCD) on a lattice, as a model for quark confinement beyond the perturbative regime^6,7. In LGTs, matter and antimatter fermionic fields are defined on lattice sites, whereas the gauge fields live on the links connecting nearest-neighbor sites. This approach has opened the doors to the application of powerful numerical methods, such as Monte Carlo (MC), to the simulations of LGTs on classical computers⁸. In the last decades, MC methods have provided a wide variety of significant results on LGTs in the context of high-energy physics, such as phases diagrams at equilibrium, characterization of the quark-gluon plasma, precise determination of the masses of quarks, mesons, and baryons, hadronic and nucleon form factors, hadronic spectra, and predictions for dark-matter models⁹. Furthermore, MC simulations of LGTs currently represent a powerful numerical tool to predict and interpret data from multiple large-scale high-energy experiments, such as the ones performed at the large hadron collider¹⁰.

Despite their impressive success, MC sampling methods are limited in some regimes of parameters of LGTs, such as in the presence of finite baryon chemical potentials, topological θ-terms, or for simulating out-of-equilibrium dynamics in real-time. In these cases, the notorious sign problems make the MC numerical approach ineffective and inaccurate¹¹.

Ranging from these problems, sign-problem circumventing methods based on tensor networks (TNs) have found significant applications in the simulations of LGTs in recent years^12,13,14. TNs were originally introduced as a class of variational wave functions in the field of quantum many-body (QMB) physics^15,16,17,18. They provide a compressed representation of physical states based on their entanglement content, capable of efficiently reproducing equilibrium properties, such as phase diagrams, and real-time dynamics of interacting quantum systems^19,20,21,22. TNs can also be employed to compute partition functions via transfer-matrix methods and tensor network renormalization algorithms^23,24,25. This approach can further be generalized to evaluate path integrals of gauge theories through field discretization²⁶. Here, we focus on the application of TNs to study ground-state properties and out-of-equilibrium dynamics in the Hamiltonian picture, where they represent one of the state-of-the-art numerical tools for simulating QMB systems, even with strong correlations.

In the context of high-energy physics, TN methods have proven noteworthy achievements in simulating LTGs in (1 + 1) dimensions for both Abelian and non-Abelian gauge groups^{27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55}. They have recently found applications to Abelian LGTs up to (3 + 1) dimensions^{56,57,58,59,60,61,62,63,64}, and also in simulating (2 + 1)-dimensional non-Abelian SU(2) models⁶⁵. Despite their effectiveness in these first important applications, further and intensive developments are still required to tackle, with TN methods, high-energy physics problems at the center of current research efforts, such as large-scale non-Abelian LGTs and their continuum limits.

In this work, we present a general overview of TN methods for LGTs, and we discuss a possible roadmap in terms of algorithmic development and strategies to improve TN capabilities toward the ambitious long-term goal of applying TNs to (3 + 1)-dimensional QCD.

Importantly, TN methods share a common language with quantum computers and simulators. Thus, these developments could also be relevant for encoding, validating, and benchmarking the current and future quantum computations and simulations of LGTs on experimental quantum hardware^{66,67,68,69,70,71,72,73,74,75,76}.

TNs overview

In this section, we present a general overview of TN methods with a particular focus on tree tensor networks (TTNs), the latter being beneficial for LTGs in higher dimensions^56,58,65. However, this work’s main concepts and ideas can be easily generalized and applied to other TN structures. Consider a QMB system defined on a lattice of N sites. The generic site j is described by a d-dimensional local Hilbert space ${{{{{\mathcal{H}}}}}}_{j}$, spanned by a local basis of vectors ${\left\vert i\right\rangle }_{1\le i\le d}$. The quantum states of the whole system live on the total Hilbert space ${{{{\mathcal{H}}}}}={{{{{\mathcal{H}}}}}}_{1}\otimes {{{{{\mathcal{H}}}}}}_{2}\otimes \cdots \otimes {{{{{\mathcal{H}}}}}}_{N}$, that is the tensor product of the local Hilbert space of the lattice sites, with dimension d^N. Then, any pure state of the system $\left\vert \psi \right\rangle$ can be exactly expanded in terms of a complete basis set of ${{{{\mathcal{H}}}}}$:

$$\left\vert \psi \right\rangle = {\sum}_{{i}_{1},{i}_{2},\ldots ,{i}_{N}=1}^{d}{c}_{{i}_{1},{i}_{2},\ldots ,{i}_{N}}\left\vert {i}_{1},{i}_{2},\ldots ,{i}_{N}\right\rangle \,,$$

(1)

where $\left\vert {i}_{1},{i}_{2},\ldots ,{i}_{N}\right\rangle$ represents the tensor product of the local basis vectors, i.e. $\left\vert {i}_{1}\right\rangle \otimes \left\vert {i}_{2}\right\rangle \otimes \left\vert \ldots \right\rangle \otimes \left\vert {i}_{N}\right\rangle$. The coefficients of the linear combination ${c}_{{i}_{1},{i}_{2},\ldots ,{i}_{N}}$ are, in general, complex scalars; their number scales as d^N, i.e., they scale exponentially with the system size N.

This is a fundamental limitation when solving a QMB problem on a classical computer since an exponential scaling with the number of degrees of freedom implies that the exact representation described in (1) is completely unfeasible from a computational and numerical point of view.

Nevertheless, a great variety of natural QMB systems happens to be described by ground and thermal equilibrium states that have little to moderate entanglement content. The physical states of these systems, instead of exploring the exponentially large dimension of the Hilbert space, live in a small corner of it, which can be efficiently targeted and parameterized. This property is formally described by the entanglement area law, fulfilled by low-energy states of local Hamiltonians⁷⁷: the entanglement between a contiguous subsystem and the rest is proportional to the area of the boundary between them, instead of its volume, as happens for the majority of states in the Hilbert space. Thus, obeying area law implies that the state contains many fewer quantum correlations than expected for a generic (or random) QMB state. Small corrections to the area law exist, for instance, close to a transition point for one-dimensional quantum systems (logarithmic corrections). However, the entanglement remains overall moderate⁷⁸. From a theoretical point of view, the entanglement area law has been rigorously proven for (i) one-dimensional gapped local Hamiltonians, where the locality means that a lattice site interacts only with neighboring sites, without two-body all-to-all interactions^79,80,81; (II) for a one-dimensional local Hamiltonian, if the Renyi entropy S_α, α < 1 is bounded from above by $c\log (N)$ for any bipartition, where c is a constant and N the system size⁸²; (iii) for quantum states at thermal equilibrium, independently from the dimensionality of the system⁸³; (iv) if the to-be-approximated state has exponential decay of correlation functions for every pair of observables (even with unbounded support)⁸⁴. Even though rigorous proof for QMB systems in higher dimensions is lacking, several numerical and phenomenological results suggest that area law still holds in the presence of local interactions^{77,85,86,87,88}.

The area law has important implications on the TN simulation of quantum lattice models: indeed, it is possible to obtain an approximate but efficient representation capable of describing the main properties of these states if the entanglement content is low-to-moderate⁷⁷; the condition applies, for example, to ground-states and first excited states of local Hamiltonians. TNs give a natural language for this representation, by replacing the complete tensor of rank-$N\,{c}_{{i}_{1},{i}_{2},\ldots ,{i}_{N}}$ of (1) with a chain of smaller tensors interconnected using auxiliary bond indices. The network keeps a number N of physical indices of dimension d (one for each lattice site), whereas the dimension of the bond indices (called bond dimension) is a control parameter χ that can be tuned in the numerical simulations and is related to the Schmidt decomposition^22,30.

The key advantage of passing from the exact representation of (1) to a TN representation is that the number of parameters in the TN is of the order O(poly(d)poly(N)poly(χ)), e.g., $O(N\chi \max {(\chi ,d)}^{2})$ for the TTN. The scaling with the system size is now polynomial and not exponential. In this way, we obtain an efficient representation of the quantum state in terms of computational complexity. It is worth noting that the bond dimension χ determines the degree of entanglement and quantum correlations encoded in the TN, e.g., for χ = 1 the TN describes a product state (no entanglement), whereas one recovers the exact but inefficient representation in the limit χ ≲ d^N. Tuning χ properly allows interpolation between these two extreme regimes, efficiently reproducing the entanglement of the quantum state.

The most widely used TN architectures are represented in Fig. 1. Matrix product states (MPS) are an established ansatz for one-dimensional systems, in which the structure of the lattice is reproduced with a network of tensors, one for each lattice site⁸⁹. As shown in Fig. 1a, each tensor in the bulk of the network has three indices: one physical leg of dimension d representing the local degrees of freedom and two virtual legs of dimension χ connected to the neighboring sites. In open boundary conditions, the tensors at the boundaries have one trivial leg together with one physical and one virtual leg. MPS intrinsically satisfies the area law and allows for efficient computation of scalar products between two states and physical observables. Currently, the MPS-based density matrix renormalization group (DMRG) stands as one of the most consolidated and accurate techniques for numerical simulations of one-dimensional QMB systems as well as quasi-one-dimensional systems such as ladder structures⁹⁰. The computational complexity of this ground state searching algorithm for MPS is of the order O(Ndχ³ + Nd²χ²) or O(Nd³χ³), depending if the algorithm optimizes a single MPS tensor at a time, or two-tensors simultaneously^90,91. Two-site optimization is usually important to avoid getting stuck in local minima or meta-stable configurations during the energy variational minimization^92,93,94. The subspace expansion is an intermediate approach with the benefits of the two-tensor update and a tunable computational cost between the two approaches³⁰.

Fig. 1: Examples of tensor network structures.

a Matrix product states (MPS); b Projected entangled pair states (PEPS); c Tree tensor networks (TTN) for an underlying one-dimensional system; d TTN for an underlying two-dimensional square lattice. The physical links with local dimension d and the virtual links with bond dimension χ are highlighted in all the panels.

The generalization of the MPS ansatz to two- or higher-dimensional lattices is represented by the projected entangled pair state (PEPS)^22,95. In this case, each tensor in the bulk has a physical leg of dimension d, and a number of χ-dimensional virtual legs depending on the coordination number of the considered lattice. For example, this coordination number is four in the case of a two-dimensional square lattice, as shown in Fig. 1b. PEPS directly encode in their structure the area law of entanglement; however, their exact contraction is an exponentially hard problem, meaning that PEPS can not be efficiently contracted for numerical computing, e.g., scalar products of states or physical observables⁹⁶. To circumvent this problem, approximate contraction methods have been developed during the last years and are still at the center of current research efforts²². But even with exploiting these approximate techniques, the computational complexity for ground state optimization remains quite high, e.g., of the order of O(Nd²χ⁸)^97,98, limiting the maximum reachable bond dimensions (typical values are of the order χ ≈ 10).

Another important family of TN ansätze is represented by TTN, in which the wave function is decomposed into a hierarchical network of tensors that do not contain internal loops^30,99. This way, the network can be efficiently contracted and manipulated in polynomial time. A particular class of TTN is represented by binary TTNs, reported in Fig. 1c–d for one- and two-dimensional lattices. In these structures, tensors in the lowest layer have two physical legs of dimension d (representing two lattice sites) and a virtual leg of dimension χ, whereas, in the upper layers, they have three virtual legs of dimensions up to χ. The network intrinsically encodes a renormalization procedure, in which, at each layer, two sites are mapped into a single effective one. In models with finite-range interactions, ground search algorithms for binary TTN architectures display a numerical complexity of the order O(Nd²χ² + Nχ⁴), see³⁰. This is a much more favorable scaling concerning equivalent algorithms for other TN structures, such as PEPS, that allows reaching quite large values of bond dimensions (χ ≈ 500)¹⁰⁰. The drawback of loopless structures, such as binary TTN, is that the area law may not be explicitly reproduced in dimensions higher than one¹⁰¹, which becomes a limiting factor when large systems are addressed. The convergence and the precision of the numerical results obtained via a variational optimization of TTN can be analyzed and kept under control, e.g., by exploiting the wide range of available bond dimensions. Furthermore, it is possible to explicitly encode the area law of high-dimensional systems in the TTN ansatz by introducing an additional layer of independent disentanglers acting on different couples of lattice sites and connected to the corresponding physical legs. This process augments the expressive power of TTN, and the resulting ansatz is known as augmented Tree Tensor Network (aTTN)¹⁰². The computational complexity of variationally optimizing an aTTN structure, which means optimizing both the tensors and the disentanglers, is of the order O(Nχ⁴d⁴ + Nχd⁷). We point out that the scaling of the computational costs with the local dimension d is particularly severe in the case of aTTN due to the presence of the disentanglers layer.

Besides variational optimization for ground state searching, the previous TN families can also be exploited to simulate the real-time dynamics of local Hamiltonians¹⁰³; in the following, we describe two popular methods. The time evolved block decimation (TEBD) algorithm, is based on a Suzuki-Trotter decomposition of the time evolution exponential¹⁰⁴. The total evolution time is discretized in small time steps. The corresponding evolution operator is computed as products of local terms, such as two-body operators, and repeatedly applied to the TN wave function to generate the time-evolved state. Each application can determine an increase in the bond dimension of the network, so an optimized truncation is needed to maintain an efficient and manageable description of the quantum state. This truncation reduces the bond dimension back to χ and is performed through a singular value decomposition that minimizes the distance between the evolved and the truncated state. In general, the TEBD method allows the simulation of the real-time dynamics for nearest-neighbor or finite-range Hamiltonians; one time-step with an MPS for a one-dimensional system with local interactions comes with a computational cost that is below a two-tensor sweep for the ground-state search algorithm.

Another method for simulating the evolution of quantum states via TN is the time-dependent variational principle (TDVP), which does not rely on the Suzuki-Trotter decomposition^105,106. In general, TDVP constrains the time evolution to the specific TN manifold considered, such as MPS or TTN, of a given initial bond dimension¹⁰⁷. This is obtained by projecting the action of the Hamiltonian into the tangent space of the TN manifold and then solving the time-dependent Schrödinger equation within this manifold. This approach automatically preserves the energy and the norm of the quantum states during the time evolution. Both the TDVP algorithm and the variational ground state search rely on a set of Krylov vectors and, hence, have the same computational scaling for one time step compared to one sweep¹⁰⁸.

These algorithms represent important and efficient tools for simulating with TN the real-time dynamics of QMB systems. While equilibrium states satisfy the aforementioned area law, out-of-equilibrium time evolution can generate a linear growth of entanglement. In this case, the time-evolved state requires an exponential growth of the bond dimension as a function of the total time⁸². For this reason, TN methods are currently limited to studying the dynamics for low-to-moderate times or close-to-equilibrium phenomena¹⁰⁹. In this framework, further developments are extremely important to avoid or at least mitigate this barrier, by devising new algorithms or optimizing existing strategies^110,111.

Hamiltonian LGTs

In the traditional MC approach to LGT, the action of a continuum gauge theory is regularized by working on a finite and discrete Euclidean spacetime—i.e., both space and (imaginary) time are discretized⁸. Instead, TN (and quantum) simulations typically rely on the Hamiltonian formalism, where time remains a real, continuous variable while a cubic lattice Λ replaces D-dimensional space. Simultaneously, Hamiltonian LGTs present features that distinguish them from other lattice models commonly simulated via TN⁷. We now discuss these properties in more detail and outline the main steps that have to be taken to exploit TN algorithms in LGT. We focus on matter-coupled LGTs of the Yang-Mills type, such as those routinely employed in high-energy physics to describe nature’s fundamental interactions; the paradigmatic example is lattice QCD, the SU(3) LGT describing quarks, gluons, and their strong interactions.

LGT building blocks

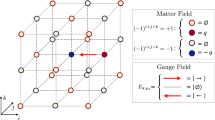
As depicted in Fig. 2, LGTs involve two types of degrees of freedom, matter, and gauge, hosted respectively on lattice sites x ∈ Λ and links (x, μ), where μ denotes one of the lattice basis vectors. Since fundamental interactions of nature involve gauge theories with compact Lie groups, the following discussion focuses on such cases. A continuous symmetry implies the existence of a color charge, which is carried by matter and gauge fields and labeled here using Greek letters.

Fig. 2: Graphical representation of 2D LGT degrees of freedom.

fermionic matter fields ${\hat{\psi }}_{{{{{\bf{x}}}}},\alpha }$, defined on lattice sites, and gauge fields (the parallel transporter, ${\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\alpha \beta }$, and the chromo-electric fields, ${\hat{L}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\nu }$ and ${\hat{R}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\nu }$), living on lattice links. A local gauge transformation at x acts on a matter site and all its attached links.

Matter fields

such as the electron or quark fields. We assume that matter consists of Dirac fermions. In general, discretizing the Dirac operator introduces additional unphysical solutions in the spectrum, known as doublers. Various approaches have been developed to tackle this problem, such as Wilson fermions^46,112,113, which, at the price of breaking the chiral symmetry, eliminate doublers in any spatial dimension. In this manuscript, we employ staggered fermions¹¹⁴, which partially resolve the doubling problem (some doublers remain in D > 1) but have a lower computational cost. Then, a color-multiplet ${\hat{\psi }}_{{{{{\bf{x}}}}},\alpha }$ of staggered fermion fields satisfies $\{{\hat{\psi }}_{{{{{\bf{x}}}}},\alpha },{\hat{\psi }}_{{{{{\bf{y}}}}},\beta }^{{{{\dagger}}} }\}={\delta }_{\alpha \beta }{\delta }_{{{{{\bf{xy}}}}}}$ Assuming a single matter flavor in the fundamental representation of the gauge group ${{{{\mathcal{G}}}}}$, gauge transformations are generated by ${\hat{Q}}_{{{{{\bf{x}}}}}}^{\nu }={\sum}_{\alpha ,\beta }{\hat{\psi }}_{{{{{\bf{x}}}}},\alpha }^{{{{\dagger}}} }{\lambda }_{\alpha \beta }^{\nu }{\hat{\psi }}_{{{{{\bf{x}}}}},\beta }$, where ${\{{\lambda }^{\nu }\}}_{\nu = 1}^{\dim {{{{\mathcal{G}}}}}}$ are the hermitian generators of ${{{{\mathcal{G}}}}}$—e.g., the electric charge for U(1) or the three spin matrices for SU(2). The discussion can be generalized to multiple matter flavors and other types of lattice fermions.

Gauge fields

such as the photon or gluon fields. They are represented by bosonic operators, namely the parallel transporter ${\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\alpha \beta }$ and the generators of its left and right gauge transformations, ${\hat{L}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\nu }$ and ${\hat{R}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\nu }$,

$${\hat{L}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\nu },{\hat{U}}_{{{{{\bf{y}}}}},{{{{\boldsymbol{\mu }}}}}^{\prime} }^{\alpha \beta }=-{\delta }_{{{{{\bf{xy}}}}}}{\delta }_{{\boldsymbol{\mu}} {\boldsymbol{\mu}} ^{\prime} }{\sum}_{\gamma }{\lambda }_{\alpha \gamma }^{\nu }{\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\gamma \beta },$$

(2a)

$${\hat{R}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\nu },{\hat{U}}_{{{{{\bf{y}}}}},{{{{\boldsymbol{\mu }}}}}^{\prime} }^{\alpha \beta }=+{\delta }_{{{{{\bf{xy}}}}}}{\delta }_{{\boldsymbol{\mu}}{\boldsymbol{\mu}}^{\prime}}{\sum}_{\gamma }{\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\alpha \gamma }{\gamma }_{\gamma \beta }^{\nu },$$

(2b)

In the Abelian U(1) case there is only one generator: the electric field, ${\hat{E}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}},={\hat{L}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}={\hat{R}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}$, for which parallel transporters act as raising operators, $[{\hat{E}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}},{\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}]={\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}$. In terms of the above ingredients, a possible discretization of a matter-coupled Yang-Mills theory is defined by the Kogut-Susskind Hamiltonian¹¹⁵

$${\hat{H}}_{{{{{\rm{LGT}}}}}} = -\frac{c\hslash }{2a}\sum\limits_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}\sum\limits_{\alpha ,\beta }\left({s}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}{\hat{\psi }}_{{{{{\bf{x}}}}},\alpha }^{{{{\dagger}}} }{\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\alpha \beta }{\hat{\psi }}_{{{{{\bf{x}}}}}+{{{{\boldsymbol{\mu }}}}},\beta }+\,{{\rm{h.c.}}}\,\right)\\ +m{c}^{2}\sum\limits_{{{{{\bf{x}}}}}}\sum\limits_{\alpha }{s}_{{{{{\bf{x}}}}}}{\hat{\psi }}_{{{{{\bf{x}}}}},\alpha }^{{{{\dagger}}} }{\hat{\psi }}_{{{{{\bf{x}}}}},\alpha }\\ +\frac{c\hslash {g}^{2}}{2{a}^{D-2}}\sum\limits_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}{\hat{E}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{2}\\ -\frac{c\hslash }{2{g}^{2}{a}^{4-D}}\sum\limits_{\square }{{{{\rm{Tr}}}}}({\hat{U}}_{\square }+{\hat{U}}_{\square }^{{{{\dagger}}} }),$$

(3)

where c is the speed of light, ℏ is the Plank constant, a is the lattice spacing, g is the gauge coupling, and m is the mass parameter. The first H_LGT term describes matter hopping between neighboring lattice sites, mediated by the gauge field; the second term is the mass-energy; s_x,μ and s_x are phases that arise due to the use of staggered fermions¹¹⁴. Namely, we have:

$${s}_{{{{{\bf{x}}}}},{{{{{\boldsymbol{\mu }}}}}}_{{{{{\boldsymbol{x}}}}}}}=1\quad {s}_{{{{{\bf{x}}}}},{{{{{\boldsymbol{\mu }}}}}}_{{{{{\boldsymbol{y}}}}}}}={(-1)}^{x+y}={s}_{{{{{\bf{x}}}}},{{{{{\boldsymbol{\mu }}}}}}_{{{{{\boldsymbol{z}}}}}}}\quad {s}_{{{{{\bf{x}}}}}}={(-1)}^{x+y+z}.$$

(4)

The last two terms of (3) represent the (chromo)electric and (chromo)magnetic energy of the gauge field, respectively. The Casimir operator gives the electric energy density:

$${\hat{E}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{2}={\sum}_{\nu }{({\hat{L}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\nu })}^{2}={\sum}_{\nu }{({\hat{R}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\nu })}^{2}.$$

(5)

The magnetic energy density is a plaquette term that, on a cubic lattice, corresponds to a four-body interaction:

$${\hat{U}}_{\square }=\sum\limits_{\alpha ,\beta ,\gamma ,\delta }\,{\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\alpha \beta }{\hat{U}}_{{{{{\bf{x}}}}}+{{{{\boldsymbol{\mu }}}}},{{{{{\boldsymbol{\mu }}}}}}^{{\prime} }}^{\beta \gamma }{\hat{U}}_{{{{{\bf{x}}}}}+{{{{{\boldsymbol{\mu }}}}}}^{{\prime} },{{{{\boldsymbol{\mu }}}}}}^{{{{\dagger}}} \gamma \delta }{\hat{U}}_{{{{{\bf{x}}}}},{{{{{\boldsymbol{\mu }}}}}}^{{\prime} }}^{{{{\dagger}}} \delta \alpha }$$

(6)

where μ and ${\boldsymbol{\mu}}^{\prime}$ span the plaquette’s plane. Plaquette terms only exist in D >1, contributing to the increased complexity of quantum and TN simulations of LGTs in higher dimensions⁷¹.

Gauge field truncation

The link Hilbert space is the space of square-integrable functions on the gauge group, ${L}^{2}({{{{\mathcal{G}}}}})$, which is infinite-dimensional for a continuous ${{{{\mathcal{G}}}}}$¹¹⁶.

In one space dimension, gauge degrees of freedom are unphysical (absence of transverse polarizations) and can thus be integrated out, albeit at the price of introducing non-local interactions¹¹⁷.

Beyond one dimension, the removal is much more delicate because it requires first decoupling the gauge field’s longitudinal component^118,119. When impossible or inconvenient to remove, gauge degrees of freedom might have to be truncated to perform TN or quantum simulation. Among known truncation recipes are quantum link Models (QLM)^{120,121,122,123}, which have already been adopted for quantum simulation of LGTs^{67,71,73,75,124,125,126,127,128}, finite subgroups^38,42,129, digitization of gauge fields¹³⁰, and fusion-algebra deformation¹³¹.

Another adopted solution is truncating the spectrum of the electric energy density operator $\parallel {\hat{E}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{2}\parallel \le \Theta$ on each link^65,132. The cutoff is conveniently imposed in the irreducible representation ( irrep) basis $\{\left\vert jmn\right\rangle \}$¹¹⁶ of ${L}^{2}({{{{\mathcal{G}}}}})$, where ${\hat{E}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{2}$ is diagonal:

$${\hat{E}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{2}\left\vert jmn\right\rangle ={C}_{2}(j)\left\vert jmn\right\rangle .$$

(7)

Here, m and n are indices in the j-irrep of ${{{{\mathcal{G}}}}}$ and C₂(j) is the quadratic Casimir of j¹¹⁶. In the strong coupling limit, where the electric energy term dominates H_LGT, this truncation is equivalent to an energy cutoff¹³².

Gauss law and the dressed site

The most distinctive feature of gauge theories is arguably the presence of local constraints, analogous to the Gauss law of classical electrodynamics, relating the configuration of the gauge field to the spatial distribution of charges¹³³. At the quantum level, Gauss law is the statement that only gauge-invariant states are physical, namely, ${\hat{G}}_{{{{{\bf{x}}}}}}^{\nu }| {\Psi }_{{{{{\rm{phys}}}}}}\left.\right\rangle =0\,\forall {{{{\bf{x}}}}},\nu$, where ${\hat{G}}_{{{{{\bf{x}}}}}}^{\nu }$ are the generators of local gauge transformations at x:

$${\hat{G}}_{{{{{\bf{x}}}}}}^{\nu }={\hat{Q}}_{{{{{\bf{x}}}}}}^{\nu }+{q}_{{{{{\bf{x}}}}}}^{\nu }+{\sum}_{{{{{\boldsymbol{\mu }}}}}}[{\hat{L}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\nu }+{\hat{R}}_{{{{{\bf{x}}}}}-{{{{\boldsymbol{\mu }}}}},{{{{\boldsymbol{\mu }}}}}}^{\nu }],$$

(8)

with ${q}_{{{{{\bf{x}}}}}}^{\nu}$ representing eventual static background charges (typically vanishing). On the lattice, Gauss law provides a set of vertex constraints, each involving a lattice site and its 2D neighboring links. Due to Gauss law, the physical Hilbert space of LGTs is much smaller than the tensor product of all local sites and link Hilbert spaces. Properly exploiting gauge symmetries can thus significantly speed up numerical simulations²⁸. Strategies that solve Gauss law by eliminating (partially or entirely) either the gauge fields or the matter fields have been developed. Nonetheless, such approaches come with specific limitations: the range of interaction has to be extended, moreover, integrating-out gauge fields become problematic in D >1¹¹⁸, while the recipe for removing matter is a model (matter content) dependent¹³⁴.

Another possibility is to enforce Gauss law using a dressed site construction, sketched in Fig. 3 and outlined below. Dressed sites have local dimensions typically larger than those resulting from the aforementioned approaches, but they are obtained from a model-independent prescription which has the advantage of preserving the locality of the interactions^28,132.

Fig. 3: Pictorial representation of the dressed site formalism adopted for TN simulations of LGTs.

a Starting from the original formulation of matter and gauge fields, b each truncated gauge link is split into two representations, one per half-link; each is equipped with a proper fermionic rishon mode ζ. c All the half-links are absorbed into the attached matter site, forming a gauge-invariant dressed site d whose Hilbert space spans all the possible gauge singlets.

Rishons

As a first step, every link is decomposed into a pair of left (L) and right (R) rishon degrees of freedom, each associated with a Hilbert space spanned by the basis states $\left\vert jm\right\rangle$, identifying $\left\vert jmn\right\rangle \hookrightarrow {\left\vert jm\right\rangle }_{L}\otimes {\left\vert jn\right\rangle }_{R}$, and writing parallel transporters as rishon bilinear⁶⁵:

$${\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\alpha \beta }\to {\sum}_{k}{\hat{\zeta}}_{{{{{\bf{x}}}}},+{{{{\boldsymbol{\mu }}}}}}^{L(k)\alpha }{\hat{\zeta}}_{{{{{\bf{x}}}}}+{{{{\boldsymbol{\mu }}}}},-{{{{\boldsymbol{\mu }}}}}}^{R(k)\beta \,{{{\dagger}}} }\,.$$

(9)

Abelian link symmetries

Physical gauge link configurations, i.e. those with the left and right rishons in the same irrep, are selected introducing a local link symmetry at the TN simulation level^28,132. Notice this is always Abelian, regardless of the Abelian or non-Abelian nature of the gauge group.

Gauge invariant computational basis

Crucially, the gauge generators ${\hat{G}}_{{{{{\bf{x}}}}}}^{\nu }$ now involve only the matter site at x and its 2D neighboring rishons. Fusing these degrees of freedom in a composite site, Gauss law becomes an internal constraint that singles out the dressed site Hilbert space as their gauge invariant subspace:

$${{{{{\mathcal{H}}}}}}_{{{{{\rm{dress}}}}}}=\ker G\subset {{{{{\mathcal{H}}}}}}_{{{{{\rm{matt}}}}}}\otimes {({{{{{\mathcal{H}}}}}}_{{{{{\rm{rish}}}}}})}^{\otimes 2D}\,.$$

(10)

The expansion of the gauge singlet basis states of ${{{{{\mathcal{H}}}}}}_{{{{{\rm{dress}}}}}}$ in terms of the matter and rishon bases is computed via Clebsch-Gordan decomposition¹³².

Defermionization

It is possible to effectively eliminate fermionic matter and treat dressed sites as large spins for any gauge theory where the gauge field has a well-defined parity. Specifically, a local parity operator ${\hat{P}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}={\hat{P}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{{{{\dagger}}} }$ such that ${\hat{P}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{2}=\hat{\mathbb{1}}$ must satisfy $\{{\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{\alpha \beta },{\hat{P}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}\}=0$, as it happens for ${{\mathbb{Z}}}_{2N}$, U(N), and SU(2N)^65,134,135. In this case, it is possible to take fermionic rishons, and as a result, all physical (gauge invariant) dressed site operators are genuinely local, i.e. they mutually commute at a nonzero distance (as spins or bosons)¹³⁶. This applies to the Hamiltonian H_LGT, making gauge-defermionization particularly convenient for higher-dimensional systems, where Jordan-Wigner strings result in long-range interactions¹³⁷.

Scaling of the local basis dimension

Table 1 lists the dressed site dimension $d=\dim {{{{{\mathcal{H}}}}}}_{{{{{\rm{dress}}}}}}$ associated with the first few nontrivial gauge truncations of three representative LGT models in D = 2, 3 space dimensions. All the considered LGTs include dynamical matter, represented by one fermionic field multiplet in the fundamental representation of the gauge group. The ℓ-th row of Table 1 is obtained keeping only the first ℓ nonzero electric energy levels (i.e., using the ℓ-th smallest quadratic Casimir eigenvalue as cutoff Θ, see subsection “Gauge field truncation”). As Table 1 shows, the local dimension increases rapidly with ℓ. For 3-dimensional non-Abelian LGTs, d ~ O(10⁴) is reached already within the first two truncations, making the study of the untruncated limit prohibitive.

Table 1 Dressed site Hilbert space dimensions

Differently from the models typically encountered in condensed matter physics, the local dimension of LGTs can thus be a limiting factor for TN simulation ∣ especially when d becomes comparable to commonly used TN bond dimensions (100 ≲ χ ≲ 500 for TTN). In these cases, strategies aimed at further compressing the local computational basis are needed (see subsection “Local basis truncation”). As just discussed, such truncation strategies are particularly crucial for high-dimensional LGTs.

Several numerical analyses suggest that, in some cases, a small-to-moderate truncation of the gauge group is enough for accurately approximating the continuum limits, at least for low-energy states^{36,38,44,138,139,140,141,142,143}. However, the optimal gauge truncation depends on the Hamiltonian parameters m and g.

As an example, we consider the (2+1)D U(1) LGT including dynamical matter (QED), whose Hamiltonian can be obtained from (3):

$${\hat{H}}_{{{{{\rm{QED}}}}}} = \frac{c\hslash }{2a}\sum\limits_{{{{{\bf{x}}}}}}\left[-\,{{\rm{i}}}\,{\hat{\psi }}_{{{{{\bf{x}}}}}}^{{{{\dagger}}} }{\hat{U}}_{{{{{\bf{x}}}}},{{{{{\boldsymbol{\mu }}}}}}_{{{{{\bf{x}}}}}}}^{{{{\dagger}}} }{\hat{\psi }}_{{{{{\bf{x}}}}}+{{{{{\boldsymbol{\mu }}}}}}_{{{{{\bf{x}}}}}}}\right.\\ -\left.{(-1)}^{x+y}{\hat{\psi }}_{{{{{\bf{x}}}}}}^{{{{\dagger}}} }{\hat{U}}_{{{{{\bf{x}}}}},{{{{{\boldsymbol{\mu }}}}}}_{{{{{\bf{y}}}}}}}+{\hat{\psi }}_{{{{{\bf{x}}}}}+{{{{{\boldsymbol{\mu }}}}}}_{{{{{\bf{y}}}}}}}+\,{{\rm{H.c.}}}\,\right]\\ +m{c}^{2}\sum\limits_{{{{{\bf{x}}}}}}{(-1)}^{x+y}{\hat{\psi }}_{{{{{\bf{x}}}}}}^{{{{\dagger}}} }{\hat{\psi }}_{{{{{\bf{x}}}}}}\\ +\frac{{g}^{2}c\hslash }{2a}\sum\limits_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}{\hat{E}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{2}-\frac{c\hslash }{2{g}^{2}a}\sum\limits_{\square }{{{{\rm{Tr}}}}}({\hat{U}}_{\square }+{\hat{U}}_{\square }^{{{{\dagger}}} }),$$

(11)

Since the Abelian U(1) group has only one generator, the gauge fields Ê_x and ${\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}$ can be represented as

$${\hat{E}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}={\hat{\sigma} }_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}^{z}(\ell )\quad {\hat{U}}_{{{{{\bf{x}}}}},{{{{\boldsymbol{\mu }}}}}}={\hat{\zeta} }_{{{{{\bf{x}}}}},+{{{{\boldsymbol{\mu }}}}}}^{{{{\dagger}}} }(\ell )\cdot {\hat{\zeta}}_{{{{{\bf{x}}}}}+{{{{\boldsymbol{\mu }}}}},-{{{{\boldsymbol{\mu }}}}}}(\ell )$$

(12)

where σ^z(ℓ) is the spin z-operator in the ℓ SU(2) irrep, while ζ(ℓ) is a ℓ × ℓ ladder operator with Fermi statistics.

We focus on a single plaquette in open boundary conditions, as it provides the minimal setting allowing for both electric and magnetic effects. Then, to characterize the convergence in the gauge truncation ℓ, we consider a candidate observable Ô and compute its ground state expectation value ${\langle \hat{O}\rangle }_{\ell }$ for increasing ℓ. We iterate until the relative deviation between consecutive truncations drops below some threshold ϵ_trunc: $| {\langle \hat{O}\rangle }_{{\ell }^{* }}-{\langle \hat{O}\rangle }_{{\ell }^{* }-1}| < {\epsilon }_{{{{{\rm{trunc}}}}}}| {\langle \hat{O}\rangle }_{{\ell }^{* }}|$ for some ℓ^*. Figure 4a shows the minimal truncation ℓ^* at which the magnetic energy operator $\hat{O}={{{{\rm{Re}}}}}{\hat{U}}_{\square }$ is converged to ϵ_trunc = 10⁻⁵. We explore a grid of model parameters, whose extent has been chosen according to standard MC literature^{8,144,145,146,147,148,149,150,151,152,153,154,155}. ${{{{\rm{Re}}}}}{\hat{U}}_{\square }$ is used as a benchmark due to its relevance in the weak coupling regime, where the continuum limit of D < 3 lattice QED is located⁸. As Fig. 4b shows, ℓ^* depends heavily on the coupling, growing asymptotically like ℓ^* ~ g⁻¹ as g is decreased, while m plays almost no role. An analogous inverse dependence of the minimal gauge truncation on the coupling is expected for non-Abelian LGT in arbitrary dimensions. Moreover, the continuum limit of non-Abelian LGTs in D≤3 is also expected at g → 0⁸, further substantiating the need to compress the local dimension in TN simulations of LGT whenever extrapolation to the continuum is in order.

Fig. 4: Exact diagonalization of a QED plaquette.

a For a grid of masses and couplings m ∈ [10⁻², 10¹] and g² ∈ [10⁻¹, 10¹], minimal gauge truncation ℓ^* required to reach a precision ϵ_trunc = 10⁻⁵ in the magnetic energy $\langle {{{{\rm{Re}}}}}\,{\hat{U}}_{\square }\rangle$. b Scaling of ℓ^* with g² for m = 0.1. c Corresponding entanglement entropy S associated with a symmetric bipartition of the plaquette (see also Supplementary Note I and Fig. S1).

Apart from the growth of the local dimension, extrapolation to the continuum is further complicated by the fact that the continuum limit of a lattice quantum field theory corresponds to a critical point of the underlying lattice model¹⁵⁶. Close to criticality, quantum correlations are boosted and violations of the entanglement area law are expected⁹⁷. The higher entanglement entropy in the proximity of the continuum (g, m ≪ 1 regime) is already captured by the single-plaquette analysis of Fig. 4c. Continuum limits of LGTs are thus an area of potential advantage for quantum computation over classical methods, as the former is not limited by entanglement. Nonetheless, quantum computation is also affected by the need to relax gauge truncations when g → 0, either by increasing the number of qubits used to encode a dressed site, which is at least $\lceil {\log }_{2}(d)\rceil$, or by using hybrid devices with both qubits and bosonic modes¹⁵⁷.

Roadmap for advanced simulations

As detailed in the previous subsections, LGT models present some peculiar features that make TN simulations particularly challenging, especially for large system sizes and for studying the continuum limits in terms of gauge field truncation, lattice spacing, and volume.

State-of-the-art techniques, such as TTN algorithms, have been applied for simulating ground state properties of QED in (2 + 1)- and (3 + 1)-dimensions for small-to-intermediate sizes^56,58. Very recently, they have also been applied to the SU(2) Yang-Mills model in (2 + 1)-dimensions⁶⁵. In all these simulations, small non-trivial representations of the gauge groups have been exploited, e.g., three electric field levels for QED and the first two IRREP of SU(2) for the Yang-Mills model.

Nowadays, lattice computations with MC-based techniques are performed on large lattices, e.g., of the order 64³ × 128 sites (space and time discretization), and with no truncation of the gauge fields. These large sizes are required to control finite-volume effects and to perform extrapolations toward the continuum limits¹⁵⁸. In the last decades, the impressive progress in algorithmic development, high-performance optimizations, and the availability of increasingly powerful supercomputer facilities have played a major role in the advancement of MC-based LGT computations. Indeed, this progress has opened the doors to large-scale simulations, that currently represent the standard approach for studying non-perturbative phenomena in quantum field theory.

However, MC techniques are generally based on computations of path integrals, in which observables are calculated as weighted sums. Many physically relevant scenarios, such as finite baryon density regimes or real-time dynamics of quarks, give rise to a change in the sign of the weights and highly oscillating behaviors. Thus, numerical evaluations suffer from the near cancellation of the opposite-sign contributions to the integrals. This is the essence of the infamous sign problem, a long-standing issue of LGT simulations with MC methods¹¹.

Hence, the quest of conceiving, developing, and optimizing alternative approaches that enable simulating these regimes, being the latter at the heart of many open problems related to our understanding of high-energy physics.

As described in the previous subsections, TNs represent a promising complementary method, which found the first applications in simulating non-trivial instances of high-dimensional LGTs on small-to-intermediate lattice sizes. TNs are intrinsically sign-problem-free, enabling the simulation of both static properties at equilibrium, such as low-energy states, and real-time dynamics, even in the presence of finite chemical potentials or non-trivial topological terms. It is worth noting that, in addition to local observables and correlation functions, TNs allow the numerical computations of entanglement properties, such as entanglement entropies and central charges, that could potentially shine new light on LGT phenomena⁴⁴.

Nevertheless, TN simulations of high-dimensional LGTs still represent a challenging problem, especially for large lattice sizes or higher representations of gauge groups needed for analyzing continuum limits. In this framework, further and intensive developments are required to tackle TNs’ current problems related to LGTs, such as QCD’s non-perturbative effects on lattices of sizes comparable with MC simulations. In this regard, sign-problem-free TN ansätze can also be used in combination with variational MC methods to tackle high-dimensional LGTs with arbitrary gauge groups¹⁵⁹.

In the following, we present a possible roadmap in terms of algorithmic development and optimization strategies that we foresee as crucial for making the TN approach competitive as a complementary method to MC techniques. Therein, the first two subsections, i.e., “Local basis truncation” and “Tailored initial states”, can be approached with existing TN algorithms and a good intuition on LGT problems; then, subsections “Leverage HPC techniques for local optimization” and “Sweeps and HPC parallelization” outline optimization for existing algorithms to leverage HPC systems; finally, we discuss new classes of ansätze to tackle finite temperature problems in subsection “Finite temperature regime.” In some parts, we focus on TTNs, but the vast majority of the presented concepts and techniques can be straightforwardly applied to other TN ansätze.

Local basis truncation

One of the main issues in simulating LGTs with TN methods lies in the very large local basis dimension d that one needs to handle to represent matter and gauge-field degrees of freedom properly. To some extent, this situation is very similar to some condensed matter models, e.g., the Holstein model, involving lattice fermions coupled with phonons¹⁶⁰, or bosonic systems coupled to optical cavities^161,162. Also, in these cases, the local Hilbert space is, in principle, infinite-dimensional, and a truncation to a fixed cutoff is needed for performing TN simulations. For one-dimensional systems of this type, some efficient algorithms based on MPS have been developed in the last years^163,164, e.g., the pseudosite DMRG (PS-DMRG) method¹⁶⁵, and the DMRG with local basis optimization (DMRG-LBO)^166,167,168.

The key idea of the PS-DMRG is to replace a single site having large local dimension d with ${n}_{ps}\approx {\log }_{2}(d)$ pseudo sites of local dimension 2, as shown Fig. 5a. Since a large class of optimization algorithms for TNs scale at least quadratically with the local dimension but linearly with the total number of sites, as detailed in subsection “TNs Overview”, one obtains a more efficient and manageable representation according to this procedure.

Fig. 5: Graphical representation of methods for handling large local bases.

a The pseudo site DMRG (PS-DMRG) approach, in which a single site having large local dimension d is replaced with n_ps pseudo sites with a smaller local dimension, e.g., two; b the local basis optimization embedded in the MPS ansatz (LBO-MPS), so that an additional layer of tensors connected to the physical legs of the MPS performs the reduction from a large local basis with dimension d into an effective basis with smaller dimension ${d}^{{\prime} }$; χ is the bond dimension of the MPS.

The price to pay lies in the range of the interactions: short-range interactions in the Hamiltonian are transformed into long-range operators due to the pseudo-site encoding of the local degrees of freedom. As a consequence, PS-DMRG should require a larger bond dimension and a larger number of variational steps to converge, and the benefits offered by the pseudo-sites could progressively fade for increasing values of n_ps at fixed bond dimension. PS-DMRG has been applied to one- and two-dimensional QMB systems with d up to O(100)^163,165.

The core of the DMRG-LBO algorithm, instead, lies in a LBO protocol that enables a controlled and efficient truncation of the local Hilbert space¹⁶⁹. For each site ${\bf{x}}^{\prime}$ of the lattice, the optimized local basis is computed by starting from its reduced density matrix, i.e.

$${\rho }_{{{{{\bf{x}}}}}^{\prime} }={{{{{\rm{Tr}}}}}}_{{{{{\bf{x}}}}}\ne {{{{\bf{x}}}}}^{\prime} }\left\vert \psi \right\rangle \left\langle \right.\psi | ,$$

(13)

where $\left\vert \psi \right\rangle$ is a general state of the whole system and the trace is over all the degrees of freedom which do not involve the site ${\bf{x}}^{\prime}$. By performing the diagonalization procedure, the eigenvalues λ_α and the eigenvectors v_α of ${\rho }_{{\bf{x}}^{\prime}}$ can be easily determined. The set of values λ_α represents the probabilities associated with the states v_α. If λ_α is small, e.g., below a certain numerical threshold, the related eigenvector v_α can be discarded from the local basis of the site ${\bf{x}}^{\prime}$, with a controllable loss of accuracy for the state $\left\vert \psi \right\rangle$. Thus, for reducing the local basis dimension of ${\bf{x}}^{\prime}$ from d to a smaller value ${d}^{{\prime} }$, an optimal choice is keeping the ${d}^{{\prime} }$ eigenvectors of ${\rho }_{{\bf{x}}^{\prime}}$ with the largest probabilities. Then, the original state $\left\vert \psi \right\rangle$ can be projected on the new basis without losing the relevant physical information. Let us notice that the site ${\bf{x}}^{\prime}$ can also be a generic unit cell of the system, composed of a certain number of lattice sites.

A crucial point of the LBO procedure is the knowledge of the original state $\left\vert \psi \right\rangle$, generally the ground state of the system, that is not known prior. This issue can be overcome in several ways: by performing exact diagonalization of the system’s Hamiltonian with local dimension d for small lattice sizes, to determine $\left\vert \psi \right\rangle$, and then truncating the basis from d to ${d}^{{\prime} }$ for increasing values of the cutoff ${d}^{{\prime} }$. From this procedure, we can obtain an optimized local basis, ensuring a controlled approximation of the original ground state. This optimized basis can then be exploited in optimization algorithms for simulating larger lattice sizes, such as DMRG. Another strategy directly incorporates the LBO procedure in the tensor network ansatz, as shown Fig. 5b: by inserting an additional tensor on each physical leg of the MPS, the large local basis with dimension d is transformed into an effective basis with a smaller dimension ${d}^{{\prime} }$. In this way, the MPS tensors only see the effective basis in the optimization procedures, with a significant reduction of the computational costs described in subsection “TNs Overview". This method has been used for both static DMRG and time evolution algorithms, such as TEBD, for the study of one-dimensional quantum impurity models and correlated electron-phonon systems^166,167,170.

Benchmarks and performance analysis concerning PS-DMRG and DMRG-LBO for QMB systems have been extensively discussed in¹⁶³. Let us mention that some of the main features of these two methods can be combined into more sophisticated algorithms, such as the projected purified DMRG¹⁷¹.

In the context of LGTs, the dimension of the local basis d can easily go beyond values of the order of 10⁶, especially for higher-dimensional non-Abelian models and large representations of the gauge groups, as shown in subsection “Hamiltonian LGTs.” In this scenario, numerical simulations with TNs are practically infeasible without an optimized scheme for truncating the local degrees of freedom. Techniques like PS-DMRG might offer some benefits for small system sizes, such as unveiling the most relevant degrees of freedom in the low-energy states, but it is not easy to scale them up for large sizes due to the long-range interactions induced between the pseudo-sites. Also, the local constraints imposed by Gauss law would become highly non-local when splitting a single site into multiple pseudo-sites representing the matter and link fields.

In principle, LBO-based procedures could instead represent a well-grounded route for addressing the problem. Their use in condensed matter, e.g., bosonic systems, is a rather consolidated approach, whereas their application to TN simulations of LGTs currently is an uncharted but promising territory. The main steps that we foresee as needed and important in this direction are the following:

• (i) Employing exact diagonalization, testing the convergence of LBO procedures for one-dimensional systems, such as the φ⁴-theory or the Schwinger model, for which analytical solutions, at least in some regimes of the phase diagram, and numerical results are widely available, also in the limit of no gauge field truncations. In this way, we can obtain valuable information about the scaling of the basis cutoffs concerning the final accuracy of the state representation for small system sizes.

• (ii) Performing the same analysis on (2 + 1)-dimensional LGTs, such as QED or SU(N) models, for one unit cell, like a single lattice-plaquette, to systematically study the effects of the magnetic interactions on the local degrees of freedom. Indeed, the QLM representation of LGTs, detailed in subsection “Hamiltonian LGT,” generally exploits the “electric field" basis, in which the electric field terms of the Hamiltonian and Gauss law are diagonal. In this scheme, the magnetic interactions correspond to non-diagonal operators which can increase the number of local electric states to include for an accurate description of the system, especially for small values of the coupling constant g of (3), as highlighted in the numerical analysis in subsection “Scaling of the local basis dimension”.

• (iii) Exploiting the optimized local bases obtained from exact diagonalization as input of TN simulations for larger sizes, testing the effects on the global ground state accuracy and in computing physically relevant quantities, such as the mass gap¹⁵⁵.

• (iv) In the same spirit of LBO-MPS, implementing LBO protocols directly in TN ansätze that are more suitable for simulating high-dimensional LGT models, such as TTN. This step could be of great benefit in particular for aTTNs, which encode the area law for the entanglement but are severely limited by large local bases (see subsection “TNs Overview”).

By following and combining all these steps, we expect to reduce the effective local basis of LGT models, potentially enabling TN simulations for large representations of Abelian and non-Abelian gauge groups.

It is worth noting that constructing optimal bases for numerical and quantum computation of LGTs is an active area of research. Several approaches that have been recently proposed involve performing canonical transformations of the gauge degrees of freedom before truncation^{129,172,173,174,175,176}. By exploiting a resource-efficient protocol of this type, ref. ¹²⁹ has shown that the number of local states required to reach a 1% accuracy level when computing the expectation value of the plaquette operators in two-dimensional (2 + 1)-dimensional QED can be reduced by more than 94% compared to the unoptimized truncation. Integrating these approaches into TN algorithms could greatly benefit LGT simulations.

Tailored initial states

In TN algorithms for ground state searching, the optimization procedure generally starts from a random TN initial state $|\psi_{{\rm{init}}}\rangle$, i.e., the tensors in the network are filled with random coefficients at the beginning. This strategy usually guarantees that the probability of overlapping with the true ground state ∣〈ψ_init∣ψ_gs〉∣² does not vanish. To reach a small error in the final energy, this procedure typically requires from 10 to 50 optimization sweeps for LGTs simulations, depending on the specific models, the Hamiltonian parameters, and the lattice size. Since the time for completing a sweep can be very long, especially for large bond dimensions, strategies for reducing the number of needed sweeps could be beneficial for scaling up system sizes. From this perspective, constructing appropriate states to be used as initial guesses can speed up the convergence, similar to the choice of the trial wave function for variational MC simulations. We consider the following options:

• (i) Physical insight: Initial states can be constructed by following physical intuition, at least in those regimes in which analytical or partial numerical results are available. For instance, initial guesses can be constructed by starting from the TN ground states numerically obtained for a lower representation to simulate large spin representations of the gauge fields.

• (ii) Machine learning: Machine learning-assisted protocols can improve the construction of tailored initial states in the different regimes of the model parameters. For instance, feed-forward neural networks have been proposed as trial wave functions for quantum MC simulations¹⁷⁷, and machine learning techniques have been used to feed TN simulations¹⁷⁸. Also, neural network quantum states (NNQS) have demonstrated their ability to represent the quantum states of many-body systems with great accuracy¹⁷⁹. Using this approach, neural networks could be trained as variational ansatzes to approximate low-energy states of LGTs. These states might then be used as initial guesses for TN simulations, potentially reducing the computational overhead associated with optimization sweeps. Furthermore, a recent study¹⁸⁰ has explored combining NNQS with TN methods to hybridize their strengths, offering a promising avenue for large-scale simulations.

• (iii) TN results: Following the idea of the physical insight, it is also possible to feed neighboring ground states as initial guesses into a ground state search. This option exists especially when scanning a phase diagram and varying parameters in a small increment, such that the overlap between neighboring wave functions is sufficient; this overlap decreases for two points on the opposite sides of a quantum critical point. The same idea can be implemented by preparing an initial guess quenching from an easily accessible ground state to the target parameters. Such an approach is well-known in the case of an adiabatic state preparation¹⁸¹, especially for challenging problems with strong localization. The quench does not necessarily have to be adiabatic or free of numerical errors, but it must only have sufficient overlap with the true ground state. The advantage here is that one quench can generate multiple initial guesses along the quench for different parameters.

Leverage HPC techniques for local optimization

We dedicate the two following subsections to the numerical optimization of the TN algorithms. In this subsection, we give an overview of the topic and discuss possible strategies to improve the optimization. The more technical steps are discussed in the following subsection, “Sweeps and HPC parallelization.”

To scale up TN simulations of LGTs, in particular regarding lattice sizes, another important factor is the number of optimization steps to be carried out. The number of optimization steps scales linearly with the number of sweeps as well as with the system size for MPS, PEPS, and TTN. The choice of the number of sweeps is set such that the algorithm reaches convergence when computing ground or low-energy states. Let us briefly describe the general procedure for ground state searches: we focus on the TTN optimization, however, the main points described here can be applied to other TN structures, such as MPS or PEPS. For a complete technical description of the algorithms and implementation details, see ref. ³⁰.

Consider a generic QMB Hamiltonian H and a generic normalized state $\left\vert \psi \right\rangle$, defined on the same Hilbert space. To numerically determine the ground state of H, the following global minimization problem has to be solved:

$${\min }_{\left\vert \psi \right\rangle }\left\{E(\left\vert \psi \right\rangle )\right\}= {\min }_{\left\vert \psi \right\rangle }\left\langle \right.\psi | H\left\vert \psi \right\rangle \,.$$

(14)

If $\left\vert \psi \right\rangle$ is written in terms of the TTN ansatz introduced in subsection “TNs Overview”, the variational parameters are the coefficients in the TTN. In this case, the global optimization problem of (14) is broken down into a sequence of smaller optimizations, each involving only a minimal subset of tensors in the TTN. The algorithm solves the optimization via an eigenproblem searching for the eigenvector with the lowest eigenvalue. Without any loss of generality, one single tensor at a time is optimized in the simplest case, as shown in Fig. 6a. In detail, the energy is computed by contracting the Hamiltonian between the TTN and its complex conjugate. Then, we start the optimization procedure from a target tensor T, by computing its environment, i.e., the network without the tensors T and T^†, which represents the effective Hamiltonian H_eff for the local problem. At this stage, an eigenproblem of H_eff is solved, and the tensor T is updated with the newly found ground state. The whole procedure is sequentially iterated for all the tensors in the network, performing an optimization sweep.

Fig. 6: Effective operators and parallel tensor networks.

a Procedure for optimizing a TTN to find the ground state of a QMB system: the energy is computed by contracting the Hamiltonian H (yellow tensor) with the TTN, representing the state $\left\vert \psi \right\rangle$, and its hermitian conjugate, representing $\left\langle \right.\psi |$. The variational optimization starts from a target tensor T (red tensor), by computing its effective Hamiltonian H_eff and then solving the local eigenvalue problem for the latter. The tensor T is then updated with the newly found ground state, and the procedure iterates over all the tensors in the network (sweep). b The workload itself consists of optimizing each tensor held by the MPI thread t, which requires effective operators calculated by other MPI threads. We dub delaysΔ_i the number of optimization cycles needed to obtain the information of tensors in the i-th MPI thread in another MPI thread via MPI communication. MPS naturally split into sub-chains, which communicate with one or two neighboring MPI threads to obtain updated effective operators. Delays for updates scale with the distance between two MPI threads along the chain. Each MPI thread can use threading or openMP, e.g., in a hybrid openMP-MPI approach. c Similarly, TTNs can be split into sub-trees for each MPI thread, allowing for optimizing the sub-tree without communication with other MPI threads. Delays due to updating scale logarithmically as any distance in a TTN.

For each operation, efficient algorithms from linear algebra are typically used, e.g., the Arnoldi algorithm implemented in the ARPACK library^182,183. We recall that the numerical complexity of this procedure for a single TTN-tensor is O(d²χ² + χ⁴). Therefore, a single optimization can be time-consuming when χ is very large, e.g., χ ≈ 1000, as for simulating high-dimensional LGTs. We point out the established and promising future parallelization schemes for the single tensor optimization:

• (i) opemMP: an efficient openMP implementation of the contraction between the effective operators with the tensor can speed up simulations. Moreover, the Arnoldi algorithm of ARPACK is optimized for large-scale linear algebra operations and supports intra-node multi-core parallelization based on openMP¹⁸⁴; thus, ARPACK does not become a bottleneck in the openMP implementation. Nonetheless, many simulations remain expensive in computation time even with 64 or more cores available in HPC facilities; therefore, we consider more approaches beyond the well-established openMP path.

• (ii) Accelerators: graphics processing units (GPU) and tensor processing units (TPU) offer a path to accelerate linear algebra routines, where both have demonstrated their usefulness¹⁸⁵: GPUs have reported speedups of up to a factor of 10 due to the efficient tensor manipulations^{186,187,188,189}; TPU have shown great potential in large-scale simulations of several quantum systems, e.g., drastically reducing the computational time of DMRG calculations with very large bond dimensions from months to hours^{190,191,192,193}. TPU are application-specific integrated circuits originally introduced for machine learning; we consider the integration and tuning of TPUs therefore as a step after the successful integration of GPUs. While single GPUs can solve TTN-problems up to a bond dimension of χ < 1000, multi-GPU support is available for libraries; HPC systems typically provide hardware with four GPUs per node.

• (iii) Multi-node approaches to local tensor optimizations: both CPU and GPU algorithms can be further scaled by using multiple nodes. The underlying linear algebra routines of the local eigenvalue problem are parallelizable via libraries such as ScaLAPACK or MAGMA. Both libraries provide routines for distributed memory machines¹⁹⁴; moreover, MAGMA supports CPU and GPUs. In this way, the workload of the eigenproblem procedure can be split into several computation nodes. Then, it is important to analyze the performance as a function of the bond dimension χ to test the effectiveness of this approach against the latency of the inter-node communications.

• (iv) Tuning of parameters and algorithms: accelerators developed for machine learning applications have excellent support for lower and real precision. Tuning parameters over the different sweeps is beneficial, e.g., increasing the precision towards the end of the sweep. This approach profits from faster single-precision implementations during the first sweeps. Selecting algorithms like random singular value decompositions can also bring benefits¹⁹⁵.

Sweeps and HPC parallelization

So far, we have parallelized single tensor optimizations within a sweep, but the sweep itself was sequential, i.e., serial. Recent works formulated parallel versions of MPS algorithms for ground state search and time evolution, e.g., via the message passing interface (MPI)^{196,197,198,199}. The main difference between the serial and parallel algorithms is the effective operators used in the optimization. In the serial version, the effective operators contain the information of the most recent version of all other tensors. This update is delayed in the parallel version, i.e., the tensor that entered the effective operator is not necessarily the one of the current sweep, but can be the version of an earlier sweep.

If the delay becomes an obstacle to convergence, there is the option to modify parameters during the sweeps. Typically, ten to fifty sweeps are necessary to converge on a solution. As the initial state is usually random, MPI can be used especially at the beginning. To ensure convergence, one can consider serial steps at the end; even a gradual reduction of the MPI processes as the sweeps proceed is possible and gradually reduces the delays.

Considering the MPS scenario of a chain in Fig. 6b, we split the chain into equal parts of (N/n_{MPI−threads}) sites. Each part of the chain communicates with its two neighbors apart from the two boundaries. The effective operators take into account the tensors of the same MPI process with zero delay as in the serial case. The tensors of the i-th neighboring MPI process have a delay of i. The worst-case scenario of the delay scales linearly with the number of MPI processes. The delay can be avoided by communicating the effective operators after each update through the chain, which is a quasi-serial step with no more than two MPI processes active at the same time.

The problem becomes more complicated for the TTNs suggested for LGT, but we expect a benefit for the parallelization of a TTN versus an MPS for higher-dimensional systems. Figure 6c shows an example of how each MPI process gets assigned a sub-tree within the complete TTN. Unlike the MPS, the number of neighboring MPI processes for communication is at least three and increases with (N/n_{MPI−threads}) tensors per thread. For simplicity, we assume equally shaped subtrees for all MPI processes. The delay of the tensor update is now $2\cdot {\log }_{2}(N)$ in the worst-case scenario.

One-dimensional systems with nearest-neighbor interactions thus exhibit a delay of 1 in the worst-case scenario in the MPS, while the delay is up to $2\cdot {\log }_{2}(N)$ for the nearest neighbors in the center of the TTN. Rather, higher-dimensional systems change this aspect, e.g., for an N × N two-dimensional system mapped to 1D via a zig-zag mapping. The MPS has a worst-case delay of the tensor update of N for the slow index. In contrast, the TTN has the same log behavior and a maximum delay at the center of the TTN as $2\cdot {\log }_{2}({N}^{2})$. Thus, the worst-case delay is equal for 16 × 16 systems; increasing N further, TTNs exhibit smaller maximum delays during parallel sweeps. Moreover, the TTN is unaffected by the type of mapping used; in contrast, the worst-case delay for the MPS grows to 2N for the snake mapping and to at least N²/2 for the Hilbert curve²⁰⁰. Equal arguments hold for 3D systems and delays of N² (MPS, zig-zag) versus $2{\log }_{2}({N}^{3})$ (TTN, any mapping).

To get an intuition of what parallelized simulations can solve, we sketch out the specifications for a parallel simulation on the pre-exascale cluster Leonardo hosted by Cineca. As an example, we focus on a 2D quantum Ising model with a transverse field in the vicinity of the quantum critical point²⁰¹:

$$\hat{H}={\sum}_{\langle i,j\rangle}{\hat{\sigma} }_{i}^{x}{\hat{\sigma}}_{j}^{x}+{{{{\rm{h}}}}}{\sum}_{i}{\hat{\sigma}}_{i}^{z}\,,$$

(15)

which, despite not resembling the previously described LGT scheme, has been demonstrated to provide the same Hilbert space dimension scaling of a gauge theory²⁸. Then, we choose an MPI approach together with the GPUs. Leonardo has 3456 nodes with four GPUs, totaling 13,824 GPUs available for the complete cluster. Bond dimensions on the order of χ = 450 consume 54 GB of memory without effective operators (assuming double complex precision, 40 Lanczos vectors) and allow for solving the eigenproblem on the GPU without temporarily storing data on the CPU. We use the single-tensor per MPI-thread with χ = 450 and initial tensor optimizations^202,203 as a baseline where we extract a rough empirical estimate with Leonardo.

Due to the delay of the tensor in the effective operators, the minimum number of sweeps must be beyond 24. Then, we consider the scaling of the TTN previously introduced and generate Table 2 with an overview of different system sizes and bond dimensions. These results provide a coarse-grained estimate, since plaquette terms, different symmetries, entanglement generation, and optimization time within later sweeps could further impact the computational time.

Table 2 Extrapolated simulation time

Our estimate predicts that a system of 256 × 256 sites takes about two months for bond dimension χ = 450 on 1024 GPU nodes of Cineca’s Leonardo. Future improvements are likely to bring this simulation time down in comparison to this single-GPU approach, requiring significant data transfer, e.g., the next-generation GPUs beyond the A100, larger GPU memory, or further optimization in data movement. In contrast, a three-dimensional system with large entanglement and many sites requires three to four orders of magnitude improvement, where cluster size and other improvements have to come together to reach this challenge. Furthermore, Table 2 provides an estimate of the boundary for a potential quantum advantage in simulating LGTs with quantum computers or simulators.

Finite temperature regime

To date, TN simulations of high-dimensional LGTs, including dynamical matter, are exploring zero temperature regimes, which are important to understand the low-energy properties of the models. To explore finite temperature phenomena, particularly relevant for open research problems, such as the QCD phase diagram, technical and numerical challenges have to be tackled, e.g., devising and testing efficient TN algorithms for targeting quantum states at equilibrium. As suggested in the next paragraph, we foresee two possible paths toward finite temperature TN states.

Matrix product density operators and locally purified tensor networks (LPTNs) provide already today the option to tackle finite temperature regimes via an imaginary time evolution^204,205,206. Herein, the algorithm starts at the infinite temperature state and starts “cooling” the system via a specified number of time steps and a specified step size to reach a given temperature. In their original formulation, both approaches are one-dimensional chains. The matrix product density operator can be formulated as TTN but faces some challenges in terms of the question of positivity²⁰⁷ or integrating symmetries. In contrast, tree tensor operators (TTO) are the tree-equivalent of an LPTN; they are also a positive loopless representation of density matrices, recently introduced in ref. ²⁰⁸. However, TTOs cannot represent the infinite temperature state necessary for the imaginary time evolution approach. Instead, a possible use of the TTO employed in LGT simulations consists of a variational algorithm to target finite-temperature states or reconstruct open-system quantum dynamics, by efficiently compressing the relevant information. The TTO enables useful measures, e.g., computing the entanglement of formation as already shown for representative one-dimensional models at finite temperature²⁰⁸.

Outlook

The field of TN methods for LGTs has shown great potential in the last decade, during which significant efforts have been devoted to developing numerical algorithms and strategies that can be seen as a complementary approach to MC simulations for high-energy physics. The validity of sign-problem-free TN algorithms has been proven for one-dimensional LGT models for both Abelian and non-Abelian scenarios. Recently, TN methods have also been applied to higher-dimensional LGTs with simple truncated gauge groups and small-to-intermediate lattice sizes. On the one hand, these results prove the effectiveness of TN methods for simulating LGTs even in regimes that are problematic for other numerical methods; on the other hand, they highlight the challenges that one needs to tackle to address state-of-the-art research problems, such as accessing the continuum limits or simulating high-dimensional QCD on large lattices.

In this work, after a general overview of TN methods and their use for LGT simulations, we have described these challenges, starting from the problem of the very large local basis required for complex gauge groups and then discussing several computational bottlenecks in terms of bond dimensions and system sizes.

To mitigate and possibly overcome these problems soon, we have presented a feasible roadmap, in terms of algorithmic developments and numerical strategies that might have a concrete impact in extending the range of applicability of TN algorithms to current research problems in high-energy physics. We foresee that all the presented steps could potentially have a key role in making the TN approach competitive as a complementary method to MC techniques for simulating high-dimensional LGTs, such as large-scale QCD.