Introduction

Gauge theories serve as a fundamental framework of modern physics through which various outstanding phenomena such as quark confinement, topological spin liquid phases, high-Tc superconductivity, and the fractional quantum Hall effect can be formulated1,2,3. This makes gauge theories relevant across various fields ranging from condensed matter to high-energy physics. Gauge theories are characterized by their principal property of gauge invariance, which is a local symmetry that enforces an intrinsic relation between local sets of degrees of freedom, and gives rise to gauge fields, the mediators of interactions between elementary particles4. The Standard Model of particle physics includes prominent gauge theories such as quantum electrodynamics, with its Abelian U(1) gauge symmetry, and quantum chromodynamics, with its non-Abelian SU(3) gauge symmetry5,6.

With the great progress achieved in the control and precision of modern quantum simulators7,8,9,10,11,12, recent years have witnessed a tremendous interest in realizing gauge theories in various synthetic quantum matter platforms such as, e.g., superconducting qubits, Rydberg setups, and optical lattices13,14,15,16,17,18. Such setups can serve as an experimental probe that can ask questions complementary to dedicated classical computations and high-energy colliders, with the exciting potential to calculate time evolution from first principles18. Until now, almost all quantum-simulation experiments of gauge theories have taken place in one spatial dimension or have been restricted to a small number of plaquettes19,20,21,22,23,24,25,26,27,28,29,30,31,32,33. Although these experiments are significant milestones in their own right, going to higher spatial dimensions is essential for probing salient high-energy phenomena in nature. Developing scalable implementations for higher dimensions has thus been identified as a major challenge in the field17.

Here, we propose an experimentally feasible quantum simulator of a large-scale 2 + 1D U(1) gauge theory with dynamical matter and gauge fields. This is achieved by mapping the model onto spinless bosonic degrees of freedom on an optical superlattice; see Fig. 1a. We provide perturbation theory derivations outlining the stability of the gauge symmetry in this mapping due to an emergent linear gauge protection term34,35, and perform time-evolution numerical benchmarks using infinite matrix product state (iMPS) techniques that demonstrate robust fidelity of the mapping. Our work complements previous proposals for implementing gauge theories in higher dimensions, which mostly concentrated on pure gauge theories (see, e.g.,36,37,38,39,40,41,42), while here we include dynamical matter (see also43,44,45), but without the use of a plaquette term. Recent theory investigations have demonstrated that even in the absence of plaquette terms, 2 + 1D gauge theories with dynamical matter can nevertheless display extremely rich physics, such as symmetry-protected topological states and spin liquid phases46,47,48,49. Importantly, our proposal is feasible to implement with existing technology in current cold-atom experiments.

Fig. 1: Diagram of the mapping.
figure 1

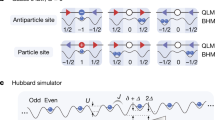
a Mapping of the 2 + 1D U(1) quantum link model (QLM) onto the two-dimensional Bose–Hubbard model (BHM) on a Lieb superlattice. A matter site (shallow) can host one or zero bosons, while a gauge site (deep) can host two or zero bosons. Forbidden sites (deepest) are never occupied. b The different matter and electric-field configurations permitted by Gauss’s law in the computational basis, shown for both the QLM and its BHM mapping.

Full size image

Methods

Model and mapping

We consider a quantum link formulation of the 2 + 1D Abelian Higgs model, where, in keeping with experimental feasibility, the infinite-dimensional gauge and electric fields are represented by spin-1/2 operators50,51. The resulting 2 + 1D U(1) quantum link model (QLM) is described by the Hamiltonian

$${\hat{H}}_{{{\rm{QLM}}}}=-\kappa {\sum}_{{{\bf{r}}},\nu }\left({\hat{\phi }}_{{{\bf{r}}}}^{{\dagger} }{\hat{s}}_{{{\bf{r}}},{{{\bf{e}}}}_{\nu }}^{-}{\hat{\phi }}_{{{\bf{r}}}+{{{\bf{e}}}}_{\nu }}^{{\dagger} }+\,{\mbox{H.c.}}\,\right)+m{\sum}_{{{\bf{r}}}}{\hat{\phi }}_{{{\bf{r}}}}^{{\dagger} }{\hat{\phi }}_{{{\bf{r}}}},$$
(1)

where \({{\bf{r}}}={({r}_{x},{r}_{y})}^{\top }\) is the vector specifying the position of a lattice site, and eν is a unit vector along the direction ν ∈ {x, y}, with the lattice spacing set to unity throughout this work. The hard-core bosonic ladder operators \({\hat{\phi }}_{{{\bf{r}}}},{\hat{\phi }}_{{{\bf{r}}}}^{{\dagger} }\) act on the matter field at site r with mass m, with κ the coupling strength, while the spin-1/2 operators \({\hat{s}}_{{{\bf{r}}},{{{\bf{e}}}}_{\nu }}^{\pm }\) and \({\hat{s}}_{{{\bf{r}}},{{{\bf{e}}}}_{\nu }}^{z}\) represent the gauge and electric fields, respectively, at the link between sites r and r + eν. Note that we do not include the gauge-coupling term \(\propto {({\hat{s}}_{{{\bf{r}}},{{{\bf{e}}}}_{\nu }}^{z})}^{2}\), as this is constant for spin-1/2 gauge fields, and we only consider dynamics via the hopping term κ, leaving the addition of plaquette interactions to this setup for future study. We have used a particle-hole transformation52 that provides a more intuitive connection to the bosonic mapping employed in this work—see Fig. 1 and Supplementary Note 1 for details.

The generator of the U(1) gauge symmetry of Hamiltonian (1) is

$${\hat{G}}_{{{\bf{r}}}}={(-1)}^{{r}_{x}+{r}_{y}}\left[{\hat{\phi }}_{{{\bf{r}}}}^{{\dagger} }{\hat{\phi }}_{{{\bf{r}}}}+{\sum}_{\nu }\left({\hat{s}}_{{{\bf{r}}},{{{\bf{e}}}}_{\nu }}^{z}+{\hat{s}}_{{{\bf{r}}}-{{{\bf{e}}}}_{\nu },{{{\bf{e}}}}_{\nu }}^{z}\right)\right],$$
(2)

which is equivalent to a discretized version of Gauss’s law, where \([{\hat{G}}_{{{\bf{r}}}},{\hat{G}}_{{{\bf{r}}}}^{{\prime} }]=0\). The gauge invariance of Hamiltonian (1) is encoded in the commutation relations \(\left[{\hat{H}}_{{{\rm{QLM}}}},{\hat{G}}_{{{\bf{r}}}}\right]=0,\,\forall {{\bf{r}}}\). The physical sector of Gauss’s law is the set of gauge-invariant states \(\{\left\vert \right.\psi \left.\right\rangle \}\) satisfying \({\hat{G}}_{{{\bf{r}}}}\left\vert \right.\psi \left.\right\rangle =0,\,\forall {{\bf{r}}}\). This restricts the allowed configurations of matter on a given site and the electric fields on its four neighboring links to those depicted in Fig. 1b, where we also show the corresponding configurations in the bosonic model onto which we map the QLM in order to quantum-simulate it. The crux of this mapping lies in first restricting the local Hilbert space of each “matter” site in the BHM superlattice to two states: \({\left\vert \right.0\left.\right\rangle }_{{{\bf{r}}}}\) and \({\left\vert \right.1\left.\right\rangle }_{{{\bf{r}}}}\), which correspond to an empty or occupied matter field on that site in the QLM. Furthermore, we restrict the local Hilbert space of each “gauge” site to the states \({\left\vert \right.0\left.\right\rangle }_{{{\bf{r}}},{{{\bf{e}}}}_{\nu }}\) and \({\left\vert \right.2\left.\right\rangle }_{{{\bf{r}}},{{{\bf{e}}}}_{\nu }}\), where an empty gauge site corresponds to a local electric field of \(\langle {\hat{s}}_{{{\bf{r}}},{{{\bf{e}}}}_{\nu }}^{z}\rangle =-1/2\), represented by an arrow pointing left (down) on the corresponding horizontal (vertical) link in the QLM, while a doublon on the gauge site of the bosonic model denotes a local electric field of \(\langle {\hat{s}}_{{{\bf{r}}},{{{\bf{e}}}}_{\nu }}^{z}\rangle =1/2\), with an arrow pointing right (up).

Such local constraints can be achieved by employing the 2D tilted Bose–Hubbard model (BHM) on a Lieb superlattice, given by the Hamiltonian

$$\begin{array}{rcl}{\hat{H}}_{{{\rm{BHM}}}}&=&\sum\limits_{{{\bf{j}}}}\left[J\sum\limits_{\nu =x,y}\left({\hat{b}}_{{{\bf{j}}}}^{{\dagger} }{\hat{b}}_{{{\bf{j}}}+{{{\bf{e}}}}_{\nu }}+\,{\mbox{H.c.}}\,\right)\right.\\ &&\left.+\frac{{U}_{{{\bf{j}}}}}{2}{\hat{n}}_{{{\bf{j}}}}\left({\hat{n}}_{{{\bf{j}}}}-1\right)+\left({{{\boldsymbol{\gamma }}}}^{\top }{{\bf{j}}}-{\delta }_{{{\bf{j}}}}-{\eta }_{{{\bf{j}}}}\right){\hat{n}}_{{{\bf{j}}}}\right],\end{array}$$
(3)

where \({{\bf{j}}}={({j}_{x},{j}_{y})}^{\top }\) is a vector denoting the position of a site on the square superlattice, \({\hat{b}}_{{{\bf{j}}}}\) and \({\hat{b}}_{{{\bf{j}}}}^{{\dagger} }\) are bosonic ladder operators satisfying the canonical commutation relations \([{\hat{b}}_{{{\bf{j}}}},{\hat{b}}_{{{\bf{l}}}}]=0\) and \([{\hat{b}}_{{{\bf{j}}}},{\hat{b}}_{{{\bf{l}}}}^{{\dagger} }]={\delta }_{{{\bf{j}}},{{\bf{l}}}}\) with \({\hat{n}}_{{{\bf{j}}}}={\hat{b}}_{{{\bf{j}}}}^{{\dagger} }{\hat{b}}_{{{\bf{j}}}}\) the singlon number operator, \({{\boldsymbol{\gamma }}}={({\gamma }_{x},{\gamma }_{y})}^{\top }\) encodes the tilt due to a magnetic gradient potential in each direction, and the chemical potential δj(ηj) equals δ(η) only on link (forbidden) sites and zero elsewhere; see Fig. 1a. The on-site interaction strength Uj is U on gauge sites and αU on matter sites, where α ≈ 1.3 (see below for experimental details).

The QLM Hamiltonian (1) can be derived from the BHM Hamiltonian (3) as a leading effective theory in second-order perturbation theory in the regime η ≫ U ~ 2δ ≫ J, m, where the parameters of both models can be related as \(\kappa \approx 4\sqrt{2}{J}^{2}/U\) and m = δ − U/2 + O(J2) (see Supplementary Note 1). We note that the value of the mass is renormalized by terms O(J2): while this renormalization is negligible for the original 1 + 1D implementation of this simulator, it cannot be ignored in 2 + 1D. Nevertheless, this renormalization does not break gauge symmetry or change the form of the simulated model. Indeed, as we detail in Supplementary Note 1, our BHM quantum simulator hosts a U(1) gauge symmetry that is stabilized through the concept of linear Stark gauge protection34,35.

Experimental setup

The BHM Hamiltonian (3) can be faithfully realized using cold atoms. Indeed, the 2 + 1D U(1) QLM can be mapped and implemented using the technology of the 1 + 1D state-of-the-art Bose–Hubbard quantum simulator28,29. Starting from degenerated quantum gases, ultracold bosons trapped in the 2D optical lattices are described by the BHM. Here, the tunneling strength J and the on-site interaction U are controlled primarily by tuning the depth of the optical lattices. When one slowly increases the ratio U/J to approach the atomic limit at U/J ≫ 1, the system undergoes a superfluid-to-Mott insulator phase transition. Other than the general Bose–Hubbard settings, our lattice gauge theory model poses strong constraints on the quantum states of the atoms. To truncate the system into the gauge-allowed subspace, we must initialize the atom occupation to fulfill Gauss’s law of Eq. (2) and meanwhile control the optical lattices to prevent gauge-violating processes.

Here, we propose a feasible way to realize the model using ultracold bosons in a special 2D superlattice53. The potential of the bichromatic superlattice can be written as \(V(x,y)={\sum }_{r = x,y}{V}_{s}(r){\cos }^{2}(4\pi r/\lambda )-{V}_{l}(r){\cos }^{2}(2\pi r/\lambda -\pi /4)\), where λ is the wavelength of the “short” lattice, and Vs,l are the lattice depths of the “short” and “long” lattices, respectively. The overlapping of the intensity minima of the lattices enables the largest imbalance between the neighboring lattice sites. The initial state shown in Fig. 2a at m → + ∞ is a special type of Mott insulating state. It can be obtained by first cooling the quantum gases in superlattices54 and then following up with a selective atom-removing operation. When the average filling factor is set to \(\bar{n}=0.625\), and the lattice depth is Vl(x) = U/2, Vl(y) ≫ U at the end stage of the Mott transition, the atoms reside only on even columns and the mean filling factor is \(\left\vert \right....,2,0.5,2,0.5,2,0.5,...\left.\right\rangle\). In this cooling scheme, number fluctuations flow into the superfluid state, thereby stabilizing the filling number of 2 for Mott insulators at the gauge sites. Next, atoms residing on the matter sites can be removed to obtain a well-defined initial state55, leading to an average filling factor of 0.5 across the lattice, as depicted in Fig. 2a.

Fig. 2: Adiabatic sweep dynamics.
figure 2

a An exemplary charge-proliferated (left) and vacuum (right) state in the quantum link model (QLM) and Bose-Hubbard model (BHM) representations. b Snapshots of the adiabatic sweep in the BHM (3) at t = 0 ms, corresponding to the charge-proliferated state in (a), and at t = 20 ms, corresponding to the wave function at the end of the sweep. Crosses denote the forbidden sites on the BHM Lieb superlattice, and these sites take on even jx and even jy in our notation, while matter sites have odd jx and odd jy, and gauge sites have one of the components jx and jy even and the second odd. c The corresponding dynamics of the chiral condensate (CC) (4) and the gauge violation (5) in both the QLM and BHM, showing good agreement and a stabilized gauge invariance. The time-evolution data is obtained using matrix-product-state numerics on an infinite cylinder of width Ly = 4 matter sites.

Full size image

Furthermore, we suggest tuning the ratio α of the on-site interactions using the difference between the Wannier states of two Bloch bands. When Vl is set close to the band gap (s to p-band) of the short lattices, the atoms can live on the s-band of the matter sites but only on the p-band of the gauge sites. The ratio is α ≈ 1.3 in the experimentally relevant regime. In this sense, the energy shifts δj and ηj denote the energy difference between the matter-site s-band and the gauge-site p-band. Such a superlattice structure forms a very deep potential on the forbidden sites, shifting the energy levels away from resonance. To further prevent atoms from tunneling to the forbidden sites, a larger energy penalty can be generated by addressing them with tightly focused laser beams56. Additionally, we need to mention that the initial state with atoms on the s-band of the gauge sites can be lifted up to the corresponding p-band with the help of a band-mapping technique57.

Results and discussion

We now present simulations for adiabatic sweep and global quench dynamics, calculated with iMPS techniques58,59,60, using the time-dependent variational principle algorithm adapted for infinite states61,62,63,64,65. We adopt the standard procedure of realizing 2D models by employing a cylindrical geometry of an infinite axis (i.e., thermodynamic limit in the x-direction: Lx → ∞) and with a finite circumference Ly (number of matter sites in the QLM, equivalent to 2Ly sites in the BHM) in the y-direction, along which periodic boundary conditions are employed. Throughout this section, we use a tilt potential of γx = 57 Hz and γy = 73 Hz, and we set the ratio α of the on-site interaction strength U for matter sites compared to other sites to be α = 1.3. Further numerical details are provided in Supplementary Note 2.

We first consider an adiabatic sweep where we start at m/κ → − ∞ in a charge-proliferated (CP) state—depicted on the left in Fig. 2a within the QLM and BHM representations—in which every matter site is occupied, and slowly ramp the Hamiltonian parameters to m/κ → ∞ in order to approach a vacuum state, where all matter sites are empty, an example of which is depicted on the right in Fig. 2a. We set Ly = 4 matter sites and fix η = 5δ. The exact ramps for the relevant parameters are within experimental validity and provided in Supplementary Note 3. Figure 2b shows singlon (doublon) density maps on the matter (link) sites in the BHM simulation at t = 0 and t = 20 ms at the end of the sweep. The time-evolved wave function at t = 20 ms is not an exact vacuum due to the finite speed of the ramp. Indeed, if we were to slow down this ramp to approach the adiabatic limit, we should expect the final state to be closer to an exact vacuum. But as we are limited by the experimental coherence time, we also cannot make the ramp time arbitrarily long. This simulation shows that we can achieve reasonable closeness to the expected vacuum state well within the experimental coherence times of ref. 28. Furthermore, we note that the exemplary vacuum shown in Fig. 2a is not unique due to the degeneracy of the vacuum states, and so it is not surprising that the quantum simulation will end in a state close to a superposition of multiple vacua. Indeed, the density snapshot at t = 20 ms shows that the initially unoccupied links at t = 0 ms are now roughly equally occupied at t = 20 ms, whereas the links that were initially fully occupied remain as such.

To better benchmark the mapping, we look at the corresponding dynamics of the chiral condensate, defined in the QLM and BHM bases as

$${{{\mathcal{C}}}}_{{{\rm{QLM}}}}(t)={\lim }_{{L}_{x}\to \infty }\frac{1}{{L}_{x}{L}_{y}}{\sum}_{{{\bf{r}}}}\left\langle \right.\psi (t)\left.\right\vert {\hat{\phi }}_{{{\bf{r}}}}^{{\dagger} }{\hat{\phi }}_{{{\bf{r}}}}\left\vert \right.\psi (t)\left.\right\rangle,$$
(4a)
$${{{\mathcal{C}}}}_{{{\rm{BHM}}}}(t)={\lim }_{{L}_{x}\to \infty }\frac{1}{{L}_{x}{L}_{y}}{\sum}_{{{\bf{j}}}\in \,{\mbox{matter}}\,}\left\langle \right.\psi (t)\left.\right\vert {\hat{n}}_{{{\bf{j}}}}\left\vert \right.\psi (t)\left.\right\rangle,$$
(4b)

respectively, where \(\left\vert \right.\psi (t)\left.\right\rangle =\hat{{{\mathcal{T}}}}{e}^{-i\int_{0}^{t}ds\hat{H}(s)}\left\vert \right.{\psi }_{0}\left.\right\rangle\), \(\hat{H}(t)\) is either the QLM or BHM Hamiltonian at time t, \(\left\vert \right.{\psi }_{0}\left.\right\rangle\) is the initial state, \(\hat{{{\mathcal{T}}}}\) is the time-ordering operator. As shown in Fig. 2c, the sweep dynamics of the chiral condensate in both the QLM and the BHM starts at unity and decreases until reaching at the end of the sweep a minimal finite value, with both models showing good agreement especially at early times. Quantitative differences between both models can be attributed to the small, albeit nonvanishing, gauge violation (orange curve), defined as the root mean square of the Gauss’s-law operator,

$$\Omega (t)={\lim }_{{L}_{x}\to \infty }\sqrt{\frac{1}{{L}_{x}{L}_{y}}{\sum }_{{{\bf{r}}}}\left\langle \right.\psi (t)\left.\right\vert {\hat{G}}_{{{\bf{r}}}}{\left\vert \right.\psi (t)\left.\right\rangle }^{2}}.$$
(5)

Throughout the whole dynamics we find that the gauge violation is restricted to below 8.4%. Importantly, we find that the gauge violation is not monotonically increasing, and shows a decrease towards the end of the sweep, highlighting the efficacy of the emergent gauge protection term in our implementation.

Next, we calculate the dynamics of these observables in the wake of global quenches starting in the CP and vacuum states, shown in Fig. 2a, with final mass values of m/κ = −1.61 and 0, respectively. For these quenches, we fix J = 30 Hz and U = 1300 Hz, and δ is then determined based on the specified value of m (we use δ = 650 Hz and 656.30 Hz, respectively), and we again set η = 5δ. Quench dynamics are numerically more costly than the adiabatic sweep. As such, due to computational overhead, we set Ly = 2 matter sites (four sites along the circumference in the case of the BHM). The corresponding dynamics is shown in Fig. 3a, b for the CP and vacuum initial states, respectively. In both cases, we see very good agreement in the dynamics between the BHM and QLM up to all investigated evolution times. The gauge violation is impressively well-suppressed, always below 3.5% in both cases.

Fig. 3: Quench dynamics.
figure 3

Evolution of the chiral condensate (CC) (4) and gauge violation (5) in the wake of a global quench, obtained using matrix-product-state numerics with a infinite cylinder of width Ly = 2 matter sites. a Starting in the charge-proliferated state of Fig. 2a and quenching to m/κ = −1.61; b starting in the vacuum initial state of Fig. 2a and quenching to m/κ = 0. The results show impressive agreement between the quantum link model (QLM) and Bose-Hubbard model (BHM) results, with gauge violation well-suppressed over all evolution times.

Full size image

As the perturbation theory connecting the effective dynamics in the BHM to the QLM is valid in the regime J ≪ U, δ, we expect the agreement to improve as we decrease J relative to the lattice parameters. Indeed, we can see this by comparing the quench dynamics (Fig. 3), which uses a flat value of J = 30 Hz, with the ramp dynamics (Fig. 2), which uses a varying J which peaks at J ~ 100 Hz (Supplementary Fig. 2): the agreement between BHM and QLM is much closer in the quench results, and the gauge violation is smaller. But since κ ∝ J2, decreasing J causes a quadratic increase in the timescale of the dynamics, which could make it difficult to extract useful results within an experimentally feasible coherence time.

Conclusions

We have shown through second-order perturbation theory and numerical benchmarks using iMPS that the 2 + 1D U(1) QLM can be faithfully mapped onto a two-dimensional Bose–Hubbard optical Lieb superlattice and quantum-simulated using spinless bosons. Although nontrivial adaptions are necessary to preserve gauge invariance in the 2 + 1D case, this quantum simulation can be readily realized using already existing technology used in the 1 + 1D case28,29. This would in principle allow the realization of a 2 + 1D U(1) QLM on a 70 × 70 BHM, equivalent to 35 matter sites along each direction. Despite impressive progress in classical computations in higher dimensions, in particular using tensor-network methods49,66, this may enable quantum simulations that in the near future outperform classical methods such as the one used in this work in terms of both size and maximal evolution times reached. Possible areas for future study regarding this simulator include incorporating gauge-field dynamics via plaquette interactions, and higher-spin representation of the gauge fields67.

Such a quantum simulator of 2 + 1D gauge theories opens the door to various exciting studies. For example, quantum many-body scars68,69 are well-established in 1 + 1D U(1) QLMs with dynamical matter19,70,71,72 and quantum link ladders without dynamical matter73. It would be interesting to explore the fate of scars in 2 + 1D U(1) QLMs with both dynamical matter and gauge fields, and further probe the connection to the quantum field theory limit suggested in 1 + 1D71,72.

Another topic of great interest in gauge theories is that of thermalization, which is still an open issue in heavy-ion and electron-proton collisions, for example74. First experimental works on the thermalization dynamics of gauge theories on a quantum simulator have been performed in 1 + 1D29, and extending this to 2 + 1D would shed more light on how gauge theories thermalize, and also allow for observing possible connections with entanglement spectra as theorized in recent work75. Furthermore, exotic topological and spin liquid phases recently theoretically demonstrated in 2 + 1D gauge theories46,49 would be interesting to probe on our proposed gauge-theory quantum simulator, as well as confinement76,77,78.

Note added: Since the completion of this manuscript, there have been experimental realizations of 2 + 1D lattice gauge theories on digital quantum platforms79,80,81,82.