Introduction

Inverse imaging and scattering1,2, trying to recover unknown material or geometry parameters from observed fields, possess extensive applications, including remote sensing3, biological imaging4,5, and geophysics6. In recent years, machine learning (ML)7,8,9,10, through learning from large datasets, has emerged as a powerful tool toward such inverse tasks11,12. Compared with traditional methods13,14 that usually develop specific algorithms for individual situations based on a good understanding of forward mechanisms, this methodology automatically identifies rules in data, offering a general data-driven framework effective for various scenarios, capable of addressing complex problems that are not easily tackled by traditional methods. Its superior capabilities have been demonstrated in electromagnetic and acoustic inverse scattering15,16,17, high-quality image construction18,19 and subwavelength imaging20, often with surpassing accuracy, resolution or efficiency. A popular approach in ML for inverse imaging is to use the so-called supervised methods that basically fit a function from the observed fields to their targets, e.g., material parameters (treated as labels in ML) of the system. In practice, it often happens that only degraded data can be measured due to problems like phase missing in measurements21,22 or limited areas attainable for detection23,24, which may result in observed data containing insufficient information to recover the target parameters, potentially leading to non-uniqueness where one observation can correspond to multiple system configurations. The straightforward supervised methods lack prior mechanisms to detect such an issue, where reconstructing the images actually requires more information than what is represented in the measured data, potentially wasting efforts on preparing data and labeling. It is thus beneficial to inspect such an issue in advance. On the other hand, another category of ML, unsupervised methods25,26,27,28,29, driven by designed criteria rather than directly fitting the ground truth, can learn from unlabeled data. Such methods have proven to be proficient at revealing the underlying structures of input data, with demonstrated applications ranging from discovering physical concepts, conservation laws, and operationally meaningful representations30,31,32, to extracting interpretable dynamics33, recognizing phase transition34,35, and learning quantum models36,37. In inverse problems of imaging, unsupervised learning offers a diversity of practical implementations, such as denoising and deblurring through latent representations38,39,40, anomaly detection through identifying deviations from learned features41,42,43, and compressed sensing utilizing generative models44,45,46. Such methods can be used alone or flexibly combined with other approaches to enhance model performance9,28,47, which can make the whole task more efficient, effective and interpretable, especially in cases of noisy or incomplete data, and scarce labeled datasets. Through learning patterns from data, they yield valuable information on the data that can reduce the complexity of tasks and benefit subsequent steps, while also holding potential on offering guidance on data preparation for inverse imaging and scattering.

In this work, we focus on one important kind of inverse problem, elastic wave imaging that extracts material or geometry parameters from wave data, which has substantial practical applications such as elasticity measurements, defect detection and non-destructive testing48,49,50,51,52. We propose to combine two unsupervised methods, variational autoencoder53,54 and independent component analysis55, to build an ML model with the capability to detect the non-uniqueness in inverse processes and significantly reduce the need for labeled data. As a demonstration, this methodology is applied to the retrieval of material and geometry parameters from the observed vibration fields on a beam. The variational autoencoder compresses the observed fields into features called latent variables. The dimension of these latent variables is leveraged to evaluate whether it is a one-to-one mapping from the collected data to the unknown parameters, thus avoiding potentially solving ambiguous inverse problems. These latent variables are further converted into independent components by independent component analysis. It turns out that each of these components corresponds to one physical parameter. As an additional step, a straightforward linear scaling can be applied to readily adjust the range of each component to match its corresponding physical quantity with the help of a small number of known values of these physical quantities. Although here we make use of the readily obtainable simulation data to train our model to boost the data collection efficiency, this model can also be applied to real-world data, even when such data come from practical conditions differing from ideal simulation. We enable our ML model to work for real-world data by carefully considering the major deviation in conditions between experiment and simulation, which is the difference in exerted excitation forces. Our testing results show that both geometry and material parameters can be well recovered by sending experimental data measured by a laser Doppler vibrometer from six fabricated elastic structures via 3D printing to the ML model.

Results

Network architecture

We begin with an elastic wave inverse imaging problem with four physical parameters to be retrieved as an illustrative example, which is simple and clear yet with no loss of generality, to demonstrate our workflow and explore the issue of non-uniqueness, as shown in Fig. 1a. In particular, we would like to retrieve the Young’s modulus and the heights of three blocks of a beam, denoted by \(\left\{{\alpha }_{i}\right\}=\left\{{E}_{0},{h}_{1},{h}_{2},{h}_{3}\right\}\), from the velocity fields measured at the back face. To predict the values of these parameters, we build an ML model containing two parts, i.e., a variational autoencoder network (VAE-Net, filled with gray color) and an independent component analysis network (ICA-Net, filled with light blue color), which are collectively termed VAE-ICA Net as a whole model, as shown in Fig. 1b, c.

Fig. 1: Workflow of our unsupervied imaging method.
figure 1

a Setup for obtaining vibration fields by a laser Doppler vibrometer for the inverse imaging of parameters \(\left\{{\alpha }_{i}\right\}=\{{E}_{0},{h}_{1},{h}_{2},{h}_{3}\}\), i.e., Young’s modulus and three heights of a beam, which is excited by a harmonic signal at one end at \(f=2{{\rm{kHz}}}\). b, c The architecture of the machine learning model, with b a variational autoencoder (VAE-Net, filled with gray color) to compress the velocity fields \(\{{v}_{i}\}\) into a low-dimensional representation \(\left\{{z}_{i}\right\}\) (each follows a Gaussian distribution with mean \({\mu }_{i}\) and standard deviation \({\sigma }_{i}\) in generating the latent variable for every input), and c an independent component analysis (ICA-Net, filled with light blue color) to further transform \(\{{z}_{i}\}\) into their independent components \(\{{z}_{i}^{{\prime} }\}\). The predicted values \(\left\{{\alpha }_{i}^{{\prime} }\right\}=\{{E}_{0}^{{\prime} },{h}_{1}^{{\prime} },{h}_{2}^{{\prime} },{h}_{3}^{{\prime} }\}\) can be readily obtained by linearly scaling \(\{{z}_{i}^{{\prime} }\}\) with a small amount of \(\left\{{z}_{i}^{{\prime} },{\alpha }_{i}\right\}\) pairs to correct the range of each \({z}_{i}^{{\prime} }\), as shown in (d) (filled with light green color).

Full size image

In this task, one crucial consideration is to ensure that the collected data can uniquely determine all four parameters. We assess this issue through the VAE-Net that consists of an encoder and a decoder. The encoder tries to shrink the inputs (the velocity data \(\{{v}_{i}\}\) on the surface of the beam) into features \(\{{z}_{i}\}\) that we call latent variables, from which the decoder then reconstructs the inputs as \(\{{v}_{i}^{{\prime} }\}\). Each latent variable \({z}_{i}\) is assumed to satisfy a normal distribution \({z}_{i} \sim N({\mu }_{i},{\sigma }_{i}^{2})\), with the reparameterization trick \({z}_{i}={\mu }_{i}+\epsilon {\sigma }_{i}\) where \(\epsilon \sim N(0,1)\) to enable training the network through back propagation54. The loss function is set to be \({L}_{{VAE}}={L}_{{rec}}+{L}_{{KL}}\), where \({L}_{{rec}}={{\rm{mean}}}\left({\left({v}_{i}-{v}_{i}^{{\prime} }\right)}^{2}\right)\) is the mean squared error of \(\{{v}_{i}\}\) and \(\{{v}_{i}^{{\prime} }\}\) driving the reconstruction of the velocity fields. The second term \({L}_{{KL}}=\beta {\sum }_{i}{D}_{{KL}}\left(N\left({\mu }_{i},{\sigma }_{i}^{2}\right){{\rm{||}}}N\left(0,1\right)\right)\) is a regularization term, trying to approach \(N({\mu }_{i},{\sigma }_{i}^{2})\) to a standard normal distribution \(N\left(0,1\right)\) as closely as possible through calculating Kullback-Leibler divergence \({D}_{{KL}}\) that measures the difference between two probability distributions, with \(\beta\) as a hyperparameter to balance the \({L}_{{rec}}\) and \({L}_{{KL}}\). Owing to this additional regularization term in the loss function, it allows us to determine the number of degrees of freedom (DOFs) of the input data (i.e., the minimum number of variables necessary to represent the data), which can help to evaluate whether the collected data are sufficient to retrieve all physical parameters, thus to avoid solving ill-posed problems with non-uniqueness, as we will demonstrate in detail later. Nevertheless, it would be laborious to evaluate this issue by experimentally collecting data in real world, given the large amount of data required to be collected for training. Instead, we tactically use the simulation data under the same settings to be implemented in experiments, which is cost-efficient and would not hinder the assessment of uniqueness, since the computational simulation, in principle, implements the same physical laws as those in experiments. For these obtained latent variables, even if the problem is unique, they are not guaranteed to be the unknown parameters that we want to recover, but only a bijective function of them. As a further step, we use another unsupervised method, namely, independent component analysis, implemented by ICA-Net in our model, to transform these latent variables to their independent component representation \(\{{z}_{i}^{{\prime} }\}\). After training, it turns out that each of \(\{{z}_{i}^{{\prime} }\}\) corresponds to one of the physical parameters \(\{{\alpha }_{i}\}\). A direct merit of this unsupervised approach is that just a small amount of labeled data is required to recover the unknown parameters in a subsequent step, simply through scaling each \({z}_{i}^{{\prime} }\) to the correct range of its corresponding physical parameter, as shown in Fig. 1d (filled with light green color). We emphasize that the labeled data are not used for training the neural networks (i.e., VAE-Net and ICA-Net), but are used solely for the scaling task described above by employing ordinary least squares linear regression which does not involve training via back propagation. Details about implementing the VAE-Net and ICA-Net can be found in Supplementary Note 1 and 2.

Training results using simulation data

Next, we go to the details of our system setup and ML results. Figure 2a depicts the size of the studied structure, a beam with length (W = 247mm) along \(x\) axis, width (D = 25mm) along \(y\) axis and thickness (h0 = 3.1mm) along \(z\) axis, with three blocks on the top. The blocks have the same area (d × d with d = 25mm) but differ in their heights, with a distance p = 35mm between adjacent blocks. The whole structure is made of the same material, with density 1167kg/m3, Young’s modulus \(2.7\)GPa, and Poisson’s ratio \(0.4\). A harmonic force along \(z\) direction with frequency f = 2kHz is applied at one end, leaving the other end clamped. We set the Young’s modulus \({E}_{0}\) and the heights of the three blocks \({h}_{1}\), \({h}_{2}\) and \({h}_{3}\) to be the pixels to be imaged, i.e., \(\left\{{\alpha }_{i}\right\}=\left\{{E}_{0},{h}_{1},{h}_{2},{h}_{3}\right\}.\) The data used to train our ML model are collected from a rectangle area of 165 × 15mm (with 89 × 9 data points) on the homogeneous face (back face in Fig. 2a).

Fig. 2: Degrees of freedom in data.
figure 2

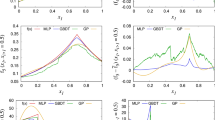
a The structure used to demonstrate inverse imaging: a beam with three blocks on top, with four parameters \({E}_{0},{h}_{1},{h}_{2},\) and \({h}_{3}\) to be recovered. b The standard deviation (Std) of \({\mu }_{i}\) and the mean of \({\sigma }_{i}\) (with \({z}_{i} \sim N({\mu }_{i},{\sigma }_{i}^{2})\) to generate latent variables) across the training dataset, indicating whether a latent variable is meaningful or not. A meaningful variable points to a definite generation with low values of \({\sigma }_{i}\) but with \({\mu }_{i}\) varying with data, in contrast to a meaningless variable, which is random with small \({\mu }_{i}\) and high \({\sigma }_{i}\). We obtain four meaningful latent variables here, exactly corresponding to the number of unknown quantities to be recovered. c The evolutions of the reconstruction error \({L}_{{rec}}\) and the number of meaningful latent variables \({n}_{M}\) as the hyperparameter \(\beta\) varies from \({10}^{-10}\) to \({10}^{1}\), indicating that the number of DOFs in the data is \(n=4\), before \({L}_{{rec}}\) significantly increasing.

Full size image

Next, we present how to identify the number of DOFs (denoted by \(n\)) in the training data. The \(n\) is equal to the number of meaningful latent variables \({n}_{M}\) in the bottleneck of VAE-Net under an appropriate setting of the hyperparameter \(\beta\) in the loss function. First, we need to determine whether a latent variable \({z}_{i} \sim N\left({\mu }_{i},{\sigma }_{i}^{2}\right)\) is meaningful or not through the statistical behaviors of \({\mu }_{i}\) and \({\sigma }_{i}\). For a latent variable \({z}_{i}\), if the standard deviation (Std) of \({\mu }_{i}\) is near zero and the mean of \({\sigma }_{i}\) is almost unity across all samples in the training set, indicating that the value of \({z}_{i}\) fluctuates drastically and thus contains no useful information, we consider such a latent variable meaningless and can be discarded. In contrast, if the standard deviation of \({\mu }_{i}\) is unity and the mean of \({\sigma }_{i}\) is near zero, \({z}_{i}\) is determined clearly, in which sense we regard as meaningful and will keep such a latent variable. According to these discussions, four out of ten latent variables (we set ten latent variables when initiating the VAE-Net) are meaningful, as can be seen from Fig. 2b. Note here the hyperparameter \(\beta\) is set to be \({10}^{-4}\) such that the number of meaningful latent variables corresponds to the number of DOFs in the data, which is clearly justified by analyzing the evolution of the reconstruction error \({L}_{{rec}}\) as \(\beta\) varies, as shown in Fig. 2c, with \({L}_{{rec}}\) and \({n}_{M}\) as functions of \(\beta\) ranging from \({10}^{-10}\) to \({10}^{1}\). When \(\beta\) is very large, the loss function focuses on the \({L}_{{KL}}\) part, trying to achieve \(\mu =0\) and \(\sigma =1\), in which case the latent variables are meaningless, along with the large reconstruction error. As \(\beta\) decreases, the latent variables turn to become meaningful, along with the decline of reconstruction error, and as \(\beta\) decreases further, the network catches more meaningful latent variables, accompanied by \({L}_{{rec}}\) dropping significantly, indicating that the latent variables better represent the information in the input data. However, when the number of meaningful latent variables reaches a certain threshold (four in this case), more meaningful latent variables achieved by smaller \(\beta\) do not improve \({L}_{{rec}}\) further, since there are already enough variables for representing the data. And \(n\) is equal to this minimum number of meaningful latent variables that effectively represent the input data, which is \(n=4\) in our case, as shown in Fig. 2c. The technique of extracting DOFs is not influenced by the variations of the prescribed number of latent variables when initiating the network, as verified in Supplementary Note 4a where we present the ML results using a setting of fifty latent variables at the bottleneck of VAE-Net. The results show that four meaningful latent variables can be identified, which aligns with what we would expect when we prescribe 10 latent variables here. The only requirement is that the dimension of the latent space should be greater than the number of actual parameters to be recovered to enable the information to flow uninterrupted through the bottleneck of VAE-Net.

After obtaining \(n\), we can evaluate whether it is unique or not in our inverse imaging problem. If \(n\) is less than the number of unknown physical quantities \(\{{\alpha }_{i}\}\), then the observation data do not capture all the information about \(\{{\alpha }_{i}\}\), and one observation \(\{{v}_{i}\}\) can correspond to multiple physical configurations, suggesting improving the intended experimental scheme or data collection method to catch more information about the system. In our case, \(n=4\) exactly corresponds to the number of unknown physical parameters, indicating that the collected velocity fields are sufficient to retrieve these parameters. When we collect fewer velocity data, \(n\) can be smaller than four, frustrating the inverse imaging task, which we illustrate in the Supplementary Note 3a to simulate the cases with less accessible areas for measurement. In one case, we remove the velocity fields under the middle block and 4 DOFs can still be found (as can be seen in Fig. S3a). If we remove the fields under all three blocks and only keep the fields at the two ends, we can only find 3 DOFs (as shown in Fig. S3b). Such a case is not suitable for imaging, since the information is not enough for recovering all four unknown parameters. Nevertheless, it would be interesting to explore such kind of situations with fewer DOFs, with potential applications other than imaging. We provide an illustration of such a scenario in Supplementary Note 3b by adding density as a varying parameter to demonstrate this promising potential. Figures S4 and S5 show that four DOFs are found despite five varying parameters, and notably, an independent component, corresponding to neither \({E}_{0}\) nor \({\rho }_{0}\) but to another physically meaningful quantity, namely, \({E}_{0}/{\rho }_{0}\), is found. The detailed investigation of this category of problems is beyond the scope of this study at present, and we will leave it for future work. This capability of discovering minimal independent representations can facilitate identifying hidden physical relationships from observation data, especially in cases involving non-uniqueness.

In addition, an understanding of how \(\{{z}_{i}\}\) quantitatively represents the underlying physical parameters can benefit retrieving these parameters from the latent space. As an illustration, we manifest one of the parameters \({h}_{2}\) (the height of the second block) in the latent space and project into two-dimensional space for visualization, as shown in Fig. 3a, with \({h}_{2}\) (represented by colormap) over each pair of {\({z}_{i}\)}. In the figure, we can see that \({h}_{2}\) has a layered structure on \(({z}_{1},{z}_{2})\), \(({z}_{2},{z}_{3})\) and (\({z}_{2}\), \({z}_{4}\)), implying that the contours of \({h}_{2}\) could be cut planes in the 4-dimensional latent space, which further suggests linear relationships between \({h}_{2}\) and \(\{{z}_{i}\}\). The panels with no layered pattern on \(({z}_{1},{z}_{3})\), \(({z}_{1},{z}_{4})\) and (\({z}_{3}\), \({z}_{4}\)) in Fig. 3a can be attributed to the weaker linear relationships of \({h}_{2}\) with \({z}_{1}\), \({z}_{3}\) and \({z}_{4}\), thus projection upsets the layered structure. Linear relations shall also apply to other parameters. If this is true, a linear regression would recover \(\{{E}_{0},{h}_{1},{h}_{2},{h}_{3}\}\) from \(\{{z}_{i}\}\). However, we prefer to continuously proceed in an unsupervised manner, by using the independent component analysis, to transform \(\{{z}_{i}\}\) to their independent components (denoted by \(\{{z}_{i}^{{\prime} }\}\)), achieved by the ICA-Net through minimizing statistical correlations between its outputs by assuming that these components satisfy a uniform distribution. It turns out that each \({z}_{i}^{{\prime} }\) corresponds to one of the physical parameters (with \({E}_{0},\,{h}_{1},\,{h}_{2}\) and \({h}_{3}\) corresponding to \({z}_{1}^{{\prime} },\,{z}_{2}^{{\prime} },\,{z}_{4}^{{\prime} }\) and \({z}_{3}^{{\prime} }\), respectively) and with no apparent relation to other parameters, as exhibited in Fig. 3b, with the digits printing the Pearson correlation coefficients on the top-right corner to indicate the strength of linear dependence. The order of \(\{{z}_{i}^{{\prime} }\}\) may not correspond to the order of the \(\{{E}_{0},{h}_{1},{h}_{2},{h}_{3}\}\), since the ICA-Net is only guided to find all the independent components without extra information to sort them in a specific order. Finally, after obtaining the \(\{{z}_{i}^{{\prime} }\}\), we can linearly transform them to the correct range to obtain the predictions of the unknown parameters by referring to a small number of \(\left\{{z}_{i}^{{\prime} }\right\}\)-\(\left\{{E}_{0},{h}_{1},{h}_{2},{h}_{3}\right\}\) pairs (we use twenty here) in the scaling part in Fig. 1d. Figure 3c shows the predictions (denoted by \({E}_{0}^{{\prime} }\), \({h}_{1}^{{\prime} }\), \({h}_{2}^{{\prime} }\) and \({h}_{3}^{{\prime} }\)) of the four parameters, exhibiting clear one-to-one correspondences with their ground truth. To quantify the prediction error, we calculate the mean absolute errors (MAEs) between the predicted values and the real values of the physical quantities, with MAE = 0.048 GPa, 0.179 mm, 0.123 mm and 0.150 mm for \({E}_{0}^{{\prime} }\), \({h}_{1}^{{\prime} }\), \({h}_{2}^{{\prime} }\), and \({h}_{3}^{{\prime} }\), respectively, shown as digits on the bottom-right corner of each panel, which are relatively small compared with the full range of these parameters. Note that the labels used for scaling are of high quality since the data are generated from these labels, which can thus be regarded as ground truth. In addition, we evaluate the effects of the number of labeled configurations used for the scaling on the accuracy of predictions, as presented in Supplementary Note 5, which shows that twenty configurations are sufficient to achieve satisfactory accuracy. The influence of noise on the accuracy of predictions is assessed in Supplementary Note 4b where we impose three different levels of noise on the testing data with signal-to-noise ratios of 20, 14, and 6 dB, respectively, to demonstrate the model’s robustness against noise. We also evaluate the extrapolation performance of our model when the range of heights in the testing data is larger than that in the training data, as detailed in Supplementary Note 4c by increasing the span of heights from 0 ~ 4 mm to 0 ~ 5 mm, demonstrating similar performance even when the testing data lie outside the range of the training data. On the other hand, for practical factors that affect model performance, such as the material parameter mismatch between simulation and fabricated samples, measurement inaccuracy of the field amplitudes in this work, we take two approaches: one is adding one more varying parameter in training the model, Young’s modulus of the material to cater for the uncertainty of material parameters even in real cases the 3D-printing samples use the same material, another is adding post-processing technique regularizing experimental data, the filtering of torsional mode, as presented in Supplementary Note 6.

Fig. 3: Latent variables and independent components.
figure 3

a The relationships between each pair of meaningful latent variables after VAE, colored by the magnitude of the height of the second block \({h}_{2}\), showing high correlation to latent variable \({z}_{2}\). b The relations between different {\({z}_{i}^{{\prime}}\)} (independent components after ICA) and {\({E}_{0}\), \({h}_{1}\), \({h}_{2}\), \({h}_{3}\)}, with the digits on the top-right corner representing Pearson correlation coefficients measuring the strength of linear dependence, indicating that one physical variable is mapped to only one independent component. c The relations between the recovered physical parameters \(\{{E}_{0}^{{\prime} },{h}_{1}^{{\prime} },{h}_{2}^{{\prime} },{h}_{3}^{{\prime} }\}\) from our ML model and their real values \(\{{E}_{0},{h}_{1},{h}_{2},{h}_{3}\}\) (ground truth), for the testing set of simulation data, with the digits on the bottom-right corner indicating the mean absolute errors.

Full size image

Thus, we begin with the observed velocity fields of elastic waves on a beam and find the quantitative representation of each unknown physical parameter by the VAE-ICA network, without even knowing the number or the values of these parameters in advance. During this process, it allows us to check the number of DOFs in the input data, thus either validating or suggesting improvements to the intended experimental schemes of the collecting schemes. The technique of extracting the DOFs can also benefit supervised methods, as it can detect whether the solution space is too large for the limited data to establish a clear mapping and thus avoid potentially solving problems with non-uniqueness, which can also reduce the risks of preparing data and labeling for an unreasonable task that attempts to link a single observation simultaneously to multiple configurations.

Test with experimental data

The above discussions are mostly based on the data from the simulation. To enable real applications of inverse imaging, it is highly desirable that such an ML model trained with simulation data can predict unknown parameters in real-world experiments. For this purpose, we first fabricate samples by 3D printing, with different configurations of \({h}_{1}\), \({h}_{2}\) and \({h}_{3}\) whose values are marked in blue on the three blocks, as shown in the first row of Fig. 4. To test the ML model on a diverse range of situations, the height configurations generally go from simple to complex, with \({h}_{1}={h}_{2}={h}_{3}=0\) in the first sample in Fig. 4a to heights of a random configuration in the sixth sample in Fig. 4f. Then, the out-of-plane velocity fields on the back face of the samples are recorded by a laser Doppler vibrometer. One thing worth noting here is that we use two transducers to excite, and the two transducers may give different magnitudes of forces under their excitation areas on the beam due to the possibly different responses of the transducers in practice, which differs from ideal conditions in simulation where we apply a uniformly distributed force on the beam. Specifically, the asymmetry of the excitation force about \(x\)-axis can excite waves with significantly different velocity patterns compared to those in simulation, which could lead to unreasonable results from the ML model. We tackle this carefully by extracting the two-dimensional velocity fields from the symmetric excitation of the force along \(y\) direction through analyzing the Green’s function of the system in response to a driven force by taking advantage of the symmetry of the structures of our samples, as detailed in Supplementary Note 6. In addition, we verify the approach’s effectiveness by comparing the predicted physical parameters from data before and after postprocessing in three representative samples, as presented also in Supplementary Note 6. After this extraction, we can get plane wave like patterns just as those in simulation, as exhibited in the second row of Fig. 4. As the configurations of \({E}_{0}\), \({h}_{1}\), \({h}_{2}\) and \({h}_{3}\) change from one to another, the velocity fields also change correspondingly in magnitude and wavelength whose characteristics serve as sources for the VAE-Net to encode into four different features \(\left\{{z}_{i}\right\}.\) If the VAE-Net can work properly for such experimental data, the decoder shall recover the input velocity fields well. To verify, we plot the reconstructed velocity fields in the third row of Fig. 4, with well agreements with the input fields in the second row of Fig. 4, confirming that the VAE-Net can work on data from experiments after our data processing strategy, since otherwise the reconstructed fields will be different from those in the input.

Fig. 4: Measured and reconstructed velocity fields.
figure 4

The first rows in a–f are photos of six 3D-printed samples with different configurations of heights of the three blocks, denoted by I, II–VI, used to obtain experimental data. The second rows are the 2D out-of-plane velocity fields at frequency \(f=2{{\rm{kHz}}}\) measured by a scanning laser Doppler vibrometer. The third rows are the reconstructed velocity fields produced by the ML model.

Full size image

To obtain the predictions from these experimental observations by our ML model, we send the obtained features \(\{{z}_{i}\}\) to the ICA-Net to get the independent components \(\{{z}_{i}^{{\prime} }\}\), which are then scaled subject to the same scaling rule established previously from the simulation data. The predicted values of the four physical parameters are displayed in the front row of each bar plot in Fig. 5, together with the predicted values from simulation data (generated by the ground truth) in the middle row, and the ground truth in the third row for convenient comparison. The digits on the top face of each bar in the figure exhibit the numerical values of that bar. Our model works well for the simulation data, as shown in the middle rows, by comparing with the ground truth in third row in Fig. 5. For the real-world data from experiments, the ML model is still effective, with both the trends and numerical values of the predictions corresponding well to those of the real parameters, as shown in the first row of Fig. 5. To quantify the error, we also calculate the MAEs of the predictions from experimental data, with MAE = 0.167 GPa, 0.140 mm, 0.279 mm and 0.262 mm for \({E}_{0}^{{\prime} }\), \({h}_{1}^{{\prime} }\), \({h}_{2}^{{\prime} }\), and \({h}_{3}^{{\prime} }\). Compared with the MAEs from simulation data in Fig. 3c, they rise slightly, yet the overall performance continues to be satisfactory. This further confirms that our ML model can apply to real circumstances after using the strategy to purify the data to eliminate disturbing factors inevitably involved in imperfect settings of experiments. Other strategies focusing on the model itself can also be considered to enable the model trained with simulation data to work for experimental data, like generalizing the ML model to take additional factors possibly occurring in experiments into account when generating the training data, with expectations that the ML model can also identify the additional factors yet does not interfere the original goals to retrieve the physical parameters of interests.

Fig. 5: Recovered physical parameters.
figure 5

a–f corresponds to the recovered Young’s modulus \({E}_{0}\) and heights of three blocks \({h}_{1}\), \({h}_{2}\), and \({h}_{3}\) of the six 3D-printed samples I, II–VI from experimental data by the ML model. For each panel, the first row of the bar plot shows the predictions from experimental data, the second row is from the simulation data, and the third row is the ground truth.

Full size image

Discussion

We have proposed an unsupervised machine learning approach combining the variational autoencoder and independent component analysis toward inverse imaging and demonstrate its effectiveness in retrieving material and geometry parameters with elastic waves. One advantage of our approach is that through VAE-Net, the number of intrinsic DOFs in the input data can be obtained from the number of meaningful latent variables, thus preventing the potential of solving ill-posed problems with non-uniqueness and providing guidance on improving data collection schemes if the number of discovered DOFs is less than the number of physical variables for recovery. Another advantage is that a clean representation with each independent component corresponding to an unknown parameter can be found through further transforming the latent variables by ICA-Net. We emphasize that the true values of the physical quantities do not input into either the VAE-Net or the ICA-Net, but are used only for scaling these independent components to match the correct ranges of those physical quantities. This final scaling step requires only twenty configurations compared with 12k configurations in the training data, holding potential to significantly relieve the work of labeling. In this architecture, the observed fields gradually turn into physical parameters in an explanatory way, which can discover issues in advance and enhance interpretability. While our method is presented in the context of unsupervised imaging, it can also be useful for other ML tasks, since it can serve as a prior process or a component within a broader framework to analyze information in data, extract essential features, and reduce data complexity, thereby facilitating subsequent tasks and improving overall performance. In our case, although the number of DOFs in the data is equal to the number of unknown physical quantities to accommodate the inverse imaging scenarios, the developed unsupervised architecture is not limited to imaging problems but could also be applied in other cases, such as those where the number of DOFs of data is less than the number of physical quantities generating these data. In these cases, the information is not enough to recover the physical quantities, but a possible representation spanned by independent variables could still be discovered. One possible application scenario involves systems modeled by effective medium theories, as effective medium theories can be viewed as non-uniqueness problems in the sense that the same effective parameters can correspond to multiple real configurations with different values of physical quantities, resulting in a one-to-many mapping with non-uniqueness. Our method is well-suited for such situations, offering potential applications for discovering the effective parameters or minimal representation of complex physical systems. The developed technique can also help identify key factors that affect observations, build understanding from data, and facilitate data-driven modeling in various physical systems.

Methods

Data preparations

The training data (N = 12k configurations in total, with 0.7 N for training, 0.2 N for validation, and 0.1 N for testing) are generated by the finite element solver COMSOL Multiphysics. The left face of one end of the sample is set to a fixed boundary condition and a force along \(z\) axis is exerted on another end at bottom surface over a rectangular area (25 × 12 mm), as shown in Fig. 2a. Free boundary conditions are set on other surfaces of the sample. In order to expose the ML model to a wide range of configurations of \(\{{E}_{0},{h}_{1},{h}_{2},{h}_{3}\}\), the Young’s modulus \({E}_{0}\) is randomly sampled from the uniform distribution with \({E}_{0} \sim U(2.6,3.1)\) (in GPa), and three block heights \({h}_{1},{h}_{2},{h}_{3} \sim U\left(0,4\right)\) (in mm) to generate the observation data. Out-of-plane velocity fields are extracted from the bottom face of the samples as training data. We randomly select twenty sets of these parameters to scale the independent components to match the ranges of their corresponding physical quantities.

Experimental setup

Six samples with different physical configurations are fabricated by 3D printing technology using a cured photosensitive resin. The experimental setup mainly consists of a laser Doppler vibrometer (optomet SWIR Scanning Vibrometer), an amplifier (Krohn-Hite Model 7602 M), two transducers, and the fabricated samples. One end of the sample is clamped (with an additional length remaining for clamping) to simulate a fixed boundary condition, while the other end is excited by two piezoelectric transducers. Here, we use two circular piezoelectric transducers (with a diameter of 12 mm) to simulate the force along \(z\) direction. The harmonic signal is generated by a built-in signal generator of the laser Doppler vibrometer, and then magnified by a power amplifier to improve the signal-to-noise ratio, exciting the transducers at a frequency of \(f=2{{\rm{kHz}}}\) to drive vibration of the samples. The out-of-plane velocities at all scanning points (89 × 9 points across a 165 × 15mm rectangular area) are measured and recorded using OptoSCAN software, designated for this vibrometer model, to obtain velocity fields in the time domain at a sampling rate of 163.840kS/s over a duration of 100 ms. Each data point is measured separately under identical excitation conditions with a reference signal to synchronize data across different scanning points. The time domain data are then subjected to a discrete Fourier transform to produce frequency domain data at \(f=2{{\rm{kHz}}}\) that can be fed into the model after data processing and normalization. A photo of the experimental setup can be found in Supplementary Note 6.