Spin-photon interaction between a ruby crystal and a high-critical-temperature superconducting microwave cavity

Abstract

High-spin systems in molecules and inorganic solids hold significant potential for advancing quantum information storage and processing technologies, owing to their multilevel structure. However, the dynamics of spin-photon interactions in these systems remain underexplored in practical device settings. Here we investigate the quantum properties of an S = 3/2 spin ensemble in a ruby crystal embedded in a high-T_c superconducting microwave cavity. Using electron spin resonance techniques, we measure the coupling strength between the quantized electromagnetic mode of the cavity and the spin ensemble across a broad temperature range and for various crystal axis orientations relative to the applied magnetic field. The coupling strength, governed by thermal polarization of the spins and quantum mechanical transition probabilities, shows quantitative agreement with theoretical predictions based on spin Hamiltonian diagonalization and electromagnetic simulations of the cavity mode. These findings establish impurity spins in solids as controllable multilevel quantum systems and provide critical insights into the factors influencing spin-cavity interactions. This work opens new avenues for optimizing quantum information processing and developing versatile quantum technologies based on high-spin systems.

Introduction

Over the past decade, quantum information processing has emerged as a revolutionary paradigm, offering unprecedented computational power and secure communication channels¹. A compelling strategy for building a quantum processor involves developing hybrid quantum systems, where information is processed using qubits that are separated from dedicated memory registers, i.e., quantum memories². Among the possible candidates, electron spin impurities in inorganic solids³, such as diamond nitrogen-vacancy centers^4,5, donor spins in silicon⁶ or rare earth ions embedded in crystals^7,8, offer several advantages for implementing quantum memories^9,10.

In the canonical framework, quantum information is encoded in qubits –the quantum analog of classical bits– by isolating two specific energy levels within a quantum system¹. However, the underlying multilevel nature of various quantum platforms represents a powerful resource for quantum computation. Qudit technology, which involves d-level quantum digits (d > 2), provides a larger state space for storing and processing information, thereby offering significant potential for improvements in algorithm efficiency and computational power^11,12. Quantum information processing with qudits has been experimentally demonstrated in a variety of systems, including superconducting circuits^13,14, trapped ions¹⁵, molecular magnets¹⁶, and nuclear spins^17,18,19.

In this context, high-electronic spins (S > 1/2) in molecules and inorganic solids present an interesting alternative for quantum applications. These systems offer several advantages : (i) relatively long coherence times, which are crucial for preserving quantum information^20,21; (ii) transition energies that typically fall within the microwave frequency range (ΔE ~ gμ_BB), where conventional solid-state qubits operate^22,23; and (iii) the ability to coherently manipulate spin states using Electron Spin Resonance (ESR) techniques in cavity. In practice, superconducting cavities are often employed due to their low conducting losses, which results in higher quality factors^24,25. These cavities enable strong coupling to be achieved between a microwave cavity field and the spins in a highly cooperative regime³. However, the use of superconducting materials limits the range of magnetic fields that can be applied, as the field must remain below the superconducting critical field. This limitation can be mitigated by using magnetically resilient superconducting materials, such as NbTi²⁶, NbN²⁷, or granular aluminum²⁸. Moreover, high-T_c superconducting cavities^29,30,31 offer extended operating ranges in both magnetic field and temperature compared to their low-T_c counterparts.

In this work, we investigate the interaction between the fundamental electromagnetic mode of a high-Tc superconducting cavity and an S = 3/2 spin ensemble, specifically Cr³⁺ spin impurities embedded in a ruby crystal. Using Electron Spin Resonance (ESR) technique, we quantify the spin-cavity coupling and the spin decay rate over an extended temperature range that spans different thermal occupation regimes of the spin energy levels. Our analysis reveals a complex temperature dependence of the coupling, driven by the interplay between thermal polarization of the spins and quantum mechanical transition probabilities, governed by Fermi’s golden rule. Furthermore, by adjusting the magnetic field orientation relative to the crystal axis, we successfully modulate the number of active transitions in the quantum system, from two to four transitions within this study. Additionally, we theoretically analyze the coupling within the Tavis–Cummings model framework^32,33, calculating the spatial distribution of the magnetic field in the ruby crystal generated by the zero-point fluctuations of the microwave current within the cavity. This allows us to evaluate the contribution of a single spin at any location and predict the temperature-dependent coupling behavior for the spin ensemble. While the absolute values of the measured coupling remain modest, our methodology provides a systematic approach for investigating spin-photon interactions in circuit quantum electrodynamics. The agreement between our model and experimental results highlights the relevance of this approach and suggests that high-spin systems warrant further exploration for their potential role in quantum technologies.

Results

Sample and experimental setup

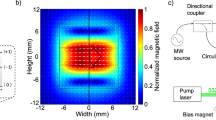
Ruby is a corundum (Al₂O₃) crystal, whose distinct red hue results from chromium dopants that replace some of the aluminum atoms. It can be manufactured artificially with a relatively low concentration of chromium, typically on the order of 0.1%, and was originally considered for its applications in lasers³⁴ and masers³⁵. When a chromium atom substitutes for an aluminum atom, it transfers three electrons to the six O²⁻ neighbor ions to form Cr³⁺ ions with electronic configuration [Ar]3d³. The three valence electrons occupy the t_2g orbitals (3d_xy,3d_xz,3d_yz), which are lower in energy than the e_g ones in the octahedral crystal field. The spin states associated with the Cr³⁺ ground state, which have a quenched orbital angular momentum, can be treated as those of an effective S = 3/2 spin. The crystal field influences the electron spins indirectly through spin-orbit coupling, resulting in a splitting of approximately 11.5 GHz between the energy levels associated with a magnetic quantum number m = ±3/2 at lower energy and m = ±1/2 at higher energy. This well-defined spin structure makes ruby an attractive platform for performing ESR experiments. In particular, superconducting coplanar waveguides and cavities have been used to probe spin-photon coupling in Cr³⁺ spin ensembles^24,36. In the following, we consider the experimental configuration presented in Fig. 1. A piece of ruby is placed in contact with a λ/2 - YBa₂Cu₃O_7−x superconducting coplanar waveguide cavity³¹ such that its crystallographic c-axis, denoted the z-axis, lies in the sample plane. Additionally, a small amount of 2,2-diphenyl-1-(2,4,6-trinitrophenyl) hydrazyl (DPPH) powder is also placed in contact with the cavity and serves as an S = 1/2 ESR standard for magnetic field calibration. The superconducting cavity has a resonant frequency ${f}_{0}=\frac{{\omega }_{0}}{2\pi }\simeq$ 5.5 GHz and a quality factor Q ≈ 8500 at zero external magnetic field (Fig. 1c). It generates a microwave AC magnetic field, suitable for inducing ESR transitions between the Cr³⁺ spin states under a Zeeman magnetic field B applied along the z₀ direction³⁷. The cavity was integrated into a microwave setup within a dilution refrigerator to measure its transmission S₂₁(ω) at temperatures ranging from 30 mK to 16 K. All the measurements were performed with an average photon number in the cavity of approximately 2 × 10⁶. Detailed information about the setup and measurement parameters is provided in the “Methods” section.

Fig. 1: Description of the Electron Spin Resonance experiment.

a Schematic description of the λ/2 - YBa₂Cu₃O_7−x superconducting coplanar waveguide cavity with the ruby and 2,2-diphenyl-1-(2,4,6-trinitrophenyl) hydrazyl (DPPH) pellet³¹. The ruby crystal is glued on the sample using a thin layer of vacuum grease (not represented here). The (x₀,y₀,z₀) coordinate system, associated with the cavity, is obtained by a rotation of angle θ of the (x,y,z) system around the y axis, such that the Zeeman magnetic field B is applied along the z₀ axis. b Distribution of the normalized amplitude of the microwave magnetic field B_ac/B_max, in the cavity, shown in color scale along cuts 1 and 2. c Transmission of the cavity S₂₁(ω) in dB scale (blue dots) centered on the resonance frequency ${{\rm{f}}}_{0}$ fitted by a Lorenztian curve providing a quality factor Q ≈ 8500 (red full line).

Spin Hamiltonian

The spin Hamiltonian for the ground state of Cr³⁺ ions in the Al₂O₃ lattice results from the contributions of two Zeeman terms and a crystal field term^38,39,40 :

$${{{{\mathcal{H}}}}}_{s} = \, {g}_{\perp }{\mu }_{{{{\rm{B}}}}}[{B}_{x}{S}_{x}+{B}_{y}{S}_{y}]+{g}_{\parallel }{\mu }_{{{{\rm{B}}}}}{B}_{z}{S}_{z} \\ + D\left[{S}_{z}^{2}-S(S+1)/3\right],$$

(1)

where g_∥ = 1.9817 and g_⊥ = 1.9819 are the in-plane and out-of-plane g-factors, respectively, μ_B is the Bohr magneton, and D represents the crystalline zero-field splitting (2D/h = 11.493 GHz). B_i=x,y,z are the components of the magnetic field, and S_i=x,y,z are the spin operators in the corresponding directions (Supplementary Note 2). Given the marginal difference between the values of g_∥ and g_⊥, we will consider the average isotropic g-factor, $\bar{g}=({g}_{\parallel }+2{g}_{\perp })/3$, in the following. In Eq. (1), we have chosen the quantization axis (z-axis) coinciding with the natural crystal symmetry axis (c-axis) to make the crystal field term diagonal. The magnetic field is applied along the z₀ direction and oriented at an angle θ with respect to the z-axis (Fig. 1a), such that B_x = $B\sin \theta$, B_y = 0, and B_z = $B\cos \theta$. At zero magnetic field, the Hamiltonian eigenstates are those of the S_z operator, $| m\left.\right\rangle$ =$| 3/2\left.\right\rangle$,$| 1/2\left.\right\rangle$, $| -1/2\left.\right\rangle$, $| -3/2\left.\right\rangle$, and the spin states consist of two doublets, $\{| \pm 3/2\left.\right\rangle \}$ with energy ${E}_{| \pm 3/2\left.\right\rangle }$ = −D/h and $\{| \pm 1/2\left.\right\rangle \}$ with energy ${E}_{| \pm 1/2\left.\right\rangle }$ = +D/h. In a finite magnetic field, the eigenenergies E_n and eigenstates $| {\phi }_{{{{\rm{n}}}}}\left.\right\rangle$ of ${{{{\mathcal{H}}}}}_{s}$ depend on the angle θ and are obtained by diagonalizing the following matrix Hamiltonian:

$$\hat{{{{{\mathcal{H}}}}}_{s}}=\left[\begin{array}{cccc}3/2\alpha -D&\sqrt{3}\beta /2&0&0\\ \sqrt{3}\beta /2&\alpha /2+D&\beta &0\\ 0&\beta &-\alpha /2+D&\sqrt{3}\beta /2\\ 0&0&\sqrt{3}\beta /2&-3\alpha /2-D\\ \end{array}\right]$$

(2)

where $\alpha =\bar{g}{\mu }_{{{{\rm{B}}}}}B \cos \theta$ and $\beta =\bar{g}{\mu }_{{{{\rm{B}}}}}B\sin \theta$. A transition between two levels E_k and E_l can occur if the ESR condition ∣E_k − E_l∣ = ℏω₀ is met. The transition probability between these two levels is given by Fermi’s golden rule and is proportional to the transition matrix element W_k,l=$\left\langle \right.{\phi }_{k}| W| {\phi }_{l}\left.\right\rangle =\bar{g}{\mu }_{B}\left\langle \right.{\phi }_{k}| {{{{\bf{B}}}}}_{{{{\rm{ac}}}}}.{{{\bf{S}}}}| {\phi }_{l}\left.\right\rangle$ with B_ac being the local AC magnetic field generated in the ruby at the spin position, by the microwave current in the cavity. The W_k,l matrix element ensures that the selection rule for magnetic dipole transitions, Δm = ±1, is satisfied.

Transitions and spin-cavity coupling

Figure 2 shows the evolution of the spin energy levels with magnetic field for three different angles, θ = 0°, θ = 36°, and θ = 98°. In the trivial case θ = 0° (panel a), the Hamiltonian is diagonal and the Zeeman effect splits the two doublets into four non-degenerate states. For this angle only, the basis vectors $\{| m\left.\right\rangle \}$ are the eigenstates of the system, regardless of the amplitude of the magnetic field. Three transitions can, in principle, be observed with our cavity: ${E}_{| 1/2\left.\right\rangle }\iff {E}_{| 3/2\left.\right\rangle }$ twice and ${E}_{| -1/2\left.\right\rangle }\iff {E}_{| 1/2\left.\right\rangle }$ (see arrows on Fig. 2a). For any angle θ ≠ 0, the spin states hybridize, and the eigenstates of $\hat{{{{{\mathcal{H}}}}}_{s}}$ become linear combinations of all basis vectors with non-zero a_n coefficients, $| {\phi }_{{{{\rm{n}}}} = 1,2,3,4}\left.\right\rangle$ = ${a}_{n,3/2}| 3/2\left.\right\rangle +{a}_{n,1/2}| 1/2\left.\right\rangle +{a}_{n,-1/2}| -1/2\left.\right\rangle + {a}_{n,-3/2}| -3/2\left.\right\rangle$. As a result, the transition matrix element W_k,l is always finite, and all the transitions satisfying the ESR condition can take place with a non-zero probability. In Fig. 2b and c, the absolute values of the a_n coefficients are encoded in a color scale to emphasize the hybridization of the levels for the angles θ₁ = 36° and θ₂ = 98° that are studied experimentally and will be discussed in the following. For θ₁, four ESR transitions are expected: the transition ${{{{\rm{T}}}}}_{1}^{{\theta }_{1}}$ (E₁ ⇔ E₂), the transitions ${{{{\rm{T}}}}}_{2{{{\rm{a}}}}}^{{\theta }_{1}}$ and ${{{{\rm{T}}}}}_{2{{{\rm{b}}}}}^{{\theta }_{1}}$ (E₂ ⇔ E₃) at two different magnetic fields, and the transition ${{{{\rm{T}}}}}_{3}^{{\theta }_{1}}$ (E₃ ⇔ E₄). For θ₂, only two ESR transitions are expected: transition ${{{{\rm{T}}}}}_{1}^{{\theta }_{2}}$ (E₁ ⇔ E₂) and transition ${{{{\rm{T}}}}}_{3}^{{\theta }_{2}}$ (E₃ ⇔ E₄). The ESR transitions observable with our superconducting cavity can be more clearly visualized by plotting the isofrequency lines at f₀ = 5.5 GHz as a function of the magnetic field B and the angle θ (Fig. 2d). Given the symmetry of the ruby crystal, the plot is π-periodic and symmetric around π/2. The two dashed lines, which indicate the angles θ₁ = 36° and θ₂ = 98°, intercept the isofrequency lines at the transitions discussed above (red circles). Figure 2d shows that the angle θ is a tunable parameter, which controls the number of active transitions in the quantum system, ranging from two transitions (θ ≳ 53°), to four transitions (17° ≲ θ ≲ 53°), and up to six transitions (θ ≲ 17°).

Fig. 2: Spin energy levels and Electron Spin Resonance (ESR) transitions experimentally accessible.

Magnetic field dependence of the spin energy levels for θ = 0° (a), θ = 36° (b), and θ = 98° (c). The spin character $| m\left.\right\rangle$ is indicated by the color scale in (b). Eigenenergies are labeled in ascending order, and arrows indicate authorized ESR transitions in our cavity with resonance frequency f₀ = 5.5 GHz. d Isofrequency plot in the magnetic field-angle plane for observable transitions at f₀ = 5.5 GHz. Red circles indicate the transition at the angles θ = 36° and θ = 98° that are addressed experimentally.

Close to the transition between two energy levels E_k ⇔ E_l, the coupling between a single Cr³⁺ spin and a quantized electromagnetic mode in the cavity can be treated within the framework of the Jaynes–Cummings Hamiltonian⁴¹,

$${{{{\mathcal{H}}}}}_{{{{\rm{JC}}}}}=\hslash {\omega }_{kl}{\sigma }^{+}{\sigma }^{-}+\hslash {\omega }_{0}{a}^{{{\dagger}} }a+\hslash \Omega ({{{{\bf{r}}}}}_{{{{\bf{i}}}}})(a{\sigma }^{+}+{a}^{{{\dagger}} }{\sigma }^{-}),$$

(3)

where ω_kl = ∣E_k − E_l∣/ℏ is the transition frequency between states $| {\phi }_{k}\left.\right\rangle$ and $| {\phi }_{l}\left.\right\rangle$. σ⁺ and σ⁻ are the spin ladder operators acting in the subspace of dimension two generated by $| {\phi }_{k}\left.\right\rangle$ and $| {\phi }_{l}\left.\right\rangle$, and a^† and a are the bosonic creation and annihilation operators of the electromagnetic mode. The spin-cavity coupling constant in Eq. (3) is $\Omega ({{{{\bf{r}}}}}_{{{{\bf{i}}}}})=\bar{g}{\mu }_{B}| \left\langle \right.{\phi }_{k}| {{{{\bf{b}}}}}_{0}({{{{\bf{r}}}}}_{{{{\bf{i}}}}}).{{{\bf{S}}}}| {\phi }_{l}\left.\right\rangle$, where b₀(r_i) is the magnetic field generated by the zero-point fluctuations of the microwave current in the cavity, at the spin location r_i. To describe an ensemble of N spins, Ω must be replaced by an effective coupling constant $\bar{\Omega }$, which accounts for the contribution of each spin at position r_i, and for the thermal occupation of the energy levels involved in the transition. For the E_k ⇔ E_l transition, the effective coupling reads⁴²,

$$\bar{\Omega }(T)=\bar{g}{\mu }_{B}\sqrt{{n}_{k,l}(T){\Sigma }_{i = 1}^{N}| \left\langle \right.{\phi }_{k}| {{{{\bf{b}}}}}_{0}({{{{\bf{r}}}}}_{{{{\bf{i}}}}}).{{{\bf{S}}}}| {\phi }_{l}\left.\right\rangle }{| }^{2},$$

(4)

where n_k,l(T)=$| {e}^{-{E}_{k}/{k}_{{{{\rm{B}}}}}T}-{e}^{-{E}_{l}/{k}_{{{{\rm{B}}}}}T}| /{\Sigma }_{j}{e}^{-{E}_{j}/{k}_{{{{\rm{B}}}}}T}$ is a thermal polarization factor derived from Boltzmann statistics (Supplementary Note 3). Equation (4) leads to a $\sim \sqrt{N}$ enhancement of the effective coupling with respect to that of a single spin as predicted in the Tavis–Cummings model for collective coupling effects^32,33,43.

ESR measurements

We now present the experimental results obtained with the configuration described in Fig. 1a. In this first experiment, the Ruby sample was placed at an unknown angle θ with respect to the magnetic field. Figure 3a shows the magnetic field dependence of S₂₁(ω) in dB scale (up panel) and its maximum value (down panel) measured at T = 186 mK. In addition to the DPPH line, which is used to calibrate the magnetic field, four transitions associated with the Cr³⁺ spin levels are observed at magnetic fields B = 83 ± 2 mT, 122.5 ± 2 mT, 143.5 ± 2 mT, and 338.5 ± 2 mT. According to the isofrequency transition lines in Fig. 2d, such configuration can unambiguously be associated with an angle θ₁ = 36 ± 2°, and corresponds to the transitions ${{{{\rm{T}}}}}_{1}^{{\theta }_{1}}$, ${{{{\rm{T}}}}}_{2{{{\rm{a}}}}}^{{\theta }_{1}}$, ${{{{\rm{T}}}}}_{2{{{\rm{b}}}}}^{{\theta }_{1}}$, and ${{{{\rm{T}}}}}_{3}^{{\theta }_{1}}$, respectively (Fig. 2b). Note that two E₂ ⇔ E₃ transitions are observed (${{{{\rm{T}}}}}_{2{{{\rm{a}}}}}^{{\theta }_{1}}$ and ${{{{\rm{T}}}}}_{2{{{\rm{b}}}}}^{{\theta }_{1}}$) due to the non-monotonous magnetic field dependence of the energy levels, which satisfy the ESR condition twice (Fig. 2b). In a second experiment, the ruby sample was rotated to investigate the ESR transitions in the right part of the isofrequency lines plot (Fig. 2d). An example of the magnetic field dependence of S₂₁(ω) and its maximum at T = 186 mK is shown in Fig. 3b. Two Cr³⁺ spin transitions are visible at magnetic fields B = 106 ± 2 mT (${{{{\rm{T}}}}}_{3}^{{\theta }_{2}}$) and 345 ± 2 mT (${{{{\rm{T}}}}}_{1}^{{\theta }_{2}}$), which corresponds to an angle θ₂ = 98 ± 2° (Fig. 2c, d).

Fig. 3: Electron Spin Resonance (ESR) transitions in the ruby sample.

a Evolution of S₂₁(ω, B) in color scale (up) and of its maximum (down) with the magnetic field, at T = 186 mK, for θ₁ = 36°. In addition to the 2,2-diphenyl-1-(2,4,6-trinitrophenyl) hydrazyl (DPPH) standard transition, the four transitions associated with Cr³⁺ ions are observed. The insets show close-up views of the ${{{{\rm{T}}}}}_{1}^{{\theta }_{1}}$ and ${{{{\rm{T}}}}}_{2{{{\rm{b}}}}}^{{\theta }_{1}}$ transitions of weak amplitude. b Evolution of S₂₁(ω, B) in color scale (up) and of its maximum (down) with the magnetic field at T = 186 mK, for θ₂ = 98°, showing the two transitions associated with Cr³⁺ ions.

To further analyze our ESR data, we consider the expression of the cavity transmission in the presence of a spin ensemble, near the E_k ⇔ E_l transition⁴⁴

$${S}_{21}(\omega ,B)\simeq \frac{{\omega }_{0}/{Q}_{{{{\rm{c}}}}}}{{\omega }_{0}/Q+2i({\omega }_{0}-\omega )+\frac{2{\bar{\Omega }}^{2}}{i({\omega }_{kl}(B)-\omega )+{\gamma }_{{{{\rm{s}}}}}}},$$

(5)

where γ_s is the decay rate of the spin ensemble, Q is the total quality factor of the cavity, and Q_c is the coupling quality factor of the cavity to its environment. For limited damping (${\gamma }_{{{{\rm{s}}}}} \, \lesssim \, \bar{\Omega }$), S₂₁(ω, B) features two resonance frequencies, which correspond to the usual vacuum Rabi splitting

$${\omega }_{\pm }={\omega }_{0}+\frac{\Delta }{2}\pm \frac{\sqrt{{\Delta }^{2}+4{\bar{\Omega }}^{2}}}{2},$$

(6)

where Δ(B) = ω_kl(B) − ω₀ is the detuning. In the opposite limit of strong damping (${\gamma }_{{{{\rm{s}}}}} \, \gtrsim \, \bar{\Omega }$), ∣S₂₁(ω)∣² can be approximated by a Lorentzian curve with quality factor²⁴

$${Q}_{{{{\rm{s}}}}}=\frac{{\Delta }^{2}+{\gamma }_{{{{\rm{s}}}}}^{2}}{2{\bar{\Omega }}^{2}{\gamma }_{{{{\rm{s}}}}}+{\omega }_{0}/Q\left({\Delta }^{2}+{\gamma }_{{{{\rm{s}}}}}^{2}\right)}{\omega }_{0}$$

(7)

While Q_s ≃ Q at large detuning, it decreases to ${Q}_{{{{\rm{s}}}}}\simeq \frac{{\gamma }_{{{{\rm{s}}}}}{\omega }_{0}}{2{\bar{\Omega }}^{2}}$ at spin resonance due to the combined effects of the spin-photon coupling rate and the spin decay rate.

As seen in Fig. 3a, b, the cavity transmission exhibits some anticrossings characteristic of spin-photon interaction close to the ESR transitions. However, for most of the transitions the damping is too strong for a direct comparison of the experimental data with Eq. (5). Nevertheless, in this regime, the coupling constant $\bar{\Omega }$ and the spin decay rate γ_s can be directly extracted from experimental data by a fit to Eq. (7). We therefore apply the following procedure. For each observed transition, the detuning Δ(B) = ω_kl(B) − ω₀ is first calculated from the magnetic field dependence of the energy levels shown in Fig. 2. Next, we determine the quality factor of the cavity Q_s from a Lorenztian fit of ∣S₂₁(ω)∣² as a function of the detuning for all the experimentally investigated temperatures. Examples of Q_s evolution with Δ across the various ESR transitions are shown in Figs. 4 and 5 for angles θ₁ and θ₂, respectively, at selected temperatures. Finally, by fitting the Q_s(Δ) curves to the theoretical model of Eq. (7) (solid lines in Figs. 4a–d and 5a, b), we extract the effective coupling constant $\bar{\Omega }$ and the spin decay rate γ_s. The close alignment of the experimental data with theoretical predictions validates our approach, though some transitions, such as ${{{{\rm{T}}}}}_{1}^{{\theta }_{1}}$ transition (Fig. 5a), show higher uncertainty due to weaker transition amplitudes. To gain a broader perspective in our analysis, we use the values of Q_s and γ_s determined by the fitting procedure to simulate S₂₁(ω) using Eq. (5) and extract the evolution of the cavity resonance frequency with detuning, ω_r(Δ), across the ESR transitions. Examples for each transition are superimposed on color plots in Figs. 4e–h and 5c, d (light blue dashed lines) at temperatures corresponding to stronger coupling. While the ω_r(Δ) line closely follows the maximum of ∣S₂₁(ω)∣² for the various transitions, it significantly departs from the vacuum Rabi frequencies ω_± (black dashed lines) as the transition is approached, which is expected in the strong damping regime. However, in the case of the ${{{{\rm{T}}}}}_{1}^{{\theta }_{2}}$ transition at 65 mK, the anticrossing is more pronounced, and ω_r(Δ) remains close to ω_± down to low detuning. The system enters a highly cooperative regime as $\bar{\Omega }/2\pi \approx$ 21 MHz becomes comparable to γ_s/2π ≈ 44 MHz, leading to a dimensionless cooperativity $C={\bar{\Omega }}^{2}/(\kappa \gamma )\approx 15$, with κ ≈ ω₀/Q denoting the cavity decay rate. Although C ≫ 1, the system does not strictly satisfy the strong coupling condition, which also requires $\bar{\Omega } > {\gamma }_{{{{\rm{s}}}}}$. In the present regime, nearly every photon entering the cavity is coherently transferred into the spins; however, the spin relaxation rate is too fast to allow coherent re-emission of photons back into the cavity. The values of the spin relaxation rates for the different transitions are discussed in Supplementary Note 1.

Fig. 4: Determination of the spin-cavity coupling for θ₁.

Evolution of the cavity quality factor Q_s with detuning Δ at selected temperatures for the transitions ${{{{\rm{T}}}}}_{1}^{{\theta }_{1}}$ (a), ${{{{\rm{T}}}}}_{2{{{\rm{a}}}}}^{{\theta }_{1}}$ (b), ${{{{\rm{T}}}}}_{3}^{{\theta }_{1}}$ (c), and ${{{{\rm{T}}}}}_{2{{{\rm{b}}}}}^{{\theta }_{1}}$ (d). Symbols correspond to data extracted from the Lorenztian fit of ∣S₂₁(ω)∣² and full lines to the fit to Eq. (7). Magnitude of S₂₁(ω) in color scale as a function of detuning across the four Electron Spin Resonance (ESR) transitions, ${{{{\rm{T}}}}}_{1}^{{\theta }_{1}}$ (e), ${{{{\rm{T}}}}}_{2{{{\rm{a}}}}}^{{\theta }_{1}}$ (f), ${{{{\rm{T}}}}}_{3}^{{\theta }_{1}}$ (g), and ${{{{\rm{T}}}}}_{2{{{\rm{b}}}}}^{{\theta }_{1}}$ (h). The light blue dashed lines represent the resonance frequency ω_r extracted from the simulations of Eq. (5) assuming the values of $\bar{\Omega }$ and γ_s determined by the fit of Q_s, while the black dashed lines represent the vacuum Rabi frequencies ω_± defined in Eq. (6).

Fig. 5: Determination of the spin-cavity coupling constant for θ₂.

Evolution of the cavity quality factor Q_s with detuning Δ at selected temperatures for the transitions ${{{{\rm{T}}}}}_{3}^{{\theta }_{2}}$ (a) and ${{{{\rm{T}}}}}_{1}^{{\theta }_{2}}$ (b). Symbols correspond to data extracted from the Lorenztian fit of ∣S₂₁(ω)∣² and full lines to the fit to Eq. (7). Magnitude of S₂₁(ω) in color scale as a function of detuning across the two Electron Spin Resonance (ESR) transitions, ${{{{\rm{T}}}}}_{3}^{{\theta }_{2}}$ (c) and ${{{{\rm{T}}}}}_{3}^{{\theta }_{2}}$ (d). The light blue dashed lines represent the resonance frequency ω_r extracted from the simulations of Eq. (5) assuming the values of $\bar{\Omega }$ and γ_s determined by the fit of Q_s, while the black dashed lines represent the vacuum Rabi frequencies ω_± defined in Eq. (6).

Discussion

Figure 6 summarizes the temperature dependence of the coupling constant $\bar{\Omega }$ extracted from the fitting procedure for the different ESR transitions for the two angles, θ₁ (panel a) and θ₂ (panel b). To determine the theoretical coupling of the spin ensemble to a single photon, we estimate the zero-point fluctuation rms current in the cavity, I_zpf, by assuming that the zero-point energy is equally distributed between the cavity’s inductor and capacitor, $\frac{1}{4}\hslash {\omega }_{0}=\frac{1}{2}L{I}_{zpf}^{2}$⁴², where L is the inductance of the lumped equivalent RLC circuit⁴⁵. Introducing the characteristic impedance of the cavity Z₀ ≃ 50 Ω, we obtain

$${I}_{zpf}={\omega }_{0}\sqrt{\frac{\hslash \pi }{4{Z}_{0}}}.$$

(8)

For our YBa₂Cu₃O_7−δ cavity, with resonance frequency f₀ ≈ 5.5 GHz, the zero-point fluctuation current is estimated to be I_zpf ≈ 44 nA. This value is used to simulate the corresponding three-dimensional distribution of the vacuum magnetic field b₀, within the volume of the ruby sample. The magnetic field maps of the three components ${b}_{0}^{{x}_{0}}$, ${b}_{0}^{{y}_{0}}$ and ${b}_{0}^{{z}_{0}}$ are shown in Supplementary Fig. 2 for both angles, along with the evolution of the field with y₀ at some characteristic locations within the resonator. From this distribution, we calculate the matrix element in Eq. (4), $\left\langle \right.{\phi }_{k}| {b}_{0}^{x}({{{{\bf{r}}}}}_{{{{\bf{i}}}}}){S}_{x}+{b}_{0}^{y}({{{{\bf{r}}}}}_{{{{\bf{i}}}}}){S}_{y}+{b}_{0}^{z}({{{{\bf{r}}}}}_{{{{\bf{i}}}}}){S}_{z}| {\phi }_{l}\left.\right\rangle$ for each spin at location r_i. Supplementary Fig. 3 provides examples of maps of the local spin-photon coupling. The effective coupling constant $\bar{\Omega }$ at a given temperature is then obtained for the six ESR transitions by summing the contributions of the spins within the volume of the ruby sample, assuming a uniform spin density n = 0.05%. Additional details on the simulation and calculation of $\bar{\Omega }$ are provided in the Supplementary Note 2. A comparison between the theoretical predictions and the coupling constants experimentally determined is shown in Fig. 6a (θ₁) and Fig. 6b (θ₂). An excellent agreement is obtained in the entire temperature range for all the transitions. The only adjustment parameter is a small shift δy₀ in the vertical position of the ruby sample, which affects the absolute value of $\bar{\Omega }$ through the b₀ magnetic field distribution inside the ruby⁴⁶. This shift accounts for the thin glue layer that holds the sample on the resonator chip. In a first-order approximation, one can consider that for a fixed angle θ, this shift corresponds to a global scaling factor that affects all the transitions the same way.

Fig. 6: Temperature evolution of the coupling constant for the different transitions.

a Temperature dependence of $\bar{\Omega }$ (symbols) for the four Cr³⁺ Electron Spin Resonance (ESR) transitions ${{{{\rm{T}}}}}_{1}^{{\theta }_{1}}$, ${{{{\rm{T}}}}}_{2{{{\rm{a}}}}}^{{\theta }_{1}}$, ${{{{\rm{T}}}}}_{3}^{{\theta }_{1}}$ and ${{{{\rm{T}}}}}_{2{{{\rm{b}}}}}^{{\theta }_{1}}$ at angle θ₁ = 36°. The values of $\bar{\Omega }$ (symbols) are extracted from the fitting procedure of Q_s described in Fig. 4 with the corresponding error bars obtained from the fitting uncertainty. The data are then fitted to Eq. (4) (solid lines) using the simulated b₀ magnetic field distribution shown in Supplementary Fig. 2 (see Supplementary Note 2). The best agreement is obtained for δy₀ = 12 μm, corresponding to a global scaling factor of 0.65 for the fit of $\bar{\Omega }$. The dashed line, corresponding to hf₀ ≈ k_BT separates the thermal regime (right, shaded red) and the quantum regime (left, shaded blue). b Temperature dependence of $\bar{\Omega }$ (symbols) for the two Cr³⁺ transitions ${{{{\rm{T}}}}}_{3}^{{\theta }_{2}}$ and ${{{{\rm{T}}}}}_{1}^{{\theta }_{2}}$ at angle θ = 98° fitted to Eq. (4) (solid lines) using the simulated ac magnetic field distribution shown in Supplementary Fig. 2 (see Supplementary Note 2). The best agreement is obtained for δy₀ = 6.5 μm, corresponding to a global scaling factor of 0.8 for the fit of $\bar{\Omega }$.

According to Eq. (4), the amplitude of the coupling constant for the different transitions, as well as their temperature dependencies, is controlled by the transition matrix element and the thermal polarization factor n_kl(T), which is shown for all transitions in Supplementary Fig. 3. For temperatures above 10K, where E_i=2,3,4 − E₁ ≪ k_BT, all energy levels are nearly equally populated, resulting in a small polarization factor n_kl(T) for all transitions. As the temperature decreases, the coupling for the transitions ${{{{\rm{T}}}}}_{2{{{\rm{a}}}}}^{{\theta }_{1}}$ (E₂ ⇔ E₃), ${{{{\rm{T}}}}}_{2{{{\rm{b}}}}}^{{\theta }_{1}}$ (E₂ ⇔ E₃), and ${{{{\rm{T}}}}}_{3}^{{\theta }_{1,2}}$ (E₃ ⇔ E₄), which occur between excited states, exhibit a non-monotonic evolution due to the interplay of two opposing processes. Cooling first increases the relative occupation difference between the energy levels, leading to an increase in n_kl(T). Nevertheless, at lower temperatures, the occupation of the excited states eventually decreases to zero and the ground state is solely populated, resulting in n₂₃(T) → 0 and n₃₄(T) → 0, while n₁₂(T) → 1. Consequently, the ${{{{\rm{T}}}}}_{2{{{\rm{a}}}}}^{{\theta }_{1}}$, ${{{{\rm{T}}}}}_{2{{{\rm{b}}}}}^{{\theta }_{1}}$, and ${{{{\rm{T}}}}}_{3}^{{\theta }_{1,2}}$ transitions disappear, whereas the transition ${{{{\rm{T}}}}}_{1}^{{\theta }_{1,2}}$ (E₁ ⇔ E₂) between the ground state and the first excited state is favored, in particular when k_BT < ℏω₀. However, at angle θ₁, the coupling remains weak for this transition due to the very small value of the transition matrix element $\left\langle \right.{\phi }_{1}| W| {\phi }_{2}\left.\right\rangle$ (Fig. 4a). Indeed, for small magnetic fields, the $| {\phi }_{1}\left.\right\rangle$ and $| {\phi }_{2}\left.\right\rangle$ states mainly retain their $| 3/2\left.\right\rangle$ and $| - 3/2\left.\right\rangle$ state character, respectively, as indicated by the green and red colors in Fig. 2b. According to the selection rule Δm = ±1, these states do not contribute to the transition. In contrast, at angle θ₂ (Fig. 4b), the stronger hybridization significantly increases the transition matrix element $\left\langle \right.{\phi }_{1}| W| {\phi }_{2}\left.\right\rangle$, resulting in an enhanced spin-cavity coupling, up to 21 MHz. As seen above in Eq. (4), the effective spin-photon coupling increases as the square root of the total number of spins. It is therefore possible to define an average coupling per spin Ω_s, considering the simple relation $\bar{\Omega }={\Omega }_{{{{\rm{s}}}}}\sqrt{N}$. Our sample includes a total number of spin N ≈ 2.6  × 10¹⁵ spins, which corresponds to Ω_s/2π ≈ 0.41 Hz. However, the contribution of an individual spin decreases with lateral and vertical distance from the resonator due to the decay of the microwave field. As a result, only a fraction of the spins make a significant contribution to the coupling, primarily those located in the regions near the resonator, as seen in Supplementary Figs. 2 and 3. If we consider only the spins located within a volume where the b₀ field reaches at least 10% of its maximum value, the estimated average coupling per spin increases to 1.25 Hz.

Conclusion

In conclusion, we employed electron spin resonance (ESR) techniques to measure the coupling strength between a Cr³⁺ S = 3/2 spin ensemble in a ruby crystal and a quantized electromagnetic mode of a high-T_c superconducting cavity across an extended range of temperatures and magnetic fields. We complemented our experimental findings with a theoretical analysis within the Tavis–Cummings model framework, simulating the spatial distribution of the magnetic field generated by the zero-point fluctuations in the cavity and summing the contribution of individual spins to the effective spin-cavity coupling. The results showed a strong agreement between theory and experiment, revealing a complex, temperature-dependent coupling driven by the interplay of thermal polarization and quantum transition probabilities. Additionally, by adjusting the magnetic field orientation relative to the crystal axis, we demonstrated control over the number of active transitions in the quantum system. This work demonstrates the potential of high-spin systems for quantum information processing, particularly in leveraging ESR techniques for spin-state manipulation. Although the present experiment does not reach the strong coupling regime necessary for direct quantum information applications, our methodology provides a valuable framework for studying spin-photon interactions. Future research focusing on optimizing spin-cavity coupling and exploring alternative spin ensembles with longer coherence times, such as NV centers or rare earth ions, will be crucial for advancing the role of high-spin systems in quantum technologies.

Methods

Sample fabrication and microwave cryogenic setup

In this study, we used distributed λ/2 - coplanar waveguide cavities fabricated from a 200 nm thick commercial YBa₂Cu₃O_7−δ thin film, provided by Ceraco GmbH (T_c ≃ 88 K). The film was grown on a sapphire substrate with a CeO₂ buffer layer and protected by a 20 nm thick Au layer. The cavity structure was defined by Ar ion beam etching through an AZ5214 optical resist, patterned using laser lithography. Alternatively, selective amorphization of the YBa₂Cu₃O_7−δ layer via high-energy ion implantation could advantageously replace the etching step^47,48,49,50. Finally, additional Ti/Au contact pads were deposited through lift-off, followed by the removal of the protective gold layer. The cavity features a central conductor 60 μm wide, separated from two lateral ground planes by a 30 μm gap. The properties of such devices have been reported in ref. ³¹. The cavity was then integrated into a microwave printed circuit board (PCB) with a ruby crystal placed on top of the cavity center, secured using a thin layer of vacuum grease (Fig. 1a). A small amount of DPPH powder, known for its highly stable free radical and common used as a reference S = 1/2 spin marker in ESR spectroscopy, was also deposited on the chip. The assembly was cooled down in a dilution refrigerator equipped with a 7 T superconducting magnet to produce an in-plane Zeeman magnetic field B (Fig. 1a). The microwave signal was coupled to the cavity through an approximately 50 dB attenuated line and the transmitted signal was amplified at the 3 K stage by a low noise cryogenic HEMT amplifier. Two isolators, placed at the mixing chamber and 3 K stages, were used to minimize back-action noise on the device. The transmission S₂₁(ω) was recorded using a Vector Network Analyzer. All the experiments were performed with a microwave power P_in ≈ −65 dBm at the input of the cavity. The corresponding average photon number in the cavity is given by $\bar{n}$ = $2{P}_{{{{\rm{in}}}}}{Q}^{2}/(\hslash {\omega }_{0}^{2}{Q}_{c})\approx 2\times 1{0}^{6}$, where Q_c≈180,000 is the coupling quality factor³¹.