Introduction

The Cr-Te compound1 is a material system that has attracted significant interest recently owing to its unique structural, transport, and magnetic properties. Many of the compounds form a layered structure and are stable down to a monolayer. The majority of the compounds exhibit strong ferromagnetism with some exceptions (e.g., antiferromagnetism in CrTe32 and Cr1+δTe23). Studies have shown that ferromagnetism persists down to a monolayer4, allowing studies on two-dimensional magnetism5,6,7. The Curie temperature typically lies in a range of 100–200 K. With proper growth conditions8,9, however, recent reports show the Curie temperature can be increased, exceeding room temperature under certain circumstances4,10,11. Owing to the crystalline anisotropy, the magnetic easy axis often points along the film normal, with the perpendicular magnetic anisotropy energy larger than that of other layered ferromagnets12,13.

The transport properties of the compounds also show unique characteristics. In particular, the compound exhibits a sizable anomalous Hall effect14,15,16. Studies have shown that the anomalous Hall resistance changes its sign as the temperature is varied9,15,17,18,19,20,21. The origin of the anomalous Hall effect as well as its sign change with temperature have been under scrutiny. It has been reported that the anomalous Hall effect in the Cr-Te compounds is caused by the large Berry curvature of the bands near the Fermi level18,20,21,22,23. As the Berry curvature induced anomalous Hall conductivity was found to be an odd function of energy, it causes a sign change in the anomalous Hall resistance as the temperature is varied due to population change of the occupied bands. However, other studies14,15,24 have shown that contribution from the skew scattering plays an essential role in the anomalous Hall effect, posing question on its origin.

Here we show that the unique characteristics of the anomalous Hall effect in Cr2Te3, one of the most stable compounds in the Cr-Te family, are defined by electron-magnon scattering. Cr2Te3 has a layered structure in which layers of CrTe2 are connected by intercalated Cr atoms. We find that the electron-magnon scattering significantly contributes to the longitudinal and anomalous Hall resistances. The scaling relation between the longitudinal and anomalous Hall resistivities is used to identify the origin of the anomalous Hall effect. We find two competing sources: magnon-induced skew scattering and impurity-induced side jump/Berry curvature effect. Model calculations show that the former is caused by the exchange interaction between the itinerant Te p-electrons and the localized Cr d-electrons modified by the spin-orbit coupling. We consider Te, which possesses significant spin-orbit coupling, plays a critical role in setting the magnon-induced skew scattering.

Experimental results

Structural and magnetic properties

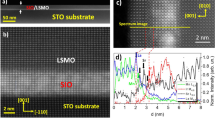
Cr2Te3 films were grown on sapphire or MgO substrates using molecular beam epitaxy (MBE). A Ti or Te layer was used as a capping layer. See “Methods" and Supplementary Note 1 for the details of sample preparation and characterization. A cross-sectional high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image of a 20 nm-thick Cr2Te3 film is displayed in Fig. 1a. The bright and dark contrasts of the image represent grains with different crystal orientations within the film plane. The grain size is of the order of a few tens of nanometers. The high magnification image, Fig. 1c, and the corresponding nanobeam electron diffraction pattern, Fig. 1d, show highly textured film with growth along the Cr2Te3 (001) direction. Energy dispersive X-ray spectroscopy (EDS) maps of the elements are shown in Fig. 1b. The images show Cr and Te are uniformly distributed within the film. Profile of the film composition along the film normal is presented in Fig. 1e. From the profile, we determine the film composition is Cr:Te~2:3. See Supplementary Fig. S1 for the reflection high energy electron diffraction (RHEED) images and the X-ray diffraction spectra of the films.

Fig. 1: Structural characterization.
figure 1

a Cross-sectional high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image and b Energy dispersive X-ray spectroscopy (EDS) maps of a 20 nm-thick Cr2Te3 film. c High magnification image of the Cr2Te3 film shown in (a). d Nanobeam electron diffraction pattern of the image shown in (c). Indices of Cr2Te3 are labeled. e Depth profile of the elements using EDS mapping.

Full size image

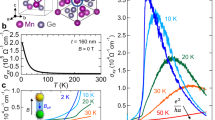
First, we study the magnetic properties of Cr2Te3. Figure 2a shows the temperature dependence of the saturation magnetization Ms for films with different thicknesses. The Curie temperature TC is  ~175 K for all samples except for the 5 nm-thick film, which exhibits TC of  ~215 K. See Supplementary Note 2 for the details of how TC is extracted. The value of Ms at 2 K for the thicker films is close to that predicted from first principles calculations, which is  ~465 emu/cm3. We find Ms is substantially larger for the thinner films (5 and 10 nm-thick). Previous studies have reported that the magnetic moments of Cr2Te3 are canted from the film normal, but the canting can be suppressed when the film thickness is reduced, thereby causing a difference in Ms against the film thickness13. Alternatively, it has been shown, using scanning tunnel microscopy, that Cr3Te4 forms at the beginning of the growth with MBE25. Since the saturation magnetization of Cr3Te4 is larger than that of Cr2Te326,27, the magnetization can be larger for the thinner films given the larger weight of the Cr3Te4 phase. Note that the transport properties of Cr3Te428,29 are not significantly different from those of Cr2Te3. In addition, Ms shows an upturn below  ~10 K for the thinner films. Such change in Ms at low temperature was reported previously9. Although the physical mechanism behind the upturn is unclear in Cr2Te3, previous studies for other systems (e.g., ultra-fine cobalt ferrite nanoparticles) suggested that it may originate from surface magnetic moments30. Further study is required to clarify the origin of the thickness dependence of Ms and the upturn below  ~10 K. In Supplementary Fig. S2, we show a few exemplary magnetization hysteresis loops. The loops show that the magnetic easy axis of the films points along the film normal, in agreement with previous studies24. For later use, we define \({M}_{{{\rm{s}}}}^{0}\) as Ms obtained at the lowest measurement temperature (~2 K).

Fig. 2: Saturation magnetization and longitudinal resistivity.
figure 2

a Temperature T dependence of the saturation magnetization Ms for films with different thicknesses. b Longitudinal resistivity ρxx of a 10 nm-thick Cr2Te3 film plotted against T. The solid red line shows fit to the data using Eq. (1) in the appropriate temperature range. Film thickness dependence of the impurity scattering coefficient \({\rho }_{xx}^{0}\) (c) and the electron-magnon scattering coefficient \({\rho }_{xx}^{{{\rm{m}}}}\) (d). For a given film thickness, results from a few devices are presented using different symbols. Definition of the symbols are the same for (c, d): see the legend shown in (c).

Full size image

Longitudinal transport properties

The transport properties are studied using the patterned Hall bars: see Supplementary Note 2 and Fig. S3 for the details of the device structure. The temperature dependence of the longitudinal resistivity ρxx of a 10 nm-thick film is shown in Fig. 2b. We find the temperature dependence of ρxx for T < TC can be fitted with the following function:

$${\rho }_{xx}={\rho }_{xx}^{0}+{\rho }_{xx}^{{{\rm{m}}}}{T}^{2}\quad (T < {T}_{{{\rm{C}}}}).$$
(1)

The fitting result, shown by the red solid line in Fig. 2b, is in good agreement with the experimental results. The change in ρxx for T > TC is almost linear and its slope is small: see also Supplementary Fig. S4.

The quadratic temperature dependence of ρxx below TC can be attributed to electron-magnon scattering31,32. (As is often the case in metals32, we neglect electron-electron scattering, which also scales with T2.) The temperature independent resistivity that is dominant at the lowest temperature is likely associated with impurity-induced scattering. We therefore assign \({\rho }_{xx}^{0}\) and \({\rho }_{xx}^{{{\rm{m}}}}\) as the impurity and electron-magnon scattering coefficients, respectively. The film thickness dependences of \({\rho }_{xx}^{0}\) and \({\rho }_{xx}^{{{\rm{m}}}}\) are shown in Fig. 2c, d, respectively. \({\rho }_{xx}^{0}\) tends to decrease with film thickness, suggesting that the film quality improves for thicker films. In contrast, \({\rho }_{xx}^{{{\rm{m}}}}\) increases with the film thickness until it saturates at  ~50 nm.

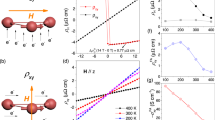
To show that electron-magnon scattering indeed contributes to the transport properties, the out-of-plane magnetic field (Hz) dependence of the longitudinal resistivity Δρxx ≡ ρxx(H) − ρxx(H = 0) is studied. Figure 3a shows representative results from a 10 nm-thick film. There are at least two major effects known to contribute to Δρxx in magnetic materials33: the Lorentz magnetoresistance and the magnon-induced magnetoresistance. Whereas the resistance quadratically increases with Hz for the former, it linearly decreases with Hz for the latter. As is evident, Δρxx decreases almost linearly with increasing Hz when the temperature is lower than Tc, suggesting that the magnon-induced magnetoresistance is dominant33. We fit the data with a linear function near zero field (from  ~0 to 10 kOe) to obtain the slope of Δρxx vs. Hz, which is defined as \(\frac{\partial \Delta {\rho }_{xx}}{\partial {H}_{z}}\). \(\frac{\partial \Delta {\rho }_{xx}}{\partial {H}_{z}}\) is plotted as a function of temperature for all films in Fig. 3b. Clearly, \(\frac{\partial \Delta {\rho }_{xx}}{\partial {H}_{z}}\) increases as the temperature approaches Tc, suggesting that electron-magnon scattering plays a larger role at higher temperatures.

Fig. 3: Longitudinal magnetoresistance.
figure 3

a Magnetoresistance Δρxx as a function of out-of-plane magnetic field Hz obtained for a 10 nm-thick film. Different symbols indicate different measurement temperatures. The solid lines show linear fits to the data when Hz is in the range of 0 to 10 kOe. b Slope of fitted linear line, \(\frac{\partial \Delta {\rho }_{xx}}{\partial {H}_{z}}\), plotted as a function of temperature. Electron-magnon scattering coefficient \({\rho }_{xx}^{{{\rm{m}}}}\) dependence of \(\frac{\partial \Delta {\rho }_{xx}}{\partial {H}_{z}}\) obtained at 2 K (c), 100 K (d), and 150 K (e). (b–e) For a given film thickness, results from a few devices are presented using different symbols. Definition of the symbols are the same for (c–e): see the legend shown in (c).

Full size image

In Fig. 3c–e, we plot \(\frac{\partial \Delta {\rho }_{xx}}{\partial {H}_{z}}\) vs. \({\rho }_{xx}^{{{\rm{m}}}}\) to study if they are correlated. At the lowest temperature [Fig. 3c], there is no significant correlation between the two quantities, as electron-magnon scattering is suppressed in this temperature range. As the temperature is raised [Fig. 3d, e], we observe a positive correlation between the two, indicating that \(\frac{\partial \Delta {\rho }_{xx}}{\partial {H}_{z}}\) is dependent on electron-magnon scattering.

Anomalous Hall resistance

Next, we study the transverse resistivity ρyx of Cr2Te3. The Hz dependence of ρyx of a 10 nm-thick film, measured at different temperatures, are plotted in Fig. 4a. A clear hysteresis loop is observed at temperatures below TC. The small hump near the magnetization switching fields may be due to the topological Hall effect or the superposition of competing anomalous Hall effects with opposite signs. Although similar features have been observed in other systems and were attributed to the topological Hall effect, e.g., Cr5Te634, CrTe2/Bi2Te335, and Cr2Te3/Cr2Se336, we cannot identify its origin in Cr2Te3 single-layer film from the current data set. The anomalous Hall resistivity Δρyx is obtained by subtracting the linear background found at high magnetic field and taking half the difference of the background subtracted ρyx at positive and negative Hz. The linear background is predominantly caused by the ordinary Hall effect: see Supplementary Fig. S5 for the carrier density and mobility estimated from the background signal. We normalize Δρyx with \(\frac{{M}_{{{\rm{s}}}}}{{M}_{{{\rm{s}}}}^{0}}\) to exclude the temperature dependence of Ms from Δρyx37. The normalized anomalous Hall resistivity \(\Delta {\tilde{\rho }}_{yx}\equiv \Delta {\rho }_{yx}/\frac{{M}_{{{\rm{s}}}}}{{M}_{{{\rm{s}}}}^{0}}\) is plotted as a function of temperature in Fig. 4b. (See Supplementary Fig. S4 for the temperature dependence of Δρyx.) As is evident, \(\Delta {\tilde{\rho }}_{yx}\) changes its sign at T ~100 K, a trend that has been reported in previous studies9,15,17,20. Similar to ρxx, \(\Delta {\tilde{\rho }}_{yx}\) exhibits a T2 scaling. The red solid line in Fig. 4b shows a parabolic fitting, which agrees well with the data. Later, we show that such T2 scaling is one of the characteristics of magnon-induced skew scattering.

Fig. 4: Anomalous Hall resistivity.
figure 4

a Transverse resistivity ρyx, measured at different temperatures, is plotted against the out-of-plane magnetic field Hz for a 10 nm-thick Cr2Te3 film. Data are shifted vertically for clarity. b Normalized anomalous Hall resistivity \(\Delta {\tilde{\rho }}_{yx}=\Delta {\rho }_{yx}/\frac{{M}_{{{\rm{s}}}}}{{M}_{{{\rm{s}}}}^{0}}\) (black circles) of a 10 nm-thick Cr2Te3 film plotted against the temperature T. Red solid lines show a parabolic fitting to the data. c The symbols indicate the longitudinal resistivity ρxx dependence of \(\Delta {\tilde{\rho }}_{yx}\). Data displayed are from a temperature range of 2–175 K. Fit to the data with a linear function is shown by the solid lines. d \(\frac{\Delta {\tilde{\rho }}_{yx}^{0}}{{\rho }_{xx}^{0}}\) plotted against the impurity scattering coefficient \({\rho }_{xx}^{0}\) (symbols). The solid line shows fit to the data using Eq. (3). The inset shows \(\Delta {\tilde{\rho }}_{yx}^{0}\), i.e., \(\Delta {\tilde{\rho }}_{yx}\) obtained at the lowest temperature, plotted as a function of \({\rho }_{xx}^{0}\). Definition of the symbols are the same as in (c): see the legend shown in (c). e The slope of the linear function used to fit the data shown in (c) plotted against \({\rho }_{xx}^{0}\) (symbols). The solid line is a linear fit to the data. f \(\Delta {\tilde{\rho }}_{yx}^{T}\equiv \Delta {\tilde{\rho }}_{yx}-\Delta {\tilde{\rho }}_{yx}^{0}\) plotted as a function of electron-magnon scattering coefficient \({\rho }_{xx}^{{{\rm{m}}}}\). The open, dot center, and solid symbols show data obtained at temperatures of 50 K, 100 K, 150 K, respectively. The color of the symbols represents the film thickness, whereas the symbol shape indicates results from different devices: see the legend shown in (e). The solid linear lines are guide to the eye. c–f For a given film thickness, results from a few devices are presented using different symbols.

Full size image

The scaling relation between the anomalous Hall and the longitudinal resistivities is studied to identify the origin of the anomalous Hall effect38,39,40. \(\Delta {\tilde{\rho }}_{yx}\) is plotted against ρxx in Fig. 4c. \(| \Delta {\tilde{\rho }}_{yx}|\) increases with increasing ρxx, with the temperature as an implicit parameter, exhibiting a predominantly linear scaling. In general, the scattering sources that cause the temperature dependence of the anomalous Hall resistivity can be classified into two categories, static and dynamic disorders. The former is caused by impurities and scales with \({\rho }_{xx}^{0}\), whereas the latter can be induced by magnons and phonons and is proportional to \({\rho }_{xx}^{T}\equiv {\rho }_{xx}-{\rho }_{xx}^{0}\). From multi-variable scaling derived by Hou et al.39, the anomalous Hall resistivity can be expressed as:

$$\Delta {\tilde{\rho }}_{yx} = \, \Delta {\tilde{\rho }}_{yx}^{{{\rm{skew}}}}+\Delta {\tilde{\rho }}_{yx}^{{{\rm{sj}}}}+\Delta {\tilde{\rho }}_{yx}^{{{\rm{int}}}},\\ \Delta {\tilde{\rho }}_{yx}^{{{\rm{skew}}}} = \, {a}_{1}{\rho }_{xx}^{0}+{a}_{2}{\rho }_{xx}^{T},\\ \Delta {\tilde{\rho }}_{yx}^{{{\rm{sj}}}} = \, {b}_{1}{\left({\rho }_{xx}^{0}\right)}^{2}+{b}_{2}{\left({\rho }_{xx}^{T}\right)}^{2}+{b}_{3}{\rho }_{xx}^{0}{\rho }_{xx}^{T},\\ \Delta {\tilde{\rho }}_{yx}^{{{\rm{int}}}} = \, c{\rho }_{xx}^{2},$$
(2)

where \(\Delta {\tilde{\rho }}_{yx}^{{{\rm{skew}}}}\), \(\Delta {\tilde{\rho }}_{yx}^{{{\rm{sj}}}}\), \(\Delta {\tilde{\rho }}_{yx}^{{{\rm{int}}}}\) are contributions from the skew scattering, the side jump, and the Berry curvature effect, respectively. a1, a2, b1, b2, b3 and c are the scaling coefficients. In contrast to the note made in ref. 39, here we have included a dynamic skew scattering (the a2-term).

We first study the effect of static disorders on the anomalous Hall resistance. We set \({\rho }_{xx}^{T}=0\) and rearrange Eq. (2) to obtain

$$\frac{\Delta {\tilde{\rho }}_{yx}^{0}}{{\rho }_{xx}^{0}}={a}_{1}+({b}_{1}+c){\rho }_{xx}^{0}$$
(3)

where \(\Delta {\tilde{\rho }}_{yx}^{0}\) is \(\Delta {\tilde{\rho }}_{yx}\) measured at the lowest temperature (2 K). In Fig. 4d, we plot \(\frac{\Delta {\tilde{\rho }}_{yx}^{0}}{{\rho }_{xx}^{0}}\) as a function of \({\rho }_{xx}^{0}\) to determine a1 and b1 + c. (As a reference, \(\Delta {\tilde{\rho }}_{yx}^{0}\) vs. \({\rho }_{xx}^{0}\) is plotted in the inset.) Data is fitted with Eq. (3): the fitted curve is shown by the solid line. We find a1 ~ −0.034 and b1 + c ~1.5 × 10−4 (μΩcm)−1. These results show that films with larger \({\rho }_{xx}^{0}\) exhibit positive \(\Delta {\tilde{\rho }}_{yx}^{0}\) due to the larger contribution from the impurity induced side-jump/Berry curvature effect, i.e., the b1 + c term. This is the case for the thinner films. For the thicker films, \(\Delta {\tilde{\rho }}_{yx}^{0}\) is negative since contribution from the impurity-induced skew scattering (a1 term) is larger.

Next, we look into the influence of dynamic disorders, which cause the temperature-dependent anomalous Hall resistance. We find that most of the data (\(\Delta {\tilde{\rho }}_{yx}\) vs. ρxx) can be described by a linear function, shown by the solid lines in Fig. 4c, particularly when the film thickness is small. The predominant linear dependence indicates that skew scattering [the a2 term in Eq. (2)] contributes to the anomalous Hall effect, consistent with previous reports on Cr-Te systems14,15,16,19. We fit the data from 2 to 100 K with a linear line. From Eq. (2), the slope of the linear line is equal to \({a}_{2}+({b}_{3}+2c){\rho }_{xx}^{0}\). (Note that the slope of \(\Delta {\tilde{\rho }}_{yx}\) vs. \({\rho }_{xx}^{T}\) is the same as that of \(\Delta {\tilde{\rho }}_{yx}\) vs. ρxx since \({\rho }_{xx}^{0}\) is a constant.) We thus plot the slope as a function of \({\rho }_{xx}^{0}\) in Fig. 4e and fit a linear function, which is shown by the solid line. From the fitting, we find a2 ~ −0.067 and b3 + 2c ~0.7 × 10−4 (μΩcm)−1. a2 is comparable in magnitude with the skew scattering coefficient in other systems41,42,43.

Before discussing the origin of the a2 term, we comment on the other terms in the anomalous Hall resistivity. As is evident in Fig. 4c, the data deviates from the linear fitting for the thicker films at higher temperatures. The deviation is caused by the side jump and/or Berry curvature contributions, i.e., b2 and c terms in Eq. (2). (For the thinner films, because of the lower resistivity at high temperature, influence from the quadratic terms is limited.) A previous study showed that the Berry curvature contribution in Cr2Te3 can vary with temperature due to thermal broadening of the Fermi surface and may depend on the film thickness via growth induced strain20,23: see Supplementary Note 3 and Fig. S6 for the first principles calculations we performed as well. The possible change of the Berry curvature contribution with temperature and thickness make it difficult to extract the coefficients b2 and c using Eq. (2). We therefore focus on the predominant linear term (a2) and simply note that the combined contributions from the quadratic terms (b2 and c) take a maximum of  ~25% for the thickest film near the Curie temperature, which is estimated from the deviation of \(\Delta {\tilde{\rho }}_{yx}\) from the linear fitting.

To identify the source of the a2 term, we plot \(\Delta {\tilde{\rho }}_{yx}^{T}\equiv \Delta {\tilde{\rho }}_{yx}-\Delta {\tilde{\rho }}_{yx}^{0}\) as a function of \({\rho }_{xx}^{m}\) in Fig. 4f. \(\Delta {\tilde{\rho }}_{yx}^{T}\) is positively related to \({\rho }_{xx}^{m}\), particularly at higher temperatures, suggesting that magnons play a dominant role in the dynamic disorder induced scattering. To corroborate this observation, the Hz dependence of the Hall resistance is measured up to 140 kOe for the 65 nm-thick film. The results obtained at measurement temperatures of 5 and 150 K are shown in Fig. 5a, b. At low temperature [Fig. 5a], ρyx scales linearly with Hz for fields outside the hysteresis loop, whereas it varies in a non-linear fashion for higher temperature [Fig. 5b]. (ρyx that scales with Hz at large field is mostly caused by the ordinary Hall effect). To display the effect more clearly, we fit the data with a linear function in the range of Hz ~130–140 kOe and subtracted it from the data. The subtracted data, defined as \({\rho }_{yx}^{{\prime} }\), are shown in Fig. 5c, d. \({\rho }_{yx}^{{\prime} }\) tends to decrease as ∣Hz∣ increases when the temperature is high, whereas it is nearly constant in the entire field range for lower temperature. Previous studies have shown that large magnetic field suppresses excitation of magnons33,44. The reduction of Δρyx at large Hz can therefore be attributed to decrease in magnon population. These results thus support the notion that electron-magnon scattering contributes to the anomalous Hall resistance at higher temperatures. We note that the saturation of \({\rho }_{yx}^{{\prime} }\) in Fig. 5d is caused by the linear background subtraction process. Measurements at even larger magnetic field are needed to determine the saturation field. Indeed, previous studies showed that suppression of magnon-induced effects requires magnetic field of the order of a few hundreds of kOe33.

Suppression of electron-magnon scattering by magnetic field can also be found in the magnetoresistance measured at higher magnetic field. Figure 5e shows the magnetoresistance Δρxx measured up to 140 kOe for the 65 nm-thick film. The slope of Δρxx vs. Hz clearly changes with Hz at higher temperatures. Note that the slope represents the strength of electron-magnon scattering: see the discussion pertaining to Fig. 3. We plot the temperature dependence of the slope ∂Δρxx/∂Hz at lower magnetic field (0–10 kOe) and higher magnetic field (130–140 kOe) in Fig. 5f. The former is significantly larger than the latter when the temperature is high, indicating that magnon excitation is suppressed at larger magnetic field. These results strongly suggest that the source of the a2 term is magnon-induced skew scattering.

Fig. 5: High field longitudinal and transverse resistivities.
figure 5

Transverse resistivity ρyx vs. out-of-plane magnetic field Hz measured at 5 K (a) and 150 K (b) for a 65 nm-thick film. (c, d) Hz dependence of the linear background-subtracted transverse resistivity \({\rho }_{yx}^{{\prime} }\). The background is determined by fitting the data in the field range of 130–140 kOe with a linear function. The horizontal dotted line in (d) is a guide to the eye. e Hz dependence of the magnetoresistance Δρxx of a 65 nm sample measured up to 140 kOe. f The slope ∂Δρxx/∂Hz of the linear line fitted to Δρxx vs. Hz in field ranges 0–10 kOe (black squares) and 130–140 kOe (red circles) are plotted as a function of temperature.

Full size image

Based on these results, we discuss the reason behind the sign change of the anomalous Hall resistance with temperature in Cr2Te3. At the lowest temperature, \(\Delta {\tilde{\rho }}_{yx}^{0}\) is governed by static disorder (impurity) \({\rho }_{xx}^{0}\). The linear (a1) and quadratic (b1 + c) terms have opposite signs. For the thinner films (with larger \({\rho }_{xx}^{0}\)), the net contribution is positive since the quadratic term dominates. In contrast, \(\Delta {\tilde{\rho }}_{yx}^{0}\) is negative for the thicker films (with smaller \({\rho }_{xx}^{0}\)) as the linear term is dominant. With increasing temperature, contribution from the magnon-induced skew scattering (a2), which is negative, increases and takes over, resulting in a sign change of \(\Delta {\tilde{\rho }}_{yx}\) only for the thinner films.

Model calculations

Finally, we discuss the microscopic origin of the magnon-induced skew scattering in Cr2Te3. The anomalous Hall resistivity \(\Delta {\tilde{\rho }}_{yx}\) that originates from magnon-induced skew scattering is obtained by including the effect of the spin-orbit coupling in a p-d exchange interaction. The Hamiltonian that describes the electron-magnon skew scattering has been proposed as45:

$${{{\mathcal{H}}}}_{pd}=i\lambda {J}_{pd}{a}_{0}^{2}{\sum}_{{{\boldsymbol{k}}},{{{\boldsymbol{k}}}}^{{\prime} }}\left({{\boldsymbol{k}}}\times {{{\boldsymbol{k}}}}^{{\prime} }\right)\cdot {\left(\delta {{\boldsymbol{S}}}\right)}_{{{\boldsymbol{k}}}-{{{\boldsymbol{k}}}}^{{\prime} }}{c}_{{{\boldsymbol{k}}}}^{{\dagger} }{c}_{{{{\boldsymbol{k}}}}^{{\prime} }},$$
(4)

where λ is a dimensionless parameter that characterizes the spin-orbit coupling, Jpd represents the p-d exchange interaction between the Te 5p conduction electrons and the Cr 3d localized moments, \({a}_{0}^{3}\) is the volume per localized spin, k and ck are the electron wave vector and annihilation operator, S represents the localized spin (∣S∣ ≡S= 3/2 for Cr) and δS is its deviation from the equilibrium direction due to magnon excitation. Assuming a free electron-like band with exchange splitting, the anomalous Hall resistivity \(\Delta {\tilde{\rho }}_{yx}^{{{\rm{cal}}}}\) is calculated by considering the process shown in Supplementary Fig. S7, as

$$\Delta {\tilde{\rho }}_{yx}^{{{\rm{cal}}}}=-{\Xi }_{yx}\frac{\lambda {a}_{0}^{2}{J}_{pd}^{3}S}{8{\hslash }^{2}{e}^{2}{v}_{{{\rm{F}}}}^{3}}{\left(\frac{{k}_{{{\rm{B}}}}T}{{A}_{{{\rm{ex}}}}}\right)}^{2}$$
(5)

where vF is the Fermi velocity and Aex is the exchange stiffness parameter. (ℏ is the reduced Planck constant, e is the elementary charge and kB is the Boltzmann constant.) Note that this process was not considered in ref. 39. The longitudinal resistivity \({\rho }_{xx}^{{{\rm{cal}}}}\) due to electron-magnon scattering is given by ref. 45

$${\rho }_{xx}^{{{\rm{cal}}}}={\Xi }_{xx}\frac{{m}^{2}{J}_{pd}^{2}S}{{(2\pi )}^{3}{\hslash }^{3}{e}^{2}{n}^{2}{a}_{0}^{3}}{\left(\frac{{k}_{{{\rm{B}}}}T}{{A}_{{{\rm{ex}}}}}\right)}^{2}$$
(6)

where Ξyx [in Eq. (5)] and Ξxx [in Eq. (6)] are constants of order unity and weakly dependent on temperature (see Supplementary Fig. S8). m is the effective electron mass and n is the electron density. See Supplementary Note 4 for the outline of the derivation of Eqs. (5) and (6), details of Ξyx and Ξxx and the Feyman diagram (Supplementary Fig. S7) used to calculate the anomalous Hall conductivity due to magnon-induced skew scattering.

Both \(\Delta {\tilde{\rho }}_{yx}^{{{\rm{cal}}}}\) and \({\rho }_{xx}^{{{\rm{cal}}}}\) scale with the temperature T quadratically, in agreement with the experiments: see Figs. 2b and 4b. Substituting the parameters listed in Supplementary Table 1, suitable for Cr2Te3, we obtain \(\Delta {\tilde{\rho }}_{yx}^{{{\rm{cal}}}} \sim -22\,\mu \Omega \cdot {{\rm{cm}}}\) and \({\rho }_{xx}^{{{\rm{cal}}}} \sim 329\,\mu \Omega \cdot {{\rm{cm}}}\) at T =  200 K from Eqs. (5) and (6). Here we adjusted λ, the dimensionless parameter that characterizes the spin-orbit interaction, to match the value of a2 = −0.067 obtained in the experiments with \(\Delta {\tilde{\rho }}_{yx}^{{{\rm{cal}}}}/({\rho }_{xx}^{{{\rm{cal}}}})\). Note that Jpd = −0.1 eV is estimated from the band structure of Cr2Te3 using first principles calculations. Jpd is normally negative when the exchange coupling is between conduction electrons and localized moments that belong to different elements. From Eq. (5), we find λ must be negative in order to account for the negative \(\Delta {\tilde{\rho }}_{yx}\) found in the experiments (see e.g., Fig. 4b). The strength of the p−d exchange interaction, characterized by λJpd, is  ~0.084 eV, which is similar in magnitude with the atomic spin-orbit coupling of Te46,47,48. We thus infer that the predominant magnon-induced skew scattering in Cr2Te3 is primarily induced by the large spin-orbit coupling of Te. A microscopic model that takes into account the band structure of host material (here Cr2Te3) is required to clarify the relation between the atomic spin orbit coupling and λ.

Conclusion

We have studied the longitudinal and anomalous Hall resistivities of Cr2Te3 thin films. We find a quadratic temperature dependence of the longitudinal resistivity below the Curie temperature, suggesting that electron-magnon scattering is one of the major sources of the resistivity. This is corroborated by a linear magnetoresistance found against the out-of-plane magnetic field. The anomalous Hall resistivity includes two major contributions: temperature-dependent and temperature-independent terms. The former exhibits a predominant linear dependence on the longitudinal resistivity and is positively correlated with the electron-magnon scattering coefficient of the longitudinal resistivity, suggesting that magnon-induced skew scattering significantly contributes to the anomalous Hall effect in Cr2Te3. We also find the anomalous Hall resistivity at higher temperatures is suppressed by a large magnetic field, supporting the scenario that the skew scattering originates from collision with magnons. For the latter (i.e., the temperature-independent term), we find that the contribution from the impurity-induced side-jump and/or the Berry curvature effect possesses the opposite sign with that of magnon-induced skew scattering. The sign change of the anomalous Hall resistivity with temperature is thus accounted for by the competition between the two effects. Using model calculations, we show that the p-d type exchange interaction modified by spin-orbit coupling can account for the significant electron-magnon scattering contribution to the anomalous Hall effect in Cr2Te3. These results suggest that magnon-induced skew scattering plays a significant role in the anomalous Hall effect in layered ferromagnets with heavy elements, a class of 2D materials that are of current interest.

Methods

Sample preparation

Cr2Te3 films were grown on sapphire (0001) or MgO (001) substrates in a commercial MBE system. The substrates were pre-annealed in vacuum at 650 °C for 150 min for degassing. After degassing, the substrate temperature Ts was set to  ~380 °C. Tellurium and chromium were co-evaporated using a Knudsen cell for Te and an electron beam gun for Cr. To form Cr2Te3, the flux ratio of Te over Cr was kept to  ~20 or higher. The growth rate of Cr2Te3 was monitored using a quartz crystal spectrometer and its typical value is  ~0.01 nm/s. Cr2Te3 thin films with different thicknesses (5, 10, 26, 49, and 65 nm) were grown. The thickness of the films were determined using X-ray reflectivity measurements. A 5 nm-thick Te or 3 nm-thick Ti capping layer was deposited at room temperature to protect the Cr2Te3 film from oxidation. We find the type of substrate (sapphire vs. MgO) and the capping layer material (Te vs. Ti) have little influence on the magnetic and transport properties of the films.

Sample characterization

Magnetic properties of the films were examined by a superconducting quantum interference diffractometer. The specimen for cross-sectional transmission electron microscopy (TEM) studies was prepared by using a focused ion beam (FIB). HAADF-STEM observation, nanobeam electron diffraction, and EDS analysis were carried out using a commercial system.

To study the transport properties, the films were patterned into Hall bars using optical lithography and Ar ion milling. Contact electrodes, made of ~50 nm thick conducting materials, were patterned on the Hall bars using standard liftoff technique. The electrodes were deposited via RF magnetron sputtering. The width w and length L of the Hall bar channel are 10 μm and 25 μm, respectively. Measurements were performed using a physical property measurement system (PPMS). A current Ix of 100 μA was applied to the sample and the longitudinal voltage Vxx and the transverse voltage Vyx were measured. The longitudinal and transverse resistivities are obtained from the relations \({\rho }_{xx}=\frac{{V}_{xx}}{{I}_{x}}\frac{wt}{L}\) and \({\rho }_{yx}=\frac{{V}_{yx}t}{{I}_{x}}\), respectively, where t is the thickness of the film. See Supplementary Note 2 and Fig. S3 for the details of the configuration used to measure the longitudinal and transverse resistivities.